Abstract
The shear span-to-effective depth ratio (a/d) is one of the factors governing the shear behavior of reinforced concrete (RC) beams, with or without shear reinforcement. In high-strength concrete (HSC), cracks may propagate between the aggregate particles and result in a brittle failure which is against the philosophy of most design guidelines. The experimental results of six HSC beams, with and without shear reinforcement, tested under four-point bending with a/d ranged from 2.0 to 3.0 are presented and compared with different model equations in design codes. The a/d ratio has higher influence on the shear strength of reinforced HSC beams without shear reinforcement than beams with shear reinforcement. Most of the shear resistance prediction models underestimate the concrete shear strength of the beams but overpredict shear resistance of beams with shear reinforcement. However, the fib Model code 2010 accurately predicted the shear resistance for all the beams within an appropriate level of approximation (LoA).
Similar content being viewed by others
1 Introduction
High-strength concrete (HSC) as defined by ACI 363R 2010 is a concrete mix with 28-day compressive strength greater than 6000 psi (41 MPa). It is preferred over normal-strength concrete (NSC) because of its superior durability and mechanical properties. In HSC, propagation of cracks through the aggregates rather than around the aggregates is possible if the hardened paste strength is higher than that of the aggregate. The propagation of cracks through the aggregates makes the crack smoother with a reduction in aggregate interlock (Regan et al. 2005). However, the reduction in aggregate interlock is a cause of concern as it can lead to brittle failure. HSC is the material of choice for use in heavily loaded columns, bridge girders, and precast elements because its improved strength can reduce member sizes and eventually overall cost.
The mechanism of shear transfer in RC members have generated extensive debate especially on the important variables to be considered in shear prediction models because shear resistance is a complex problem. These variables are transverse and longitudinal steel ratios; to a/d ratio; compressive strength of concrete; yield strength of steel reinforcement; crack spacing; bond stress between steel and concrete, and size of the beam (ACI 426-1973; CSA23.3- 2004; EC 2- 1992). An experimental approach has been developed for RC members to evaluate shear strength provided by concrete (Vc) and steel reinforcements (Vs) (Wu et al. 2020). The variations of the a/d ratios have been taken into consideration to develop model. The results showed that Vc and Vs were significantly affected by a/d and they vary with the same cross section; therefore, they cannot be considered as cross-section property.
Table 1 summarizes the important variables considered in some commonly used design guidelines and models for shear prediction. Early theories of shear transfer mechanism in NSC beams were empirically based on codes, such as ACI 318-2014 and EC 2-1992, while some were based on modified compression field theory (MCFT), such as the case of CSA23.3- 2004, and fib model Code 2010 (Béton et al. 2013 and SIA 262-2012), which are based on critical shear crack theory (CSCT). The stress distribution in a RC section is represented by the stress block diagram (ACI 318- 2014), which can be used to determine section capacity. The HSC stress–strain curve is more linear than the parabolic stress–strain curve for NSC, resulting in a different shapes of stress block diagram to calculate the HSC beams flexural capacity (Pastor et al. 1984 and Leslie et al. 1976). The empirical approaches use beam and arch actions (Kani et al. 1964 and Park et al. 1975) that neglect the bond action of the steel reinforcement and aggregate interlock. The MCFT considers the tensile steel reinforcement, the compression zone, the aggregate interlock, and shear transfer across the cracks (Taylor et al. 1970), and MCFT was proposed by the fib concrete model based on shear transfer across cracks (Béton et al. 2013). Other theories are based on truss analogy (ACI 318-2014), variable truss angle (EC 2-1992), and a combination of beam and arch actions with dowel action and aggregate interlock (CSA23.3- 2004).
The experimental evaluation of shear cracking in RC beams has been reported by Hu et al. (2017). Shear crack widths and shear strains have been reported and evaluated by digital image correlation. The results have correlated crack width to deflection and shear strength. The addition of shear strength provided by concrete (Vc) and steel reinforcements (Vs) to predict the overall RC beams shear strength has been used by designers for years and years (Hu et al. 2018). ACI and AASHTO provide various formulas to predict the first diagonal shear crack Vcr and the total Vc. Hu et al. (2018) provided experimental evaluation of the effect of a/d on the Vc and the Vs. Results showed that varying small a/d shows larger Vc compared to Vcr. In addition, not all stirrups cross shear cracks reach yield ultimate strength. It was found also that the design codes provide unconservative values for Vc at higher a/d.
In a hypothetical model developed by JC et al. (1981), concrete was described to be a two-phase composite material, where rigid sphere aggregates are surrounded by the cement paste. Cracks were modeled to propagate around the aggregates whose contact area between them depends on the crack kinematics (width and sliding), aggregate size, and the ratio of the coarse aggregate to the total aggregate volume. The fib Model code 2010 (Béton et al. 2013) was based on this premise to establish the importance of aggregate interlock on shear resistance of RC members.
Experimental studies conducted by different authors (ACI 426-1973; Grebović et al. 2015; Perera et al. 2013) have shown that the compressive strength of concrete and a/d ratio have a greater influence on the behavior of RC beams, with and without web reinforcement. For example, when the a/d ratio is less than 1.0, an inclined crack joining the load and the support would be formed. The formation of the inclined crack destroys the horizontal shear flow from the beam longitudinal reinforcement to the concrete compression zone and changes its behavior from the beam action to the arch action. For an a/d between 1.0 and 2.5, an inclined crack forms after a redistribution of internal forces such that the beam is dominated by the arching action, and for a/d between 2.5 and 6.0, the behavior is dominated by beam action before ultimately fails in flexure.
Chen et al. (2013) have reported that the shear strength of high-strength concrete beams does not improve with the same proportion as the compressive strength improvement. They tested high-strength concrete beams without shear reinforcement to investigate the overall behavior. Chen et al. (2013) showed that the variation of shear strength in HSC is related to the fracture failure roughness, where they found that the roughness index decreases when compressive strength increases, which means that failure surfaces in HSC is smoother than failure surfaces in normal weight concrete.
Sudheer et al. (2010) have attempted to investigate the shear strength of high-strength concrete beams with compressive strength close to 70 MPa. The parametric study has included various shear span-to-depth ratios (a/d = 1, 2, 3, and 4) without shear reinforcement. The results have been compared with the shear models found in the literature, such as ACI 318, Canadian Standard, CEP-FIP Model, Zsutty Equation, and Bazant Equation. The main conclusion was found that the best fit to the testing results was Zsutty’s model; in addition, the authors provided simplified equation to predict shear strength of HSC.
The ACI 318-2014 limits concrete compressive strength for shear calculation in beams without web reinforcement to 68 MPa and underestimates the effect of longitudinal reinforcement ratio as well as the a/d ratio. The EC 2-1992 limits the compressive strength of concrete to 50 MPa, while BS 8110-1997 limits concrete compressive strength to 41 MPa, longitudinal reinforcement ratio to 0.03, and a/d ratio to 2.0. In contrast, the fib Model Code 2010 (Béton et al. 2013) limits the concrete strength to 64 MPa because HSC produces smoother crack faces where cracks pass through rather than around aggregate particles, especially in beams without shear reinforcements.
The objective of this paper is to study the influence of the a/d ratio on the behavior of high-strength RC beams in comparison with state-of-the-art models and design guidelines; it is not to say that one model or design guideline is better than the other. As future RC construction will more likely use HSC more and more, this study points out the need for more research in understanding shear mechanisms in high-strength RC beams.
2 Experimental Procedure
2.1 Concrete and Reinforcement Bars Properties
The fine and coarse aggregates were obtained from Premix Concrete at Pullman, WA. The coarse aggregate used was a basalt rock with a maximum aggregate size of 20 mm, while the fine aggregate was obtained from Atlas Rock in Northern Idaho. The aggregates were well blended and graded to ensure optimum packing. Ordinary Portland cement blended with supplementary cementitious materials (50% fly ash and 50% slag) was used with a water to cementitious (w-cm) ratio of 0.32. To achieve sufficient workability, Daracem was used as high-range water-reducing agent (HRWRA), and Daravar (DAV) as air-entraining agent. The mixing proportion and fresh properties of the concrete are summarized in Table 2. Concrete samples were taken from each concrete batch during mixing to make three concrete cylinders of 101.6 mm by 203.2 mm for compressive strength test on the day of testing the beams. The concrete cylinders and the beam specimens were cured in a humidity chamber for 28 days. The average 28-day compressive strength of the concrete cylinders was 69.5 MPa.
The mechanical properties of the steel reinforcement used in this study were obtained from uniaxial tension testing of three samples of the stirrups and the longitudinal reinforcement. The stirrups, made from 10 mm diameter bar, had an average yield stress of 400 MPa, and the longitudinal reinforcement was made from 16 mm diameter bar with an average yield stress of 420 MPa. The average ultimate strength for the stirrup and longitudinal bars is 490 MPa and 520 MPa, respectively. All the rebar has elastic modulus of 210 GPa.
2.2 Specimen Design
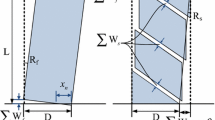
To study the influence of a/d on the behavior of reinforced HSC beams, six specimens were designed according to ACI 318-2014 and tested using a four-point bending, under a displacement-control regime at a rate of 0.5 mm/min until failure, by varying the a/d as summarized in Table 3. All beams were simply supported having a length of 2133.6 mm and a clear span (length between supports) of 1879.6 mm, and 25.4 mm clear concrete cover. The cross sections of the beams are shown in Fig. 1. To design the beams to have shear failure, no stirrups were used as shown in Fig. 1a, while to force beams to have flexural failure, \(\emptyset\) 10 mm stirrups @ 75 mm spacing were provided. The shear and flexural design have been conducted using the ACI [3] design provisions.
The specimens were named according to the Beam Number-Loading Type-Stirrups-Spacing-Shear and a/d ratio. For example, 2Cont-MN-2 represents beam specimen number 2 as a control specimen (CONT)-tested under monotonic loading (M) without stirrups (N) and a/d of 2.0.
As shown in Fig. 1, specimens 2Cont-MN-2 and 3Cont-MN-2.5 did not have shear reinforcement, while minimum shear reinforcement was provided in specimens 4Cont-M8-2, 5Cont-M8-2.5, 6Cont-M8-3, and 7Cont-M3-2.5 to prevent brittle shear failure and to compensate for the reduced concrete contribution to shear strength caused by the reduction in aggregate interlock (ACI 363R 2010). The proposed minimum shear reinforcement was calculated from Eq. (1) as suggested in ACI 363R-2010.
A technical report (CSTR-49 1998) proposed the minimum shear reinforcement for HSC beams according to Eq. (2), where Eq. (3) is used to calculate the tensile strength of the concrete. Equation (2) was developed to account for the reduction in aggregate interlock:
Comparison of Eq. (1) and (2) denotes that (Reagan et al. 2005) is conservative in shear resistance prediction of RC beams. A plot of Eqs. (1) and (2) for concrete grades greater than 60 MPa is shown in Fig. 2.
2.3 Instrumentation and Test Setup
The necessary data collected during the experimental testing were the strain in the concrete and rebar, beam mid-span deflection, and crack evolution/propagation. To capture these data, strain gauges were installed at mid-span of the bottom (tensile) steel reinforcements and on the shear reinforcement (the second stirrup from the support) where the bending and shear stresses are maximum, respectively. The steel strain gauges were installed and marked before the concrete was poured. A day prior to testing, concrete strain gauges were installed on the compression side of the beam to capture the concrete strain. During testing, a linear variable differential transformer (LVDT) was placed at the mid-span and close to the supports of the specimen to capture the mid-span displacement and any rotation at either support. All the strain gauges and the LVDT were connected to a data acquisition system to continuously record the data electronically. A 220 kN servo-valve hydraulic actuator was used to apply load to the specimens through a steel spreader beam placed on top of the beam at a loading distance corresponding to each a/d. To prevent local crushing of concrete, 150 mm by 30 mm thick neoprene pads were placed under the load. The beam was hinged at one end and supported by a roller at the other end. A complete setup of the specimen before testing is shown in Fig. 3 All beams were loaded until failure. The load and deflections corresponding to the concrete cracks and steel yielding were marked, recorded, and analyzed.
3 Test Results and Discussions
The results of the experimental testing are presented in the following subsections.
3.1 Cracking Moments and Moment Capacity
The first crack in all the specimens was a flexural crack which occurred at the mid-span of the beams and propagated to other parts of beam as the test continued with subsequent development of shear cracks inclined toward the loading points. The corresponding load at first crack was recorded and converted to moment by multiplying it with the shear distance in each loading case. This cracking moment was compared with those suggested by ACI 363R (2010) and ACI 318- (2014) as summarized in Table 4, by using Eqs. 4(a) and (b), respectively:
Comparison of the cracking moment with ACI code equations is summarized in Table 4. The results showed that the beam cracking moment is lower than those predicted by ACI 318-2014 and ACI 363R-2010. The ACI codes overpredicted the cracking moment for beams without shear reinforcements by 30.76%, but for beams with shear reinforcement, the results were fairly consistent with the ACI except beam 5Cont-M8-2.5. The inconsistency of the early cracking could be attributed to shrinkage of the concrete where restraint was provided by the steel reinforcement within the concrete. It has been suggested that using a reduced tensile strength of concrete to calculate the cracking moment of reinforced HSC beams would account for free shrinkage strain and translating it into equivalent tensile stress (Gilbert et al. 1998 and Large et al. 1969).
The parameters for the stress block were modified to account for the greater brittleness of HSC (Campione et al. 2014). Whitney’s equivalent stress block for under-reinforced (tension-controlled) beam can be used if the section analysis is based on bending theory. Using the stress–strain curves for uniaxially loaded specimens showed close values to the experimental data in terms of moment–curvature relationship and ultimate moment capacity of HSC beams (Mansur et al. 1997). ACI 318-2014 can be used to calculate the beam flexural capacity using Eq. (5):
Comparisons of experimentally obtained moment capacities and Eq. (5) are summarized in Table 4. The ratio of ultimate moment from ACI 318 to ultimate moment from experiment, Mu-ACI 318 /Mu-Expt., had an average value of 0.92 for a total of 16 reinforced HSC beams tested (Mansur et al. 1997) under different a/d ratios. It can be observed that the equation from ACI 318-2014 greatly underestimates the flexural capacity of reinforced HSC beams, especially for beams with a/d between 2.0 and 3.0. The flexural capacities of the specimens did not show a well-defined trend with various a/d, and the provision of shear reinforcement in the beams prevented premature flexural failure. Technically, the flexural capacities of the specimens should be the same because all the specimens had the same cross section and the same amount of flexural reinforcement. However, it was the difference in the shear capacities that resulted in the difference in applied shear load in the specimens when concrete beams failed.
3.2 Load–Deflection and Behavior of Beam Specimens
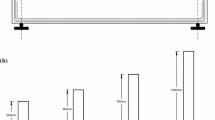
The load–deflection curves for all the beam specimens were plotted and compared with deflections calculated using the elastic theory. An idealized load–displacement curve for reinforced HSC beam is shown in Fig. 4 and compared with the experimental results. The specimens were classified into two groups: the first group comprised two beams having the same flexural reinforcement ratio, but different a/d ratios without shear reinforcement. In the second group, beams have equal flexural reinforcement ratio but different shear reinforcement ratios.
An under-reinforced beam that shows ductility before failure when loaded could be idealized with four segments labeled A to D on the load–deflection curve of Fig. 4a. The first two points of Fig. 4a depict the first cracking and tension steel yielding (points A and B), respectively, and the stiffness of the beam is then reduced at points of “B” to “D” (beyond yielding). If shear reinforcement is provided to preclude brittle shear failure, the beam would develop its full flexural capacity and ultimately fail by flexure (points “B”–“D”). However, in the absence of shear reinforcement, the full flexural capacity of the beam will not be reached, and the section fails before yielding (between points “A” and “B”) in a brittle manner.
The load–deflection curves for the tested beams are shown in Fig. 4b and 4c, with behaviors similar to the idealized load–deflection curve of Fig. 4a. In the first group (3CONT-MN-2 and 2CONT-MN-2.5), the specimens failed in brittle shear without steel yielding; this failure corresponds between points “A” and “B” shown in Fig. 4a. After the first crack in specimen 3CONT-MN-2, diagonal shear cracks occurred in the region of combined moment and shear, which propagated to the compression zone (top) of the beam followed by crushing of the concrete under the load. Similarly, 2CONT-MN-2.5 had an inclined shear crack that extended to the bottom of the beam with a splitting crack along the tension reinforcement of the beam as shown in Fig. 5. The splitting crack along the tension reinforcement was due to dowel action in the tension reinforcement. The two beams, 3CONT-MN-2 and 2CONT-MN-2.5, failed ultimately by shear-compression and shear-tension, respectively. The observed failure modes were similar to the results of reinforced NSC beams (ACI 426- 1973).
In the second group (4CONT-M8-2, 5CONT-M8-2.5, 6CONT-M8-3, and 7CONT-M3-2.5), the load-displacements shown in Fig. 4(c) displayed a pattern similar to those in group one. Specimens with a/d equals 2.0 and 2.5 (4CONT-M8-2, 5CONT-M8-2.5, and 7CONT-M3-2.5) failed between points “A” and “B” in a brittle shear manner without yielding of the steel reinforcement. Comparison of these specimens with those without shear reinforcement showed that beams in group 2 are stiffer and possess higher load capacities than those in group one. The cracks started as flexural cracks at the region of maximum moment and propagated along the beam length with formation of diagonal shear cracks as shown in Fig. 6a through c.
In specimen 6Cont-M8-3, the load–displacement curve was similar to the idealized load–displacement curve with failure between points “B” and “D”, beyond yielding as shown in Fig. 4c. As the test progressed, yielding of the steel reinforcement was observed and the beam ultimately failed in flexure. The load-strain curve for the longitudinal and transverse reinforcement is shown in Fig. 7.
3.3 Deflection Predictions
The basic approach to calculate deflection is by using elastic beam theory given in Eq. (6a), considering the effective moment of inertia. The most commonly accepted empirical expression to calculate the effective moment of inertia is shown in Eq. (6b):
The Mcr suggested by ACI 363R- (2010) and ACI 318- (2014) were used to calculate the effective moment of inertia in Eq. (6b). The deflection values obtained from the calculations named \(\delta_{ACI - 318 }\) are based on Mcr-ACI 318 and \(\delta_{ACI - 363 }\) based on Mcr-ACI 363 are compared with the experimental results, as shown in Table 5.
The equations (ACI 318- 2014) underestimated the deflections of the beams without shear reinforcements. However, for beams reinforced with stirrups, the deflection values from ACI 318-2014 were higher than the experimental deflection values as shown in Table 5. Beam with stirrups (shear reinforcement) had higher deflection because, with the introduction of shear reinforcement, the beam would sustain higher load which would also translate to higher deflection as long as the beam remains elastic.
For example, beams reinforced with stirrups (200 mm spacing) showed predicted deflection of 50%, and 37% increase for a/d = 2 and 2.5, respectively, and when a/d was increased to 3.0, the deflection was significantly increased to (45%) compared to the experimental results. The code equations shown in Eq. 6(a) through (b) were used taking into consideration the concrete elastic modulus and the cracking moment based on the tensile strength of the concrete. As previously described, equations from ACI 318-2014 do not consider the effect of shrinkage and creep in the calculation of cracking moment, especially for HSC.
In the modified method of deflection calculation presented by Ghali et al. (2012), a basic deflection value is calculated by assuming that the RC beam is a homogeneous elastic material without cracking. This basic deflection value was then multiplied by factors to account for creep, shrinkage, cracking, and reinforcement stiffening (Ghali et al. 2012). This modified method of calculating deflection improved the accuracy of the deflection predictions as shown in Table 5. Improvement in deflection values for beams without shear reinforcement was observed with an overprediction of 20% for a/d = 2.0. For beams with higher values of a/d and with shear reinforcements, the deflection predicted by Ghali et al. (2012) showed higher results. As a/d was increased, the beam would be subjected to higher effect of shear and flexure, which would result in higher deflection. The combined effect of flexure-shear on deflection of beams has not been fully developed and hence needs further study to understand this interaction. The effect of shrinkage and cracking should be accounted for in deflection prediction for reinforced HSC beam (Rashid et al. 2005).
3.4 Shear Prediction Models
The shear resistance of reinforced HSC beams can be calculated in different ways using empirical approaches based on the assumptions of the shear stress distribution theories in the beam section. One such theory assumes 25% of the shear stresses to be transferred through the compression zone, 25% through dowel action, and 50% through aggregate interlock along the crack (Taylor et al. 1970).
In the fib Model Code 2010, four levels of shear strength approximation (LoA I to LoA IV) were suggested as presented in Muttoni et al. (2012). For members without shear reinforcement, LoA II provides a base model and Level I is its simplification. Similarly, for members with shear reinforcement, Level III provides a base model while Level II is its simplified form. The level of approximation (LoA) contains β, a value that accounts for cracked concrete to transfer shear stress across the crack through aggregate interlock. The higher the aggregate interlock, the higher the β value. It should be noted that for a concentrated load placed between 1 ≤ a/d ≤ 2, the β value would account for arching action. In this study, LoA I and II were used for specimens without shear reinforcement and with shear reinforcement, respectively.
Using the critical shear crack theory, Zsutty’ s model (1971) and Huber et al. (2019) proposed a model which combined aggregate interlock, effective shear span-to-depth ratio and failure zone roughness to predict the shear capacity of RC beams with and without shear reinforcement. The effect of shear reinforcement depends on the bond action between the stirrups and the concrete, and the inclination of the diagonal cracks or the number of stirrups crossing the diagonal cracks (Huber et al. 2016).
Several shear prediction models are summarized in Table 6 for different concrete grades and based on different shear transfer mechanisms. The shear capacities of beams from the experimental testing were compared with the results from the models summarized in Table 6. These results are as summarized in Table 7.
For beams without shear reinforcement (2Cont-MN-2.5 and 3Cont-MN-2), a comparison of the experimental and analytical results showed that all the models except the fib 2010 model with LoA1 (Béton et al. 2013) and Huber’s et al. (2019) displayed a wide variation in the shear capacities. It is interesting to note that both Bazant et al. (1984) model and fib model (Béton et al. 2013) considered the same factors in their models, but the Bazant model overpredicted the shear capacity of the beams. The reason for the disparity could be the assumption of crack propagation through rather than around the aggregate which is accounted for by a strain factor in the fib model code. The Huber et al. 2016 and 2019 models, which are modifications of the fib model, had a calibration factor to account for surface roughness. The predictions were based on perfectly smooth crack agreed well with the experimental results.
In beams with shear reinforcements, similar results were obtained. The fib model code (Béton et al. 2013) and the Huber et al. 2016 model satisfactorily predicted the shear capacities of the beams, although the LoA II for Béton et al. (2013) was more accurate than LoA for beams with shear reinforcement. Other models provided relatively accurate shear resistance values when compared with the experimental results, especially the model suggested by BS (1997) for a/d of 2.0–2.50 and fewer stirrups (4Cont-M8-2, 5Cont-M8-2.5, and 6Cont-M8-3). At higher stirrups content, (7Cont-M3-2.5), the shear capacity was overestimated by a factor of two compared the experimental result, except for Béton et al. (2013) and Huber et al. (2016). The a/d had a higher effect on the shear capacity of the beams with stirrups in contrast to the beams without stirrups.
A modified equation based on a truss angle analogy and the arch crushing action (Campione et al. 2014) displayed the lowest shear capacity for beams without stirrups. The model of Bazant et al. (1984) accounted for the strength contribution due to beam action in NSC by considering the influence of the aggregate size, while the model of Zsutty 1971 accounted for the effect of longitudinal reinforcement and a/d ratio.
4 Conclusions
In this paper, the effect a/d ratio on the behavior of reinforced HSC beams was investigated and the results were compared with different empirical state-of-the-art models and design guidelines. Although the number of tested beams were quite few to develop a new model, comparisons of the experimental results with well-established models provided insight on the behavior of HSC beams under shear loading. The following conclusions have been drawn:
-
The failure modes of reinforced HSC beams were similar to those of NSC beams which depend on the a/d as it influences the shear transfer mechanisms.
-
In beams with stirrups, the effect of a/d on the shear strength was higher in contrast to beams without stirrups. The influence of a/d in addition to the aggregate interlock was unaccounted for in most shear models. This was evident as most of the models either underestimate the shear strength (up to 50%) or overestimate the shear capacities, with exceptions of the fib Model code 2010 and Huber et al. models. Therefore, prior to the use of any model, the understanding of the model assumption is necessary, especially in HSC construction.
-
The ACI 363R and ACI 318 codes were quite conservative in predicting cracking moment and moment capacity of HSC beams and therefore should be used with caution because the section could crack earlier than the predicted values of cracking moment by the code equations.
Availability of data and materials
The experimental data used to support the observations of this study are included in this article and the data will be available to share with whom is interested.
Abbreviations
- A st :
-
Area of steel reinforcement
- f y :
-
Yield stress of reinforcement
- P cr :
-
Cracking force
- A v ,min :
-
Minimum area of shear reinforcement
- h :
-
Beam height
- S :
-
Stirrup spacing
- a v :
-
Shear span
- I cr :
-
Cracked moment of inertia
- V :
-
Shear force
- b w :
-
Beam width
- I e :
-
Effective moment of inertia
- ρ i :
-
Percentage area of longitudinal reinforcement
- d :
-
Effective depth of beam
- I g :
-
Gross moment of inertia
- Ρ w :
-
Percentage area of shear reinforcement
- Expt:
-
Experiment
- L :
-
Beam span (between supports)
- δ :
-
Deflection
- \(f^{\prime}_{c}\) :
-
Concrete 28th day compressive strength
- M a :
-
Applied ment
- w-cm:
-
Water-to-cementitious ratio
- \(f_{ct,m} f_{ct}\) :
-
Concrete tensile strength
- M cr :
-
Cracking moment
References
ACI-ASCE Committee 426, The Shear Strength of Reinforced Concrete Members. Journal Proceedings, 1973. 70(7): p. 471–473.
ACI Committee 318, Building Code Requirements for Structural Concrete (ACI 318–14) and Commentary. (2014). American Concrete Institute: Farmington Hills, MI. p. 524.
ACI Committee 363R-10, Report on High-Strength Concrete. 2010, American Concrete Institute: Farmington Hills, MI. p. 69.
Bazant, Z. P., & Kim, J. K. (1984). Size effect in shear failure of longitudinally reinforced beams. ACI Struct. J., 85(5), 456–468.
Béton, F.F.I.d., fib Model Code for Concrete Structures 2010. (2013). Ernst & Sohn: Berlin.
British Standard Institution. (1997). Structural use of concrete, Part 1, Code of Practice for design and construction (p. 168). London: BSI.
Campione, G., Monaco, A., & Minafò, G. (2014). Shear strength of high-strength concrete beams: modeling and design recommendations. Engineering Structures, 69,(Supplement C), 116–122.
Chen, S., Li, J. (2013) Shear Behavior of Reinforced High-Strength Concrete Beams, ACI Structural Journal (Discussion Section), V. 110, pp. 1112–1114.
Concrete Society Technical Report TR-49. (1998). Design guidance for high strength concrete. United Kingdom. p. 168.
CSA A23.3–04. (2004) Design of Concrete Structures. Canadian Standard Association: Ontario. p. 258.
Eurocode 2, Design of concrete structures. Part 1–1: General Rules and Rules for Building (ENV 1992–1–1). (2004). Brussels. p. 225.
Ghali, A., Favre, R., & Elbadry, M. (2012). Concrete structures (4th ed.). NY: Taylor and Francis.
Gilbert, R.I. (1998). Serviceability considerations and requirements for high performance reinforced concrete slabs, in International Conference on High Performance High Strength Concrete. Perth. p. 15.
Grebović, R. S., & Radovanović, Ž. (2015). Shear strength of high strength concrete beams loaded close to the support. Procedia Engineering, 117,(Supplement C), 487–494.
Hu, B., & Wu, Y. F. (2018). Effect of shear span-to-depth ratio on shear strength components of RC beams. Engineering Structures, 168, 770–783.
Hu, B., & Yu-Fei, W. (2017). Quantification of shear cracking in reinforced concrete beams. Engineering Structures., 147, 666–678.
Huber, P., Huber, T., & Kollegger, J. (2016). Investigation of the shear behavior of RC beams on the basis of measured crack kinematics. Engineering Structures, 113, 41–58.
Huber, T., Huber, P., & Kollegger, J. (2019). Influence of aggregate interlock on the shear resistance of reinforced concrete beams without stirrups. Engineering Structures, 186, 26–42.
JC, W. (1981). Fundamental analysis of aggregate interlock. ASCE J Struct Div., 107(11), 2245–2270.
Kani, G. (1964). The riddle of shear failure and its solution. ACI Struct. J., 61(4), 27.
Large, G. E., & Chen, T. Y. (1969). Reinforced concrete design (p. 481). New York: The Ronald Press Co.
Leslie, K. E., Rajagopalan, K. S., & Everard, N. J. (1976). Flexural behavior of high-strength concrete beams. ACI Journal, Proceedings, 73(9), 517–521.
Mansur, M. A., Chin, M. S., & Wee, T. H. (1997). Flexural behavior of high-strength concrete beams. Structural Journal, 94(6), 663–673.
Muttoni, A., & Ruiz, M. F. (2012). Levels-of-approximation approach in codes of practice. Structural Engineering International, 22(2), 190–194.
Park, R., & Paulay, T. (1975). Reinforced concrete structures (p. 769). New York: Wiley.
Pastor, J. A., Nilson, A. H., Slate, F. O., & Behavior of High Strength Concrete Beams. (1984). Department of Structural Engineering (p. 311). NY: Cornell University.
Perera, S., & Mutsuyoshi, H. (2013). Shear behavior of reinforced high-strength concrete beams. ACI Struct. J., 110(1), 43–53.
Rashid, M. A., & Mansur, M. A. (2005). Reinforced high-strength concrete beams in flexure Structural Journal, 102(3), 462–471.
Regan, P. E., Kennedy-Reid, I. L., Pullen, A. D., & Smith, D. A. (2005). The influence of aggregate type on the shear resistance of reinforced concrete. Struct Engineer, 8(23), 27–32.
SIA, Construction en béton (Concrete construction—in French). (2012). Société Suisse des Ingénieurs et Architectes Ed.
Sudheer, R. L., Ramana, R. N. V., & Gunneswara, R. T. D. (2010). Shear resistance of high strength concrete beams without shear reinforcement. International Journal of Civil and Structural Engineering, 1(1), 101–113.
Taylor, H.P.J. (1970). Investigation of forces carried across cracks in reinforced concrete beams in shear by interlock of aggregate. Cement and Concrete Association: London. p. 22.
Y.F., Hu B. (2020). Variation of Shear Strength Components of RC Beams. Wang C., Ho J., Kitipornchai S. (eds) ACMSM25. Lecture Notes in Civil Engineering. 37. Springer, Singapore.
Zsutty, T. C. (1971). Shear strength prediction for separate categories of simple beam tests. ACI Journal, 68(2), 138–143.
Acknowledgements
The authors would like to thank Pre-Mix Inc. at Pullman, Washington for providing the concrete used for this study. The support of the Department of Civil and Environmental Engineering at the University of Idaho is appreciated.
Funding
The authors have not received financial funding for this research.
Author information
Authors and Affiliations
Contributions
AI and RN planned the experimental program, analyzed the data, and drafted the paper. OA, AA, and NS performed the experimental program, data collection, and analysis of data. All the authors read and approved the final manuscript.
Authors' information
Olaniyi Arowojolu is a PhD candidate at the department of civil and environmental engineering, University of Idaho. His research is focused on behavior of concrete structures, experimental testing, and simulation.
Ahmed Ibrahim is an Associate professor at the department of civil and environmental engineering, University of Idaho. His research is focused on Non-linear behavior and modeling of reinforced and prestressed concrete elements, Mechanistic damage modeling of reinforced concrete elements under blast loading, and Experimental testing of reinforced concrete members.
Abdullah Almakrab is a PhD candidate at the department of civil and environmental engineering, University of Idaho. His research is focused on behavior of concrete materials.
Nicholas Saras is a former graduate student at the department of civil and environmental engineering, University of Idaho.
Richard Nielsen is an Associate professor at the department of civil and environmental engineering, University of Idaho. His research is focused on seismic behavior of structures, reliability, and structural dynamics and random vibrations.
Corresponding author
Ethics declarations
Competing interests
The authors declare that there is no conflict of interest in any form.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Journal information: ISSN 1976-0485 / eISSN 2234-1315
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arowojolu, O., Ibrahim, A., Almakrab, A. et al. Influence of Shear Span-to-Effective Depth Ratio on Behavior of High-Strength Reinforced Concrete Beams. Int J Concr Struct Mater 15, 14 (2021). https://doi.org/10.1186/s40069-020-00444-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40069-020-00444-7