Optimum Locations of Outriggers in a Concrete Tall Building to Reduce Differential Axial Shortening

Abstract

Differential axial shortening (DAS) in a tall building can produce adverse effects on its structural and nonstructural elements. Therefore, DAS should be considered in the design phase and appropriate measures should be taken to reduce its unfavorable effects. In this study, the utilization of outriggers, which has been originally designed to reduce lateral displacements, is proposed to reduce DAS. The optimum locations of outriggers that minimize the maximum DAS are determined by an optimization method. The integrality requirement posed by the outrigger locations, which should be given as integer numbers, is resolved by piecewise quadratic interpolation with discrete analysis results. The proposed optimization method stably yielded optimum solutions for a total of 24 design cases. The optimum design results show that although the maximum DAS decreases as the number of outriggers increases, the maximum DAS does not decrease significantly when the number of outriggers is greater than 2.

1 Introduction

Differential axial shortening (DAS), which is often also called differential column shortening, is the difference between the vertical displacements developed in the column and wall at the same floor in a building. DAS in a low-rise building is so small that it does not cause any adverse effect. However, it has been one of the most important issues that need special attention in the design and construction of a tall building because of the accumulated amount of vertical displacement. Furthermore, owing to the long-term behavior of concrete such as creep and shrinkage, DAS becomes more significant in concrete tall buildings than in steel tall buildings. DAS can cause adverse effects not only on the structural members but also on nonstructural elements, such as the curtain wall, partitions, and mechanical pipelines. Therefore, DAS in a tall building should be predicted and appropriate measures should be taken to reduce its unfavorable effects.

The most widely known method to predict column shortening in a tall building is the method proposed by Fintel et al. (1987) and published by the Portland Cement Association (PCA). It calculates column shortening using a series of vertical truss elements, which are subjected to sequential vertical loads according to the construction sequence. The PCA method takes into consideration the stress distribution between concrete and reinforcement bars by using the transformed section and the reinforcement coefficient. However, the so-called frame effect, which is the force distribution between interconnected structural members, is not considered.

Recently developed methods for column shortening have dealt with this drawback. Kwak and Kim (2006) studied the effect of the construction sequence on the long-term behavior of a reinforced concrete frame structure using layered beam elements. Moragaspitiya et al. (2010) proposed a numerical procedure to predict the DAS in a high-rise concrete building and reported that a rigid outrigger system has a mitigating impact on the DAS between the perimeter columns and cores. Kim (2013) proposed a time-dependent analysis method for reinforced concrete frames, which iterates a linear elastic analysis and considers the equivalent nodal load of creep and shrinkage, transformed section, and effective elastic modulus. Kurc and Lulec (2013) studied the different analysis approaches for estimating axial loads on vertical elements of tall buildings. Zou et al. (2014) carried out a construction sequence analysis using the long-term properties of a reinforced concrete shear wall. Recently, Samarakkody et al. (2017) studied DAS and its effects in tall buildings with composite concrete-filled tube columns. In particular, they noted the possibility of using an outrigger and belt system to mitigate the DAS in a tall building, in addition to their role in lateral load resistance. Afefy and El-Tony (2016) proposed a simplified design procedure for eccentrically loaded columns and Georgoussis (2017) presented a preliminary structural design of wall-frame building systems.

The most commonly used method to compensate for the adverse effects of DAS consists in raising the columns that are expected to exhibit significant shortening (Park et al. 2013). However, compensation during construction by, for instance, raising columns is not a solution that can eliminate the unfavorable effects of DAS. Compensation could level the floors at the target time, but it cannot prevent the development of the DAS itself. Kim (2015) proposed placing additional reinforcement as a measure to reduce DAS in the design phase, and a mathematical optimization method was developed to determine the optimum distribution of the additional reinforcement along the stories.

In this study, outriggers, which are horizontal structures connecting a building core to distant columns to increase the lateral stiffness of a tall building, are proposed to reduce DAS. Conventionally, the permanent connection of outriggers to perimeter columns is delayed until the completion of the structure to avoid the development of shear forces that could be caused by DAS because the outriggers have been conventionally designed to reduce the lateral displacement caused by wind or earthquake loads. Special construction methods, such as delayed joints and adjustment joints with shim plates or oil jacks, have been proposed or used to minimize the impact of DAS during construction (Choi and Joseph 2012; Park et al. 2010). Although the main purpose of the outriggers is to limit the lateral drift of a tall building within an acceptable level (Wu and Li 2003; Hoenderkamp 2008; Lee and Tovar 2014), it is proposed that outriggers can also function as a measure to reduce DAS between core walls and perimeter columns. If the outriggers are designed to reduce DAS and lateral displacement, the additional stresses caused by DAS should be evaluated and considered during the design phase of a tall building.

The optimum locations of the outriggers to reduce DAS can be determined by an optimization method. Because the floors where the outriggers are installed are given as integer numbers, conventional gradient-based optimization methods cannot be directly used. In this study, a piecewise quadratic interpolation method was used to resolve the integrality requirement posed by the optimum locations of the outriggers.

2 Analysis of Axial Shortening

2.1 Construction Sequence Analysis

The axial shortening analysis of a concrete tall building essentially requires a construction sequence analysis and a creep analysis of the concrete structure. The construction sequence analysis is a series of static analyses, where new construction activities are applied to an already deformed and stressed structure (Kurc and Lulec 2013). Before defining the geometry of the newly added structure for the construction sequence analysis, it is necessary to determine what type of shortening is considered. Total shortening in a tall building can be divided into pre-installation and post-installation shortening (Fintel et al. 1987). Pre-installation shortening and post-installation shortening are sometimes called up-to-slab shortening and subsequent shortening, respectively. In cast-in-place concrete building structures, pre-installation shortening, which is the amount of shortening developed before slab installation, is meaningless since it is automatically compensated by leveling the forms. On the other hand, in steel building structures where columns are prepared to exact lengths, the total shortening, which is the sum of the pre-installation and the post-installation shortenings, is of significance because the slabs are built at a predetermined position. In this study, the analysis models are reinforced concrete tall buildings and the post-installation shortenings are calculated. In an analysis model, the displacement of each node is assumed to be zero until the node is generated. The incremental displacements are calculated for each construction step. The incremental vertical displacements at the columns and walls are accumulated to yield the post-installation shortening at the target time.

2.2 Long-term Analysis of Concrete Structures

The total strain at time t under a constant stress $\sigma (t_{0} )$ applied at time t₀ is the sum of the elastic strain and non-mechanical strain such as creep strain, shrinkage strain, and temperature strain. The temperature strain is not considered in this study because it does not accumulate along time. Creep is usually presented as a creep coefficient $\phi (t,t_{0} )$, which is the ratio of the creep strain to the elastic strain. The sum of the creep strain and the elastic strain is sometimes given by the creep function (often called the compliance function) $J(t,t_{0} )$, which represents the strain at time t produced by a unit constant stress that has been acting since time t₀ (Bazant and Wittmann 1982). Thus, the total strain of unrestrained plain concrete under constant stress is given by Eq. (1).

$$\begin{aligned} \varepsilon (t) &= \frac{{\sigma (t_{0} )}}{{E_{c} (t_{0} )}}\left[ {1 + \phi (t,t_{0} )} \right] + \varepsilon_{sh} (t,t_{0} ) \\ &= J(t,t_{0} )\sigma (t_{0} ) + \varepsilon_{sh} (t,t_{0} ) \\ \end{aligned}$$

(1)

where $E_{c} (t_{0} )$ is the elastic modulus of concrete at time t₀, and $\varepsilon_{sh} (t,t_{0} )$ is the shrinkage strain developed from t₀ to t.

If the concrete is restrained by other structural members or reinforcing bars, the stress in the concrete changes over time. The total strain developed in the restrained concrete can be obtained by integrating the strain over time as given in Eq. (2).

$$\begin{aligned} \varepsilon (t) &= \frac{{\sigma (t_{0} )}}{{E_{c} (t_{0} )}}\left[ {1 + \phi (t,t_{0} )} \right] + \int_{{t_{0} }}^{t} {\frac{{1 + \phi (t,t_{0} )}}{{E_{c} (\tau )}}\frac{\partial \sigma (\tau )}{\partial \tau }d\tau + } \varepsilon_{sh} (t,t_{0} ) \\ &= J(t,t_{0} )\sigma (t_{0} ) + \int_{{t_{0} }}^{t} {J(t,t_{0} )\frac{\partial \sigma (\tau )}{\partial \tau }d\tau + } \varepsilon_{sh} (t,t_{0} ) \\ \end{aligned}$$

(2)

Several analysis methods have been developed to solve Eq. (2). The rate of creep method, effective modulus method, age-adjusted modulus method, and step-by-step method (SSM) are well-known analysis methods to solve Eq. (2) (Bazant and Wittmann 1982; Neville et al. 1983; Ghali and Favre 1994). This study uses the SSM because it can give the most accurate analysis of the time-dependent behavior of concrete structures such as axial shortenings in a tall building.

In the SSM, the analysis time is divided into several intervals. The stress is assumed to be constant in each interval and the strain variation in the i-th interval can be given by

$$\begin{aligned} (\Delta \varepsilon )_{i} &= \frac{{(\Delta \sigma )_{i} }}{{E_{c} (t_{i - 1/2} )}}\left[ {1 + \phi (t_{i} ,t_{i - 1/2} )} \right] + \sum\limits_{j = 1}^{i - 1} {\left( {\frac{{(\Delta \sigma )_{j} }}{{E_{c} (t_{j - 1/2} )}}\left[ {\phi (t_{i} ,t_{j - 1/2} ) - \phi (t_{i - 1} ,t_{j - 1/2} )} \right]} \right)} + (\Delta \varepsilon_{sh} )_{i} \\ &= J(t_{i} ,t_{i - 1/2} ) \cdot (\Delta \sigma )_{i} + \sum\limits_{j = 1}^{i - 1} {\left( {\left[ {J(t_{i} ,t_{j - 1/2} ) - J(t_{i - 1} ,t_{j - 1/2} )} \right] \cdot (\Delta \sigma )_{j} } \right)} + (\Delta \varepsilon_{sh} )_{i} \\ \end{aligned}$$

(3)

where $t_{i - 1/2}$ denotes the middle of the interval $(t_{i - 1} ,t_{i} )$ in the log $(t - t_{0} )$ scale.

Long-term analyses of columns and horizontal beams are carried out using a specially developed beam element, which can take into account the restraining effect of the reinforcing bars and creep effects in the axial deformation and curvatures at the nodes (Kim 2013). Although the axial shortening of walls can be approximated by the beam elements, in this study, the plane stress element with incompatible modes (Taylor et al. 1976) is modified to obtain higher accuracy in the long-term behavior of the reinforced concrete walls as follows.

The strain vector in the plane stress elements can be given from Eq. (3) as the following equation.

$$\left\{ {\Delta \varepsilon } \right\}_{i} = \left[ {J(t_{i} ,t_{i - 1/2} )} \right]\left\{ {\Delta \sigma } \right\}_{i} + \sum\limits_{j = 1}^{i - 1} {\left( {\left[ {J(t_{i} ,t_{j - 1/2} )} \right] - \left[ {J(t_{i - 1} ,t_{j - 1/2} )} \right]} \right)} \left\{ {\Delta \sigma } \right\}_{j} + \{ \Delta \varepsilon_{sh} \}_{i}$$

(4)

where $\left\{ {\Delta \varepsilon } \right\}_{i}$, $\left\{ {\Delta \sigma } \right\}_{i}$, and $\left\{ {\Delta \varepsilon_{sh} } \right\}_{i}$ are the strain increment vector, stress increment vector, and shrinkage strain increment vector for the plane stress elements, respectively. These vectors have three components as follows.

$$\left\{ {\Delta \varepsilon } \right\}_{i} = \left\{ {\begin{array}{*{20}c} {(\Delta \varepsilon_{x} )_{i} } \\ {\,(\Delta \varepsilon_{y} )_{i} } \\ {(\Delta \gamma_{xy} )_{i} } \\ \end{array} } \right\}$$

(5)

$$\left\{ {\Delta \sigma } \right\}_{i} = \left\{ {\begin{array}{*{20}c} {(\Delta \sigma_{x} )_{i} } \\ {(\Delta \sigma_{y} )_{i} } \\ {(\Delta \tau_{xy} )_{i} } \\ \end{array} } \right\}$$

(6)

$$\left\{ {\Delta \varepsilon_{sh} } \right\}_{i} = \left\{ {\begin{array}{*{20}c} {(\Delta \varepsilon_{sh} )_{i} } \\ {\,(\Delta \varepsilon_{sh} )_{i} } \\ 0 \\ \end{array} } \right\}$$

(7)

It was assumed that shrinkage causes normal strains only (i.e., no shear strain). If the isotropy of materials is kept unchanged and Poisson’s ratio is uniform in whole time steps, then the creep function matrix $[J(t_{i} ,t_{j} )]$ can be obtained by the inverse matrix of the stress–strain constitutive matrix of the plane stress elements (Bazant and Wittmann 1982).

$$[J(t_{i} ,t_{j} )] = J(t_{i} ,t_{j} )\left[ {\begin{array}{*{20}c} 1 & { - v} & 0 \\ { - v} & 1 & 0 \\ 0 & 0 & {2(1 + v)} \\ \end{array} } \right]$$

(8)

where $v$ is the Poisson’s ratio of concrete.

The increment of the total strain $(\Delta \varepsilon )_{i}$ on the left-hand side of Eqs. (3) and (4) denotes the strain change of concrete rather than that of reinforced concrete. The incremental strain is therefore converted to an equivalent nodal load that can be used in the finite element analysis to obtain the strain change of the reinforced concrete members, which are internally and externally restrained by the reinforcing bars and other connected members such as outriggers. The internal restraint due to the reinforcing bars is represented by the area and second moment of the transformed section that is used for calculating the stiffness matrix of the beam element (Kim 2013). For the wall element, the internal restraint of vertical reinforcing bars was considered by adding truss elements, and the effect of horizontal reinforcing bars was neglected because the horizontal reinforcing bars have no significant effect on vertical displacement. The stiffness matrix of the plane stress elements can be obtained by 2 by 2 Gauss quadrature; however, the stress and the strain vectors are calculated at the center of the elements for efficiency.

The shortening of each column or wall at the end of the i-th interval $\left\{ {\text{u}} \right\}_{i}$, which is the sum of the change in the vertical displacement until the i-th interval, is given by

$$\left\{ u \right\}_{i} = \sum\limits_{j = 1}^{i} {\left\{ {\Delta u} \right\}_{j} }$$

(9)

where $\left\{ {\Delta u} \right\}_{j}$ is the increment in the vertical displacement at the j-th interval.

3 Effect of Outriggers on Differential Axial Shortening

3.1 Analysis Models

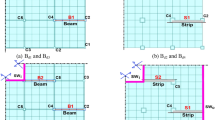
The effects of an outrigger on the DAS of tall buildings were investigated before determining its optimum location. Three 80-story reinforced concrete building structures with the outrigger as shown in Fig. 1 were analyzed. The three analysis models have different sectional profiles for the column and shear walls, as listed in Table 1. The constant-section model has the same column and wall sections for all stories. In the constant-stress model, the column and wall sections were determined according to the applied gravity loads such that the members developed approximately equal axial stresses from the gravity loads. The general model has four different section groups for the vertical members. Although the constant-section and constant-stress models were not likely applicable for an actual tall building, they represented extreme cases of the simplest and the most refined sectional profiles for tall building structures. The four-story high outrigger truss, which is made of steel, has two inclined members and two horizontal members as shown in Fig. 1. The initial sectional area of the horizontal member is 0.1256 m², which was determined in a previous study (Kim 2017). The sectional area of the inclined member in the outrigger was proportioned to $\sqrt 2$ times that of the horizontal member because the inclined member is expected to develop an axial force $\sqrt 2$ times that of the horizontal member. The outrigger floor, which indicates the floor where the outrigger is installed, is assigned to the floor where the inclined member is connected to the wall, as shown in Fig. 1. The beams between the perimeter columns and interior core were assumed to be shear connected, as they are in most tall building structures. The elastic modulus of the outrigger was 210 GPa and that of the other members was 23 GPa. The Poisson’s ratio of concrete for the plane stress elements was 0.18.

Fig. 1

Analysis models and outrigger configuration.

Table 1 Properties of elements and loads used in 80-story analysis models.

The two-dimensional plane frame indicated with red dashed line in Fig. 1a were analyzed. Two plane-stress elements were used to model the wall on every floor, and the beam elements were used to model the perimeter columns. The shear connected beams, outriggers, and vertical reinforcing bars embedded in the walls were modeled with the truss elements. The CEB model (CEB 1993) was used to estimate the long-term behavior of plain concrete. The relative humidity was 60%, and the cement type was normal. Each floor had a 5-day construction cycle. The dead loads listed in Table 1 were applied on the third day after placing each column and wall. The live loads, which are uniformly distributed loads of 20 kN/m applied on the beams spanning 14 m, were applied at the same time 700 days after the beginning of construction. The dead loads, including the uniformly distributed load of 60 kN/m, were applied at the columns and the walls. The differential shortenings to be compared are the post-installation differential shortenings, measured 10,000 days after the beginning of construction when the long-term behavior of concrete structures is considered to be converged. These shortenings include inelastic deformation due to creep and shrinkage, and elastic deformation.

3.2 Reduction of Differential Shortening

The post-installation shortenings of the general model with and without an outrigger are shown in Fig. 2. It is assumed that the outrigger is placed at the 40-th floor and is connected at 195 days, the same time as the construction of the wall at the 40-th floor. It is noted that the DAS with an outrigger is significantly smaller than without it, especially at the 40-th floor, where the inclined member of the outrigger is connected to the wall.

Fig. 2

Shortening of the general model without and with an outrigger placed at the 40-th floor.

The three analysis models show greater shortenings in columns than in walls. The maximum DAS of the models without an outrigger are 109.9, 105.7, and 100.1 mm for the general, constant-section, and constant-stress models, respectively. When the outrigger is placed at the middle of the story, the shortenings of the column decreased and those of the core wall increased. Consequently, the maximum DAS decreased to 83.9, 57.6, and 74.7 mm, respectively. The solid red line in Fig. 2, which represents the DAS with an outrigger placed at the 40-th floor, indicates that the maximum DAS develops at around the 65-th floor and the DAS below the 40-th floor are significantly smaller than the maximum DAS. It can be expected that the maximum DAS would be reduced if the outrigger is placed at a higher floor than the 40-th, for instance, the 55-th floor. Therefore, it is clear that the 40-th floor is not the optimum location, although the optimum location cannot be determined from Fig. 2. The optimum locations of the outrigger are studied in Sect. 4.2.

In this study, to compare the effectiveness of the outriggers, a reduction ratio $R_{d}$ is defined as follows:

$$R_{d} = \frac{\text{maximum DAS with outrigger}}{\text{maximum DAS without outrigger}}$$

(10)

The smaller the reduction ratio, the greater the reduction obtained in the maximum DAS. The reduction ratio of the three analysis models with an outrigger at the 40-th story are calculated as 0.764, 0.545, and 0.746, respectively.

3.3 Effects of Sectional Area

The stiffness of the outrigger can be changed through the cross-sectional area of the outrigger truss. The sectional area of the horizontal members is increased in 50 steps, from zero to 0.1216 m². The sectional area of the inclined members is also proportionally increased. The location of the outrigger, at the 40-th floor, is the same as in the previous analysis. Figure 3 shows the relation between the reduction ratio and the sectional area of the outrigger. It is noted that the effect of the sectional area on the reduction ratio is not the same among the three analysis models. It is worth noting that the relation is non-linear such that the efficiency of the outrigger with smaller sectional area is better than that with larger area. It can be expected that a dual or even triple outrigger system would be better than a single outrigger system in terms of efficiency.

Fig. 3

Relation between sectional area of the outrigger and reduction ratio.

3.4 Effects of Location

As mentioned in Sect. 3.2 and shown in Fig. 2, the middle of the height is not the optimum location of an outrigger to minimize the maximum DAS. The location of the outrigger was changed from the 4-th floor to the 80-th floor in 1 story steps. The construction time of the outrigger changed accordingly to the time when the wall at the outrigger floor was constructed. Figure 4 shows the relation between the location of the outrigger and the reduction ratio. It shows a definite optimum location of a single outrigger to minimize the maximum DAS exists. The optimum location is at the 60-, 45-, and 58-th floors for the general, constant-section, and constant-stress models, respectively. The optimum location is close to 2/3 of the height for the general and the constant-stress models and close to the middle of the height for the constant-section model.

Fig. 4

Relation between location of the outrigger and reduction ratio.

4 Optimum Location of Outriggers

4.1 Formulation of Optimum Problem

As demonstrated above, the DAS of a tall building can be controlled by changing the location and stiffness of the outrigger. The optimum locations of the outriggers can be determined using a mathematical optimization method. The optimization problem can be formulated in the following standard form:

$$\begin{array}{*{20}l}{{\text{Minimize}}} \quad g{\mathbf{(y)}} \\ {\text{subject \, to}}\quad {\mathbf{y}} \in {\mathbf{Z}^{n}} \qquad \qquad {\text{(I-NLP)}}\\ \qquad \qquad \quad y_{\bar{i}\, {\text{min}}} \le y_{\bar{i}\, {\text{max}}} \quad i = 1, \ldots, n\end{array}$$

(11)

where ${\mathbf{y}}$ is a vector of the integer variables and its element y_i represents the location of the i-th outrigger. n is the number of the outriggers. The integer design variable y_i should not be greater than the highest floor and not less than the lowest feasible floor, which are the 80-th and 4-th floor, respectively, in the analysis models. $g({\mathbf{y}})$ is the objective function representing the maximum value of DAS, as given in Eq. (12). The vertical displacements of the wall and column are calculated through a long-term analysis of the reinforced concrete structure.

$$\begin{aligned} g({\mathbf{y}}) &= \hbox{max} (\delta_{1} , \ldots ,\delta_{N} ) \\ & = \hbox{max} ((u_{1}^{wall} - u_{1}^{col} ), \ldots ,(u_{N}^{wall} - u_{N}^{col} ))\end{aligned}$$

(12)

where $N$ is the number of stories in the building. $\delta_{i}$ is the DAS at the i-th floor.$\,u_{i}^{wall}$ and $u_{i}^{col}$ are the vertical displacements of the wall and column at the i-th floor, respectively.

The problem given in Eq. (11) is an unconstrained nonlinear programming with integer variables (I-NLP, hereafter) and it cannot be directly solved by the gradient–based optimization methods, owing to the integrality requirement. In this study, a piecewise quadratic interpolation was applied to obtain the differentiable function $\bar{g}({\tilde{\mathbf{y}}})$. The integer nonlinear programming given in Eq. (11) can be substituted with the following nonlinear programming with the interpolated polynomial function with real variables (P-NLP, hereafter).

$$\begin{array}{*{20}l}{{\text{Minimize}}} \quad {\bar{g}}{( \tilde{\mathbf{y}} )} \\ {\text{subject \, to}}\quad \tilde{{\mathbf{y}}} \in {\mathbf{R}^{n}} \qquad \qquad {\text{(P-NLP)}}\\ \qquad \qquad \quad y_{\bar{i}\, {\text{min}}} \le {\tilde{y}}_{{i}} \le y_{\bar{i}\, {\text{max}}}\quad i = 1, \ldots, n\end{array}$$

(13)

$$y_{i} = \left\| {\tilde{y}_{i} } \right\| = round(\,\tilde{y}_{i} )$$

(14)

where ${\tilde{\mathbf{y}}}$ is the relaxed variable vector of ${\mathbf{y}}$ and $\tilde{y}_{i}$ is the relaxed variable of $y_{i}$. $y_{i}$ can be obtained by rounding $\tilde{y}_{i}$ to the nearest integer. $g({\mathbf{y}})$ is substituted with the interpolated function $\bar{g}({\tilde{\mathbf{y}}})$, as given in Eq. (15):

$$\bar{g}({\tilde{\mathbf{y}}}) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\bar{g}({\tilde{\mathbf{y}}}_{{\mathbf{i}}} )}$$

(15)

$$\begin{aligned} \bar{g}({\tilde{\mathbf{y}}}_{{\mathbf{i}}} ) = \,\frac{1}{2}g({\mathbf{y}} - {\hat{\mathbf{y}}}_{{\mathbf{i}}} )(\tilde{y}_{i} - y_{i} )(\tilde{y}_{i} - y_{i} - 1) \\ \quad -g({\mathbf{y}})(\tilde{y}_{i} - y_{i} + 1)(\tilde{y}_{i} - y_{i} - 1) \\ \quad +\frac{1}{2}g({\mathbf{y}} + {\hat{\mathbf{y}}}_{{\mathbf{i}}} )(\tilde{y}_{i} - y_{i} + 1)(\tilde{y}_{i} - y_{i} ) \\ \end{aligned}$$

(16)

where ${\tilde{\mathbf{y}}}_{{\mathbf{i}}}$ is the same vector as ${\mathbf{y}}$ except the i-th component, which is replaced with the relaxed variable $\tilde{y}_{i}$. $\bar{g}({\tilde{\mathbf{y}}}_{{\mathbf{i}}} )$ is the interpolated function by the Lagrange quadratic polynomial with successive three integers about the i-th variable. ${\hat{\mathbf{y}}}_{{\mathbf{i}}}$ is the unit vector of the i-th direction, such as $\left\{ {0,1,0,0} \right\}^{T}$ when $i = 2$ and $n = 4$.

Figure 5 shows the concept of the piecewise quadratic interpolation function with two integer variables, $y_{1}$ and $y_{2}$. As shown in Fig. 5 and Eqs. (15) and (16), $2n + 1$ times finite element analyses (FEA) are needed to evaluate $\bar{g}({\tilde{\mathbf{y}}})$ for every design state. However, the integer requirement in $g({\mathbf{y}})$ can be utilized to reduce the central processing unit (CPU) time by storing and reusing the function values in the optimization. It is worth noting that the interpolation function $\bar{g}({\tilde{\mathbf{y}}})$ is not a complete quadratic polynomial and the Hessian matrix of the function is a diagonal matrix; this is because the interpolation function used $2n + 1$ sampling points rather than $(n + 1)(n + 2)/2$, which is the required number of sampling points for the complete quadratic interpolation function. Because of the uncoupling between the design variables, the search method which requires a Hessian matrix should be avoided in the P-NLP. The steepest descent method with a quadratic line search (Parkinson et al. 2013), which requires only a gradient vector, was used in this study.

Fig. 5

Piecewise quadratic interpolation with two integer variables.

The gradient of $\bar{g}({\tilde{\mathbf{y}}})$ can be obtained as given in Eqs. (17) and (18).

$$\frac{{\partial \,\bar{g}({\tilde{\mathbf{y}}})}}{{\partial \,\tilde{y}_{i} }} = \frac{1}{n}\frac{{\partial \,\bar{g}({\tilde{\mathbf{y}}}_{{\mathbf{i}}} )}}{{\partial \,\tilde{y}_{i} }}$$

(17)

$$\begin{aligned} \frac{{\partial \,\bar{g}({\tilde{\mathbf{y}}}_{{\mathbf{i}}} )}}{{\partial \,\tilde{y}_{i} }} &= \,\frac{1}{2}g({\mathbf{y}} - {\hat{\mathbf{y}}}_{{\mathbf{i}}} )(2\tilde{y}_{i} - 2y_{i} - 1) \\ \,\,\,\,\,\,&\quad -g({\mathbf{y}})(2\tilde{y}_{i} - 2y_{i} ) \\ \,&\quad +\frac{1}{2}g({\mathbf{y}} + {\hat{\mathbf{y}}}_{{\mathbf{i}}} )(2\tilde{y}_{i} - 2y_{i} + 1) \\ \end{aligned}$$

(18)

The piecewise quadratic interpolation function given in Eq. (16) is differentiable but discontinuous at $y_{i} + 0.5$ owing to the rounding off of $\tilde{y}_{i}$ to the nearest integer $y_{i}$ or $y_{i} + 1$. Figure 6 shows the discontinuity of the piecewise quadratic interpolation function with one integer variable $y_{1}$. This discontinuity can be overcome in the P-NLP if the search algorithm has a condition for breaking the search iteration when $\bar{g}({\tilde{\mathbf{y}}})$ oscillates between the discontinuous points.

Fig. 6

Discontinuity in the piecewise quadratic interpolation with one variable.

When the line search terminates, the integer solution that was rounded from the P-NLP may not be the correct optimum solution because of the discontinuity, as shown in Fig. 6. In this study, the branch-and-test module (BT, hereafter) was added to find the correct optimum solution. The BT branches the two adjacent integer locations from the real number variables of the last P-NLP, and then tests the objective function to find the correct optimum locations. For the BT, the evaluation of the objective function needs to be performed $2^{n}$ times. However, the added burden for the BT is almost negligible because most of the $2^{n}$ branches have been tested and stored during the P-NLP.

4.2 Optimum Design Examples

The optimum locations of the outriggers to minimize the maximum value of the DAS in the three analysis models described in Sect. 3.1 were obtained by the proposed optimization method. The design variables for the optimum problem were the outrigger floors; therefore, the sectional areas of the outriggers were predetermined according to two schemes: divided-area and constant-area. The divided-area scheme divides the outrigger sectional area by the number of outriggers. For example, the sectional area of the horizontal members with one outrigger is 0.1256 m² and that with two outriggers is 0.0628 m², and so on. The total area of the outriggers does not change as the number of outriggers varies. In the constant-area scheme, the sectional area of the horizontal members does not change, regardless of the number of outriggers. Consequently, the total area of the outriggers proportionally increases as the number of outriggers increases. As mentioned above, the sectional area of the inclined members in the outrigger was proportioned to $\sqrt 2$ times that of the horizontal members.

The initial locations of the outriggers were the middle points, such as $y_{i} = \left\| {\,80 \times i/(n + 1)\,} \right\|$. Table 2 presents the objective function values, which are the maximum DAS, and the design variables, which are the optimum locations of the outriggers, for the three analysis models when the divided-area scheme was applied. The locations are given in integer numbers and the maximum DAS is given as a real number with five decimal places. The number in bracket refers to the reduction ratio $R_{d}$ given in Eq. (10), which is the ratio of the maximum DAS of the analysis model with outriggers to that of the model without outriggers. Table 3 presents the optimum locations of the outriggers and the maximum DAS for the three analysis models when the constant-area scheme is applied. It is noted that the optimum locations with two outriggers for both schemes are similar. However, the optimum locations with three and four outriggers for the constant-area scheme are slightly expanded outward than those for the divided-area scheme.

Table 2 Optimum locations and maximum DAS with the divided-area scheme.

Table 3 Optimum locations and maximum DAS with the constant-area scheme.

Figure 7 shows the DAS along the story of the general models with zero, one, two, and three outriggers. The colored arrows indicate the optimum locations with one, two, and three outriggers, respectively. Figure 7 indicates that the optimum locations of the outriggers are the locations that can push the peak DAS toward the left side. Moreover, it can be observed that as the number of outriggers increases, the maximum DAS decreases. However, the efficiency of the outriggers is significantly reduced when the number of outriggers is greater than 2.

Fig. 7

Optimum locations and DAS for the general model.

Figure 8 shows the maximum DAS according to the number of outriggers for the divided-area scheme and the constant-area scheme. It is noted that the maximum DAS is not significantly reduced when the number of the outriggers is greater than 2, even with the constant-area scheme, which linearly increases the total sectional area of the outriggers.

Fig. 8

Maximum differential axial shortenings according to number of outriggers.

The most time-consuming part of the proposed method is the finite element analysis (FEA) for column shortening; the number of analysis executions requested and performed during the optimization of the analysis models was thus investigated, as presented in Table 4. The number of analyses requested corresponds to the analyses looked up during the search for optimum solutions, while the number of analyses performed corresponds to the analyses actually executed. The number of analyses performed is much less than the number of analyses requested because the design variables are integer numbers and the maximum DAS and the design variables were stored and reused. Meanwhile, the locations of the outriggers before and after the BT are the same for all 24 cases; therefore, it can be concluded that the BT is not necessary.

Table 4 Number of FEA requested and performed for the divided-area scheme.

5 Conclusions

The differential axial shortenings (DAS) in a tall building should be considered in the design phase, and proper measures should be taken to reduce their unfavorable effects. In this study, outriggers, which have been designed to reduce the lateral displacements caused by wind and earthquake loads, were used to reduce DAS. The optimum locations of the outriggers to minimize the maximum DAS were determined by an optimization method. Since the floors where the outriggers were installed were given as integer numbers, a piecewise quadratic interpolation method was newly developed and applied to overcome the integrality requirement of the integer nonlinear programming. With the interpolated function, it was possible to carried out an unconstrained nonlinear optimization using the discrete analysis results from the finite element analysis of the axial shortening. A branch-and-test (BT) was added to complement the discontinuity of the piecewise quadratic interpolation. However, the solutions were not changed after the BT was used; therefore, it can be concluded that the BT is not required, and the piecewise quadratic interpolation method can be used for the integer nonlinear programming. The proposed optimization method stably yielded optimum solutions for a total of 24 cases that were examined with three analysis models, four outriggers, and two schemes for the sectional area of the outriggers. The optimum design results show that the optimum locations of the outriggers were the locations that can reduce the peak DAS. It was also noted that increasing the number of outriggers reduced the maximum DAS in the tall building. However, the maximum DAS was not significantly reduced when the number of the outriggers was greater than 2, even with the constant-area scheme, which linearly increased the total sectional area of the outriggers.

The proposed method can be effectively used in other structural engineering applications that involve finite element analysis. A further direction of this study is to improve the algorithm to accommodate multiple objectives, such as minimizing the lateral and the vertical displacements.