1 Introduction

Let H be a real Hilbert space with norm \(\Vert \cdot \Vert \) and C be a nonempty subset of H. A mapping \(T:C\rightarrow H\) is said to be L-Lipschitz if there exists \(L \geq 0\) such that

$$\begin{aligned} \Vert Tx-Ty \Vert \leq L\Vert x-y \Vert \quad \mbox{for all }x,y\in C. \end{aligned}$$
(1)

T is said to be contraction if \(L\in [0,1)\) and is called nonexpansive mapping if \(L=1\). We observe that every contraction mapping is nonexpansive and every nonexpansive mapping is Lipschitz.

A mapping \(T:C\rightarrow H\) is said to be k-strictly pseudocontractive if there exists \(k\in [0,1)\) such that

$$\begin{aligned} \Vert Tx-Ty \Vert ^{2}\leq \Vert x-y \Vert ^{2}+k \bigl\Vert x-y-(Tx-Ty) \bigr\Vert ^{2},\quad \forall x,y\in C. \end{aligned}$$
(2)

We remark that every k-strictly pseudocontractive mapping is Lipschitz and hence the class of k-strictly pseudocontractive mappings includes properly the class of nonexpansive mappings.

An important class of mappings more general than the class of k-strictly pseudocontractive mappings is the class of pseudocontractive mappings. T is said to be pseudocontractive if

$$\begin{aligned} \Vert Tx-Ty \Vert ^{2}\leq \Vert x-y \Vert ^{2}+ \bigl\Vert x-y-(Tx-Ty) \bigr\Vert ^{2}, \quad \forall x,y\in C. \end{aligned}$$
(3)

The class of pseudocontractive mappings is related to one of the important classes of operators known as monotone mappings. A mapping \(A:C\to {H}\) is said to be monotone if

$$\begin{aligned} \langle Ax-Ay, x-y\rangle \geq 0, \quad \forall x,y\in C. \end{aligned}$$

Note that a mapping \(A:C\to {H}\) is monotone if and only if \(T:=I-A\) is pseudocontractive, where I is an identity mapping on C. Thus, the zeros of A are fixed points of T, that is, \(N(A):=\{x\in C: Ax=0\}=F(T):=\{x\in C:x= Tx\}\).

Several authors have studied iterative methods for approximating fixed points of nonexpansive, k-strictly pseudocontractive and pseudocontractive mappings (see, e.g., [3, 6, 15, 17, 22, 27, 28] and the references contained therein). In 1953, Mann [15] introduced the following scheme, which is refereed to as Mann iteration method:

$$\begin{aligned} x_{n+1} =\alpha_{n} x_{n} + (1 - \alpha_{n}) Tx_{n}, \end{aligned}$$
(4)

where the initial guess \(x_{0}\in C\) is arbitrary and \(\{\alpha_{n}\} \subseteq [0,1]\) such that \(\lim_{n\to \infty }\alpha_{n}=0\) and \(\sum \alpha_{n}=\infty \). The Mann iteration method has been extensively investigated for approximating fixed points of nonexpansive mappings (see, e.g., [17]). In an infinite-dimensional Hilbert space, the Mann iteration method can provide only weak convergence (see, e.g., [7]). To obtain strong convergence, numerous authors have modified the Mann iterative method (see, e.g., [8, 10, 11]) in many ways.

In 1967, Halpern [8] studied the following recursive formula:

$$\begin{aligned} x_{n+1} =\alpha_{n}u + (1-\alpha_{n})Tx_{n},\quad n\geq 0, \end{aligned}$$
(5)

where \(\alpha_{n}\) is a sequence of numbers in \((0,1)\). He proved strong convergence of \(\{x_{n}\}\) to a fixed point of T, where \(\alpha _{n} := n^{-a}\), for \(a\in (0,1)\), in the framework of Hilbert spaces. Halpern’s scheme (5) has been studied extensively by many authors (see, e.g., [2, 12, 18, 21]). In particular, Reich [18] proved that the result of Halpern remains true in uniformly smooth Banach spaces (see also [19]).

In 1977, Lions [12] improved the result of Halpern, still in Hilbert spaces, by proving strong convergence of \(\{x_{n}\}\) to a fixed point of T, where the real sequence \(\{\alpha_{n}\}\) satisfies the following conditions:

$$\begin{aligned} \mbox{(i)} \quad \lim_{n\to \infty } \alpha_{n}=0;\qquad \mbox{(ii)} \quad \sum_{n=0}^{\infty } \alpha_{n}=\infty ;\qquad \mbox{(iii)}\quad \lim _{n\to \infty }\frac{\alpha_{n}-\alpha_{n-1}}{\alpha_{n}^{2}}=0. \end{aligned}$$

In 2002, Xu [24] (see also [25]) improved the result of Lion in two directions. First, he weakened the condition (iii) by removing the square in the denominator so that we can choose the sequence \(\alpha_{n}=\frac{1}{n+1}\). Second, he proved the strong convergence of Halpern’s scheme (5) in the framework of real uniformly smooth Banach spaces.

For approximating fixed points of a Lipschitz pseudocontractive self-mapping T, Ishikawa [9] introduced the following process known as Ishikawa iteration:

$$\begin{aligned} \textstyle\begin{cases} x_{0} \in C, \\ y_{n}=\beta_{n} x_{n}+(1-\beta_{n})Tx_{n}, \\ x_{n+1} =\alpha_{n} x_{n} + (1 -\alpha_{n}) Ty_{n}, \quad n\geq 0, \end{cases}\displaystyle \end{aligned}$$
(6)

where \(\{\alpha_{n}\}\), \(\{\beta_{n}\}\) are sequences of positive numbers satisfying the conditions:

  1. (i)

    \(0 \leq \alpha_{n}\leq \beta_{n}\leq 1\);

  2. (ii)

    \(\lim_{n\to \infty } \beta_{n} =0\);

  3. (iii)

    \(\sum \alpha_{n}\beta_{n}=\infty \).

He showed that the sequence \(\{x_{n}\}\) converges strongly to a fixed point of the mapping T, provided that C is a compact convex subset of a Hilbert space H. Several authors have extended the results of Ishikawa [9] to Banach spaces without compactness assumption on C (see, e.g., [13, 23]).

However, we observe that all the above results are valid only for self-mappings. For approximating fixed points of non-self mappings, several iterative schemes have been studied (see, e.g., [16, 20]) with the use of metric projection or sunny nonexpansive retraction mapping which are generally difficult to compute in practical applications.

In 2015, Colao and Marino [4] introduced a new searching strategy for the coefficient \(\alpha_{n}\) which makes the Mann algorithm well-defined for non-self mappings in the setting of a real Hilbert space H. In fact, they studied the following scheme:

$$\begin{aligned} \textstyle\begin{cases} x_{0}\in C, \\ \alpha_{0}=\max \{\frac{1}{2},h(x_{0})\}, \\ x_{n+1}=\alpha_{n} x_{n}+ (1-\alpha_{n})Tx_{n}, \\ \alpha_{n+1}=\max \{\alpha_{n},h(x_{n+1})\}, \quad n\geq 0, \end{cases}\displaystyle \end{aligned}$$
(7)

where \(h(x):=\inf \{\lambda \geq 0: \lambda x+(1-\lambda )Tx \in C\}, \forall x\in C\subseteq H\) and T is a non-self mapping of C into H. Indeed, they obtained weak and strong convergence of the algorithm to a fixed point of nonexpansive non-self mappings under appropriate conditions.

Recently, Colao et al. [5] extended this result of Colao and Marino [4] to a class of k-strictly pseudocontractive mappings. We observe that these results (the results obtained in [4] and [5]) provide a way forward to avoid the use of metric projection or sunny nonexpansive mapping in constructing algorithms for approximating fixed points of a more general class of non-self mappings.

It is our purpose in this paper to construct and study a Halpern–Ishikawa type iterative scheme for non-self mappings in the setting of Hilbert spaces. As a result, we obtain strong convergence of the scheme to a fixed point of a Lipschitz pseudocontractive non-self mapping under some mild conditions. Our results extend and generalize many results in the literature.

2 Preliminaries

Let C be a nonempty subset of a Hilbert space H. A mapping \(T:C\to H\) is said to be inward if, for any \(x\in C\), we have

$$ Tx\in I_{C}(x) := \bigl\{ x + \lambda (w-x): \mbox{ for some } w\in C \mbox{ and } \lambda \geq 1\bigr\} . $$

The set \(I_{C}(x)\) is called inward set of C at x. A mapping \(I -T\), where I is an identity mapping on C, is called demiclosed at zero if for any sequence \(\{x_{n}\}\) in C such that \(x_{n}\rightharpoonup x\) and \(Tx_{n}-x_{n}\to 0\) as \(n\to \infty \), then \(x=Tx\).

In what follows, we shall make use of the following lemmas.

Lemma 2.1

Let H be a real Hilbert space. Then, for any given \(x,y\in H\), the following inequality holds:

$$ \Vert x+y \Vert ^{2}\leq \Vert x \Vert ^{2}+2\langle y,x+y\rangle . $$

Lemma 2.2

([1])

Let C be a convex subset of a real Hilbert space H and let \(x\in H\). Then \(x_{0}=P_{C}x\) if and only if

$$ \langle z-x_{0}, x-x_{0}\rangle \leq 0, \quad \forall z\in C. $$

Lemma 2.3

([24])

Let \(\{a_{n}\}\) be a sequence of nonnegative real numbers satisfying the following relation:

$$ a_{n+1} \leq (1-\alpha_{n})a_{n} + \alpha_{n}\delta_{n} , \quad n\geq 0, $$

where \(\{\alpha_{n}\} \subset (0,1)\) and \(\{\delta_{n}\}\subset R\) satisfy the conditions \(\sum_{n=0}^{\infty } \alpha_{n}=\infty \) and \(\limsup_{n\to \infty }\delta_{n}\leq 0\). Then \(\lim_{n\to \infty }a_{n}=0\).

Lemma 2.4

([28])

Let C be a closed convex subset of a real Hilbert space H and \(T : C \to C \) be a continuous pseudo-contractive mapping. Then

  1. (i)

    \(F (T )\) is a closed convex subset of C;

  2. (ii)

    \(I -T\) is demiclosed at zero.

Lemma 2.5

([14])

Let \(\{a_{n}\}\) be sequence of real numbers such that there exists a subsequence \(\{n_{i}\}\) of \(\{n\}\) such that \(a_{n_{i}}< a_{{n_{i}}+1}\) for all \(i\in N\). Then there exists a nondecreasing sequence \(\{m_{k}\}\subset N\) such that \(m_{k}\to \infty \) and the following properties are satisfied by all (sufficiently large) numbers \(k\in N\):

$$ a_{m_{k}}\leq a_{{m_{k}}+1} \quad \textit{and} \quad a_{k}\leq a_{{m_{k}}+1}. $$

In fact, \(m_{k}=\max \{j\leq k:a_{j}< a_{j+1}\}\).

Lemma 2.6

([26])

Let H be a real Hilbert space. Then, for all \(x,y\in H\) and \(\alpha \in [0,1]\), the following equality holds:

$$ \bigl\Vert \alpha x +(1-\alpha )y \bigr\Vert ^{2}= \alpha \Vert x \Vert ^{2}+(1-\alpha )\Vert y \Vert ^{2}- \alpha (1- \alpha )\Vert x-y \Vert ^{2}. $$

Lemma 2.7

([4])

Let C be a nonempty, closed and convex subset of a real Hilbert space H and \(T:C\to H\) be a mapping. Define \(h:C\to \mathbb{R}\) by

$$ h(x)=\inf \bigl\lbrace \lambda \geq 0: \lambda x + (1-\lambda ) Tx\in C \bigr\rbrace . $$

Then, for any \(x\in C\), the following hold:

  1. (1)

    \(h(x)\in [0,1]\) and \(h(x)=0\) if and only if \(Tx\in C\);

  2. (2)

    if \(\beta \in [h(x), 1]\), then \(\beta x +(1-\beta ) Tx \in C\);

  3. (3)

    if T is inward, then \(h(x)<1\);

  4. (4)

    if \(Tx \notin C\), then \(h(x)x +(1-h(x))Tx\in \partial C\).

3 Results and discussion

Now, let C be a nonempty, closed and convex subset of a real Hilbert space H and let \(T:C\rightarrow H\) be an inward L-Lipschitz mapping. Let \(\beta \in (1-\frac{1}{1+\sqrt{L^{2}+1}},1 )\) and \(\{\alpha_{n}\}\subseteq (0,1)\) such that \(\lim_{n\to \infty } \alpha_{n}=0\) and \(\sum \alpha_{n}=\infty \). We define a Halpern–Ishikawa type iterative scheme as follows.

Choose \(u,x_{0}\in C\). Let

$$ h(x_{0}):=\inf \bigl\lbrace \lambda \geq 0: \lambda x_{0}+ (1-\lambda )Tx _{0}\in C \bigr\rbrace \quad \mbox{and}\quad \lambda_{0}\in \bigl[\max \bigl\{ \beta ,h(x_{0}) \bigr\} ,1\bigr). $$

Then by Lemma 2.7 it follows that \(y_{0}:=\lambda_{0} x_{0}+(1-\lambda_{0})Tx_{0}\in C\).

Let \(l(y_{0}):=\inf \lbrace \theta \geq 0: \theta x_{0} +(1-\theta )Ty _{0}\in C\rbrace \) and \(\theta_{0}\in [\max \{\lambda_{0},l(y_{0})\},1)\). Again by Lemma 2.7, \(\theta_{0} x_{0}+(1-\theta_{0})Ty_{0}\in C\), and hence it follows that

$$ x_{1}:=\alpha_{0} u+ (1-\alpha_{0}) \bigl( \theta_{0}x_{0}+(1-\theta_{0})Ty _{0} \bigr)\in C. $$

Thus, by mathematical induction, we have

$$\begin{aligned} \textstyle\begin{cases} \lambda_{n}\in [\max \{\beta , h(x_{n})\}, 1); \\ y_{n}=\lambda_{n}x_{n}+(1-\lambda_{n}) Tx_{n}; \\ \theta_{n}\in [\max \{\lambda_{n},l(y_{n})\},1); \\ x_{n+1}=\alpha_{n} u + (1-\alpha_{n}) (\theta_{n}x_{n}+(1-\theta _{n}) Ty_{n} ), \end{cases}\displaystyle \end{aligned}$$
(8)

where \(h(x_{n}):=\inf \{\lambda \geq 0: \lambda x_{n}+ (1-\lambda ) Tx _{n} \in C\}\) and \(l(y_{n}):=\inf \{\theta \geq 0: \theta x_{n}+ (1-\theta ) Ty_{n} \in C\}\).

Next, we prove the following theorem.

Theorem 3.1

Let C be a nonempty, closed and convex subset of a real Hilbert space H. Let \(T:C\to H\) be an L-Lipschitz pseudocontractive inward mapping with \(F(T)\neq\emptyset \). Let \(\{x_{n}\}\) be a sequence defined by (8). If there exists \(\epsilon >0\) such that \(\theta_{n}\leq 1-\epsilon\) \(\forall n\geq 0\), then \(\{x_{n}\}\) converges strongly to a fixed point of T nearest to u.

Proof

We make use of some ideas of the paper [27]. Let \(p\in F(T)\). Then from (8) and Lemma 2.6, we have

$$\begin{aligned} \Vert x_{n+1}-p \Vert ^{2} &=\bigl\Vert \alpha_{n} u + (1-\alpha_{n}) \bigl(\theta_{n}x_{n}+(1- \theta_{n})Ty_{n}\bigr)-p \bigr\Vert ^{2} \\ &\leq \alpha_{n}\Vert u-p \Vert ^{2}+ (1- \alpha_{n})\bigl\Vert \theta_{n}(x_{n}-p)+(1- \theta_{n}) (Ty_{n}-p) \bigr\Vert ^{2} \\ &\leq \alpha_{n}\Vert u-p \Vert ^{2}+ (1- \alpha_{n}) \bigl[\theta_{n}\Vert x_{n}-p \Vert ^{2}+(1- \theta_{n}) \Vert Ty_{n}-p \Vert ^{2} \bigr] \\ & \quad {} -(1-\alpha_{n})\theta_{n} (1-\theta_{n}) \Vert Ty_{n}-x_{n} \Vert ^{2}, \end{aligned}$$

and hence from (3) we obtain

$$\begin{aligned} \Vert x_{n+1}-p \Vert ^{2} &\leq \alpha_{n} \Vert u-p \Vert ^{2}+(1-\alpha_{n})\theta _{n} \Vert x_{n}-p \Vert ^{2} + (1-\alpha_{n}) (1- \theta_{n}) \\ & \quad {} \times \bigl[\Vert y_{n}-p \Vert ^{2}+\Vert y_{n}-Ty_{n} \Vert ^{2} \bigr]-(1-\alpha _{n})\theta_{n} (1- \theta_{n}) \Vert Ty_{n}-x_{n} \Vert ^{2} \\ &\leq \alpha_{n}\Vert u-p \Vert ^{2}+ (1- \alpha_{n}) (1-\theta_{n})\Vert y_{n}-p \Vert ^{2} \\ &\quad {} +(1-\alpha_{n}) (1-\theta_{n}) \Vert y_{n}-Ty_{n} \Vert ^{2} \\ & \quad {} +(1-\alpha_{n})\theta_{n} \bigl( \Vert x_{n}-p \Vert ^{2} -(1-\theta_{n}) \Vert Ty _{n}-x_{n} \Vert ^{2} \bigr). \end{aligned}$$
(9)

Moreover, from (8), Lemma 2.6, and (3), we have

$$\begin{aligned} \Vert y_{n}-p \Vert ^{2} =& \bigl\Vert \lambda_{n} (x_{n}-p)+(1-\lambda_{n}) (Tx_{n}-p) \bigr\Vert ^{2} \\ = & \lambda_{n} \Vert x_{n}-p \Vert ^{2}+(1- \lambda_{n})\Vert Tx_{n}-p \Vert ^{2} \\ &{} -\lambda_{n} (1-\lambda_{n} )\Vert x_{n}-Tx_{n} \Vert ^{2} \\ \leq & \lambda_{n}\Vert x_{n}-p \Vert ^{2}+(1-\lambda_{n}) \bigl[\Vert x_{n}-p \Vert ^{2}+ \Vert x_{n}-Tx_{n} \Vert ^{2} \bigr] \\ &{} -\lambda_{n} (1-\lambda_{n} )\Vert x_{n}-Tx_{n} \Vert ^{2} \\ = & \Vert x_{n}-p \Vert ^{2}+(1-\lambda_{n})^{2} \Vert x_{n}-Tx_{n} \Vert ^{2}. \end{aligned}$$
(10)

Furthermore, (8) and Lemma 2.6 imply that

$$\begin{aligned} \Vert y_{n}-Ty_{n} \Vert ^{2} &= \bigl\Vert \lambda_{n}(x_{n}-Ty_{n})+(1-\lambda_{n}) (Tx_{n}-Ty_{n}) \bigr\Vert ^{2} \\ &= \lambda_{n} \Vert x_{n}-Ty_{n} \Vert ^{2}+(1-\lambda_{n}) \Vert Tx_{n}-Ty_{n} \Vert ^{2} \\ & \quad {} -\lambda_{n} (1-\lambda_{n} )\Vert x_{n}-Tx_{n} \Vert ^{2} \\ &\leq \lambda_{n} \Vert x_{n}-Ty_{n} \Vert ^{2}+(1-\lambda_{n}) L^{2}\Vert x_{n}-y_{n} \Vert ^{2} \\ & \quad {} -\lambda_{n} (1-\lambda_{n} )\Vert x_{n}-Tx_{n} \Vert ^{2} \\ &= \lambda_{n} \Vert x_{n}-Ty_{n} \Vert ^{2}+(1-\lambda_{n})^{3}L^{2}\Vert x_{n}-Tx_{n} \Vert ^{2} \\ & \quad {} -\lambda_{n} (1-\lambda_{n} )\Vert x_{n}-Tx_{n} \Vert ^{2} \\ &= \lambda_{n}\Vert x_{n}-Ty_{n} \Vert ^{2} \\ & \quad {} -(1-\lambda_{n}) \bigl(\lambda_{n}-L^{2}(1- \lambda_{n})^{2} \bigr)\Vert x_{n}-Tx_{n} \Vert ^{2}. \end{aligned}$$
(11)

Substituting (10) and (11) into (9), we obtain

$$\begin{aligned} \Vert x_{n+1}-p \Vert ^{2} &\leq \alpha_{n}\Vert u-p \Vert ^{2}+ (1-\alpha_{n}) (1-\theta_{n}) \bigl(\Vert x_{n}-p \Vert ^{2} \\ &\quad {} +(1-\lambda_{n})^{2}\Vert x_{n}-Tx_{n}\Vert ^{2} \bigr) + (1-\alpha_{n}) (1-\theta_{n}) \bigl(\lambda_{n}\Vert x_{n}-Ty_{n}\Vert ^{2} \\ & \quad {} - (1-\lambda_{n}) \bigl(\lambda_{n}-L^{2}(1- \lambda_{n})^{2}\bigr)\Vert x_{n}-Tx_{n} \Vert ^{2} \bigr) \\ & \quad {} +(1-\alpha_{n})\theta_{n}\Vert x_{n}-p \Vert ^{2} -(1-\alpha_{n})\theta_{n} (1- \theta_{n}) \Vert Ty_{n}-x_{n} \Vert ^{2} \\ &= \alpha_{n}\Vert u-p \Vert ^{2}+ (1- \alpha_{n})\Vert x_{n}-p \Vert ^{2}- (1-\alpha _{n}) (1-\theta_{n}) (1-\lambda_{n}) \\ & \quad {} \times\bigl(1-\bigl(L^{2}(1-\lambda_{n})^{2}+2(1- \lambda_{n}) \bigr)\bigr)\Vert x_{n}-Tx_{n} \Vert ^{2} \\ & \quad {} +(1-\alpha_{n}) (1-\theta_{n}) (\lambda_{n}- \theta_{n})\Vert Ty_{n}-x_{n} \Vert ^{2}. \end{aligned}$$
(12)

Then since, from the hypothesis, we have

$$\begin{aligned} 1-2(1-\lambda_{n})-L^{2}(1-\lambda_{n})^{2} \geq 1-2(1-\beta )-L^{2}(1- \beta )^{2}>0, \end{aligned}$$
(13)

and

$$\begin{aligned} \theta_{n}\geq \lambda_{n}, \quad \mbox{for all }n\geq 0\mbox{,} \end{aligned}$$
(14)

inequality (12) implies that

$$\begin{aligned} \Vert x_{n+1}-p \Vert ^{2} \leq & \alpha_{n} \Vert u-p \Vert ^{2}+ (1-\alpha_{n})\Vert x_{n}-p \Vert ^{2}. \end{aligned}$$
(15)

Thus, by induction,

$$\begin{aligned} \Vert x_{n+1}-p \Vert ^{2} \leq &\max \bigl\{ \Vert u-p \Vert ^{2}, \Vert x_{0}-p \Vert ^{2} \bigr\} , \quad \forall n\geq 0, \end{aligned}$$

which provides that \(\{x_{n}\}\) and hence \(\{y_{n}\}\) are bounded.

Now, let \(x^{*}=P_{F(T)}(u)\). Then, using (8), Lemma 2.1, and following the methods used to get (12), we obtain

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} =& \bigl\Vert \alpha_{n} u+ (1-\alpha_{n}) \bigl( \theta_{n}x_{n}+(1-\theta_{n})Ty_{n} \bigr) -x^{*} \bigr\Vert ^{2} \\ = & \bigl\Vert \alpha_{n} \bigl(u-x^{*}\bigr) + (1- \alpha_{n}) \bigl[\theta_{n}x_{n}+ (1- \theta_{n})Ty_{n}-x^{*} \bigr] \bigr\Vert ^{2} \\ \leq & (1-\alpha_{n}) \bigl\Vert \theta_{n}x_{n} +(1-\theta_{n})Ty_{n} -x^{*} \bigr\Vert ^{2} +2\alpha_{n}\bigl\langle u- x^{*}, x_{n+1}-x^{*} \bigr\rangle \\ \leq & (1-\alpha_{n})\theta_{n}\bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+(1- \alpha_{n}) (1- \theta_{n}) \bigl\Vert Ty_{n}-x^{*} \bigr\Vert ^{2} \\ &{} -(1-\alpha_{n})\theta_{n}(1-\theta_{n})\Vert Ty_{n}-x_{n} \Vert ^{2} +2 \alpha_{n} \bigl\langle u- x^{*}, x_{n+1}-x^{*}\bigr\rangle , \end{aligned}$$

and

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \leq & (1-\alpha_{n})\theta_{n} \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2} \\ &{} +(1-\alpha_{n}) (1-\theta_{n}) \bigl[ \bigl\Vert y_{n}-x^{*} \bigr\Vert ^{2}+\Vert y_{n}-Ty_{n} \Vert ^{2} \bigr] \\ &{} -(1-\alpha_{n})\theta_{n}(1-\theta_{n})\Vert Ty_{n}-x_{n} \Vert ^{2}+2 \alpha_{n} \bigl\langle u-x^{*}, x_{n+1}-x^{*}\bigr\rangle \\ \leq &(1-\alpha_{n})\theta_{n} \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+ (1- \alpha_{n}) (1- \theta_{n}) \\ &{} \times \bigl[ \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+ (1-\lambda_{n})^{2}\Vert x_{n}-Tx_{n} \Vert ^{2} \bigr]+(1- \alpha_{n}) (1-\theta_{n}) \\ &{}\times \bigl[ \lambda_{n} \Vert x_{n}-Ty_{n} \Vert ^{2}-(1-\lambda_{n}) \bigl( \lambda_{n}-L^{2}(1- \lambda_{n})^{2}\bigr) \Vert x_{n}-Tx_{n} \Vert ^{2} \bigr] \\ & {} -(1-\alpha_{n})\theta_{n}(1-\theta_{n})\Vert Ty_{n}-x_{n} \Vert ^{2}+2\alpha _{n} \bigl\langle u-x^{*}, x_{n+1}-x^{*}\bigr\rangle , \end{aligned}$$

which implies that

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \leq & (1-\alpha_{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2} -(1- \alpha_{n}) (1-\theta_{n}) (1- \lambda_{n}) \\ &{} \times \bigl[ 1-L^{2}(1-\lambda_{n})^{2} -2(1- \lambda_{n})\bigr]\Vert x_{n}-Tx_{n} \Vert ^{2} \\ &{}+(1-\alpha_{n}) (1-\theta_{n}) ( \lambda_{n}- \theta_{n})\Vert x_{n}-Ty_{n} \Vert ^{2} \\ & {} +2\alpha_{n}\bigl\langle u-x^{*}, x_{n+1}-x^{*} \bigr\rangle \end{aligned}$$
(16)
$$\begin{aligned} \leq & (1-\alpha_{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2} +2\alpha_{n}\bigl\langle u-x ^{*}, x_{n}-x^{*}\bigr\rangle \\ &{} {}+2\alpha_{n}\bigl\Vert u-x^{*} \bigr\Vert \Vert x_{n+1}-x_{n} \Vert . \end{aligned}$$
(17)

Now, we consider two cases.

Case 1. Suppose that there exists \(n_{0}\in \mathbb{N}\) such that \(\{\Vert x_{n}-x^{*} \Vert \}\) is decreasing for all \(n\geq n_{0}\). Then it follows that \(\{\Vert x_{n}-x^{*} \Vert \}\) is convergent. Thus, from (16), (13), and (14), we have

$$\begin{aligned} x_{n}-Tx_{n}\to 0 \quad \mbox{as }n\to \infty. \end{aligned}$$
(18)

Moreover, from (8) and (18), we obtain

$$\begin{aligned} &\Vert y_{n}-x_{n} \Vert =(1-\lambda_{n}) \Vert x_{n}-Tx_{n} \Vert \to 0\quad \mbox{as }n\to \infty \mbox{, } \end{aligned}$$
(19)

and hence the Lipschitz continuity of T, (19), and (18) imply that

$$\begin{aligned} \Vert Ty_{n}-x_{n} \Vert \leq &\Vert Ty_{n}-Tx_{n} \Vert +\Vert Tx_{n}-x_{n} \Vert \\ \leq &L\Vert y_{n}-x_{n} \Vert +\Vert Tx_{n}-x_{n} \Vert \to 0 \quad \mbox{as }n\to \infty. \end{aligned}$$
(20)

In addition, from (3.1) and (18), we obtain

$$\begin{aligned} \Vert x_{n+1}-x_{n} \Vert \leq \alpha_{n}\Vert u-x_{n} \Vert +(1-\alpha_{n}) (1-\theta _{n}) \Vert Ty_{n}-x_{n} \Vert \to 0. \end{aligned}$$
(21)

Furthermore, since \(\{x_{n} \}\) is a bounded subset of H which is reflexive, we can choose a subsequence \(\{x_{n_{i}}\}\) of \(\{x_{n}\}\) such that

$$ x_{n_{i}}\rightharpoonup w \quad \mbox{and} \quad \limsup _{n\to \infty }\bigl\langle u-x^{*}, x_{n}-x^{*} \bigr\rangle = \lim_{i\to \infty }\bigl\langle u-x^{*},x_{n_{i}}-x^{*} \bigr\rangle . $$

Then from (18) and Lemma 2.4, we have \(w\in F(T)\). Therefore, by Lemma 2.2, we immediately obtain

$$\begin{aligned} \limsup_{n\to \infty }\bigl\langle u-x^{*},x_{n}-x^{*} \bigr\rangle =& \lim_{i\to \infty }\bigl\langle u-x^{*}, x_{n_{i}}-x^{*}\bigr\rangle \\ =&\bigl\langle u-x^{*}, w-x^{*}\bigr\rangle \leq 0. \end{aligned}$$
(22)

Then it follows from (17), (22), and Lemma 2.3 that \(\Vert x_{n}-x^{*} \Vert \to 0\) as \(n\to \infty \). Consequently, \(x_{n}\to x ^{*}=P_{F(T)}(u)\).

Case 2. Suppose that there exists a subsequence \(\{n_{i}\}\) of \(\{n\}\) such that

$$ \bigl\Vert x_{n_{i}}-x^{*} \bigr\Vert < \bigl\Vert x_{n_{i}+1}-x^{*} \bigr\Vert , \quad \forall i\in \mathbb{N}. $$

Then, by Lemma 2.5, there exists a nondecreasing sequence \(\{m_{k}\}\subset \mathbb{N}\) such that \(m_{k}\to \infty \) and

$$\begin{aligned} \bigl\Vert x_{m_{k}}-x^{*} \bigr\Vert \leq \bigl\Vert x_{m_{k}+1}-x^{*} \bigr\Vert \quad \mbox{and}\quad \bigl\Vert x_{k}-x^{*}\bigr\Vert \leq \bigl\Vert x_{m_{k}+1}-x^{*}\bigr\Vert , \end{aligned}$$
(23)

for all \(k\in N\). Now, from (16), (13), and (14), it follows that \(x_{m_{k}}-Tx_{m_{k}}\to 0\) as \(k\to \infty \). Thus, like in Case 1, we obtain

$$\begin{aligned} \limsup_{k\to \infty }\bigl\langle u-x^{*}, x_{m_{k}}-x^{*}\bigr\rangle \leq 0. \end{aligned}$$
(24)

Now, from (17), we have

$$\begin{aligned} \bigl\Vert x_{m_{k}+1}-x^{*} \bigr\Vert ^{2} \leq & (1-\alpha_{m_{k}})\bigl\Vert x_{m_{k}}-x^{*} \bigr\Vert ^{2}+ 2\alpha_{m_{k}}\bigl\langle u-x ^{*}, x_{m_{k}}-x^{*}\bigr\rangle \\ &{} + 2\alpha_{m_{k}}\bigl\Vert u-x^{*} \bigr\Vert \Vert x_{m_{k}+1}-x_{m_{k}} \Vert , \end{aligned}$$
(25)

and hence (23) and (25) imply that

$$\begin{aligned} \alpha_{m_{k}}\bigl\Vert x_{m_{k}}-x^{*} \bigr\Vert ^{2} \leq &\bigl\Vert x_{m_{k}}-x^{*} \bigr\Vert ^{2}-\bigl\Vert x_{{m_{k}}+1}-x^{*} \bigr\Vert ^{2} +2\alpha_{m_{k}}\bigl\langle u-x^{*}, x_{m_{k}}-x ^{*}\bigr\rangle \\ &{} +2\alpha_{m_{k}}\bigl\Vert u-x^{*} \bigr\Vert \Vert x_{m_{k}+1}-x_{m_{k}} \Vert \\ \leq & 2 \alpha_{m_{k}}\bigl\langle u-x^{*}, x_{m_{k}}-x^{*}\bigr\rangle + 2 \alpha_{m_{k}}\bigl\Vert u-x^{*} \bigr\Vert \Vert x_{m_{k}+1}-x_{m_{k}} \Vert . \end{aligned}$$

Thus, using (21), (24), and the fact that \(\alpha_{m _{k}}>0\), we obtain

$$\begin{aligned} \bigl\Vert x_{m_{k}}-x^{*} \bigr\Vert ^{2}\leq 0\quad \mbox{and hence} \quad \bigl\Vert x_{m_{k}}-x^{*} \bigr\Vert \to 0 \quad \mbox{as } k\to \infty . \end{aligned}$$

This together with (25) implies that \(\Vert x_{{m_{k}}+1}-x^{*} \Vert \to 0\) as \(k\to \infty \). But, since \(\Vert x_{k}-x^{*} \Vert \leq \Vert x_{{m_{k}}+1}-x^{*} \Vert \), for all \(k\in \mathbb{N}\), it follows that \(x_{k}\to x^{*}=P_{F(T)}(u)\). Therefore, from the above two cases, we can conclude that \(\{x_{n}\}\) converges strongly to the fixed point of T nearest to u. □

If, in Theorem 3.1, we assume that T is k-strictly pseudocontractive, then T is Lipschitz pseudocontractive with \(L=\frac{1+k}{k}\), and hence we get the following corollary.

Corollary 3.2

Let C be a nonempty, closed and convex subset of a real Hilbert space H. Let \(T:C\to H\) be a k-strictly pseudocontractive inward mapping with \(F(T)\neq\emptyset \). Let \(\beta \in (1-\frac{k}{k+\sqrt{(k+1)^{2}+k ^{2}}},1 )\) and \(\{\alpha_{n}\}\subseteq (0,1)\) such that \(\lim_{n\to \infty } \alpha_{n}=0\) and \(\sum \alpha_{n}=\infty \). Let a sequence \(\{x_{n}\}\) be generated from arbitrary \(x_{0},u\in C\) by

$$\begin{aligned} \textstyle\begin{cases} \lambda_{n}\in [\max \{\beta ,h(x_{n})\},1); \\ y_{n}=\lambda_{n}x_{n}+(1-\lambda_{n}) Tx_{n}; \\ \theta_{n}\in [\max \{\lambda_{n},l(y_{n})\},1); \\ x_{n+1}=\alpha_{n} u + (1-\alpha_{n}) (\theta_{n}x_{n}+(1-\theta _{n}) Ty_{n} ), \end{cases}\displaystyle \end{aligned}$$
(26)

where \(h(x_{n}):=\inf \{\lambda \geq 0: \lambda x_{n}+ (1-\lambda ) Tx _{n} \in C\}\) and \(l(y_{n}):=\inf \{\theta \geq 0: \theta x_{n}+ (1-\theta ) Ty_{n} \in C\}\).

If there exists \(\epsilon >0\) such that \(\theta_{n}\leq 1-\epsilon\) \(\forall n\geq 0\), then \(\{x_{n}\}\) converges strongly to a fixed point of T nearest to u.

If, in Theorem 3.1, we assume that T is nonexpansive, then we have that T is Lipschitz pseudocontractive with \(L=1\), and hence we get the following corollary.

Corollary 3.3

Let C be a nonempty, closed and convex subset of a real Hilbert space H, and let \(T:C\to H\) be a nonexpansive inward mapping with \(F(T)\neq\emptyset \). Let \(\beta \in (2-\sqrt{2},1)\) and \(\{\alpha_{n}\}\subseteq (0,1)\) such that \(\lim_{n\to \infty } \alpha_{n}=0\) and \(\sum \alpha_{n}=\infty \). Let a sequence \(\{x_{n}\}\) be generated from arbitrary \(x_{0},u\in C\) by

$$\begin{aligned} \textstyle\begin{cases} \lambda_{n}\in [\max \{\beta ,h(x_{n})\},1); \\ y_{n}=\lambda_{n}x_{n}+(1-\lambda_{n}) Tx_{n}; \\ \theta_{n}\in [\max \{\lambda_{n},l(y_{n})\},1); \\ x_{n+1}=\alpha_{n} u + (1-\alpha_{n}) (\theta_{n}x_{n}+(1-\theta _{n}) Ty_{n} ), \end{cases}\displaystyle \end{aligned}$$
(27)

where \(h(x_{n}):=\inf \{\lambda \geq 0: \lambda x_{n}+ (1-\lambda ) Tx _{n} \in C\}\) and \(l(y_{n}):=\inf \{\theta \geq 0: \theta x_{n}+ (1-\theta ) Ty_{n} \in C\}\).

If there exists \(\epsilon >0\) such that \(\theta_{n}\leq 1-\epsilon \) \(\forall n\geq 0\), then \(\{x_{n}\}\) converges strongly to a fixed point of T nearest to u.

We now state and prove a convergence result for a monotone mapping.

Corollary 3.4

Let C be a nonempty, closed and convex subset of a real Hilbert space H. Let \(A:C\to H\) be an L-Lipschitz monotone inward mapping with \(N(A)\neq\emptyset \). Let \(\beta \in (1-\frac{1}{1+ \sqrt{1+(1+L)^{2}}},1 )\) and \(\{\alpha_{n}\} \subset (0,1)\) such that \(\lim_{n\to \infty } \alpha_{n}=0\) and \(\sum \alpha_{n}=\infty \). Let a sequence \(\{x_{n}\}\) be generated from arbitrary \(x_{0},u\in C\) by

$$\begin{aligned} \textstyle\begin{cases} \lambda_{n}\in [\max \{\beta ,h(x_{n})\},1); \\ y_{n}=x_{n}-(1-\lambda_{n})Ax_{n}; \\ \theta_{n} \in [\max \{\lambda_{n},l(y_{n})\},1); \\ x_{n+1}=\alpha_{n} u + (1-\alpha_{n}) (\theta_{n}x_{n}+(1-\theta _{n}) (I-A)y_{n} ), \end{cases}\displaystyle \end{aligned}$$
(28)

where \(h(x_{n}):=\inf \{\lambda \geq 0: x_{n}-(1-\lambda )Ax_{n}\in C\}\) and \(l(y_{n}):=\inf \{\theta \geq 0: \theta x_{n}+ (1-\theta) (I-A)y_{n} \in C\}\).

If there exists \(\epsilon >0\) such that \(\theta_{n}\leq 1-\epsilon\) \(\forall n\geq 0\), then \(\{x_{n}\}\) converges strongly to the zero point of A nearest to u.

Proof

Let \(Tx:=(I-A)x\). Then T is a Lipschitz pseudocontractive mapping with Lipschitz constant \(L':=(1+L)\) and \(F(T)=N(A)\neq \emptyset \). Moreover, if A is replaced with \((I-T)\), then scheme (28) reduces to scheme (8), and hence the conclusion follows from Theorem 3.1. □

We observe that the method of proof of Theorem 3.1 provides the following result for approximating the minimum-norm point of fixed points of Lipschitz pseudocontractive non-self mappings.

Theorem 3.5

Let C be a nonempty, closed and convex subset of a real Hilbert space H containing 0, and let \(T:C\to H\) be an L-Lipschitz pseudocontractive inward mapping with \(F(T)\neq\emptyset \). Let \(\{x_{n}\}\) be a sequence defined by (8) with \(u=0\). If there exists \(\epsilon >0\) such that \(\theta_{n}\leq 1-\epsilon\) \(\forall n\geq 0\), then \(\{x_{n}\}\) converges strongly to the minimum-norm point \(x^{*}\) of \(F(T)\).

Remark 3.6

Note that, in the above results, the coefficients \(\lambda_{n}\) and \(\theta_{n}\) can be chosen simply as follows: \(\lambda_{n}=\max \{ \beta ,h(x_{n})\}\) and \(\theta_{n}=\max \{\lambda_{n},l(y_{n})\}\).

Remark 3.7

If, in all the above theorems and corollaries, the set \(F(T)\) is a subset of interior of C, then the assumption that there exists \(\epsilon >0\) such that \(\theta_{n}\leq 1-\epsilon \) \(\forall n\geq 0\) may not be required.

4 Numerical example

Now, we give an example of a nonlinear mapping which satisfies the conditions of Theorem 3.1.

Example 4.1

Let \(H=\mathbb{R}\) with Euclidean norm. Let \(C=[-1,1]\) and \(T:C\to \mathbb{R}\) be defined by

$$\begin{aligned} Tx= \textstyle\begin{cases} -3x,&x\in [-1,0], \\ x,&x\in (0, 1]. \end{cases}\displaystyle \end{aligned}$$
(29)

Then we observe that T satisfies the inward condition and \(F(T)=[0,1]\). One can also easily verify that

$$ \bigl\langle x-Tx-(y-Ty) , x-y\bigr\rangle \geq 0, \quad \forall x,y \in C. $$

Thus, \(I-T\) is monotone and hence T is a pseudocontractive mapping. To show that T is a Lipschitz mapping, we consider the following cases.

Case 1: Let \(x,y \in [-1,0]\). Then we have

$$\begin{aligned} \vert Tx-Ty \vert =\vert {-}3x+3y \vert =3\vert x-y \vert . \end{aligned}$$

Case 2: Let \(x,y \in (0,1]\). Then we have

$$\begin{aligned} \vert Tx-Ty \vert =\vert x-y \vert . \end{aligned}$$

Case 3: Let \(x\in [-1,0]\) and \(y\in (0,1]\). Then we have

$$\begin{aligned} \vert Tx-Ty \vert =&\vert {-}3x-y \vert \\ =& \vert 3x+y \vert \\ =& \vert x-y+2x+2y \vert \\ \leq & \vert x-y \vert +2\vert x+y \vert \\ \leq & \vert x-y \vert +2\vert x-y \vert \\ =&3\vert x-y \vert . \end{aligned}$$

From the above cases, it follows that T is L-Lipschitz with \(L=3\).

Now, let \(\beta =\frac{5}{6}, u=\frac{1}{2}, x_{0}=-1\), and \(\alpha_{n}=\frac{2}{n+5}\). Then \(Tx_{0}=3\) and

$$\begin{aligned} h(x_{0}) =&\inf \bigl\{ \lambda \geq 0: \lambda x_{0}+(1- \lambda )Tx_{0} \in C\bigr\} \\ =& \inf \bigl\{ \lambda \geq 0: - \lambda +3(1-\lambda )\in C \bigr\} \\ =& \frac{1}{2}. \end{aligned}$$

Now, let \(\lambda_{0}=\frac{5}{6}\). Then \(y_{0}=\lambda_{0} x_{0}+(1- \lambda_{0})Tx_{0}=-\frac{1}{3}\) and \(Ty_{0}=1\), which gives

$$ l(x_{0})=\inf \bigl\{ \theta \geq 0: \theta x_{0}+(1-\theta )Ty_{0}\in C\bigr\} =0. $$

If we choose \(\theta_{0}=\frac{5}{6}\), then we have

$$ x_{1}=\alpha_{0} u+(1-\alpha_{0})\bigl[ \theta_{0}x_{0}+(1-\theta_{0})Ty _{0} \bigr]=-\frac{1}{5}. $$

Thus, \(Tx_{1}=\frac{3}{5}\), which implies that \(h(x_{1})=0\). Now, if we choose \(\lambda_{1}=\frac{5}{6}\), then we obtain

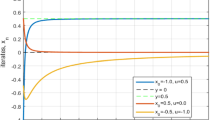
$$ y_{1}=\lambda_{1}x_{1}+(1-\lambda_{1})Tx_{1}=- \frac{1}{15}, \qquad Ty_{1}= \frac{1}{5} \quad \mbox{and}\quad l(y_{1})=0. $$

Again, we can choose \(\theta_{1}=\frac{5}{6}\), which yields \(x_{2}=0.0778\). In general, we observe that for \(u=0.5, x_{0}=-1\) and \(\alpha_{n}=\frac{2}{n+5}\), we can choose \(\lambda_{n}=\theta_{n}= \frac{5}{6}\). Thus, all the conditions of Theorem 3.1 are satisfied and \(x_{n}\) converges to \(0.5=P_{F(T)}u\) (see Fig. 1).

Figure 1
figure 1

Convergence of \(x_{n}\) with different values of \(x_{0}\) and u

Full size image

On the other hand, for \(u=-0.8, x_{0}=1\), and \(\alpha_{n}= \frac{2}{n+5}\), we obtain that \(x_{n}\) converges to \(0.0=P_{F(T)}u\). Figure 1 is obtained using MATLAB version 7.5.0.342(R2007b).

5 Conclusion

In this paper, we have constructed and studied a Halpern–Ishikawa type iterative scheme for non-self mappings in the setting of Hilbert spaces. As a result, we obtained strong convergence of the scheme to a fixed point of a Lipschitz pseudocontractive non-self mapping under some mild conditions. In addition, we provided a numerical example to support our results. Our study can open the door for further research activity in the field for a more general class of mappings in Hilbert and/or Banach spaces more general than Hilbert spaces. Our results extend and generalize many results in the literature. More particularly, Theorem 3.1 extends Theorem 8 of Colao et al. [5] in the sense that it provides a convergent scheme for approximating fixed points of Lipschitz pseudocontractive non-self mappings more general than that of k-strictly pseudocontractive non-self mappings.