1 Introduction

Fall armyworm (FAW), Spodoptera frugiperda, a highly destructive and fast spreading agricultural pest native to North and South America, poses a real threat to global food security. Spodoptera frugiperda remains an important pest of members of family Poaceace including major food crops such as corn, sorghum, rice wheat, maize, and diverse pasture [1]. According to FAO [2], food security is defined as a “situation that exists when all people, at all times, have physical, social, and economic access to sufficient, safe, and nutritious food that meets their dietary needs and food preferences for an active and healthy life” [2]. In recent years, the FAW has spread globally and emerged in countries where it had rarely or never before been presented, posing a real threat to global food security [3, 4]. Prior studies suggest that FAW pest is native to and widely distributed in the tropical and subtropical regions of America [1], and its invasion into Africa was reported for the first time in January 2016 [1]. Since then, it has become an epidemic pest in and beyond several African countries [1, 3–5]. FAW is regarded to be a major pest of maize biomass and other crops, such as rice, millet, sorghum, and cotton [5]. Due to the importance of maize biomass in many countries, there is a need to explore the implications of FAW outbreak in a field of maize biomass to increase the harvest of this crop.

Mathematical modeling has become a tool used to explore many real-world phenomena. Ordinary differential equations (ODEs) and partial differential equations (PDEs) with and without memory effects are some of the tools that have been commonly used to formulate equation(s) that mirror the real-world problem(s) [6–12]. In recent years a number of mathematical models were developed to explore plant–pest interaction [11–19]. Tang et al. [17] proposed impulsive differential equation models or hybrid dynamical system to model the introduction of a periodic IPM strategy, which includes periodic spraying of pesticide and release of natural enemies at critical time [14–17]. On the other hand, Tang et al. [17] developed an impulsive pest-natural enemy model, in which pulsing actions such as spraying pesticide and releasing natural enemies were considered with the assumption that the pesticide kills a pest instantly, whereas Chowdhury [18] formulated and extensively investigated continuous and discrete predator–prey models concerning IPM strategy. Discrete host parasitoid models were also proposed in circumstances where the timing of pesticide application leads to the death of parasitoid, and four different cases involving the timing of applications were investigated [11, 18].

The aforementioned studies and several other cited therein have certainly produced many useful results and improved the existing knowledge on plant–pest interaction. However, one of the limitations of these studies is that their models were based on integer-order ordinary differential equations. Recent studies suggest that models that use integer-order differential equations do not adequately capture memory effects and hereditary properties, which are inherent in many real-world problems [20]. As such, in recent years, fractional calculus has become an intriguing field. Several researchers have shown that models that utilize fractional calculus are more likely to replicate real-world problems compared those that use integer-order differential equations since fractional-order differential equations are able to capture memory effects [20, 21].

Therefore the present work aims to utilize fractional calculus to explore the implications of FAW infestation in a field planted with initial number of maize biomass at time \(t=0\) and obtaining maximum harvest of the biomass at the end of the season. The proposed model incorporates all the relevant biological information. In particular, the FAW population has been subdivided into egg population, larvae population, pupae population, and the adult population, also known as moth. Although the FAW has six larval instar stages, we have considered this as a single group to reduce complexity of the model. The proposed model also incorporates the use of nonbiological control methods such as use of pesticides and commonly known traditional methods such as hand picking of caterpillars. The role of biological control on FAW dynamics was comprehensively explored in [12], and hence we did not consider this aspect. At larval stage cannibalism is known to occur in FAW dynamics, and we also incorporate this aspect. We support qualitative and quantitative analytical results obtained in this study by numerical illustration.

We organize the paper as follows. In Sect. 2, we give some necessary definitions and some known properties of fractional calculus. In Sect. 3, we propose a fractional-order model for fall armyworm and maize biomass interaction. We investigate the local and global stability of the model equilibria. To support analytical findings, we carry out numerical simulation and present their results in Sect. 4. In the last section, we present the conclusions of this paper.

2 Preliminaries on the Caputo fractional calculus

We begin by introducing the definition of Caputo fractional derivative and state related theorems (see [22–24]), which we will utilize to derive important results in this work.

Definition 2.1

([22–24])

Suppose that \(q, a,t\in \mathbb{R}\), \(q>0, t>a\). The Caputo fractional derivative is given by

$$\begin{aligned} ^{c}_{a}D^{q}_{t}f(t)=\frac{1}{\Gamma (n-q)} \int ^{t}_{a} \frac{f^{n}(\xi )}{(t-\xi )^{q+1-n}}\,d\xi ,\quad n-1< q,n\in \mathbb{N}, \end{aligned}$$

where Γ is the gamma function.

Definition 2.2

([22, 24])

The Riemann–Liouville fractional integral of arbitrary real order \(q>0\) of a function \(f(t)\) is defined by the integral

$$\begin{aligned} J^{q}f(t)=\frac{1}{\Gamma (q)} \int ^{t}_{0}(t-\xi )^{q-1}f(\xi )\,d\xi , \end{aligned}$$

and \(J^{0}f(t)=f(t)\).

Definition 2.3

([25])

Let \(q>0\), \(n-1< q< n\), \(n\in \mathbb{N}\). Suppose that \(f(t), f^{\prime }(t),\ldots,f^{(n-1)}(t)\) are continuous on \([t_{0},\infty )\) and have the exponential order and that \({}^{c}_{t_{0}}D^{q}_{t}f(t)\) is piecewise continuous on \([t_{0},\infty )\). Then

$$\begin{aligned} {\mathcal{L}}\bigl\{ ^{c}_{t_{0}}D^{q}_{t}f(t) \bigr\} = s^{q} {\mathcal{F}} (s)-\sum^{n-1}_{k=0} s^{q-k-1} f^{(k)}(t_{0}), \end{aligned}$$

where \({\mathcal{F}} (s)= {\mathcal{L}}\{f(t)\}\).

Lemma 2.1

([26])

Let \(x(\cdot )\) be a continuous and differentiable function with \(x(t) \in \mathbb{R}_{+}\). Then, for any time instant \(t\geq t_{0}\), we have

$$\begin{aligned} ^{c}_{t_{0}}D^{q}_{t} \biggl(x(t)-x^{*}-x^{*} \ln \frac{x(t)}{x^{*}} \biggr)\leq \biggl(1-\frac{x^{*}}{x(t)} \biggr) {}^{c}_{t_{0}}D^{q}_{t}x(t),\quad x^{*}\in \mathbb{R}^{+}, \forall q\in (0,1). \end{aligned}$$

3 Model formulation and analysis

3.1 Model formulation

A fractional-order model we introduce consists of two populations, maize biomass and the FAW population, where one of the populations is a stage-structured giving a total of five populations. Meanwhile, the FAW population is divided into four classes, which represent the FAW life cycle and are the egg stage \(E(t)\), Larvae \(L(t)\), pupal \(P(t)\), and the adult stage (Moth) \(A(t)\). Although the FAW typically has six larval instars, to reduce complexity of the model in a biological sensible way, all larval instars are represented by class \(L(t)\). The life cycle of FAW starts when eggs are laid in masses on maize biomass, mostly underside of these biomass. The following equation describes the FAW egg population dynamics:

$$\begin{aligned} ^{c}_{a}D^{q}_{t} E(t)=b^{q} \biggl(1-\frac{E}{K_{E}^{q}} \biggr)WA-\bigl( \alpha ^{q}_{E}+u^{q}_{E}+ \mu _{E}^{q}\bigr)E, \end{aligned}$$

where b represents the egg laying rate for an adult female FAW, that is, an average number of eggs each female adult FAW will lay per day, \(K_{E}\) represents the egg carrying capacity, that is, the availability of space to lay eggs, W is the proportion of adult FAW that are females, \(\alpha _{E}\) is the egg hatching rate, and \(u_{E}\) accounts for the effects of intervention strategies a farmer will implement once they observe eggs laid on the maize biomass, \(\mu _{E}\) is the egg mortality rate. FAW larvae generally emerge simultaneously three to five days following oviposition. The following equation summarizes the population dynamics of the larvae stage:

$$\begin{aligned} ^{c}_{a}D^{q}_{t} L(t)=\alpha ^{q}_{E} \biggl(1-\frac{L}{K^{q}_{L}} \biggr)E+\theta ^{q} LM-\bigl(\alpha ^{q}_{L}+u^{q}_{L}+ \mu ^{q}_{L}\bigr)L, \end{aligned}$$

where the transition rate from the egg stage to larvae is \(\alpha _{E}\). Prior studies [3, 27] suggest that whenever the food is limited, the older larvae of FAW exhibit a cannibalistic behavior on the smaller larvae. Hence to account for this aspect, we assume that the death rate due to lack of food is proportional to the smaller larvae \(\alpha _{E}E\) and to the coefficient \(L/K_{L}\) that represent the availability of food for each larvae. Therefore \(K_{L}\) models the availability of food and space for the larvae population, \(\mu _{L}\) represents the natural mortality rate of the larvae, and \(1/\alpha _{L}\) is the average duration of the larvae stage, which is estimated to the of 14–30 days [3, 28, 29]. In particular, it is estimated that this duration is shorter, around 14 days during warm summer months and longer, and around 30 days during cooler weather [28, 29]. The parameter \(u_{L}\) models the role of intervention strategies implemented by the farmer, which may be use of pesticides or handpicking of the larvae. The term \(\theta ^{q} LM\) represents the interaction of larvae and maize biomass, which results in conversion of maize biomass into larvae biomass. Hence we can write \(\theta ^{q}=e^{q}\beta ^{q}\), where the parameter e represents the efficiency with which caterpillar (FAW larvae) convert consumed maize biomass.

Pupation of the FAW normally occurs in the soil at a depth of 2–8 cm [29]. Here the larva constructs a loose cocoon, oval in shape and 20–30 mm in length, through tying together particles of soil with silk [3]. In areas where the soil is too hard, larvae web together leaf debris and other material to form a cocoon on the soil surface [3]. The following equation represents the dynamics of pupae stage:

$$\begin{aligned} ^{c}_{a}D^{q}_{t} P(t)=\alpha ^{q}_{L}L-\bigl(\mu ^{q}_{P}+\alpha ^{q}_{p}+u^{q}_{P}\bigr)P, \end{aligned}$$

where \(\mu _{P}\) is the natural mortality rate, \(1/\alpha _{P}\) represents the duration of the pupae stage, which is approximately 8–9 days during the summer; however, during winter it may reach 20–30 days [3, 28]. It is worth noting that the pupal stage of FAW does not enter a diapause period to withstand protracted periods winter or summer seasons in the absence of the host plant biomass [3, 30]. The effects of intervention strategies on reducing the population of the pupae is modeled by \(u_{P}\). Adult FAW are 20–25-mm long with a wingspan of approximately 30–40 mm. Female and male adult FAW have different color pattern on their forewing. Adult female FAW are responsible for laying eggs on the surface of maize biomass, and this process usually starts after a preoviposition period of 3–4 days and continues until they become 3-week old. The following equation summarizes the population dynamics of the adult FAW:

$$\begin{aligned} ^{c}_{a}D^{q}_{t} A(t)=\alpha ^{q}_{P} P-\bigl(\mu ^{q}_{A}+u^{q}_{A} \bigr)A, \end{aligned}$$

where \(\alpha _{P}\) accounts for the proportion of FAW pupa population that successfully progresses to the adult stage, \(u_{A}\) denotes the effects of intervention strategies, and \(1/\mu _{A}\) is the life span, which is estimated to average about 10 days, with a range of about 7–21 days [3]. It is worth noting that the duration of the life cycle for FAW lasts for about 30 days at 28∘C and may take longer, 60–90 days, when the weather is cooler [28]. In addition, under favorable conditions, the FAW larvae have a potential to feed and breed on maize biomass year-round [28].

Plant biomass (plant seeds) planted at time \(t=0\) emerges in a period of 0 to 7 days. We assume that planting of maize seed per hectare at the beginning of the season is done in a day. In this regard, we let \(M(t)\) represent the population density of maize biomass per hectare Therefore the population dynamics of the maize biomass is governed by the equation

$$\begin{aligned} ^{c}_{a}D^{q}_{t} M(t)=r^{q} M \biggl(1-\frac{M}{K^{q}_{M}} \biggr)- \beta ^{q} LM, \end{aligned}$$

where r is the growth rate of maize biomass, \(K_{M}\) is the maximum biomass of maize plants, and β is rate at which larvae (FAW larva) attacks the biomass of the maize plants.

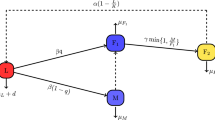
Our assumptions on the dynamics of fall armyworm in a maize biomass population density are demonstrated in Fig. 1, and equations are presented in the system

$$ \left . \textstyle\begin{array}{l} ^{c}_{a}D^{q}_{t} M(t)=r^{q} M (1-\frac{M}{K^{q}_{M}} )- \beta ^{q} LM, \\ {}^{c}_{a}D^{q}_{t} E(t)=b^{q} (1-\frac{E}{K_{E}^{q}} )WA-( \alpha ^{q}_{E}+u^{q}_{E}+\mu _{E}^{q})E, \\ {}^{c}_{a}D^{q}_{t} L(t)=\alpha ^{q}_{E} (1-\frac{L}{K^{q}_{L}} )E+\theta ^{q} LM-(\alpha ^{q}_{L}+u^{q}_{L}+\mu ^{q}_{L})L, \\ {}^{c}_{a}D^{q}_{t} P(t)=\alpha ^{q}_{L}L-(\mu ^{q}_{P}+\alpha ^{q}_{p}+u^{q}_{P})P, \\ {}^{c}_{a}D^{q}_{t} A(t)=\alpha ^{q}_{P} P-(\mu ^{q}_{A}+u^{q}_{A})A. \end{array}\displaystyle \right \} $$
(1)
Figure 1
figure 1

Model flow diagram illustrating the dynamics of fall armyworm in a field of maize biomass. The fall armyworm life cycle is divided into four classes: the egg stage \(E(t)\), Larvae \(L(t)\), pupal \(P(t)\), and the adult stage (Moth) \(A(t)\). The compartment \(M(t)\) represents maize plant population. The dotted line demonstrates that fall armyworm larvae are responsible for attacking the maize plant

Full size image

3.2 Positivity and boundedness of solutions to model (1)

Theorem 3.1

There exists a unique solution for the fractional-order model (1) in \((0,\infty )\). Moreover, the solution is nonnegative for all \(t>0\) and remains in \(\mathbb{R}^{5}_{+}\).

Proof

We begin by demonstrating that \(\mathbb{R}^{5}_{+}=\{(M,E,L,P,A)\in \mathbb{R}^{5}_{+}:M\geq 0, E \geq 0,L\geq 0,P\geq 0,A\geq 0\}\) is positively invariant. For that, we have to demonstrate that on each hyperplane bounding the nonnegative orthant the vector field points to \(\mathbb{R}^{5}_{+}\). Let us consider the following cases.

Case 1. Assume that the exists \(t_{*}>t_{0}\) such that \(M(t_{*})=0\) and \(M(t)<0\) for \(t\in (t_{*},t_{1}]\), where \(t_{1}\) is sufficiently close to \(t_{*}\). If \(M(t_{*})=0\), then

$$\begin{aligned} {}^{c}_{t_{0}}D^{q}M(t_{*})=0. \end{aligned}$$

Therefore \({}^{c}_{t_{0}}D^{q}M(t)\geq 0\) for all \(t\in [t_{*},t_{1}]\).

Case 2. Assume that the exists \(t_{*}>t_{0}\) such that \(E(t_{*})=0\) and \(E(t)<0\) for \(t\in (t_{*},t_{1}]\), where \(t_{1}\) is sufficiently close to \(t_{*}\). If \(E(t_{*})=0\), then

$$\begin{aligned} ^{c}_{t_{0}}D^{q}E(t_{*})=b^{q}WA>0. \end{aligned}$$

Therefore \({}^{c}_{t_{0}}D^{q}E(t)>0\) for all \(t\in [t_{*},t_{1}]\).

Case 3. Assume that the exists \(t_{*}>t_{0}\) such that \(L(t_{*})=0\) and \(L(t)<0\) for \(t\in (t_{*},t_{1}]\), where \(t_{1}\) is sufficiently close to \(t_{*}\). If \(L(t_{*})=0\), then

$$\begin{aligned} ^{c}_{t_{0}}D^{q}L(t_{*})=\alpha ^{q}_{E} E>0. \end{aligned}$$

From the last two equations of system (1) we can easily verify that

$$ \left . \textstyle\begin{array}{l} {}^{c}_{t_{0}}D^{q}P(t)=\alpha ^{q}_{L}L>0, \\ {}^{c}_{t_{0}}D^{q}A(t)=\alpha ^{q}_{P}P>0. \end{array}\displaystyle \right \} $$

From the discussion above we observe that each hyperplane bounding the nonnegative orthant, the vector field points to \(\mathbb{R}^{5}_{+}\), that is, all solutions of system (1), remains nonnegative for all \(t\geq 0\). □

Theorem 3.2

Let \({\mathcal{X}}(t)=(E(t),L(t), P(t), A(t))\) be a unique solution of the model (1) for \(t\geq 0\). Then the solution \({\mathcal{X}}(t)\) is bounded above, that is, \({\mathcal{X}}(t)\in \Omega \), where Ω denotes the feasible region given by

$$ \Omega =\left \{ \textstyle\begin{array}{ll} (E(t),L(t),P(t),A(t) )\left| \textstyle\begin{array}{l} {}0\leq E(t)\leq K_{E} \\ {}0\leq L(t)\leq C_{L} \\ {}0\leq P(t)\leq C_{P} \\ {}0\leq A(t)\leq C_{A} \end{array}\displaystyle \right. \end{array}\displaystyle \right \} . $$

Proof

Here we will now demonstrate that the solutions of system (1) are bounded for all \(t\geq 0\). For biological relevance, the least possible lower bound for each of the variables in system (1) is zero. Based on this, our discussion will be on determining the upper bound for these variables. Moreover, we can easily establish that the following conditions should hold: \(0\leq M(t)\leq K_{M}\) and \(0\leq E(t)\leq K_{E}\). For instance, we have

$$\begin{aligned} ^{c}_{a}D^{q}_{t} M(t)&=r^{q} M \biggl(1-\frac{M}{K^{q}_{M}} \biggr)- \beta ^{q} LM \\ &\leq r^{q} M \biggl(1-\frac{M}{K^{q}_{M}} \biggr). \end{aligned}$$

Therefore it follows that \(\limsup_{t\rightarrow \infty }M(t)\leq K_{M}\). Based on these bounds, we have

$$\begin{aligned} ^{c}_{a}D^{q}_{t} L(t) &=\alpha ^{q}_{E} \biggl(1-\frac{L}{K^{q}_{L}} \biggr)E+\theta ^{q} LM-\bigl(\alpha ^{q}_{L}+u^{q}_{L}+ \mu ^{q}_{L}\bigr)L \\ &\leq \alpha ^{q}_{E} K^{q}_{E} - \biggl[ \biggl(\alpha ^{q}_{L}+u^{q}_{L}+ \mu ^{q}_{L}+\frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} \biggr)- \theta ^{q} K^{q}_{M} \biggr]L. \end{aligned}$$

Applying the Laplace transform leads to

$$\begin{aligned} s^{q}{\mathcal{L}} \bigl[L(t)\bigr]-s^{{q}-1} L(0)\leq \frac{\alpha ^{q}_{E} K^{q}_{E}}{s}- \biggl[ \biggl(\alpha ^{q}_{L}+u^{q}_{L}+ \mu ^{q}_{L}+\frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} \biggr)- \theta ^{q} K^{q}_{M} \biggr]{\mathcal{L}}\bigl[L(t) \bigr]. \end{aligned}$$

Grouping like terms, we get

$$\begin{aligned} {\mathcal{L}}\bigl(L(t)\bigr)\leq{} &\frac{ \alpha ^{q}_{E} K^{q}_{E} s^{-1}}{s^{q}+ [ (\alpha ^{q}_{L}+u^{q}_{L}+\mu ^{q}_{L}+\frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} )-\theta ^{q} K^{q}_{M} ]} \\ &{}+ \frac{s^{q-1} L(0)}{s^{q}+ [ (\alpha ^{q}_{L}+u^{q}_{L}+\mu ^{q}_{L}+\frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} )-\theta ^{q} K^{q}_{M} ]} \\ ={}&\frac{\alpha ^{q}_{E} K^{q}_{E} s^{q-(1+q)}}{s^{q}+ [ (\alpha ^{q}_{L}+u^{q}_{L}+\mu ^{q}_{L}+\frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} )-\theta ^{q} K^{q}_{M} ]} \\ &{}+ \frac{s^{q-1}L(0}{s^{q}+ [ (\alpha ^{q}_{L}+u^{q}_{L}+\mu ^{q}_{L}+\frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} )-\theta ^{q} K^{q}_{M} ]}. \end{aligned}$$

Applying the inverse Laplace transform leads to

$$\begin{aligned} L(t)\leq{} &{\mathcal{L}}^{-1} \biggl\{ \frac{\alpha ^{q}_{E} K^{q}_{E} s^{q-(1+q)}}{s^{q}+ [ (\alpha ^{q}_{L}+u^{q}_{L}+\mu ^{q}_{L}+\frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} )-\theta ^{q} K^{q}_{M} ]} \biggr\} \\ &{}+ {\mathcal{L}}^{-1} \biggl\{ \frac{s^{q-1}L(0}{s^{q}+ [ (\alpha ^{q}_{L}+u^{q}_{L}+\mu ^{q}_{L}+\frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} )-\theta ^{q} K^{q}_{M} ]} \biggr\} \\ \leq{} &\alpha ^{q}_{E} K^{q}_{E} t^{q} E_{q,q+1} \biggl(- \biggl[ \biggl( \alpha ^{q}_{L}+u^{q}_{L}+\mu ^{q}_{L}+ \frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} \biggr)-\theta ^{q} K^{q}_{M} \biggr] t^{q} \biggr) \\ &{}+ L(0)E_{q,1} \biggl(- \biggl[ \biggl(\alpha ^{q}_{L}+u^{q}_{L}+ \mu ^{q}_{L}+ \frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} \biggr)-\theta ^{q} K^{q}_{M} \biggr] t^{q} \biggr) \\ \leq{} &\max \biggl\{ \frac{\alpha ^{q}_{E} K^{q}_{E}}{ [ (\alpha ^{q}_{L}+u^{q}_{L}+\mu ^{q}_{L}+\frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} )-\theta ^{q} K^{q}_{M} ]}, L(0) \biggr\} \\ &{}\times \biggl( \biggl[ \biggl(\alpha ^{q}_{L}+u^{q}_{L}+ \mu ^{q}_{L}+ \frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} \biggr)-\theta ^{q} K^{q}_{M} \biggr]t^{q} E_{q,q+1} \\ &{}\times \biggl(- \biggl[ \biggl(\alpha ^{q}_{L}+u^{q}_{L}+ \mu ^{q}_{L}+ \frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} \biggr)-\theta ^{q} K^{q}_{M} \biggr] t^{q} \biggr) \\ &{}+E_{q,1} \biggl(- \biggl[ \biggl(\alpha ^{q}_{L}+u^{q}_{L}+ \mu ^{q}_{L}+ \frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} \biggr)-\theta ^{q} K^{q}_{M} \biggr] t^{q}\biggr) \biggr) \\ ={}&\frac{C}{\Gamma (1)}:= C_{L}, \end{aligned}$$

where \(C_{L}=\max \{ [ (\alpha ^{q}_{L}+u^{q}_{L}+\mu ^{q}_{L}+ \frac{\alpha ^{q}_{E} K^{q}_{E}}{K^{q}_{L}} )-\theta ^{q} K^{q}_{M} ], L(0) \} \). Thus \(L(t)\) is bounded from above. From the equation for pupa population we have

$$\begin{aligned} ^{c}_{a}D^{q}_{t} P(t)=\alpha ^{q}_{L}L-\bigl(\mu ^{q}_{P}+\alpha ^{q}_{p}+u^{q}_{P}\bigr)P \leq \alpha ^{q}_{L}C_{L}-\bigl(\mu ^{q}_{P}+ \alpha ^{q}_{p}+u^{q}_{P}\bigr)P. \end{aligned}$$

Applying the Laplace transform leads to

$$\begin{aligned} s^{q}{\mathcal{L}} \bigl[P(t)\bigr]-s^{{q}-1} P(0)\leq \frac{\alpha ^{q}_{L} C_{L}}{s}-\bigl(\mu ^{q}_{P}+\alpha ^{q}_{p}+u^{q}_{P}\bigr){ \mathcal{L}} \bigl[P(t)\bigr]. \end{aligned}$$

Combining the like terms, we get

$$\begin{aligned} {\mathcal{L}}\bigl(P(t)\bigr)&\leq \alpha ^{q}_{L}C_{L} \frac{s^{-1}}{s^{q}+(\mu ^{q}_{P}+\alpha ^{q}_{p}+u^{q}_{P})}+P(0) \frac{s^{q-1}}{s^{q}+(\mu ^{q}_{P}+\alpha ^{q}_{p}+u^{q}_{P})} \\ &=\alpha ^{q}_{L}C_{L} \frac{s^{q-(1+q)}}{s^{q}+(\mu ^{q}_{P}+\alpha ^{q}_{p}+u^{q}_{P})}+P(0) \frac{s^{q-1}}{s^{q}+(\mu ^{q}_{P}+\alpha ^{q}_{p}+u^{q}_{P})}. \end{aligned}$$

Applying the inverse Laplace transform leads to

$$\begin{aligned} P(t)\leq {}&{\mathcal{L}}^{-1} \biggl\{ \alpha ^{q}_{L}C_{L} \frac{s^{q-(1+q)}}{s^{q}+(\mu ^{q}_{P}+\alpha ^{q}_{p}+u^{q}_{P})} \biggr\} + P(0){\mathcal{L}}^{-1} \biggl\{ \frac{s^{q-1}}{s^{q}+(\mu ^{q}_{P}+\alpha ^{q}_{p}+u^{q}_{P})} \biggr\} \\ \leq{} &\alpha ^{q}_{L}C_{L}t^{q} E_{q,q+1}\bigl(-\bigl(\mu ^{q}_{P}+\alpha ^{q}_{p}+u^{q}_{P}\bigr) t^{q}\bigr)+ P(0)E_{q,1}\bigl(-\bigl(\mu ^{q}_{P}+ \alpha ^{q}_{p}+u_{P}^{q}\bigr) t^{q}\bigr) \\ \leq{} &\frac{\alpha ^{q}_{L}C_{L}}{(\alpha ^{q}_{P}+\mu _{p}^{q}+u^{q}_{P})}{\bigl( \mu ^{q}_{P}+\alpha ^{q}_{p}+u^{q}_{P}\bigr)}t^{q} E_{q,q+1}\bigl(-\bigl(\alpha ^{q}_{P}+ \mu _{p}^{q}+u^{q}_{P}\bigr) t^{q}\bigr) \\ &{}+ P(0)E_{q,1}\bigl(-\bigl(\alpha ^{q}_{P}+\mu _{p}^{q}+u^{q}_{P}\bigr) t^{q}\bigr) \\ \leq{} &\max \biggl\{ \frac{\alpha ^{q}_{L}C_{L}}{(\alpha ^{q}_{P}+\mu _{p}^{q}+u^{q}_{P})}, P(0) \biggr\} \bigl(\bigl(\alpha ^{q}_{P}+\mu _{p}^{q}+u^{q}_{P} \bigr)t^{q} E_{q,q+1}\bigl(-\bigl( \alpha ^{q}_{P}+ \mu _{p}^{q}+u^{q}_{P}\bigr) t^{q}\bigr) \\ &{}+E_{\alpha ,1}\bigl(-\bigl(\alpha ^{q}_{P}+\mu _{p}^{q}+u^{q}_{P}\bigr) t^{q}\bigr)\bigr) \\ ={}&\frac{C}{\Gamma (1)}:= C_{P}, \end{aligned}$$

where \(C_{P}=\max \{ \frac{\alpha ^{q}_{L}C_{L}}{(\alpha ^{q}_{P}+\mu _{p}^{q})}, P(0) \} \). Thus \(P(t)\) is bounded from above. From the last equation of system (1) we have

$$\begin{aligned} ^{c}_{a}D^{q}_{t} A(t)=\alpha ^{q}_{P}P-\bigl(\mu ^{q}_{A}+u^{q}_{A} \bigr)A \leq \alpha ^{q}_{P}C_{P}-\bigl(\mu ^{q}_{A}+u^{q}_{A}\bigr)A. \end{aligned}$$

By applying the Laplace transform it follows that

$$\begin{aligned} s^{q}{\mathcal{L}} \bigl[A(t)\bigr]-s^{{q}-1} A(0)\leq \frac{\alpha ^{q}_{L} C_{P}}{s}-\bigl(\mu ^{q}_{A}+u^{q}_{A} \bigr){\mathcal{L}}\bigl[A(t)\bigr]. \end{aligned}$$

Grouping similar terms, we have

$$\begin{aligned} {\mathcal{L}}\bigl(A(t)\bigr)&\leq \alpha ^{q}_{P}C_{P} \frac{s^{-1}}{s^{q}+(\mu ^{q}_{A}+u^{q}_{A})}+A(0) \frac{s^{q-1}}{s^{q}+(\mu ^{q}_{A}+u^{q}_{A})} \\ &=\alpha ^{q}_{L}K^{q}_{L} \frac{s^{q-(1+q)}}{s^{q}+(\mu ^{q}_{P}+\alpha ^{q}_{p})}+P(0) \frac{s^{q-1}}{s^{q}+(\mu ^{q}_{P}+\alpha ^{q}_{p})}. \end{aligned}$$

Utilizing inverse Laplace transform, we get

$$\begin{aligned} A(t)\leq {}&{\mathcal{L}}^{-1} \biggl\{ \alpha ^{q}_{P}C_{P} \frac{s^{q-(1+q)}}{s^{q}+(\mu ^{q}_{A}+u^{q}_{A})} \biggr\} + A(0){ \mathcal{L}}^{-1} \biggl\{ \frac{s^{q-1}}{s^{q}+(\mu ^{q}_{A}+u^{q}_{A})} \biggr\} \\ \leq{} &\alpha ^{q}_{P}C_{P}t^{q} E_{q,q+1}\bigl(-\bigl(\mu ^{q}_{A}+u^{q}_{A} \bigr) t^{q}\bigr)+ A(0)E_{q,1}\bigl(-\bigl(\mu ^{q}_{A}+u^{q}_{A}\bigr) t^{q}\bigr) \\ \leq{} &\frac{\alpha ^{q}_{P}C_{P}}{(\alpha ^{q}_{A}+u^{q}_{A})}{\bigl(\mu ^{q}_{A}+u^{q}_{A} \bigr)}t^{q} E_{q,q+1}\bigl(-\bigl(\mu ^{q}_{A}+u^{q}_{A} \bigr) t^{q}\bigr)+ A(0)E_{q,1}\bigl(-\bigl(\mu ^{q}_{A}+u^{q}_{A}\bigr)t^{q} \bigr) \\ \leq {}&\max \biggl\{ \frac{\alpha ^{q}_{P}C_{P}}{(\mu ^{q}_{A}+u^{q}_{A})}, A(0) \biggr\} \bigl(\bigl( \mu ^{q}_{A}+u^{q}_{A}\bigr)t^{q} \\ &{}\times E_{q,q+1}\bigl(-\bigl(\mu ^{q}_{A}+u^{q}_{A} \bigr) t^{q}\bigr)+E_{q,1}\bigl(-\bigl(\mu ^{q}_{A}+u^{q}_{A} \bigr) t^{q}\bigr)\bigr) \\ ={}&\frac{C}{\Gamma (1)} = C_{A}, \end{aligned}$$

where \(C_{P}=\max \{ \frac{\alpha ^{q}_{P}C_{P}}{(\mu ^{q}_{A}+u^{q}_{A})}, A(0) \} \). Thus \(A(t)\) is bounded from above. This completes the proof. □

3.3 Model equilibria

By direct calculations we can observe that system (1) has four equilibrium points:

  1. (i)

    Trivial equilibrium

    $$\begin{aligned} {\mathcal{E}}^{1}=\bigl\{ E^{1}=0, L^{1}=0, P^{1}=0, A^{1}=0, M^{1}=0\bigr\} . \end{aligned}$$
  2. (ii)

    First axial equilibrium point

    $$\begin{aligned} {\mathcal{E}}^{2}=\bigl\{ M^{2}=K_{M}^{q}, E^{2}=0, L^{2}=0, P^{2}=0, A^{2}=0 \bigr\} . \end{aligned}$$
  3. (iii)

    Second axial equilibrium point \({\mathcal{E}}^{3}=\{M^{3} E^{3}, L^{3}, P^{3}, A^{3}\}\), where

    $$ {\mathcal{E}}^{3}:\left \{ \textstyle\begin{array}{l} E^{3}= \frac{K^{q}_{E}K^{q}_{L}m_{1}m_{2}m_{3}m_{4}}{\alpha ^{q}_{E}(b^{q}WK^{q}_{L}\alpha ^{q}_{L}\alpha ^{q}_{P}+K^{q}_{E}m_{1}m_{3}m_{4})} ( \frac{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}}{m_{1}m_{2}m_{3}m_{4}}-1 ), \\ L^{3}= \frac{K^{q}_{E}K^{q}_{L}m_{1}m_{2}m_{3}m_{4}}{b^{q} W(K_{E}\alpha _{E}+K^{q}_{L}m_{2})\alpha ^{q}_{L}\alpha ^{q}_{P}} ( \frac{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{P}\alpha ^{q}_{L}}{m_{1}m_{2}m_{3}m_{4}}-1 ), \\ P^{3}= \frac{K^{q}_{E}K^{q}_{L}m_{1}m_{2}m_{3}m_{4}}{b^{q} W(K_{E}\alpha _{E}+K^{q}_{L}m_{2})\alpha ^{q}_{P}m_{3}} ( \frac{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}}{m_{1}m_{2}m_{3}m_{4}}-1 ), \\ A^{3}= \frac{K^{q}_{E}K^{q}_{L}m_{1}m_{2}m_{3}m_{4}}{b^{q} W(K_{E}\alpha _{E}+K^{q}_{L}m_{2})m_{3}m_{4}} ( \frac{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}}{m_{1}m_{2}m_{3}m_{4}}-1 ), \\ M^{3}=0, \end{array}\displaystyle \right \} $$
    (2)

    with

    $$\begin{aligned} &m_{1}=\bigl(\mu ^{q}_{E}+\alpha ^{q}_{E}+u^{q}_{E}\bigr),\qquad m_{2}=\bigl(\mu ^{q}_{L}+ \alpha ^{q}_{L}+u^{q}_{L}\bigr), \\ &m_{3}=\bigl(\mu ^{q}_{P}+\alpha ^{q}_{p}+u^{q}_{P}\bigr),\qquad m_{4}=\bigl(\mu ^{q}_{A}+u^{q}_{A} \bigr). \end{aligned}$$

    We can observe that this equilibrium point makes biological sense whenever

    $$\begin{aligned} {} \frac{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}}{m_{1}m_{2}m_{3}m_{4}}>1 . \end{aligned}$$

    Let

    $$\begin{aligned} {} {\mathcal{R}}_{0}&=b^{q}W \biggl( \frac{\alpha ^{q}_{E}}{\mu ^{q}_{E}+\alpha ^{q}_{E}+u^{q}_{E}} \biggr) \biggl(\frac{\alpha ^{q}_{L}}{\mu ^{q}_{L}+\alpha ^{q}_{L}+u^{q}_{L}} \biggr) \biggl( \frac{\alpha ^{q}_{P}}{\mu ^{q}_{P}+\alpha ^{q}_{P}+u^{q}_{P}} \biggr) \biggl(\frac{1}{\mu ^{q}_{A}+u^{q}_{A}} \biggr) \\ &=\frac{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}}{m_{1}m_{2}m_{3}m_{4}}. \end{aligned}$$

    Biologically, \({\mathcal{R}}_{0}\) is a threshold quantity that accounts for the persistence of the FAW population, and thus when \({\mathcal{R}}_{0}>1\), the population of FAW persists and will be an attack on maize plants leaves, and finally the population of maize plants is extinct. Hence we can precisely define \({\mathcal{R}}_{0}\) as the average number of off-spring generated by an adult female FAW during its entire life span. Precisely, we can note that a proportion W of moth will each lay b eggs per day for an average duration of \(\frac{1}{\mu ^{q}_{A}+u^{q}_{A}}\); laid egg has the probability \(\frac{\alpha ^{q}_{E}}{\mu ^{q}_{E}+\alpha ^{q}_{E}+u^{q}_{E}}\) of surviving to become larva. Caterpillars that emerge following oviposition have the probability \(\frac{\alpha ^{q}_{L}}{\mu ^{q}_{L}+\alpha ^{q}_{L}+u^{q}_{L}}\) of surviving to become pupa, which also has the probability \(\frac{\alpha ^{q}_{P}}{\mu ^{q}_{P}+\alpha ^{q}_{P}+u^{q}_{P}}\) of surviving to become moth.

  4. (iv)

    Interior equilibrium point

    $$ {\mathcal{E}}^{4}:\left \{ \textstyle\begin{array}{l} E^{4}= \frac{-b^{q}K^{q}_{E}W\alpha ^{q}_{L}\alpha ^{q}_{P}h_{2}+ b^{q}K^{q}_{E}W\alpha ^{q}_{P}\sqrt{h_{2}^{2}-4h_{1}h_{3}}}{-b^{q}W\alpha ^{q}_{L}\alpha ^{q}_{P}h_{2}+ b^{q} W\alpha ^{q}_{P}\sqrt{h_{2}^{2}-4h_{1}h_{3}}-2K^{q}_{E}h_{1}m_{1}m_{4}}, \\ L^{4}=\frac{-h_{2}+\sqrt{h_{2}^{2}-4h_{1}h_{3}}}{2h_{1}}, \\ P^{4}= \frac{-\alpha ^{q}_{L}h_{2}+\alpha ^{q}_{L}\sqrt{h_{2}^{2}-4h_{1}h_{3}}}{2h_{1}m_{3}}, \\ A^{4}= \frac{-\alpha ^{q}_{P}\alpha ^{q}_{L}h_{2}+ \alpha ^{q}_{P}\alpha ^{q}_{L}\sqrt{h_{2}^{2}-4h_{1}h_{3}}}{2h_{1}m_{3}m_{4}}, \\ M^{*}= \frac{2h_{1}r^{q}K^{q}_{M}-\beta _{q} K^{q}_{M}h_{2}+ \beta ^{q} K^{q}_{M}\sqrt{h_{2}^{2}-4h_{1}h_{3}}}{2h_{1}r}, \end{array}\displaystyle \right \}, $$
    (3)

    where

    $$ \left . \textstyle\begin{array}{l} h_{1}=b^{q}K^{q}_{L}\theta ^{q}K^{q}_{M}W\alpha ^{q}_{P}\alpha ^{q}_{L}, \\ h_{2}=-( b^{q}\theta ^{q} r^{q}WK^{q}_{L}K^{q}_{M}\alpha ^{q}_{L} \alpha ^{q}_{P}+\theta ^{q}\beta ^{q}e^{q}K^{q}_{E}K^{q}_{L}K^{q}_{M}m_{1}m_{2}m_{3} \\ \phantom{h_{2}=}{} +b^{q}r^{q}WK^{q}_{E}K^{q}_{L}\alpha ^{q}_{E}\alpha ^{q}_{L} \alpha ^{q}_{P} -b^{q}r^{q}WK^{q}_{L}\alpha ^{q}_{L}\alpha ^{q}_{P}m_{2}), \\ h_{3}=-(\theta ^{q} K_{E}K^{q}_{L}K^{q}_{M}m_{1}m_{2}m_{3}+r^{q}K^{q}_{E}K^{q}_{L}m_{1}m_{2}^{2}m_{3}) , \end{array}\displaystyle \right \} $$

    Based on (3), \(h_{1},h_{2}\), and \(h_{3}\), \(\Delta =(h_{2}^{2}-4h_{1}h_{3})>0\) implies that the equilibrium point \({\mathcal{E}}^{4}\) has a unique feasible equilibrium.

3.4 Local stability of equilibrium points

In this section, we study the local stability behavior of the four equilibrium points computed earlier by using the Jacobian matrix

$$\begin{aligned} J= \begin{bmatrix} {}r^{q}-\frac{2Mr^{q}}{K_{M}}-\beta ^{q}L&0&-\beta ^{q}M &0 &0 \\ 0&-m_{1}-\frac{b^{q}WA}{K_{E}}&0&0&b^{q}W (1-\frac{E}{K_{E}} ) \\ {}\theta ^{q} L& (1-\frac{L}{K^{q}_{L}} )\alpha ^{q}_{E} & \theta ^{q} M -m_{2}-\frac{\alpha ^{q}_{E} E}{K_{L}}&0&0 \\ 0&0&\alpha ^{q}_{L} &-m_{3} &0 \\ 0&0&0&\alpha ^{q}_{P} &-m_{4} \end{bmatrix} . \end{aligned}$$
(4)
  1. (a)

    Trivial equilibrium point. Evaluating the Jacobian matrix (4) about \({\mathcal{E}}^{1}\) leads to

    $$\begin{aligned} J\bigl({\mathcal{E}}^{1}\bigr)= \begin{bmatrix} r^{q}&0&0&0&0 \\ 0&-m_{1}&0&0&b^{q}W \\ 0&\alpha ^{q}_{E} & -m_{2}&0&0 \\ 0&0&\alpha ^{q}_{L} &-m_{3} &0 \\ 0&0&0&\alpha ^{q}_{P} &-m_{4} \end{bmatrix} . \end{aligned}$$
    (5)

    The trivial equilibrium point is locally stable if all eigenvalues \(\lambda _{i}\) \((i=1,2,3,4)\) of \(J({\mathcal{E}}^{1})\) satisfy the condition \(\vert \text{arg}(\lambda _{i}) \vert >\frac{q\pi }{2} \) [31]. We can observe that one of the eigenvalues of (5) is \(r^{q}>0\). The other equilibrium points are obtained from the characteristic equation

    $$\begin{aligned} \lambda ^{4}+c_{1}\lambda ^{3}+c_{2} \lambda ^{2}+c_{3}\lambda +c_{4}=0 \end{aligned}$$
    (6)

    with

    $$ \left . \textstyle\begin{array}{l} c_{1}=m_{1}+m_{2}+m_{4}, \\ c_{2}=m_{1}m_{2}+(m_{1}+m_{2})(m_{3}+m_{4})+m_{3}m_{4}, \\ c_{3}=m_{1}m_{2}(m_{3}+m_{4})+m_{3}m_{4}(m_{1}+m_{2}), \\ c_{4}=m_{1}m_{2}m_{3}m_{4}-b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L} \alpha ^{q}_{P} \\ \phantom{c_{4}}=m_{1}m_{2}m_{3}m_{4}(1-{\mathcal{R}}_{0}). \end{array}\displaystyle \right \} $$

    The Routh–Hurwitz criteria for local asymptotic stability of the equilibrium point \({\mathcal{E}}^{1}\) are

    $$ \left . \textstyle\begin{array}{l} {\mathcal{H}}_{1}=c_{1}>0,\qquad c_{3}>0, \qquad c_{4}>0, \\ {\mathcal{H}}_{2}= c_{1}c_{2}c_{3}-c_{3}^{2}-c_{1}^{2}c_{4}>0. \end{array}\displaystyle \right \} $$
    (7)

    As we can observe, all the coefficients of the characteristic polynomial (6) are positive whenever \({\mathcal{R}}_{0}<1\), implying that condition \({\mathcal{H}}_{1}\) holds for \({\mathcal{R}}_{0}<1\). Since we have established that the trivial equilibrium point \({\mathcal{E}}^{1}\) has another eigenvalue \(r^{q}\), which is always positive, we will not investigate the positivity of condition \({\mathcal{H}}_{2}\), and hence we conclude that \({\mathcal{E}}^{1}\) is an unstable equilibrium point.

  2. (b)

    First axial equilibrium point \({\mathcal{E}}^{2}\). Evaluating the Jacobian matrix (4) about \({\mathcal{E}}^{2}\) leads to

    $$\begin{aligned} J\bigl({\mathcal{E}}^{2}\bigr)= \begin{bmatrix} -r^{q}&0&-\beta ^{q}K_{M}^{q}&0&0 \\ 0&-m_{1}&0&0&b^{q}W \\ 0&\alpha ^{q}_{E} & \theta ^{q}K^{q}_{M}-m_{2}&0&0 \\ 0&0&\alpha ^{q}_{L} &-m_{3} &0 \\ 0&0&0&\alpha ^{q}_{P} &-m_{4} \end{bmatrix} . \end{aligned}$$
    (8)

    From (8) we can observe that one of the eigenvalues is \(-r^{q}<0\), and the other eigenvalues are roots of the characteristic equation

    $$\begin{aligned} \lambda ^{4}+b_{1}\lambda ^{3}+b_{2} \lambda ^{2}+b_{3}\lambda +b_{4}=0 \end{aligned}$$
    (9)

    with

    $$ \left . \textstyle\begin{array}{l} b_{1}=m_{1}+m_{2}+m_{4}-\theta ^{q}K^{q}_{M}, \\ b_{2}=(m_{1}+m_{2})(m_{3}+m_{4})+m_{1}m_{2}+m_{3}m_{4}-\theta ^{q}K^{q}_{M}(m_{1}+m_{3}+m_{4}), \\ b_{3}=m_{1}(m_{3}m_{4}+m_{2}(m_{3}+m_{4}))+m_{2}m_{3}m_{4}-\theta ^{q}K^{q}_{M}(m_{1}(m_{3}+m_{4})+m_{3}m_{4}), \\ b_{4}=m_{1}m_{2}m_{3}m_{4}((1-{\mathcal{R}}_{0})-\theta ^{q}K^{q}_{M}). \end{array}\displaystyle \right \} $$

    The Routh–Hurwitz criteria for local asymptotic stability of the equilibrium point \({\mathcal{E}}^{2}\) are

    $$ \left . \textstyle\begin{array}{l} \widehat{{\mathcal{H}}}_{1}=b_{1}>0,\quad b_{3}>0,\quad b_{4}>0, \\ \widehat{{\mathcal{H}}}_{2}= b_{1}b_{2}b_{3}-b_{3}^{2}-b_{1}^{2}b_{4}>0. \end{array}\displaystyle \right \} $$
    (10)

    If conditions specified in (10) hold, then the equilibrium point \({\mathcal{E}}^{2}\) is locally asymptotically stable.

  3. (c)

    Second axial equilibrium point \({\mathcal{E}}^{3}\). Evaluating the Jacobian matrix (4) about \({\mathcal{E}}^{3}\), we get

    $$\begin{aligned} J\bigl({\mathcal{E}}^{3}\bigr) = \begin{bmatrix} r^{q}-\beta ^{q}L^{3}&0&0&0&0 \\ 0&-\widehat{n_{1}}&0&0&\widehat{n_{2}} \\ \widehat{n_{3}}&\widehat{n_{4}}&-\widehat{n_{5}}&0&0 \\ 0&0&\alpha ^{q}_{L} &-m_{3} &0 \\ 0&0&0&\alpha ^{q}_{P} &-m_{4} \end{bmatrix} \end{aligned}$$
    (11)

    with

    $$\begin{aligned} &\widehat{n_{1}} = -m_{1}-\frac{b^{q}WA^{3}}{K_{E}},\qquad \widehat{n_{2}}=b^{q}W \biggl(1-\frac{E^{3}}{K_{E}} \biggr),\qquad \widehat{n_{3}}=\theta ^{q} L, \\ &\widehat{n_{4}} = \biggl(1-\frac{L^{3}}{K^{q}_{L}} \biggr),\qquad \widehat{n_{5}}= m_{2}+\frac{\alpha ^{q}_{E} E}{K_{L}}. \end{aligned}$$

    From (11) we can observe that \(-r^{q} (\frac{\beta ^{q}L^{3}}{r^{q}}-1 )\) is an eigenvalue, and other eigenvalues can be determined from the characteristic polynomial

    $$\begin{aligned} \lambda ^{4}+d_{1}\lambda ^{3}+d_{2} \lambda ^{2}+d_{3}\lambda +d_{4}=0 \end{aligned}$$

    with

    $$\begin{aligned} &d_{1} = m_{1}+m_{3}+m_{4}+ \widehat{n_{5}}, \\ &d_{2} = \widehat{n_{1}}\widehat{n_{5}}+m_{3}m_{4}+(m_{3}+m_{4}) ( \widehat{n_{1}}+\widehat{n_{5}}), \\ &d_{3} = \widehat{n_{1}}\widehat{n_{5}}(m_{3}+m_{4})+m_{3}m_{4}( \widehat{n_{1}}+\widehat{n_{5}}), \\ &d_{4} = m_{3}m_{4}\widehat{n_{1}} \widehat{n_{5}}-\widehat{n_{2}} \widehat{n_{4}} \alpha ^{q}_{L}\alpha ^{q}_{P}. \end{aligned}$$

    Ahmed et al. [31] presented some Routh–Hurwitz stability conditions for fractional-order systems. One well-known Routh–Hurwitz condition is that an equilibrium point is locally stable if all eigenvalues of the community matrix satisfy the condition \(\vert \text{arg}(\lambda _{i}) \vert >\frac{q\pi }{2}\). The Routh–Hurwitz criteria for the local asymptotic stability of the equilibrium point \({\mathcal{E}}^{3}\) are

    $$ \left . \textstyle\begin{array}{l} \xi _{1}=d_{1}>0,\qquad d_{3}>0,\qquad d_{4}>0, \\ \xi _{2}= d_{1}d_{2}d_{3}-d_{3}^{2}-d_{1}^{2}d_{4}>0. \end{array}\displaystyle \right \} $$
    (12)

    Since the existence of the equilibrium point \({\mathcal{E}}^{3}\) is based on \({\mathcal{R}}_{0}>1\), (2), we conclude that the equilibrium point \({\mathcal{E}}^{3}\) is locally asymptotically stable provided that conditions (12) hold and (i) \(r^{q}<\beta ^{q}L^{3}\) and (ii) \({\mathcal{R}}_{0}>1\).

  4. (d)

    Interior equilibrium point \({\mathcal{E}}^{4}\). Evaluating the Jacobian matrix (4) about \({\mathcal{E}}^{4}\), we get

    $$\begin{aligned} J\bigl({\mathcal{E}}^{4}\bigr) = \begin{bmatrix} n_{1}&0&-n_{2}&0&0 \\ 0&-n_{3}&0&0&n_{4} \\ n_{5}&n_{6}&n_{7}&0&0 \\ 0&0&\alpha ^{q}_{L} &-m_{3} &0 \\ 0&0&0&\alpha ^{q}_{P} &-m_{4} \end{bmatrix} \end{aligned}$$
    (13)

    with

    $$\begin{aligned} &n_{1} = r^{q}-\frac{2Mr^{q}}{K_{M}}-\beta ^{q}L,\qquad n_{2}=-\beta ^{q}M,\qquad n_{3}=-m_{1}- \frac{b^{q}WA}{K_{E}}, \\ &n_{4} = b^{q}W \biggl(1-\frac{E}{K_{E}} \biggr),\qquad n_{5}=\theta ^{q} L,\qquad n_{6}= \biggl(1- \frac{L}{K^{q}_{L}} \biggr)\alpha ^{q}_{E}, \\ &n_{7} = \theta ^{q} M -m_{2}-\frac{\alpha ^{q}_{E} E}{K_{L}}. \end{aligned}$$

    The characteristic equation of (13) is

    $$\begin{aligned} \lambda ^{5}+z_{1}\lambda ^{4}+z_{2} \lambda ^{3}+z_{3}\lambda ^{2}+z_{4} \lambda +z_{5}=0, \end{aligned}$$

    where

    $$\begin{aligned} z_{1}={}&m_{3}+m_{4}+n_{3}-n_{1}-n_{7}, \\ z_{2}={}&n_{2}n_{5}-n_{1}n_{3}+m_{3}(m_{4}+n_{3}-n_{1}-n_{7})+n_{1}n_{7}-n_{3}n_{7}-m_{4}(n_{1}-n_{3}+n_{7}), \\ z_{3}={}&n_{3}(n_{1}n_{7}+n_{2}n_{5})+m_{4} \bigl(n_{2}n_{5}-n_{3}n_{7}+n_{1}(n_{7}-n_{3}) \bigr) \\ &{}-m_{3}\bigl(n_{1}(n_{3}-n_{7})+n_{3}n_{7}+m_{4}(n_{1}-n_{3}+n_{7})-n_{2}n_{5} \bigr), \\ z_{4}={}&n_{3}m_{4}(n_{2}n_{5}+n_{1}n_{7})+m_{3} \bigl(n_{3}(n_{2}n_{5}+n_{1}n_{7})+m_{4} \bigl(n_{2}n_{5}-n_{3}n_{7}+n_{1}(n_{7}-n_{3}) \bigr)\bigr) \\ &{}-\alpha _{L}^{q}\alpha ^{q}_{P}n_{4}n_{6}, \\ z_{5}={}&\alpha _{L}^{q}\alpha ^{q}_{P}n_{1}n_{4}n_{6}+n_{3}m_{3}m_{4}(n_{2}n_{5}+n_{1}n_{7}). \end{aligned}$$

    The Routh–Hurwitz criteria necessary and sufficient for local asymptotic stability of the equilibrium point \({\mathcal{E}}^{4}\) are that the Hurwitz determinants \(H_{i}\) are all positive [32]. For a fifth-degree polynomial, these criteria are

    $$ \left . \textstyle\begin{array}{l} H_{1}=z_{1}>0, \\ H_{2}= z_{1}z_{2}-z_{3}>0, \\ H_{3}=z_{1}z_{2}z_{3}+z_{1}z_{5}-z_{1}^{2}z_{4}-z^{2}_{3}>0, \\ H_{4}=(Z_{3}z_{4}-z_{2}z_{5})(z_{1}z_{2}-z_{3})-(z_{1}z_{4}-z_{5})^{2}>0, \\ H_{5}=c_{5}H_{4}>0. \end{array}\displaystyle \right \} $$
    (14)

Thus we have the following result.

Theorem 3.3

The interior equilibrium point \({\mathcal{E}}^{4}\) is locally asymptotically stable if conditions in (14) hold; otherwise, it is unstable.

3.5 Global stability of equilibrium points

In this section, we study the global stability of the equilibrium points \({\mathcal{E}}^{1}\), \({\mathcal{E}}^{2}\), \({\mathcal{E}}^{3}\), and \({\mathcal{E}}^{4}\) determined earlier.

  1. (a)

    Trivial equilibrium point \({\mathcal{E}}^{1}\). Let us consider the Lyapunov function

    $$\begin{aligned} {\mathcal{U}}_{1}( M,E,L,P,A)={}&M(t)+ \biggl(\frac{m_{4}}{b^{q}W} \biggr)E(t)+ \biggl(\frac{m_{1}m_{4}}{b^{q}W\alpha ^{q}_{E}} \biggr)L(t) \\ &{}+ \biggl( \frac{m_{1}m_{2}m_{4}}{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}} \biggr)P(t) + \biggl( \frac{m_{1}m_{2}m_{3}m_{4}}{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}} \biggr)A(t). \end{aligned}$$

    As we can observe, the Lyapunov functional \({\mathcal{U}}_{1}( M,E,L,P,A)\) is defined, continuous, and positive definite for all \(M(t)\), \(E(t)\), \(L(t)\), \(P(t)\), and \(A(t)\). It is evident that \({\mathcal{U}}_{1}\) vanishes at \({\mathcal{E}}^{1}\). The fractional derivative of \({\mathcal{U}}(t)\) along the solutions of system (1) leads to

    $$\begin{aligned} ^{c}_{t_{0}}D^{q}_{t} { \mathcal{U}}_{1}(t)={}& {}^{c}_{t_{0}}D^{q}_{t}M(t)+ \biggl(\frac{m_{4}}{b^{q}W} \biggr){}^{c}_{t_{0}}D^{q}_{t}E(t) + \biggl(\frac{m_{1}m_{4}}{b^{q}W\alpha ^{q}_{E}} \biggr){}^{c}_{t_{0}}D^{q}_{t} L(t) \\ &{}+ \biggl( \frac{m_{1}m_{2}m_{4}}{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}} \biggr) {}^{c}_{t_{0}}D^{q}_{t}P(t) + \biggl( \frac{m_{1}m_{2}m_{3}m_{4}}{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}} \biggr){}^{c}_{t_{0}}D^{\alpha }_{t}A(t) \\ ={}& r^{q} M(t) \biggl(1-\frac{M(t)}{K^{q}_{M}} \biggr)-\beta ^{q} L(t)M(t) \\ &{}+ \biggl(\frac{m_{4}}{b^{q}W} \biggr) \biggl(b^{q} \biggl(1- \frac{E(t)}{K^{q}_{E}} \biggr)WA(t)-m_{1}E(t) \biggr) \\ &{}+ \biggl(\frac{m_{1}m_{4}}{b^{q}W\alpha ^{q}_{E}} \biggr) \biggl( \alpha ^{q}_{E} \biggl(1-\frac{L(t)}{K^{q}_{L}} \biggr)E(t)+\theta ^{q} L(t)M(t)-m_{2}L(t) \biggr) \\ &{}+ \biggl( \frac{m_{1}m_{2}m_{4}}{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}} \biggr) \bigl(\alpha ^{q}_{L}L(t)-m_{3}P(t) \bigr) \\ &{} + \biggl( \frac{m_{1}m_{2}m_{3}m_{4}}{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}} \biggr) \bigl(\alpha ^{q}_{P}P(t)-m_{4}AV \bigr) \\ ={}&{-}m_{4}\frac{E(t)A(t)}{K_{E}} -m_{1}m_{2} \frac{E(t)L(t)}{K_{L}}- \frac{m_{1}m_{2}m_{3}m_{4}^{2}}{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}} \\ &{}\times \biggl(1- \frac{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}}{m_{1}m_{2}m_{3}m_{4}} \biggr)A(t) -\theta ^{q} \biggl( \frac{ b^{q}W\alpha ^{q}_{E}\beta ^{q}}{m_{1}m_{4}\theta ^{q}}-1 \biggr)L(t)M(t) \\ &{}+r^{q} M(t) \biggl(1-\frac{M(t)}{K^{q}_{M}} \biggr) \\ ={}&{-}m_{4}\frac{E(t)A(t)}{K_{E}} -m_{1}m_{2} \frac{E(t)L(t)}{K_{L}}- \frac{m_{4}}{{\mathcal{R}}_{0}} (1-{\mathcal{R}}_{0} )A(t) \\ &{}-\theta ^{q} \biggl( \frac{ b^{q}W\alpha ^{q}_{E}\beta ^{q}}{m_{1}m_{4}\theta ^{q}}-1 \biggr)L(t)M(t)+r^{q} M(t) \biggl(1-\frac{M(t)}{K^{q}_{M}} \biggr) . \end{aligned}$$

    Note that \({}^{c}_{t_{0}}D^{q}_{t} {\mathcal{U}}_{1}(t)=0\) if \(M(t)=K^{q}_{M}\), \({\mathcal{R}}_{0}=1\), and \(m_{1}m_{4}\theta ^{q} \leq b^{q} W\alpha ^{q}_{E}\beta ^{q}\). Thus \({}^{c}_{t_{0}}D^{q}_{t} {\mathcal{U}}_{1}(t)\) is negative definite if \(M(t)=K^{q}_{M}\), \({\mathcal{R}}_{0}\leq 1\), and \(m_{1}m_{4}\theta ^{q} \leq b^{q} W\alpha ^{q}_{E}\beta ^{q}\). Therefore we have the following theorem.

Theorem 3.4

The trivial equilibrium point \({\mathcal{E}}^{1}\) is globally asymptotically stable if \(M(t)=K^{q}_{M}\), \({\mathcal{R}}_{0}\leq 1\), and \(m_{1}m_{4}\theta ^{q} \leq b^{q} W\alpha ^{q}_{E}\beta ^{q}\); otherwise, it is unstable.

  1. (b)

    First axial equilibrium point \({\mathcal{E}}^{2}\). Define the function

    $$\begin{aligned} {\mathcal{U}}_{2}( M,E,L,P,A)={}&M(t)-M^{*}-M^{*} \ln \frac{M(t)}{M^{*}}+ \biggl(\frac{m_{4}}{b^{q}W} \biggr)E(t) \\ &{}+ \biggl(\frac{m_{1}m_{4}}{b^{q}W\alpha ^{q}_{E}} \biggr)L(t) + \biggl(\frac{m_{1}m_{2}m_{4}}{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}} \biggr)P(t) \\ &{}+ \biggl( \frac{m_{1}m_{2}m_{3}m_{4}}{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}} \biggr)A(t). \end{aligned}$$

    Evidently, the function \({\mathcal{U}}_{2}( M,E,L,P,A)\) is defined, continuous, and positive definite for all \(M(t)\), \(E(t)\), \(L(t)\), \(P(t)\), and \(A(t)\). Furthermore, \({\mathcal{U}}_{2}\) vanishes at \({\mathcal{E}}^{2}\). Hence the fractional derivative of \({\mathcal{U}}_{2}(t)\) along the solutions of the system satisfies

    $$\begin{aligned} ^{c}_{t_{0}}D^{q}_{t} { \mathcal{U}}_{2}(t)\leq {}& \biggl(1- \frac{M^{*}}{M(t)} \biggr){}^{c}_{t_{0}}D^{q}_{t}M(t)+ \biggl( \frac{m_{4}}{b^{q}W} \biggr){}^{c}_{t_{0}}D^{q}_{t}E(t) + \biggl( \frac{m_{1}m_{4}}{b^{q}W\alpha ^{q}_{E}} \biggr){}^{c}_{t_{0}}D^{q}_{t} L(t) \\ &{}+ \biggl( \frac{m_{1}m_{2}m_{4}}{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}} \biggr) {}^{c}_{t_{0}}D^{q}_{t}P(t) + \biggl( \frac{m_{1}m_{2}m_{3}m_{4}}{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}} \biggr){}^{c}_{t_{0}}D^{\alpha }_{t}A(t) \\ ={}&{-}r^{q} M^{*} \biggl(1-\frac{M(t)}{K^{q}_{M}} \biggr) \biggl(1- \frac{M(t)}{M^{*}} \biggr) -m_{4}\frac{E(t)A(t)}{K_{E}} -m_{1}m_{2} \frac{E(t)L(t)}{K_{L}} \\ &{}- \frac{m_{1}m_{2}m_{3}m_{4}^{2}}{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}} \biggl(1- \frac{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}}{m_{1}m_{2}m_{3}m_{4}} \biggr)A(t) \\ &{}- \frac{\beta ^{q}b^{q}W\alpha ^{q}_{E}+m_{1}m_{4}\theta ^{q}}{b^{q}W\alpha ^{q}_{E}} \biggl(1- \frac{\beta ^{q} b^{q}W\alpha ^{q}_{E}}{m_{1}m_{4}\theta ^{q}+\beta ^{q}b^{q}W\alpha ^{q}_{E}} \frac{M^{*}}{M(t)} \biggr) \\ ={}&{-}r^{q} M^{*} \biggl(1-\frac{M(t)}{K^{q}_{M}} \biggr) \biggl(1- \frac{M(t)}{M^{*}} \biggr) -m_{4}\frac{E(t)A(t)}{K_{E}} -m_{1}m_{2} \frac{E(t)L(t)}{K_{L}} \\ &{}- \frac{\beta ^{q}b^{q}W\alpha ^{q}_{E}+m_{1}m_{4}\theta ^{q}}{b^{q}W\alpha ^{q}_{E}} \biggl(1- \frac{\beta ^{q} b^{q}W\alpha ^{q}_{E} M^{*}}{(m_{1}m_{4}\theta ^{q}+\beta ^{q}b^{q}W\alpha ^{q}_{E})M(t)} \biggr) \\ &{}- \frac{m_{1}m_{2}m_{3}m_{4}^{2}}{b^{q}W\alpha ^{q}_{E}\alpha ^{q}_{L}\alpha ^{q}_{P}} (1-{\mathcal{R}}_{0} )A(t). \end{aligned}$$

    Therefore \({}^{c}_{t_{0}}D^{q}_{t} {\mathcal{U}}_{2}(t)\) is negative definite if the following conditions hold: (i) \({\mathcal{R}}_{0}\leq 1\), (ii) \(M< M^{*}\), (iii) \(\beta ^{q} b^{q}W\alpha ^{q}_{E} M^{*}\leq (m_{1}m_{4}\theta ^{q}+ \beta ^{q}b^{q}W\alpha ^{q}_{E})M(t)\). Therefore we have the following theorem.

Theorem 3.5

The trivial equilibrium point \({\mathcal{E}}^{2}\) is globally asymptotically stable if the following conditions hold: (i) \({\mathcal{R}}_{0}\leq 1\), (ii) \(M< M^{*}\), and (iii) \(\beta ^{q} b^{q}W\alpha ^{q}_{E} M^{*}\leq (m_{1}m_{4}\theta ^{q}+ \beta ^{q}b^{q}W\alpha ^{q}_{E})M(t)\); otherwise, it is unstable.

  1. (c)

    Global stability of equilibrium points \({\mathcal{E}}^{3}\) and \({\mathcal{E}}^{4}\). We will use the following Lyapunov function to investigate the global stability of the equilibrium points \({\mathcal{E}}^{3}\) and \({\mathcal{E}}^{4}\):

    $$\begin{aligned} {\mathcal{U}}_{3}(t)={}& a_{0} \biggl[M(t)-M^{*}-M^{*} \ln \biggl( \frac{M(t)}{M^{*}} \biggr) \biggr]+a_{1} \biggl[ E(t)-E^{*}-E^{*}\ln \biggl( \frac{E(t)}{E^{*}} \biggr) \biggr] \\ &{}+a_{2} \biggl[ L(t)-L^{*}-L^{*}\ln \biggl( \frac{L(t)}{L^{*}} \biggr) \biggr]+a_{3} \biggl[P(t)-P^{*}-P^{*} \ln \biggl(\frac{P(t)}{P^{*}} \biggr) \biggr] \\ &{}+ a_{4} \biggl[A(t)-A^{*}-A^{*}\ln \biggl( \frac{A(t)}{A^{*}} \biggr) \biggr] , \end{aligned}$$

    where \(a_{1}\), \(a_{2}\), \(a_{3}\), and \(a_{4}\) are positive constants to be determined. Let \(g_{0}(M)=r^{q} (1-\frac{M}{K^{q}_{M}} )\), \(g_{1}(E,A)=b^{q} (1-\frac{E}{K^{q}_{E}} )WA\), and \(g_{2}(E,L)=\alpha ^{q}_{E} (1-\frac{L}{K^{q}_{L}} )E\). Recall that at this equilibrium, we have the following identities:

    $$ \left . \textstyle\begin{array}{l} g_{0}(M)=\beta ^{q}L^{*}M^{*},\qquad g_{1}(E^{*},A^{*})=m_{1}E^{*},\qquad g_{2}(E^{*},L^{*})+\theta ^{q}L^{*}M^{*}=m_{2}L^{*}, \\ \alpha ^{q}_{L}L^{*}-m_{3}P^{*}, \qquad \alpha ^{q}_{P}P^{*}=m_{4}A^{*}. \end{array}\displaystyle \right \} $$

    Setting

    $$ \left . \textstyle\begin{array}{l} a_{1}=g_{2}(E^{*},L^{*}), \qquad a_{3}= \frac{g_{1}(E^{*},A^{*})g_{2}(E^{*},L^{*})}{\alpha ^{q}_{L} L^{*}}, \\ a_{2}=g_{1}(E^{*},A^{*}),\qquad a_{4}= \frac{g_{1}(E^{*},A^{*})g_{2}(E^{*},L^{*})}{\alpha ^{q}_{P} P^{*}}, \end{array}\displaystyle \right \} $$

    it follows from Lemma 2.1 that

    $$\begin{aligned} &{}^{c}_{t_{0}}D^{\alpha }_{t} { \mathcal{U}}_{2}(t)\\ &\quad\leq \biggl(1- \frac{M^{*}}{M(t)} \biggr){}^{c}_{t_{0}}D^{q}_{t}M(t)+ g_{2}\bigl(E^{*},L^{*}\bigr) \biggl(1- \frac{E^{*}}{E(t)} \biggr){}^{c}_{t_{0}}D^{q}_{t}E(t) \\ &\qquad{}+ g_{1}\bigl(E^{*},A^{*}\bigr) \biggl(1- \frac{L^{*}}{L(t)} \biggr){}^{c}_{t_{0}}D^{q}_{t}L(t) \biggl( \frac{g_{1}(E^{*},A^{*})g_{2}(E^{*},L^{*})}{\alpha ^{q}_{L} L^{*}} \biggr) \biggl(1-\frac{P^{*}}{P(t)} \biggr){}^{c}_{t_{0}}D^{q}_{t}P(t) \\ &\qquad{}+ \biggl( \frac{g_{1}(E^{*},A^{*})g_{2}(E^{*},L^{*})}{\alpha ^{q}_{P} P^{*}} \biggr) \biggl(1-\frac{A^{*}}{A(t)} \biggr){}^{c}_{t_{0}}D^{q}_{t}A(t) \\ &\quad= g_{0}\bigl(M^{*}\bigr) \biggl(1-\frac{M^{*}}{M} \biggr) \biggl( \frac{g(M)}{g(M^{*})}-\frac{LM}{L^{*}M^{*}} \biggr)+ \theta ^{q}g_{1}\bigl(E^{*},A^{*}\bigr) \biggl(1-\frac{L}{L^{*}} \biggr) \biggl(1-\frac{M}{M^{*}} \biggr) \\ &\qquad{}+g_{2}\bigl(E^{*},L^{*}\bigr) \biggl(1- \frac{E^{*}}{E} \biggr) \biggl(g_{1}(E,A)- g_{1} \bigl(E^{*},A^{*}\bigr)\frac{E}{E^{*}} \biggr) \\ &\qquad{}+ g_{1}\bigl(E^{*},A^{*}\bigr) \biggl(1- \frac{L^{*}}{L} \biggr) \biggl(g_{2}(E,L)-g_{2} \bigl(E^{*},L^{*}\bigr) \frac{L}{L^{*}} \biggr) \\ &\qquad{}+ \biggl( \frac{g_{1}(E^{*},A^{*})g_{2}(E^{*},L^{*})}{\alpha ^{q}_{L} L^{*}} \biggr) \biggl(1-\frac{P^{*}}{P} \biggr) \biggl(\alpha ^{q}_{L}L- \alpha _{L}^{q} L^{*}\frac{P}{P^{*}} \biggr) \\ &\qquad{}+ \biggl( \frac{g_{1}(E^{*},A^{*})g_{2}(E^{*},L^{*})}{\alpha ^{q}_{P} P^{*}} \biggr) \biggl(1-\frac{A^{*}}{A} \biggr) \biggl(\alpha ^{q}_{P}P- \alpha ^{q}_{P}P^{*} \frac{A}{A^{*}} \biggr) \\ &\quad= g_{0}\bigl(M^{*}\bigr) \biggl(1-\frac{M^{*}}{M} \biggr) \biggl( \frac{g(M)}{g(M^{*})}-\frac{LM}{L^{*}M^{*}} \biggr)+ \theta ^{q}g_{1}\bigl(E^{*},A^{*}\bigr) \biggl(1-\frac{L}{L^{*}} \biggr) \biggl(1-\frac{M}{M^{*}} \biggr) \\ &\qquad{}+g_{1}\bigl(E^{*},A^{*}\bigr)g_{2} \bigl(E^{*},L^{*}\bigr) \biggl(1-\frac{E}{E^{*}}- \frac{E^{*}g_{1}(E,A)}{Eg_{1}(E^{*},A^{*})}+ \frac{g_{1}(E,A)}{g_{1}(E^{*},A^{*})} \biggr) \\ &\qquad{}+g_{1}\bigl(E^{*},A^{*}\bigr)g_{2} \bigl(E^{*},L^{*}\bigr) \biggl(3-\frac{A}{A^{*}}- \frac{A^{*}P}{AP^{*}}- \frac{P^{*}L}{PL^{*}}- \frac{L^{*}g_{2}(E,L)}{Lg_{2}(E^{*},L^{*})}+ \frac{g_{2}(E,L)}{g_{2}(E^{*},L^{*})} \biggr). \end{aligned}$$

    Let \(\Phi (x)=1-x+\ln x\) for \(x>0\). It follows that \(\Phi (x)\leq 0\) with the equality if and only if \(x=1\). Using this relation, we have

    $$\begin{aligned} &1-\frac{E}{E^{*}}-\frac{E^{*}g_{1}(E,A)}{Eg_{1}(E^{*},A^{*})}+ \frac{g_{1}(E,A)}{g_{1}(E^{*},A^{*})} \\ &\quad =\Phi \biggl(\frac{E^{*}g_{1}(E,A)}{Eg_{1}(E^{*},A^{*})} \biggr)- \frac{E}{E^{*}}\\ &\qquad{}+ \frac{g_{1}(E,A)}{g_{1}(E^{*},A^{*})}-\ln \biggl( \frac{E^{*}g_{1}(E,A)}{Eg_{1}(E^{*},A^{*})} \biggr) \\ &\quad \leq \frac{g_{1}(E,A)}{g_{1}(E^{*},A^{*})}- \ln \biggl( \frac{g_{1}(E,A)}{g_{1}(E^{*},A^{*})} \biggr) - \frac{E}{E^{*}}+ \ln \biggl(\frac{E}{E^{*}} \biggr). \end{aligned}$$

    Similarly, we can write

    $$\begin{aligned} &3-\frac{A}{A^{*}}- \frac{A^{*}P}{AP^{*}}- \frac{P^{*}L}{PL^{*}}- \frac{L^{*}g_{2}(E,L)}{Lg_{2}(E^{*},L^{*})}+ \frac{g_{2}(E,L)}{g_{2}(E^{*},L^{*})} \\ &\quad = \Phi \biggl(\frac{A^{*}P}{AP^{*}} \biggr)+ \Phi \biggl( \frac{A^{*}P}{AP^{*}} \biggr)+ \Phi \biggl( \frac{L^{*}g_{2}(E,L)}{Lg_{2}(E^{*},L^{*})} \biggr) -\frac{A}{A^{*}} \\ &\qquad{}+ \frac{g_{2}(E,L)}{g_{2}(E^{*},L^{*})}- \ln \biggl( \frac{A^{*}g_{2}(E,L)}{A g_{2}(E^{*},L^{*})} \biggr) \\ &\quad \leq \frac{g_{2}(E,L)}{g_{2}(E^{*},L^{*})}-\ln \biggl( \frac{g_{2}(E,L)}{ g_{2}(E^{*},L^{*})} \biggr) - \frac{A}{A^{*}}+ \ln \biggl(\frac{A}{A^{*}} \biggr). \end{aligned}$$

Therefore \({}^{c}_{t_{0}}D^{q}_{t} {\mathcal{U}}_{3}(t)\) is negative definite if the following conditions hold:

  1. (i)

    \((1-\frac{M^{*}}{M} ) (\frac{g(M)}{g(M^{*})}- \frac{LM}{L^{*}M^{*}} )\leq 0\),

  2. (ii)

    \((1-\frac{L}{L^{*}} ) (1-\frac{M}{M^{*}} ) \leq 0\).

Therefore we have the following theorem.

Theorem 3.6

The equilibrium points \({\mathcal{E}}^{3}\) and \({\mathcal{E}}^{4}\) are globally asymptotically stable if the following conditions hold:

  1. (i)

    \((1-\frac{M^{*}}{M} ) (\frac{g(M)}{g(M^{*})}- \frac{LM}{L^{*}M^{*}} )\leq 0\)

  2. (ii)

    \((1-\frac{L}{L^{*}} ) (1-\frac{M}{M^{*}} ) \leq 0\);

otherwise, they are unstable.

4 Numerical results

4.1 Model parameterization

In this section, we present the baseline values for the model parameters. Majority of the parameter values are taken from previously published studies, and a few not available in literature were estimated within plausible and reasonable ranges so as to draw reasonably realistic scenarios.

  1. (i)

    Natural mortality rate of adult FAW \(\mu _{A}\): The life span of female adult FAW is 15–21 days. It follows that the natural mortality rate of the moth is

    $$\begin{aligned} \mu _{A}=\frac{\text{1}}{\text{expected lifetime}}. \end{aligned}$$
  2. (ii)

    Egg laying rate b and life span of adult moth \(\mu _{A}^{-1}\): During its entire life span of 15–21 days and adult female FAW’s total egg production per female averages about 1500 with a maximum of over 2000 [28]. The average daily egg laying rate can be expressed as follows:

    $$\begin{aligned} \text{eggs laid per day}= \frac{\text{eggs laid in a lifetime}}{\text{expected lifetime}}. \end{aligned}$$

    Westbrook et al. [33] estimated that a female adult moth with a life span of 18 days can oviposit about 125 eggs. Hence in our simulations, we set \(b=125\) eggs per day and \(\mu _{A}=1/18\) per day.

  3. (iii)

    Egg hatching rate \(\alpha _{E}\) and gender ratio W: Mathematically, the egg hatching rate is the inverse of average duration of the egg stage, that is,

    $$\begin{aligned} \alpha _{E}=\frac{1}{\text{Average duration of the egg stage}}. \end{aligned}$$

    Depending on the climate, the duration of egg stage takes an average period of 2–3 days [3, 28]. Westbrook et al. [33] estimated a gender ratio of 50:50 males/females.

  4. (iv)

    Average duration of the larval stage \(\alpha _{L}^{-1}\): The duration of the larval stage is influenced by climate changes. During summer periods, the larval stage is about 14 days and 30 days during cool weather [3, 28, 29].

  5. (v)

    Average duration of the pupal stage \(\alpha _{P}^{-1}\): Similarly to the larval stage, the pupal stage also depends on the climate. It is about 8–9 days during summer but reaches 20–30 days during the winter [3, 28].

4.2 Sensitivity analysis of the reproduction number

Analytical results of the model have shown that the basic reproduction number is an important threshold parameter for the persistence and extinction of FAW during any outbreak. Since the parameters of the proposed model have either been drawn from literature or estimated, there is need to investigate the influence of each parameter on the magnitude of the basic reproduction number \({\mathcal{R}}_{0}\) so as to understand the uncertainty regarding their values. To infer on the relationship between the model parameters and individual parameters, we conduct sensitivity analysis as follows.

Definition 4.1

(See [34])

The normalized sensitivity index of \({\mathcal{R}}_{0}\), which depends differentiably on a parameter, say κ, is defined by

$$\begin{aligned} {\Theta }^{{\mathcal{R}}_{0}}_{\kappa }= \frac{\partial {\mathcal{R}}_{0}}{\partial \kappa }\times \frac{\kappa }{{\mathcal{R}}_{0}}. \end{aligned}$$
(15)

The model parameters whose sensitivity index is positive will increase the size of \({\mathcal{R}}_{0}\) whenever they are increased, whereas those with negative index decrease \({\mathcal{R}}_{0}\) whenever they are increased. It follows from (15) that the normalized sensitivity of \({\mathcal{R}}_{0}\) with regard to the model parameters that define it is given by

$$ \left . \textstyle\begin{array}{l} {\Theta }^{{\mathcal{R}}_{0}}_{b}=1, \qquad {\Theta }^{{\mathcal{R}}_{0}}_{W}=1,\qquad {\Theta }^{{\mathcal{R}}_{0}}_{\alpha _{i}}= \frac{\mu _{i}+u_{i}}{\mu _{i}+\alpha _{i}+u_{i}}>0, \\ {\Theta }^{{\mathcal{R}}_{0}}_{\mu _{i}}=- \frac{\mu _{i}}{\mu _{i}+\alpha _{i}+u_{i}}< 0, \qquad {\Theta }^{{\mathcal{R}}_{0}}_{ \mu _{A}}=-\frac{\mu _{A}}{\mu _{A}+u_{A}}< 0, \\ {\Theta }^{{\mathcal{R}}_{0}}_{u_{i}}=- \frac{u_{i}}{\mu _{i}+\alpha _{i}+u_{i}}< 0,\qquad {\Theta }^{{\mathcal{R}}_{0}}_{u_{j}}=- \frac{u_{A}}{\mu _{A}+u_{A}}< 0 \quad \text{for } i=E,P,L. \end{array}\displaystyle \right \} $$
(16)

As we can observe from (16), the model parameters b, W, and \(\alpha _{j}\) \((j=E,L,P,A)\) increase the size of \({\mathcal{R}}_{0}\) whenever they are increased, whereas the model parameters \(\mu _{j}\) and \(u_{j}\) decrease the size of \({\mathcal{R}}_{0}\) whenever they are increased. It is worth noting that an increase in either b or W by 10% may result in an increase in the magnitude of \({\mathcal{R}}_{0}\) by 10%. However, an increase by 10% of \(\alpha _{j}\) increases the size of \({\mathcal{R}}_{0}\) by a value less than 10%. In addition, note that \(u_{j}\) has a negative effect on \({\mathcal{R}}_{0}\), implying that intervention strategy has an impact on extinction and persistence of FAW in the environment. Without loss of generality, we set \(u_{E}=u_{L}=u_{P}=u_{A}=0.3\) and computed the sensitivity index for each model parameter that defines \({\mathcal{R}}_{0}\). The results are presented in Table 1 and Fig. 2.

Figure 2
figure 2

Sensitivity analysis of the basic reproduction number \({\mathcal{R}}_{0}\) with respect to model parameters. Baseline values used given in Table 2. The exact numerical indices are also presented in Table 1, whereas control parameters are set to \(u_{E}=u_{L}=u_{P}=u_{A}=0.3\). Overall, we can note that model parameters b and W are highly correlated with \({\mathcal{R}}_{0}\). In particular, an increase in either b or W by 10% may result in an increase in the magnitude of \({\mathcal{R}}_{0}\) by 10%

Full size image
Table 1 Sensitivity index of the basic reproduction number
Full size table

Numerical results in Table 1 suggests that pest control intervention strategies more effects on minimizing the FAW population in the field if such strategies target the adult FAW population. Simulation results in Fig. 3 demonstrate the effects of varying the intervention strategies on extinction and persistence of pests in the field. For simplicity, we set \(u=u_{E}=u_{L}=u_{P}=u_{A}\), whereas the other parameter values are taken from Table 2. From the results we can note that any value of \(u>0.5\) leads to the extinction of the pest, and persistence of the pests occurs for \(u<0.5\).

Figure 3
figure 3

Effects of varying intervention strategies on the magnitude of \({\mathcal{R}}_{0}\). Here we set \(u=u_{E},u_{L}=u_{P}=u_{A}\). (a) Dynamics of \({\mathcal{R}}_{0}\) on a wide ranges of values for u. (b) Zoomed graph, that is, an illustration of the dynamics of \({\mathcal{R}}_{0}\) for a refined range of values for u. From the results we can note that any value of \(u>0.5\) leads to the extinction of the pest, and persistence of the pests occurs for \(u<0.5\)

Full size image
Table 2 Model parameters and their baseline values
Full size table

4.3 Population level effects

In this section, we conducted additional simulations to numerically illustrate the dynamical behavior of system (1) and to validate the analytical results such as the stability of the equilibria. We used the fractional Adam–Bashforth–Moulton method [35] to conduct the simulations, that is, for a differential equation

$$\begin{aligned} \frac{d^{\alpha }x(t)}{dt^{\alpha }} =f\bigl(t,x(t)\bigr), \end{aligned}$$

the fractional variant of the one step Adam–Moulton method is given by

$$\begin{aligned} x_{n+1}=\sum^{[\alpha ]-1}_{i=0} \frac{t^{i}_{n+1}}{i!}x_{0}^{i}+ \frac{h^{\alpha }}{\Gamma (\alpha +2)}\sum ^{n}_{i=0}a_{i, n+1}f(t_{i},x_{i})+ \frac{h^{\alpha }}{\Gamma (\alpha +2)}f\bigl(t_{n+1},x^{p}_{n+1}\bigr), \end{aligned}$$

where \(t_{i}=ih\) with some fixed h, and

$$ a_{i,n+1}= \textstyle\begin{cases} n^{\alpha +1}-(n-\alpha )(n+1)^{\alpha },& i=0, \\ (n-i+2)^{\alpha +1}+(n-i)^{\alpha +1}-2(n-i+1)^{\alpha +1}, & 1 \leq i\leq n. \end{cases} $$

To determine the error in this method, by assuming that \(t_{i}=ih=\frac{i\tau }{N}\) with some \(N\in \mathbb{N}\), we have (see [35])

$$ \max_{0\leq i\leq N} \bigl\vert x(t_{i})-x_{i} \bigr\vert = \textstyle\begin{cases} \mathcal{O}(h^{2}),& \alpha \leq 1, \\ \mathcal{O}(h^{1+\alpha }),& \alpha < 1. \end{cases} $$

Simulating system (1), we assumed the following initial population levels: \(E(0)=1000\), \(L(0)=P(0)=0\), \(A(0)=500\), and \(M(0)=15\).

Numerical results in Fig. 4 illustrate the dynamics of the pest and maize biomass whenever the reproduction ratio \({\mathcal{R}}_{0}\) is less than unity. As we can note, if the moth cannot produce more than one off-spring, then within a period of 200 days, all the FAW populations (eggs, larvae, pupae, and moth) will become extinct, whereas the maize biomass will increase with time till it reaches the expected maximum biomass per plant (50 kg plant−1). We can also observe that the convergence of solutions to their respective limiting points in time depends on the fractional order q: as q approaches unity, the time taken by solutions to converge to the limiting point increases. From the simulation results shown in Fig. 5 we can observe that whenever each female moth reproduces more than one off-spring, that is, \({\mathcal{R}}_{0}>1\), then the pest population will persist in the field till the final harvesting time \(t=300\) day. In addition, the final maize biomass per plant will be less than the expected 50 k,plant−1. Precisely, maize biomass increases from the start and reaches a maximum of 50 kg plant−1 after approximately 100 days, and after that, it decreases gradually till it stabilizes at approximated 18 kg plant−1. Figure 6 shows the solutions of model system (1) for an experiment set up with small population sizes for the pest, that is, \(E(0)=100\), \(L(0)=P(0)=0\), and \(A(0)=50\), together with a control rate of \(u_{E}=u_{L}=u_{P}=u_{A}=0.45\) day −1, leading to \({\mathcal{R}}_{0}=1.3583\). Furthermore, q was fixed to 0.8. As we can observe, the pest population increases rapidly within the first 100 days, and then it stabilizes. The maize biomass also increases during the first 50 days and attains a maximum approximately close to the expected value 50 kg plant−1, and then the biomass decreases gradually for approximately 50 days before it becomes stable at approximately 50 kg plant−1. Overall, the egg population will dominate all the pest populations.

Figure 4
figure 4

Numerical results of system (1) demonstrating the convergence of solutions to the pest-free equilibrium for \({\mathcal{R}}_{0} \leq 1\). On construction of the simulations, we considered initial population levels discussed earlier, while baseline values for the model parameters are as in Table 2. In addition, we set \(u_{E}=u_{L}=u_{P}=u_{A}=0.52\) to obtain \({\mathcal{R}}_{0}=0.8630\). We can note that whenever \({\mathcal{R}}_{0}<1\), the pest population becomes extinct while maize biomass increases with time, reaching its expected maximum of 50 kg plant−1

Full size image
Figure 5
figure 5

Numerical results of system (1) demonstrating the convergence of solutions to the pest persistence equilibrium point for \({\mathcal{R}}_{0} > 1\). Baseline values for the model parameters are as in Table 2. In addition, we set \(u_{E}=u_{L}=u_{P}=u_{A}=0.35\) to obtain \({\mathcal{R}}_{0}=2.8931\). As we can observe, the solutions suggest that the pest will persist in the field and the final maize biomass will be less than the expected 50 kg plant−1

Full size image
Figure 6
figure 6

Model solutions showing the effects of a FAW outbreak with a small initial pest life cycle population. We considered \(E(0)=100\), \(L(0)=P(0)=0\), and \(A(0)=50\). Furthermore, we fixed \(q=0.8\) and \(u_{E}=u_{L}=u_{P}=u_{A}=0.45\) to obtain \({\mathcal{R}}_{0}=1.3583\)

Full size image

Numerical results in Fig. 7 depicts the effects of a FAW outbreak with a large initial pest life cycle population, \(E(0)=2000\), \(L(0)=P(0)=0\), and \(A(0)=15\), combined with less effective control measures, that is, \(u_{E}=u_{L}=0.45\), and \(u_{P}=u_{A}=0\). More often, pesticides, which are known to effectively control FAW, are expensive such that farmers in some areas rely on traditional methods of controlling the pest such as hand picking of caterpillars, picking and destroying egg masses, spraying lime, salt, oil, and soap solution. Prior studies suggests that traditional methods are less effective and are likely to eliminate the egg and larvae population. Hence, in Fig. 7, we explore the effects of a FAW outbreak with a large initial pest life cycle population coupled with less effective control measures. As we can observe, an outbreak with a large pest population coupled with less effective control measure may result in the pest population increasing rapidly so that in less than 100 days, they will reach their respective maximum. After an initial increase, the maize biomass would gradually decrease to a level below its initial biomass. The results highlight the importance of effective control measure on increasing maize biomass whenever there is a FAW outbreak.

Figure 7
figure 7

Model solutions showing the effects of a FAW outbreak with a large initial pest life cycle population, \(E(0)=2000\), \(L(0)=P(0)=0\), and \(A(0)=15\), coupled with less effective control measures, that is, \(u_{E}=u_{L}=0.45\) and \(u_{P}=u_{A}=0\), leading to \({\mathcal{R}}_{0}=58\). We set \(q=0.8\)

Full size image

5 Concluding remarks

In this study, we presented a Caputo fractional-order model for fall armyworm (Spodoptera frugiperda) infestation in a maize field. Fall armyworm (Spodoptera frugiperda) commonly known as FAW remain a major pest of maize. The pest has already been considered as one of the greatest threat to food security in Africa despite the fact that it was first detected in 2016. The pest is highly destructive and fast spreading. Moth are capable of flying up to 100 km in one night. Based on its destructiveness, there is need to gain understanding the dynamics of this pest and the maize plant whenever there is an outbreak. Through the use of mathematical models, it is possible to predict many real-world problems in various fields such as agriculture, economics, biology, engineering, and so on. In particular, mathematical models are capable of providing solutions to phenomena that are difficult to measure in the field. Here fractional derivatives model have been utilized to model the dynamics of FAW infestation in a maize field based on the fact that fractional calculus is naturally related to many adaptive systems with memory and hereditary properties, which widely exist in several fields such as biology, agriculture, medicine, physics, chemistry, and engineering [21].

Mathematical analysis of the proposed model reveals that there exists a threshold parameter, the basic reproduction number, which governs the persistence and extinction of FAW in the field. Biologically, this basic reproduction number represents the average number of newborns produced by one individual female moth during its life span. We have noted that if one female moth is not capable of producing more than one off-spring, then the pest population becomes extinct; otherwise, it persists. The basic reproduction number was qualitatively and quantitatively used to investigate the local and global stability of the model steady state. For two steady states, the model has the pest-free equilibrium and the pest persistence equilibrium. We have observed that both are locally and globally stable. In particular, the pest-free equilibrium point is both locally and globally stable whenever the basic reproduction number is less than unity. However, when the basic reproduction number is greater than unity, there exists a pest persistence equilibrium point, which is also both locally and globally stable.

We have also noted that the model parameters, the egg laying rate and proportion of female moth in the environment, have a strong positive influence on increasing the size of the basic reproduction number. Precisely, increasing in the proportion of female moth in the environment by a certain percent increases the size of the basic reproduction by a similar percentage. FAW intervention strategies aimed at reducing moth population were observed to have a stronger impact on reducing the size of the basic reproduction number than any other model parameter. Numerical illustrations are included to support analytical results and to explore optimal intervention levels essential to minimize persistence of the pest population. We also used numerical simulations to illustrate the impact of initial pest population level during an outbreak on maize growth in a field.

The proposed model is not exhaustive. In the future work, we will explore the effects of temperature and seasonal variation on the dynamics of FAW and its implications on maize growth. In the current study, we found that there is a need for better metadata in plant population studies to help explain calibration and validation of proposed models. Although we did not manage to validate the proposed model with data, due to its unavailability, the proposed model and results will certainly improve the existing knowledge on FAW dynamics and its implications in maize crops.