A new extension to the controlled metric type spaces endowed with a graph

Abstract

In this paper, we initiate a new extension of b-metric spaces, called controlled metric-like spaces, by changing the condition

$$ \bigl[\wp (s,r)=0 \Leftrightarrow s=r\bigr]\quad \text{by } \bigl[\wp (s,r)=0 \Rightarrow s=r\bigr] $$

and that means basically we may have a non-zero self-distance. We prove some fixed point theorems which generalize many results in the literature. Also, we present an interesting application to illustrate our results by considering controlled metric-like spaces endowed with a graph.

1 Introduction

Banach [1] in 1922 started a new field in mathematics, so called fixed point theory. That was the starting point for researchers around the globe to start generalize his result whether by changing the contractions or by generalizing the type of metric spaces, so it can cover a larger class of metrics; see [2–23]. Lately, in [24], an extension of b-metric spaces to extended b-metric spaces was given by Kamran et al. For related work, see [25–30]. Not much later, Mlaiki et al. in [31], introduced another generalization to the b-metric spaces, so called controlled metric type spaces.

In this manuscript, we introduce the concept of controlled metric-like spaces, which involves a generalization of the controlled metric type spaces, that is, by assuming that the “self-distance” of an element is not necessary zero. However, if the value of the metric between two elements is zero, then these two elements are equal. One may ask: what is the point of all these generalizations? In fact the answer to that is quite simple: the larger the class of functions or metrics, the more fields that results can be applied to, such as computer science and engineering. Inspired by the work of Jachymski in [32], where he introduced the concept of metric spaces endowed with a graph, we present in the last section some fixed point results on a controlled metric-like space endowed with a graph.

2 Preliminaries

In 2017, Kamran et al. [24] introduced the notion of extended b-metric spaces.

Definition 2.1

([24])

Given $F\neq \emptyset$ and $\theta : F\times F \rightarrow [1,\infty )$. The function $\Omega :F\times F\rightarrow [0,\infty )$ is called an extended b-metric if

• (1) $\Omega (s,r)=0 \Longleftrightarrow s=r$;

• (2) $\Omega (s,r) = \Omega (r,s)$;

• (3) $\Omega (s,r) \leq \theta (s,r) [\Omega (s,z) + \Omega (z,r)]$,

for all $s,r,z \in F$. In 2018, Mlaiki et al. in [31] introduced the following generalization of extended b-metric spaces, called controlled metric type spaces.

Definition 2.2

([31])

Given $F\neq \emptyset$ and $\eta : F\times F\rightarrow [1,\infty )$. The function $\Omega : F\times F\rightarrow [0,\infty )$ is said to be of controlled metric type if

• (1) $\Omega (s,r)=0$ ⇔ $s=r$;

• (2) $\Omega (s,r)=\Omega (r,s)$;

• (3) $\Omega (s,r)\leq \eta (s,z) \Omega (s,z)+\eta (z,r) \Omega (z,r)$,

for all $s,r,z\in F$. The pair $(F,\Omega )$ is called a controlled metric type space.

Now, we present the definition of controlled metric-like spaces.

Definition 2.3

Given $F\neq \emptyset$ and $\eta : F\times F\rightarrow [1,\infty )$. The function $\Omega : F\times F\rightarrow [0,\infty )$ verifying:

• (CL1) $\wp (s,r)=0$ ⇒ $s=r$;

• (CL2) $\wp (s,r)=\wp (r,s)$;

• (CL3) $\wp (s,r)\leq \eta (s,z) \wp (s,z)+\eta (z,r) \wp (z,r)$,

for all $s,r,z\in F$, is called a controlled metric-like space on F.

Notice that every space called a controlled metric type is a controlled metric-like space, but the converse is not always true, and to prove it we present the following example of a controlled metric-like space, that is not a controlled metric type space.

Example 2.4

Choose $F=\{1,2,\ldots \}$. Take $\wp :F \times F \to [0,\infty )$ as

$$ \wp (s,r)= \textstyle\begin{cases} 0, &\text{if $r=s$ and both even,} \\ \frac{1}{s+r}, &\text{if $s=r$ and both odd,} \\ \frac{1}{s}, &\text{if $s$ is even and $r$ is odd,} \\ \frac{1}{r}, &\text{if $s$ is odd and $r$ is even,} \\ 1, &\text{otherwise}. \end{cases} $$

Given $\eta : F\times F\rightarrow [1,\infty )$ as

$$ \eta (s,r)= \textstyle\begin{cases} s, &\text{if $s$ is even and $r$ is odd,} \\ r, &\text{if $s$ is odd and $r$ is even,} \\ 1, &\text{otherwise}. \end{cases} $$

$(CL1)$ and $(CL2)$ are obvious. We claim that ($CL3$) is satisfied.

Case 1: If $z=s$ or $z=r$, ($CL3$) is satisfied.

Case 2: If $z\neq s$ and $z\neq r$, ($CL3$) holds if $s=r$. Now, assume that $s\neq r$, so $s\neq r\neq z$. Again, ($CL3$) is verified in the following subcases:

• (s1): s, z are even and r is odd;

• (s2): s is even and r, z are odd;

• (s3): s, z are odd and r is even;

• (s4): s, z are even and r is odd;

• (s5): s, r, z are even;

• (s6): s, r are even and z is odd;

• (s7): s, r are odd and z is even;

• (s8): s, r, z are odd.

Thus, $(F,\wp )$ is a controlled metric-like space. It is not difficult to see that $(F,\wp )$ is not a controlled metric type space.

Example 2.5

Take $F=\{0,1,2\}$. Define the function ℘ by

$$ \wp (0,0)=\wp (1,1)=0,\quad\quad \wp (2,2)=\frac{1}{10} $$

and

$$ \wp (0,1)=\wp (1,0)=1,\quad\quad \wp (0,2)=\wp (2,0)=\frac{1}{2},\quad \quad \wp (1,2)=\wp (2,1)=\frac{2}{5}. $$

Take $\eta : F\times F\rightarrow [1,\infty )$ to be symmetric and to be defined by

$$ \eta (0,0)=\eta (1,1)=\eta (2,2)=\eta (0,2)=1, \quad\quad \eta (1,2)= \frac{5}{4}, \quad\quad \eta (0,1)=\frac{11}{10}. $$

Here, ℘ is controlled metric-like on F.

We have $\wp (2,2)=\frac{1}{10}\neq 0$, which implies that $(F,\wp )$ is not a controlled metric type space.

For work in the same direction, see [33]. The definition of being of Cauchy type and of convergence in controlled metric-like spaces is given as follows.

Definition 2.6

Let $(F,\wp )$ be a controlled metric-like space and $\{s_{n}\}_{n\ge 0}$ be a sequence in F.

• (1) $\{s_{n}\}$ is convergent to s in F, if and only if

  $$ \lim_{n\rightarrow \infty }\wp (s_{n},s)=\wp (s,s). $$

  Here, one writes $\lim_{n \rightarrow \infty }{s_{n}=s}$.

• (2) $\{s_{n}\}$ is Cauchy, if and only if $\lim_{n,m\rightarrow \infty }\wp (s_{n},s_{m})$ exists and is finite.

• (3) $(F,\wp )$ is called complete if, for each Cauchy sequence $\{s_{n}\}$, there is some $s\in F$ so that

  $$ \lim_{n\rightarrow \infty }\wp (s_{n},s)=\wp (s,s)=\lim _{n,m \rightarrow \infty }\wp (s_{n},s_{m}). $$

Definition 2.7

Let $(F,\wp )$ be a controlled metric-like space. Let $s\in F$ and $\tau >0$.

• (i) The open ball $B(s,\tau )$ is

  $$ B(s,\tau )=\bigl\{ y\in F, \bigl\vert \wp (s,r)-\wp (s,s) \bigr\vert < \tau \bigr\} . $$

• (ii) The mapping $\zeta :F\rightarrow F$ is called continuous at $s\in F$ if for $\upsilon >0$, there is $\nu >0$ so that $\zeta (B(s,\nu ))\subseteq B(\zeta (s),\upsilon )$. Thus, if ζ is continuous at s, then, for any sequence $\{s_{n}\}$ converging to s, we have $\lim_{n \rightarrow \infty }\zeta s_{n}=\zeta s$, that is,

  $$ \lim_{n\rightarrow \infty }\wp (\zeta s_{n},\zeta s)=\wp (\zeta s, \zeta s). $$

Notice that each controlled metric-like space is a controlled metric space. But the converse is not always true (see Example 2.4 and Example 2.5).

3 Main results

The following result corresponds to the Banach contraction principle on controlled metric-like spaces.

Theorem 3.1

Let ζ be a self-mapping on a complete controlled metric-like space $(F,\wp )$ so that

$$ \wp \bigl(\zeta (s),\zeta (r)\bigr)\leq k\wp (s,r), $$

(3.1)

for all $s,r\in F$, where $k\in (0,1)$. For $s_{0}\in F$, take $s_{n}=\zeta ^{n}(s_{0})$. Suppose that

$$ \sup_{m\geq 1}\lim_{i\rightarrow \infty } \frac{\eta (s_{i+1},s_{i+2})}{\eta (s_{i},s_{i+1})}\eta (s_{i+1},s_{m})< \frac{1}{k}. $$

(3.2)

Also, assume for each $s\in F$,

$$ \lim_{n\rightarrow \infty }\eta (s_{n},s) \quad \textit{and}\quad \lim_{n \rightarrow \infty }\eta (s,s_{n}) \quad \textit{exist and are finite}. $$

(3.3)

Then ζ possesses a unique fixed point, say $\tau \in F$. We have $\wp (\tau ,\tau )=0$.

Proof

Take the sequence $\{s_{n}=\zeta ^{n}(s_{0})\}$. By using (3.1), we get $\wp (s_{n},s_{n+1})\le k^{n}\wp (s_{0},s_{1})$ for all $n\geq 0$. For all integers $n< m$, one writes

$$\begin{aligned} \wp (s_{n},s_{m})&\le \eta (s_{n},s_{n+1}) \wp (s_{n},s_{n+1})+\eta (s_{n+1},s_{m}) \wp (s_{n+1},s_{m}) \\ &\le \eta (s_{n},s_{n+1})\wp (s_{n},s_{n+1})+ \eta (s_{n+1},s_{m}) \eta (s_{n+1},s_{n+2}) \wp (s_{n+1},s_{n+2}) \\ &\quad {} +\eta (s_{n+1},s_{m})\eta (s_{n+2},s_{m}) \wp (s_{n+2},s_{m}) \\ &\le \eta (s_{n},s_{n+1})\wp (s_{n},s_{n+1})+ \eta (s_{n+1},s_{m}) \eta (s_{n+1},s_{n+2}) \wp (s_{n+1},s_{n+2}) \\ &\quad {} +\eta (s_{n+1},s_{m})\eta (s_{n+2},s_{m}) \eta (s_{n+2},s_{n+3})\wp (s_{n+2},s_{n+3}) \\ &\quad {} +\eta (s_{n+1},s_{m})\eta (s_{n+2},s_{m}) \eta (s_{n+3},s_{m})\wp (s_{n+3},s_{m}) \\ &\le \cdots \\ &\le \eta (s_{n},s_{n+1})\wp (s_{n},s_{n+1})+ \sum_{i=n+1}^{m-2} \Biggl(\prod _{j=n+1}^{i}\eta (s_{j},s_{m}) \Biggr)\eta (s_{i},s_{i+1}) \wp (s_{i},s_{i+1}) \\ &\quad {} +\prod_{k=n+1}^{m-1} \eta (s_{k},s_{m})\wp (s_{m-1},s_{m}) \\ &\le \eta (s_{n},s_{n+1})k^{n}\wp (s_{0},s_{1})+\sum_{i=n+1}^{m-2} \Biggl(\prod_{j=n+1}^{i}\eta (s_{j},s_{m}) \Biggr)\eta (s_{i},s_{i+1}) k^{i}\wp (s_{0},s_{1}) \\ &\quad {} +\prod_{i=n+1}^{m-1} \eta (s_{i},s_{m})k^{m-1}\wp (s_{0},s_{1}) \\ &\le \eta (s_{n},s_{n+1})k^{n}\wp (s_{0},s_{1})+\sum_{i=n+1}^{m-2} \Biggl(\prod_{j=n+1}^{i}\eta (s_{j},s_{m}) \Biggr)\eta (s_{i},s_{i+1}) k^{i}\wp (s_{0},s_{1}) \\ &\quad {} + \Biggl(\prod_{i=n+1}^{m-1} \eta (s_{i},s_{m}) \Biggr)k^{m-1}\eta (s_{m-1},s_{m}) \wp (s_{0},s_{1}) \\ &= \eta (s_{n},s_{n+1})k^{n}\wp (s_{0},s_{1})+\sum_{i=n+1}^{m-1} \Biggl(\prod_{j=n+1}^{i}\eta (s_{j},s_{m}) \Biggr)\eta (s_{i},s_{i+1}) k^{i}\wp (s_{0},s_{1}). \end{aligned}$$

Thus, due to $\eta (s,r) \geq 1$,

$$ \wp (s_{n},s_{m})\leq \eta (s_{n},s_{n+1})k^{n} \wp (s_{0},s_{1})+ \sum_{i=n+1}^{m-1} \Biggl(\prod_{j=0}^{i}\eta (s_{j},s_{m}) \Biggr) \eta (s_{i},s_{i+1}) k^{i}\wp (s_{0},s_{1}). $$

Let

$$ \Upsilon _{p}= \sum_{i=0}^{p} \Biggl(\prod_{j=0}^{i}\eta (s_{j},s_{m}) \Biggr)\eta (s_{i},s_{i+1}) k^{i}. $$

Hence, we have

$$ \wp (s_{n},s_{m})\leq \wp (s_{0},s_{1}) \bigl[ k^{n} \eta (s_{n},s_{n+1})+( \Upsilon _{m-1}-\Upsilon _{n}) \bigr]. $$

(3.4)

Condition (3.2), by using the ratio test, implies that $\lim_{n\rightarrow \infty }\Upsilon _{n}$ exists. Hence, $\{\Upsilon _{n}\}$ is a real Cauchy sequence. Letting $n,m\rightarrow \infty$ in the inequality (3.4), we get

$$ \lim_{n,m\rightarrow \infty }\wp (s_{n},s_{m})=0, $$

(3.5)

that is, the sequence $\{s_{n}\}$ is Cauchy in $(F,\wp )$, which is a complete controlled metric-like space, so $\{s_{n}\}$ converges to some $s\in F$. We have

$$ \lim_{n\rightarrow \infty }\wp (s_{n},s)=\wp (s,s)= \lim_{n,m \rightarrow \infty }\wp (s_{n},s_{m})=0. $$

(3.6)

Then $\wp (s,s)=0$. We claim that $\zeta s=s$. Applying $(CL3)$, one writes

$$ \wp (s,s_{n+1})\leq \eta (s,s_{n})\wp (u, s_{n})+ \eta (s_{n},s_{n+1}) \wp (s_{n},s_{n+1}). $$

Using (3.2), (3.3), (3.5) and (3.6),

$$ \lim_{n\rightarrow \infty }\wp (s,s_{n+1})=0. $$

(3.7)

Again, in view of $(CL3)$ and using (3.1),

$$\begin{aligned} \wp \bigl(s,\zeta (s)\bigr)&\leq \eta (s,s_{n+1})\wp (s, s_{n+1})+ \eta \bigl(s_{n+1}, \zeta (s)\bigr)\wp \bigl(s_{n+1}, \zeta (s)\bigr) \\ &\le \eta (s,s_{n+1})\wp (s, s_{n+1})+ k\eta \bigl(s_{n+1},\zeta (s)\bigr)\wp (s_{n}, s). \end{aligned}$$

Letting $n\rightarrow \infty$ and inserting (3.3) and (3.7), we conclude that $\wp (s,\zeta (s))=0$, i.e., $\zeta (s)=s$.

Assume that $\zeta \sigma =\sigma$ and $\zeta \varsigma =\varsigma$. Here,

$$ \wp (\sigma ,\varsigma )=\wp \bigl(\zeta (\sigma ),\zeta (\varsigma )\bigr)\le k \wp (\sigma ,\varsigma ). $$

It holds unless $\wp (\sigma ,\varsigma )=0$, so $\sigma =\varsigma$. □

Theorem 3.1 is supported by the two following examples.

Example 3.2

Choose $F=\{0,1,2\}$. Take ℘ to be symmetric and to be defined by

$$ \wp (0,0)=0,\quad\quad \wp (1,1)=0,\quad\quad \wp (2,2)=\frac{1}{100}, $$

and

$$ \wp (0,1)=1,\quad\quad \wp (0,2)=\frac{11}{20},\quad\quad \wp (1,2)= \frac{2}{5}. $$

Given $\eta : F\times F\rightarrow [1,\infty )$ as

$$ \eta (0,0)=\eta (1,1)=\eta (2,2)=\eta (0,2)=\eta (2,0)=1, \quad\quad \eta (1,2)= \eta (2,1)=\frac{49}{40}, $$

and

$$ \eta (0,1)=\eta (1,0)=\frac{11}{10}. $$

Clearly, ℘ is controlled metric-like (℘ is not a controlled metric type on F). Define the self-mapping ζ on F by

$$ \zeta (0)=2\quad \text{and}\quad \zeta (1)=\zeta (2)=1. $$

Set $k=\frac{4}{5}$. It is clear that (3.1) is verified. For each $s_{0}\in F$, (3.2) holds. All hypotheses of Theorem 3.1 are fulfilled, and hence ζ possesses a unique fixed point, which is $s=1$.

Example 3.3

Let $F =[0,\infty )$. Define $\wp :F ^{2}\rightarrow {}[ 0,\infty )$ by

$$ \wp (x,y)= \textstyle\begin{cases} 0&\text{if } x=y=0, \\ \frac{y}{1+y}&\text{if } x=0,y\neq 0, \\ \frac{x}{1+x}&\text{if } y=0,x\neq 0, \\ x+y&\text{if } x\neq 0,y\neq 0. \end{cases} $$

Consider $\eta :F^{2}\rightarrow {}[ 1,\infty )$ as $\eta (x,y )=2+2x +2y$. Note that ℘ is controlled metric-like on F.

First, $(CL1)$ and $(CL2)$ are obvious. We need to prove $(CL3)$. For this, let x, y and z in F. We state the following cases:

Case 1: $x=z=0$. Here, $(CL3)$ holds.

Case 2: $x=0$ and $z\neq 0$.

Subcase 1: $y=0$. We have

$$ \begin{aligned} \wp (x,z)&=\frac{z}{1+z} \\ &\leq (2) (0)+(2+2z)\frac{z}{1+z} \\ &= \eta (x,y)\wp (x,y)+\eta (y,z)\wp (y,z). \end{aligned} $$

Subcase 2: $y\neq 0$. We have

$$ \begin{aligned} \wp (x,z)&=\frac{z}{1+z} \\ &\leq (2+2y)\frac{y}{1+y}+(2+2z) (y+z) \\ &= \eta (x,y)\wp (x,y)+\eta (y,z)\wp (y,z). \end{aligned} $$

Case 3: $z=0$ and $x\neq 0$. Proceeding similarly to Case 2, $(CL3)$ holds.

Case 4: $x\neq 0$ and $z\neq 0$.

Subcase 1: $y=0$. We have

$$ \begin{aligned} \wp (x,z)&=x+z \\ &\leq (2+2x)\frac{x}{1+x}+(2+2z)\frac{z}{1+z} \\ &= \eta (x,y)\wp (x,y)+\eta (y,z)\wp (y,z). \end{aligned} $$

Subcase 2: $y\neq 0$. We have

$$ \begin{aligned} \wp (x,z)&=x+z \\ &\leq (2+2x+2y) (x+y)+(2+2y+2z) (y+z) \\ &= \eta (x,y)\wp (x,y)+\eta (y,z)\wp (y,z). \end{aligned} $$

On the other hand, $(F,\wp )$ is not a b-metric-like space. We argue by contradiction by assuming that $(F ,\wp )$ is a b-metric-like space with a coefficient $s\geq 1$ (a constant). Then, for any real $y>0$, we have

$$ \wp (y,y+1)\leq s\bigl[\wp (y,0)+\wp (0,y+1)\bigr]. $$

That is,

$$ 2y+1\leq s\biggl[\frac{y}{1+y}+\frac{y+1}{2+y}\biggr]. $$

Letting $y\rightarrow \infty$, we get $+\infty \leq 2s$, which is a contradiction.

Consider the self-mapping ζ on F defined by $\zeta (x)=\frac{x}{3}$. It is clear that (3.1) holds for all $x,y\in F$, with $k=\frac{2}{5}$. Take $s_{0}=1$. The sequence $\{s_{n}\}$ given as $s_{n}=\zeta ^{n}(s_{0})$ is written as

$$ s_{n}=\frac{1}{3^{n}},\quad n=0,1,\ldots . $$

A simple calculation yields

$$ \sup_{m\geq 1}\lim_{i\rightarrow \infty } \frac{\eta (s_{i+1},s_{i+2})}{\eta (s_{i},s_{i+1})}\eta (s_{i+1},s_{m})=\biggl(2+ \frac{1}{3}\biggr)=\frac{7}{3}< \frac{5}{2}= \frac{1}{k}. $$

That is, (3.2) is verified. Moreover, we have, for each $s\in F$,

$$ \lim_{n\rightarrow \infty }\eta (s_{n},s)=\lim _{n\rightarrow \infty } \eta (s,s_{n})=(2+2s) \quad \text{exists}. $$

All hypotheses of Theorem 3.1 hold. Hence, ζ admits a unique fixed point, which is $\tau =0$. It verifies $\wp (\tau ,\tau )=0$.

Definition 3.4

Let $\zeta :F \longrightarrow F$. For some $s_{0}\in F$, let $O (s_{0})=\{s_{0},\zeta s_{0},\zeta ^{2}s_{0},\ldots\}$ be the orbit of $s_{0}$. Given $P:F\longrightarrow \mathbb{R}$. Such a P is called ζ-orbitally lower semi-continuous at $\varrho \in F$ if for $\{s_{n}\}\subset O (s_{0})$ so that $s_{n}\longrightarrow \varrho$, we have $P(\varrho )\leq \lim_{n\rightarrow \infty }\inf P(s_{n})$.

As in [24], using Definition 3.4, a consequence of Theorem 3.1 (it is a generalization of Theorem 1 in [13]) is as follows.

Corollary 3.5

Let $\zeta \colon F\rightarrow F$ be a self-mapping on a complete controlled metric-like space $(F,\wp )$. Given $s_{0}\in F$. Assume there is $k\in (0,1)$ so that

$$ \wp \bigl(\zeta (z),\zeta ^{2}(z)\bigr)\leq k\wp \bigl(z,\zeta (z) \bigr), \quad \textit{for each } z\in O(s_{0}). $$

(3.8)

Take $s_{n}=\zeta ^{n}(s_{0})$. Suppose that

$$ \sup_{m\geq 1}\lim_{i\rightarrow \infty } \frac{\eta (s_{i+1},s_{i+2})}{\eta (s_{i},s_{i+1})}\eta (s_{i+1},s_{m})< \frac{1}{k}. $$

(3.9)

Then $s_{n}\rightarrow l\in F$ as $n\rightarrow \infty$. Further, if the functional $\delta \mapsto \wp (s,\zeta (\delta ))$ is ζ-orbitally lower semi-continuous at l, we get $\zeta (l)=l$.

4 Controlled metric-like spaces endowed with a graph

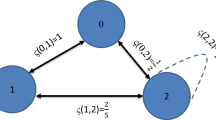
Throughout this section, we denote controlled metric-like spaces by $(CMLS)$. Now, we present $(CMLS)$ endowed with a graph. Figure 1 is an example of a controlled metric-like space endowed with a graph.

Figure 1

Controlled metric-like space as in Example 2.5

Consider the $(CMLS)$ $(F,\wp )$, let Δ be the diagonal of $F^{2}$. A graph G is defined by the pair $(V,E)$ where V is a set of vertices coinciding with F and E is the set of its edges with $\Delta \subset E$. From now on, assume that G has no parallel edges.

Definition 4.1

([32])

Let t and s be two vertices of a graph G. We define $q\in \mathbb{N}\cup \{0\}$ to be the length of the path between t and s in G by a sequence $(k_{i})_{i=0}^{q}$ of $q+1$ distinct vertices where $k_{0}=t$, $k_{n}=s$ and $(k_{i},k_{i+1})\in E(G)$ for $i=1,2,\ldots,q$.

Note that the graph G can be converted to a weighted graph and associate to each edge the value of $(CMLS)$.

Notation

Let $F^{g}=\{x\in F/ (x,gx)\in E(G) \text{ or } (gx,x)\in E(G)\}$.

Definition 4.2

Let $(F,\wp )$ be a complete $(CMLS)$ endowed with a graph G. The mapping $\zeta \colon F\rightarrow F$ is said to be a $G_{\phi }$-contraction if

• $$ \text{for all } t,s\in F, \quad (t,s)\in E(G) \quad \Longrightarrow \quad (\zeta t, \zeta s)\in E(G); $$

  (4.1)

• there is $\phi :[0,\infty )\longrightarrow [0,\infty )$ so that

  $$ \xi \bigl(\zeta t,\zeta ^{2}t\bigr)\leq \phi \bigl(\xi (t,\zeta t) \bigr)\quad \forall t \in X^{\zeta }, $$

  (4.2)

  where ϕ is nondecreasing and $\{\phi ^{n}(t)\}_{n\in \mathbb{N}}\rightarrow 0$ $\forall t>0$.

Definition 4.3

The mapping $\zeta :F\longrightarrow F$ is called orbitally G-continuous if for all $\tau ,\rho \in X$ and $\{s_{n}\}_{n\in \mathbb{N}}$ a positive sequence,

$$ \zeta ^{s_{n}}\tau \longrightarrow \rho , \quad\quad \bigl(\zeta ^{s_{n}}\tau , \zeta ^{s_{n+1}}\tau \bigr)\in E(G) \quad \Longrightarrow \quad \zeta \bigl(\zeta ^{s_{n}} \tau \bigr)\longrightarrow \zeta \rho \quad \text{as } n\rightarrow \infty . $$

Lemma 4.4

Let $(F,\wp )$ be a complete $(CMLS)$ equipped by a graph G. Suppose that $\zeta \colon F\rightarrow F$ be a $G_{\phi }$-contraction. If $t\in X^{\zeta }$ then there is $q(t)\geq 0$ so that

$$ \wp \bigl(\zeta ^{n}t,\zeta ^{n+1}t\bigr)\leq \phi ^{n}\bigl(q(t)\bigr) \quad \forall n \in \mathbb{N} , $$

(4.3)

where $q(t)=\wp (t,\zeta t)$.

Proof

Let $t\in F^{\zeta }$, then $(t,\zeta t)\in E(G)$ or $(\zeta t,t)\in E(G)$. Assume that w.l.o.g. $(t,\zeta t)\in E(G)$. Hence,

$$ \bigl(\zeta ^{n},\zeta ^{n+1}t\bigr)\in E(G)\quad \forall n\in \mathbb{N}. $$

(4.4)

Hence, we deduce

$$\begin{aligned} \wp \bigl(\zeta ^{n}t,\zeta ^{n+1}t\bigr) \leq & \phi \bigl( \wp \bigl(\zeta ^{n-1}t, \zeta ^{n}t\bigr)\bigr) \\ \leq & \phi ^{2}\bigl(\wp \bigl(\zeta ^{n-2}t,\zeta ^{n-1}t\bigr)\bigr) \\ \leq & \vdots \\ \leq & \phi ^{n}\bigl(\wp (t,\zeta t)\bigr)=\phi ^{n} \bigl(q(t)\bigr). \end{aligned}$$

 □

Theorem 4.5

Let $(F,\wp , G)$ be a complete $(CMLS)$ equipped by a graph G. Suppose that $\zeta \colon F\rightarrow F$ be a $G_{\phi }$-contraction, which is orbitally G-continuous. Consider the property $(P)$ as follows: $\forall \{t_{n}\}_{n\in \mathbb{N}}$ in F, if $t_{n}\longrightarrow t$ and $(t_{n},t_{n+1})\in E(G)$, then there is $\{t_{k_{n}}\}_{n\in \mathbb{N}}$ where $(t_{k_{n}},t)\in E(G)$, holds. Further, suppose that, for each $s\in F$,

$$ \lim_{n\rightarrow \infty }\eta \bigl(\zeta ^{i}s,\zeta ^{n}s\bigr) \quad ( \forall i\geq 1)\quad \textit{and}\quad \lim _{n\rightarrow \infty }\eta \bigl( \zeta ^{n}s,\zeta ^{n+1}s \bigr) \quad \textit{exist and are finite} $$

(4.5)

and

$$ \textit{if} \quad \lim_{n\rightarrow \infty }\zeta ^{n}s \rightarrow u\in F , \quad \textit{then}\quad \wp (\zeta u,u)> \limsup_{n\rightarrow \infty } \eta \bigl( \zeta u,\zeta ^{n}s\bigr)\wp (\zeta u,\zeta u). $$

(4.6)

Thus, the restriction of $\zeta _{| [s]_{\tilde{G}}}$ to $[s]_{\tilde{G}}$ possesses a fixed point. Moreover, if for every two fixed points $v_{1}$, $v_{2}$ we have $\eta (v_{1}, v_{2})>1$, then we have uniqueness of the fixed point.

Proof

Consider $s\in F^{\zeta }$. By Lemma 4.4, there is $q(s)\geq 0$ so that

$$ \wp \bigl(\zeta ^{n}s,\zeta ^{n+1}s\bigr)\leq \phi ^{n}\bigl(q(s)\bigr). $$

First, we show that $(\zeta ^{n}s)_{n\in \mathbb{N}}$ converges to some $u\in F$. It should be enough to ensure that $\{\zeta ^{n}t\}_{n\in \mathbb{N}}$ is Cauchy. Take the integers n, m. Using again Lemma 4.4, we get

$$\begin{aligned} \wp \bigl(\zeta ^{n}s,\zeta ^{n+m}s\bigr) \leq & \eta \bigl( \zeta ^{n}s,\zeta ^{n+1}s\bigr) \wp \bigl(\zeta ^{n}s,\zeta ^{n+1}s\bigr)+\eta \bigl(\zeta ^{n+1}s, \zeta ^{n+m}s\bigr) \wp \bigl(\zeta ^{n+1}s,\zeta ^{n+m}s\bigr) \\ \leq & \eta \bigl(\zeta ^{n}s,\zeta ^{n+1}s\bigr)\wp \bigl( \zeta ^{n}s,\zeta ^{n+1}s\bigr)+ \eta \bigl(\zeta ^{n+1}s,\zeta ^{n+m}s\bigr)\eta \bigl(\zeta ^{n+1}s, \zeta ^{n+2}s\bigr) \\ & {} \times \wp \bigl(\zeta ^{n+1}s,\zeta ^{n+2}s\bigr) \\ & {} + \eta \bigl(\zeta ^{n+1}s,\zeta ^{n+m}s\bigr)\eta \bigl(\zeta ^{n+2}s,\zeta ^{n+m}s\bigr) \wp \bigl(\zeta ^{n+2}s,\zeta ^{n+m}s\bigr) \\ \leq & \vdots \\ \leq & \eta \bigl(\zeta ^{n}s,\zeta ^{n+1}s\bigr)\wp \bigl( \zeta ^{n}s,\zeta ^{n+1}s\bigr)+ \sum _{i=n+1}^{n+m-2}\Biggl( \prod_{j=n+1}^{i} \eta \bigl(\zeta ^{j}s,\zeta ^{n+m}s\bigr)\Biggr)\eta \bigl( \zeta ^{i}s,\zeta ^{i+1}s\bigr) \\ & {} \times \wp \bigl(\zeta ^{i}s,\zeta ^{i+1}s\bigr)+ \prod_{k=n+1}^{n+m-1} \eta \bigl(\zeta ^{k}s,\zeta ^{n+m}s\bigr)\wp \bigl(\zeta ^{n+m-1}s, \zeta ^{n+m}s\bigr) \\ \leq & \eta \bigl(\zeta ^{n}s,\zeta ^{n+1}s\bigr)\phi ^{n}\bigl(q(s)\bigr)+ \sum_{i=n+1}^{n+m-2} \Biggl( \prod_{j=n+1}^{i} \eta \bigl(\zeta ^{j}s,\zeta ^{n+m}s\bigr)\Biggr)\eta \bigl(\zeta ^{i}s,\zeta ^{i+1}s\bigr) \phi ^{i}\bigl(q(s)\bigr) \\ & {} + \prod_{k=n+1}^{n+m-1}\eta \bigl(\zeta ^{k}s,\zeta ^{n+m}s\bigr) \phi ^{n+m-1}\bigl(q(s) \bigr)\eta \bigl(\zeta ^{n+m-1}s,\zeta ^{n+m}s\bigr) \\ \leq & \eta \bigl(\zeta ^{n}s,\zeta ^{n+1}s\bigr)\phi ^{n}\bigl(q(s)\bigr)+ \sum_{i=n+1}^{n+m-1} \Biggl( \prod_{j=0}^{i} \eta \bigl(\zeta ^{j}s,\zeta ^{n+m}s\bigr)\Biggr)\eta \bigl(\zeta ^{i}t,\zeta ^{i+1}s\bigr) \phi ^{i}\bigl(q(s)\bigr) \\ \leq & \prod_{j=0}^{n}\eta \bigl(\zeta ^{j}t,\zeta ^{n+m}s\bigr)) \eta \bigl(\zeta ^{n}s, \zeta ^{n+1}s\bigr)\phi ^{n}\bigl(q(s)\bigr) \\ & {} + \sum_{i=n+1}^{n+m-1}\Biggl( \prod _{j=0}^{i} \eta \bigl(\zeta ^{j}s, \zeta ^{n+m}s\bigr)\Biggr)\eta \bigl(\zeta ^{i}s,\zeta ^{i+1}s\bigr) \phi ^{i}\bigl(q(s)\bigr) \\ = & \sum_{i=n}^{n+m-1}\Biggl( \prod _{j=0}^{i} \eta \bigl(\zeta ^{j}s,\zeta ^{n+m}s\bigr)\Biggr)\eta \bigl(\zeta ^{i}s,\zeta ^{i+1}s\bigr) \phi ^{i}\bigl(q(s)\bigr) \\ = & \sum_{i=n}^{n+m-1}\Gamma _{i} \phi ^{i}\bigl(q(s)\bigr),\quad \text{where } \Gamma _{i}=\Biggl( \prod_{j=0}^{i}\eta \bigl(\zeta ^{j}s, \zeta ^{n+m}s\bigr)\Biggr)\eta \bigl(\zeta ^{i}s,\zeta ^{i+1}s\bigr) \\ = & \sum_{i=1}^{m}\Gamma _{i}^{n+i-1}\phi ^{n+i-1}\bigl(q(s)\bigr). \end{aligned}$$

In view of the property of ϕ and using (4.5), we deduce that $\sum_{i=1}^{m}\Gamma _{i}^{n+i-1}\phi ^{n+i-1}(q(s))$ is convergent to 0 as $n,m\longrightarrow \infty$. Thus,

$$ \lim_{n,m\rightarrow \infty }\wp \bigl(\zeta ^{n}s,\zeta ^{m}s\bigr)=0, $$

(4.7)

that is, the sequence $\{\zeta ^{n}s\}$ is Cauchy in $(F,\wp )$. Its completeness entails that $\{\zeta ^{n}s\}$ converges to some $u\in F$, so that

$$ \lim_{n\rightarrow \infty }\wp \bigl(\zeta ^{n}s,u \bigr)=\wp (u,u)=\lim_{n,m \rightarrow \infty }\wp \bigl(\zeta ^{n}s,\zeta ^{m}s\bigr)=0. $$

(4.8)

We have $\wp (u,u)=0$.

Since $s\in F^{\zeta }$, one writes that $\zeta ^{n}s\in F^{\zeta }$ for every $n\in \mathbb{N}$. We suppose that $(s,\zeta s)\in E(G)$, by $(P)$, we deduce that there is $\{\zeta ^{k_{n}}s\}_{n\in \mathbb{N}}$ of $\{\zeta ^{n}s\}_{n\in \mathbb{N}}$ so that $(\zeta ^{k_{n}}s,u)\in E(G)$ for any $n\in \mathbb{N}$. We consider the path in G as follows: $s,\zeta s,\ldots,\zeta ^{k_{1}}s,u$ and so $u\in [s]_{\tilde{G}}$. The orbital G-continuity of ζ yields

$$ \lim_{n\rightarrow \infty } \wp \bigl(\zeta \bigl(\zeta ^{k_{n}}s\bigr), \zeta u\bigr)= \wp (\zeta u,\zeta u). $$

(4.9)

Suppose that $\wp (\zeta u,u)>0$. Applying $(CL3)$, one writes

$$\begin{aligned} \wp (\zeta u,u) \leq \eta (\zeta u,\zeta ^{k_{n}}\wp \bigl(\zeta u,\zeta ^{k_{n}}s\bigr)+ \eta \bigl(\zeta ^{n}s,u\bigr)\wp \bigl(\zeta ^{k_{n}} s,u\bigr). \end{aligned}$$

Letting $n\rightarrow \infty$ and using (4.5), (4.8) and (4.9), we get

$$ \wp (\zeta u,u)\leq \limsup_{n\rightarrow \infty } \eta \bigl(\zeta u, \zeta ^{k_{n}} s\bigr)\wp (\zeta u,\zeta u). $$

It contradicts (4.6). Hence, $\wp (\zeta u,u)=0$, so $\zeta u=u$, that is, u is a fixed point of $\zeta| _{[s]_{\tilde{G}}}$.

For its uniqueness, suppose there are two fixed points $v_{1}$ and $v_{2}$, i.e., $\zeta v_{1}=v_{1}$ and $\zeta v_{2}=v_{2}$. We have

$$\begin{aligned} \wp (v_{1},v_{2}) \leq & \eta (v_{1},v_{1}) \wp (v_{1},v_{1})+ \eta (v_{1},v_{2}) \wp (v_{1},v_{2}) \\ \leq & \frac{\eta (v_{1},v_{1})}{1-\eta (v_{1},v_{2})}\wp (v_{1},v_{1}). \end{aligned}$$

Since $\eta >1$, we have $\wp (v_{1},v_{2})\leq 0$, and so $v_{1}=v_{2}$. □

5 Conclusion

The $(CMLS)$ endowed with a graph introduced in this paper can be successfully used in different branches of scientific knowledge, for example when studying the kinetics of biochemical reaction networks, where we have the serious problem of the choice of “appropriate distance” in the analysis of a “K-angle general kinetic reaction system”; see [34].