Abstract
In this paper, we investigate a class of fractional-order gene regulatory networks with time-varying delays and structured uncertainties (UDFGRNs). First, we deduce the existence and uniqueness of the equilibrium for the UDFGRNs by using the contraction mapping principle. Next, we derive a novel global uniform asymptotic stability criterion of the UDFGRNs by using a Lyapunov function and the Razumikhin technique, and the conditions relating to the criterion depend on the fractional order of the UDFGRNs. Finally, we provide two numerical simulation examples to demonstrate the correctness and usefulness of the novel stability conditions. One of the most interesting findings is that the structured uncertainties indeed have an impact on the stability of the system.
Similar content being viewed by others
1 Introduction
In recent years, tremendous progress has been made in modern biology because of the development of gene sequencing, especially the third generation gene sequencing technology. Based on gene sequencing and other experimental methods, it has been found that most biological functions are controlled not only by several molecules or genes, but also by complex interactions between many components. A large number of DNAs, RNAs, proteins, and small molecules in an organism together with the mechanisms which regulate the expression of genes form gene regulatory networks (GRNs) [1]. Now GRNs comprise one of the important research directions in the field of system biology. Researchers have established various GRN models from their respective perspectives, such as Boolean networks [2], Petri networks [3], Bayesian networks [4], differential equation models [5–7], etc.
A lot of research has focused on integer-order differential equation model of GRNs [8–10]. Fractional-order calculus is a generalization of integer-order derivative and integral theory to arbitrary real order. Because fractional derivative operators are nonlocal, possess memory and hereditary properties, they have more advantages than integer-order systems in modeling GRNs. So with the development of fractional differential equation theory, the research on GRNs has gradually shifted from integer-order model to fractional-order model [1, 5, 11, 12].
As GRNs are modeled from time-series data of real-world gene expression, it has been well recognized that the modeling errors and parameter fluctuations are unavoidable primarily due to certain limitations to the current experimental techniques in GRNs. Moreover, it has been pointed out that the system parameters identified from experimental data may form an unknown, but bounded time-varying function, which incorporates structured or parameter uncertainties (also called variations or fluctuations) [13]. It is obtained that structured uncertainties in GRNs may cause poor performance or even instability of real genetic networks [13–17]. Therefore, it may be essential to take the structured uncertainties into account when investigating the dynamical behaviors of DFGRNs.
According to bioinformatics theory, some time is needed to complete the process of transcription and translation of gene information in GRNs. For example, in eukaryotic cells, it takes time for RNA and protein synthesis and to transport RNA and protein from nucleus to cytoplasm at different locations. Therefore, time delay has become a key factor affecting gene expression. Many literature sources have reported the effects of time delay in gene regulatory networks [8, 10, 18–20]. These results show that the stability of a gene regulatory network system may even be affected due to the existence of time delay. In recent years, fractional-order gene regulatory networks with constant delays have attracted more and more researchers’ interest [6, 10, 19, 21]. Moreover, some researchers have paid attention to the fractional-order dynamic systems with time-varying delays [7, 22–26]. Zhang et al. [7] discussed the stability for a fractional-order gene regulatory network with time-lag by using Jensen and Wirtinger inequalities, etc., and obtained the model stability results. Recently, Zhang et al. put forward a novel stability condition on fractional-order composite systems with time delay based on the vector Lyapunov function [27], and investigated the asymptotic stability of nonlinear fractional-order systems with multiple time delays via two new control methods [28], which provide us a new idea to find stability conditions and control of fractional-order dynamic systems with time-varying delays in the future research. In [22], Razumikhin-type stability for fractional-order differential equation with time-varying delays is investigated. The authors obtained global uniform asymptotic stability results for the considered systems. However, the stability conditions didn’t include the fractional order of the systems. Wu et al. [21] investigated global asymptotic stability for fractional-order GRNs (FGRNs) with constant time delay by using the Lyapunov method and comparison theorem. Wu et al. [26] studied the finite-time stability for DFGRNs with structured uncertainties and controllers by using a generalized Gronwall inequality and norm technique. The results showed that the structured uncertainties can shorten the “estimated time” of finite-time stability. We naturally ask whether the structured uncertainties affect the global asymptotic stability of DFGRNs. What are the global uniform asymptotic stability conditions related to fractional order for FGRNs with time-varying delays and structured uncertainties?
This paper answers the above questions. We investigate a class of FGRNs with time-varying delays and structured uncertainties by virtue of a Lyapunov function and Razumikhin technique. Compared with some recent results [21, 22, 26], the chief contributions of our study are as follows: (1) we obtain sufficient conditions related to fractional order of the global uniform asymptotic stability for FGRNs with time-varying delays and structured uncertainties, and illustrate the advantages of our stability conditions in numerical examples; (2) It is shown that bigger structured uncertainties can make DFGRNs unstable in numerical examples. The rest of this paper is organized as follows: Sect. 2 mainly introduces the model studied in this paper and some necessary concepts and lemmas. In Sect. 3, the existence and uniqueness of the equilibrium point are obtained, and the sufficient conditions on global uniform asymptotical stability for the DFGRNs are given. In Sect. 4, two examples are provided to show the effectiveness of the obtained results. Finally, some conclusions are drawn in Sect. 5.
2 Preliminaries
Definition 1
([29])
The fractional integral of order q for a function \(f(t)\) is defined as
where \(t\geq a, a\in R,q>0\). The Gamma function \(\Gamma (q)\) is defined by the integral \(\Gamma (q)=\int _{0}^{\infty }t^{q-1}e^{-t}\,dt\).
Definition 2
([29])
The Riemann–Liouville fractional derivative of order q for a function f is defined as
where \(t\geq a\) and n is a positive integer such that \(n-1< q< n\).
Definition 3
([29])
Caputo’s fractional derivative of order q for a function f is defined by
where \(t\geq a\) and n is a positive integer such that \(n-1< q< n\).
For convenience, we choose the notation \(I^{q}_{t}={_{0}}I^{q}_{t}\), \({}^{C}D^{q}_{t} = {_{0}^{C}}D^{q}_{t}\), \({^{RL}}D_{t}^{q}={_{0}^{RL}}D_{t}^{q}\).
In [26], we have investigated the finite-time stability of the following FGRNs with time-varying delays and structured uncertainties:
where \(q\in (0,1),m_{i}(t),p_{i}(t)\in R^{+}\) are the concentrations of mRNA and protein of the ith node, respectively; the parameters \(a_{i}>0\) and \(c_{i}>0\) are the decay rates of mRNA and protein, respectively; \(d_{i}>0\) and \(e_{i}\geq 0\) are the translation rates; \(\Delta a_{i}(t), \Delta c_{i}(t), \Delta d_{i}(t), \Delta e_{i}(t), \Delta w_{ij}(t), \Delta k_{ij}(t)\) are the norm-bounded unknown functions; the transcriptional delay \(\tau _{1}(t)\) and translational delay \(\tau _{2}(t)\) are bounded continuous functions on R with \(0\leq \tau _{i}(t)\leq \tau _{i}^{*}\ (i=1,2)\), here \(\tau _{i}^{*}\) are positive constants. Both \(f_{j}(p_{j}(t))\) and \(g_{j}(p_{j}(t-\tau _{1}(t)))\) represent the feedback regulation of the protein on the transcription. Generally, both functions are nonlinear but monotonic. As monotonic increasing or decreasing regulatory functions, \(f_{j}\) and \(g_{j}\) usually have the Michaelis–Menten or Hill forms [30]; \(B_{i}=\sum_{j\in I_{i}}b_{ij}+\sum_{j\in \bar{I}_{i}} \bar{b}_{ij}\), \(b_{ij}\) and \(\bar{b}_{ij}\) are bounded constants which are respectively the dimensionless transcriptional rate of transcription factor j to i at time t and \(t-\tau _{1}(t)\), and \(I_{i}, \bar{I}_{i}\), respectively, are the sets of all j’s where the transcription factor j is a repressor of gene i at time t and \(t-\tau _{1}(t)\); the matrices \(W=(w_{ij})\in R^{n\times n}\), \(K=(k_{ij}) \in R^{n\times n}\) are the coupling matrices of the gene network, which are defined as follows:
In order to investigate whether structured uncertainties can affect the global asymptotical stability of FGRNs and get the global stability conditions related to the fractional order, we consider the global uniform asymptotical stability of DFGRN (1).
The initial conditions for system (1) are as follows:
where \(\tau ^{*}=\max \{\tau _{1}^{*},\tau _{2}^{*}\}, \phi _{i}(t)\in C([-\tau ^{*},0],R^{n})\ (i=1,2)\) are the given initial functions with
Definition 4
The vector \((m^{*},p^{*})\) is an equilibrium point of DFGRN (1) if and only if
where \(m^{*}=(m_{1}^{*},\dots,m_{n}^{*})^{T},p^{*}=(p_{1}^{*},\dots,p_{n}^{*})^{T}\).
3 Main results
In order to prove our theorems, we need the following lemmas.
Lemma 1
([31])
If \(h(t)\in C^{1}([0,+\infty ),R)\) is a continuously differentiable function, then the following inequality holds almost everywhere:
Lemma 2
([29])
If \(f(t)\in C^{1}[a,+\infty )\) and \(0< q<1\), then the following properties hold:
-
(i)
\(_{a}^{C}D_{t}^{q}f(t)=_{a}^{RL}D_{t}^{q}f(t)- \frac{f(a)}{\Gamma (1-q)}(t-a)^{-q} \)
-
(ii)
If \(f(t)\) and φ, along with all its derivatives, are continuous in \([a,t]\), then Leibniz rule for fractional differentiation takes the form:
$$ _{a}^{RL}D_{t}^{q}\bigl(\varphi (t)f(t) \bigr)=\sum_{k=0}^{n}\binom{q}{k} \frac{d^{k}\varphi (t)}{dt^{k}}{_{a}^{RL}D}_{t}^{q-k}f(t)-R_{n}^{q}(t), $$where \(n\geq q+1, t\geq a, a \in R\),
$$\begin{aligned} &R_{n}^{q}(t)=\frac{(-1)^{n}(t-q)^{n-q+1}}{n!\Gamma (-q)} \int _{0}^{1} \int _{0}^{1}F_{q}(t,\xi,\eta )\,d\xi\, d \eta, \\ &F_{q}(t,\xi,\eta )=f\bigl(a+\eta (t-a)\bigr)\varphi ^{(n+1)} \bigl(a+(t-a) (\xi + \eta -\xi \eta )\bigr), \end{aligned}$$and
$$ \binom{q}{k}=\frac{\Gamma (q+1)}{k!\Gamma (q-k+1)}. $$
In order to prove our theorems, we still need the following lemmas. Consider the following system:
where \(q\in (0,1), 0\leq \tau (t)\leq \tau ^{*},f:R^{+}\times R^{n}\times R^{n} \rightarrow R^{n}\) is continuous in t and locally Lipschitz in x on \([a,\infty ), a\in R\).
Lemma 3
([22])
Suppose that \(\omega _{1},\omega _{2}: R\rightarrow R\) are continuous nondecreasing functions, \(\omega _{1}(s)\) and \(\omega _{2}(s)\) are positive for \(s>0\), and \(\omega _{1}(0)=\omega _{2}(0)=0\), \(\omega _{2}\) strictly increasing. If there exists a continuously differentiable function \(V: R\times R^{2n}\rightarrow R\) such that
and for any given \(a\in R\), the Caputo fractional derivative of V along the solution \(x(t)\) of system (3) satisfies
then system (3) is uniformly stable.
Lemma 4
([22])
Suppose all of the conditions of Lemma 3are satisfied. If, in addition, there exist three positive constants \(\mu _{1},\mu _{2},\mu _{3}\) with \(\mu _{3}>\tau ^{*}\) and \(\frac{q^{2}-q+1}{\mu _{3}^{q}\Gamma (1-q)}+ \frac{\mu _{1}}{(1-\frac{\tau ^{*}}{\mu _{3}})^{q}}-\mu _{2}\leq 0\) such that
for \(t\geq a\), then system (3) is globally uniformly asymptotically stable.
Proof
See the Appendix. □
In addition, we introduce the following assumptions:
- (\(H_{1}\)):
-
The feedback regulation functions \(f_{i},g_{i}\) are Lipschitz continuous. That is, there exist positive constants \(\gamma _{i}, L_{i},i=1,2,\dots,n\), such that
$$ \bigl\vert f_{i}(x)-f_{i}(y) \bigr\vert < \gamma _{i} \vert x-y \vert , \text{ } \bigl\vert g_{i}(x)-g_{i}(y) \bigr\vert < L_{i} \vert x-y \vert ,\quad i=1,2,\dots,n $$(7)for all \(x,y\in R\) with \(x\neq y\).
- (\(H_{2}\)):
-
There exist positive constants \(\delta _{i} \ (i=1,2,\dots,2n)\) such that \(\lambda >0\),
where \(\lambda _{i} = (a_{i}-\widetilde{a}_{i}) - \frac{\delta _{n+i}}{\delta _{i}}(d_{i}+\widetilde{d}_{i}+e_{i}+ \widetilde{e}_{i})\), \(\lambda _{n+i} = (c_{i}-\widetilde{c}_{i}) - \sum_{j=1}^{n}\frac{\delta _{j}}{\delta _{n+i}}((|w_{ji}|+ \widetilde{w}_{ji})\gamma _{i}+(|k_{ji}|+\widetilde{k}_{ji})L_{i})\), \(i=1,2,\dots,n,\lambda =\min_{1\leq i\leq 2n}\{\lambda _{i} \}\).
- (\(H_{3}\)):
-
The norm-bounded structured uncertainties’ functions \(\Delta a_{i}(t)\), \(\Delta c_{i}(t)\), \(\Delta d_{i}(t)\), \(\Delta e_{i}(t)\), \(\Delta w_{ij}(t)\), \(\Delta k_{ij}(t)\) satisfy: \(| \Delta a_{i}(t)|<\widetilde{a}_{i}\), \(|\Delta c_{i}(t)|<\widetilde{c}_{i}\), \(|\Delta d_{i}(t)|<\widetilde{d}_{i}\), \(|\Delta e_{i}(t)|<\widetilde{e}_{i}\), \(|\Delta w_{ij}(t)|<\widetilde{w}_{ij}\), \(|\Delta k_{ij}(t)|<\widetilde{k}_{ij}\), where \(\widetilde{a}_{i}\), \(\widetilde{c}_{i}\), \(\widetilde{d}_{i}\), \(\widetilde{e}_{i}\), \(\widetilde{w}_{ij}\), \(\widetilde{k}_{ij}\) are positive constants.
- (\(H_{4}\)):
-
There exists a constant \(\mu >\tau ^{*}\) such that
$$ \frac{q^{2}-q+1}{\mu ^{q}\Gamma (1-q)}+ \frac{\hat{K}}{(1-\frac{\tau ^{*}}{\mu })^{q}}-\lambda \leq 0, $$(8)where \(\hat{K}=\max_{1\leq i\leq n} \{ \frac{\delta _{n+i}}{\delta _{i}}(e_{i}+\widetilde{e}_{i}),\sum_{j=1}^{n} \frac{\delta _{j}}{\delta _{n+i}}(|k_{ji}|+\widetilde{k}_{ji})L_{i} \} \).
Remark 1
The proof method of Lemma 4 is similar to that of Theorem 3.2 in [22], but the conditions are different.
The inequality \(\frac{q^{2}-q+1}{\mu _{3}^{q}\Gamma (1-q)}+ \frac{\mu _{1}}{(1-\frac{\tau ^{*}}{\mu _{3}})^{q}}-\mu _{2}\leq 0\) can imply \(\mu _{1}<\mu _{2}\) in [22], but not the converse. If we choose \(\mu _{1}\) and \(\mu _{3}\), there exists \(\mu _{2}\) satisfying
moreover, we find that \(\mu _{2}\) satisfying the above inequality is unstable in the numerical example, which shows that the condition of Lemma 4 is better than that of Theorem 3.2 in [22].
Remark 2
The condition of Lemma 4 depends on the fractional-order q.
3.1 The existence and uniqueness of the equilibrium point of DFGRNs
By using the contraction mapping theorem, we have the following conclusion.
Theorem 1
If assumptions (\(H_{1}\)), (\(H_{2}\)), and (\(H_{3}\)) hold, then DFGRN (1) has a unique equilibrium point \((m^{*},p^{*})\), where \(m^{*}=(m_{1}^{*},\dots,m_{n}^{*})^{T},p^{*}=(p_{1}^{*},\dots,p_{n}^{*})^{T}\).
Proof
Let \(w=(u_{1},\dots,u_{n},v_{1},\dots,v_{n})^{T}\) and \(m=(m_{1},\dots,m_{n}, p_{1},\dots,p_{n})^{T}\). Define a mapping \(H:R^{2n}\rightarrow R^{2n}\) as
where \(H(w)=(H_{1}(w),H_{2}(w),\dots,H_{2n}(w))^{T}\), and H is endowed with the \(l_{1}\) norm.
Due to (\(H_{2}\)), we obtain
Denote
Obviously, we have \(0 \leq \theta _{1} <1, 0 \leq \theta _{2} <1\), and \(0 \leq \theta <1\).
For any two different vectors \(w\in R^{2n}\) and \(m\in R^{2n}\), from (10), we get
and
According to the above two formulas and due to assumptions (\(H_{2}\)) and (\(H_{3}\)), we obtain
Due to the definition of the \(l_{1}\) norm, we have
which means that the mapping \(H(w)\) is a contraction mapping on \(R^{2n}\). Hence, there is a unique fixed point \(u^{*}=(u_{1}^{*},u_{2}^{*},\dots,u_{n}^{*},v_{1}^{*},v_{2}^{*}, \dots,v_{n}^{*})^{T} \in R^{2n}\) such that \(H(u^{*})=u^{*}\), i.e.,
Denote \(m_{i}^{*}=\frac{u^{*}_{i}}{(a_{i}+\Delta a_{i})\delta _{i}}\) and \(p_{j}^{*}=\frac{v^{*}_{j}}{(c_{j}+\Delta {c_{j}})\delta _{n+j}}\), where \(i,j=1,2,\dots,n\). We have
and this, together with the uniqueness of \(u^{*}\), implies that DFGRN (1) has a unique equilibrium point \((m^{*},p^{*})\), where \(m^{*}=(m_{1}^{*},\dots,m_{n}^{*})^{T},p^{*}=(p_{1}^{*},\dots,p_{n}^{*})^{T}\). □
3.2 Global uniform asymptotical stability
According to Theorem 1, DFGRN (1) has a unique equilibrium point \((m^{*},p^{*})\), where \(m^{*}=(m_{1}^{*},\dots,m_{n}^{*})^{T},p^{*}=(p_{1}^{*},\dots,p_{n}^{*})^{T}\). Let \(x_{i}(t)=m_{i}(t)-m^{*}_{i},y_{i}(t)=p_{i}(t)-p^{*}_{i}, i=1,2, \dots,n\). Then system (1) will be transformed into
Theorem 2
If assumptions (\(H_{1}\)),(\(H_{2}\)), (\(H_{3}\)), and (\(H_{4}\)) hold, then system (1) is globally uniformly asymptotically stable.
Proof
Suppose that \((x(t),y(t))^{T}\) is an arbitrary solution of system (15), where \(x(t)=(x_{1}(t), x_{2}(t), \dots, x_{n}(t))^{T}, y(t)=(y_{1}(t),y_{2}(t),\dots,y_{n}(t))^{T}\).
Let \(\delta _{*}=\min_{1\leq i\leq 2n}\{\delta _{i}\}\), \(\delta ^{*}=\max_{1\leq i\leq 2n}\{\delta _{i}\}\), \(X(t)=(x_{1}(t),\dots,x_{n}(t),y_{1}(t),\dots,y_{n}(t))^{T}\), \(\|X(t)\|=\sum_{i=1}^{n}|x_{i}(t)|+\sum_{i=1}^{n}|y_{i}(t)|\). Take \(V(t)=\sum_{i=1}^{n}\delta _{i}|x_{i}(t)|+\sum_{i=1}^{n} \delta _{n+i}|y_{i}(t)|\), \(\omega _{1}(\|X\|)=\delta _{*}\|X\|\), \(\omega _{2}(\|X\|)=\delta ^{*}\|X\|\). Then we have \(\omega _{1}(\|X\|)\leq V(t)\leq \omega _{2}(\|X\|) \).
From Lemma 1, we know that the solution \((x(t),y(t))^{T}\) of system (15) satisfies \({^{C}D}_{t}^{q}|x_{i}(t)| \leq \operatorname{sgn} (x_{i}(t)){^{C}D}_{t}^{q}x_{i}(t)\) and \({^{C}D}_{t}^{q}|y_{i}(t)| \leq \operatorname{sgn} (y_{i}(t)){^{C}D}_{t}^{q}y_{i}(t), 0< q\leq 1, i=1,2,\dots,n\), respectively.
After calculating the fractional-order derivative of \(V(t)\) along the solutions of system (15), due to (\(H_{1}\)), (\(H_{2}\)), and (\(H_{3}\)), we obtain
By (\(H_{2}\)), we have \(\lambda >0, \hat{K}>0\). By virtue of (\(H_{4}\)), we obtain \(\hat{K}<\lambda \), so we have \({^{C}D}_{t}^{q} V(t) \leq -(\lambda -\hat{K})V(t)\leq 0\) when the Razumikhin condition \(V(t-\tau (t))\leq V(t), 0\leq \tau (t)\leq \tau ^{*}\) holds. According to Lemma 4, the system (1) is globally uniformly asymptotically stable. □
Remark 3
If we adopt \(\Delta a_{i}(t)=\Delta w_{ij}(t)=\Delta k_{ij}(t)=\Delta c_{i}(t)= \Delta d_{i}(t)=\Delta e_{i}(t)=0\) in system (1), the conditions \((H_{2})\) and \((H_{4})\) become the following \((\hat{H}_{2})\) and \((\hat{H}_{4})\), respectively.
\((\hat{H}_{2})\) There exist positive constants \(\delta _{i}\ (i=1,2,\dots, 2n)\) such that \(\bar{\lambda }>0\), where
\((\hat{H}_{4})\) There exists a constant \(\mu >\tau ^{*}\) such that
where
Then we obtain the following result.
Corollary 1
If assumptions \((H_{1})\), \((\hat{H}_{2})\), and \((\hat{H}_{4})\) hold, then system (1) without structured uncertainties is globally uniformly asymptotically stable.
Remark 4
Corollary 1 is still new.
Remark 5
If we adopt \(\Delta a_{i}(t)=\Delta w_{ij}(t)=\Delta k_{ij}(t)=\Delta c_{i}(t)= \Delta d_{i}(t)=\Delta e_{i}(t)=0\) and \(\tau _{1}(t)=\tau _{2}(t)=\tau \) (constant), DFGRN (1) will degenerate into system (2.2) in [21]. The conclusion of Corollary 1 in this paper is stronger than that of Theorem 3.6 in [21].
4 Numerical example
In this section, we give two numerical examples to illustrate the effectiveness of our theoretical results obtained in Sect. 3. In the following examples, the functions \(f_{j}\) and \(g_{j}\) have the Hill form, the initial conditions are random. In addition, we improve the Adams–Bashforth–Moulton predictor–corrector scheme [32] with Matlab to make it available for the fractional-order differential equations with time-varying delays. When \(t\in [-\tau ^{*},0]\), we take \(m_{i}(t)=h_{i}(t) \) and \(p_{i}(t)=\hat{h}_{i}(t)\), respectively, where \(h_{i}(t)\) and \(\hat{h}_{i}(t)\) are random functions, \(i=1,2,3\). We repeat the computations 5 times with different initial values and the step-length \(h=0.1\). In order to better illustrate the global uniform asymptotic stability, we take five different initial values for \((m_{1},m_{2},m_{3},p_{1},p_{2},p_{3})^{T}\) as
-
\((0.2147, 0.5058, 0.1270, 0.0913, 0.2324, 0.0975)^{T}\),
-
\((0.0278, 0.2469, 0.3575, 0.0049, 0.2576, 0.1970)^{T}\),
-
\((0.1655, 0.0152, 0.0186, 0.0489, 0.0456,0.1463)^{T}\),
-
\((0.3094, 0.4547, 0.2760, 0.2797, 0.1551, 0.1626)^{T}\), and
-
\((0.0119, 0.3284, 0.0695, 0.3404, 0.3853,0.0220)^{T}\),
respectively.
Example 1
Consider the following DFGRN of three mRNA and protein nodes with time-varying delays and structured uncertainties:
where \(\tau _{1}(t)=\tau _{2}(t)=20\cos t,r=s=2,a_{i}=3,c_{i}=3.5,d_{i}=1,e_{i}=0.3,i=1,2,3\). Let
and
Obviously, \(\tau ^{*}=20\). By calculating we can find positive constants \(\gamma _{i}=1\) and \(L_{i}=1\ (i=1,2,3)\) such that (7) holds, which implies that the condition (\(H_{1}\)) is satisfied. We can take \(\delta _{1}=0.14,\delta _{2}=0.15,\delta _{3}=0.16,\delta _{4}=0.21, \delta _{5}=0.22\), and \(\delta _{6}=0.23\). Since \(\lambda _{i} = (a_{i}-\widetilde{a}_{i}) - \frac{\delta _{3+i}}{\delta _{i}}(d_{i}+\widetilde{d}_{i}+e_{i}+ \widetilde{e}_{i})\) and \(\lambda _{3+i} = (c_{i}-\widetilde{c}_{i}) -\sum_{j=1}^{3} \frac{\delta _{j}}{\delta _{3+i}}((|w_{ji}|+\widetilde{w}_{ji}) \gamma _{i}+(|k_{ji}|+\widetilde{k}_{ji})L_{i}), i=1,2,3\), we have \(\lambda _{1}=1.0350>0\), \(\lambda _{2}= 1.0786>0,\lambda _{3}= 1.1167>0,\lambda _{4}=1.3967>0, \lambda _{5}= 2.4775>0\), and \(\lambda _{6}= 2.7067>0\). So, the condition \((H_{2})\) holds. Furthermore, letting \(\hat{k}_{i}=\sum_{j=1}^{3} \frac{\delta _{j}}{\delta _{3+i}}(|k_{ji}|+\widetilde{k}_{ji})L_{i}, i=1,2,3\), we have \(\hat{k}_{1}=0.3445,\hat{k}_{2}= 0.3398,\hat{k}_{3}=0.2438\). Then we obtain \(\hat{K}=\max \{\frac{\delta _{4}}{\delta _{1}}(e_{1}+ \widetilde{e}_{1}),\frac{\delta _{5}}{\delta _{2}}(e_{2}+ \widetilde{e}_{2}), \frac{\delta _{6}}{\delta _{3}}(e_{3}+ \widetilde{e}_{3}),\hat{k}_{1},\hat{k}_{2},\hat{k}_{3} \}= 0.4552\) and \(\lambda =\min \{ \lambda _{1},\lambda _{2},\lambda _{3}, \lambda _{4},\lambda _{5},\lambda _{6} \} =1.0350\). Due to Theorem 1, DFGRN (17) has a unique equilibrium point \((m^{*},p^{*})\), where \(m^{*}=( 0.0507, 0.3643, 0.0924)^{T}\), \(p^{*}=(0.0189, 0.1357, 0.0344)^{T}\). When we take \(q=0.95\) and \(\mu =34.6001>20=\tau ^{*}\), then \(\frac{q^{2}-q+1}{\mu ^{q}\Gamma (1-q)}+ \frac{\hat{K}}{(1-\frac{\tau ^{*}}{\mu })^{q}}-\lambda \leq 0\). According to Theorem 2, DFGRN (17) is globally uniformly asymptotically stable. Similarly, if we take \(q=0.6\) and \(\mu = 27.6001>20=\tau ^{*}\), then the conclusion also holds.
Subsequently, we use the improved predictor–corrector method [32] to calculate the numerical solutions of DFGRN (17). The trajectories of variables \(m_{i}(t)\) and \(p_{i}(t)\ (i=1,2,3)\) with \(q=0.95\), \(q=0.6\) and different initial values are shown in Figs. 1 and 2, respectively. The convergence behaviors are obvious.
Response curves of system (17) with \(q=0.95\) and (a) \(m_{1}(t),m_{2}(t),m_{3}(t)\); (b) \(p_{1}(t),p_{2}(t),p_{3}(t)\)
Response curves of system (17) with \(q=0.60\) and (a) \(m_{1}(t),m_{2}(t),m_{3}(t)\); (b) \(p_{1}(t),p_{2}(t),p_{3}(t)\)
Example 2
Consider the following DFGRN of three mRNA and protein nodes with time-varying delays and without structured uncertainties:
All parameters are the same as in Example 1. We can take \(\delta _{1}=0.14,\delta _{2}=0.15,\delta _{3}=0.16,\delta _{4}=0.21, \delta _{5}=0.22\), and \(\delta _{6}=0.23\). Due to \(\lambda _{i} \triangleq a_{i} -\frac{\delta _{3+i}}{\delta _{i}}(d_{i}+e_{i})\) and \(\lambda _{3+i} \triangleq c_{i} -\sum_{j=1}^{3} \frac{\delta _{j}}{\delta _{3+i}}(|w_{ji}|\gamma _{i}+|k_{ji}|L_{i})\), we have \(\lambda _{1}=1.05>0\), \(\lambda _{2}=1.0933>0,\lambda _{3}=1.1312>0,\lambda _{4}=1.4106>0, \lambda _{5}=2.4916>0\), and \(\lambda _{6}=2.7209>0\). So, the condition \((H_{2})\) holds. Furthermore, letting \(\hat{k}_{i}=\sum_{j=1}^{3} \frac{\delta _{j}}{\delta _{3+i}}|k_{ji}|L_{i}, i=1,2,3\), we have \(\hat{k}_{1}=0.3401,\hat{k}_{2}=0.3352,\hat{k}_{3}=0.2393\). Then we obtain \(\hat{K}=\max \{\frac{\delta _{4}}{\delta _{1}}e_{1}, \frac{\delta _{5}}{\delta _{2}}e_{2}, \frac{\delta _{6}}{\delta _{3}}e_{3}, \hat{k}_{1},\hat{k}_{2},\hat{k}_{3} \}=0.45\) and \(\lambda =\min \{ \lambda _{1},\lambda _{2},\lambda _{3}, \lambda _{4},\lambda _{5},\lambda _{6} \} =1.05\). Due to Theorem 1, DFGRN (18) has a unique equilibrium point \((m^{*},p^{*})\), where \(m^{*}=( 0.0508, 0.3644, 0.0925)^{T}\), \(p^{*}=(0.0189, 0.1353, 0.0343)^{T}\). When we take \(q=0.95\) and \(\mu =34.0001>20=\tau ^{*}\), so \(\frac{q^{2}-q+1}{\mu ^{q}\Gamma (1-q)}+ \frac{\hat{K}}{(1-\frac{\tau ^{*}}{\mu })^{q}}-\lambda \leq 0\). According to Theorem 2, DFGRN (18) is globally uniformly asymptotically stable. Similarly, if we take \(q=0.6\) and \(\mu = 27.2001>20=\tau ^{*}\), then the conclusion also holds.
Subsequently, we also calculate the numerical solutions of DFGRN (18). The trajectories of variables \(m_{i}(t)\) and \(p_{i}(t)\ (i=1,2,3)\) with \(q=0.95\), \(q=0.6\) and different initial values are shown in Figs. 3 and 4, respectively. The convergence behaviors are obvious.
Response curves of system (18) with \(q=0.95\) and (a) \(m_{1}(t),m_{2}(t),m_{3}(t)\); (b) \(p_{1}(t),p_{2}(t),p_{3}(t)\)
Response curves of system (18) with \(q=0.60\) and (a) \(m_{1}(t),m_{2}(t),m_{3}(t)\); (b) \(p_{1}(t),p_{2}(t),p_{3}(t)\)
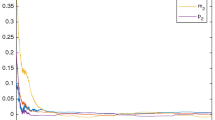
From Figs. 1–4, we find that the effect of small structured uncertainties on stability of DFGRNs is not obvious. Meanwhile, we also find that the fractional-order q can affect the time of stability of DFGRNs. To illustrate the bigger structured uncertainties’ effect on the stability of DFGRN (17), we set
and
Then we calculate \(\frac{q^{2}-q+1}{\mu ^{q}\Gamma (1-q)}+ \frac{\hat{K}}{(1-\frac{\tau ^{*}}{\mu })^{q}}-\lambda =1.4002>0\) with \(q=0.95\) and \(1.3848>0\) with \(q=0.6\), respectively. So the condition \((H_{4})\) doesn’t hold. The trajectories of variables \(m_{i}(t)\) and \(p_{i}(t)\ (i=1,2,3)\) with \(q=0.95\) and \(q=0.6\) are shown in Figs. 5 and 6, respectively. The DFGRN (17) is obviously unstable.
Response curves of system (17) with \(q=0.95\) and (a) \(m_{1}(t),m_{2}(t),m_{3}(t)\); (b) \(p_{1}(t),p_{2}(t),p_{3}(t)\)
Response curves of system (17) with \(q=0.60\) and (a) \(m_{1}(t),m_{2}(t),m_{3}(t)\); (b) \(p_{1}(t),p_{2}(t),p_{3}(t)\)
From Figs. 5–6, we find that bigger structured uncertainties can make DFGRN (17) unstable.
5 Conclusion
In this paper, we have proposed a class of fractional-order gene regulatory network models with time-varying delays and structured uncertainties, and we have obtained the following results related to DFGRNs: (1) By using the contraction mapping theorem, we obtained that DFGRNs have a unique equilibrium point; (2) Based on Lyapunov function and Razumikhin technique, we proved that DFGRNs are globally uniformly asymptotically stable. Furthermore, numerical simulations showed the stability condition \(\frac{q^{2}-q+1}{\mu ^{q}\Gamma (1-q)}+ \frac{\hat{K}}{(1-\frac{\tau ^{*}}{\mu })^{q}}-\lambda \leq 0\), which depends on the fractional-order q, is better than that of Theorem 3.2 in [22]; (3) We found that the influence of smaller structured uncertainties on the stability is not obvious, but bigger structured uncertainties can change the stability of DFGRNs in a numerical example.
Availability of data and materials
All authors declare that all the data can be accessed in our manuscript in the numerical simulation section.
References
Huang, C., Cao, J., Xiao, M.: Hybrid control on bifurcation for a delayed fractional gene regulatory network. Chaos Solitons Fractals 87, 19–29 (2016)
De Jong, H.: Modeling and simulation of genetic regulatory systems: a literature review. J. Comput. Biol. 9(1), 67–103 (2002)
Chaouiya, C., Remy, E., Thieffry, D.: Petri net modelling of biological regulatory networks. J. Discret. Algorithms 6(2), 165–177 (2008)
Friedman, N., Linial, M., Nachman, I., Pe’er, D.: Using Bayesian networks to analyze expression data. J. Comput. Biol. 7(3–4), 601–620 (2000)
Tao, B., Xiao, M., Sun, Q., Cao, J.: Hopf bifurcation analysis of a delayed fractional-order genetic regulatory network model. Neurocomputing 275, 677–686 (2018)
Yu, T., Zhang, X., Zhang, G., Niu, B.: Hopf bifurcation analysis for genetic regulatory networks with two delays. Neurocomputing 164, 190–200 (2015)
Zhang, Z., Zhang, J., Ai, Z.: A novel stability criterion of the time-lag fractional-order gene regulatory network system for stability analysis. Commun. Nonlinear Sci. Numer. Simul. 66, 96–108 (2019)
Fan, X., Xue, Y., Zhang, X., Ma, J.: Finite-time state observer for delayed reaction–diffusion genetic regulatory networks. Neurocomputing 227, 18–28 (2017)
Wu, L., Liu, K., Lü, J., Gu, H.: Finite-time adaptive stability of gene regulatory networks. Neurocomputing 338, 222–232 (2019)
Yue, D., Guan, Z., Li, J., Liu, F., Xiao, J., Ling, G.: Stability and bifurcation of delay-coupled genetic regulatory networks with hub structure. J. Franklin Inst. Eng. Appl. Math. 356(5), 2847–2869 (2019)
Ren, F., Cao, F., Cao, J.: Mittag-Leffler stability and generalized Mittag-Leffler stability of fractional-order gene regulatory networks. Neurocomputing 160, 185–190 (2015)
Zhang, Y., Pu, Y., Zhang, H., Cong, Y., Zhou, J.: An extended fractional Kalman filter for inferring gene regulatory networks using time-series data. Chemom. Intell. Lab. Syst. 138, 57–63 (2014)
Wang, Y., Wang, Z., Liang, J.: On robust stability of stochastic genetic regulatory networks with time delays: a delay fractioning approach. IEEE Trans. Syst. Man Cybern., Part B, Cybern. 40(3), 729–740 (2010)
He, Y., Zeng, J., Wu, M., Zhang, C.-K.: Robust stabilization and H∞ controllers design for stochastic genetic regulatory networks with time-varying delays and structured uncertainties. Math. Biosci. 236(1), 53–63 (2012)
Chesi, G., Hung, Y.S.: Stability analysis of uncertain genetic sum regulatory networks. Automatica 44(9), 2298–2305 (2008)
Kim, T.-H., Hori, Y., Hara, S.: Robust stability analysis of gene–protein regulatory networks with cyclic activation–repression interconnections. Syst. Control Lett. 60(6), 373–382 (2011)
Zhang, W., Fang, J.-A., Tang, Y.: Robust stability for genetic regulatory networks with linear fractional uncertainties. Commun. Nonlinear Sci. Numer. Simul. 17(4), 1753–1765 (2012)
Wang, Q., Perc, M., Duan, Z., Chen, G.: Synchronization transitions on scale-free neuronal networks due to finite information transmission delays. Phys. Rev. E 80(2), 026206 (2009)
Zang, H., Zhang, T., Zhang, Y.: Bifurcation analysis of a mathematical model for genetic regulatory network with time delays. Appl. Math. Comput. 260, 204–226 (2015)
Zhang, J., Jin, Z., Yan, J., Sun, G.: Stability and Hopf bifurcation in a delayed competition system. Nonlinear Anal., Theory Methods Appl. 70(2), 658–670 (2009)
Wu, Z., Wang, Z., Zhou, T.: Global stability analysis of fractional-order gene regulatory networks with time delay. Int. J. Biomath. 12(6), 1950067 (2019)
Chen, B., Chen, J.: Razumikhin-type stability theorems for functional fractional-order differential systems and applications. Appl. Math. Comput. 254, 63–69 (2015)
Stamova, I.: Global Mittag-Leffler stability and synchronization of impulsive fractional-order neural networks with time-varying delays. Nonlinear Dyn. 77(4), 1251–1260 (2014)
Stamova, I., Stamov, G.: Mittag-Leffler synchronization of fractional neural networks with time-varying delays and reaction-diffusion terms using impulsive and linear controllers. Neural Netw. 96, 22–32 (2017)
Wu, Z., Wang, Z., Zhou, T., Tan, S.: Global synchronization and anti-synchronization of fractional-order complex-valued gene regulatory networks with time-varying delays. IEEE Access 8, 150555–150572 (2020)
Wu, Z., Wang, Z., Zhou, T.: Finite-time stability of fractional-order time-varying delays gene regulatory networks with structured uncertainties and controllers. Complexity 2020, 2315272 (2020)
Zhang, Z., Toshimitsu, U., Ai, Z., Zhang, J.: Novel stability condition for delayed fractional-order composite systems based on vector Lyapunov function. Nonlinear Dyn. 99, 1253–1267 (2020)
Zhang, Z., Zhang, J.: Asymptotic stabilization of general nonlinear fractional-order systems with multiple time delays. Nonlinear Dyn. 102, 605–619 (2020)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Ren, F., Cao, J.: Asymptotic and robust stability of genetic regulatory networks with time-varying delays. Neurocomputing 71(4), 834–842 (2008)
Zhang, S., Yu, Y., Hu, W.: Robust stability analysis of fractional-order Hopfield neural networks with parameter uncertainties. Math. Probl. Eng. 2014, Article ID 302702 (2014)
Diethelm, K., Ford, N.J., Freed, A.D., Gray, H.R.: A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 29, 3–22 (2002)
Acknowledgements
The authors are grateful to the editor and the anonymous referees for their valuable comments and suggestions on the paper.
Funding
This work is supported by the Hunan Provincial Natural Science Foundation (No. 2019JJ50222, 13JJ4065), the Scientific Research Fund of Hunan Provincial Education Department (No. 19C0911).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Appendix
Appendix
Proof of Lemma 4
Let
From properties (i) and (ii) in Lemma 2, for \(t\geq a\), we have
For any given \(t\geq a\), there exists a \(\theta ^{*}\in [-\tau ^{*},0]\) such that \(\sup_{ -\tau ^{*}\leq \theta \leq 0}V(t+\theta )=V(t+ \theta ^{*})\). From condition (6), we have
Then, for \(t\geq a\), we have
From (19)–(21), we can show that
By the above arguments, we can get
Now, for any given \(\varepsilon >0, \delta >0\), and \(\|\phi \|\leq \delta \), we have
but this implies that \(\|x(t)\|\leq \varepsilon \), for \(t\geq a+T\), where \(T=[(\frac{\omega _{2}(\delta )}{\omega _{1}(\varepsilon )})^{ \frac{1}{q}}-1]\mu _{3}\).
The system (3) is globally uniformly stable. The proof is completed. □
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wu, Z., Wang, Z. & Zhou, T. Global uniform asymptotical stability for fractional-order gene regulatory networks with time-varying delays and structured uncertainties. Adv Differ Equ 2021, 93 (2021). https://doi.org/10.1186/s13662-021-03243-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03243-w