1 Introduction

Leishmaniasis is a group of vector-borne diseases. Cutaneous and visceral strains are two main types of the disease. The disease is caused by protozoa which belong to Leishmania genus. The protozoa is transmitted/carried from one individual to another by a vector/sandfly. The three causative pathogens of visceral leishmaniasis are L. infantum, L. donovani, and L. chagasi. The incubation/latency period varies from three to six months with a minimum of 10 days, however, a longer period of one year has also been reported [1–4]. Each year \(500{,}000\) new cases of \(V_{l}\) strain are reported worldwide [5]. The causative agents of cutaneous strain are L. major and L. tropica, however, in some cases L. infantum may also cause \(C_{l}\) strain [6].

In very rare cases, very few individuals who seem to be recovered from visceral strain develop complications of the disease. The period in which complications may appear is from 2 to 3 years in India, and about 6 months in Sudan. In such a case nodules appear on the whole body of the victim, this form of the disease is known as post kala-azar dermal leishmaniasis (PKDL) [7, 8]. PKDL is in general not fatal. Therefore the poor community, in particular, does not focus on treatment and hence remains undiagnosed and untreated [9].

The flies belong to the genus Phlebotomus or Lutzomyia [10]. About, 900 species of phlebotomine sandfly exist, and only 30% of them work as vector of leishmaniasis. The carrier sandfly is blood-feeding, and ovigenesis in the fly depends upon the quality of the blood [11]. The disease latency period in the fly is observed from 3 to 7 days [12, 13].

Disease control is a great challenge for scientists and physicians. The disease clinical structure, human immune system response, and drug resistance are the main causes of treatment’s failure. Cross-immunity between \(C_{l}\) and \(V_{l}\) can play an important role in the reduction of the disease [14].

Recently different optimal control models have been formulated to control different infectious diseases utilizing minimum resources [15, 16]. In this work we present a mathematical model for the transmission dynamics of the cutaneous and visceral strains of leishmaniasis. The model incorporates the complications of visceral leishmaniasis, called PKDL. The model consists of 22 compartments. The incubation periods of the different strains are included. The individuals in the latent period are distributed into 6 compartments on the basis of strain and attack types (e.g., recovered from one strain and attacked by another, or initial attack by some strain). The model also includes an exposed class for both reservoir and sandfly populations. We take into account the role of cross-immunity between cutaneous and visceral strains of leishmaniasis. The immunity losing periods, k and \(\omega _{d}\), which denote the rate of loss of immunity in humans and reservoirs, respectively, are also included into the model.

Furthermore, the model includes \(Z_{r}\), the recovered class of reservoirs, and \(\tau _{d}\), the natural recovery of dogs. Also, humans, reservoirs, and sandflies almost live in the same vicinity, particularly in poor communities. Therefore we consider homogenous mixing of the populations involved in the model, in the sense that sandflies distribute equally over \(N_{h}+N_{r}\).

2 Model formulation

In what follows, \(N_{h}\) is the density of the human class and is divided into the following further subclasses:

  • \(S_{h}\), the susceptible human class;

  • \(E_{1}\) and \(E_{2}\), the human classes exposed/latent for \(C_{l}\) and \(V_{l}\) infection, respectively;

  • \(E_{12}\), the human class recovered from \(C_{l}\) and exposed to the infection of \(V_{l}\);

  • \(E_{21}\), the humans recovered from \(V_{l}\) and exposed to the infection of \(C_{l}\);

  • \(E_{23}\), the dormant/exposed class of PKDL, the class which otherwise seems recovered from \(V_{l}\);

  • \(E_{123}\), the exposed class of PKDL after being recovered from \(C_{l}\);

  • \(I_{1}\) and \(I_{2}\), the infectious classes of \(C_{l}\) and \(V_{l}\);

  • \(I_{12}\) and \(I_{21}\), the infectious classes of \(V_{l}\) and \(C_{l}\), developing from \(E_{12}\) and \(E_{21}\);

  • \(P_{2}\), the infectious class of PKDL;

  • \(P_{12}\), the infectious class of PKDL after being recovered from \(C_{l}\);

  • \(R_{1}\), \(R_{2}\), and M, the classes recovered from \(C_{l}\) strain, \(V_{l}\) strain, and both strains, respectively.

Next \(N_{r}\) is the total reservoir population, divided into the following subclasses:

  • \(S_{r}\), the susceptible reservoir class;

  • \(I_{r}\), the infectious class of reservoir;

  • \(Z_{r}\), the reservoir class being recovered from infection.

Then \(N_{v}\) is the total vector population, divided in the following classes:

  • \(S_{v}\), the susceptible-vector class;

  • \(E_{v}\), the exposed-vector class, and

  • \(I_{v}\), the infectious-vector class.

A susceptible human after catching infection follows Path-1 or Path-2, according to as the infection causing fly or the source fly was infected with \(C_{l}\) or \(V_{l}\), respectively:

  • Path-1, \(E_{1} \longrightarrow I_{1} \longrightarrow R_{1} \longrightarrow E_{12} \longrightarrow I_{12} \longrightarrow M \longrightarrow S_{h}\);

  • Path-2, \(E_{2} \longrightarrow I_{2} \longrightarrow R_{2} \longrightarrow E_{21} \longrightarrow I_{21} \longrightarrow M \longrightarrow S_{h}\).

In case of complication of \(V_{l}\) strain, the transmission follows Path-3 or Path-4:

  • Path-3, \(I_{2} \longrightarrow P_{2} \longrightarrow R_{2} \);

  • Path-4, \(I_{12} \longrightarrow E_{123} \longrightarrow P_{12} \).

The infection follows the following path of transmission in dogs (reservoir):

  • \(S_{r} {\longrightarrow } I_{r} \longrightarrow Z_{r}\).

The infection follows the following path of transmission in vectors:

  • \(S_{v} \longrightarrow E_{v} \longrightarrow I_{v}\).

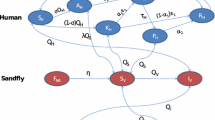
The overall path of transmission of leishmaniasis in all the three populations is shown in the following Fig. 1. The mathematical model of the 3-strains of leishmaniasis is given by the following set of coupled differential equations:

$$ \textstyle\begin{cases} \dot{S_{h}} = (1- \epsilon _{1} - \epsilon _{2})\Gamma _{h} + kM - ( \Pi _{1} + \Pi _{2} )S_{h} - \mu _{h} S_{h}, \\ \dot{E_{1}} = \Pi _{1} S_{h} - (k_{1} + \mu _{h})E_{1}, \\ \dot{E_{2}} = \Pi _{2} S_{h} - (k_{2} + \mu _{h})E_{2}, \\ \dot{I_{1}} = k_{1} E_{1} - (\gamma _{1} + \mu _{h}) I_{1}, \\ \dot{I_{2}} = k_{2} E_{2} - (\gamma _{2} + \delta _{1} + \mu _{h}) I_{2}, \\ \dot{E}_{23}= \gamma _{2} I_{2}-(k_{6}+\mu _{h})E_{23}, \\ \dot{P_{2}} = k_{6}E_{23} -(\beta _{1}+\delta _{3} + \mu _{h}) P_{2}, \\ \dot{R_{1}} = \epsilon _{2} \Gamma _{h} + \gamma _{1} I_{1} - (\rho \Pi _{2} +\mu _{h} )R_{1}, \\ \dot{R}_{2} = \epsilon _{1} \Gamma _{h}+ (\beta _{1})P_{2} - (\rho \Pi _{1} + \mu _{h})R_{2}, \\ \dot{E}_{12} = \rho \Pi _{2} R_{1} - (k_{4} + \mu _{h})E_{12}, \\ \dot{E}_{21} = \rho \Pi _{1} R_{2} - (k_{3} +\mu _{h})E_{21}, \\ \dot{I}_{12} = k_{4} E_{12} - (\gamma _{5}+ \delta _{2}+ \mu _{h})I_{12}, \\ \dot{E}_{123}= \gamma _{5} I_{12}-(k_{6}+\mu _{h})E_{123}, \\ \dot{P}_{12} = k_{6}E_{123} - (\beta _{2}+ \delta _{3}+\mu _{h})P_{12}, \\ \dot{I}_{21} = k_{3} E_{21}- (\gamma _{4} + \mu _{h})I_{21}, \\ \dot{M} =(\beta _{2})P_{12} + \gamma _{4} I_{21} -(k+ \mu _{h}) M, \\ \dot{S_{r}} = \Gamma _{r}+\omega _{d}Z_{r} - (\Pi _{r} + \mu _{r}) S_{r}, \\ \dot{I_{r}} = \Pi _{r} S_{r} -(\alpha _{d}+\tau _{d}+ \mu _{r}) I_{r}, \\ \dot{Z_{r}}=\tau _{d}I_{r}-(\omega _{d}+\mu _{r})Z_{r}, \\ \dot{S_{v}} = \Gamma _{v} -(\Pi _{v} + \mu _{v}) S_{v}, \\ \dot{E_{v}} = \Pi _{v} S_{v} -( \mu _{v}+\varrho _{v}) E_{v}, \\ \dot{I_{v}}=\varrho _{v} E_{v} -\mu _{v} I_{v}. \end{cases} $$
(1)

The terms of interaction \(\Pi _{1}\), \(\Pi _{2}\), \(\Pi _{r}\), and \(\Pi _{v} \) between the three populations are defined as follows:

$$\begin{aligned}& \Pi _{1} = ab_{1} \frac{I_{v}}{N_{h} + N_{r}}, \\ & \Pi _{2} = ab_{2} \frac{I_{v}}{N_{h} + N_{r}}, \\ & \Pi _{r} = ab \frac{I_{v}}{N_{h} + N_{r}}, \\ & \Pi _{v}=\frac{a}{N_{h} + N_{r}} \bigl( \rho (c_{1}I_{21}+c_{2}I_{12}+c_{2}P_{12})+c_{1}I_{1}+c_{2}(I_{2}+P_{2})+cI_{r} \bigr). \end{aligned}$$
Figure 1
figure 1

Disease flow chart

Full size image

Table 1 contains the values of the different parameters used in the model (1).

Table 1 Parameter values
Full size table

3 Model analysis

Here, in Sect. 3, the properties of the model, namely the disease-free equilibrium, invariant region, and basic reproduction number, are discussed.

3.1 Invariant region

The state variables and parameters used in the model are taken nonnegative because the model concerns the living population:

$$\begin{aligned}& \dot{N}_{h} = \Gamma _{h}-\mu _{h} N_{h}-\delta _{1} I_{2} -\delta _{2} I_{12}-\delta _{3}(P_{2}+P_{12}), \end{aligned}$$
(2)
$$\begin{aligned}& \dot{N}_{r} = \Gamma _{r} -\mu _{r} N_{r}-(\alpha _{d}+ \tau _{d})I_{r}, \end{aligned}$$
(3)
$$\begin{aligned}& \dot{N}_{v} = \Gamma _{v} -\mu _{v} N_{v}. \end{aligned}$$
(4)

From(2), (3), and (4), we have

$$\begin{aligned}& N_{h}\le N_{h}(0)e^{-\mu _{h}t}+ \frac{\Gamma _{h}}{\mu _{h}} \bigl(1-e^{-\mu _{h}t} \bigr), \\& N_{r}\le N_{r}(0)e^{-\mu _{r}t}+ \frac{\Gamma _{r}}{\mu _{r}} \bigl(1-e^{-\mu _{r}t} \bigr), \\& N_{v}\le N_{v}(0)e^{-\mu _{v}t}+ \frac{\Gamma _{v}}{\mu _{h}} \bigl(1-e^{-\mu _{v}t} \bigr). \end{aligned}$$

Thus

$$ \biggl(N_{h} \le \frac{\Gamma _{h}}{\mu _{h}}, N_{r} \le \frac{\Gamma _{r}}{\mu _{r}}, N_{v} \le \frac{\Gamma _{v}}{\mu _{v}} \biggr) \quad \text{as } t\rightarrow \infty . $$

Using [29], we claim the following result:

Proposition 1

The region Ω defined by

$$\begin{aligned} \Omega ={}& \biggl[ \bigl(S_{h}, E_{1}, E_{2}, I_{1}, I_{2},E_{23}, P_{2}, R_{1}, R_{2}, E_{12}, E_{21}, I_{12},E_{123}, \\ &{} P_{12},I_{21},M,S_{r},I_{r},Z_{r},S_{v},E_{v},I_{v} \bigr) \in \mathbb{R}_{+}^{22} ,N_{h}\leq \frac{\Gamma _{h}}{\mu _{h}}{;N_{r} \leq \frac{\Gamma _{r}}{\mu _{r}}; N_{v}\leq \frac{\Gamma _{v}}{\mu _{v}}} \biggr] \end{aligned}$$

is a positively invariant domain, also the model is epidemiologically and mathematically well-posed as all the trajectories are forward-bounded.

3.2 Reproduction number

The number of secondary infections caused by a single primary infection in the completely susceptible population is called the reproduction number and denoted by \(R_{0}\). The reproduction number is found from the next generation matrix [17, 30]. Here

$$ R_{0} =\sqrt{R_{1} + R_{2} + R_{3} + R_{4} + R_{5}} , $$

where

$$\begin{aligned}& R_{1}=r_{1}r_{2}, \quad\quad R_{2}=r_{3}r_{4}, \quad\quad R_{3}=r_{5}r_{6}, \quad\quad R_{4}=r_{7}r_{8}, \quad\quad R_{5}=r_{9}r_{10}, \\ & r_{1} = \frac{ab_{1}\mu _{r} \Gamma _{h}}{\mu _{v} (\Gamma _{h} \mu _{r} +\Gamma _{r} \mu _{h})}, \quad\quad r_{2}= \frac{a c_{1} \Gamma _{v} \mu _{r} \mu _{h}}{\mu _{v} (\Gamma _{h} \mu _{r} + \Gamma _{r} \mu _{h})} \biggl(\frac{k_{1}\epsilon \varrho _{v}}{a_{1}a_{3}a_{14}} \biggr), \\ & r_{3} = \frac{a b_{2} \mu _{r} \Gamma _{h}}{{\mu _{v} (\Gamma _{h} \mu _{r} + \Gamma _{r} \mu _{h})}}, \\ & r_{4} = \frac{a c_{2} \mu _{r} \mu _{h} \Gamma _{v}}{{\mu _{v} (\Gamma _{h} \mu _{r} + \Gamma _{r} \mu _{h})}} \biggl[\frac{\epsilon k_{2}\varrho _{v}}{a_{2}a_{4}a_{14}} \biggl(1+ \frac{\gamma _{2}k_{6}}{a_{5}a_{6}} \biggr) \biggr], \\ & r_{5} = \frac{a b\mu _{h}\Gamma _{r}}{\mu _{v} (\Gamma _{h} \mu _{r} + \Gamma _{r} \mu _{h})}, \quad\quad r_{6}= \frac{ac\mu _{h}\mu _{r}\Gamma _{v}}{\mu _{v} (\Gamma _{h} \mu _{r} +\Gamma _{r} \mu _{h})} \biggl(\frac{\varrho _{v}}{a_{13}a_{14}} \biggr), \\ & r_{7} = \frac{a b_{1}\mu _{r} \Gamma _{h} \rho }{{\mu _{v} (\Gamma _{h} \mu _{r} + \Gamma _{r} \mu _{h})}}, \\ & r_{8} = \frac{ac_{2}\mu _{r} \mu _{h}\Gamma _{v}}{{\mu _{v} (\Gamma _{h} \mu _{r} +\Gamma _{r} \mu _{h})}} \biggl[\frac{\epsilon _{1} k_{4}\rho \varrho _{v}}{a_{7}a_{9}a_{14}} \biggl(1+ \frac{\gamma _{5}k_{6}}{a_{10}a_{11}} \biggr) \biggr], \\ & r_{9} = \frac{ab_{2}\mu _{r} \Gamma _{h} \rho }{{\mu _{v} (\Gamma _{h} \mu _{r} +\Gamma _{r} \mu _{h})}},\qquad r_{10} = \frac{ac_{1}\mu _{r} \mu _{h}\Gamma _{v}}{{\mu _{v} (\Gamma _{h} \mu _{r} +\Gamma _{r} \mu _{h})}} \biggl[\frac{\epsilon _{2}\rho k_{3}\varrho _{v}}{a_{8} a_{12}a_{14}} \biggr], \end{aligned}$$

where \(a_{1} =\mu _{h}+k_{1}\), \(a_{2} =\mu _{h}+k_{2}\), \(a_{3}=\mu _{h}+ \gamma _{1}\), \(a_{4}=\delta _{1}+\gamma _{2}+\mu _{h}\), \(a_{5}=\mu _{h}+k_{6}\), \(a_{6}=\delta _{3}+\beta _{1}+\mu _{h}\), \(a_{7} = \mu _{h}+k_{4}\), \(a_{8}=\mu _{h}+k_{3}\), \(a_{9} =\delta _{2}+\gamma _{5}+ \mu _{h}\), \(a_{10}=\upsilon +k_{6}\), \(a_{11}=\delta _{3}+\beta _{2}+\mu _{h}\), \(a_{12}=\mu _{h}+\gamma _{4}\), \(a_{13}=\tau _{d}+\mu _{r}+\alpha _{d}\), \(a_{14}=\mu _{v}+\varrho _{v}\).

3.3 Sensitivity analysis of \(R_{0}\)

Different parameters used in the model influence the evolution of the disease differently. The role of parameter K in the phenomenon Z is called the sensitivity of Z with respect to K and is given by [18, 31]

$$ \Upsilon _{Z}^{K}= \frac{\partial Z}{\partial K} \frac{K}{Z}. $$

The sensitivity indices of different parameters are shown in Table 2

Table 2 Sensitivity indices of parameters
Full size table

4 Control strategies

To control the further transmission of the disease in the community, we use sensitivity test to check the absolute value of the index of a parameter. The greater the absolute value of the index of a parameter, the higher would be the role of this parameter. The contact rate of the fly has sensitivity index of 1. This index is the highest, hence a plays the most significant role in the disease transmission. The probabilities of disease transmission from flies to dogs and from dogs to flies, denoted by b and c, respectively, have the indices of 0.47 each, while the index of sandfly birth rate, \(\Gamma _{v}\) has the index of 0.5 as shown in Table 2. So these three parameters need intervention. Alternatively, we address the biting rate, a, by introducing a control variable \(q_{1}\). This intervention consequently helps in controlling b, c, and \(\Gamma _{v}\). Control variable \(q_{1}\) is associated with insecticide-treated bed nets, sandfly repulsive lotion, and electric devices, etc.

The sensitivity index of “elimination of seropositive/infected dogs” is −0.38. That is, an increase of 10% in the culling rate of infectious dogs will decrease \(R_{0}\) by 3.8%. We introduce control variable \(q_{2}\) for the control of seropositive dogs.

The mortality rate of flies has the sensitivity index of −1. This means that an increase in mortality of flies will cause a decrease in \(R_{0}\). To increase the death rate of flies, we introduce a control variable \(q_{3}\). As such, \(q_{3}\) is associated with residual DDT sprays in animal and human shelters.

Based on the above control variables, we propose the following optimal control model:

$$ \textstyle\begin{cases} \dot{S_{h}} = (1- \epsilon _{1} - \epsilon _{2})\Gamma _{h} + kM - ( \Pi _{1} + \Pi _{2} )(1-q_{1})S_{h} - \mu _{h} S_{h}, \\ \dot{E_{1}} = \Pi _{1}(1-q_{1}) S_{h} - (k_{1} + \mu _{h})E_{1}, \\ \dot{E_{2}} = \Pi _{2}(1-q_{1}) S_{h} - (k_{2} + \mu _{h})E_{2}, \\ \dot{I_{1}} = k_{1} E_{1} - (\gamma _{1} + \mu _{h}) I_{1}, \\ \dot{I_{2}} = k_{2} E_{2} - (\gamma _{2} + \delta _{1} + \mu _{h}) I_{2}, \\ \dot{E}_{23}= \gamma _{2} I_{2}-(k_{6}+\mu _{h})E_{23}, \\ \dot{P_{2}} = k_{6}E_{23} -( \beta _{1}+\delta _{3} + \mu _{h}) P_{2}, \\ \dot{R_{1}} = \epsilon _{2} \Gamma _{h} + \gamma _{1} I_{1} - (\rho \Pi _{2}(1-q_{1}) +\mu _{h} )R_{1}, \\ \dot{R}_{2} = \epsilon _{1} \Gamma _{h} + (\beta _{1})P_{2} - (\rho \Pi _{1}(1-q_{1}) + \mu _{h})R_{2}, \\ \dot{E}_{12} = \rho \Pi _{2}(1-q_{1}) R_{1} - (k_{4} + \mu _{h})E_{12}, \\ \dot{E}_{21} = \rho \Pi _{1}(1-q_{1}) R_{2} - (k_{3} +\mu _{h})E_{21}, \\ \dot{I}_{12} = k_{4} E_{12} - (\gamma _{5}+ \delta _{2}+ \mu _{h})I_{12}, \\ \dot{E}_{123}= \gamma _{5} I_{12}-(k_{6}+\mu _{h})E_{123}, \\ \dot{P}_{12} = k_{6}E_{123} - ( \beta _{2}+ \delta _{3}+\mu _{h})P_{12}, \\ \dot{I}_{21} = k_{3} E_{21}- (\gamma _{4} + \mu _{h})I_{21}, \\ \dot{M} = (\beta _{2})P_{12} + \gamma _{4} I_{21} -(k+ \mu _{h}) M, \\ \dot{S_{r}} = \Gamma _{r}+\omega _{d}Z_{r} - (\Pi _{r}(1-q_{1}) + \mu _{r}) S_{r}, \\ \dot{I_{r}} = \Pi _{r}(1-q_{1}) S_{r} -(\tau _{d}+\alpha _{d}+ \mu _{r}+q_{2}) I_{r}, \\ \dot{Z_{r}}=\tau _{d}I_{r}-(\omega _{d}+\mu _{r})Z_{r}, \\ \dot{S_{v}} = \Gamma _{v} -(\Pi _{v}(1-q_{1}) + \mu _{v}+q_{3}) S_{v}, \\ \dot{E_{v}} = \Pi _{v}(1-q_{1}) S_{v} -( \mu _{v}+\varrho _{v}+q_{3}) E_{v}, \\ \dot{I_{v}}=\varrho _{v} E_{v} -(\mu _{v}+q_{3}) I_{v}. \end{cases} $$
(5)

To reduce the density of sandflies, infected humans, and infected reservoir, we define an objective function (OF) as:

$$ J(q_{1},q_{2},q_{3})= \int ^{T}_{0} \biggl(Q+g_{8}( N_{v})+\frac{1}{2} \bigl(d_{1} q_{1}^{2}(t)+d_{2} q_{2}^{2}(t)+d_{3} q_{3}^{2}(t) \bigr) \biggr)\,dt,$$
(6)

where

$$ Q= g_{1}I_{1}+g_{2}I_{2}+g_{3}P_{2}+g_{4}I_{12}+g_{5}P_{12}+g_{6}I_{21}+g_{7}I_{r}. $$

Here \(N_{v}\) denotes the total vector population and \(g_{i}\) for \(i=1,2,3,\ldots,8\) denote the concerned weight constants; \(\frac{1}{2}(d_{1} q_{1}^{2}(t)+d_{2} q_{2}^{2}(t)+d_{3} q_{3}^{2}(t))\) denotes the cost associated with interventions.

Next we need to find the control function \(J_{1}\), subject to system (5), such that

$$ J_{1}=\min \bigl\{ J (q_{1},q_{2},q_{3}), \text{if } (q_{1},q_{2},q_{3})\in D) \bigr\} , $$

where D denotes the set of control variables and is defined as

$$ D= \bigl\{ (q_{1},q_{2},q_{3})\mid {q_{i}(t)} \text{ is Lebesgue measurable on } {[0 , T]} , 0 \le q_{i} ( t ) < 1 , i = 1 , 2 , 3 \bigr\} . $$

4.1 Solution of the proposed optimal control (OC) model

Here we investigate existence of OC for the proposed model (5) at \(t=0\). Using [32], we claim that the solution of the state system (5) is bounded. This is because the control variables are bounded and Lebesgue measurable, and the initial conditions are nonnegative.

Next we prove that the system has an optimal solution. For this, we introduce a Lagrangian and Hamiltonian as follows:

$$ L(t)=Q+g_{8}Nv(t)+\frac{1}{2} \bigl(d_{1}q_{1}^{2}+d_{2}q_{2}^{2}+d_{3}q_{3}^{2} \bigr),$$
(7)

where

$$ N_{v}(t)=S_{v}(t)+E_{v}(t)+I_{v}(t) $$

and

$$\begin{aligned}& Q= g_{1}I_{1}+g_{2}I_{2}+g_{3}P_{2}+g_{4}I_{12}+g_{5}P_{12}+g_{6}I_{21}+g_{7}I_{r}; \\& \begin{aligned} H(t)&=L(t)+\lambda _{1} \frac{dS_{h}}{dt}+\lambda _{2} \frac{dE_{1}}{dt}+\lambda _{3}\frac{dE_{2}}{dt}+\lambda _{4} \frac{dI_{1}}{dt}+ \lambda _{5}\frac{dI_{2}}{dt}+\lambda _{6} \frac{dE_{23}}{dt}+\lambda _{7}\frac{dP_{2}}{dt} \\ & \quad {} + \lambda _{8}\frac{dR_{1}}{dt}+\lambda _{9} \frac{dR_{2}}{dt}+ \lambda _{10}\frac{dE_{12}}{dt}+\lambda _{11}\frac{dE_{21}}{dt}+ \lambda _{12}\frac{dI_{12}}{dt}+ \lambda _{13}\frac{dE_{123}}{dt}+ \lambda _{14} \frac{dP_{12}}{dt} \\ &\quad {} + \lambda _{15}\frac{dI_{21}}{dt}+\lambda _{16} \frac{dM}{dt}+\lambda _{17} \frac{dS_{r}}{dt}+\lambda _{18}\frac{dI_{r}}{dt}+\lambda _{19} \frac{dZ_{r}}{dt}+ \lambda _{20}\frac{dS_{v}}{dt}+\lambda _{21} \frac{dE_{v}}{dt}+\lambda _{22}\frac{dI_{v}}{dt}. \end{aligned} \end{aligned}$$
(8)

Theorem 1

The set \((q_{1}^{*},q_{2}^{*},q_{3}^{*})\)of optimal controls minimizes \(J_{1}\)over D, subject to the initial conditions specified at \(t=0\).

Proof 1

Since both the state and control variables are nonnegative, using [33], the objective function is convex in the control variables \(q_{i}\), \(i=1,2,3\).

Clearly, from the definition, D is closed and convex. Further, since the optimal system is bounded, the set of optimal controls is compact.

And the control variables \(q_{1}\), \(q_{2}\), and \(q_{3} \) enter as quadratic terms. Therefore the integrand in (6) is convex on the control set D.

Also, all Y, for \(Y \in \Omega \), are bounded. So we can find a constant \(\partial > 1\) and positive numbers \(\Re _{1}\) and \(\Re _{2}\) such that \(J(q_{1}, q_{2}, q_{3})\ge \Re _{1}( \vert q_{1} \vert ^{2}, \vert q_{2} \vert ^{2}, \vert q_{3} \vert ^{2})^{\frac{\partial }{2}}-\Re _{2}\), as the state variables are bounded.

The proof of existence of optimal control is completed.

Next we characterize the control variables of the proposed model. We use Pontryagin’s maximum principle [34] stated here for convenience. Let

$$\begin{aligned}& F= \bigl(E_{1}^{*},I_{1}^{*},E_{2}^{*},I_{2}^{*},E_{23}^{*},P_{2}^{*},R_{1}^{*},R_{2}^{*},E_{12}^{*},I_{12}^{*},E_{21}^{*},I_{21}^{*},E_{123}^{*},P_{12}^{*},M^{*},I_{r}^{*},Z_{r}^{*},E_{v}^{*},I_{v}^{*},S_{h}^{*},S_{r}^{*},S_{v}^{*} \bigr)^{ T} \end{aligned}$$

be the states associated with control variables \((q_{1}^{*},q_{2}^{*},q_{3}^{*})\). Let \((y,q)\) be the solution of the control model/problem, for \(y\in \Omega \) and \(q=(q_{1}^{*},q_{2}^{*},q_{3}^{*})\), then there exists a vector function \(\lambda =(\lambda _{1},\lambda _{2},\ldots,\lambda _{n})\) satisfying the following:

$$\begin{aligned}& \frac{dy}{dt}= \frac{\partial H(t,y,q,\lambda )}{\partial \lambda }, \\& 0= \frac{\partial H(t,y,q,\lambda )}{\partial q}, \\& \lambda '=- \frac{\partial H(t,y,q,\lambda )}{\partial y}. \end{aligned}$$

To establish the necessary condition on H, we prove the following result.

Theorem 2

The necessary condition for a control \(q=(q_{1}^{*},q_{2}^{*},q_{3}^{*})\)to be optimal with corresponding state F is that there exists an adjoint variable, \(\lambda _{i}\), for \(i = 1,2,\ldots,22\), satisfying:

$$\begin{aligned}& \textstyle\begin{cases} \frac{d\lambda _{1}}{dt}= \frac{(\lambda _{1}(t)-\lambda _{2}(t))ab_{1}(W_{1})(1-q_{1}(t))I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{1}(t)-\lambda _{3}(t))(W_{1})ab_{2}(1-q_{1}(t))I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{1}}{dt}=}{}+\frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{1}}{dt}=}{}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{21}(t)-\lambda _{20}(t))(W)}{(N_{h}(t)+N_{r}(t))^{2}}+ \mu _{h}\lambda _{1}(t), \\ \frac{d\lambda _{2}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{2}}{dt}=}{} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{2}}{dt}=}{}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{21}(t)-\lambda _{20}(t))(W)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{2}}{dt}=}{}+(\lambda _{2}(t)-\lambda _{4}(t))k_{1}+\mu _{h}\lambda _{2}(t), \\ \frac{d\lambda _{3}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{3}}{dt}=} {} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-u_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{3}}{dt}=}{}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{21}(t)-\lambda _{20}(t))(W)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{3}}{dt}=}{}+(\lambda _{3}(t)-\lambda _{5}(t))k_{2}+\mu _{h}\lambda _{3}(t), \\ \frac{d\lambda _{4}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{4}}{dt}=} {} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{4}}{dt}=}{}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+( \lambda _{4}(t)-\lambda _{8}(t))\gamma _{1}+\mu _{h}\lambda _{4}(t)-g_{1} \\ \hphantom{\frac{d\lambda _{4}}{dt}=}{}+\frac{(\lambda _{21}(t)-\lambda _{20}(t))( c I_{r}(t)+S_{v}a(1-q_{1}))(W_{2}-c_{1}(W_{3}+N_{r})}{(N_{h}(t)+N_{r}(t))^{2}}, \end{cases}\displaystyle \\& \textstyle\begin{cases} \frac{d\lambda _{5}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))H_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{5}}{dt}=} {} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{5}}{dt}=}{}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+( \lambda _{5}(t)-\lambda _{6}(t))\gamma _{2}+\lambda _{5}(t)(\delta _{1}+ \mu _{h})-g_{2} \\ \hphantom{\frac{d\lambda _{5}}{dt}=}{} + \frac{(\lambda _{21}(t)-\lambda _{20}(t))( c I_{r}(t)+S_{v}a(1-q_{1}))(W_{4}-c_{2}(W_{5}+N_{r})}{(N_{h}(t)+N_{r}(t))^{2}}, \\ \frac{d\lambda _{6}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{6}}{dt}=} {} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{6}}{dt}=}{}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{21}(t)-\lambda _{20}(t))(W)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{6}}{dt}=}{}+(\lambda _{6}(t)-\lambda _{7}(t))k_{6}+\mu _{h}\lambda _{6}(t), \\ \frac{d\lambda _{7}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{7}}{dt}=}{} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{7}}{dt}=}{}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+( \lambda _{7}(t)-\lambda _{9}(t))\beta _{1}+\lambda _{7}(t)(\delta _{3}+ \mu _{h})-g_{3} \\ \hphantom{\frac{d\lambda _{7}}{dt}=} {} + \frac{(\lambda _{21}(t)-\lambda _{20}(t))(S_{v}a(1-q_{1}))(W_{4}-c_{2}(W_{5}+N_{r})}{(N_{h}(t)+N_{r}(t))^{2}}, \\ \frac{d\lambda _{8}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{8}}{dt}=} {} + \frac{(\lambda _{8}(t)-\lambda _{10}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)(W_{6}+N_{r})}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{21}(t)-\lambda _{20}(t))(W)}{(N_{h}(t)+N_{r}(t))^{2}}+ \mu _{h}\lambda _{8}(t) \\ \hphantom{\frac{d\lambda _{8}}{dt}=}{} + \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}, \\ \frac{d\lambda _{9}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{9}}{dt}=} {} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{9}}{dt}=}{}+\frac{(\lambda _{9}(t)-\lambda _{11}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)(W_{7}+N_{r}(t))}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{21}(t)-\lambda _{20}(t))(W)}{(N_{h}(t)+N_{r}(t))^{2}}+ \mu _{h}\lambda _{9}(t), \end{cases}\displaystyle \\& \textstyle\begin{cases} \frac{d\lambda _{10}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{10}}{dt}=} {} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{10}}{dt}=}{}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-u_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{21}(t)-\lambda _{20}(t))(W)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{10}}{dt}=}{} +(\lambda _{10}(t)-\lambda _{12}(t))k_{4}+\lambda _{10}(t)\mu _{h}, \\ \frac{d\lambda _{11}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{11}}{dt}=} {} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-u_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{11}}{dt}=}{}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{21}(t)-\lambda _{20}(t))(W)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{11}}{dt}=} {} +(\lambda _{11}(t)-\lambda _{15}(t))k_{3}+\lambda _{11}(t)\mu _{h}, \\ \frac{d\lambda _{12}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{12}}{dt}=} {} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{12}}{dt}=}{}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+( \lambda _{12}(t)-\lambda _{13}(t))\gamma _{5}+\lambda _{12}(t)( \delta _{2}+\mu _{h})-g_{4} \\ \hphantom{\frac{d\lambda _{12}}{dt}=}{}+\frac{(\lambda _{21}(t)-\lambda _{20}(t))(S_{v}(t)a(1-q_{1}(t)))(W_{8}-c_{2}\rho (W_{9}+N_{r}))}{(N_{h}(t)+N_{r}(t))^{2}}, \\ \frac{d\lambda _{13}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{13}}{dt}=} {} + \frac{(\lambda _{8}(t)-\lambda _{10}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)(W_{6}+N_{r})}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{21}(t)-\lambda _{20}(t))(W)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{13}}{dt}=}{}+\frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{13}}{dt}=}{}+(\lambda _{13}(t)-\lambda _{14}(t))k_{6}+\mu _{h}\lambda _{13}(t), \\ \frac{d\lambda _{14}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{14}}{dt}=} {} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{14}}{dt}=}{}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)_{r}S(t)}{(N_{h}(t)+N_{r}(t))^{2}}+( \lambda _{14}(t)-\lambda _{16}(t))(\beta _{2}+\gamma _{2}) \\ \hphantom{\frac{d\lambda _{14}}{dt}=}{}+\frac{(\lambda _{21}(t)-\lambda _{20}(t))(S_{v}(t)a(1-q_{1}(t)))(W_{8}-c_{2}\rho (W_{9}+N_{r}))}{(N_{h}(t)+N_{r}(t))^{2}}+ \lambda _{14}(t)(\delta _{3}+\mu _{h})-g_{5}, \end{cases}\displaystyle \end{aligned}$$

also

$$\begin{aligned}& \textstyle\begin{cases} \frac{d\lambda _{15}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{15}}{dt}=}{} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\\hphantom{\frac{d\lambda _{15}}{dt}=} {}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+( \lambda _{15}(t)-\lambda _{16}(t))\gamma _{4}+\lambda _{15}(t)\mu _{h}-g_{6} \\ \hphantom{\frac{d\lambda _{15}}{dt}=} {}+\frac{(\lambda _{21}(t)-\lambda _{20}(t))(S_{v}(t)a(1-q_{1}(t)))(W_{10}-c_{1}\rho (W_{11}+N_{r}))}{(N_{h}(t)+N_{r}(t))^{2}}, \\ \frac{d\lambda _{16}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-u_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{16}}{dt}=}{} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{16}}{dt}=} {}+\frac{(\lambda _{17}(t)-\lambda _{18}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)(N_{h}(t)-(I_{r}(t)+Z_{r}(t)))}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{21}(t)-\lambda _{20}(t))W}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{16}}{dt}=} {}+(\lambda _{16}(t)-\lambda _{1}(t))k+\lambda _{16}(t)\mu _{h}, \\ \frac{d\lambda _{17}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{17}}{dt}=} {} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{17}}{dt}=} {}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{21}(t)-\lambda _{20}(t))W}{(N_{h}(t)+N_{r}(t))^{2}}+ \lambda _{17}(t)\mu _{h}, \\ \frac{d\lambda _{18}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{18}}{dt}=}{} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{18}}{dt}=} {}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{21}(t)-\lambda _{20}(t))((W_{12}-\rho c(N_{h}-(S_{r}+Z_{r}))}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{18}}{dt}=} {} +(\lambda _{18}(t)-\lambda _{19}(t))\tau _{d}+\lambda _{18}(t)( \zeta _{d}+\mu _{r}+q_{2})-g_{7}, \\ \frac{d\lambda _{19}}{dt}= \frac{(\lambda _{2}(t)-\lambda _{1}(t))ab_{1}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{3}(t)-\lambda _{1}(t))ab_{2}(1-q_{1}(t))S_{h}(t)I_{v}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{19}}{dt}=} {} + \frac{(\lambda _{10}(t)-\lambda _{8}(t))ab_{2}(1-q_{1}(t))\rho I_{v}(t)R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{11}(t)-\lambda _{9}(t))ab_{1}(1-q_{1}(t))\rho I_{v}(t)R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{19}}{dt}=} {}+\frac{(\lambda _{18}(t)-\lambda _{17}(t))ab(1-q_{1}(t))I_{v}(t)S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{21}(t)-\lambda _{20}(t))(W)}{(N_{h}(t)+N_{r}(t))^{2}} \\ \hphantom{\frac{d\lambda _{19}}{dt}=}{} +(\lambda _{19}(t)-\lambda _{17}(t))\omega _{d}+\lambda _{19}(t)( \mu _{h}), \end{cases}\displaystyle \\& \textstyle\begin{cases} \frac{d\lambda _{20}}{dt}= \frac{(\lambda _{21}(t)-\lambda _{20}(t))a(1-q_{1}(t))}{(N_{h}(t)+N_{r}(t))^{2}}(c_{1}I_{1}(t)+c_{2}(I_{2}(t)+P_{2}(t))+ \rho (c_{1}I_{21}(t) \\\hphantom{\frac{d\lambda _{20}}{dt}=} {}+c_{2}I_{12}(t)+c_{2}P_{12}(t)))+\lambda _{20}(t)(\mu _{v}+q_{3}(t))-g_{8}, \\ \frac{d\lambda _{21}}{dt}= \frac{(\lambda _{21}(t)-\lambda _{20}(t))\varrho _{v}}{(N_{h}(t)+N_{r}(t))^{2}}+ \lambda _{21}(t)(\mu _{v}+q_{3}(t))-g_{8}, \\ \frac{d\lambda _{22}}{dt}= \frac{(\lambda _{1}(t)-\lambda _{2}(t))ab_{1}(1-q_{1}(t))S_{h}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{1}(t)-\lambda _{3}(t))ab_{2}(1-q_{1}(t))S_{h}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\\hphantom{\frac{d\lambda _{22}}{dt}=} {}+\frac{(\lambda _{8}(t)-\lambda _{10}(t))ab_{2}(1-q_{1}(t))\rho R_{1}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \frac{(\lambda _{9}(t)-\lambda _{11}(t))ab_{1}(1-q_{1}(t))\rho R_{2}(t)}{(N_{h}(t)+N_{r}(t))^{2}} \\\hphantom{\frac{d\lambda _{22}}{dt}=} {}+\frac{(\lambda _{17}(t)-\lambda _{18}(t))ab(1-q_{1}(t))S_{r}(t)}{(N_{h}(t)+N_{r}(t))^{2}}+ \lambda _{22}(t)(\mu _{v}+q_{3}(t))-g_{8} \end{cases}\displaystyle \end{aligned}$$
(9)

with transversality/boundary conditions

$$ \lambda _{i}(t_{end})=\lambda _{i}(T) = 0 \quad \textit{for } i = 1,2,\ldots,22.$$
(10)

And the optimal controls \(q_{2}^{*}\), \(q_{3}^{*}\), and \(q_{1}^{*}\)are given by

$$\begin{aligned}& q_{1}^{*}=\max \bigl\{ \min \{Z,1 \},0 \bigr\} , \end{aligned}$$
(11)
$$\begin{aligned}& q_{2}^{*}=\max \biggl\{ \min \biggl\{ \frac{\lambda _{18} I^{*}_{r}}{d_{2}},1 \biggr\} ,0 \biggr\} , \end{aligned}$$
(12)
$$\begin{aligned}& q_{3}^{*}=\max \biggl\{ \min \biggl\{ \frac{\lambda _{20}S^{*}_{v}+\lambda _{21}E^{*}_{v}+\lambda _{22}I^{*}_{v}}{d_{3}},1 \biggr\} ,0 \biggr\} , \end{aligned}$$
(13)

where

$$\begin{aligned}& \begin{aligned} Z={}& \frac{(\lambda _{1}-\lambda _{2})ab_{1}I^{*}_{v}S^{*}_{h}+(\lambda _{1}-\lambda _{3})ab_{2}I^{*}_{v}S^{*}_{h}+(\lambda _{8}(t)-\lambda _{10}(t))ab_{2}\rho I^{*}_{v}(t)R^{*}_{1}(t)}{d_{1}(N_{h}+N_{r})} \\ &{} + \frac{(\lambda _{9}(t)-\lambda _{11}(t))ab_{1}\rho I^{*}_{v}(t)R^{*}_{2}(t)+(\lambda _{17}(t)-\lambda _{18}(t))abI^{*}_{v}(t)S^{*}_{r}(t)}{d_{1}(N_{h}+N_{r})} \\ &{} + \bigl(\bigl(\lambda _{20}(t)-\lambda _{21}(t)\bigr) \bigl(S^{*}_{v}(t) \bigl(c_{1}I^{*}_{1}(t) +c_{2} \bigl(I^{*}_{2}(t)+P^{*}_{2}(t)\bigr)+ \rho \bigl(c_{1}I^{*}_{21}(t) \\ &{}+ c_{2}\bigl(I^{*}_{12}(t)+P^{*}_{12}(t) \bigr)\bigr)\bigr) + c I^{*}_{r}(t)\bigr)\bigr)/ \bigl({d_{1}(N_{h}+N_{r})}\bigr), \end{aligned} \\ & \begin{aligned} W={}&a \bigl(1-q_{1}(t) \bigr) S_{v}(t) \bigl(c_{1}I_{1}(t)+c_{2}I_{2}(t)+c_{2}P_{2}(t)+ \rho c_{1}I_{21}(t)+\rho c_{2}I_{12}(t) \\ &{}+ \rho c_{2}P_{12}(t)+ c I_{r}(t) \bigr), \end{aligned} \\ & \begin{aligned} W_{1}={}&E_{1}(t)+E_{2}(t)+I_{1}(t)+I_{2}(t)+E_{23}(t)+P_{2}(t)+R_{1}(t)+R_{2}(t)+E_{12}(t)+E_{21}(t) \\ &{}+I_{12}(t) + E_{123}(t)+P_{12}(t)+I_{21}(t)+M(t)+N_{r}(t),\end{aligned} \\ & W_{2}= \bigl(c_{2}I_{2}(t)+c_{2}P_{2}(t)+ \rho c_{1}I_{21}(t)+\rho c_{2}I_{12(t)}+ \rho c_{2}P_{12}(t)+ c I_{r}(t) \bigr),\\ & \begin{aligned} W_{3}={}&S_{h}(t)+E_{1}(t)+E_{2}(t)+I_{2}(t)+E_{23}(t)+P_{2}(t)+R_{1}(t)+R_{2}(t) \\ &{} + E_{12}(t)+E_{21}(t)+I_{12}(t)+E_{123}(t)+P_{12}(t)+I_{21}(t)+M(t),\end{aligned} \\ & W_{4}= \bigl(c_{1}I_{1}(t)+\rho c_{1}I_{21}(t)+ \rho c_{2}I_{12}(t)+ \rho c_{2}P_{12}(t)+c I_{r}(t) \bigr),\\ & \begin{aligned} W_{5}={}&S_{h}(t)+E_{1}(t)+E_{2}(t)+I_{1}(t)+E_{23}(t)+R_{1}(t)+R_{2}(t)+E_{12}(t)+E_{21}(t) \\ &{} + I_{12}(t)+E_{123}(t)+P_{12}(t)+I_{21}(t)+M(t),\end{aligned} \\ & \begin{aligned} W_{6}={}&S_{h}(t)+E_{1}(t)+E_{2}(t)+I_{1}(t)+I_{2}(t)+E_{23}(t)+P_{2}(t)+R_{2}(t)+E_{12}(t)+E_{21}(t) \\ &{} + I_{12}(t)+E_{123}(t)+P_{12}(t)+I_{21}(t)+M(t),\end{aligned} \\ & \begin{aligned} W_{7}={}&S_{h}(t)+E_{1}(t)+E_{2}(t)+I_{1}(t)+I_{2}(t)+E_{23}(t)+P_{2}(t)+R_{1}(t)+E_{12}(t)+E_{21}(t) \\ &{} + I_{12}(t)+E_{123}(t)+P_{12}(t)+I_{21}(t)+M(t),\end{aligned} \\ & W_{8}= \bigl(c_{1}I_{1}(t)+c_{2}I_{2}(t)+c_{2}P_{2}(t)+ \rho c_{1}I_{21}(t)+c I_{r}(t) \bigr),\\ & \begin{aligned} W_{9}={}&S_{h}(t)+E_{1}(t)+E_{2}(t)+I_{1}(t)+I_{2}(t)+E_{23}(t)+P_{2}(t)+R_{1}(t)+R_{2}(t)+E_{12}(t) \\ &{} + E_{21}(t)+E_{123}(t)+I_{21}(t)+M(t),\end{aligned} \\ & W_{10}= \bigl(c_{1}I_{1}(t)+c_{2}I_{2}(t)+c_{2}P_{2}(t)+ \rho c_{2}I_{12}(t)+\rho c_{2}P_{12}(t)+c I_{r}(t) \bigr),\\ & \begin{aligned} W_{11}={}&S_{h}(t)+E_{1}(t)+E_{2}(t)+I_{1}(t)+I_{2}(t)+E_{23}(t)+P_{2}(t)+R_{1}(t)+R_{2}(t)+E_{12}(t) \\ &{} + E_{21}(t)+I_{12}(t)+E_{123}(t)+P_{12}(t)+M(t),\end{aligned} \\ & W_{12}=a \bigl(1-q_{1}(t) \bigr) S_{v}(t) \bigl(c_{1}I_{1}(t)+c_{2}I_{2}(t)+c_{2}P_{2}(t)+ \rho c_{1}I_{21}(t)+\rho c_{2}I_{12}(t)+ \rho c_{2}P_{12}(t) \bigr). \end{aligned}$$

Proof 2

First we differentiate H given in (8) with respect to the state variables involved in the model. As a result we get the system involving \(\frac{d\lambda _{i}}{dt}\) for \(i=1,2,3,\ldots,22\).

To find \((q_{1}^{*},q_{2}^{*},q_{3}^{*})\), we solve the following system, using the properties of control set and optimality conditions:

$$ \frac{\partial H}{\partial q_{1}}=0, \quad\quad \frac{\partial H}{\partial q_{2}}=0, \quad\quad \frac{\partial H}{\partial q_{3}}=0. $$

Solving the above system, we have the results (11)–(13).

Here, the second derivative of Lagrangian L with respect to \(q_{3}^{*}\), \(q_{2}^{*}\), and \(q_{1}^{*}\) is \(+ve\). This shows that the optimal control is a maximum at control \(q_{3}^{*}\), \(q_{2}^{*}\), and \(q_{1}^{*}\). We put these values in system (5) and propose the following optimal control model.

$$\begin{aligned} \textstyle\begin{cases} \dot{S^{*}_{h}} = (1- \epsilon _{1} - \epsilon _{2})\Gamma _{h} + kM^{*} - (\Pi ^{*}_{1} + \Pi ^{*}_{2} )(1-\max \{\min \{Z,1 \},0 \})S^{*}_{h} - \mu _{h} S_{h}^{*}, \\ \dot{E^{*}_{1}} = \Pi ^{*}_{1}(1-\max \{\min \{Z,1 \},0 \}) S^{*} - (k_{1} + \mu _{h})E^{*}_{1}, \\ \dot{E^{*}_{2}} = \Pi ^{*}_{2}(1-\max \{\min \{Z,1 \},0 \}) S^{*}_{h} - (k_{2} + \mu _{h})E^{*}_{2}, \\ \dot{I^{*}_{1}} = k_{1} E^{*}_{1} - (\gamma _{1} + \mu _{h}) I^{*}_{1}, \\ \dot{I^{*}_{2}} = k_{2} E^{*}_{2} - (\gamma _{2} + \delta _{1} + \mu _{h}) I^{*}_{2}, \\ \dot{E^{*}_{23}} = \gamma _{2} I^{*}_{2}-(k_{6}+\mu _{h})E^{*}_{23}, \\ \dot{P^{*}_{2}} = k_{6}E^{*}_{23} -( \beta _{1}+\delta _{3} + \mu _{h}) P^{*}_{2}, \\ \dot{R^{*}_{1}} = \epsilon _{2} \Gamma _{h} + \gamma _{1} I^{*}_{1} - (\rho \Pi ^{*}_{2}(1-\max \{\min \{Z,1 \},0 \}) + \mu _{h} )R^{*}_{1}, \\ \dot{R^{*}_{2}} = \epsilon _{1} \Gamma _{h} +\beta _{1}P^{*}_{2} - ( \rho \Pi ^{*}_{1}(1-\max \{\min \{Z,1 \},0 \}) + \mu _{h})R^{*}_{2}, \\ \dot{E^{*}_{12}} = \rho \Pi ^{*}_{2}(1-\max \{\min \{Z,1 \},0 \}) R^{*}_{1} - (k_{4} + \mu _{h})E^{*}_{12}, \\ \dot{E^{*}_{21}} = \rho \Pi ^{*}_{1}(1-\max \{\min \{Z,1 \},0 \}) R^{*}_{2} - (k_{3} +\mu _{h})E^{*}_{21}, \\ \dot{I^{*}_{12}} = k_{4} E^{*}_{12} - (\gamma _{5}+ \delta _{2}+ \mu _{h})I^{*}_{12}, \\ \dot{E^{*}_{123}} = \gamma _{5} I^{*}_{12}-(k_{6}+\mu _{h})E^{*}_{123}, \\ \dot{P^{*}_{12}} = k_{6}E^{*}_{123} - ( \beta _{2}+ \delta _{3}+\mu _{h})P^{*}_{12}, \\ \dot{I^{*}_{21}} = k_{3} E^{*}_{21}- (\gamma _{4} + \mu _{h})I^{*}_{21}, \\ \dot{M^{*}} = \beta _{2} P^{*}_{12} + \gamma _{4} I^{*}_{21} -(k+ \mu _{h}) M^{*}, \\ \dot{S_{r}^{*}} = \Gamma _{r}+\omega _{d}Z^{*}_{r} - (\Pi ^{*}_{r}(1- \max \{\min \{Z,1 \},0 \}) + \mu _{r}) S_{r}^{*}, \\ \dot{I_{r}^{*}} = \Pi ^{*}_{r}(1-\max \{\min \{Z,1 \},0 \}) S_{r}^{*} -(\tau _{d}+\alpha _{d}+ \mu _{r}+\max \{ \min \{\frac{\lambda _{18} I_{r}^{*}}{d_{2}},1 \},0 \}) I_{r}^{*}, \\ \dot{Z_{r}^{*}} =\tau _{d}I_{r}^{*}-(\omega _{d}+\mu _{r})Z_{r}^{*}, \\ \dot{S_{v}^{*}} = \Gamma _{v} -(\Pi ^{*}_{v}(1-\max \{\min \{Z,1 \},0 \}) + (\mu _{v}+q^{*}_{3}) S_{v}^{*}, \\ \dot{E_{v}^{*}} = \Pi ^{*}_{v}(1-\max \{\min \{Z,1 \},0 \}) S_{v}^{*}-(\mu _{v}+\varrho _{v}+q^{*}_{3}) E_{v}^{*}, \\ \dot{I_{v}^{*}} =\varrho _{v} E_{v}^{*} -(\mu _{v}+\max \{\min \{ \frac{\lambda _{20}S_{v}^{*}+\lambda _{21}E_{v}^{*}+\lambda _{22}I_{v}^{*}}{d_{3}},1 \},0 \}) I_{v}^{*}. \end{cases}\displaystyle \end{aligned}$$
(14)

with

$$\begin{aligned} H^{*}={}&g_{1}I_{1}+g_{2}I_{2}+g_{3}P_{2}+g_{4}I_{12}+g_{5}P_{12}+g_{6}I_{21}+g_{7}I_{r}+g_{8}N_{v}^{*} \\ &{}+\frac{1}{2} \biggl(d_{1} \bigl(\max \bigl\{ \min \{Z,1 \},0 \bigr\} \bigr)^{2} +d_{2} \biggl(\max \biggl\{ \min \biggl\{ \frac{\lambda _{18}I_{r}^{*}}{d_{2}},1 \biggr\} ,0 \biggr\} \biggr)^{2} \\ &{}+d_{3} \biggl(\max \biggl\{ \min \biggl\{ \frac{\lambda _{20}S_{v}^{*}+\lambda _{21}E_{v}^{*}+\lambda _{22}I_{v}^{*}}{d_{3}},1 \biggr\} ,0 \biggr\} \biggr)^{2} \biggr) +\lambda _{1} \frac{dS_{h}^{*}}{dt}+ \lambda _{2}\frac{dE_{1}^{*}}{dt} \\ &{}+\lambda _{3}\frac{dE_{2}^{*}}{dt}+\lambda _{4} \frac{dI_{1}^{*}}{dt}+ \lambda _{5}\frac{dI_{2}^{*}}{dt}+\lambda _{6}\frac{dE_{23}^{*}}{dt}+ \lambda _{7}\frac{dP_{2}^{*}}{dt}+ \lambda _{8}\frac{dR_{1}^{*}}{dt}+ \lambda _{9} \frac{dR_{2}^{*}}{dt}+\lambda _{10}\frac{dE_{12}^{*}}{dt} \\ &{}+\lambda _{11}\frac{dE_{21}^{*}}{dt}+\lambda _{12} \frac{dI_{12}^{*}}{dt}+\lambda _{13}\frac{dE_{123}^{*}}{dt}+ \lambda _{14} \frac{dP_{12}^{*}}{dt}+\lambda _{15}\frac{dI_{21}^{*}}{dt}+ \lambda _{16} \frac{dM^{*}}{dt}+\lambda _{17} \frac{dS_{r}^{*}}{dt} \\ &{}+ \lambda _{18}\frac{dI_{r}^{*}}{dt}+\lambda _{19} \frac{dZ_{r}^{*}}{dt}+\lambda _{20}\frac{dS_{v}^{*}}{dt}+\lambda _{21} \frac{dE_{v}^{*}}{dt}+\lambda _{22}\frac{dI_{v}^{*}}{dt}. \end{aligned}$$
(15)

5 Numerical simulations and discussion

We solve the optimality system (14) numerically using RK4 method. The method solves the state system (5), forward in time, and the adjoint system (9), backward in the time, and system (10), the controls are updated continuously using systems (11) to (13). The process is continued until the results at the consecutive iterations (CI) are close. For details, see [35].

We assign the following values to weight constants (WC): \(g_{1}=0.5\), \(g_{2}=0.5\), \(g_{3}=0.5\), \(g_{4}=0.5\), \(g_{5}=0.5\), \(g_{6}=0.5\), \(g_{7}=0.5\), \(g_{8}=0.7\), \(d_{1}=1\), \(d_{2}=10\), and \(d_{3}=20\). We have used \(S_{h}=1000\), \(E_{1}=30\), \(E_{2}=30\), \(I_{1}=30\), \(I_{2}=30\), \(E_{23}=30\), \(P_{2}=30\), \(R_{1}=30\), \(R_{2}=30\), \(E_{12}=30\), \(E_{21}=30\), \(I_{12}=30\), \(E_{123}=30\), \(P_{12}=30\), \(I_{21}=30\), \(M=30\), \(S_{r}=10\), \(I_{r}=5\), \(Z_{r}=2\), \(S_{v}=10{,}000\), \(E_{v}=1000\), and \(I_{v}=500\).

Note

Stage 1 infection means that a susceptible human at the first time is attacked by some strain. Stage 2 infection means that the individual has recovered form some strain of leishmaniasis and after recovery is attacked by another stain of leishmaniasis.

In the following figures we have presented the behavior of different subclasses of the total population involved in the model. Figure 2 represents two subclasses: \(S_{h}\), the susceptible human class, and \(E_{1}\), the \(C_{l}\)-exposed human class. The figure shows that without intervention or control variables (presented by red lines), the density of the susceptible human class decreases because the susceptible humans are infected and they move from the susceptible class to the infected class \(E_{1}\). At the same time the density of the infected class increases. However, in case of proper intervention, the density of the exposed class decreases, and there is no notable decrease in the density of the susceptible human population. Figure 3 presents the behavior of \(E_{2}\), the \(V_{l}\)-exposed human class, and \(I_{1}\), the infectious human class of \(C_{l}\) strain. The gap between the red and blue lines represents the effectiveness of the control variables. Figure 4 presents the behavior of \(I_{2}\), the \(V_{l}\)-infectious human class, and \(E_{23}\), the human class in the dormant period of developing PKDL. The figures show that the interventions have a notable effect on the control of \(I_{2}\) and \(E_{23}\). Figure 5 represents the behaviors of \(P_{2}\), the human class infected with PKDL, and \(R_{1}\), the human class recovered from the cutaneous strain. Here too the effect of interventions is notable. The effect of interventions on \(R_{2}\) is not so high. The reason might be the prolonged dormancy period of PKDL. All the above mentioned cases are concerned with Stage 1 infection and the effect of interventions is high.

Figure 2
figure 2

Comparison of behaviors with and without control in case of \(S_{h}\) and \(E_{1}\)

Full size image
Figure 3
figure 3

Comparison of behaviors with and without control in case of \(E_{2}\) and \(I_{1}\)

Full size image
Figure 4
figure 4

Comparison of behaviors with and without control in case of \(I_{2}\) and \(E_{23}\)

Full size image
Figure 5
figure 5

Comparison of behaviors with and without control in case of \(P_{2}\) and \(R_{1}\)

Full size image

From Fig. 6 to Fig. 9, these behaviors are associated with Stage 2 infection. Like in Fig. 6, \(E_{12}\) represents the human class recovered from cutaneous leishmaniasis and infected/attacked by visceral leishmaniasis after the said recovery. In all Stage 2 infection cases, the effect of the interventions is not high. Figure 10 presents the behavior of \(S_{r}\), the susceptible reservoir, and \(I_{r}\), the infectious reservoir. The intervention involving “culling of seropositive dogs” directly addresses the infectious class of the reservoir population and hence the density of \(I_{r}\) reduces rapidly. Similarly, the density of all the subclasses in the vector population reduces very rapidly because the use of residual sprays directly affects all the subclasses. Figure 11 represents the behavoir of susceptible sanflies and recovered resorvoirs. it takes 5-10 days to elimanate susceptible vectors using control variable. Figure 12 represents the behavoirs of exposed and infectious vectors with and without control. The density of exposed vectors reduces to zero in five days while that of infectious vectors reduces to zero in ten days. Figure 13 suggests that the interventions should be continue for a long time.

Figure 6
figure 6

Comparison of behaviors with and without control in case of \(R_{2}\) and \(E_{12}\)

Full size image
Figure 7
figure 7

Comparison of behaviors with and without control in case of \(E_{21}\) and \(I_{12}\)

Full size image
Figure 8
figure 8

Comparison of behaviors with and without control in case of \(E_{123}\) and \(P_{12}\)

Full size image
Figure 9
figure 9

Comparison of behaviors with and without control in case of \(I_{21}\) and M

Full size image
Figure 10
figure 10

Comparison of behaviors with and without control in case of \(S_{r}\) and \(I_{r}\)

Full size image
Figure 11
figure 11

Comparison of behaviors with and without control in case of \(Z_{r}\) and \(S_{v}\)

Full size image
Figure 12
figure 12

Comparison of behaviors with and without control in case of \(E_{v}\) and \(I_{v}\)

Full size image
Figure 13
figure 13

Control variables \(q_{1}\), \(q_{2}\), and \(q_{3}\)

Full size image

6 Conclusion

A model of three populations, namely sandflies, dogs, and humans, was considered for the epidemic of leishmaniasis. The main aim of the study was the minimization of the objective function, that is, the reduction of total sandflies population and the minimization of infected classes in the human and dog populations. Three control variables, \(q_{1}\), \(q_{2}\), and \(q_{3}\), were introduced to control the biting rate of sandflies and the densities of the infectious class of dog and vector populations. For this, first of all we investigated the sensitivity of the initial rate of transmission, \(R_{0}\), for different parameters involved in the transmission. Different parameters used in \(R_{0}\) have different sensitivity indices. We needed to address the parameters with high sensitivity. However, some parameters are beyond the human control, like the birth and death rates of human and reservoir populations. The sensitivity index of a, the biting rate of sandfly, is 1. That is, a decrease of 20% in a would cause a decrease of 20% in \(R_{0}\), the initial rate of disease transmission. Similarly, \(\mu _{v}\), \(\Gamma _{v}\), \(\mu _{r}\), and \(\Gamma _{r}\) have high sensitivity indices and hence a high impact on the disease transmission. The most sensitive parameters, namely a, the biting rate of sandfly, \(\mu _{v}\), the mortality rate of sandflies, and \(\mu _{r}\), the death rate of dogs, are directly influenced by using control variables \(q_{1}\), \(q_{2}\), and \(q_{3}\). Aso \(\Gamma _{v}\), the birth rate of sandflies, is addressed indirectly by imposing restrictions on the collection of blood meal, and hence reducing ovigenesis. Numerical simulations show that as a result of these interventions cutaneous leishmaniasis can be eliminated in the period of 1200 days. However, \(I_{2}\), \(P_{2}\), and \(I_{12}\) reduce to zero in 750, 1750, and 1150 days, respectively. Moreover, \(P_{12}\), \(I_{21}\), \(I_{r}\), and \(I_{v}\) reduce to zero in 1700, 950, 7, and 7 days, respectively.