1 Introduction

Applications of fractional differential equation (FDE) in science and engineering are becoming vibrant, particularly in the fields of physics, finance, viscoelasticity, chemistry, and fluid mechanics. For this reason many authors are attracted to knowing the properties of FDEs (for details, see [2, 13, 15, 16, 18–20, 24, 25, 28]) and vast applications in modeling and engineering fields [1, 6, 11, 12]. Also see the literature [3, 5, 21, 23] for further applications of FDE in different disciplines.

The Fokker–Planck equation (FPE) was studied for the first time by Risken [22]. In addition, several researchers [4, 17] have worked on fractional Fokker–Planck equations among mathematical models developed in physical and biological sciences. It results from a diffusion estimation of certain stochastic processes that have been re-enacted as Markovian and continuous. It is a generalized diffusion equation that governs the evolution of the probability density in time. In most cases, fractional differential equations (FDEs) cannot be solved using the exact methods [8–10], that is why the recent research has used the properties of shifted Chebyshev polynomials [14, 27] and the finite difference method (FDM) to simplify the fractional initial value problem (IVP) to a set of nonlinear equations. In this paper, we are limited to the computational solution for the two-variable time-fractional Fokker–Planck equation [17] as follows:

$$ \frac{\partial ^{\alpha } u}{\partial t^{\alpha } } = \Biggl[-\sum _{i=1}^{n} \frac{\partial u}{\partial x_{i} } A_{i} (x, t, u)+\sum_{i=1}^{n} \sum_{j=1}^{n}\frac{\partial ^{2} u}{\partial x_{i} \partial x_{j} } B_{i} (x, t, u) \Biggr]u, $$
(1.1)

where \(u= u(x, t), \alpha \) is a parameter that defines the fractional derivative order (\(0<\alpha \le 1\)). \(A_{i} (x, t, u)\) and \(B_{i} (x, t, u)\) are arbitrary constants and n is an integer such that \(n\ne 0\).

In recent decades, Chebyshev polynomials have been among the most useful approximations because of their suitability for solving complex problems in science and engineering that can be expressed in integral equations, ordinary differential equations, and partial differential equations in integer and fractional orders. In this article, we use the fourth-kind Chebyshev polynomials with some important properties and their analytical form. Here, the approximate solution of FFPE is computed with the help of the shifted Chebyshev collocation method and the finite difference scheme. The shifted Chebyshev collocation method is used to reduce FFPE into systems of nonlinear differential equations, while FDM can be used for rewriting these systems into systems of nonlinear equations, and hence the Newton–Raphson method is used to arrive at the required approximate solution.

The organization of the paper is as follows. In Sect. 2, we provide the basic properties of Chebyshev polynomials of the fourth kind. In Sect. 3, the shifted Chebyshev collocation method and the finite difference method (FDM) are implemented to solve the fractional Fokker–Planck equation. In Sect. 4, conclusions are provided.

2 Preliminaries

This section discusses mathematical description, fractional derivative notation, and some essential properties for the fourth-kind Chebyshev polynomials.

Definition 2.1

In the Caputo sense the fractional derivative of \(f(z)\) is defined as in [19]:

$$ D^{\alpha } f(z)=\frac{1}{\varGamma (m-\alpha )} \int _{0}^{z}(z-s)^{m- \alpha -1} f^{(m)} (s)\,ds, $$
(2.1)

where \(z>0\), \(m\in \mathbb{C}\), and \(m-1<\alpha <m\).

The sequential property of the Caputo fractional derivative emerges analogous to the integer order differentiation

$$ D^{\alpha } \bigl(ap(z)+bq(z) \bigr)=a D^{\alpha }p(z)+b D^{\alpha }p(z),\quad a,b \in \Re . $$
(2.2)

For the Caputo fractional derivative, we have

$$\begin{aligned}& D^{\alpha }K=K,\quad K \text{ is a constant}, \end{aligned}$$
(2.3)
$$\begin{aligned}& D^{\alpha }(z)^{\epsilon }= \textstyle\begin{cases} \frac{\varGamma (\epsilon +1)}{\varGamma (\epsilon -\alpha +1)} z^{ \epsilon -\alpha }, & \text{for } \epsilon \in \mathbb{N}_{0} \text{ and } \epsilon \ge \lceil \alpha \rceil , \\ 0, & \text{for } \epsilon \in \mathbb{N}_{0} \text{ and } \epsilon \ge \lceil \alpha \rceil , \end{cases}\displaystyle \end{aligned}$$
(2.4)

the notation \(\lceil \alpha \rceil \) is used in the sense of a ceiling function which gives an integer smaller than or equal to α.

We recall from Mason and Handscomb [14] that the fourth-kind Chebyshev polynomials \(W_{n} (t)\) are orthogonal degree polynomials of n in t based on \([-1, 1]\). Hence, for \(t=\cos \theta \) and \(\theta \in [0, \pi ]\),

$$ W_{n} (t)= \frac{\sin (n+\frac{1}{2} )\theta }{\sin \frac{\theta }{2} }, $$
(2.5)

and it can be extracted from the special case \(\beta =-\alpha =\frac{1}{2} \) of the Jacobi polynomial \(P_{n}^{(\alpha , \beta )} (t)\) explicitly:

$$ W_{n} (t)= \frac{2^{2n} }{\binom{2n}{n}} P_{n}^{ (\frac{-1}{2} , \frac{1}{2} )} (t), $$
(2.6)

where

$$\begin{aligned} P_{n}^{(\alpha , \beta )} (t) =&\frac{\varGamma (\alpha +n+1)}{\varGamma (n+1)\varGamma (\alpha +\beta +n+1)} \\ &{} \times \sum_{m=0}^{n} \begin{pmatrix} {n} \\ {m} \end{pmatrix} \frac{\varGamma (\alpha +\beta +n+m+1)}{\varGamma (\alpha +m+1)} \biggl(\frac{t-1}{2} \biggr)^{m}, \end{aligned}$$
(2.7)

and \(W_{n} (t)\) is the orthogonal polynomial on \([-1, 1]\) w.r.t. the inner product as follows:

$$ \bigl\langle W_{n} (t), W_{m} (t) \bigr\rangle = \int _{-1}^{1} \sqrt{\frac{1-t}{1+t} } W_{n} (t)W_{m} (t)\,dt= \textstyle\begin{cases} 0, & n\ne m, \\ \pi ,& n=m, \end{cases} $$
(2.8)

where \(W_{n} (t)\) has a weight function \(\sqrt{\frac{1-t}{1+t} } \).

The Chebyshev polynomials of the fourth kind \(W_{n} (t)\) can be generated using the recurrence relation

$$ W_{n+1} (t)=2tW_{n} (t)-W_{n-1} (t), \quad n=1, 2,\ldots $$
(2.9)

starting with the values \(W_{0} (t)=1\), \(W_{1} (t)=2t+1\), \(W_{2} (t)=4t^{2} +2t-1\).

The analytical form of the fourth-kind Chebyshev polynomial \(W_{n} (t)\) of degree n can be expressed using (2.6) and the properties of Jacobi polynomial in the following form:

$$ W_{n} (t)=\sum_{i=0}^{n} \frac{(-1)^{i} \varGamma (2n-i+1)}{(2)^{i-n} \varGamma (i+1)\varGamma (2n-2i+1)} (t+1)^{n-i}, \quad n\in \mathbb{Z}^{+}. $$
(2.10)

Further, we can define the polynomial of Chebyshev in any finite range of \([a, b]\), but here it is more convincing to use \([0, 1]\) than \([-1, 1]\) to map the independent variable \(t \in [0, 1]\) to the variable \(s\in [-1, 1]\) by the linear transformation \(t=\frac{s (b-a )+(a+b)}{2} \). However, in this paper, we are only concerned with the fourth-kind shifted Chebyshev polynomial of degree n symbolized by \(W_{n}^{*} (t)\):

$$ W_{n}^{*} (t)=W_{n} (2t-1). $$
(2.11)

These shifted polynomials of the fourth kind are orthogonal at the support interval \([0, 1]\) under the inner product shown as follows:

$$ \bigl\langle W_{n}^{*} (t), W_{m}^{*} (t) \bigr\rangle = \int _{0}^{1} \sqrt{\frac{1-t}{t} } W_{n}^{*} (t)W_{m}^{*} (t)\,dt= \textstyle\begin{cases} 0,& n\ne m, \\ \frac{\pi }{2} ,& n=m. \end{cases} $$
(2.12)

On the right-hand side of (2.12), \(\sqrt{\frac{1-t}{t} } \) is the weight function of \(W_{n}^{*} (t)\) and is normalized by \(W_{n}^{*} (1)=1\). The fourth-kind shifted Chebyshev polynomial is obtained by means of a recurrence connection:

$$ W_{n+1}^{*} (t)=2(2t-1)W_{n}^{*} (t)-W_{n-1}^{*} (t),\quad n=1, 2,\ldots $$
(2.13)

starting with the values \(W_{0}^{*} (t)=1\), \(W_{1}^{*} (t)=4t-1\), \(W_{2}^{*} (t)=16t^{2} -12t+1\). The possible expression of the analytic form for the fourth-kind shifted Chebyshev polynomials \(W_{n}^{*} (t)\) of degree n is shown as follows:

$$ W_{n}^{*} (t)=\sum _{i=0}^{n} \frac{(-1)^{i} \varGamma (2n-i+1)}{(2)^{2i-2n}\varGamma (i+1)\varGamma (2n-2i+1)} t^{n-i},\quad n\in \mathbb{Z}^{+}. $$
(2.14)

In a spectral method, it is possible to expand \(g(t)\), the square integrable function, in \([0, 1]\) and define it by an infinite \(W_{n}^{*} (t)\) expansion as follows:

$$ g(t)=\sum_{i=0}^{\infty }c_{i} W_{i}^{*} (t) , $$
(2.15)

where \(c_{i} \) are constants. Now, we can estimate a number of the coefficients \(c_{i} \), and then \(g(t)\) can be approximated by a finite sum of terms \((m+1)\) such as

$$ g_{m} (t)=\sum_{i=0}^{m}c_{i} W_{i}^{*} (t), $$
(2.16)

where the coefficients \(c_{i}\) (\(i=0, 1, 2,\ldots,m\)) are given by

$$ c_{i} =\frac{1}{\pi } \int _{-1}^{1}g \biggl(\frac{t+1}{2} \biggr) \sqrt{\frac{1-t}{1+t} } W_{i} (t)\,dt $$
(2.17)

or

$$ c_{i} =\frac{2}{\pi } \int _{0}^{1}g (t )\sqrt{ \frac{1-t}{t} } W_{{t} }^{*} (t)\,dt. $$
(2.18)

3 Main results

The approximate formula for the function \(g_{m} (t)\) given in (2.16) is presented in the following theorem.

Theorem 3.1

Let\(g_{m} (t)\)be an approximate function in terms of the fourth-kind shifted Chebyshev polynomials given by (2.16). Suppose that\(\alpha >0\), we get

$$ D^{\alpha } \bigl(g_{m} (t) \bigr)=\sum _{i= \lceil \alpha \rceil }^{m} \sum _{k=0}^{i- \lceil \alpha \rceil }c_{i} V_{i, k}^{( \alpha )} t^{i-k-\alpha }, $$
(3.1)

where

$$ V_{i,k}^{(\alpha )} =(-1)^{k} 2^{(2i-2k)} \frac{\varGamma (i-k+1)\varGamma (2i-k+1)}{\varGamma (2i-2k+2)\varGamma (i-k+1-\alpha )\varGamma (k+1)}. $$
(3.2)

Proof

Using the definition of approximated function \(g_{m}(t)\) given in (2.16) and the Caputo fractional differentiation properties given in (2.2), we obtain

$$ D^{\alpha } \bigl(g_{m}(t) \bigr)=\sum _{0}^{m} c_{i} D^{\alpha } \bigl(V_{i}^{*}(t) \bigr). $$
(3.3)

Applying equations (2.3) and (2.4), we get

$$ D^{\alpha } \bigl(V_{i}^{*}(t) \bigr)=\sum_{k=0}^{i- \lceil \alpha \rceil }(-1)^{k} 2^{(2i-2k)} \frac{\varGamma (i-k+1)\varGamma (2i-k+1)}{\varGamma (2i-2k+2)\varGamma (i-k+1-\alpha )\varGamma (k+1)}. $$
(3.4)

From (3.3) and (3.4), we obtain the desired result (3.1). □

4 Numerical examples

In this section, we present numerical examples to show the efficacy and validity of the proposed method and to compare it with the existing method.

Example 4.1

Let us consider the time-fractional Fokker–Planck equation

$$ \frac{\partial ^{\alpha } u}{\partial t^{\alpha } } - \frac{\partial u}{\partial x} - \frac{\partial ^{2} u}{\partial x^{2} } =0 $$
(4.1)

with the initial condition

$$ u(x, 0)=x. $$
(4.2)

The exact solution to equation (4.1) for the non-fractional case at \(\alpha =1\) is \(u(x, t)=x+t\).

In order to use the shifted Chebyshev polynomials of the fourth kind, we approximate \(u(x, t)\) with \(m=3\):

$$ u_{3} (x,t)=\sum_{i=0}^{3}u_{i} (x)W_{i}^{*} (t). $$
(4.3)

From [26], we have

$$ \frac{\partial ^{\alpha } u}{\partial t^{\alpha } } =D^{\alpha } \bigl(u_{3} (x, t) \bigr)=\sum_{i= \lceil \alpha \rceil }^{3}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t^{i-k- \alpha }, $$
(4.4)

where

$$ V_{i, k}^{(\alpha )} =(-1)^{k} 2^{(2i-2k)} \frac{\varGamma (2i-k+1)\varGamma (i-k+1)}{\varGamma (k+1)\varGamma (2i-2k+2)\varGamma (i-k+1-\alpha )}. $$

Now, we have

$$\begin{aligned}& D^{\alpha } \bigl(g_{m} (t) \bigr)=\sum _{i= \lceil \alpha \rceil }^{m}c_{i} D^{\alpha } \bigl(W_{i}^{*} (t) \bigr), \\& \frac{\partial u}{\partial x} =\sum_{i=0}^{3}u'_{i} (x)W_{i}^{*} (t), \end{aligned}$$
(4.5)
$$\begin{aligned}& \frac{\partial ^{2} u}{\partial x^{2} } =\sum_{i=0}^{3} \ddot{u}_{i} (x) (x)W_{i}^{*} (t). \end{aligned}$$
(4.6)

Substituting (4.4), (4.5), and (4.6) into (4.1), we get

$$ \sum_{i= \lceil \alpha \rceil }^{3}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t^{i-k- \alpha } -\sum _{i=0}^{3}u'_{i} (x) W_{i}^{*} (t) -\sum_{i=0}^{3} \ddot{u}_{i} (x)W_{i}^{*} (t) =0. $$
(4.7)

For suitable collocation points \(t_{p} \), we use the roots of shifted Chebyshev polynomials of the fourth kind \(W_{m+1- \lceil \alpha \rceil }^{*} (t)\), \(p=0, 1, 2,\ldots, m- \lceil \alpha \rceil \). For non-fractional case \(\alpha =1\) and \(m=3\), we have \(W_{3}^{*} (t_{p} )=0\), \(p=0, 1, 2\). The roots of \(64t^{3}_{p} -80t^{2}_{p} +24t_{p} -1=0\) are \(t_{0} =0.04952\), \(t_{1} =0.38874\), \(t_{2} =0.81174\).

From (4.7) and the Chebyshev collocation method, we have

$$\begin{aligned}& \sum_{i=0}^{3} \ddot{u}_{i} (x)W_{i}^{*} (t_{p} ) =\sum_{i= \lceil \alpha \rceil }^{3} \sum_{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{p} {}^{i-k-\alpha } - \sum_{i=0}^{3}u_{i} ^{\prime} (x)W_{i}^{*} (t_{p} ) ,\quad p=0, 1, 2, \end{aligned}$$
(4.8)
$$\begin{aligned}& \ddot{u}_{0} (x)W_{0}^{*} (t_{p} )+\ddot{u} (x)W_{1}^{*} (t_{p} )+ \ddot{u}_{2} (x)W_{2}^{*} (t_{p} ) \\& \quad =\sum_{i= \lceil \alpha \rceil }^{3}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{p} {}^{i-k-\alpha } -\sum_{i=0}^{3}u_{i} ^{\prime} (x)W_{i}^{*} (t_{p} ). \end{aligned}$$
(4.9)

By the property of shifted Chebyshev polynomials of the fourth kind with \(W_{0}^{*} (t_{p} )=1\), we obtain a nonlinear system of differential equations:

$$\begin{aligned}& \ddot{u}_{0} (x)+K_{1} \ddot{u}_{1} (x)+K_{2} \ddot{u}_{2} (x)=\sum _{i= \lceil \alpha \rceil }^{3}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{0} {}^{i-k- \alpha } -\sum_{i=0}^{3}u_{i} ^{\prime} (x)W_{i}^{*} (t_{0} ), \end{aligned}$$
(4.10)
$$\begin{aligned}& \ddot{u}_{0} (x)+H_{1} \ddot{u}_{1} (x)+H_{2} \ddot{u}_{2} (x)=\sum _{i= \lceil \alpha \rceil }^{3}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{1} {}^{i-k- \alpha } -\sum_{i=0}^{3}u_{i} ^{\prime} (x)W_{i}^{*} (t_{1} ), \end{aligned}$$
(4.11)
$$\begin{aligned}& \ddot{u}_{0} (x)+F_{1} \ddot{u}_{1} (x)+F_{2} \ddot{u}_{2} (x)=\sum _{i= \lceil \alpha \rceil }^{3}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{2} {}^{i-k- \alpha } -\sum_{i=0}^{3}u_{i} ^{\prime} (x)W_{i}^{*} (t_{2} ), \end{aligned}$$
(4.12)

where

$$\begin{aligned}& K_{1} =W_{1}^{*} (t_{0} )=-0.80192;\qquad F_{1} =W_{1}^{*} (t_{2} )=2.24696;\qquad H_{1} =W_{1}^{*} (t_{1} )=0.55496; \\& K_{2} =W_{2}^{*} (t_{0} )=0.45500; \qquad F_{2} =W_{2}^{*} (t_{2} )=1.80191;\qquad H_{2} =W_{2}^{*} (t_{1} )=-1.24787. \end{aligned}$$

Using the finite difference method to solve the systems of ordinary differentials (4.10)–(4.12), we use the notations \(T=T_{\mathrm{final}}\), \(0< t_{j} \le T\), \(t_{j} =j\Delta t\)\(\Delta t=\frac{T}{N}\), \(j=1, 2,\ldots ,N \). System (4.10)–(4.12) is discretized and takes the following form:

$$\begin{aligned}& \frac{u_{0}^{n+1} -2u_{0}^{n} +u_{0}^{n-1} }{\Delta t^{2} } +K_{1} \frac{u_{1}^{n+1} -2u_{1}^{n} +u_{1}^{n-1} }{\Delta t^{2} } +K_{2} \frac{u_{2}^{n+1} -2u_{2}^{n} +u_{2}^{n-1} }{\Delta t^{2} } \\& \quad =\sum_{i= \lceil \alpha \rceil }^{3}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} (t_{0} )^{i-k-\alpha } - \sum_{i=0}^{3}u_{i} ^{\prime} (x)W_{i}^{*} (t_{0} ), \end{aligned}$$
(4.13)
$$\begin{aligned}& \frac{u_{0}^{n+1} -2u_{0}^{n} +u_{0}^{n-1} }{\Delta t^{2} } +H_{1} \frac{u_{1}^{n+1} -2u_{1}^{n} +u_{1}^{n-1} }{\Delta t^{2} } +H_{2} \frac{u_{2}^{n+1} -2u_{2}^{n} +u_{2}^{n-1} }{\Delta t^{2} } \\& \quad = \sum_{i= \lceil \alpha \rceil }^{3}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} (t_{1} )^{i-k-\alpha } - \sum_{i=0}^{3}u_{i} ^{\prime} (x)W_{i}^{*} (t_{1} ), \end{aligned}$$
(4.14)
$$\begin{aligned}& \frac{u_{0}^{n+1} -2u_{0}^{n} +u_{0}^{n-1} }{\Delta t^{2} } +F_{1} \frac{u_{1}^{n+1} -2u_{1}^{n} +u_{1}^{n-1} }{\Delta t^{2} } +F_{2} \frac{u_{2}^{n+1} -2u_{2}^{n} +u_{2}^{n-1} }{\Delta t^{2} } \\& \quad =\sum_{i= \lceil \alpha \rceil }^{3}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} (t_{2} )^{i-k-\alpha } - \sum_{i=0}^{3}u_{i} ^{\prime} (x)W_{i}^{*} (t_{2}), \end{aligned}$$
(4.15)
$$\begin{aligned}& u_{0}^{n+1} -u_{1}^{n+1} +u_{2}^{n+1} -u_{3}^{n+1} =x. \end{aligned}$$
(4.16)

Rearranging (4.13)–(4.16) and applying the Newton–Raphson method, we arrive at the required solution for the problem on (4.1).

Graphs and Table: In Fig. 1, the numerical solutions attained for Example 4.1 using the shifted Chebyshev collocation method are presented and are compared with the previous method [7] and with the exact solution as well. And it is easy to observe, the proposed method has an excellent agreement with the exact solution.

Figure 1
figure 1

Comparison between the exact solution and the approximate solution of Example 4.1 for different values of α

Full size image

Table 1 presents the numerical results of Example 4.1 at various levels of value of α. The results obtained by our method with \(\alpha =0.2\), \(\alpha =0.4\), \(\alpha =0.6\), and \(\alpha =0.8\) are given in the 3rd, 5th, 7th, and 9th columns, respectively. To validate the accuracy of the proposed method, the numerical solution is compared with the previous findings provided in Habenom et al. [7] and the exact solutions, which shows that the present method is in good agreement with the exact solution. The findings in Table 1 demonstrate that the accuracy of the method presented is better than that of other methods. In comparison, the computing expense (CPU time) of the suggested approach tends to be lower than in other approaches, since we require just a few terms to find an answer with high accuracy. We provide a comparative study of two methods (TSM = Taylor series method (see [7]); CPFK = Chebyshev polynomial of the fourth kind (present method)) in the numerical form as follows.

Table 1 The comparative numerical value of the present method with the method [7] for Example 4.1
Full size table

Example 4.2

Consider the time-fractional Fokker–Planck equation (FFPE) \(f(x)=1+x\), \(x\in \mathbb{R}\). Let in equation (1.1) \(n=1\), \(x_{1} =x\), \(A_{1} (x, t)=-(1+x)\), \(B_{1} (x, t)=e^{t} x^{2} \) in the form

$$ \frac{\partial ^{\alpha } u}{\partial t^{\alpha } } -(1+x) \frac{\partial u}{\partial x} - \bigl(e^{t} x^{2} \bigr) \frac{\partial ^{2} u}{\partial x} =0, $$
(4.17)

with the initial condition

$$ u(x, 0)=1+x. $$
(4.18)

The exact solution of equation (4.17) is \(u(x,t)=(x+1) e^{t}\).

To use the shifted fourth-type Chebyshev polynomials, we approximate \(u(x, t)\) with \(m=5\) on (2.16) as follows:

$$ u_{5} (x,t)=\sum_{i=0}^{5}u_{i} (x)W_{i}^{*} (t). $$
(4.19)

From the above theorem, we have

$$\begin{aligned}& \frac{\partial ^{\alpha } u}{\partial t^{\alpha } } =D^{\alpha } \bigl(u_{5} (x, t) \bigr)=\sum_{i= \lceil \alpha \rceil }^{5}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t^{i-k- \alpha }, \end{aligned}$$
(4.20)
$$\begin{aligned}& \frac{\partial u}{\partial x} =\sum_{i=0}^{5}u_{i} ^{\prime} (x)W_{i}^{*} (t), \end{aligned}$$
(4.21)
$$\begin{aligned}& \frac{\partial ^{2} u}{\partial x^{2} } =\sum_{i=0}^{5} \ddot{u}_{i} (x) (x)W_{i}^{*} (t). \end{aligned}$$
(4.22)

Putting (4.20), (4.21), and (4.22) into (4.17), we obtain

$$ \sum_{i= \lceil \alpha \rceil }^{5}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t^{i-k- \alpha } -(1+x)\sum _{i=0}^{5}u_{i} ^{\prime} (x)W_{i}^{*} (t) -e^{t} x^{2} \sum_{i=0}^{5}\ddot{u}_{i} (x)W_{i}^{*} (t) =0. $$
(4.23)

For suitable collocation points \(t_{p} \), we use the roots of shifted Chebyshev polynomials of the fourth kind \(W_{m+1- \lceil \alpha \rceil }^{*} (t)\), \(p=0, 1, 2,\ldots, m- \lceil \alpha \rceil \). For fractional α with \(m=5\), we have

$$\begin{aligned}& W_{m+1- \lceil \alpha \rceil }^{*} (t_{p} )=W_{5}^{*} (t_{p} )=0,\quad p=0, 1, 2, 3, 4, \end{aligned}$$
(4.24)
$$\begin{aligned}& 1024 t_{p} ^{5} -2304 t_{p} ^{4} +1792 t_{p} ^{3} -560 t_{p} ^{2} +60 t_{p} -1=0. \end{aligned}$$
(4.25)

The roots of polynomial (4.25) are

$$ t_{0} =0.0202, \qquad t_{1} =0.1726, \qquad t_{2} =0.4288,\qquad t_{3} =0.7077, \qquad t_{4} =0.9206. $$

From (4.23) and the Chebyshev collocation method, we get

$$\begin{aligned} e^{t} x^{2} \sum_{i=0}^{5} \ddot{u}_{i} (x)W_{i}^{*} (t_{p} ) =&\sum_{i= \lceil \alpha \rceil }^{5} \sum_{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{p} ^{i-k- \alpha } \\ &{}-(1+x)\sum_{i=0}^{5}u_{i} ^{\prime} (x)W_{i}^{*} (t_{p} ) \quad (p=0, 1, 2, 3, 4). \end{aligned}$$
(4.26)

Of the property of the fourth-kind shifted Chebyshev polynomials, \(W_{0}^{*} (t_{p} )=1\). Equation (4.26) will lead us to a nonlinear system of ODE given below.

$$\begin{aligned}& e^{t} x^{2} \bigl(\ddot{u}_{0} (x)+A_{1} \ddot{u}_{1} (x)+A_{2} \ddot{u}_{2} (x) +A_{3} \ddot{u}_{3} (x)+A_{4} \ddot{u}_{4} (x) \bigr) \\& \quad =\sum_{i= \lceil \alpha \rceil }^{5}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{0} ^{i-k-\alpha }-(1+x) \sum_{i=0}^{5}u_{i} ^{\prime} (x)W_{i}^{*} (t_{0} ) , \end{aligned}$$
(4.27)
$$\begin{aligned}& e^{t} x^{2} \bigl(\ddot{u}_{0} (x)+B_{1} \ddot{u}_{1} (x)+B_{2} \ddot{u}_{2} (x) +B_{3} \ddot{u}_{3} (x)+B_{4} \ddot{u}_{4} (x) \bigr) \\& \quad =\sum_{i= \lceil \alpha \rceil }^{5}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{1} ^{i-k-\alpha } -(1+x)\sum_{i=0}^{5}u_{i} ^{\prime} (x)W_{i}^{*} (t_{1} ), \end{aligned}$$
(4.28)
$$\begin{aligned}& e^{t} x^{2} \bigl(\ddot{u}_{0} (x)+C_{1} \ddot{u}_{1} (x)+C_{2} \ddot{u}_{2} (x) +C_{3} \ddot{u}_{3} (x)+C_{4} \ddot{u}_{4} (x) \bigr) \\& \quad =\sum_{i= \lceil \alpha \rceil }^{5}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{2} ^{i-k-\alpha } -(1+x) \sum_{i=0}^{5}u_{i} ^{\prime} (x)W_{i}^{*} (t_{2} ), \end{aligned}$$
(4.29)
$$\begin{aligned}& e^{t} x^{2} \bigl(\ddot{u}_{0} (x)+D_{1} \ddot{u}_{1} (x)+D_{2} \ddot{u}_{2} (x) +D_{3} \ddot{u}_{3} (x)+D_{4} \ddot{u}_{4} (x) \bigr) \\& \quad =\sum_{i= \lceil \alpha \rceil }^{5}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{3} ^{i-k-\alpha } -(1+x)\sum_{i=0}^{5}u_{i} ^{\prime} (x)W_{i}^{*} (t_{3} ), \end{aligned}$$
(4.30)
$$\begin{aligned}& e^{t} x^{2} \bigl(\ddot{u}_{0} (x)+E_{1} \ddot{u}_{1} (x)+E_{2} \ddot{u}_{2} (x) +E_{3} \ddot{u}_{3} (x)+E_{4} \ddot{u}_{4} (x) \bigr) \\& \quad =\sum_{i= \lceil \alpha \rceil }^{5}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{4} ^{i-k-\alpha } -(1+x)\sum_{i=0}^{5}u_{i} ^{\prime} (x)W_{i}^{*} (t_{4} ). \end{aligned}$$
(4.31)

From the initial condition (IC) given at (4.18), we have

$$ u(x,0)=u_{0} (x)-u_{1} (x)+u_{2} (x)-u_{3} (x)+u_{4} (x)-u_{5} (x)= \sum_{i=0}^{5}(-1)^{i} u_{i} (x) =1+x, $$
(4.32)

where

$$\begin{aligned}& A_{1} =W_{1}^{*} (t_{0} )=-0.9192; \qquad A_{2} =W_{2}^{*} (t_{0} )=0.7641;\qquad A_{3} =W_{3}^{*} (t_{0} )=-0.5473; \\& A_{4} =W_{4}^{*} (t_{0} )=0.2863. \\& B_{1} =W_{1}^{*} (t_{1} )=-0.3096;\qquad B_{2} =W_{2}^{*} (t_{1} )=-0.5945; \qquad B_{3} =W_{3}^{*} (t_{1} )=1.0882; \\& B_{4} =W_{4}^{*} (t_{1} )=-0.8306. \\& C_{1} =W_{1}^{*} (t_{2} )=0.7152;\qquad C_{2} =W_{2}^{*} (t_{2} )=-1.2037; \qquad C_{3} =W_{3}^{*} (t_{2} )=-0.3724; \\& C_{4} =W_{4}^{*} (t_{2} )=1.3097. \\& D_{1} =W_{1}^{*} (t_{3} )=1.8308;\qquad D_{2} =W_{2}^{*} (t_{3} )=0.5210;\qquad D_{3} =W_{3}^{*} (t_{3} )=-1.3979; \\& D_{4} =W_{4}^{*} (t_{3} )=-1.6824. \\& E_{1} =W_{1}^{*} (t_{4} )=2.6824; \qquad E_{2} =W_{2}^{*} (t_{4} )=3.5129; \qquad E_{3} =W_{3}^{*} (t_{4} )=3.2276; \\& E_{4} =W_{4}^{*} (t_{4} )=1.9173. \end{aligned}$$

Applying the concept of finite difference method (FDM) to the system of nonlinear ODEs (4.27)–(4.32), considering that \(T=T_{\mathrm{final}}\), \(0< t_{j} \le T\), \(t_{j} =j\Delta t\)\(\Delta t=\frac{T}{N} \), \(j=1, 2, \ldots,N\),

$$\begin{aligned}& \begin{aligned}[b] &e^{t} x^{2} \biggl( \frac{u_{0}^{n+1} -2u_{0}^{n} +u_{0}^{n-1} }{\Delta t^{2} } +A_{1} \frac{u_{1}^{n+1} -2u_{1}^{n} +u_{1}^{n-1} }{\Delta t^{2} } +A_{2} \frac{u_{2}^{n+1} -2u_{2}^{n} +u_{2}^{n-1} }{\Delta t^{2} } \\ &\qquad {} +A_{3} \frac{u_{3}^{n+1} -2u_{3}^{n} +u_{3}^{n-1} }{\Delta t^{2} }+A_{4} \frac{u_{4}^{n+1} -2u_{4}^{n} +u_{4}^{n-1} }{\Delta t^{2} } \biggr) \\ &\quad =\sum_{i= \lceil \alpha \rceil }^{5}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} (t_{0} )^{i-k-\alpha } -(1+x) \sum_{i=0}^{5}u_{i} ^{\prime} (x)W_{i}^{*} (t_{0} ) , \end{aligned} \end{aligned}$$
(4.33)
$$\begin{aligned}& \begin{aligned}[b] &e^{t} x^{2} \biggl( \frac{u_{0}^{n+1} -2u_{0}^{n} +u_{0}^{n-1} }{\Delta t^{2} } +B_{1} \frac{u_{1}^{n+1} -2u_{1}^{n} +u_{1}^{n-1} }{\Delta t^{2} } +B_{2} \frac{u_{2}^{n+1} -2u_{2}^{n} +u_{2}^{n-1} }{\Delta t^{2} } \\ &\qquad {} +B_{3} \frac{u_{3}^{n+1} -2u_{3}^{n} +u_{3}^{n-1} }{\Delta t^{2} }+B_{4} \frac{u_{4}^{n+1} -2u_{4}^{n} +u_{4}^{n-1} }{\Delta t^{2}} \biggr) \\ &\quad =\sum_{i= \lceil \alpha \rceil }^{5}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} (t_{1} )^{i-k-\alpha } - (1+x)\sum_{i=0}^{5}u_{i} ^{\prime} (x)W_{i}^{*} (t_{1} ), \end{aligned} \end{aligned}$$
(4.34)
$$\begin{aligned}& \begin{aligned}[b] &e^{t} x^{2} \biggl( \frac{u_{0}^{n+1} -2u_{0}^{n} +u_{0}^{n-1} }{\Delta t^{2} } +C_{1} \frac{u_{1}^{n+1} -2u_{1}^{n} +u_{1}^{n-1} }{\Delta t^{2} } +C_{2} \frac{u_{2}^{n+1} -2u_{2}^{n} +u_{2}^{n-1} }{\Delta t^{2} } \\ &\qquad {} +C_{3} \frac{u_{3}^{n+1} -2u_{3}^{n} +u_{3}^{n-1} }{\Delta t^{2} }+C_{4} \frac{u_{4}^{n+1} -2u_{4}^{n} +u_{4}^{n-1} }{\Delta t^{2}} \biggr) \\ &\quad =\sum_{i= \lceil \alpha \rceil }^{5}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} (t_{2} )^{i-k-\alpha } - (1+x)\sum_{i=0}^{5}u_{i} ^{\prime} (x)W_{i}^{*} (t_{2} ) , \end{aligned} \end{aligned}$$
(4.35)
$$\begin{aligned}& \begin{aligned}[b] &e^{t} x^{2} \biggl( \frac{u_{0}^{n+1} -2u_{0}^{n} +u_{0}^{n-1} }{\Delta t^{2} } +D_{1} \frac{u_{1}^{n+1} -2u_{1}^{n} +u_{1}^{n-1} }{\Delta t^{2} } +D_{2} \frac{u_{2}^{n+1} -2u_{2}^{n} +u_{2}^{n-1} }{\Delta t^{2} } \\ &\qquad {} +D_{4} \frac{u_{4}^{n+1} -2u_{4}^{n} +u_{4}^{n-1} }{\Delta t^{2} }+D_{3} \frac{u_{3}^{n+1} -2u_{3}^{n} +u_{3}^{n-1} }{\Delta t^{2}} \biggr) \\ &\quad =\sum_{i= \lceil \alpha \rceil }^{5}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} (t_{3} )^{i-k-\alpha } - (1+x)\sum_{i=0}^{5}u_{i} ^{\prime} (x)W_{i}^{*} (t_{3} ) , \end{aligned} \end{aligned}$$
(4.36)
$$\begin{aligned}& \begin{aligned}[b] &e^{t} x^{2} \biggl( \frac{u_{0}^{n+1} -2u_{0}^{n} +u_{0}^{n-1} }{\Delta t^{2} } +E_{1} \frac{u_{1}^{n+1} -2u_{1}^{n} +u_{1}^{n-1} }{\Delta t^{2} } +E_{2} \frac{u_{2}^{n+1} -2u_{2}^{n} +u_{2}^{n-1} }{\Delta t^{2} } \\ &\qquad {} +E_{3} \frac{u_{3}^{n+1} -2u_{3}^{n} +u_{3}^{n-1} }{\Delta t^{2} } +E_{4} \frac{u_{4}^{n+1} -2u_{4}^{n} +u_{4}^{n-1} }{\Delta t^{2}} \biggr) \\ &\quad =\sum_{i= \lceil \alpha \rceil }^{5}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} (t_{4} )^{i-k-\alpha } - (1+x)\sum_{i=0}^{5}u_{i} ^{\prime} (x)W_{i}^{*} (t_{4} ) , \end{aligned} \end{aligned}$$
(4.37)
$$\begin{aligned}& u_{0}^{n+1} -u_{1}^{n+1} +u_{2}^{n+1} -u_{3}^{n+1} +u_{4}^{n+1} -u_{5}^{n+1} =1+x. \end{aligned}$$
(4.38)

Using the points \(t_{0}\), \(t_{1}\), \(t_{2}\) obtained from the roots of (4.25) and collecting like terms of (4.33)–(4.38), we arrive at the following matrix form:

$$ U^{n+1} =A^{-1} BU^{n} +A^{-1} CU^{n-1} +A^{-1} X ;\quad n=1, 2, 3,\ldots, $$

where

$$ A=\Im \begin{bmatrix} {1} & {-0.9192} & {0.7641} & {-0.5473} & {0.2863} & {0} \\ {1} & {-0.3096} & {-0.5945} & {1.0882} & {-0.8306} & {0} \\ {1} & {0.7152} & {-1.2037} & {-0.3724} & {1.3097} & {0} \\ {1} & {1.8308} & {0.5210} & {-1.3979} & {-1.6824} & {0} \\ {1} & {2.6824} & {3.5129} & {3.2276} & {1.9173} & {0} \\ {\frac{1}{\Im } } & {\frac{-1}{\Im } } & {\frac{1}{\Im } } & { \frac{-1}{\Im } } & {\frac{1}{\Im } } & {\frac{-1}{\Im } } \end{bmatrix}, $$

where \(\Im =e^{t} x^{2} +(1+x)\Delta t\).

$$ B= \begin{bmatrix} {b_{11} } & {b_{12} } & {b_{13} } & {b_{14} } & {b_{15} } & {b_{16} } \\ {b_{21} } & {b_{22} } & {b_{23} } & {b_{24} } & {b_{25} } & {b_{26} } \\ {b_{31} } & {b_{32} } & {b_{33} } & {b_{34} } & {b_{35} } & {b_{36} } \\ {b_{41} } & {b_{42} } & {b_{43} } & {b_{44} } & {b_{45} } & {b_{46} } \\ {b_{51} } & {b_{52} } & {b_{53} } & {b_{54} } & {b_{55} } & {b_{56} } \\ {0} & {0} & {0} & {0} & {0} & {0} \end{bmatrix}, $$

where

$$\begin{aligned}& b_{11} =b_{21} =b_{31} =b_{41} =b_{51} =2e^{t} x^{2} +(1+x)\Delta t , \\& b_{12} = \bigl(V_{1, 0}^{(\alpha )} t_{0} ^{1-\alpha } \bigr) \Delta t^{2} -0.9191(1+x) \Delta t-1.8384e^{t} x^{2} , \\& b_{13} = \bigl(V_{2, 0}^{(\alpha )} t_{0} ^{2-\alpha } +V_{2, 1}^{( \alpha )} t_{0} ^{1-\alpha } \bigr)\Delta t^{2} +0.7641(1+x) \Delta t+1.5282e^{t} x^{2} , \\& b_{14} = \bigl(V_{3, 0}^{(\alpha )} t_{0} ^{3-\alpha } +V_{3, 1}^{( \alpha )} t_{0} ^{2-\alpha } +V_{3, 2}^{(\alpha )} t_{0} ^{1- \alpha } \bigr)\Delta t^{2} -0.5473(1+x) \Delta t-1.0946e^{t} x^{2}, \\& b_{15} = \bigl(V_{4, 0}^{(\alpha )} t_{0} ^{4-\alpha } +V_{4, 1}^{( \alpha )} t_{0} ^{3-\alpha } +V_{4, 2}^{(\alpha )} t_{0} ^{2- \alpha } +V_{4, 3}^{(\alpha )} t_{0} ^{1-\alpha } \bigr)\Delta t^{2} +0.2863(1+x) \Delta t \\& \hphantom{b_{15} ={}}{}+0.5726e^{t} x^{2}, \\& b_{16} = \bigl(V_{5, 0}^{(\alpha )} t_{0} ^{5-\alpha } +V_{5, 1}^{( \alpha )} t_{0} ^{4-\alpha } +V_{5, 2}^{(\alpha )} t_{0} ^{3- \alpha } +V_{5, 3}^{(\alpha )} t_{0} ^{2-\alpha } +V_{5, 4}^{( \alpha )} t_{0} ^{1-\alpha } \bigr)\Delta t^{2} , \\& b_{22} = \bigl(V_{1, 0}^{(\alpha )} t_{1} ^{1-\alpha } \bigr) \Delta t^{2} -0.3096(1+x) \Delta t-0.6192e^{t} x^{2}, \\& b_{23} = \bigl(V_{2, 0}^{(\alpha )} t_{1} ^{2-\alpha } +V_{2, 1}^{( \alpha )} t_{1} ^{1-\alpha } \bigr)\Delta t^{2} -0.5945(1+x) \Delta t-1.1890e^{t} x^{2}, \\& b_{24} = \bigl(V_{3, 0}^{(\alpha )} t_{1} ^{3-\alpha } +V_{3, 1}^{( \alpha )} t_{1} ^{2-\alpha } +V_{3, 2}^{(\alpha )} t_{1} ^{1- \alpha } \bigr)\Delta t^{2} +1.0882(1+x) \Delta t+2.1764e^{t} x^{2}, \\& b_{25} = \bigl(V_{4, 0}^{(\alpha )} t_{1} ^{4-\alpha } +V_{4, 1}^{( \alpha )} t_{1} ^{3-\alpha } +V_{4, 2}^{(\alpha )} t_{1} ^{2- \alpha } +V_{4, 3}^{(\alpha )} t_{1} ^{1-\alpha } \bigr)\Delta t^{2} -0.8306(1+x) \Delta t \\& \hphantom{b_{25} ={}}{}-1.6612e^{t} x^{2}, \\& b_{26} = \bigl(V_{5, 0}^{(\alpha )} t_{1} ^{5-\alpha } +V_{5, 1}^{( \alpha )} t_{1} ^{4-\alpha } +V_{5, 2}^{(\alpha )} t_{1} ^{3- \alpha } +V_{5, 3}^{(\alpha )} t_{1} ^{2-\alpha } +V_{5, 4}^{( \alpha )} t_{1} ^{1-\alpha } \bigr)\Delta t^{2}, \\& b_{32} = \bigl(V_{1, 0}^{(\alpha )} t_{2} ^{1-\alpha } \bigr) \Delta t^{2} +0.7152(1+x) \Delta t+1.4304e^{t} x^{2}, \\& b_{33} = \bigl(V_{2, 0}^{(\alpha )} t_{2} ^{2-\alpha } +V_{2, 1}^{( \alpha )} t_{2} ^{1-\alpha } \bigr)\Delta t^{2} -1.2037(1+x) \Delta t-2.4074e^{t} x^{2}, \\& b_{34} = \bigl(V_{3, 0}^{(\alpha )} t_{2} ^{3-\alpha } +V_{3, 1}^{( \alpha )} t_{2} ^{2-\alpha } +V_{3, 2}^{(\alpha )} t_{2} ^{1- \alpha } \bigr)\Delta t^{2} -0.3724(1+x) \Delta t-0.7448e^{t} x^{2}, \\& b_{35} = \bigl(V_{4, 0}^{(\alpha )} t_{2} ^{4-\alpha } +V_{4, 1}^{( \alpha )} t_{2} ^{3-\alpha } +V_{4, 2}^{(\alpha )} t_{2} ^{2- \alpha } +V_{4, 3}^{(\alpha )} t_{2} ^{1-\alpha } \bigr)\Delta t^{2} +1.3097(1+x) \Delta t \\& \hphantom{b_{35} ={}}{}+2.6194e^{t} x^{2}, \\& b_{36} = \bigl(V_{5, 0}^{(\alpha )} t_{2} ^{5-\alpha } +V_{5, 1}^{( \alpha )} t_{2} ^{4-\alpha } +V_{5, 2}^{(\alpha )} t_{2} ^{3- \alpha } +V_{5, 3}^{(\alpha )} t_{2} ^{2-\alpha } +V_{5, 4}^{( \alpha )} t_{2} ^{1-\alpha } \bigr)\Delta t^{2}, \\& b_{42} = \bigl(V_{1, 0}^{(\alpha )} t_{3} ^{1-\alpha } \bigr) \Delta t^{2} +1.8308(1+x) \Delta t+3.6616e^{t} x^{2}, \\& b_{43} = \bigl(V_{2, 0}^{(\alpha )} t_{3} ^{2-\alpha } +V_{2, 1}^{( \alpha )} t_{3} ^{1-\alpha } \bigr)\Delta t^{2} +0.5210(1+x) \Delta t+1.0420e^{t} x^{2}, \\& b_{44} = \bigl(V_{3, 0}^{(\alpha )} t_{3} ^{3-\alpha } +V_{3, 1}^{( \alpha )} t_{3} ^{2-\alpha } +V_{3, 2}^{(\alpha )} t_{3} ^{1- \alpha } \bigr)\Delta t^{2} -1.3979(1+x) \Delta t-2.7958e^{t} x^{2}, \\& b_{45} = \bigl(V_{4, 0}^{(\alpha )} t_{3} ^{4-\alpha } +V_{4, 1}^{( \alpha )} t_{3} ^{3-\alpha } +V_{4, 2}^{(\alpha )} t_{3} ^{2- \alpha } +V_{4, 3}^{(\alpha )} t_{3} ^{1-\alpha } \bigr)\Delta t^{2} -1.6824(1+x) \Delta t \\& \hphantom{b_{45} ={}}{}-3.3648e^{t} x^{2}, \\& b_{46} = \bigl(V_{5, 0}^{(\alpha )} t_{3} ^{5-\alpha } +V_{5, 1}^{( \alpha )} t_{3} ^{4-\alpha } +V_{5, 2}^{(\alpha )} t_{3} ^{3- \alpha } +V_{5, 3}^{(\alpha )} t_{3} ^{2-\alpha } +V_{5, 4}^{( \alpha )} t_{3} ^{1-\alpha } \bigr)\Delta t^{2}, \\& b_{52} = \bigl(V_{1, 0}^{(\alpha )} t_{4} ^{1-\alpha } \bigr) \Delta t^{2} +2.6824(1+x) \Delta t+5.3648e^{t} x^{2}, \\& b_{53} = \bigl(V_{2, 0}^{(\alpha )} t_{4} ^{2-\alpha } +V_{2, 1}^{( \alpha )} t_{4} ^{1-\alpha } \bigr)\Delta t^{2} +3.5129(1+x) \Delta t+7.0258e^{t} x^{2}, \\& b_{54} = \bigl(V_{3, 0}^{(\alpha )} t_{4} ^{3-\alpha } +V_{3, 1}^{( \alpha )} t_{4} ^{2-\alpha } +V_{3, 2}^{(\alpha )} t_{4} ^{1- \alpha } \bigr)\Delta t^{2} +3.2276(1+x) \Delta t+6.4552e^{t} x^{2}, \\& b_{55} = \bigl(V_{4, 0}^{(\alpha )} t_{4} ^{4-\alpha } +V_{4, 1}^{( \alpha )} t_{4} ^{3-\alpha } +V_{4, 2}^{(\alpha )} t_{4} ^{2- \alpha } +V_{4, 3}^{(\alpha )} t_{4} ^{1-\alpha } \bigr)\Delta t^{2} +1.9173(1+x) \Delta t \\& \hphantom{b_{55} ={}}{} +3.8346e^{t} x^{2}, \\& b_{56} = \bigl(V_{5, 0}^{(\alpha )} t_{4} ^{5-\alpha } +V_{5, 1}^{( \alpha )} t_{4} ^{4-\alpha } +V_{5, 2}^{(\alpha )} t_{4} ^{3- \alpha } +V_{5, 3}^{(\alpha )} t_{4} ^{2-\alpha } +V_{5, 4}^{( \alpha )} t_{4} ^{1-\alpha } \bigr)\Delta t^{2}, \\& C=e^{t} x^{2} \begin{bmatrix} {-1} & {0.9122} & {-0.7641} & {0.5473} & {-0.2863} & {0} \\ {-1} & {0.3096} & {0.5945} & {-1.0882} & {0.8306} & {0} \\ {-1} & {-0.7152} & {1.2037} & {0.3724} & {-1.3097} & {0} \\ {-1} & {-1.8308} & {-0.5210} & {1.3979} & {1.6824} & {0} \\ {-1} & {-2.6824} & {-3.5129} & {-3.2276} & {-1.9173} & {0} \\ {0} & {0} & {0} & {0} & {0} & {0} \end{bmatrix}. \end{aligned}$$

Solving the above system with the help of Newton–Raphson method, using the initial approximations \(U_{i}^{0}\) and \(U_{i}^{1} \) at \(n=1\) from the initial condition given on (4.18) yields the numerical solution of the fractional Fokker–Planck equation (4.17). For \(m=3\), and the Chebyshev collocation method and FDM on (4.17), we obtain the following nonlinear system of ordinary differential equations:

$$\begin{aligned}& \begin{aligned}[b] &e^{t} x^{2} \bigl( \ddot{u}_{0} (x)+k_{1} \ddot{u}_{1} (x)+k_{2} \ddot{u}_{2} (x) \bigr) \\ &\quad =\sum_{i= \lceil \alpha \rceil }^{3}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{0} ^{i-k-\alpha } -(1+x)\sum_{i=0}^{3}u_{i} ^{\prime} (x)W_{i}^{*} (t_{0} ), \end{aligned} \end{aligned}$$
(4.39)
$$\begin{aligned}& \begin{aligned}[b] & e^{t} x^{2} \bigl( \ddot{u}_{0} (x)+h_{1} \ddot{u}_{1} (x)+h_{2} \ddot{u}_{2} (x) \bigr) \\ & \quad =\sum_{i= \lceil \alpha \rceil }^{3}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{1} ^{i-k-\alpha } -(1+x)\sum_{i=0}^{3}u_{i} ^{\prime} (x)W_{i}^{*} (t_{1} ), \end{aligned} \end{aligned}$$
(4.40)
$$\begin{aligned}& \begin{aligned}[b] & e^{t} x^{2} \bigl( \ddot{u}_{0} (x)+g_{1} \ddot{u}_{1} (x)+g_{2} \ddot{u}_{2} (x) \bigr) \\ &\quad =\sum_{i= \lceil \alpha \rceil }^{3}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{2} ^{i-k-\alpha } -(1+x)\sum_{i=0}^{3}u_{i} ^{\prime} (x)W_{i}^{*} (t_{2} ), \end{aligned} \end{aligned}$$
(4.41)

where

$$\begin{aligned}& k_{1} =W_{1}^{*} (t_{0} )=-0.8020, \qquad k_{2} =W_{2}^{*} (t_{0} )=0.4452, \qquad h_{1} =W_{1}^{*} (t_{1} )=0.5548, \\& g_{1} =W_{1}^{*} (t_{2} )=2.2468,\qquad g_{2} =W_{2}^{*} (t_{2} )=1.8013,\qquad h_{2} =W_{2}^{*} (t_{1} )=-1.2470. \end{aligned}$$

For \(m=4\), and the Chebyshev collocation method and FDM on (4.17), we obtain the following nonlinear system of ordinary differential equations:

$$\begin{aligned}& \begin{aligned}[b] &e^{t} x^{2} \bigl( \ddot{u}_{0} (x)+K_{1} \ddot{u}_{1} (x)+K_{2} \ddot{u}_{2} (x) +K_{3} \ddot{u}_{3} (x) \bigr) \\ &\quad =\sum_{i= \lceil \alpha \rceil }^{4}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{0} ^{i-k-\alpha } -(1+x)\sum_{i=0}^{4}u_{i} ^{\prime} (x)W_{i}^{*} (t_{0} ), \end{aligned} \end{aligned}$$
(4.42)
$$\begin{aligned}& \begin{aligned}[b] &e^{t} x^{2} \bigl( \ddot{u}_{0} (x)+H_{1} \ddot{u}_{1} (x)+H_{2} \ddot{u}_{2} (x) +H_{3} \ddot{u}_{3} (x) \bigr) \\ &\quad =\sum_{i= \lceil \alpha \rceil }^{4}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{1} ^{i-k-\alpha } -(1+x)\sum_{i=0}^{4}u_{i} ^{\prime} (x)W_{i}^{*} (t_{1} ), \end{aligned} \end{aligned}$$
(4.43)
$$\begin{aligned}& \begin{aligned}[b] & e^{t} x^{2} \bigl( \ddot{u}_{0} (x)+F_{1} \ddot{u}_{1} (x)+F_{2} \ddot{u}_{2} (x) +F_{3} \ddot{u}_{3} (x) \bigr) \\ &\quad =\sum_{i= \lceil \alpha \rceil }^{4}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{2} ^{i-k-\alpha } -(1+x)\sum_{i=0}^{4}u_{i} ^{\prime} (x)W_{i}^{*} (t_{2} ), \end{aligned} \end{aligned}$$
(4.44)
$$\begin{aligned}& \begin{aligned}[b] &e^{t} x^{2} \bigl( \ddot{u}_{0} (x)+G_{1} \ddot{u}_{1} (x)+G_{2} \ddot{u}_{2} (x) +G_{3} \ddot{u}_{3} (x) \bigr) \\ &\quad =\sum_{i= \lceil \alpha \rceil }^{4}\sum _{k=0}^{i- \lceil \alpha \rceil }u_{i} (x)V_{i, k}^{(\alpha )} t_{3} ^{i-k-\alpha } -(1+x)\sum_{i=0}^{4}u_{i} ^{\prime} (x)W_{i}^{*} (t_{3} ), \end{aligned} \end{aligned}$$
(4.45)

where

$$\begin{aligned}& K_{1} =W_{1}^{*} (t_{0} )=-0.8792, \qquad K_{2} =W_{2}^{*} (t_{0} )=0.6522, \qquad K_{3} =W_{3}^{*} (t_{0} )=-0.3464, \\& H_{1} =W_{1}^{*} (t_{1} )=0.0000, \qquad H_{2} =W_{2}^{*} (t_{1} )=-1.0000 \qquad H_{3} =W_{3}^{*} (t_{1} )=1.0000, \\& F_{1} =W_{1}^{*} (t_{2} )=1.3472 , \qquad F_{2} =W_{2}^{*} (t_{2} )=-0.5322 \qquad F_{3} =W_{3}^{*} (t_{2} )=-1.5320, \\& G_{1} =W_{1}^{*} (t_{2} )=2.5320,\qquad G_{2} =W_{2}^{*} (t_{2} )=2.8790 , \qquad G_{3} =W_{3}^{*} (t_{2} )=1.8787. \end{aligned}$$

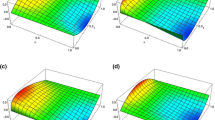
Graphs and Table: The graphical depictions in Fig. 2 show the exact solution and an approximate solution obtained through the shifted Chebyshev spectral method of FFPE on Example 4.2. Also, the absolute error of the present method for \(m=3,4\), and 5 is displayed in Table 2. As it is expected, accuracy of the method increases, i.e., the absolute error gets very small upon increasing the value of m, since the proposed method is based on the idea of infinite series.

Figure 2
figure 2

Comparison between the exact solution and the approximate solution of Example 4.2 for different values of α

Full size image
Table 2 The absolute error of \(u(x, t)\) for different values of m
Full size table

5 Conclusion

In this paper, to solve a Fokker–Planck time-fractional equation, the Chebyshev collocation method and the finite difference method are applied. Using the properties of the shifted Chebyshev fourth-kind polynomials, we reduce the time-fractional Fokker–Planck equation to the system of differential equations. Also, using FDM we reduce such systems of DEs into nonlinear equations where the Newton–Raphson method can be used to solve them. As it can be observed from the tabulated values and graphical solutions in Sect. 3, the behavior of numerical solution for different values of α is presented, which shows that the proposed method is dominant over the previous study in [7] taking the exact solutions as reference values. From this we conclude that the shifted Chebyshev polynomial of the fourth kind gives us better approximation, and we recommend other scholars in this area to increase the accuracy of such methods even more than this by taking a large value of the series (2.16).

The advantage of the methods is that the approximation requires only few terms of fourth-kind Chebyshev polynomials. Also, we compared the present method with the method in [7] to show that the present method demonstrated the effectiveness and high accuracy. All the numerical results were obtained with the help of MATLAB 2018a.