Abstract
In this paper, we consider a predator–prey model with Allee effect, fear effect and prey refuge. By considering the prey refuge as a parameter, we give the threshold condition for the stability of the system, and prove that the system undergoes a supercritical Hopf bifurcation. We show that increasing the prey refuge or Allee effect can make the dynamical behavior of the system more complicated; the fear effect or Allee effect has no influence on the prey density, but can lead to a decrease of the predator population at positive equilibrium.
Similar content being viewed by others
1 Introduction
The predator–prey model is one of the basic models in the theoretical studies of ecology, and it has been studied extensively (see [1–14] and the references cited therein). On the other hand, prey species usually make use of refuges to decrease predation risk. Chen et al. [15] investigated the stable property of a predator–prey system with a constant number of prey refuges. The authors [16] showed that prey refuge has no influence on the stability of the system. Khajanchi and Banerjee [17] studied the uniform persistence and global asymptotic stability of a stage structured predator–prey model with prey refuge. Xiao et al. [18] considered the global stability of a stage structure predator–prey system with prey refuge, and pointed out that the model undergoes a Hopf bifurcation when the delay crosses some critical values. Xie et al. [19] studied the persistence and stability of a modified Leslie–Gower predator–prey model with prey refuge, and showed that the prey refuge has a positive effect on the persistence property. For more details in this direction, see [20–23].
Most studies of predator systems only consider direct killing by predators, because such predation can be easily observed in nature. However, prey respond to predation risk and exhibit different types of anti-predator responses, including habitat change, foraging, alertness, and different physiological changes. Apart from the direct killing, based on many experiments, Zanette et al. [24] showed that the song sparrows reduce by 40% the offspring by predation fears. Motivated by this, Wang et al. [25] considered the cost of fear into prey reproduction and investigated the following predator–prey system
where a is the birth rate of prey; d is the natural death rate of prey; b is the density dependent coefficient; m is the capture rate; n is the conversion efficiency; e is the death rate of predator; f is the level of fear; \(F (f, v)\) is the cost of anti-predator defence due to fear. From a biological point of view, \(F(f,v)\) can be reasonably assumed to obey
They showed the cost of fear has no influence on the stability of the system (1). Considering the Holling type II functional response for system (1), [25] studied the stability of equilibria, and showed that a high amount of fear can stabilize the predator–prey system. Zhang et al. [26] investigated a Holling-II predator–prey model incorporating the fear effect and a prey refuge. They found that the fear effect cannot only reduce the population density of the predator at the positive equilibrium, but also stabilize the system. Kumar and Dubey [27] studied the stability of a delay prey-predator model with prey refuge and fear effect, and showed that the refuge below the threshold level is conducive to the system. Xiao and Li [28] considered a mutual interference predator–prey model with fear effect. Comparing with the corresponding predator–prey model without mutual interference, they concluded that the mutual interference can stabilize the predator–prey system. Sasmal and Takeuchi [29] studied a predator–prey system with fear effect, and discussed the multi-stability and Hopf bifurcation of the system. For more details in this direction, see [30–33].
On the other hand, the Allee effect can lead to the decrease of the intrinsic growth at low population densities, and make the system become unstable. Lin [34] studied the stability of a single species logistic model with Allee effect and feedback control, and showed the Allee effect makes the system become unstable. Ibarra and Flores [35] discussed the bifurcation of a Holling–Tanner predator–prey model with Allee effect. Wu et al. [36] concluded that the unique positive equilibrium is globally stable, and the Allee effect has no impact on the final density of the species. Guan and Chen [37] studied the bifurcation and stability of an amensalism with Allee effect, considering the growth reduction due to predator fear consider, Sasmal [38] studied a predator model with Allee effect in prey as follows:
where all the coefficients are positive constants; r is the intrinsic growth rate; k is the carrying capacity of the environment; a represents predation rate; α is the conversion efficiency of predator by consuming prey; m is the predator’s natural mortality rate; \(0<\theta <k\) is expressed by a strong Allee effect; \(F(f,v)=\frac{1}{1+fv}\) is the same meaning as (1). In the presence of fear, they showed that the fear effect can lead to the decrease of the per-capita growth rate, pointed out that fear does not affect the equilibrium stability, and the system has bi-stability among different equilibria.
Motivated by the above papers, the main purpose of this paper is to study the influence of the prey refuge on the stability of the system (3) as follows:
where \(0<\eta <1\) is the prey refuge constant; \(\eta u(t)\) is the capacity of a refuge at time t; the rest of the parameters have the same meaning as system (3).
For simplicity, let
Rewriting τ as t, system (4) is reduced to
where \(0<\theta <1\) and \(0<\eta <1\), the remaining parameters are positive constants.
The organization of this paper is as follows. In Sect. 2, the stability of the equilibria of the system (5) is investigated. In Sect. 3, the impacts of the fear effect, Allee effect and prey refuge on the species are discussed. Finally, a brief conclusion is drawn.
2 Main results
In this section, we study the existence and stability of the equilibria point of the system (5). Obviously, system (5) always has a trivial equilibrium \(E_{0}(0,0)\) and two boundary equilibria \(E_{1}(1,0)\) and \(E_{2}(\theta,0)\). The positive equilibrium point of the system (5) is determined by the following equation:
Substituting \(N=\frac{m}{1-\eta }\) into the first equation of (6), we have
where \(H=\frac{(1-\eta -m)(m-\theta (1-\eta ))}{(1-\eta )^{3}}\). If \(m\geq 1\), that is \(H<0\), then there does not exist a positive equilibrium. If \(1-\frac{m}{\theta }<\eta <1-m\), then \(H>0\). Hence, Eq. (7) has a positive solution,
Let \(N^{*}=\frac{m}{1-\eta }\), then system (5) has a positive equilibrium \(E^{*} (N^{*}, P^{*} )\).
Now we discuss the stability of equilibria, and we obtain the following lemmas.
Lemma 1
The trivial equilibrium\(E_{0}(0,0)\)of the system (5) is always a stable node.
Proof
The Jacobian matrix of the system (5) at \(E_{0}\) is calculated as
We obtain \(\operatorname{Tr} J_{E_{0}}=-\frac{\theta }{\epsilon }-m<0\) and \(\operatorname{Det} J_{E_{0}}= \frac{m \theta }{\epsilon } >0\), thus the equilibrium \(E_{0}\) is a stable node. This completes the proof of Lemma 1. □
Lemma 2
-
(1)
If\(0<\eta <1-m\), \(E_{1}(1,0)\)of the system (5) is a saddle point.
-
(2)
If\(\eta =1-m\), \(E_{1}(1,0)\)of the system (5) is an attracting saddle node, which includes a stable parabolic sector.
-
(3)
If\(1-m<\eta <1\), \(E_{1}(1,0)\)of the system (5) is locally asymptotically stable.
Proof
The Jacobian matrix of the system (5) at \(E_{1}\) is calculated as
Then the eigenvalues \(\lambda _{1}=\frac{\theta -1}{\epsilon }<0\) and \(\lambda _{2}=1-\eta -m\). If \(0<\eta <1-m\), that is \(\lambda _{2}>0\), the boundary equilibrium \(E_{1}\) is a saddle point. If \(1-m<\eta <1\), that is \(\lambda _{2}<0\), the boundary equilibrium \(E_{1}\) is stable.
When \(\eta =1-m\), we have \(\lambda _{2}=0\). Then system (5) can be rewritten as
We transform the equilibrium \(E_{1}\) to the origin by making a transformation that \(X=N-1, Y=P\). Then we have a Taylor expansion at the origin as follows:
where \(Q_{1}(X,Y)\) is \(C^{\infty }\) functions of at least the third order in terms of \((X,Y)\).
Let \(X_{1}=\frac{\theta -1}{\epsilon }X-\frac{m}{\epsilon }Y, Y_{1}=Y\). Introducing a new time variable τ by \(\tau =-\frac{1-\theta }{\epsilon }t\), rewriting τ as t, we have
where \(Q_{2}(X_{1},Y_{1})\) is a \(C^{\infty }\) function of at least the third order in terms of \((X_{1},Y_{1})\).
Therefore, the coefficient of \(Y_{1}^{2}\) is \(\frac{\epsilon m^{2}}{(\theta -1)^{2}}>0\). According to Theorem 7.1 in Zhang et al. [39], we can conclude that \(E_{1}(1,0)\) is an attracting saddle node, which includes a stable parabolic sector. This completes the proof of Lemma 2. □
Lemma 3
-
(1)
If\(0<\eta <1-\frac{m}{\theta }\), \(E_{2}(\theta,0)\)of the system (5) is unstable.
-
(2)
If\(\eta =1-\frac{m}{\theta }\), \(E_{2}(\theta,0)\)of the system (5) is a repelling saddle node, which includes a unstable parabolic sector.
-
(3)
If\(1-\frac{m}{\theta }<\eta <1\), \(E_{2}(\theta,0)\)of the system (5) is a saddle point.
Proof
The Jacobian matrix of the system (5) at \(E_{2}\) is calculated as
Then the eigenvalues \(\lambda _{1}=\frac{\theta (1-\theta )}{\epsilon }>0\) and \(\lambda _{2}=\theta (1-\eta )-m\). If \(0<\eta <1-\frac{m}{\theta }\), that is, \(\lambda _{2}>0\), the boundary equilibrium \(E_{2}\) is unstable. If \(1-\frac{m}{\theta }<\eta <1\), that is, \(\lambda _{2}<0\), the boundary equilibrium \(E_{2}\) is a saddle point.
When \(\eta =1-\frac{m}{\theta }\), we obtain \(\lambda _{2}=0\). Then system (5) can be rewritten as
We transform the equilibrium \(E_{2}\) to the origin by making a transformation that \(X=N-\theta, Y=P\). Then we have a Taylor expansion at the origin as follows:
where \(Q_{3}(X,Y)\) is a \(C^{\infty }\) function of at least the third order in terms of \((X,Y)\).
Let \(X_{1}=\frac{\theta (1-\theta )}{\epsilon }X- \frac{m}{\epsilon }Y, Y_{1}=Y\). Introducing a new time variable τ by \(\tau =\frac{\theta (1-\theta )}{\epsilon }t\), rewriting τ as t, we have
where \(Q_{4}(X_{1},Y_{1})\) is a \(C^{\infty }\) function of at least the third order in terms of \((X_{1},Y_{1})\).
Therefore, the coefficient of \(Y_{1}^{2}\) is \(\frac{\epsilon m^{2}}{\theta ^{3}(\theta -1)^{2}}>0\). According to Theorem 7.1 in Zhang et al. [39], we can conclude that \(E_{2}(\theta,0)\) is a repelling saddle node, which includes an unstable parabolic sector. This completes the proof of Lemma 3. □
Lemma 4
-
(1)
If\(1-\frac{m}{\theta }<\eta <1-\frac{2m}{\theta +1}\), \(E^{*} (N^{*}, P^{*} )\)of the system (5) is stable.
-
(2)
If\(1-\frac{2m}{\theta +1}<\eta <1-m\), \(E^{*} (N^{*}, P^{*} )\)of the system (5) is unstable.
Proof
The Jacobian matrix of the system (5) at \(E^{*}\) is calculated as
By calculation, we obtain \(\operatorname{Det} J_{E^{*}}=\frac{mP^{*}}{\epsilon } (\frac{(1-m-\eta )(m-\theta (1-\eta ))f}{(1-\eta )^{2}(1+fP^{*})^{2}}+(1- \eta ) )> 0\) and \(\operatorname{Tr} J_{E^{*}}=\frac{m((1+\theta )(1-\eta )-2m)}{\epsilon (1-\eta )^{2}(1+fP^{*})}\).
Therefore, if \(1-\frac{m}{\theta }<\eta <1-\frac{2m}{\theta +1}\), that is \(\operatorname{Tr} J_{E^{*}}>0\), then the boundary equilibrium \(E^{*}\) of the system (5) is unstable. If \(1-\frac{2m}{\theta +1}<\eta <1-m\), that is \(\operatorname{Tr} J_{E^{*}}<0\), then the boundary equilibrium \(E^{*}\) of the system (5) is stable. This completes the proof of Lemma 4. □
Lemma 5
If\(\eta =1-\frac{2m}{\theta +1}\), system (5) undergoes a supercritical Hopf bifurcation at positive equilibrium\(E^{*}\)and there exists a stable limit cycle around\(E^{*}\).
Proof
Form the proof of Lemma 4, when \(\eta =1-\frac{2m}{\theta +1}\), we have \(\operatorname{Det} J_{E^{*}}>0\) and \(\operatorname{Tr} J_{E^{*}}=0\). The positive equilibrium \(E^{*}\) becomes a non-hyperbolic equilibrium, and the Jacobian matrix at \(E^{*}\) has a pair of imaginary roots. In order to ensure the occurrence of the Hopf bifurcation, the transverse conditions of Hopf bifurcation should be checked. By a straightforward computation, we have
Hence, the positive equilibrium \(E^{*}\) loses its stability through a non-degenerate Hopf bifurcation.
Now we will calculate the Lyapunov number \(l_{1}\) at \(E^{*}\) to determine the stability of the limit cycle. We first translate the equilibrium \(E^{*}\) of the system (5) to the origin by employing the transformations \(N=\hat{x}-N^{*}\) and \(P=\hat{y}-P^{*}\). Note that \(N^{*}=\frac{1+\theta }{2}\) and \(\eta =1-{ \frac{ (1-\theta )^{2} }{4 P^{*} ( f{ P^{*}}+1 ) }}\). Thus, system (5) in a neighborhood of the origin can be written as
where \(a_{10}=0\), \(a_{01}=-\frac{(1+\theta )(1-\theta )^{2} (2fP^{*}+1 )}{8\epsilon P^{*}(fP^{*}+1)^{2}}\), \(a_{20}=-\frac{1+\theta }{2\epsilon (fP^{*}+1)}\), \(a_{11}=-\frac{(1-\theta )^{2}(2fP^{*}+1)}{4\epsilon P^{*}(fP^{*}+1)^{2}}\), \(a_{02}=\frac{(1+\theta )(1-\theta )^{2}f^{2}}{8\epsilon (fP^{*}+1)^{3}}\), \(a_{30}=-\frac{1}{\epsilon (fP^{*}+1)}\), \(a_{12}=\frac{(1-\theta )^{2}f^{2}}{4\epsilon (fP^{*}+1)^{3}}\), \(a_{21}=\frac{(1+\theta )(fP^{*}+1)^{2}f}{2\epsilon (fP^{*}+1)^{4}}\), \(a_{03}=-\frac{(1+\theta )(1-\theta )^{2}f^{3}}{8\epsilon (fP^{*}+1)^{4}}\), \(b_{10}=\frac{(1-\theta )^{2}}{4(fP^{*}+1)}\), \(b_{01}=\frac{(1-\theta )^{2}(1+\theta )}{8P^{*}(fP^{*}+1)}-m\), \(b_{11}=\frac{(1-\theta )^{2}}{4P^{*}(fP^{*}+1)} \), \(b_{20}=b_{02}=b_{30}=b_{21}=b_{12}=b_{03}=0\).
The first Lyapunov number \(l_{1}\) [40] to determine the stability of limit cycle for a planar system (14) is given by the following formula:
where \(\varPhi =\sqrt{\frac{(1+\theta )(1-\theta )^{4}(2fP^{*}+1)}{32\epsilon (fP^{*}+1)^{3}P^{*}}}\).
Obviously \(l_{1}<0\), the system (5) undergoes a supercritical Hopf bifurcation at positive equilibrium \(E^{*}\) and there exists a stable limit cycle around \(E^{*}\). This completes the proof of Lemma 5.
It follows from Lemma 6 that the trivial equilibrium point \(E_{0}\) is always a stable node. Hence, in the rest of this section, we only consider the stability of the boundary equilibria \(E_{1}, E_{2}\) and the positive equilibrium \(E^{*}\) of the system with the prey refuge and Allee effect varies. When \(m\ge 1\), there does not exist a positive equilibrium point of the system (5). According to Lemmas 2 and 3, we have the following theorem. □
Theorem 1
When\(m\ge 1\)and\(0<\eta <1\), the boundary equilibrium\(E_{1}\)is stable and the boundary equilibrium\(E_{2}\)is a saddle point.
From Theorem 1, if the death rate of the predator is large enough, then the predator will be extinct, and the prey will tend to extinction or the carrying capacity of the environment depending on the choices of the initial density of prey.
In the following, we only discuss \(0< m<1\). According to Lemmas 2–4 and considering the prey refuge as a parameter, we have the following theorems.
Theorem 2
When\(\theta \le 2m-1\)and\(m<1\), we have:
-
(1)
If\(0<\eta <1-m\), \(E_{1}\)and\(E_{2}\)are saddle points, \(E^{*}\)is stable.
-
(2)
If\(\eta =1-m\), \(E_{1}\)is an attracting saddle node, including a stable parabolic sector, and\(E_{2}\)is a saddle point.
-
(3)
If\(1-m<\eta <1\), \(E_{1}\)is stable and\(E_{2}\)is a saddle point.
Theorem 3
When\(2m-1<\theta \le m<1\), we have:
-
(1)
If\(0<\eta <1-\frac{2m}{1+\theta }\), \(E_{1}\)and\(E_{2}\)are saddle points, \(E^{*}\)is unstable.
-
(2)
If\(\eta =1-\frac{2m}{1+\theta }\), \(E_{1}\)and\(E_{2}\)are saddle points, and a Hopf bifurcation exists at\(E^{*}\).
-
(3)
If\(1-\frac{2m}{1+\theta }<\eta <1-m\), \(E_{1}\)and\(E_{2}\)are saddle points and\(E^{*}\)is stable.
-
(4)
If\(\eta =1-m\), \(E_{1}\)is an attracting saddle node, including a stable parabolic sector and\(E_{2}\)is a saddle point.
-
(5)
If\(1-m<\eta <1\), \(E_{1}\)is stable and\(E_{2}\)is a saddle point.
Theorem 4
When\(m<\theta <1\), we get:
-
(1)
If\(0<\eta <1-\frac{m}{\theta }\), \(E_{1}\)is a saddle point, \(E_{2}\)is unstable.
-
(2)
If\(\eta =1-\frac{m}{\theta }\), \(E_{1}\)is a saddle point, and\(E_{2}\)is a repelling saddle node, which includes a unstable parabolic sector.
-
(3)
If\(1-\frac{m}{\theta }<\eta <1-\frac{2m}{1+\theta }\), \(E_{1}\)and\(E_{2}\)are saddle points and\(E^{*}\)is unstable.
-
(4)
If\(\eta =1-\frac{2m}{1+\theta }\), \(E_{1}\)and\(E_{2}\)are saddle points, and a Hopf bifurcation exists at\(E^{*}\).
-
(5)
If\(1-\frac{2m}{1+\theta }<\eta <1-m\), \(E_{1}\)and\(E_{2}\)are saddle points and\(E^{*}\)is stable.
-
(6)
If\(\eta =1-m\), \(E_{1}\)is an attracting saddle node, which includes a stable parabolic sector, and\(E_{2}\)is a saddle point.
-
(7)
If\(1-m<\eta <1\), \(E_{1}\)is stable and\(E_{2}\)is a saddle point.
Note that the trivial equilibrium point \(E_{0}\) is always a stable node. If \(m<\theta <1\) and \(0<\eta \leq 1-\frac{m}{\theta }\), it follows from Theorem 4 that \(E_{1}\) is a saddle point and \(E_{2}\) is unstable. Obviously, the solutions of the system (5) are positive and bounded. Also, for system (1.5) there do not exist limit cycles. Hence, \(E_{0}\) is globally asymptotically stable. Then we have the following remark.
Remark 1
If \(m<\theta <1\) and \(0<\eta \leq 1-\frac{m}{\theta }\), the trivial equilibrium \(E_{0}\) is globally asymptotically stable.
If \(m\leq \theta \), without the prey refuge, the author [38] pointed out that both prey and predator will be extinct. However, it follows from Theorems 3 and 4, the dynamics behavior of the system (5) becomes more complicated. With increase of the prey refuge, the behavior of the positive equilibrium \(E^{*}\) changes from instability to stability. System (5) undergoes a supercritical Hopf bifurcation and there exists a stable limit cycle around \(E^{*}\). If the prey refuge is large enough, the positive equilibrium \(E^{*}\) disappears, that is, the predator will be extinct.
3 Discussion and numerical simulations
In this section, we show the influence of the Allee effect, fear effect and prey refuge on the dynamics behavior of the system (5).
Firstly, we study the impact of the fear effect on the dynamics behavior of the system (5). Note that \(N^{*}=\frac{m}{1-\eta }\), then the fear effect has no influence on the prey density. By calculating, we have
that is, the predator density is a strictly decreasing function with respect to fear effect. Then we show that increasing the fear effect can decrease the predator density, that is, fear effect can lead to the decrease of the predator population. It follows from Theorems 2–4 that the cost of the fear effect has no influence on the stability of the system (5), which is in accord with that for the predator–prey model with the linear functional response [25].
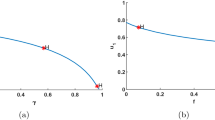
Secondly, we study the impact of the Allee effect on the dynamics behavior of the system (5). Obviously, the Allee effect has no impact on the prey density. The existence of the positive equilibrium point \(E^{*}(N^{*},P^{*})\) implies that \(1-\frac{m}{\theta }<\eta <1-m\). By simple computation, one has
that is the predator density is a strictly decreasing function with respect to the Allee effect. With the increase of Allee effect, the density of the predator population decreases, while the density of the prey population does not change. From Theorem 2, if the Allee effect is small enough, then the dynamics behavior of the system (5) is relatively simple, that is the positive equilibrium \(E^{*}\) is stable when it exists (see Fig. 1(a)). However, if the Allee effect is large enough, the dynamics behavior of the system (5) becomes more complicated. From Theorems 3 and 4, the behavior of the positive equilibrium \(E^{*}\) changes from stability to instability, and there exists a stable limit cycle around \(E^{*}\) (see Fig. 1(b)). If the prey refuge is small enough, the positive equilibrium \(E^{*}\) can even disappear (see Fig. 1(c)). Hence, increasing the amount of the Allee effect has a negative effect on the stability of the system (5).
Dynamic behavior of the system (5) with \(\eta =0.1, \varepsilon =1, f=0.2, m=0.6\)
Thirdly, we investigate the impact of prey refuge on the dynamics behavior of the system (5). By computing the derivative along the \(N^{*}\) and \(P^{*}\) with respect to η, respectively, we obtain
and
The above inequality shows that \(N^{*}\) is a strictly increasing function with respect to prey refuge. That is, increasing the value of prey refuge can increase prey density.
Let \(F(z)=-\theta z^{2}+2m(1+\theta )z-3m^{2}\), where \(z=1-\eta \). Then the sign of \(\frac{\partial P^{*}}{\partial \eta }\) is determined by the sign of \(F(z)\). Note that the existence of the positive equilibrium point \(E^{*}(N^{*},P^{*})\) implies that \(m<1\) and \(1-\frac{m}{\theta }<\eta <1-m\). Hence, we only consider \(m< z<\frac{m}{\theta }\).
By calculation, \(F(m)=-(1-\theta )m^{2}<0\) and \(F(\frac{m}{\theta })=\frac{(1-\theta )m^{2}}{\theta }>0\). Solving the equation \(F(z)=0\), we have \(z_{1}=\frac{m(1+\theta )-m\sqrt{\theta ^{2}-\theta +1}}{\theta }\), where \(m< z_{1}<\frac{m}{\theta }\). Then \(F(z)<0\) for \(m< z< z_{1}\) and \(F(z)>0\) for \(z_{1}< z<\frac{m}{\theta }\). Hence, we have
and
Therefore, when \(1-z_{1}<\eta <1-m\) or \(1-\frac{m}{\theta }<\eta <1-z_{1}\), the predator density is a strictly decreasing or increasing function with respect to prey refuge, respectively (see Fig. 2). With the increase of prey refuge, the density of the prey population increases. Then the prey refuge is benefit to the density of the prey population. However, when \(1-z_{1}<\eta <1-m\), increasing the amount of prey refuge can protect more prey from predation. Due to lack of food resources, it leads to the decrease of the density of the predator population. When \(1-\frac{m}{\theta }<\eta <1-z_{1}\), the predator density is an increasing function with respect to prey refuge. Then with the increase of the prey population, more and more preys have to leave the shelter. It leads to more food for the predator. Hence, the predator density is increasing.
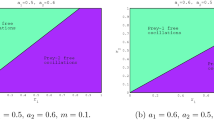
In the case without the prey refuge, that is \(\eta =0\), system (5) is reduced to the system in [38]. The author [38] pointed out that both prey and predator converge to O for every initial conditions if \(m\leq \theta \). However, with influence of prey refuge, it follows from Theorems 3 and 4 that the dynamics behavior of the system (5) becomes even more complicated than that of the corresponding system in[38]. Figure 3 shows the dynamics behavior of positive equilibrium \(E^{*}\) in \((\eta,\theta )\) plane when \(m<\theta <1\).
Now, we consider the dynamics behavior of the system (5) when \(m<\theta \), that is the Allee effect is large enough. More precisely, if prey refuge η is larger than \(1-m\), there does not exist the positive equilibrium \(E^{*}\) (see Fig. 4(a)). That is, if the shelter is large enough, then it leads to less food resources for the predator. Hence, the predator is extinct. With the decrease of prey refuge, a stable positive equilibrium \(E^{*}\) appears (see Fig. 4(b)). Then both prey and predator can survive. When prey refuge passes through \(1-\frac{2m}{1+\theta }\), system (5) undergoes a supercritical Hopf bifurcation at positive equilibrium \(E^{*}\) and there exists a stable limit cycle around \(E^{*}\) (see Fig. 4(c)). When prey refuge is small enough, the positive equilibrium \(E^{*}\) becomes unstable. Then both prey and predator are extinct (see Fig. 4(d)). Finally, if the prey refuge is less than \(1-\frac{m}{\theta }\), the positive equilibrium \(E^{*}\) disappears. Then system (5) is still extinct (see Fig. 4(e)). In this situation, the shelter is not enough for sustaining the prey and predator to survival.
Dynamic behavior of the system (5) with \(\theta =0.6, \varepsilon =1, f=0.2, m=0.4\)
4 Conclusion
In this paper, we consider a fear effect predator–prey model with the Allee effect and a prey refuge. By analyzing the characteristic equation of the corresponding linearized system and considering prey refuge as parameter, we obtain the threshold condition for the stability of the system (5). We show that prey refuge plays an important role in the dynamics of the system (5). Comparing with the corresponding predator–prey model without prey refuge [38], we find that the prey refuge can make the dynamics behavior of the system (5) more complicated.
References
Xiao, A., Lei, C.: Dynamic behaviors of a non-selective harvesting single species stage-structured system incorporating partial closure for the populations. Adv. Differ. Equ. 2018(1), 245 (2018)
He, M., Chen, F.: Extinction and stability of an impulsive system with pure delays. Appl. Math. Lett. 91, 128–136 (2019)
Lin, Y., Xie, X., Chen, F., et al.: Convergences of a stage-structured predator–prey model with modified Leslie–Gower and Holling-type II schemes. Adv. Differ. Equ. 2016(1), 1 (2016)
He, M., Chen, F., Li, Z.: Permanence and global attractivity of an impulsive delay logistic model. Appl. Math. Lett. 62, 92–100 (2016)
Xue, Y., Xie, X., Lin, Q.: Almost periodic solutions of a commensalism system with Michaelis–Menten type harvesting on time scales. Open Math. 17(1), 1503–1514 (2019)
Guo, Z., Huo, H., Ren, Q., et al.: Bifurcation of a modified Leslie–Gower system with discrete and distributed delays. J. Nonlinear Model. Anal. 1(1), 73–91 (2019)
Chen, B.: The influence of commensalism on a Lotka–Volterra commensal symbiosis model with Michaelis–Menten type harvesting. Adv. Differ. Equ. 2019(1), 43 (2019)
Song, Y., Zhang, T.: Spatial pattern formations in diffusive predator–prey systems with non-homogeneous Dirichlet boundary conditions. J. Appl. Anal. Comput. 10(1), 165–177 (2019)
Lei, C.: Dynamic behaviors of a stage-structured commensalism system. Adv. Differ. Equ. 2018(1), 301 (2018)
Lei, C.: Dynamic behaviors of a non-selective harvesting may cooperative system incorporating partial closure for the populations. Commun. Math. Biol. Neurosci. 2018, Article ID 12 (2018)
An, Y., Luo, X.: Global stability of a stochastic Lotka–Volterra cooperative system with two feedback controls. J. Nonlinear Model. Anal. 2(1), 131–142 (2020)
Song, Y., Jiang, H., Yuan, Y.: Turing–Hopf bifurcation in the reaction-diffusion system with delay and application to a diffusive predator–prey model. J. Appl. Anal. Comput. 9(3), 1132–1164 (2019)
Lin, Q., Xie, X., Chen, F., et al.: Dynamical analysis of a logistic model with impulsive Holling type-II harvesting. Adv. Differ. Equ. 2018(1), 112 (2018)
Dai, Y., Yang, P., Luo, Z., et al.: Bogdanov–Takens bifurcation in a delayed Michaelis–Menten type ratio-dependent predator–prey system with prey harvesting. J. Appl. Anal. Comput. 9(4), 1333–1346 (2019)
Chen, F., Ma, Z., Zhang, H.: Global asymptotical stability of the positive equilibrium of the Lotka–Volterra prey-predator model incorporating a constant number of prey refuges. Nonlinear Anal., Real World Appl. 13(6), 2790–2793 (2012)
Chen, F., Chen, L., Xie, X.: On a Leslie–Gower predator–prey model incorporating a prey refuge. Nonlinear Anal., Real World Appl. 10(5), 2905–2908 (2009)
Khajanchi, S., Banerjee, S.: Role of constant prey refuge on stage structure predator–prey model with ratio dependent functional response. Appl. Math. Comput. 314, 193–198 (2017)
Xiao, Z., Li, Z., Zhu, Z., et al.: Hopf bifurcation and stability in a Beddington–DeAngelis predator–prey model with stage structure for predator and time delay incorporating prey refuge. Open Math. 17(1), 141–159 (2019)
Xie, X., Xue, Y., Chen, J., et al.: Permanence and global attractivity of a nonautonomous modified Leslie–Gower predator–prey model with Holling-type II schemes and a prey refuge. Adv. Differ. Equ. 2016(1), 1 (2016)
Yang, P.: Hopf bifurcation of an age-structured prey-predator model with Holling type II functional response incorporating a prey refuge. Nonlinear Anal., Real World Appl. 49, 368–385 (2019)
Yue, Q.: Dynamics of a modified Leslie–Gower predator–prey model with Holling-type II schemes and a prey refuge. SpringerPlus 5(1), 1–12 (2016)
Dubey, B., Kumar, A., Maiti, A.P.: Global stability and Hopf-bifurcation of prey-predator system with two discrete delays including habitat complexity and prey refuge. Commun. Nonlinear Sci. Numer. Simul. 67, 528–554 (2019)
Chakraborty, B., Bairagi, N.: Complexity in a prey-predator model with prey refuge and diffusion. Ecol. Complex. 37, 11–23 (2019)
Zanette, L.Y., White, A.F., Allen, M.C., et al.: Perceived predation risk reduces the number of offspring songbirds produce per year. Science 334(6061), 1398–1401 (2011)
Wang, X., Zanette, L., Zou, X.: Modelling the fear effect in predator–prey interactions. J. Math. Biol. 73(5), 1179–1204 (2016)
Zhang, H., Cai, Y., Fu, S., et al.: Impact of the fear effect in a prey-predator model incorporating a prey refuge. Appl. Math. Comput. 356, 328–337 (2019)
Kumar, A., Dubey, B.: Modeling the effect of fear in a prey-predator system with prey refuge and gestation delay. Int. J. Bifurc. Chaos 29(14), 1950195 (2019)
Xiao, Z., Li, Z.: Stability analysis of a mutual interference predator–prey model with the fear effect. J. Appl. Sci. Eng. 22(2), 205–211 (2019)
Sasmal, S.K., Takeuchi, Y.: Dynamics of a predator–prey system with fear and group defense. J. Math. Anal. Appl. 481(1), 123471 (2020)
Pal, S., Pal, N., Samanta, S., et al.: Effect of hunting cooperation and fear in a predator–prey model. Ecol. Complex. 39, 100770 (2019)
Wang, X., Zou, X.: Modeling the fear effect in predator–prey interactions with adaptive avoidance of predators. Bull. Math. Biol. 79(6), 1325–1359 (2017)
Wang, X., Zou, X.: Pattern formation of a predator–prey model with the cost of anti-predator behaviors. Math. Biosci. Eng. 15(3), 775 (2017)
Pal, S., Pal, N., Samanta, S., et al.: Fear effect in prey and hunting cooperation among predators in a Leslie–Gower model. Math. Biosci. Eng. 16(5), 5146–5179 (2019)
Lin, Q.: Stability analysis of a single species logistic model with Allee effect and feedback control. Adv. Differ. Equ. 2018(1), 190 (2018)
Arancibia-Ibarra, C., Flores, J.D., Pettet, G., et al.: A Holling–Tanner predator–prey model with strong Allee effect. Int. J. Bifurc. Chaos 29(11), 1930032 (2019)
Wu, R., Li, L., Lin, Q.: A Holling type commensal symbiosis model involving Allee effect. Commun. Math. Biol. Neurosci. 2018, Article ID 6 (2018)
Guan, X., Chen, F.: Dynamical analysis of a two species amensalism model with Beddington–DeAngelis functional response and Allee effect on the second species. Nonlinear Anal., Real World Appl. 48, 71–93 (2019)
Sasmal, S.K.: Population dynamics with multiple Allee effects induced by fear factors—a mathematical study on prey-predator interactions. Appl. Math. Model. 64, 1–14 (2018)
Zhang, Z., Ding, T., Huang, W., Dong, Z.: Qualitative Theory of Differential Equation. Science Press, Beijing (1992)
Perko, L.: Differential equations and dynamical systems. In: Texts in Applied Mathematics, 3rd edn. vol. 7. Springer, New York (2001)
Acknowledgements
The authors would like to thank Dr. Hang Deng for bringing our attention to the paper of A. Basheer.
Availability of data and materials
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
Funding
The research was supported by the Natural Science Foundation of Fujian Province (2019J01841).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that there is no conflict of interests.
Consent for publication
Not applicable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huang, Y., Zhu, Z. & Li, Z. Modeling the Allee effect and fear effect in predator–prey system incorporating a prey refuge. Adv Differ Equ 2020, 321 (2020). https://doi.org/10.1186/s13662-020-02727-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02727-5