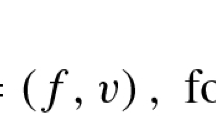Two computational approaches for solving a fractional obstacle system in Hilbert space

Abstract

The primary motivation of this paper is to extend the application of the reproducing-kernel method (RKM) and the residual power series method (RPSM) to conduct a numerical investigation for a class of boundary value problems of fractional order 2α, $0<\alpha\leq1$, concerned with obstacle, contact and unilateral problems. The RKM involves a variety of uses for emerging mathematical problems in the sciences, both for integer and non-integer (arbitrary) orders. The RPSM is combining the generalized Taylor series formula with the residual error functions. The fractional derivative is described in the Caputo sense. The representation of the analytical solution for the generalized fractional obstacle system is given by RKM with accurately computable structures in reproducing-kernel spaces. While the methodology of RPSM is based on the construction of a fractional power series expansion in rapidly convergent form and apparent sequences of solution without any restriction hypotheses. The recurrence form of the approximate function is selected by a well-posed truncated series that is proved to converge uniformly to the analytical solution. A comparative study was conducted between the obtained results by the RKM, RPSM and exact solution at different values of α. The numerical results confirm both the obtained theoretical predictions and the efficiency of the proposed methods to obtain the approximate solutions.

1 Introduction

The concept of variational inequality problems (VIPs) has become an influential mathematical methodology for qualitatively analyzing free boundary, equilibrium, optimization, complementarity, obstacle, unilateral, and environmental network issues in numerous disciplines including economics, finance, management, mechanics, elasticity and engineering [1,2,3]. This concept has been generalized and improved as an interesting branch in applied mathematics, which was formulated and investigated as special cases of equilibrium analysis. In 1966, Hartman and Stampacchia introduced the theory of VIP for studying a class of partial differential equations with applications that were derived mainly from mechanics. Later, Kikuchi and Oden [3] have shown that the equilibrium problems for elastic objects touching a rigid base can be handled in the context of the theory of VIP. The obstacle model is essential in the development of the VIPs theory that arises in a variety of pure and differential applied sciences. Anyhow, scholars have considered the following obstacle system with second-order derivatives by utilizing other numerical methods, including finite difference, spline, and collocation methods [4,5,6,7]:

$$ u''(x)= \textstyle\begin{cases} f ( x ),&x\in [ a,c ] \cup [ d,b ], \\ g ( x ) u ( x ) +f ( x ) +r,& x\in [ c, d ], \end{cases} $$

(1.1)

with boundary conditions

$$ u ( a ) = \mu_{1},\qquad u ( b ) = \mu_{2}, $$

(1.2)

and with the assumptions that the required solution $u ( x )$ for boundary value problems (BVPs) (1.1) and (1.2) is unique smooth function and its first derivative satisfies the continuity conditions at internal points c and d. Moreover, the functions $g(x)$ and $f(x)$ are given analytical real-valued functions on $[ c, d ]$ and on $[ a,b ]$, respectively, where $a< c< d< b$. The parameters $\mu_{1}, \mu_{2}$ and r are real finite constants. These kinds of BVPs arise in the study of obstacle, moving, unilateral, and free BVPs that have many powerful applications in the field of mathematics [5,6,7,8].

Many obstacle problems of integer order have been studied and solved using several numerical approaches such as variation of parameters, collocation, finite difference, spline and residual power series techniques. For instance, the collocation technique was applied in [4] for solving the obstacle BVPs (1.1) and (1.2) utilizing B-cubic splines basis functions that yields approximate solution of first-order accuracy. Later, similar results were drawn to obstacle BVPs (1.1) and (1.2) utilizing finite difference and spline methods [4, 7]. While the Numerov technique was modified and employed in solving the obstacle system by Al-Said and Noor [9]. Further, the quadratic and cubic splines techniques were implemented and analyzed by Al-Said [8] to produce a smooth approximate solution of the obstacle BVPs (1.1) and (1.2) over the domain [$a,b$]. Also, quartic-spline functions were presented to get some consistent relations that utilized in developing a numeric approach in finding smooth approximate solutions for the proposed obstacle system [10].

Furthermore, it is very difficult to achieve an analytic solution for obstacle BVPs (1.1) and (1.2) for arbitrary choices of the functions $f(x)$ and $g(x)$, so numerical methods are commonly resorted to for obtaining an approximate solution to such obstacles. For instance, the author in [11] applied a classical Rayleigh–Ritz method in solving special case of obstacle BVPs (1.1) and (1.2) in the form

$$ u''(x)= \textstyle\begin{cases} 0, &x\in [ 0, \frac{\pi}{4} ],\\ u ( x ) -1,& x\in [ \frac{\pi}{4}, \frac{3\pi}{4} ],\\ 0,& x\in [ \frac{3\pi}{4}, \pi ], \end{cases} $$

(1.3)

in which $f ( x ) =0,g ( x ) =1$, the parameter $r=-1$ and with the BCs $u ( 0 ) =0, u ( \pi ) =0$, whereas $u^{ ( i )} ( x ),i=0,1$, is continuous function at the internal points $\frac{\pi}{4}$ and $\frac{3\pi}{4}$.

However, in the last few decades, fractional calculus has attracted the attention of many researchers for its considerable importance in many applications in fluid dynamics, viscoelasticity, physics, entropy theory and engineering. Therefore, many boundary differential equations and initial differential equations of integer order were generalized to fractional order and several powerful methods were modified to approximate their solutions. The Adomian decomposition method [12], the variational iteration method [13], the differential transformation method [14], the finite difference method [15], the homotopy analysis method [16], and the homotopy perturbation method [17] are some of these methods. Also, MOL-GPS and theta methods have been applied for solving Burgers equation [18], and fractional telegraph differential equation [19], respectively. For using Riesz Riemann–Liouville, Riesz–Caputo, and other fractional concepts, we refer to [20, 21].

This paper aims to generalize the classical obstacle system described in (1.1) and (1.2) of integer order into the following obstacle system of the fractional order α under certain assumptions:

$$ D_{a}^{2\alpha} u(x)= \textstyle\begin{cases} f ( x ), &a\leq x< c,\\ g ( x ) u ( x ) +f ( x ) +r,&c\leq x< d, \\ f ( x ),&d\leq x\leq b, \end{cases} $$

(1.4)

with the boundary conditions

$$ u ( a ) = \mu_{1},\qquad u ( b ) = \mu_{2}, $$

(1.5)

where $0<\alpha\leq1, D_{a}^{2\alpha}$ is the Caputo-fractional derivative, $\mu_{1}, \mu_{2}\in \mathbb{R}$, the parameter r is real finite constant, $g ( x )$ is an analytical continuous function on $[ c,d ],f ( x )$ is a continuous on $[ a,b ]$, the function $u ( x )$ is unknown smooth to be obtained such that $u^{ ( i )} ( x ),i=0,1$, is continuous function at internal points c and d of $[ a,b ]$.

In this aspect, the reproducing-kernel method (RKM) is applied for finding smooth approximations to the solution of the modified obstacle system of fractional order (1.4) and (1.5), and its derivative. However, many definitions in the literature have been proposed for the derivatives of arbitrary order because all the utilized concepts do not preserve the classical integer-order derivative properties. For the concept of fractional derivative, we adopt the definition of the Caputo-fractional derivative due to the derivative of any constant function in the Caputo sense is equal to zero and are no initial conditions of fractional order are needed according to the proposed fractional models. However, the Caputo-fractional derivative of order $n-1<\alpha<n, n\in \mathbb{{N}}$, is defined for $u\in \mathcal{C}^{n} (0,\infty)$ by

$$ D_{a}^{\alpha} u ( x ) = \frac{1}{\varGamma(n-\alpha)} \int_{a}^{x} \frac{u^{(n)} (\xi)}{(x-\xi)^{\alpha-n+1}} \,d\xi,\quad x>a, $$

(1.6)

and $D_{a}^{\alpha} u ( x ) = u^{(n)} (x)$ for $\alpha=n \in \mathbb{N}$.

The reproducing-kernel approach has been developed as an efficacious numeric-analytic method in treating different type of ordinary and partial differential, integral, integrodifferential equations with singularity, fuzziness, nonlocal, and non-classical constraint conditions [22,23,24,25,26,27]. Recently, the RKM has been improved and successfully applied in obtaining approximations of solutions for many initial and boundary problems that appear in natural sciences and engineering. The RKM was successfully used for solving the Thomas–Fermi equation [28], the Poisson–Boltzmann equation for semiconductor devices [29], variable-order fractional differential equations [30] and second-order partial differential equations [31] and others [32,33,34]. Moreover, Cui and Lin [24] have efficiently solved obstacle third-order BVP using RKM. It should be noted here that the obstacle system of fractional order has not been solved using RKM before. The RPSM is an analytical as well as an approximate method for handling several kinds of FDEs. This method has been applied effectively to construct a fractional power series solution for numerous linear and nonlinear equations without linearization, perturbation, or discretization [35]. The FRPS method is basically utilized for the residual functions and the generalized Taylor expansion by selecting a proper initial guess approximation to introduce a suitable analytical solution.

The present analysis extends the application of the RKM and RPSM for finding approximate solutions of fractional obstacle system in the Caputo sense. The structure of the present article is organized as follows. In Sect. 2, some necessary definitions and mathematical preliminaries are introduced, including several reproducing-kernel spaces required in establishing the results of our analysis and the generalized Taylor’s expansion. In Sect. 3, short description of the RK and RPS techniques for solving fractional obstacle system (1.4) and (1.5) is given. In Sect. 4, numerical application is presented to show the capability and validity of the kernel method. This analysis ends with Sect. 5 with some conclusions.

2 Basic concepts and fundamentals

In this section, we have given some basic definitions and theorems regarding the reproducing-kernel spaces and the generalized power series representations. For more details about these definitions and properties, one can refer to [22,23,24,25,26,27]. Throughout the current paper, $L^{2} [ a,b ]$ stands for the set of all square integrable functions on $[ a,b ]$ while $AC [ a,b ]$ stands for the set of all absolutely continuous functions on $[ a,b ]$ such that $AC [ a,b ] = \{ u: [ a,b ]\rightarrow\mathbb{ R}: u\mbox{ is absolutely continuous on }[ a,b ] \}$.

Definition 2.1

For a universal set Λ, the function $\psi: \varLambda \times \varLambda\rightarrow \mathbb{R}$ is called a reproducing-kernel function to Hilbert space H if and only if

• (a) For each τ in Λ, we have $\psi ( {\cdot},\tau ) \in H$,

• (b) For each τ in Λ and any function ϕ in H, we have $\langle \phi ( {\cdot} ),\psi ( {\cdot},\tau ) \rangle_{H} =\phi ( \tau )$.

The last condition indicates that function’s value ϕ at any τ in Λis reproduced through the inner product for ϕ and $\psi ( {\cdot},\tau )$, where the function ψ is called the reproducing-kernel function of H that possesses some important properties such as being unique, conjugate symmetric and positive-definite.

Consequently, two RKHSs are introduced as follows.

Definition 2.2

The function space $\mathcal{W}_{1} [ a,b ]$ is given by

$$\mathcal{W}_{1} [ a,b ] = \bigl\{ u: [ a,b ]\rightarrow \mathbb{R}: u\in AC [ a,b ], \mbox{ and } u ' \in L^{2} [ a,b ] \bigr\} . $$

The inner product for $\varphi,\vartheta\in \mathcal{W}_{1} [ a,b ]$ is given by $\langle \varphi,\vartheta \rangle_{\mathcal{W}_{1}} = \int_{a}^{b} ( \varphi ' (\xi) \vartheta ' (\xi)+\varphi(\xi)\vartheta(\xi) ) \,d\xi$, and the norm of φ is $\Vert \varphi \Vert _{\mathcal{W}_{1}} = \sqrt{ \langle \varphi ( \xi ), \varphi (\xi) \rangle_{\mathcal{W}_{1}}}$.

Theorem 2.1

The reproducing-kernel function $\mathcal{T}_{x} ( {v} )$ of the complete Hilbert space $\mathcal{W}_{1} [ a, b ]$ can be obtained by

$$\mathcal{T}_{x} ( {v} ) = \frac{1}{2} \bigl( \sinh ( b-a ) \bigr)^{-1} \bigl( \cosh ( x +{v}- a-b ) + \cosh \bigl( \vert x -{v} \vert +a-b \bigr) \bigr). $$

Definition 2.3

The function space $\mathcal{W}_{2} [ a,b ]$ is defined by

$$\mathcal{W}_{2} [ a,b ] = \bigl\{ u: u ', u^{\prime\prime} \in AC [ a,b ], u'''\in L^{2} [a,b], u(a)=0,u(b)=0 \bigr\} . $$

An inner product for $\varphi,\vartheta\in \mathcal{W}_{2} [ a,b ]$ and the norm can be equipped, respectively, as follows:

$$\langle \varphi,\vartheta \rangle_{\mathcal{W}_{2}} = \varphi ' ( a ) \vartheta ' ( a ) + \int_{a}^{b} \varphi^{\prime\prime\prime} ( \xi ) \vartheta^{\prime\prime\prime} (\xi)\,d\xi, $$

and $\Vert \varphi \Vert _{\mathcal{W}_{2}} = \sqrt{ \langle \varphi ( \xi ), \varphi (\xi) \rangle_{\mathcal{W}_{2}}}$.

The unique representation to reproducing-kernel function $\mathcal{Q}_{x} ( {v} )$ within the space $\mathcal{W}_{2} [ a,b ]$ can be formulated as in the following theorem.

Theorem 2.2

The function $\mathcal{Q}_{x} ( {v} )$ is the reproducing kernel of the complete Hilbert space $\mathcal{W}_{2} [ a, b ]$ that can be written in the following form:

$$ \mathcal{Q}_{x} ( {v} ) = \textstyle\begin{cases} {h} ( x, {v} ),& {v} \leq x;\\ {h}( {v},x) &{v} >x, \end{cases} $$

(2.1)

where ${h} ( x, {v} )$ for ${v} \leq x$ is given by

$$\begin{aligned} {h} ( x, {v} ) ={}& \frac{1}{120 ( a-b )^{2}} ( a- {v} ) ( -4 a^{4} ( b-x ) ( b- {v} ) -6 b^{3} x^{2} {v} \\ &{} + a^{3} ( b-x ) ( b- {v} ) ( 6b+7x+3 {v} ) + x^{2} {v} \bigl( x^{3} + {v}^{3} -120 \bigr) \\ &{}-3 a^{2} ( b- {v} ) \bigl( x {v} ( {v} -3x ) +2 b^{2} ( 2x+ {v} ) -b \bigl( 4 x^{2} -x {v} + {v}^{2} \bigr) \bigr) \\ &{}-5bx \bigl( x^{3} {v} -24 {v} +x \bigl( {v}^{3} -24 \bigr) \bigr) \\ &{}+ b^{2} \bigl( 10 x^{3} {v} - {v}^{4} +5x \bigl( {v}^{3} -24 \bigr) \bigr) \\ &{}+a \bigl( 6 b^{3} x ( x+2 {v} ) - b^{2} \bigl( 10 x^{3} +12 x^{2} {v} +15x {v}^{2} + {v}^{3} -120 \bigr) \\ &{}+x \bigl( x {v}^{3} - x^{4} -2 {v} \bigl( -60+ {v}^{3} \bigr) \bigr) \\ &{}+b \bigl( 5 x^{4} +15 x^{2} {v}^{2} -120x+2 {v} \bigl( -60+ {v}^{3} \bigr) \bigr) \bigr) ). \end{aligned}$$

(2.2)

Proof

To construct $\mathcal{Q}_{x} ( {v} )$, let $u ( x ) \in \mathcal{W}_{2} [ a,b ]$. Then, $\langle u ( {v} ), \mathcal{Q}_{x} ( {v} ) \rangle_{\mathcal{W}_{2}} = u ' ( a ) \mathcal{Q}_{x} ' ( a ) + \int_{a}^{b} u^{\prime\prime\prime} ( \xi ) \mathcal{Q}_{x}^{\prime\prime\prime} ( \xi ) \,d\xi$. By doing integrations by parts for $\int_{a}^{b} u^{\prime\prime\prime} ( \xi ) \mathcal{Q}_{x}^{\prime\prime\prime} (\xi)\,d\xi$, we obtain $\langle u ( {v} ), \mathcal{Q}_{x} ( {v} ) \rangle_{\mathcal{W}_{2}} = u ' ( a ) [ \mathcal{Q}_{x} ' ( a ) + \mathcal{Q}_{x}^{(4)} ( a ) ] - u^{\prime\prime} ( a ) \mathcal{Q}_{x}^{ ( 3 )} (a)+ u^{\prime\prime} ( b ) \mathcal{Q}_{x}^{ ( 3 )} (b)- u ' ( b ) \mathcal{Q}_{x}^{ ( 4 )} (b)- \int_{a}^{b} u ( \xi ) \mathcal{Q}_{x}^{(6)} (\xi)\,d\xi$.

Since $\mathcal{Q}_{x} ( {v} )$ is reproducing-kernel function in $\mathcal{W}_{2} [ a,b ]$, $\mathcal{Q}_{x} ( {v} )$ should satisfy the homogeneous boundary conditions (1.5) as follows:

$$ \mathcal{Q}_{x} ( a ) = \mathcal{Q}_{x} ( b ) =0. $$

(2.3)

Also, if $\mathcal{Q}_{x} ( {v} )$ is the solution of the following generalized differential equation:

$$ \mathcal{Q}_{x}^{ ( 6 )} ( \xi ) =-\delta ( \xi -x ), $$

(2.4)

then the characteristic equation is $\lambda^{6} =0$ whose characteristic value is $\lambda=0$ with six multiple roots. Hence, the general solution of (2.4) at $\xi \neq x$ can be given by

$$ \mathcal{Q}_{x} ( {v} ) =\textstyle\begin{cases} \sum_{j=0}^{5} c_{j} (x) {v}^{j},& {v} \leq x;\\ \sum_{j=0}^{5} d_{j} (x) {v}^{j}, &{v} >x, \end{cases} $$

(2.5)

where the coefficients $c_{j} (x)$ and $d_{j} ( x )$ for $j=0,1,\dots,5$, can be determined by solving the following differential equations via Mathematica software package 7.0:

$$\begin{aligned} &\mathcal{Q}_{x} ' ( a ) + \mathcal{Q}_{x}^{ ( 4 )} ( a ) =0, \qquad \mathcal{Q}_{x}^{ ( 3 )} ( a ) =0,\qquad \mathcal{Q}_{x}^{ ( 3 )} ( b ) =0,\qquad \mathcal{Q}_{x}^{ ( 4 )} ( b ) =0, \end{aligned}$$

(2.6)

$$\begin{aligned} &\mathcal{Q}_{x}^{ ( k )} \bigl( {v}^{+} \bigr) = \mathcal{Q}_{x}^{ ( k )} \bigl( {v}^{-} \bigr),\quad k=0,1,\dots,4, \end{aligned}$$

(2.7)

$$\begin{aligned} & \mathcal{Q}_{x}^{ ( 5 )} \bigl( {v}^{+} \bigr) - \mathcal{Q}_{x}^{ ( 5 )} \bigl( {v}^{-} \bigr) =-1. \end{aligned}$$

(2.8)

 □

Definition 2.4

([35])

A power series (PS) expansion at $x= x_{0}$ of the following form:

$$\sum_{i=0}^{\infty} a_{i} (x- x_{0} )^{i\alpha} = a_{0} + a_{1} ( x- x_{0} )^{\alpha} + a_{1} ( x- x_{0} )^{2\alpha} +\cdots $$

for $n-1<\alpha\leq n$, $n\in \mathbb{N}$ and $x\leq x_{0}$, is called the fractional-power series (FPS).

Theorem 2.3

([35])

Suppose that $u(x)$ has a FPS representation at $x= x_{0}$ of the form

$$u ( x ) = \sum_{i=0}^{\infty} a_{i} ( x- x_{0} )^{i \alpha}. $$

If $u(x)\in C[ x_{0}, x_{0} +R)$, and $D^{i \alpha} u ( x ) \in C( x_{0}, x_{0} +R)$, for $i=0,1,2,\dots$, then coefficients $a_{i}$ will be in the form $a_{i} = \frac{\mathcal{D}_{0}^{i \alpha} u ( x_{0} )}{\varGamma ( n \alpha +1 )}$, where R is radius of convergence, and $\mathcal{D}^{i \alpha} = \mathcal{D}^{\alpha} {\cdot} \mathcal{D}^{\alpha} \cdots \mathcal{D}^{\alpha}$ (i-times).

3 The application of fractional RKM and RPSM

In this section, the iterative reproducing-kernel method will be executed to handle the fractional obstacle system in the complete Hilbert space $\mathcal{W}_{2} [ a,b ]$ and the procedure of the RPSM is presented. Meanwhile, description of the modified RKM, solution formula and error analysis are introducing in the same Hilbert space.

To illustrate the basic ideas of the RKM, consider the following linear differential operator $\mathcal{P}: \mathcal{W}_{2} [ a,b ] \rightarrow \mathcal{W}_{1} [ a,b ]$ such that $\mathcal{ P} u ( \xi ) = D_{a}^{2\alpha} u ( \xi )$ for each $\xi\in [ a,b ]$ and $u\in \mathcal{W}_{2} [ a,b ]$. Subsequently, obstacle BVPs (1.4) and (1.5) can be given equivalently by

$$\begin{aligned} \begin{aligned} &\mathcal{P} u ( x ) =\mathcal{S} \bigl( x,u ( x ) \bigr),\quad x\in [ a,b ], \\ &u ( a ) =u ( b ) =0, \end{aligned} \end{aligned}$$

(3.1)

after homogenizing the boundary conditions. In which, $\mathcal{S} ( x,u ( x ) ) = f ( x )$ for each $x\in [ a,c ] \cup[d,b]$ and $\mathcal{S} ( x,u ( x ) ) =g ( x ) u ( x ) +f ( x ) +r$ for each $x\in [ c,d ]$, and $\mathcal{S} ( x,u ( x ) ) \in \mathcal{W}_{1} [ a,b ]$. It turns out that the differential operator $\mathcal{P}$ is bounded, that is, $\Vert \mathcal{P} u \Vert _{\mathcal{W}_{1}} \leq c_{0} \Vert u \Vert _{\mathcal{W}_{2}}, c_{0} >0$.

For a countable dense $\{ x_{i} \}_{i=1}^{\infty}$ subset of the compact interval $[ a,b ]$, the characteristic orthogonal functions are constructed by letting ${w}_{i} ( x ) = \mathcal{T}_{x_{i}} ( x )$ and $\psi_{i} ( x ) = \mathcal{P}^{*} \varphi_{i} ( x )$, where $\mathcal{P}^{*}$ is the conjugate operator of $\mathcal{P}$, and $\psi_{i} ( x ) \in \mathcal{W}_{2} [ a, b ]$. Consequently, the characteristic orthonormal functions $\{ \overline{\psi}_{i} ( x ) \}_{i=1}^{\infty}$ of $\mathcal{W}_{2} [ a, b ]$ will be found by utilizing the modified Gram–Schmidt procedure to $\{ \psi_{i} ( x ) \}_{i=1}^{\infty}$ such that

$$ \overline{\psi}_{i} ( x ) = \sum_{k=1}^{i} \sigma_{ik} \psi_{k} ( x ) \quad ( i=1, 2, \dots ), $$

(3.2)

where the coefficients $\sigma_{ik}$ are given by

$$\begin{aligned} &\sigma_{11} = \frac{1}{ \Vert \psi_{1} \Vert }, \qquad \sigma_{ii} = \frac{1}{\sqrt{ \Vert \psi_{i} \Vert ^{2} - \sum_{n=1}^{i-1} ( \langle \psi_{i}, \overline{\psi}_{n} \rangle_{\mathcal{W}_{2}} )^{2}}}, \\ & \sigma_{ik} = \frac{- \sum_{k=n}^{i-1} \langle \psi_{i},\overline{\psi}_{n} \rangle_{\mathcal{W}_{2}} \sigma_{jk}}{\sqrt{ \Vert \psi_{i} \Vert ^{2} - \sum_{n=1}^{i-1} ( \langle \psi_{i}, \overline{\psi}_{n} \rangle_{\mathcal{W}_{2}} )^{2}}}. \end{aligned}$$

Theorem 3.1

Let $\{ x_{i} \}_{i=1}^{\infty}$ be a dense subset of $[ a, b ]$, then the system $\{ \overline{\psi}_{i} ( x ) \}_{i=1}^{\infty}$ will be a complete normal basis to $\mathcal{W}_{2} [ a, b ]$ with $\psi_{i} ( x ) = \mathcal{P}_{{v}} \mathcal{Q}_{x} ( {v} ) |_{{v}= x_{i}}$, where the subscript v by the operator $\mathcal{P}$ indicate that $\mathcal{P}$ employ directly to the function of v.

Proof

For fixed $u ( x )$ in $\mathcal{W}_{2} [ a, b ]$, it follows that $\langle u(x), \psi_{i} ( x ) \rangle =0,i\in \mathbb{N}$, which mean that $\langle u(x), \mathcal{P}^{*} {w}_{i} ( x ) \rangle_{\mathcal{W}_{2}} = \langle \mathcal{P} u(x), {w}_{i} ( x ) \rangle_{\mathcal{W}_{1}} = ( \mathcal{P} u ) ( x_{i} ) =0$. But$\{ x_{i} \}_{i=1}^{\infty}$ is dense on the compact interval $[ a, b ]$ that leads to $( \mathcal{P} u ) ( x ) =0$. Since $\mathcal{P}$ is invertible operator, $u ( x ) \equiv0$. Further and in terms of the reproducing property, it follows that $\psi_{i} ( x ) = ( \mathcal{P}^{*} {w}_{i} ) ( x ) = \langle \mathcal{P}^{*} {w}_{i} ( {v} ), \mathcal{Q}_{x} ( {v} ) \rangle_{\mathcal{W}_{2}} = \langle {w}_{i} ( {v} ), \mathcal{P}_{{v}} \mathcal{Q}_{x} ( {v} ) \rangle_{\mathcal{W}_{2}} = \mathcal{P}_{{v}} \mathcal{Q}_{x} ( {v)} |_{{v} = x_{i}}$. □

Theorem 3.2

Let $u ( x )$ be a unique solution of Eq. (3.1), then $u ( x )$ has the following form:

$$ u ( x ) = \sum_{i=1}^{\infty} \sum _{k=1}^{i} \sigma_{ik} \mathcal{ S}\bigl( x_{k}, u( x_{k} )\bigr) \overline{\psi_{i}} ( x ), $$

(3.3)

for a dense subset, $\{ x_{i} \}_{i=1}^{\infty}$, of $[ a, b ]$.

Proof

It is worth mentioning that $\{ \overline{\psi}_{i} ( x ) \}_{i=1}^{\infty}$ is complete normal set for $\mathcal{W}_{2} [ a, b ]$. So, the solution $u(x)$ will be written in terms of $\overline{\psi}_{i} ( x )$ by $u ( x ) = \sum_{i=1}^{\infty} \langle u ( x ), \overline{\psi}_{i} ( x ) \rangle \overline{\psi}_{i} ( x )$. Using the reproducing property $\langle u ( x ), {w}_{i} (x) \rangle = u_{i} (x)$ for each $u(x)\in \mathcal{W}_{2} [ a, b ]$, it follows that

$$\begin{aligned} u ( x ) &= \sum_{i=1}^{\infty} \sum _{k=1}^{i} \sigma_{ik} \bigl\langle u ( x ), \mathcal{P}^{*} {w}_{i} ( x ) \bigr\rangle \overline{\psi_{i}} ( x ) = \sum_{i=1}^{\infty} \sum_{k=1}^{i} \sigma_{ik} \bigl\langle \mathcal{P} u ( x ), {w}_{i} ( x ) \bigr\rangle \overline{\psi_{i}} ( x ) \\ &= \sum_{i=1}^{\infty} \sum_{k=1}^{i} \sigma_{ik} \bigl\langle \mathcal{S} \bigl( x_{k}, u( x_{k} )\bigr), {w}_{k} ( x ) \bigr\rangle \overline{\psi_{i}} ( x ) = \sum_{i=1}^{\infty} \sum _{k=1}^{i} \sigma_{ik} \mathcal{S} \bigl( x_{k}, u( x_{k} )\bigr) \overline{\psi_{i}} ( x ). \end{aligned}$$

A representation of the nth approximation $u_{n} (x)$ of $u ( x )$ can be obtained directly by truncating the series representation of Eq. (3.3) as follows:

$$ u_{n} ( x ) = \sum_{i=1}^{n} \sum _{k=1}^{i} \sigma_{ik} \mathcal{ S}\bigl( x_{k}, u( x_{k} )\bigr) \overline{ \psi_{i}} ( x ). $$

(3.4)

 □

Theorem 3.3

Let ${r}_{n} (x)$ be the actual error between the analytical, $u ( x )$, and the approximate, $u_{n} (x)$ solutions. Then, ${r}_{n} (x)$ be a monotonic decreasing function within $\Vert {\cdot} \Vert _{\mathcal{W}_{2}}$ and $\Vert {r}_{n} (x) \Vert _{\mathcal{W}_{2}}$ approaches 0.

Proof

From Theorem 3.2, the proof of monotone decreasing of ${r}_{n} (x)$ is straightforward as follows: $\Vert {r}_{n} (x) \Vert _{\mathcal{W}_{2}}^{2} = \Vert u ( x ) - u_{n} (x) \Vert _{\mathcal{W}_{2}}^{2} = \Vert \sum_{i=n+1}^{\infty} \sum_{k=1}^{i} \sigma_{ik} \mathcal{ S}( x_{k}, u( x_{k} )) \overline{\psi_{i}} ( x ) \Vert _{\mathcal{W}_{2}}^{2} = \sum_{i=n+1}^{\infty} ( \sum_{k=1}^{i} \sigma_{ik} \mathcal{ S}( x_{k}, u( x_{k} )) )^{2} = \sum_{i=n+1}^{\infty} \mathcal{E}_{i}^{2}, \mathcal{E}_{i} = \sum_{k=1}^{i} \sigma_{ik} \mathcal{ S}( x_{k}, u( x_{k} ))$.

Consequently, $\{ {r}_{n} (x) \}$ is monotone decreasing function in the space $\mathcal{W}_{2} [ a, b ]$. Also, since the series $\sum_{i=1}^{\infty} \mathcal{E}_{i} \overline{\psi}_{i} ( x )$ is convergent, then $\Vert {r}_{n} (x) \Vert _{\mathcal{W}_{2}} \rightarrow0$. □

Corollary 3.1

For $u ( x ) \in \mathcal{W}_{2} [ a, b ]$, the approximation $u_{n}^{ ( i )} ( x ),i=0,1,2$, are uniformly converging to analytic solution $u^{ ( i )} ( x ),i=0,1,2$, as soon as $n\rightarrow\infty$.

Proof

Let x lies in the compact interval [$a,b$], then

$$\begin{aligned} \bigl\vert u_{n}^{ ( i )} ( x ) - u^{ ( i )} ( x ) \bigr\vert & = \bigl\vert \bigl\langle u_{n} ( x ) -u ( x ), \mathcal{Q}_{x}^{(i)} ( x ) \bigr\rangle _{\mathcal{W}_{2}} \bigr\vert \\ &\leq \bigl\Vert \mathcal{Q}_{x}^{ ( i )} ( x ) \bigr\Vert _{\mathcal{W}_{2}} \bigl\Vert u_{n} ( x ) -u ( x ) \bigr\Vert _{\mathcal{W}_{2}} \\ &\leq \mathcal{M}_{i} \bigl\Vert u_{n} ( x ) -u ( x ) \bigr\Vert _{\mathcal{W}_{2}}, \quad\mathcal{M}_{i} >0, i=0,1,2. \end{aligned}$$

Hence, when as $\lim_{n\rightarrow\infty} \Vert u_{n} ( x ) -u ( x ) \Vert _{\mathcal{W}_{2}} =0$, the approximation $u_{n}^{ ( i )} ( x ), n=0,1,2$, will be converging to analytical solutions $u ( x )$ and its derivative, respectively, uniformly.

Now, to apply the fractional RPS technique, there are three cases to obtain the approximate solution, $u_{n} ( x )$, for the obstacle BVPs (1.4) and (1.5) depending on the corresponding intervals. These cases are as follows:

• Case one, the RPS solution, $u_{1} ( x )$, on $[ a,c ]$ can be presented as follows:

Let $D_{a}^{2\alpha} u_{1} (x) =f(x)$ on $[ a,c ]$ and let the solution, $u_{1} ( x )$, has the following FPS expansion about the initial point a:

$$ u_{1} ( x ) = \sum_{n =0}^{\infty} c_{n} ( x - a )^{n \alpha}, $$

(3.5)

and the kth truncated series

$$ u_{1, k} ( x ) = \sum_{n =0}^{k} c_{n} ( x - a )^{n\alpha}. $$

(3.6)

Here $u_{1} ( x )$ satisfies the initial condition $u_{1} ( a ) = \mu_{1} = c_{0}$. Thus, $u_{1,k} ( x )$ can be written as

$$ u_{1,k} ( x ) = \mu_{1} + c_{1} ( x - a )^{\alpha} + \sum_{n=2}^{k} c_{n} ( x - a )^{n \alpha}. $$

(3.7)

According to the RPS method, the kth-residual error function, $\operatorname{Res}_{u_{1}}^{k} ( x )$, can be defined by

$$ \operatorname{Res}_{u_{1}}^{k} ( x ) = D_{a}^{2\alpha} u_{1,k} ( x ) -f(x), $$

(3.8)

where the residual error function, $\operatorname{Res}_{u_{1}} ( x )$, can be given as follows:

$$\operatorname{Res}_{u_{1}} ( x ) = \lim_{k\rightarrow\infty} \operatorname{Res}_{u_{1}}^{k} ( x ). $$

Consequently, we need to minimize $\operatorname{Res}_{u_{1}}^{k} ( x )$ and utilize the relation $D_{a}^{(k-2)\alpha} \operatorname{Res}_{u_{1}}^{k} ( x ) |_{x=a} =0, k=2,3,\dots$, to determine the unknown coefficients $c_{n},n=2,3, \dots,k$, of Eq. (3.7). At this point, we note that the value of $c_{1} =A$ will be determined later by using the continuity conditions of Eq. (1.4).

However, to illustrate the main steps of the RPS algorithm in finding the unknown coefficients $c_{n},n=2,3, \dots,k$, let $k=2$ and substitute the approximation $u_{1,2} ( x ) = \mu_{1} +A ( x-a )^{\alpha} + {c}_{2} (x-a)^{2\alpha}$ into the kth-residual error function, $\operatorname{Res}_{u_{1}}^{2} ( x )$, such that

$$\begin{aligned} \operatorname{Res}_{u_{1}}^{2} ( x ) &= D_{a}^{2\alpha} u_{1,2} ( x ) -f ( x ) = D_{a}^{2\alpha} \bigl( \mu_{1} +A ( x-a )^{\alpha} + {c}_{2} ( x-a )^{2\alpha} \bigr) - f ( x ) \\ &= c_{2} \varGamma ( 2\alpha+1 ) -f ( x ), \end{aligned}$$

and then, by $D_{a}^{(k-2)\alpha} \operatorname{Res}_{u_{1}}^{k} ( x ) | _{x=a} =0, k=2$, we obtain $c_{2} \varGamma ( 2\alpha+1 ) -f ( a ) =0$, that is, $c_{2} = \frac{f ( a )}{\varGamma ( 2\alpha+1 )}$. Therefore, $u_{1,2} ( x ) = \mu_{1} +A ( x-a )^{\alpha} + \frac{f ( a )}{\varGamma ( 2\alpha+1 )} (x-a)^{2\alpha}$.

Likewise, to find the unknown coefficient $c_{3}$, substitute the third truncated series $u_{1,3} ( x ) = \mu_{1} +A ( x-a )^{\alpha} + \frac{f ( a )}{\varGamma ( 2\alpha+1 )} (x-a)^{2\alpha} + {c}_{3} (x-a)^{3\alpha}$ into $\operatorname{Res}_{u_{1}}^{3} ( x )$ such that

$$\begin{aligned} \operatorname{Res}_{u_{1}}^{3} ( x ) ={}& D_{a}^{2\alpha} u_{1,3} ( x ) -f ( x ) \\ ={}& D_{a}^{2\alpha} \biggl( \mu_{1} +A ( x-a )^{\alpha} + \frac{f ( a )}{\varGamma ( 2\alpha+1 )} (x-a)^{2\alpha} + {c}_{3} (x-a)^{3\alpha} \biggr) - f ( x ) \\ ={}&f ( a ) + c_{3} \frac{\varGamma ( 3\alpha+1 )}{\varGamma ( \alpha+1 )} ( x-a )^{\alpha} -f ( x ), \end{aligned}$$

and then, by using $D_{a}^{\alpha} \operatorname{Res}_{u_{1}}^{3} ( x ) | _{x=a} =0$, we obtain $c_{3} \varGamma ( 3\alpha+1 ) - D_{a}^{\alpha} f ( a ) =0$, that is, $c_{3} = \frac{D_{a}^{\alpha} f ( a )}{\varGamma ( 3\alpha+1 )}$. Therefore, $u_{1,3} ( x ) = \mu_{1} +A ( x-a )^{\alpha} + \frac{f ( a )}{\varGamma ( 2\alpha+1 )} (x-a)^{2\alpha} + \frac{D_{a}^{\alpha} f ( a )}{\varGamma ( 3\alpha+1 )} (x-a)^{3\alpha}$.

Now, to find the unknown coefficient $c_{4}$, substitute the fourth truncated series $u_{1,4} ( x ) = \mu_{1} +A ( x-a )^{\alpha} + \frac{f ( a )}{\varGamma ( 2\alpha+1 )} (x-a)^{2\alpha} + \frac{D_{a}^{\alpha} f ( a )}{\varGamma ( 3\alpha+1 )} (x-a)^{3\alpha} + {c}_{4} (x-a)^{4\alpha}$ into $\operatorname{Res}_{u_{1}}^{4} ( x )$ such that

$$\begin{aligned} \operatorname{Res}_{u_{1}}^{4} ( x ) = {}&D_{a}^{2\alpha} u_{1,4} ( x ) -f ( x ) \\ ={}& D_{a}^{2\alpha} \biggl( \mu_{1} +A ( x-a )^{\alpha} + \frac{f ( a )}{\varGamma ( 2\alpha+1 )} ( x-a )^{2\alpha} \\ &{}+ \frac{D_{a}^{\alpha} f ( a )}{\varGamma ( 3\alpha+1 )} ( x-a )^{3\alpha} + {c}_{4} ( x-a )^{4\alpha} \biggr) - f ( x ) \\ ={}&f ( a ) + \frac{D_{a}^{\alpha} f ( a )}{\varGamma ( \alpha+1 )} ( x-a )^{\alpha} + {c}_{4} \frac{\varGamma ( 4\alpha+1 )}{\varGamma ( 2\alpha+1 )} ( x-a )^{2\alpha} -f ( x ), \end{aligned}$$

and then, by using $D_{a}^{2\alpha} \operatorname{Res}_{u_{1}}^{4} ( x ) | _{x=a} =0$, we obtain $c_{4} \varGamma ( 4\alpha+1 ) - D_{a}^{2\alpha} f ( a ) =0$, that is, $c_{4} = \frac{D_{a}^{2\alpha} f ( a )}{\varGamma ( 4\alpha+1 )}$. Therefore, the fourth RPS-approximation is given by

$$ u_{1,4} ( x ) = \mu_{1} +A ( x-a )^{\alpha} + \sum _{n=2}^{4} \frac{D_{a}^{(n-2)\alpha} f ( a )}{\varGamma ( n\alpha+1 )} ( x - a )^{n \alpha}. $$

(3.9)

• Case two, the RPS solution, $u_{2} ( x )$, on $[ c,d ]$ can be presented as follows:

Let $D_{a}^{2\alpha} u_{2} (x) = g ( x ) u_{2} ( x ) +f ( x ) +r$ on $[ c,d ]$ and let the solution, $u_{2} ( x )$, has the kth truncated series expansion about the initial point c in the form

$$ u_{2,k} ( x ) = \sum_{n=0}^{k} c_{n} ( x - c )^{n \alpha}. $$

(3.10)

Here there is no condition at the initial point c. Then, $u_{2,k} ( x )$ can be written as

$$ u_{2,k} ( x ) = c_{0} + c_{1} ( x - c )^{\alpha} + \sum_{n=2}^{k} c_{n} ( x - c )^{n \alpha}. $$

(3.11)

According to the RPS method, the kth-residual error function, $\operatorname{Res}_{u_{2}}^{k} ( x )$, can be defined by

$$ \operatorname{Res}_{u_{2}}^{k} ( x ) = D_{a}^{2\alpha} u_{2,k} ( x ) - g ( x ) u_{2,k} ( x ) -f ( x ) -r. $$

(3.12)

Consequently, to obtain the unknown coefficients $c_{n},n=2,3, \dots,k$, of Eq. (3.11), we need to minimize $\operatorname{Res}_{u_{2}}^{k} ( x )$ and utilize the relation $D_{a}^{(k-2)\alpha} \operatorname{Res}_{u_{2}}^{k} ( x ) | _{x=c} =0, k=2,3,\dots$. In this point, the values of $c_{0} =B$ and $c_{1} =C$ will be determined later by using the continuity conditions of Eq. (1.4). Now, to apply the RPS algorithm in finding the coefficient $c_{2}$, substitute $u_{2,2} ( x ) = B +C ( x-c )^{\alpha} + c_{2} (x-c)^{2\alpha}$ into $\operatorname{Res}_{u_{2}}^{2} ( x )$ such that

$$\begin{aligned} \operatorname{Res}_{u_{2}}^{2} ( x ) = {}&D_{a}^{2\alpha} u_{2,2} ( x ) - g ( x ) u_{2,2} ( x ) -f ( x ) -r \\ ={}& D_{a}^{2\alpha} \bigl( B +C ( x-c )^{\alpha} + c_{2} (x-c)^{2\alpha} \bigr)\\ &{} - g ( x ) \bigl( B +C ( x-c )^{\alpha} + c_{2} (x-c)^{2\alpha} \bigr) -f ( x ) -r \\ ={}& b_{2} \varGamma ( 2\alpha+1 ) - g ( x ) \bigl( B +C ( x-c )^{\alpha} + c_{2} (x-c)^{2\alpha} \bigr) -f ( x ) -r, \end{aligned}$$

and then, by using $\operatorname{Res}_{u_{2}}^{2} ( x ) | _{x=c} =0$, we obtain $c_{2} \varGamma ( 2\alpha+1 ) - B g ( c ) -f ( c ) -r =0$, that is, $c_{2} = \frac{B g ( c ) +f ( c ) +r}{\varGamma ( 2\alpha+1 )}$. Therefore, the second approximation is

$$u_{2,2} ( x ) = B +C ( x-c )^{\alpha} + \frac{B g ( c ) +f ( c ) +r}{\varGamma ( 2\alpha+1 )} (x-c)^{2\alpha}. $$

Again, the third approximation has the form

$$u_{2,3} ( x ) = B +C ( x-c )^{\alpha} + \frac{B g ( c ) +f ( c ) +r}{\varGamma ( 2\alpha+1 )} (x-c)^{2\alpha} + c_{3} (x-c)^{3\alpha}. $$

Thus, to obtain the value of $c_{3}$, substitute $u_{2,3} ( x )$ into $\operatorname{Res}_{u_{2}}^{3} ( x )$ such that

$$\begin{aligned} \operatorname{Res}_{u_{2}}^{3} ( x ) ={}& D_{a}^{2\alpha} u_{2,3} ( x ) - g ( x ) u_{2,3} ( x ) -f ( x ) -r \\ ={}& D_{a}^{2\alpha} \biggl( B +C ( x-c )^{\alpha} + \frac{B g ( c ) +f ( c ) +r}{\varGamma ( 2\alpha+1 )} (x-c)^{2\alpha} + c_{3} (x-c)^{3\alpha} \biggr) \\ &{}- g ( x ) \biggl( B +C ( x-c )^{\alpha} + \frac{B g ( c ) +f ( c ) +r}{\varGamma ( 2\alpha+1 )} (x-c)^{2\alpha} + c_{3} (x-c)^{3\alpha} \biggr) -f ( x ) -r \\ ={}& \bigl( B g ( c ) +f ( c ) +r \bigr) + c_{3} \frac{\varGamma ( 3\alpha+1 )}{\varGamma ( \alpha+1 )} ( x-c )^{\alpha} \\ &{}- g ( x ) \biggl( B +C ( x-c )^{\alpha} + \frac{B g ( c ) +f ( c ) +r}{ \varGamma ( 2\alpha+1 )} (x-c)^{2\alpha} + c_{3} (x-c)^{3\alpha} \biggr) -f ( x ) -r, \end{aligned}$$

and then, by using $D_{a}^{\alpha} \operatorname{Res}_{u_{2}}^{3} ( x ) | _{x=c} =0$, we obtain $c_{3} \varGamma ( 3\alpha+1 ) -B D_{a}^{\alpha} g ( c ) -C D_{a}^{\alpha} ( g ( x ) ( x-c )^{\alpha} ) | _{x=c} - \frac{B g ( c ) +f ( c ) +r}{\varGamma ( 2\alpha+1 )} D_{a}^{\alpha} ( g ( x ) ( x-c )^{2\alpha} ) | _{x=c} - c_{3} D_{a}^{\alpha} ( g ( x ) ( x-c )^{3\alpha} ) | _{x=c} - D_{a}^{\alpha} f ( c ) =0$, that is, $c_{3} = \frac{\psi ( c )}{\varGamma ( 3\alpha+1 )}$, $\psi ( c ) =B D_{a}^{\alpha} g ( c ) +C D_{a}^{\alpha} ( g ( x ) ( x-c )^{\alpha} ) | _{x=c} + D_{a}^{\alpha} f ( c )$. Therefore, $u_{2,3} ( x ) = B +C ( x-c )^{\alpha} + \frac{B g ( c ) +f ( c ) +r}{\varGamma ( 2\alpha+1 )} (x-c)^{2\alpha} + \frac{\psi ( c )}{\varGamma ( 3\alpha+1 )} (x-c)^{3\alpha}$. Similarly, the fourth approximation $u_{2,4} ( x )$ can be obtained.

• Case three, the RPS solution, $u_{3} ( x )$, on $[ d,b ]$ can be presented as follows:

Let $D_{a}^{2\alpha} u_{3} (x) = f ( x )$ on $[ c,d ]$ and let the solution, $u_{3} ( x )$, have the kth truncated series expansion at b in the form

$$ u_{3,k} ( x ) = \sum_{n=0}^{k} c_{n} ( x - b )^{n \alpha}. $$

(3.13)

Here $u_{3} ( x )$ satisfies the condition $u_{3} ( b ) = \mu_{2} = a_{0}$. Thus, $u_{3,k} ( x )$ can be written as

$$ u_{3,k} ( x ) = \mu_{2} + c_{1} ( x - b )^{\alpha} + \sum_{n=2}^{k} c_{n} ( x - b )^{n \alpha}. $$

(3.14)

According to the RPS method, the kth-residual error function, $\operatorname{Res}_{u_{3}}^{k} ( x )$, can be defined by

$$ \operatorname{Res}_{u_{3}}^{k} ( x ) = D_{a}^{2\alpha} u_{3,k} ( x ) -f ( x ). $$

(3.15)

However, to obtain the unknown coefficients $c_{n},n=2,3, \dots,k$, of Eq. (3.14), we need to minimize $\operatorname{Res}_{u_{3}}^{k} ( x )$ and utilize the relation $D_{a}^{(k-2)\alpha} \operatorname{Res}_{u_{3}}^{k} ( x ) | _{x=b} =0, k=2,3,\dots$. At this point we note the value of $c_{1} =D$ will be determined later by using the continuity conditions of Eq. (1.4). Thus, to apply the FRPS algorithm in finding the coefficients $a_{2}$, substitute $u_{3,2} ( x ) = \mu_{2} + D ( x - b )^{\alpha} + c_{2} (x-b)^{2\alpha}$ into $\operatorname{Res}_{u_{3}}^{2} ( x )$ such that

$$\begin{aligned} \operatorname{Res}_{u_{3}}^{2} ( x ) &= D_{a}^{2\alpha} u_{3,2} ( x ) -f ( x ) = D_{a}^{2\alpha} \bigl( \mu_{2} + D ( x - b )^{\alpha} + c_{2} (x-b)^{2\alpha} \bigr) -f ( x ) \\ &= c_{2} \varGamma ( 2\alpha+1 ) -f ( x ), \end{aligned}$$

and then, by using $\operatorname{Res}_{u_{3}}^{2} ( x ) | _{x=b} =0$, we obtain $c_{2} \varGamma ( 2\alpha+1 ) -f ( b ) =0$, that is, $c_{2} = \frac{f ( b )}{\varGamma ( 2\alpha+1 )}$. Therefore, the second approximation is

$$u_{3,2} ( x ) = \mu_{2} +D ( x-b )^{\alpha} + \frac{f ( b )}{\varGamma ( 2\alpha+1 )} (x-b)^{2\alpha}. $$

In the same manner, substitute the third truncated series $u_{3,3} ( x ) = \mu_{2} +D ( x-b )^{\alpha} + \frac{f ( b )}{\varGamma ( 2\alpha+1 )} (x-b)^{2\alpha} + c_{3} (x-b)^{3\alpha}$ into $\operatorname{Res}_{u_{3}}^{3} ( x )$ such that

$$\begin{aligned} \operatorname{Res}_{u_{3}}^{3} ( x ) ={}& D_{a}^{2\alpha} u_{1,3} ( x ) -f ( x ) \\ ={}& D_{a}^{2\alpha} \biggl( \mu_{2} +D ( x-b )^{\alpha} + \frac{f ( b )}{\varGamma ( 2\alpha+1 )} (x-b)^{2\alpha} + c_{3} (x-b)^{3\alpha} \biggr) - f ( x ) \\ ={}&f ( b ) + c_{3} \frac{\varGamma ( 3\alpha+1 )}{ \varGamma ( \alpha+1 )} ( x-b )^{\alpha} -f ( x ), \end{aligned}$$

and then, by using $D_{a}^{\alpha} \operatorname{Res}_{u_{3}}^{3} ( x ) | _{x=b} =0$, we obtain $c_{3} \varGamma ( 3\alpha+1 ) - D_{a}^{\alpha} f ( b ) =0$, that is, $c_{3} = \frac{D_{a}^{\alpha} f ( b )}{\varGamma ( 3\alpha+1 )}$. Therefore, $u_{3,3} ( x ) = \mu_{2} +D ( x-b )^{\alpha} + \frac{f ( b )}{\varGamma ( 2\alpha+1 )} (x-b)^{2\alpha} + \frac{D_{a}^{\alpha} f ( b )}{\varGamma ( 3\alpha+1 )} (x-b)^{3\alpha}$. Hence, the fourth RPS-approximation on [$d,b$] is given by

$$ u_{3,4} ( x ) = \mu_{2} +D ( x-b )^{\alpha} + \sum _{n=2}^{4} \frac{D_{a}^{(n-2)\alpha} f ( b )}{\varGamma ( n\alpha+1 )} ( x - b )^{n \alpha}. $$

(3.16)

Moreover, the same routine can be repeated until an arbitrary order k, so the unknown coefficients $c_{n},n=4,5,6,\dots,k$, can be obtained. Furthermore, the values of the parameters $A,B,C$, and D can be found by utilizing the continuity conditions of Eq. (1.4) and solving the obtained system of algebraic equations,

$$ \begin{aligned} &u_{1,k} ( c ) = u_{2,k} ( c ),\qquad u_{2,k} ( d ) = u_{3,k} ( d ), \\ & D_{a}^{\alpha} u_{1,k} ( c ) = D_{a}^{\alpha} u_{2,k} ( c ),\qquad D_{a}^{\alpha} u_{2,k} ( d ) = D_{a}^{\alpha} u_{3,k} ( d ). \end{aligned}$$

(3.17)

Therefore, the kth approximate solution on [$a,b$] can be finally given by

$$ u_{k} ( x ) = \textstyle\begin{cases} u_{1,k} ( x ),& a\leq x\leq c,\\ u_{2,k} ( x ), &c\leq x\leq d,\\ u_{3,k} ( x ),& d\leq x\leq b. \end{cases} $$

(3.18)

Hence, the kth RPS-approximate solution is completely constructed for the BVPs (1.4) and (1.5). □

4 Numerical outcomes

To test simplicity, applicability and accuracy of the proposed RK and RPS algorithms, the numerical experiment is presented in this section. The methodology is directly employed without using discretization, transformation, and restrictive assumptions. The appropriateness and effectiveness of the proposed methods are evident when we compare it with each other for different values of α. Numerical comparison between the RKM, RPSM and other well-known methods are also presented for $\alpha=1$. The motivation of the current section is to obtain the RK-solution and RPS-solution for the obstacle BVP (1.4) and (1.5).

Consider the integer-order obstacle BVP in normal form [36]

$$ \begin{aligned} &{-} u^{\prime\prime} ( x ) \geq f ( x ),\qquad u ( x ) \geq\psi ( x ),\\ & \bigl[ u^{\prime\prime} ( x ) +f ( x ) \bigr] \bigl[ u ( x ) -\psi ( x ) \bigr] =0,\quad x\in [ a,b ],\\ & u ( a ) =u ( b ) =0, \end{aligned}$$

(4.1)

where $f ( x )$ is an analytical function, $\psi ( x )$ is an obstacle term, and $u ( x )$ is an unknown function, which can be converted to the following equivalent form:

$$ u''(x)= \textstyle\begin{cases} f(x),& x\in [ a,c ],\\ u ( x ) +f(x)-1,& x\in [ c,d ],\\ f(x),& x\in [ d,b ], \end{cases} $$

(4.2)

subject to the BCs $u ( a ) =u ( b ) =0$, by setting $a=0,c=(3a+b)/4,d=(a+3b)/4$, and $b=\pi$, in which $u ( x )$ and $u' ( x )$ are continuous at the internal points $x= \frac{3a+b}{ 4}$ and $x= \frac{a+3b}{4}$.

Without loss of generality, we consider the following fractional obstacle BVP to develop the approximate solution of the obstacle BVP (4.2) by utilizing the Caputo-fractional operator $D_{a}^{2\alpha}$ with $\alpha\in ( 0,1 ]$:

$$\begin{aligned} \begin{aligned} &\bigl( D_{a}^{2\alpha} u\bigr) ( x ) = \textstyle\begin{cases} 0,& x\in [ 0, \frac{\pi}{4} ],\\ u ( x ) -1,& x\in [ \frac{\pi}{4}, \frac{3\pi}{4} ],\\ 0,& x\in [ \frac{3\pi}{4}, \pi ], \end{cases}\displaystyle \\ & u ( 0 ) =u ( \pi ) =0. \end{aligned} \end{aligned}$$

(4.3)

The exact solution when $\alpha=1$ is given by

$$u ( x ) = \textstyle\begin{cases} \frac{4x}{\pi+4 \coth ( \frac{\pi}{4} )},& x\in [ 0, \frac{\pi}{4} ],\\ 1- \frac{4 \cosh ( \frac{\pi}{2} -x )}{\pi \sinh ( \frac{\pi}{4} ) +4 \cosh ( \frac{\pi}{4} )},& x\in [ \frac{\pi}{4}, \frac{3\pi}{4} ],\\ \frac{4(\pi-x)}{\pi+4 \coth ( \frac{\pi}{4} )},& x\in [ \frac{3\pi}{4}, \pi ]. \end{cases} $$

To achieve our goal by using the RKM, divide the interval [$0, \pi$] into n equal subintervals utilizing the standard grid points $x_{i} =ih,i=0,1,\dots,n, x_{0} =0, x_{n} =\pi$, and the step size $h=\pi/n$, $n \in \mathbb{N}$. Using the RK algorithm, a numerical comparison of the obtained results with the exact solution to some selected grid points for $n = 10$, $h=\pi/10$ and the fractional order $\alpha=1$ are shown in Table 1. Meanwhile Table 2 is allocated for maximum absolute errors associated with $u'_{n} (x)$ for different values of n using the RKM.

Table 1 Numerical results of BVP (4.3) at $\alpha=1$ using RKM

Table 2 The maximum absolute error $| u' ( x_{i} ) - u '_{n} ( x_{i} ) |$ at $\alpha=1$ using RKM

To show the powerful features of the proposed methods, numerical comparison between our computed results with variety values of h and the corresponding experimental results obtained by the methods presented in [4,5,6,7,8,9,10,11] is given in Table 3. Anyway, numerical results at some values of the fractional order α such that $\alpha\in\{1,0.8,0.6\}$ are also given in Table 4 to justify the advantages of the proposed methods.

Table 3 Numerical comparison via maximum absolute error at $\alpha=2$

Table 4 Numerical results of BVP (4.3) for different values of α

Figure 1 shows the relevant behavior of the RK approximate solution for $\alpha=1$ over the interval [$0, \pi$]. On the other hand, the maximum absolute errors are presented in Fig. 2, while the approximate solutions $u_{n} (x)$ of BVP (4.3) at different values of the fractional order α with $\alpha=1,\alpha=0.8$ and $\alpha=0.6$ over the interval [$0, \pi$] are shown in Fig. 3. These figures clearly indicate the convergence of approximate solutions to the exact solution. All necessary computations and graphical analyses were carried out by using Mathematica 10.

Figure 1

The RK approximate solutions of BVP (4.3) at $\alpha=1$

Figure 2

Absolute errors of the obstacle BVP (4.3) at $\alpha=1$

Figure 3

The RKHS solutions of BVP (4.3) for different values of α

5 Conclusion

The main goal of this analysis is to implement reliable numeric-analytic techniques that depend on the use of reproducing-kernel theory and the generalized Taylor expansion for the solution of BVPs of fractional order associated with obstacle in the Caputo sense. This goal has been achieved by improving the RK and RPS algorithms to handle such class of obstacle problems. A numerical investigation has been presented to demonstrate the approximate solution of a well-known example in the literature. The solution behavior of approximation of some values of the fractional order α is shown quantitatively and graphically. Anyway, results acquired explicitly show the full reliability and regularity of the proposed methods. The applications of BVPs fractional order with the Riesz derivative, which is a two-sided space-fractional derivative, should be investigated for future work.