1 Introduction

In recent decades, it was acknowledged that fractional operators are appropriate tools for differentiation as compared to the local differentiation particularly in physical real word problems. These fractional operators can be constructed by the convolutions of the local derivative as the kernel of fractional operators; various kernels for fractional operators have been suggested in the literature but the most common is the power law kernel (\(x^{ - \alpha} \)), which is used in the construction of Riemann–Liouville and Caputo fractional operators (see [1], p. 65–106). However, the exponential decay law \(\exp ( - \alpha x )\) was used by Caputo and Fabrizio (see [2], p. 1–13). Atangana and Baleanu developed fractional operators in the Caputo and Riemann–Liouville sense using the generalized Mittag–Leffler law \(E_{\alpha} ( - \phi x^{\alpha} )\) as a kernel (see [3], p. 763–769). All these fractional operators have some shortcomings and challenges but at the same time this area is growing fast, and researchers devoted their attention to this field (see [4,5,6,7,8,9,10] and the references therein).

It is important to mention here that fractional order calculus has many applications in almost every field of science and technology which includes diffusion, relaxation process, control, electrochemistry and viscoelasticity (see [11], p. 79–85). Zafar and Fetecau ([12], p. 2789–2769) applied Caputo–Fabrizio fractional derivative to the flow of Newtonian viscous fluid flowing over the infinite vertical plate. Markis et al. ([13], p. 1663–1679) analyzed the flow of a fractional Maxwell’s fluid. According to their report, the fractional results showed excellent agreement with experimental work by adjusting the fractional parameter. Alkahtani and Atangana ([14], p. 106–113) used different fractional operators to analyze the memory effect in a potential energy field caused by a charge. They presented some novel numerical approaches to the solutions of a fractional system of equations. Vieru et al. ([15], p. 85–96) presented exact solutions for the time-fraction model of viscous fluid flow near a vertical plate taking into consideration mass diffusion and Newtonian heating. Abro et al. ([16], p. 1–10) presented exact analytical solutions for the flow of an Oldroyd-B fluid in a horizontal circular pipe. Jain ([17], p. 1–11) introduced a novel and powerful numerical scheme and implemented to different fractional order differential equations. Some other interesting and significant studies on fractional derivatives can be found in [18,19,20,21,22,23,24,25,26] and the references therein.

The nanofluid is an innovation of nanotechnology to overcome the problems of heat transport in many engineering and industrial sectors. A detailed discussion on nanofluids with a list of applications is reported by Wang et al. ([27], p. 1–19) in a review paper. Sheikholeslam et al. ([28], p. 71–82) numerically studied the shape effect and the external magnetic field effect on the \(F_{3}O_{4} - H_{2}0\) nanofluid inside a porous enclosure. Hassanan et al. ([29], p. 482–488) developed exact solutions for nanofluids with different nanoparticles for the unsteady flow of a micropolar fluid. The literature of nanofluids has exponentially increased and has reached a next level by introducing hybrid nanofluids which are the suspensions of two or more types of nanoparticles in the composite form with low concentration. Hybrid nanofluids are introduced to overcome the drawbacks of single nanoparticle suspensions and connect the synergetic effect of nanoparticles. The hybrid nanofluid is branded to further improve the thermal conductivity and heat transport, which leads to industrial and engineering applications with low cost (see [30], p. 262–273). Hussain et al. ([31], p. 1054–1066) carried out an entropy generation analysis on a hybrid nanofluid in a cavity. Farooq et al. ([32], p. 1–14) presented a numerical study on hybrid nanofluids keeping into consideration suction/injection, entropy generation, and viscous dissipation.

In the existing literature, experimental, theoretical and numerical studies on hybrid nanofluids are very limited. A study of a hybrid nanofluid fluid with exact solutions and the Caputo fractional derivative even does not exist. So, there is an urgent need to contribute to the literature of hybrid nanofluids using the application of fractional differential equations. Motivated by the above discussion, the present study focused on the heat transfer in hybrid nanofluid in two vertical parallel plates using fractional derivative approach. A water-based hybrid nanofluid is characterized here with composite hybrid nanoparticles of cupper (Cu) and alumina (\(Al_{2}O_{3}\)). The fractional Brinkman type fluid model with physical initial and boundary conditions is considered for the flow phenomena. The Laplace transform technique is used to obtain exact analytical solutions for the velocity and temperature profiles. Using the properties of the Caputo–Fabrizio fractional derivative the obtained solutions are reduced to the classical form for \(\alpha = 1\) and \(\beta = 1\). To explore the physical aspect of the flow parameters the solutions are numerically computed and plotted in different graphs with a physical explanation.

2 Problem’s description

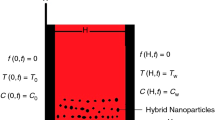
Let us consider the unsteady free convection flow of a generalized incompressible hybrid nanofluid in two infinite vertical parallel plates at a distance d. The plates are taken along the x-axis and the y-axis is chosen normal to it. At \(t \le 0\), the plates and fluid are at rest with ambient temperature \(T_{0}\). After \(t = 0^{ +} \), the temperature of the plate at \(y = d\) rises or lowers from \(T_{0}\) to \(T_{W}\) due to which the free convection takes place. At this moment, the fluid starts motion in the x− direction due to the temperature gradient which gives rise to the buoyancy forces. The Brinkman type fluid model is utilized to describe flow phenomena of the hybrid nanofluid. Under the assumptions of ([33], p. 1472–1488) the governing equations of the \(Cu - Al_{2}O_{3} - H_{2}O\) hybrid nanofluid are given by

$$\begin{aligned} &\rho_{hnf} \biggl( \frac{\partial u ( y,t )}{\partial t} + \beta_{b}^{*}u ( y,t ) \biggr) = \mu_{hnf}\frac{\partial^{2}u ( y,t )}{\partial y^{2}} + g ( \rho \beta_{T} )_{hnf} \bigl( T ( y,t ) - T_{0} \bigr), \end{aligned}$$
(1)
$$\begin{aligned} & ( \rho Cp )_{hnf}\frac{\partial T ( y,t )}{\partial t} = k_{hnf} \frac{\partial^{2}T ( y,t )}{\partial y^{2}} + Q_{0} ( T - T_{0} ), \end{aligned}$$
(2)

together with the following appropriate initial and boundary conditions:

$$\begin{aligned} &u ( y,0 ) = 0, \qquad T ( y,0 ) = T_{0}, \quad\forall y \ge 0, \end{aligned}$$
(3)
$$\begin{aligned} &\left . \textstyle\begin{array}{l} u ( 0,t ) = 0,\qquad T ( 0,t ) = T_{0}\quad \mbox{for } t > 0 \\ u ( d,t ) = 0, \qquad T ( d,t ) = T_{W}\quad \mbox{for } t > 0 \end{array}\displaystyle \right \}, \end{aligned}$$
(4)

where \(\rho_{hnf}\) is the density, \(u ( y,t )\) is the velocity, \(\beta_{b}^{*}\) is the Brinkmann parameter, \(\mu_{hnf}\) is the dynamic viscosity, \(\beta_{hnf}\) is the volumetric thermal expansion, \(( C_{p} )_{hnf}\) is the specific heat, \(T ( y,t )\) is the temperature, \(k_{hnf}\) is the thermal conductivity and \(Q_{0}\) is the heat generation of the hybrid nanofluid.

3 Thermophysical properties of hybrid nanofluid

This section demonstrates the modification of thermophysical properties of a conventional nanofluid and a hybrid nanofluid \(Cu - Al_{2}O_{3} - H_{2}O\) in a spherical shape.

3.1 The effective density

The effective density \(\rho_{nf}\) of conventional nanofluid is defined by Aminossadati and Ghasemi (see [34], p. 630–640) and can be expressed as

$$ \rho_{nf} = ( 1 - \phi )\rho_{f} + \phi \rho_{s}, $$
(5)

where ϕ is the volume concentration of the nanoparticles, \(\rho_{f}\) and \(\rho_{s}\) are the densities of the base fluid and solid particles respectively. The mathematical expression for the effective density of the hybrid nanofluid can be obtained by modifying Eq. (5) (see [31], p. 1054–1066):

$$ \rho_{hnf} = ( 1 - \phi_{hnf} )\rho_{f} + \phi_{Al_{2}O_{3}}\rho_{Al_{2}O_{3}} + \phi_{Cu}\rho_{Cu}, $$
(6)

where \(\rho_{hnf}\) is the density of the hybrid nanofluid, \(\phi_{hnf}\) is the volume concentration of solid particles such that \(\phi_{hnf} = \phi_{Al_{2}O_{3}} + \phi_{Cu}\), \(\rho_{f}\) is the density of the base fluid, \(\phi_{Al_{2}O_{3}}\) is the volume concentration of alumina, \(\rho_{Al_{2}O_{2}}\) is the density of alumina, \(\phi_{Cu}\) is the volume concentration of cupper and \(\rho_{Cu}\) is the density of cupper.

3.2 The effective dynamic viscosity

The dynamics viscosity \(\mu_{nf}\) of an ordinary nanofluid is expressed by Brinkman (see [35], p. 571) by

$$ \mu_{nf} = \frac{\mu_{f}}{ ( 1 - \phi )^{2.5}}, $$
(7)

which leads to the following modified form for a hybrid nanofluid:

$$ \mu_{hnf} = \frac{\mu_{f}}{ \{ 1 - ( \phi_{Al_{2}O_{3}} + \phi_{Cu} ) \}^{2.5}}. $$
(8)

3.3 The effective volumetric thermal expansion and heat capacitance

The thermal expansion and heat capacitance are, respectively, defined by Bourantas and Loukopoulos (see [36], p. 35–41) in the form

$$\begin{aligned} & ( \beta_{T}\rho )_{nf} = ( 1 - \phi ) ( \beta_{T}\rho )_{f} + \phi ( \beta_{T}\rho )_{s}, \end{aligned}$$
(9)
$$\begin{aligned} & ( \rho C_{p} )_{nf} = ( 1 - \phi ) ( \rho C_{p} )_{f} + \phi ( \rho C_{p} )_{s}, \end{aligned}$$
(10)

with the following altered form for a hybrid nanofluid:

$$\begin{aligned} & ( \rho \beta_{T} )_{hnf} = ( 1 - \phi_{hnf} ) ( \rho \beta_{T} )_{f} + \phi_{Al_{2}O_{3}} ( \rho \beta_{t} )_{Al_{2}O_{3}} + \phi_{Cu} ( \rho \beta_{T} )_{Cu}, \end{aligned}$$
(11)
$$\begin{aligned} & ( \rho Cp )_{hnf} = ( 1 - \phi_{hnf} ) ( \rho Cp )_{f} + \phi_{Al_{2}O_{3}} ( \rho Cp )_{Al_{2}O_{3}} + \phi_{Cu} ( \rho Cp )_{Cu}. \end{aligned}$$
(12)

3.4 The effective thermal conductivity

The effective thermal conductivity for a conventional nanofluid is based on Maxwell’s model (see [37], p. 87–92), which is defined by

$$ \frac{K_{nf}}{K_{f}} = \frac{k_{s} + 2k_{f} - 2\phi ( k_{s} - k_{f} )}{k_{s} + 2k_{f} + 2\phi ( k_{s} - k_{f} )}, $$
(13)

where \(K_{nf}\) is the thermal conductivity of the nanofluid, \(K_{s}\) is the thermal conductivity of solid nanometer-sized particles and \(K_{f}\) is the thermal conductivity of the base fluid. For the hybrid nanofluid, Maxwell’s model can be modified:

$$ \frac{k_{hnf}}{k_{f}} = \frac{\frac{\phi_{Al_{2}O_{3}}k_{Al_{2}O_{3}} + \phi_{Cu}k_{{Cu}}}{\phi_{hnf}} + 2k_{f} + 2 ( \phi_{Al_{2}O_{3}}k_{Al_{2}O_{3}} + \phi_{{Cu}}k_{{Cu}} ) - 2k_{f}\phi_{hnf}}{\frac{\phi_{Al_{2}O_{3}}k_{Al_{2}O_{3}} + \phi_{{Cu}}k_{{Cu}}}{\phi_{hnf}} + 2k_{f} - ( \phi_{Al_{2}O_{3}}k_{Al_{2}O_{3}} + \phi_{{Cu}}k_{{Cu}} ) - 2k_{f}\phi_{hnf}}. $$
(14)

It is important to highlight here that by making \(\phi_{Al_{2}O_{3}} = 0\) or \(\phi_{Cu} = 0\) the effective thermophysical properties of the hybrid nanofluid presented in Eqs. (8), (11), (12) and (14) can be reduced to the effective thermophysical properties of a conventional nanofluid presented in Eqs. (7), (9), (10) and (13), respectively. Furthermore, the typo mistake made in [31], p. 1054–1066) and [32], p. 1–14 has been corrected here in the expression of the thermal conductivity for the hybrid nanofluid. The numerical values of the base fluid and nanoparticles are given in Table 1.

Table 1 Numerical values of thermophysical properties of base fluid and nanoparticles
Full size table

4 Generalization of local model

In this section, the dimensional system is first transformed to dimensionless form using non-similarity variables to reduce the number of variables and get rid of units. The dimensionless system is then artificially converted to time-fractional form or generalized form using the Caputo–Fabrizio fractional operator (see [2], p. 1–13). It is worth to mention here that the fractional models are more general and convenient in the description of flow behavior and memory effect. Moreover, the results obtained from the fractional model are additionally realistic because by adjusting the fractional parameter the obtained results can be compared with experimental data to reach excellent agreement as obtained by Markis et al. (see [13], p. 1663–1679). Now introducing the following non-similarity dimensionless variables:

$$v = \frac{d}{\nu_{f}}u,\qquad \xi = \frac{y}{d}, \qquad \tau = \frac{\nu_{f}}{d^{2}}t,\qquad \theta = \frac{T - T_{0}}{T_{W} - T_{0}}, $$

into Eqs. (1)–(4) yields the following:

$$\begin{aligned} &a_{0} \biggl( \frac{\partial v ( \xi,\tau )}{\partial \tau} + \beta_{b}v ( \xi,\tau ) \biggr) = a_{1}\frac{\partial^{2}v ( \xi,\tau )}{\partial \xi^{2}} + a_{2}\operatorname{Gr}\theta ( \xi, \tau ), \end{aligned}$$
(15)
$$\begin{aligned} &a_{3}\Pr \frac{\partial \theta ( \xi,\tau )}{\partial \tau} = \lambda_{hnf} \frac{\partial^{2}\theta ( \xi,\tau )}{\partial \xi^{2}} + Q\theta ( \xi,\tau ), \end{aligned}$$
(16)
$$\begin{aligned} &v ( \xi,0 ) = 0,\qquad \theta ( \xi,0 ) = 0,\quad \forall \xi \ge 0, \end{aligned}$$
(17)
$$\begin{aligned} & \left . \textstyle\begin{array}{l} v ( 0,\tau ) = 0,\qquad \theta ( 0,\tau ) = 0\quad\mbox{for } \tau > 0 \\ v ( 1,\tau ) = 0, \qquad\theta ( 1,\tau ) = 1\quad \mbox{for } t > 0 \end{array}\displaystyle \right \}, \end{aligned}$$
(18)

where

$$\begin{aligned} &\beta_{b} = \frac{d^{2}\beta_{b}^{*}}{\nu_{f}^{2}},\qquad \operatorname{Gr} = \frac{d^{3}g ( \beta_{T} )_{f}}{\nu_{f}^{2}} ( T_{W} - T_{0} ),\qquad \Pr = \frac{ ( \mu C_{p} )_{f}}{k_{f}},\\ &Q = \frac{d^{2}Q_{0}}{k_{f}},\qquad \lambda_{hnf} = \frac{k_{hnf}}{k_{f}},\qquad a_{0} = ( 1 - \phi ) + \frac{\phi_{Al_{2}O_{3}}\rho_{Al_{2}O_{3}} + \phi_{Cu}\rho_{Cu}}{\rho_{f}},\\ & a_{1} = \frac{1}{ \{ 1 - ( \phi_{Al_{2}O_{3}} + \phi_{Cu} ) \}^{2.5}}\qquad a_{2} = ( 1 - \phi ) + \frac{\phi_{Al_{2}O_{3}} ( \rho \beta_{t} )_{Al_{2}O_{3}} + \phi_{Cu} ( \rho \beta_{T} )_{Cu}}{ ( \rho \beta_{T} )_{f}},\\ & a_{3} = ( 1 - \phi ) + \frac{\phi_{Al_{2}O_{3}} ( \rho Cp )_{Al_{2}O_{3}} + \phi_{Cu} ( \rho Cp )_{Cu}}{ ( \rho Cp )_{f}}, \end{aligned}$$

is the dimensionless Brinkman type fluid parameter, the thermal Grashof number, the Prandtl number and heat generation parameter, respectively. Here \(\lambda_{hnf}, a_{0}, a_{1}, a_{2} \mbox{ and } a_{3}\) are the constant terms produced during the calculation. The time-fractional form of Eqs. (15) and (16) in terms of Caputo–Fabrizio fractional operator is given by

$$\begin{aligned} &\frac{a_{0}}{a_{1}}{}^{CF}D_{\tau}^{\alpha} v ( \xi,\tau ) + \frac{a_{0}}{a_{1}}\beta_{b}v ( \xi,\tau ) = \frac{\partial^{2}v ( \xi,\tau )}{\partial \xi^{2}} + \frac{a_{2}}{a_{1}}\operatorname{Gr}\theta ( \xi,\tau ), \end{aligned}$$
(19)
$$\begin{aligned} &a_{3}\Pr{}^{CF}D_{\tau}^{\beta} \theta ( \xi, \tau ) = \lambda_{hnf}\frac{\partial^{2}\theta ( \xi,\tau )}{\partial \xi^{2}} + Q\theta ( \xi,\tau ), \end{aligned}$$
(20)

where \({}^{CF}D_{\tau}^{\alpha} v ( \xi,\tau )\), and \({}^{CF}D_{\tau}^{\beta} \theta ( \xi,\tau )\) is for the Caputo–Fabrizio fractional operators of fractional order α and β. Equations (19) and (20) are the Caputo–Fabrizio generalized form of Eqs. (15) and (16), while the initial and boundary conditions will remain the same as in Eqs. (17) and (18). The Caputo–Fabrizio fractional operator is defined by (see [2], p. 1–13)

$$ {}^{CF}D_{t}^{\delta} f ( t ) = \frac{N ( \delta )}{1 - \delta} \int_{0}^{t} \exp \biggl( - \frac{\delta ( t - \tau )}{1 - \delta} \biggr) \frac{\partial f ( \tau )}{\partial \tau} \,d\tau, \quad 0 < \delta < 1, $$
(21)

which is the convolution product of the function \(\frac{N ( \delta )}{1 - \delta} \exp ( - \frac{\delta t}{1 - \delta} )\) and \(f ( t )\) of fractional order δ. In this study the following two properties of Caputo–Fabrizio fractional operator will be utilized.

  1. 1.

    Property 1: According to Losanda and Nieto (see [38], p. 87–92) \(N ( \delta )\) is the normalization function such that

    $$ N ( 1 ) = N ( 0 ) = 1. $$
    (22)
  2. 2.

    Property 2: taking into consideration Eq. (22), the Laplace transform of Eq. (21) yields

    $$ L \bigl\{ {}^{CF}D_{t}^{\delta} f ( t ) \bigr\} ( q ) = \frac{q\bar{f} ( q ) - f ( 0 )}{ ( 1 - \delta )q + \delta},\quad 0 < \delta < 1, $$
    (23)

    such that

    $$ \lim_{\delta \to 1} \bigl[ L \bigl\{ {}^{CF}D_{t}^{\delta} f ( t ) \bigr\} ( q ) \bigr] = \lim_{\delta \to 1} \biggl\{ \frac{q\bar{f} ( q ) - f ( 0 )}{ ( 1 - \delta )q + \delta} \biggr\} = q\bar{f} ( q ) - f ( 0 ) = L \biggl\{ \frac{\partial f ( t )}{\partial t} \biggr\} , $$
    (24)

    where \(\bar{f} ( q )\) is the Laplace transform of \(f ( t )\) and \(f ( 0 )\) is the initial value of the function.

5 Solution of the problem

To solve Eqs. (19) and (20) the Laplace transform method \(L \{ f ( t ) \} ( q ) = \bar{f} ( q ) = \int_{0}^{\infty} f ( t )e^{ - qt}\,dt\), will be applied by using the corresponding initial and boundary conditions from Eqs. (17) and (18) to develop exact analytical solutions for the velocity and temperature profiles.

5.1 Solutions of the energy equation

Applying the Laplace transform to Eq. (20) keeping in mind the definition and properties of the Caputo–Fabrizio fractional operator defined in Eq. (21)–(24) and using the corresponding initial condition from Eq. (17) yield

$$ a_{3}\Pr \frac{q\theta ( \xi,\tau ) - \theta ( \xi,0 )}{ ( 1 - \beta )q + \beta} = \lambda_{hnf}\frac{d^{2}\bar{\theta} ( \xi,q )}{\partial \xi^{2}} + Q\bar{\theta} ( \xi,q ), \quad 0 < \beta < 1, $$
(25)

and after further simplification of Eq. (25)

$$ \frac{d^{2}\bar{\theta} ( \xi,q )}{\partial \xi^{2}} - \frac{b_{4}q - b_{1}b_{3}}{q + b_{1}} = 0, \quad 0 < \beta < 1, $$
(26)

with transformed boundary conditions

$$ \left . \textstyle\begin{array}{l} \bar{v} ( 0,q ) = 0, \qquad\bar{\theta} ( 0,q ) = 0 \quad\mbox{for } q > 0 \\ \bar{v} ( 1,q ) = 0,\qquad \bar{\theta} ( 1,q ) = \frac{1}{q} \quad\mbox{for } q > 0 \end{array}\displaystyle \right \}, $$
(27)

where

$$b_{0} = \frac{1}{1 - \beta},\qquad b_{1} = b_{0}\beta,\qquad b_{2} = \frac{a_{3}\Pr}{ \lambda_{hnf}},\qquad b_{3} = \frac{Q}{\lambda_{hnf}},\qquad b_{4} = b_{0}b_{2} - b_{3}. $$

The exact solution of Eq. (26) using the corresponding boundary conditions from Eq. (27) is given by

$$ \bar{\theta} ( \xi,q ) = \frac{1}{q} \biggl( \sinh \xi \sqrt{ \frac{b_{4}q - b_{1}b_{3}}{q + b_{1}}} \biggr) \biggl( \sinh \sqrt{\frac{b_{4}q - b_{1}b_{3}}{q + b_{1}}} \biggr)^{ - 1},\quad 0 < \beta < 1. $$
(28)

Equation (28) represents the solutions of the energy equation in the Laplace transformed domain. In order to invert the Laplace transform, this equation can be written in a more suitable and simplified form:

$$ \bar{\theta} ( \xi,q ) = \sum_{n = 0}^{\infty} \biggl( \frac{1}{q}e^{ - ( 1 + 2n - \xi )\sqrt{\frac{b_{4}q - b_{1}b_{3}}{q + b_{1}}}} - \frac{1}{q}e^{ - ( 1 + 2n + \xi )\sqrt{\frac{b_{4}q - b_{1}b_{3}}{q + b_{1}}}} \biggr), \quad 0 < \beta < 1. $$
(29)

Let us consider

$$ \bar{\theta} ( \xi,q ) = \bar{\theta}_{1} ( \xi,q ) - \bar{ \theta}_{2} ( \xi,q ),\quad 0 < \beta < 1, $$
(30)

where

$$\begin{aligned} &\bar{\theta}_{1} ( \xi,q ) = \sum_{n = 0}^{\infty} \frac{1}{q}e^{ - ( 1 + 2n - \xi )\sqrt{\frac{b_{4}q - b_{1}b_{3}}{q + b_{1}}}},\quad 0 < \beta < 1, \end{aligned}$$
(31)
$$\begin{aligned} & \bar{\theta}_{2} ( \xi,q ) = \sum_{n = 0}^{\infty} \frac{1}{q}e^{ - ( 1 + 2n + \xi )\sqrt{\frac{b_{4}q - b_{1}b_{3}}{q + b_{1}}}},\quad 0 < \beta < 1. \end{aligned}$$
(32)

Upon taking the inverse Laplace transform, Eq. (30) yields

$$ \theta ( \xi,\tau ) = \theta_{1} ( \xi,\tau ) - \theta_{2} ( \xi,\tau ),\quad 0 < \beta < 1, $$
(33)

and to derive the functions \(\theta_{1} ( \xi,\tau )\) and \(\theta_{2} ( \xi,\tau )\), the compound formula for the Laplace inversion is used. The function \(\bar{\varPhi} ( \xi,q )\) is chosen as

$$ \bar{\varPhi} ( \xi,q ) = e^{ - (1 + 2n - \xi )\sqrt{\frac{b_{4}q - b_{1}b_{3}}{q + b_{1}}}} = e^{(1 + 2n - \xi )\sqrt{W_{1} ( q )}}. $$
(34)

According to Khan (see [39], p. 397–401), the inverse Laplace transform of the functions \(\bar{\varPhi} ( \xi,q )\) can be obtained as

$$ \varPhi ( \xi,\tau ) = L^{ - 1} \bigl\{ \bar{\varPhi} ( \xi,q ) \bigr\} = \int_{0}^{\infty} f \bigl( ( 1 + 2n - \xi ),u \bigr)g ( u,\tau ) \,d\tau, $$
(35)

where

$$\begin{aligned} &f \bigl( ( 1 + 2n - \xi ),u \bigr) = \frac{ ( 1 + 2n - \xi )}{2u\sqrt{\pi u}} e^{ - \frac{ ( 1 + 2n - \xi )}{4u}}, \end{aligned}$$
(36)
$$\begin{aligned} & g ( u,\tau ) = e^{ - b_{4}u}\delta ( \tau ) - e^{ - b_{4}u}\sqrt{ \frac{pu}{\tau}} I_{1}\sqrt{pu\tau} e^{ - b_{1}\tau}. \end{aligned}$$
(37)

and

$$p = - b_{1} ( b_{3} + b_{4} ). $$

The values of functions \(f ( ( 1 + 2n - \xi ),u )\) and \(g ( u,\tau )\), defined in Eqs. (36) and (37), are used in Eq. (35) yielding the following simplified form:

$$ \varPhi ( \xi,\tau ) = e^{ - ( 1 + 2n - \xi )\sqrt{b_{4}}} \delta ( \tau ) - \frac{ ( 1 + 2n - \xi )\sqrt{p}}{2\sqrt{\pi \tau}} e^{ - b_{1}\tau} \int_{0}^{\infty} \frac{1}{u}e^{ - \frac{ ( 1 + 2n - \xi )^{2}}{4u} - b_{4}u} I_{1}\sqrt{pu\tau} \,du. $$
(38)

To evaluate the function \(\theta_{1} ( \xi,\tau )\), we need to find the convolution product of \(L^{ - 1} \{ \frac{1}{q} \} = 1\) and the function \(\bar{\varPhi} ( \xi,q )\) which yields

$$\begin{aligned} \theta_{1} ( \xi,\tau ) ={}& \sum_{n = 0}^{\infty} \biggl( e^{ - ( 1 + 2n - \xi )\sqrt{b_{4}}} - \int_{0}^{\infty} \int_{0}^{\tau} \frac{ ( 1 + 2n - \xi )\sqrt{p}}{2\sqrt{\pi s}} e^{ - b_{1}s} \\ &{}\times \frac{1}{u}e^{ - \frac{ ( 1 + 2n - \xi )^{2}}{4u} - b_{4}u}I_{1}\sqrt{pus} \,du\,ds \biggr). \end{aligned}$$
(39)

Similarly, the function \(\theta_{2} ( \xi,\tau )\) is given by

$$\begin{aligned} \theta_{1} ( \xi,\tau ) ={}& \sum_{n = 0}^{\infty} \biggl( e^{ - ( 1 + 2n + \xi )\sqrt{b_{4}}} - \int_{0}^{\infty} \int_{0}^{\tau} \frac{ ( 1 + 2n + \xi )\sqrt{p}}{2\sqrt{\pi s}} e^{ - b_{1}s} \\ &{}\times \frac{1}{u}e^{ - \frac{ ( 1 + 2n + \xi )^{2}}{4u} - b_{4}u}I_{1}\sqrt{pus} \,du\,ds \biggr). \end{aligned}$$
(40)

To reduce the solutions obtained in Eq. (33) to classical or local form, Eq. (24) is used for the following.

For \(\beta \to 1\), Eq. (24) is used which reduced Eq. (25) to the following form:

$$ \frac{d^{2}\bar{\theta} ( \xi,q )}{\partial \xi^{2}} - ( b_{2}q + b_{2} )\bar{\theta} ( \xi,q ) = 0. $$
(41)

With the solutions in the Laplace transform domain one finds

$$ \bar{\theta} ( \xi,q ) = \frac{1}{q}\frac{\sinh \xi \sqrt{b_{2}q - b_{3}}}{\sinh \sqrt{b_{2}q - b_{3}}}. $$
(42)

After further simplification, Eq. (42) takes the following form:

$$ \bar{\theta} ( \xi,q ) = \sum_{n = 0}^{\infty} \biggl( \frac{1}{q}e^{ - ( 1 + 2n - \xi )\sqrt{b_{2}q - b_{3}}} - \frac{1}{q}e^{ - ( 1 + 2n + \xi )\sqrt{b_{2}q - b_{3}}} \biggr),\quad \beta = 1. $$
(43)

Taking the inverse Laplace transform, Eq. (43) gives the following local solutions for the temperature profile:

$$ \theta ( \xi,\tau ) = A_{1} ( \xi,\tau ) - A_{2} ( \xi,\tau ), \quad \beta = 1, $$
(44)

where

A 1 (ξ,τ)= 1 2 ∑ n = 0 ∞ ( e − ( 1 + 2 n − ξ ) b 2 − b 3 b 2 erfc ( ( 1 + 2 n − ξ ) 2 τ − − b 3 b 2 τ ) + e ( 1 + 2 n − ξ ) b 2 − b 3 b 2 erfc ( ( 1 + 2 n − ξ ) 2 τ + − b 3 b 2 τ ) ) ,
(45)
A 2 (ξ,τ)= 1 2 ∑ n = 0 ∞ ( e − ( 1 + 2 n + ξ ) b 2 − b 3 b 2 erfc ( ( 1 + 2 n − ξ ) 2 τ − − b 3 b 2 τ ) + e ( 1 + 2 n + ξ ) b 2 − b 3 b 2 erfc ( ( 1 + 2 n − ξ ) 2 τ + − b 3 b 2 τ ) ) .
(46)

5.2 Solution of momentum equation

Applying the Laplace transform on Eq. (19) using the corresponding initial condition from Eq. (15) yields

$$ \frac{a_{0}}{a_{1}} \frac{q\bar{v} ( \xi,q ) - v ( \xi,0 )}{ ( 1 - \alpha )q + \alpha} + \frac{a_{0}}{a_{1}}\beta_{b} \bar{v} ( \xi,q ) = \frac{d^{2}\bar{v} ( \xi,q )}{d\xi^{2}} + \frac{a_{2}}{a_{1}}\operatorname{Gr}\bar{\theta} ( \xi, \tau ). $$
(47)

After further simplification of Eq. (47)

$$ \frac{d^{2}\bar{v} ( \xi,q )}{d\xi^{2}} - \frac{d_{5}q + d_{1}d_{3}}{q + d_{1}}\bar{v} ( \xi,q ) = - d_{4} \bar{\theta} ( \xi,q ), $$
(48)

where

$$\begin{aligned} &d_{0} = \frac{1}{1 - \alpha},\qquad d_{1} = \alpha d_{0},\qquad d_{2} = \frac{a_{0}}{a_{1}},\qquad d_{3} = d_{2}\beta_{b},\\ & d_{4} = \frac{a_{2}}{a_{1}}\operatorname{Gr},\qquad d_{5} = d_{0}d_{2} + d_{3}. \end{aligned}$$

In the Laplace transform domain, the exact solution of Eq. (48) is given by

$$\begin{aligned} \bar{v} ( \xi,q ) ={}& \frac{ ( q + b_{1} )(q + b_{1})}{ ( d_{6}q^{2} + d_{7}q + d_{8} )q}\frac{\sinh \xi \sqrt{\frac{d_{5}q + d_{1}d_{3}}{q + d_{1}}}}{\sinh \sqrt{\frac{d_{5}q + d_{1}d_{3}}{q + d_{1}}}} \\ &{}- \frac{ ( q + b_{1} )(q + b_{1})}{ ( d_{6}q^{2} + d_{7}q + d_{8} )q} \frac{\sinh \xi \sqrt{\frac{b_{4}q - b_{1}b_{3}}{q + b_{1}}}}{\sinh \sqrt{\frac{b_{4}q - b_{1}b_{3}}{q + b_{1}}}}, \end{aligned}$$
(49)

where

$$\begin{aligned} &W_{1} ( q ) = \frac{d_{5}q + d_{1}d_{3}}{q + d_{1}},\qquad d_{6} = b_{4} - d_{5},\\ & d_{7} = b_{4}d_{1} - b_{1} ( b_{3} + d_{5} ),\qquad d_{8} = - b_{1}d_{1} ( b_{3} + d_{3} ). \end{aligned}$$

In order to find the inverse Laplace transform, Eq. (49) can be written in a more convenient and simplified form as

$$\begin{aligned} \bar{v} ( \xi,q ) ={}& \frac{ ( q + b_{1} )(q + b_{1})}{ ( d_{6}q^{2} + d_{7}q + d_{8} )q}\sum_{n = 0}^{\infty} \bigl( e^{ - ( 1 + 2n - \xi )\sqrt{\frac{d_{5}q + d_{1}d_{3}}{q + d_{1}}}} - e^{ - ( 1 + 2n + \xi )\sqrt{\frac{d_{5}q + d_{1}d_{3}}{q + d_{1}}}} \bigr) \\ &{}- \frac{ ( q + b_{1} )(q + b_{1})}{ ( d_{6}q^{2} + d_{7}q + d_{8} )q} \sum_{n = 0}^{\infty} \bigl( e^{ - ( 1 + 2n - \xi )\sqrt{\frac{b_{4}q - b_{1}b_{3}}{q + b_{1}}}} - e^{ - ( 1 + 2n + \xi )\sqrt{\frac{b_{4}q - b_{1}b_{3}}{q + b_{1}}}} \bigr), \\ & 0 < \alpha,\beta < 1. \end{aligned}$$
(50)

Let us consider

$$\begin{aligned} \bar{v} ( \xi,q ) ={}& \bar{v}_{1} ( \xi,q ) \times \bigl\{ \bar{v}_{2} ( \xi,q ) - \bar{v}_{3} ( \xi,q ) \bigr\} - \bar{v}_{1} ( \xi,q ) \\ &{}\times \bigl\{ \bar{v}_{4} ( \xi,q ) - \bar{v}_{5} ( \xi,q ) \bigr\} , \quad 0 < \alpha,\beta < 1. \end{aligned}$$
(51)

Here

$$\begin{aligned} &\bar{v}_{1} ( \xi,q ) = \frac{ ( q + b_{1} )(q + b_{1})}{ ( d_{6}q^{2} + d_{7}q + d_{8} )}, \end{aligned}$$
(52)
$$\begin{aligned} &\bar{v}_{2} ( \xi,q ) = \frac{1}{q}\sum _{n = 0}^{\infty} e^{ - ( 1 + 2n - \xi )\sqrt{\frac{d_{5}q + d_{1}d_{3}}{q + d_{1}}}}, \end{aligned}$$
(53)
$$\begin{aligned} &\bar{v}_{3} ( \xi,q ) = \frac{1}{q}\sum _{n = 0}^{\infty} e^{ - ( 1 + 2n + \xi )\sqrt{\frac{d_{5}q + d_{1}d_{3}}{q + d_{1}}}}, \end{aligned}$$
(54)
$$\begin{aligned} & \bar{v}_{4} ( \xi,q ) = \frac{1}{q}\sum _{n = 0}^{\infty} e^{ - ( 1 + 2n - \xi )\sqrt{\frac{b_{4}q - b_{1}b_{3}}{q + b_{1}}}}, \end{aligned}$$
(55)
$$\begin{aligned} & \bar{v}_{5} ( \xi,q ) = \frac{1}{q}\sum _{n = 0}^{\infty} e^{ - ( 1 + 2n + \xi )\sqrt{\frac{b_{4}q - b_{1}b_{3}}{q + b_{1}}}}, \end{aligned}$$
(56)

and taking the inverse Laplace transform yields

$$\begin{aligned} v ( \xi,\tau ) ={}& v_{1} ( \xi,\tau )* \bigl\{ v_{2} ( \xi, \tau ) - v_{3} ( \xi,\tau ) \bigr\} \\ &{}- v_{1} ( \xi,\tau )* \bigl\{ v_{4} ( \xi,\tau ) - v_{5} ( \xi,\tau ) \bigr\} , \quad 0 < \alpha,\beta < 1, \end{aligned}$$
(57)

where ∗ represents a convolution product and the terms \(v_{2} ( \xi,\tau )\), \(v_{3} ( \xi,\tau ) v_{4} ( \xi,\tau )\) and \(v_{5} ( \xi,\tau )\) are given by

$$\begin{aligned} v_{2} ( \xi,\tau ) ={}& \sum_{n = 0}^{\infty} \biggl\{ e^{ - ( 1 + 2n - \xi )\sqrt{d_{5}}} \delta ( \tau ) \\ &{}- \frac{ ( 1 + 2n - \xi )\sqrt{p_{2}}}{2\sqrt{\pi \tau}} e^{ - d_{1}\tau} \int_{0}^{\infty} \frac{1}{u}e^{ - \frac{ ( 1 + 2n - \xi )^{2}}{4u} - b_{4}u} I_{1}\sqrt{p_{2}u\tau} \,du \biggr\} , \end{aligned}$$
(58)
$$\begin{aligned} v_{3} ( \xi,\tau ) ={}& \sum_{n = 0}^{\infty} \biggl\{ e^{ - ( 1 + 2n + \xi )\sqrt{d_{5}}} \delta ( \tau ) \\ &{}- \frac{ ( 1 + 2n + \xi )\sqrt{p_{2}}}{2\sqrt{\pi \tau}} e^{ - d_{1}\tau} \int_{0}^{\infty} \frac{1}{u}e^{ - \frac{ ( 1 + 2n + \xi )^{2}}{4u} - b_{4}u} I_{1}\sqrt{p_{2}u\tau} \,du \biggr\} , \end{aligned}$$
(59)
$$\begin{aligned} v_{4} ( \xi,\tau ) ={}& \sum_{n = 0}^{\infty} \biggl\{ e^{ - ( 1 + 2n - \xi )\sqrt{b_{4}}} \delta ( \tau ) \\ &{}- \frac{ ( 1 + 2n - \xi )\sqrt{p_{2}}}{2\sqrt{\pi \tau}} e^{ - b_{1}\tau} \int_{0}^{\infty} \frac{1}{u}e^{ - \frac{ ( 1 + 2n - \xi )^{2}}{4u} - b_{4}u} I_{1}\sqrt{p_{2}u\tau} \,du \biggr\} , \end{aligned}$$
(60)
$$\begin{aligned} v ( \xi,\tau ) ={}& \sum_{n = 0}^{\infty} \biggl\{ e^{ - ( 1 + 2n + \xi )\sqrt{b_{4}}} \delta ( \tau ) \\ &{}- \frac{ ( 1 + 2n + \xi )\sqrt{p_{2}}}{2\sqrt{\pi \tau}} e^{ - b_{1}\tau} \int_{0}^{\infty} \frac{1}{u}e^{ - \frac{ ( 1 + 2n + \xi )^{2}}{4u} - b_{4}u} I_{1}\sqrt{p_{2}u\tau} \,du \biggr\} , \end{aligned}$$
(61)

where

$$p_{2} = \frac{d_{1}d_{3} - d_{5}d_{1}}{d_{1}^{2}}. $$

The term \(v_{1} ( \xi,\tau )\) is numerically obtained using Zakian’s algorithm. In the literature, it is proven that the Zakian algorithm is a stable way for the inverse Laplace transform because the truncated error for five multiple terms is negligible ([40], p. 83).

For the velocity profile, the local solutions can be recovered by making \(\alpha,\beta \to 1\) in Eq. (47) which leads to the following solutions in the Laplace transform domain:

$$\begin{aligned} \bar{v} ( \xi,q ) ={}& \frac{d_{4}}{ ( b_{2} - d_{3} )q - ( b_{3} + d_{3} )}\frac{1}{q}\frac{\sinh \xi \sqrt{d_{2}q + d_{3}}}{\sinh \sqrt{d_{2}q + d_{3}}} \\ &{}- \frac{d_{4}}{ ( b_{2} - d_{3} )q - ( b_{3} + d_{3} )}\frac{1}{q}\frac{\sinh \xi \sqrt{b_{2}q - b_{3}}}{\sinh \sqrt{b_{2}q - b_{33}}}, \end{aligned}$$
(62)

with the following simplified form:

$$\begin{aligned} \bar{v} ( \xi,q ) ={}& \frac{d_{9}}{q^{2} + qd_{10}}\sum_{n = 0}^{\infty} \bigl( e^{ - ( 1 + 2n - \xi )\sqrt{d_{2}q + d_{3}}} - e^{ - ( 1 + 2n + \xi )\sqrt{d_{2}q + d_{3}}} \bigr) \\ &{}- \frac{d_{9}}{q^{2} + qd_{10}} \sum_{n = 0}^{\infty} \bigl( e^{ - ( 1 + 2n - \xi )\sqrt{b_{2}q - b_{3}}} - e^{ - ( 1 + 2n + \xi )\sqrt{b_{2}q - b_{3}}} \bigr),\quad \alpha,\beta = 1 , \end{aligned}$$
(63)

where

$$d_{9} = \frac{d_{4}}{b_{2} - d_{2}}, \qquad d_{10} = \frac{b_{3} + d_{3}}{b_{2} - d_{2}}. $$

The inverse Laplace transform of Eq. (63) yields

$$ v ( \xi,\tau ) = B_{1} ( \xi,\tau ) - B_{2} ( \xi,\tau ) - B_{3} ( \xi,\tau ) + B_{4} ( \xi,\tau ),\quad \alpha,\beta = 1, $$
(64)

where

B 1 (ξ,τ)= d 10 2 ∑ n = 0 ∞ ∫ 0 τ e − d 7 ( τ − s ) ( e − ( 1 + 2 n − ξ ) b 2 d 3 d 2 erfc ( ( 1 + 2 n − ξ ) 2 s − d 3 d 2 s ) + e ( 1 + 2 n − ξ ) b 2 − b 3 b 2 erfc ( ( 1 + 2 n − ξ ) 2 s + d 3 d 2 s ) ) ds,
(65)
B 2 (ξ,τ)= d 10 2 ∑ n = 0 ∞ ∫ 0 τ e − d 7 ( τ − s ) ( e − ( 1 + 2 n + ξ ) b 2 d 3 d 2 erfc ( ( 1 + 2 n − ξ ) 2 s − d 3 d 2 s ) + e ( 1 + 2 n + ξ ) b 2 − d 3 d 2 erfc ( ( 1 + 2 n − ξ ) 2 s + d 3 d 2 s ) ) ds,
(66)
B 3 (ξ,τ)= d 10 2 ∑ n = 0 ∞ ∫ 0 τ e − d 7 ( τ − s ) ( e − ( 1 + 2 n − ξ ) b 2 − b 3 b 2 erfc ( ( 1 + 2 n − ξ ) 2 s − − b 3 b 2 s ) + e ( 1 + 2 n − ξ ) b 2 − b 3 b 2 erfc ( ( 1 + 2 n − ξ ) 2 s + − b 3 b 2 s ) ) ds,
(67)
B 4 (ξ,τ)= d 10 2 ∑ n = 0 ∞ ∫ 0 τ e − d 7 ( τ − s ) ( e − ( 1 + 2 n + ξ ) b 2 − b 3 b 2 erfc ( ( 1 + 2 n − ξ ) 2 s − − b 3 b 2 s ) + e ( 1 + 2 n + ξ ) b 2 − b 3 b 2 erfc ( ( 1 + 2 n − ξ ) 2 s + − b 3 b 2 s ) ) ds.
(68)

6 Results and discussion

In this article, the idea of the fractional derivative is used for the generalization of the free convection flow of the hybrid nanofluid. The governing equations of the Brinkman type fluid along with the energy equation is fractionalized using the Caputo–Fabrizio fractional derivative. The fractional PDEs are more general and are known as master PDEs. The momentum and energy equations are solved analytically using the Laplace transform technique. The obtained results are displayed in various graphs to study the influence of the pertinent corresponding parameters, such as the fractional parameters \(\alpha \mbox{ and } \beta\), the volume fraction of hybrid nanofluid \(\phi_{hnf}\), the heat generation parameter Q, the Brinkman parameter \(\beta_{b}\) and the thermal Grashof number Gr on velocity and temperature profiles.

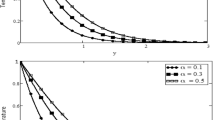
Figures 1(a) and (b) and 2(a) and (b) depict the impact of the fractional parameter α and β on the velocity and temperature profiles. From these figures, it is noticed that the velocity and the temperature profiles show the same trend for variations in the fractional parameters. The velocity and temperature profiles exhibited increasing behavior for increasing values of α, β for a longer time. When \(\alpha,\beta\) are increased, the thickness of thermal and momentum boundary layers are increased and become thickest at \(\alpha,\beta = 1\), which corresponds to the increasing performance of the velocity and temperature profiles. This trend of the fractional parameter is the same here for velocity and temperature profiles as reported by ([25], p. 7) for fractional nanofluids using the Caputo–Fabrizio fractional derivatives. But this effect reverses for a shorter time in the case of fractional velocity and temperature distributions.

Figure 1
figure 1

Variation in temperature profile against ξ due to β

Full size image
Figure 2
figure 2

Variation in velocity profile against ξ due to α and β

Full size image

The influence of \(\phi_{hnf}\) on the velocity and temperature profiles is studied in Figs. 3 and 4. The trends of velocity and temperature profiles are opposite to each other. The hybrid nanofluid velocity decreases with increasing \(\phi_{hnf}\). This can be physically justified as the hybrid nanofluid became more viscous with increasing \(\phi_{hnf}\), which leads to a decrease in the nanofluid velocity. Nevertheless, the temperature profile increases with increase in \(\phi_{hnf}\) when the temperature is less than 180°C. The is due to the thermal conductivity enhancing with the enhancement of \(\phi_{hnf}\) and the hybrid nanofluid conducting more heat as a result of heat transfer increases, which leads to an increase in the temperature profile.

Figure 3
figure 3

Variation in temperature profile against ξ due to \(\phi_{hnf}\)

Full size image
Figure 4
figure 4

Variation in velocity profile against ξ due to \(\phi_{hnf}\)

Full size image

In Figs. 5 and 6 the temperature and velocity profiles are compared for \(Cu - Al_{2}O_{3} - H_{2}O\), \(Cu - H_{2}O\), \(Al_{2}O_{3} - H_{2}O\) and pure water. It is noticed that the temperature profile is higher for \(Cu - H_{2}O\) followed by \(Cu - Al_{2}O_{3} - H_{2}O\), \(Al_{2}O_{3} - H_{2}O\) and pure water. This due to the fact that the thermal conductivity of Cu is higher than hybrid nanoparticles, alumina, and pure water. But the hybrid nanofluid is more stable. In the case of the velocity profile, the velocity of \(Al_{2}O_{3} - H_{2}O\) is higher, followed by the velocity of \(Cu - Al_{2}O_{3} - H_{2}O\), \(Cu - H_{2}O\) and pure water. It can be physically justified as the \(Al_{2}O_{3}\) conducting a high quantity of heat due to the effective thermal conductivity but being less dense. Therefore, the velocity of \(Al_{2}O_{3} - H_{2}O\) is higher among all the fluids under consideration.

Figure 5
figure 5

Compression of the temperature profile against ξ for different nanofluids

Full size image
Figure 6
figure 6

Compression of the temperature profile against ξ for different nanofluids

Full size image

Figures 7 and 8 depict the influence of Q on velocity and temperature profiles. It is found that the velocity and temperature distributions increase with increasing values of Q. When a larger value is assigned to Q this means that the system absorbed more heat due to which the intermolecular attractive force became weaker; as a result, the temperature and velocity profiles increase. The effect of the Brinkman parameter is presented in Fig. 9. It is noticed that the velocity distribution decreases with increasing values of \(\beta_{b}\). The higher values \(\beta_{b}\) correspond to stronger drag forces, which lead to the retardation of the velocity profile. The same effect of \(\beta_{b}\) is reported by [33].

Figure 7
figure 7

Variation in temperature profile against ξ due to Q

Full size image
Figure 8
figure 8

Variation in velocity profile against ξ due to Q

Full size image
Figure 9
figure 9

Variation in velocity profile against ξ due to \(\beta_{b}\)

Full size image

The effect of Gr is studied in Fig. 10 for negative and positive values. Positive values of Gr correspond to heating of the plate, while negative values correspond to cooling of the plate. In this figure, it is noticed that for greater values of Gr the velocity profile shows an increasing trend. This is because when Gr is increased the buoyancy forces become stronger due to which more convection takes place; as a result, the velocity profile increases. But this effect reverses for negative values of Gr due to cooling of the plate.

Figure 10
figure 10

Variation in velocity profile against ξ due to Gr

Full size image

7 Concluding remarks

In this article, the idea of free convection is generalized using the Caputo–Fabrizio fractional derivative. The natural convection flow of a hybrid nanofluid in two vertical infinite parallel plates is studied. Exact analytical solutions are developed for temperature and velocity profiles via the Laplace transform technique. The effects of various pertinent parameters are numerically studied through graphs and discuss physically. The major points extracted from this study are as follows:

  • The velocity and temperature profiles show an increasing behavior for increasing values \(\alpha \mbox{ and } \beta\) being most dominant for \(\alpha,\beta = 1\) for a larger time. But this effect reverses for a shorter time.

  • The fractional velocity and temperature are more general. Hence, the numerical values for \(v ( \xi,\tau )\) and \(\theta ( \xi,\tau )\) can be calculated for any value of \(\alpha \mbox{ and } \beta\) such that \(0 < \alpha,\beta < 1\).

  • The temperature distribution shows a very similar variation for different shapes of the hybrid nanoparticles, so the density of the nanoparticles is a significant factor as compared to thermal conductivity.

  • The velocity profile decreases with increasing values of \(\phi_{hnf}\) but this effect is opposite in the case of the temperature profile.

  • With increasing values of Gr, the free convection became dominant, increasing the nanofluid velocity for positive values but this trend reverses for negative values of Gr.

  • The velocity retards for larger values of \(\beta_{b}\) due the enhancement in the drag forces.