Comparative simulations for solutions of fractional Sturm–Liouville problems with non-singular operators

Abstract

In this study, we consider fractional Sturm–Liouville (S–L) problems within non-singular operators. A fractional S–L problem with exponential and Mittag-Leffler kernels is given with different versions in the Riemann–Liouville and Caputo sense. Also, we obtain representation of solutions for S–L problems by the Laplace transform and find analytical solutions of the problems. Finally, we compare the solutions of the problem with these different versions, and we also compare the solutions of the problem with exponential and Mittag-Leffler kernels together by simulation under different potentials, different orders, and different eigenvalues.

1 Introduction

Fractional calculus has a lot of application areas in engineering, nature sciences, and mathematics. This range of application areas gave rise to new fractional definitions, especially for the real world modelling problems. More recently, several new fractional derivative definitions have been studied. One of those definitions is fractional derivative with exponential kernel defined by Caputo and Fabrizio [1], and another definition is fractional derivative with Mittag-Leffler kernel defined by Atangana and Baleanu [2]. Fractional operator with Mittag-Leffler kernel is a general form of the operator with exponential kernel because of α order in its definition. These new definitions enable more suitable results for some modelling problems in the real world because of having nonsingularity in the kernels.

Baleanu et al. [3–7], Atangana et al. [8, 9], and Abdeljawad et al. [10, 11] studied a fractional operator with exponential kernel for some modelling problems and their solution methods. After the emergence of the definition of fractional derivative with Mittag-Leffler kernel by Atangana and Baleanu [2], many scientists studied this operator [12–24]. Baleanu et al. [25–27], Atangana et al. [28, 29] studied the operator with Mittag-Leffler kernel. Many other scientists studied comparisons of these two new definitions, see Abro et al. [30], Sheikh et al. [31, 32], Saad et al. [33], and Gomez et al. [34].

The emergence of Sturm–Liouville operators began as a one-dimensional Schrödinger equation in quantum mechanics. Fractional Sturm–Liouville differential equations were studied by Klimek et al. [35], Bas et al. [36, 37], Zayernouri et al. [38], Khosravian et al. [39], and Dehghan et al. [40].

In this study, we consider fractional Sturm–Liouville (S–L) problems within non-singular operators. A fractional S–L problem with exponential and Mittag-Leffler kernels is given with different versions in the Riemann–Liouville and Caputo sense. Also, we obtain the representation of solutions for S–L problems by the Laplace transform and find the analytical solutions of the problems. We analyze solutions of these different versions and display them by simulation under different potentials, different orders, and different eigenvalues. However, we compare the solutions of the problem with these different versions, and we also compare the solutions of the problem with exponential and Mittag-Leffler kernels together by simulation.

2 Preliminaries

Definition 1

([1])

Fractional derivative with exponential kernel is defined as follows: left and right derivatives in the Caputo sense

$$\begin{aligned}& {}_{\hspace{9pt}a}^{CFC}D^{\alpha } f ( t ) = \frac{M ( \alpha ) }{1 - \alpha } \int_{a}^{t}f' ( s ) \exp \biggl( \frac{ - \alpha }{1 - \alpha } ( t - s ) \biggr)\,ds, \end{aligned}$$

(1)

$$\begin{aligned}& {}^{CFC}D_{b}^{\alpha } f ( t ) = \frac{ - M ( \alpha ) }{1 - \alpha } \int_{t}^{b}f' ( s ) \exp \biggl( \frac{ - \alpha }{1 - \alpha } ( s - t ) \biggr)\,ds, \end{aligned}$$

(2)

left and right derivatives in the Riemann–Liouville sense

$$ {}_{\hspace{9pt}a}^{CFR}D^{\alpha } f ( t ) = \frac{M ( \alpha ) }{1 - \alpha } \frac{d}{dt} \int_{a}^{t}f ( s ) \exp \biggl( \frac{ - \alpha }{1 - \alpha } ( t - s ) \biggr)\,ds, $$

(3)

where $f \in H^{1} ( a, b )$, $a < b$, $\alpha \in [ 0, 1 ]$,

$$ ^{CFR}D_{b}^{\alpha } f ( t ) = \frac{ - M ( \alpha ) }{1 - \alpha } \frac{d}{dt} \int_{t}^{b}f ( s ) \exp \biggl( \frac{ - \alpha }{1 - \alpha } ( s - t ) \biggr)\,ds, $$

(4)

where $M ( \alpha ) > 0$ is a normalization function with $M(0) = M(1) = 1$.

Definition 2

([1])

Left and right fractional integrals for fractional derivatives with exponential kernel are defined respectively by

$$\begin{aligned}& {}_{\hspace{4pt}a}^{CF}I^{\alpha } f ( t ) = \frac{1 - \alpha }{M ( \alpha ) }f ( t ) + \frac{\alpha }{M ( \alpha ) } \int_{a}^{t}f ( s )\,ds, \\& {}^{CF}I_{b}^{\alpha } f ( t ) = \frac{1 - \alpha }{M ( \alpha ) }f ( t ) + \frac{\alpha }{M ( \alpha ) } \int_{t}^{b}f ( s )\,ds. \end{aligned}$$

Theorem 3

([25])

Let $\alpha > 0$, $p \ge 1$, $q \ge 1$, $\frac{1}{p} + \frac{1}{q} \le 1 + \alpha$, $f ( x ) \in{}^{CF}I _{b}^{\alpha } ( L_{p} )$, and $g ( x ) \in {}_{\hspace{4pt}a}^{CF}I^{\alpha } ( L_{q} )$, then integration by parts formulas are given as follows:

$$\begin{aligned}& \int_{a}^{b}f ( x ) {}_{\hspace{9pt}a}^{CFR}D^{\alpha } g ( x )\,dx = \int_{a}^{b}{}^{CFR}D_{b}^{\alpha } f ( x ) g ( x )\,dx, \end{aligned}$$

(5)

$$\begin{aligned}& \int_{a}^{b}g ( t ) {}_{\hspace{9pt}a}^{CFC}D^{\alpha } f ( t )\,dt = \int_{a}^{b}{}^{CFR}D_{b}^{\alpha } g ( t ) f ( t )\,dt + \frac{B ( \alpha ) }{1 - \alpha } f ( t ) e_{\frac{ - \alpha }{1 - \alpha }, b^{ -}} g ( t ) | _{a}^{b}, \end{aligned}$$

(6)

$$\begin{aligned}& \int_{a}^{b}g ( t ) {}^{CFC}D_{b}^{\alpha } f ( t )\,dt = \int_{a}^{b}{}_{\hspace{9pt}a}^{CFR}D^{\alpha } g ( t ) f ( t )\,dt - \frac{B ( \alpha ) }{1 - \alpha } f ( t ) e_{\frac{ - \alpha }{1 - \alpha }, a^{ +}} g ( t ) | _{a}^{b}, \end{aligned}$$

(7)

where $e_{\frac{ - \alpha }{1 - \alpha }, b^{ -}}$ and $e_{\frac{ - \alpha }{1 - \alpha }, a^{ +}}$ are the left and right exponential integral operators respectively,

$$\begin{aligned}& e_{\frac{ - \alpha }{1 - \alpha }, b^{ -}} = \int_{a}^{x}e^{\frac{ - \alpha }{1 - \alpha } ( t - a ) } \varphi ( t )\,dt, \quad x > a, \\& e_{\frac{ - \alpha }{1 - \alpha }, a^{ +}} = \int_{x}^{b}e^{\frac{ - \alpha }{1 - \alpha } ( b - t ) } \varphi ( t )\,dt,\quad x < b, \end{aligned}$$

and function spaces ${}^{CF}I_{b}^{\alpha } ( L_{p} )$ and ${}_{\hspace{4pt}a}^{CF}I^{\alpha } ( L_{q} )$ are defined by

$$\begin{aligned}& {}_{\hspace{4pt}a}^{CF}I^{\alpha } ( L_{p} ) = \bigl\{ f: f ={}_{\hspace{4pt}a}^{CF}I ^{\alpha } \varphi, \varphi \in L_{p} ( a, b ) \bigr\} , \\& {}^{CF}I_{b}^{\alpha } ( L_{p} ) = \bigl\{ f: f ={}^{CF}I _{b}^{\alpha } \varphi, \varphi \in L_{p} ( a, b ) \bigr\} . \end{aligned}$$

Definition 4

([2])

Fractional derivative with Mittag-Leffler kernel is defined as follows: left and right derivatives in the Caputo sense

$$\begin{aligned}& {}_{\hspace{9pt}a}^{ABC}D^{\alpha } f ( t ) = \frac{B ( \alpha ) }{1 - \alpha } \int_{a}^{t}f' ( s ) E _{\alpha } \biggl( \frac{ - \alpha }{1 - \alpha } ( t - s ) ^{\alpha } \biggr)\,ds, \end{aligned}$$

(8)

$$\begin{aligned}& {}^{ABC}D_{b}^{\alpha } f ( t ) = \frac{ - B ( \alpha ) }{1 - \alpha } \int_{t}^{b}f' ( s ) E _{\alpha } \biggl( \frac{ - \alpha }{1 - \alpha } ( s - t ) ^{\alpha } \biggr)\,ds, \end{aligned}$$

(9)

left and right derivatives in the Riemann–Liouville sense

$$ {}_{\hspace{9pt}a}^{ABR}D^{\alpha } f ( t ) = \frac{B ( \alpha ) }{1 - \alpha } \frac{d}{dt} \int_{a}^{t}f ( s ) E_{\alpha } \biggl( \frac{ - \alpha }{1 - \alpha } ( t - s ) ^{\alpha } \biggr)\,ds, $$

(10)

where $f \in H^{1} ( a, b )$, $a < b$, $\alpha \in [ 0, 1 ]$,

$$ {}^{ABR}D_{b}^{\alpha } f ( t ) = \frac{ - B ( \alpha ) }{1 - \alpha } \frac{d}{dt} \int_{t}^{b}f ( s ) E_{\alpha } \biggl( \frac{ - \alpha }{1 - \alpha } ( s - t ) ^{\alpha } \biggr)\,ds, $$

(11)

where $B ( \alpha ) > 0$ is a normalization function with $B(0) = B(1) = 1$.

Definition 5

([26])

Left and right fractional integrals for fractional derivative with Mittag-Leffler kernel are defined respectively by

$$\begin{aligned}& {}_{\hspace{5pt}a}^{AB}I^{\alpha } f ( t ) = \frac{1 - \alpha }{B ( \alpha ) }f ( t ) + \frac{\alpha }{B ( \alpha ) }_{a}I^{\alpha } f ( t ), \\& ^{AB}I_{b}^{\alpha } f ( t ) = \frac{1 - \alpha }{B ( \alpha ) }f ( t ) + \frac{\alpha }{B ( \alpha ) } I_{b}^{\alpha } f ( t ) s. \end{aligned}$$

Theorem 6

([1, 8])

The Laplace transform of fractional definitions with exponential kernel (1) and (3) is given as follows:

$$\begin{aligned}& \mathfrak{L} \bigl\{ {}_{\hspace{9pt}a}^{CFR}D^{\alpha } f ( t ) \bigr\} ( s ) = \frac{M ( \alpha ) }{1 - \alpha } \frac{s \mathfrak{L} \{ f ( t ) \} ( s ) }{s + \frac{ \alpha }{1 - \alpha }}, \\& \mathfrak{L} \bigl\{ \bigl( {}_{\hspace{9pt}a}^{CFC}D^{\alpha } f \bigr) ( t ) \bigr\} ( s ) = \frac{M ( \alpha ) }{1 - \alpha } \frac{s\mathfrak{L} \{ f ( t ) \} ( s ) }{s + \frac{\alpha }{1 - \alpha }} - \frac{M ( \alpha ) }{1 - \alpha } f ( a ) e^{ - as}\frac{1}{s + \frac{ \alpha }{1 - \alpha }}. \end{aligned}$$

Theorem 7

([3])

The Laplace transform of fractional definitions with Mittag-Leffler kernel (8) and (10) is given as follows:

$$\begin{aligned}& \mathfrak{L} \bigl\{ {}_{\hspace{9pt}a}^{ABR}D^{\alpha } f ( t ) \bigr\} ( s ) = \frac{B ( \alpha ) }{1 - \alpha } \frac{s ^{\alpha } \mathfrak{L} \{ f ( t ) \} ( s ) }{s ^{\alpha } + \frac{\alpha }{1 - \alpha }}, \\& \mathfrak{L} \bigl\{ {}_{\hspace{9pt}a}^{ABC}D^{\alpha } f ( t ) \bigr\} ( s ) = \frac{B ( \alpha ) }{1 - \alpha } \frac{s ^{\alpha } \mathfrak{L} \{ f ( t ) \} ( s ) - s^{\alpha - 1}f ( a ) }{s^{\alpha } + \frac{\alpha }{1 - \alpha }}. \end{aligned}$$

Definition 8

The convolution of $f ( t )$ and $g ( t )$ is defined as follows:

$$ ( f * g ) ( t )= \int_{0}^{t}f ( s ) g ( t - s )\,ds ,\quad f, g: [ 0,\infty ) \to \mathrm{R}. $$

Definition 9

([41])

The Mittag-Leffler function $E_{\delta } ( z )$ is defined by

$$ E_{\delta } ( z ) = \sum_{k = 0}^{\infty } \frac{z^{k}}{ \Gamma ( \delta k + 1 ) }\quad \bigl( z \in \mathrm{C}, \operatorname{Re}( \delta ) > 0 \bigr), $$

and the Mittag-Leffler function with two parameters is defined by

$$ E_{\delta, \theta } ( z ) = \sum_{k = 0}^{\infty } \frac{z ^{k}}{\Gamma ( \delta k + \theta ) }\quad \bigl( z, \theta \in \mathrm{C}, \operatorname{Re}( \delta ) > 0 \bigr). $$

Property 10

The inverse Laplace transform of some special functions has the following properties:

• (i) $\mathfrak{L}^{ - 1} \{ \frac{a}{s ( s^{\delta } + a ) } \} = 1 - E _{\delta } ( - at^{\delta } )$,

• (ii) $\mathfrak{L}^{ - 1} \{ \frac{1}{s^{\delta } + a} \} = t^{\delta - 1}E_{\delta, \delta } ( - at^{\delta } )$.

Property 11

$\mathfrak{L} \{ ( f * g ) ( t ) \} = \mathfrak{L} \{ f ( t ) \} \mathfrak{L} \{ g ( t ) \}$.

In the following section, firstly we give fractional S–L problems within different versions of the operators with exponential kernel in the Riemann–Liouville and Caputo sense and compare them. Secondly, we give fractional S–L problems within different versions of the operators with Mittag-Leffler kernel in the Riemann–Liouville and Caputo sense and compare them. We obtain the representation of solutions for S–L problems by the Laplace transform and find the analytical solutions of the problem. We analyze the solutions of these different versions and display them by simulation under different potentials, different orders, and different eigenvalues. Finally, we compare the solutions of the problem with these different versions, and we also compare the solutions of the problem with exponential and Mittag-Leffler kernels together by simulation.

3 Main results

3.1 Representations of solutions of fractional Sturm–Liouville problems with exponential and Mittag-Leffler kernels

Theorem 12

Let us consider the fractional Sturm–Liouville initial value problem with exponential kernel:

$$\begin{aligned}& {}^{CF}L_{1}f ={}_{\hspace{9pt}0}^{CFC}D^{\alpha } \bigl( {}_{\hspace{9pt}0}^{CFR}D^{\alpha } f ( x ) \bigr) + q ( x ) f ( x ) = \lambda f ( x ), \quad x \in [ 0, n ] , n \in \mathrm{R}^{ +}, \end{aligned}$$

(12)

$$\begin{aligned}& {}_{\hspace{9pt}0}^{CFR}D^{\alpha } f ( 0 ) = c_{1}, \end{aligned}$$

(13)

where $0 < \alpha < 1$, $q ( x )$ is a real-valued continuous function on $[ 0, n ]$. Then the representation of solution of problem (12)–(13) is as follows: $\lambda \ne \{ 0, 1 \}$,

$$\begin{aligned} f ( x, \lambda ) =& c_{1}\frac{e^{\frac{\alpha \lambda x}{( \alpha - 1)(\lambda - 1)}} ( \sinh ( \frac{\alpha \sqrt{ \lambda } x}{(\alpha - 1)(\lambda - 1)} ) + \sqrt{\lambda } \cosh ( \frac{\alpha \sqrt{\lambda } x}{(\alpha - 1)(\lambda - 1)} ) ) }{(\alpha - 1)(\lambda - 1)\sqrt{\lambda }} \\ &{}+ \frac{\alpha [ - 2\sqrt{\lambda } + (\lambda + 1) + ( \lambda + 1) ( - e^{\frac{2\alpha \lambda x}{(\lambda - 1)(\alpha - 1)\sqrt{\lambda }}} ) ] e^{ - \frac{x\alpha ( \sqrt{ \lambda } - \lambda ) }{(\alpha - 1)(\lambda - 1)}}}{2(\alpha - 1)( \lambda - 1)^{2}\sqrt{\lambda }} \\ &{}+ \frac{\alpha ( - 2\sqrt{\lambda } e^{\frac{2\alpha \sqrt{ \lambda } x}{(\lambda - 1)(\alpha - 1)}} ) e^{ - \frac{x\alpha ( \sqrt{\lambda } - \lambda ) }{(\alpha - 1)(\lambda - 1)}}}{2( \alpha - 1)(\lambda - 1)^{2}\sqrt{\lambda }} \\ &{}+ \biggl( \frac{\alpha [ - 2\sqrt{\lambda } + (\lambda + 1) + (\lambda + 1) ( - e^{\frac{2\alpha \sqrt{\lambda } x}{(\alpha - 1)(\lambda - 1)}} ) ] e^{ - \frac{x\alpha ( \sqrt{ \lambda } - \lambda ) }{(\alpha - 1)(\lambda - 1)}}}{2(\alpha - 1)( \lambda - 1)^{2}\sqrt{\lambda }} \biggr) * q ( x ) f ( x ) \\ &{}+ \biggl( \frac{\alpha ( - 2\sqrt{\lambda } e^{\frac{2\alpha \lambda x}{(\alpha - 1)(\lambda - 1)\sqrt{\lambda }}} ) e^{ ( - \frac{x\alpha ( \sqrt{\lambda } - \lambda ) }{( \alpha - 1)(\lambda - 1)} ) }}{2(\alpha - 1)(\lambda - 1)^{2}\sqrt{ \lambda }} - \frac{\delta (x)}{\lambda - 1} \biggr) * q ( x ) f ( x ). \end{aligned}$$

(14)

Proof

If we apply the Laplace transform to both sides of equation (12) and by the help of Theorem 6, let $q ( x ) f ( x ) = g ( x )$,

$$\begin{aligned}& \mathfrak{L} \bigl\{ {}_{\hspace{9pt}0}^{CFC}D^{\alpha } \bigl( {}_{\hspace{9pt}0}^{CFR}D^{ \alpha } f \bigr) \bigr\} ( s ) + \mathfrak{L} \{ g \} ( s ) = \lambda \mathfrak{L} \{ f \} ( s ) \\& \quad = \frac{M ( \alpha ) }{1 - \alpha } \frac{s\mathfrak{L} \{ ( {}_{\hspace{9pt}0}^{CFR}D^{\alpha } f ) \} ( s ) }{s + \frac{\alpha }{1 - \alpha }} - \frac{M ( \alpha ) }{1 - \alpha } \frac{ ( {}_{\hspace{9pt}0}^{CFR}D^{\alpha } f ) ( 0 ) }{s + \frac{\alpha }{1 - \alpha }} + \mathfrak{L} \{ g \} ( s ) = \lambda \mathfrak{L} \{ f \} ( s ) \\& \quad = \frac{M ( \alpha ) }{1 - \alpha } \frac{s\frac{M ( \alpha ) }{1 - \alpha } \frac{s\mathfrak{L} \{ ( f ) \} ( s ) }{s + \frac{\alpha }{1 - \alpha }}}{s + \frac{ \alpha }{1 - \alpha }} - \frac{M ( \alpha ) }{1 - \alpha } \frac{ ( {}_{\hspace{9pt}0}^{CFR}D^{\alpha } f ) ( 0 ) }{s + \frac{ \alpha }{1 - \alpha }} + \mathfrak{L} \{ g \} ( s ) = \lambda \mathfrak{L} \{ f \} ( s ) \\& \quad = \biggl[ \frac{M ( \alpha ) }{1 - \alpha } \frac{s}{s + \frac{ \alpha }{1 - \alpha }} \biggr] ^{2}\mathfrak{L} \bigl\{ ( f ) \bigr\} ( s ) - c_{1} \frac{M ( \alpha ) }{1 - \alpha } \frac{1}{s + \frac{\alpha }{1 - \alpha }} + \mathfrak{L} \{ g \} ( s ) = \lambda \mathfrak{L} \{ f \} ( s ) \\& \quad \Rightarrow\quad \mathfrak{L} \bigl\{ ( f ) \bigr\} ( s ) = \frac{c_{1}\frac{M ( \alpha ) }{1 - \alpha } \frac{1}{s + \frac{\alpha }{1 - \alpha }}}{ ( \frac{M ( \alpha ) }{1 - \alpha } \frac{s}{s + \frac{\alpha }{1 - \alpha }} ) ^{2} - \lambda } - \frac{1}{ ( \frac{M ( \alpha ) }{1 - \alpha } \frac{s}{s + \frac{ \alpha }{1 - \alpha }} ) ^{2} - \lambda } \mathfrak{L} \{ g \} ( s ). \end{aligned}$$

(15)

Now, if we apply the inverse Laplace transform to equation (15) and use a convolution theorem, so we can find the sum representation of solution, noted by (14), of problem (12)–(13). □

Theorem 13

Let us consider the fractional Sturm–Liouville initial value problem with exponential kernel:

$$\begin{aligned}& ^{CF}L_{2}f ={}_{\hspace{9pt}0}^{CFC}D^{\alpha } \bigl( {}_{\hspace{9pt}0}^{CFC}D^{\alpha } f ( x ) \bigr) + q ( x ) f ( x ) = \lambda f ( x ), \quad x \in [ 0, n ] , n \in \mathrm{R}^{ +}, \end{aligned}$$

(16)

$$\begin{aligned}& {}_{\hspace{9pt}0}^{CFC}D^{\alpha } f ( 0 ) = c_{1}, \quad f ( 0 ) = c_{2}, \end{aligned}$$

(17)

where $0 < \alpha < 1$, $q ( x )$ is a real-valued continuous function on $[ 0, n ]$. Then the representation of solution of problem (16)–(17) is as follows: $\lambda \ne \{ 0, 1 \}$,

$$\begin{aligned} f ( x, \lambda ) =& c_{1}\biggl( - \frac{ - \alpha ( e ^{\frac{x\alpha \sqrt{\lambda }}{1 + ( \alpha - 1 ) \sqrt{ \lambda }}} ( - 1 + ( \alpha - 1 ) \sqrt{\lambda } ) ^{2} + e^{\frac{x\alpha \sqrt{\lambda }}{ - 1 + ( \alpha - 1 ) \sqrt{\lambda }}} ( 1 + ( \alpha - 1 ) \sqrt{ \lambda } ) ^{2} ) }{2 ( - 1 + ( \alpha - 1 ) ^{2}\lambda ) ^{2}} \\ &{} + \frac{ ( \alpha - 1 ) \delta ( x ) }{ - 1 + ( \alpha - 1 ) ^{2}\lambda } \biggr) \\ &{}- c_{2}\frac{ ( e^{\frac{x\alpha \sqrt{\lambda }}{1 + ( \alpha - 1 ) \sqrt{\lambda }}} ( 1 - ( \alpha - 1 ) \sqrt{\lambda } ) + e^{\frac{x\alpha \sqrt{\lambda }}{ - 1 + ( \alpha - 1 ) \sqrt{\lambda }}} ( 1 + ( \alpha - 1 ) \sqrt{\lambda } ) ) }{2 ( - 1 + ( \alpha - 1 ) ^{2}\lambda ) } \\ &{}+ \biggl( \frac{ - \alpha ( - e^{\frac{x\alpha \sqrt{\lambda }}{1 + ( \alpha - 1 ) \sqrt{\lambda }}} ( - 1 + ( \alpha - 1 ) \sqrt{\lambda } ) ^{2} + e^{\frac{x \alpha \sqrt{\lambda }}{ - 1 + ( \alpha - 1 ) \sqrt{ \lambda }}} ( 1 + ( \alpha - 1 ) \sqrt{\lambda } ) ^{2} ) }{2\sqrt{\lambda } ( - 1 + ( \alpha - 1 ) ^{2}\lambda ) ^{2}} \\ &{} - \frac{ ( \alpha - 1 ) ^{2}\delta ( x ) }{ - 1 + ( \alpha - 1 ) ^{2}\lambda } \biggr) * q ( x ) f ( x ). \end{aligned}$$

(18)

Proof

Proof is straightforward from the proof of Theorem 12. □

Theorem 14

Let us consider the fractional Sturm–Liouville initial value problem with exponential kernel:

$$\begin{aligned}& ^{CF}L_{3}f ={}_{\hspace{9pt}0}^{CFR}D^{\alpha } \bigl( {}_{\hspace{9pt}0}^{CFC}D^{\alpha } f ( x ) \bigr) + q ( x ) f ( x ) = \lambda f ( x ),\quad x \in [ 0, n ] , n \in \mathrm{R}^{ +}, \end{aligned}$$

(19)

$$\begin{aligned}& f ( 0 ) = c_{2}, \end{aligned}$$

(20)

where $0 < \alpha < 1$, $q ( x )$ is a real-valued continuous function on $[ 0, n ]$. Then the representation of solution of problem (19)–(20) is as follows: $\lambda \ne \{ 0, 1 \}$,

$$\begin{aligned} f ( x, \lambda ) =& - c_{2} \biggl( - \frac{e^{\frac{x\alpha \sqrt{\lambda }}{1 + ( \alpha - 1 ) \sqrt{\lambda }}} ( 1 - ( \alpha - 1 ) \sqrt{\lambda } ) + e ^{\frac{x\alpha \sqrt{\lambda }}{ - 1 + ( \alpha - 1 ) \sqrt{ \lambda }}} ( 1 + ( \alpha - 1 ) \sqrt{\lambda } ) }{2 ( 1 - \alpha ) ( - 1 + ( \alpha - 1 ) ^{2} \lambda ) ^{2}} \biggr) \\ &{} - \biggl( \frac{\alpha ( - e^{\frac{x\alpha \sqrt{\lambda }}{1 + ( \alpha - 1 ) \sqrt{\lambda }}} ( - 1 + ( \alpha - 1 ) \sqrt{\lambda } ) ^{2} + e^{\frac{x\alpha \sqrt{ \lambda }}{ - 1 + ( \alpha - 1 ) \sqrt{\lambda }}} ( 1 + ( \alpha - 1 ) \sqrt{\lambda } ) ^{2} ) }{2\sqrt{ \lambda } ( - 1 + ( \alpha - 1 ) ^{2}\lambda ) ^{2}} \\ &{}- \frac{ ( \alpha - 1 ) ^{2}\delta ( x ) }{ - 1 + ( \alpha - 1 ) ^{2}\lambda } \biggr) * q ( x ) f ( x ). \end{aligned}$$

(21)

Proof

Proof is straightforward from the proof of Theorem 12. □

Remark

Approximate solutions of the problems according to the Mittag-Leffler function $E_{\delta, \theta } ( z ) = \sum_{k = 0}^{500} \frac{z^{k}}{\Gamma ( \delta k + \theta ) }$ will be simulated in all of the figures, also let $B ( \alpha ) = M ( \alpha ) = 1$.

Theorem 15

Let us consider the fractional Sturm–Liouville initial value problem with exponential kernel:

$$ ^{CF}L_{4}f ={}_{\hspace{9pt}0}^{CFR}D^{\alpha } \bigl( {}_{\hspace{9pt}0}^{CFR}D^{\alpha } f ( x ) \bigr) + q ( x ) f ( x ) = \lambda f ( x ), \quad x \in [ 0, n ] , $$

(22)

where $0 < \alpha < 1$, $q ( x )$ is a real-valued continuous function on $[ 0, n ]$. Then the representation of solution of equation (22) is as follows: $\lambda \ne \{ 0, 1 \}$,

$$\begin{aligned} f ( x, \lambda ) =& - \biggl( \frac{\alpha ( - e^{\frac{x \alpha \sqrt{\lambda }}{1 + ( \alpha - 1 ) \sqrt{ \lambda }}} ( - 1 + ( \alpha - 1 ) \sqrt{\lambda } ) ^{2} + e^{\frac{x\alpha \sqrt{\lambda }}{ - 1 + ( \alpha - 1 ) \sqrt{\lambda }}} ( 1 + ( \alpha - 1 ) \sqrt{ \lambda } ) ^{2} ) }{2\sqrt{\lambda } ( - 1 + ( \alpha - 1 ) ^{2}\lambda ) ^{2}} \\ &{}- \frac{ ( \alpha - 1 ) ^{2}\delta ( x ) }{ - 1 + ( \alpha - 1 ) ^{2} \lambda } \biggr) * q ( x ) f ( x ). \end{aligned}$$

(23)

Proof

Proof is straightforward from the proof of Theorem 12. □

Theorem 16

Let us consider the fractional Sturm–Liouville initial value problem with Mittag-Leffler kernel:

$$\begin{aligned}& {}^{AB}L_{1}f ={}_{\hspace{9pt}0}^{ABC}D^{\alpha } \bigl( {}_{\hspace{9pt}0}^{ABR}D^{\alpha } f ( x ) \bigr) + q ( x ) f ( x ) = \lambda f ( x ),\quad x \in [ 0, 1 ] , \end{aligned}$$

(24)

$$\begin{aligned}& {}_{\hspace{9pt}0}^{ABR}D^{\alpha } f ( 0 ) = c_{3}, \end{aligned}$$

(25)

where $0 < \alpha < 1$, $q ( x )$ is a real-valued continuous function on $[ 0, 1 ]$. Then the representation of solution of problem (24)–(25) is as follows: $\lambda \ne \{ 0, 1 \}$,

$$\begin{aligned} f ( x,\lambda ) =& c_{3} \biggl[ \frac{ ( 1 - \alpha ) }{1 - \lambda ( 1 - \alpha ) ^{2}} - \frac{\sqrt{ \lambda } ( 1 - \alpha ) ^{2}}{B ( \alpha ) ( B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2} ) } \biggl\{ 1 - E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr\} \\ &{}+ \frac{\sqrt{\lambda } ( 1 - \alpha ) ^{2}}{B ( \alpha ) ( B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2} ) } \biggl\{ 1 - E_{\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr\} \\ &{}- \frac{ ( 1 - \alpha ) }{2B ( \alpha ) ( B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) ) } \biggl\{ 1 - E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr\} \\ &{}- \frac{ ( 1 - \alpha ) }{2B ( \alpha ) ( B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) ) } \biggl\{ 1 - E_{\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x ^{\alpha } \biggr) \biggr\} \\ &{} + \alpha \biggl( \frac{1}{ - 2B ( \alpha ) \sqrt{ \lambda }} \biggl\{ 1 - E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x ^{\alpha } \biggr) \biggr\} \\ &{} + \frac{1}{2B ( \alpha ) \sqrt{ \lambda }} \biggl\{ 1 - E_{\alpha } \biggl( \frac{ - \alpha \sqrt{ \lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr\} \biggr) \biggr] \\ &{} + \biggl[ \frac{\delta ( x ) }{B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2}} \\ &{}+ \frac{\lambda \alpha ( 1 - \alpha ) }{B ( \alpha ) ( B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2} ) } \biggl[ \frac{x^{\alpha - 1}}{B ( \alpha ) - \sqrt{ \lambda } ( 1 - \alpha ) }E_{\alpha,\alpha } \biggl( \frac{ \alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{} + \frac{x^{\alpha - 1}}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }E _{\alpha,\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr] \\ &{}+ \frac{\sqrt{\lambda } \alpha }{B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2}} \biggl[ \frac{x^{\alpha - 1}}{2B ( \alpha ) }E_{\alpha,\alpha } \biggl( \frac{\alpha \sqrt{ \lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{}- \frac{x^{\alpha - 1}}{2B ( \alpha ) }E_{\alpha,\alpha } \biggl( \frac{ - \alpha \sqrt{ \lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr] \\ &{}+ \frac{\alpha ( 1 - \alpha ) }{B ( \alpha ) } \biggl[ \frac{x^{\alpha - 1}}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }E_{\alpha,\alpha } \biggl( \frac{\alpha \sqrt{ \lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{} + \frac{x^{\alpha - 1}}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }E_{ \alpha,\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr] \\ &{} + \alpha \biggl( \frac{x^{\alpha - 1}}{2\sqrt{\lambda } B ( \alpha ) }E_{\alpha,\alpha } \biggl( \frac{\alpha \sqrt{ \lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{} - \frac{x^{\alpha - 1}}{2\sqrt{ \lambda } B ( \alpha ) }E_{\alpha,\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr) \biggr] *q(x)f(x). \end{aligned}$$

(26)

Proof

Let us apply the Laplace transform to both sides of equation (24) and, by the help of Theorem 7, let $q ( x ) f ( x ) = g ( x )$,

$$\begin{aligned}& \mathfrak{L} \bigl\{ {}_{\hspace{9pt}0}^{ABC}D^{\alpha } \bigl( {}_{\hspace{9pt}0}^{ABR}D^{ \alpha } f \bigr) \bigr\} ( s ) + \mathfrak{L} \{ g \} ( s ) = \lambda \mathfrak{L} \{ f \} ( s ) \\& \quad = \frac{B ( \alpha ) }{1 - \alpha } \frac{s^{\alpha } \mathfrak{L} \{ ( {}_{\hspace{9pt}0}^{ABR}D^{\alpha } f ) \} ( s ) }{s^{\alpha } + \frac{\alpha }{1 - \alpha }} - \frac{B ( \alpha ) }{1 - \alpha } \frac{s^{\alpha - 1} ( {}_{\hspace{9pt}0}^{ABR}D^{\alpha } f ) ( 0 ) }{s^{\alpha } + \frac{ \alpha }{1 - \alpha }} + \mathfrak{L} \{ g \} ( s ) = \lambda \mathfrak{L} \{ f \} ( s ) \\& \quad = \frac{B ( \alpha ) }{1 - \alpha } \frac{s\frac{B ( \alpha ) }{1 - \alpha } \frac{s^{\alpha } \mathfrak{L} \{ ( f ) \} ( s ) }{s^{\alpha } + \frac{ \alpha }{1 - \alpha }}}{s + \frac{\alpha }{1 - \alpha }} - \frac{B ( \alpha ) }{1 - \alpha } \frac{s^{\alpha - 1} ( {}_{\hspace{9pt}0}^{ABR}D^{\alpha } f ) ( 0 ) }{s^{\alpha } + \frac{ \alpha }{1 - \alpha }} + \mathfrak{L} \{ g \} ( s ) = \lambda \mathfrak{L} \{ f \} ( s ) \\& \quad = \biggl( \frac{B ( \alpha ) }{1 - \alpha } \frac{s^{\alpha }}{s ^{\alpha } + \frac{\alpha }{1 - \alpha }} \biggr) ^{2}\mathfrak{L} \bigl\{ ( f ) \bigr\} ( s ) - c_{3} \frac{B ( \alpha ) }{1 - \alpha } \frac{s^{\alpha - 1} ( {}_{\hspace{9pt}0}^{ABR}D^{\alpha } f ) ( 0 ) }{s^{\alpha } + \frac{ \alpha }{1 - \alpha }} + \mathfrak{L} \{ g \} ( s ) = \lambda \mathfrak{L} \{ f \} ( s ) \\& \quad \Rightarrow \quad \mathfrak{L} \bigl\{ ( f ) \bigr\} ( s ) = c_{1}\frac{s^{\alpha - 1}}{\frac{B ( \alpha ) }{1 - \alpha } ( \frac{s^{2\alpha }}{s^{\alpha } + \frac{\alpha }{1 - \alpha }} ) - \lambda ( s^{\alpha } + \frac{\alpha }{1 - \alpha } ) } - \frac{1}{ ( \frac{B ( \alpha ) }{1 - \alpha } \frac{s^{\alpha }}{s^{\alpha } + \frac{\alpha }{1 - \alpha }} ) ^{2} - \lambda } \mathfrak{L} \{ g \} ( s ). \end{aligned}$$

 □

Now, if we apply the inverse Laplace transform to the last equation and use a convolution theorem, so we can find the sum representation of solution, noted by (26), of problem (24)–(25).

Theorem 17

Let us consider the fractional Sturm–Liouville initial value problem with Mittag-Leffler kernel:

$$\begin{aligned}& ^{AB}L_{2}f ={}_{\hspace{9pt}0}^{ABC}D^{\alpha } \bigl( {}_{\hspace{9pt}0}^{ABC}D^{\alpha } f ( x ) \bigr) + q ( x ) f ( x ) = \lambda f ( x ),\quad x \in [ 0, 1 ] , \end{aligned}$$

(27)

$$\begin{aligned}& {}_{\hspace{9pt}0}^{ABR}D^{\alpha } f ( 0 ) = c_{3},\quad f ( 0 ) = c_{4}, \end{aligned}$$

(28)

where $0 < \alpha < 1$, $q ( x )$ is a real-valued continuous function on $[ 0, n ]$. Then the representation of solution of problem (27)–(28) is as follows: $\lambda \ne \{ 0, 1 \}$,

$$\begin{aligned} f ( x,\lambda ) =& c_{3} \bigg[ \frac{1}{B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2}} \\ &{}+ \frac{\sqrt{\lambda } ( 1 - \alpha ) }{B ( \alpha ) ( B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2} ) } \biggl\{ E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x ^{\alpha } \biggr) \\ &{} - E_{\alpha } \biggl( \frac{ - \alpha \sqrt{ \lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr\} \\ &{}+ \frac{1}{B ( \alpha ) ( B ( \alpha ) + \sqrt{ \lambda } ( 1 - \alpha ) ) } \biggl\{ - \frac{1}{2} \biggl( 1 - E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr) \biggr\} \\ &{}- \frac{1}{B ( \alpha ) ( B ( \alpha ) + \sqrt{ \lambda } ( 1 - \alpha ) ) } \biggl\{ - \frac{1}{2} \biggl( 1 - E_{\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x ^{\alpha } \biggr) \biggr) \biggr\} \\ &{}+ \frac{ ( 1 - \alpha ) }{\sqrt{\lambda } B ( \alpha ) } \biggl\{ E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \\ &{}- E_{\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x ^{\alpha } \biggr) \biggr\} \\ &{}+ \frac{1}{\lambda B ( \alpha ) } \biggl\{ \frac{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }{ - 2} \biggl[ 1 - E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr] \\ &{} - \frac{B ( \alpha ) + \sqrt{ \lambda } ( 1 - \alpha ) }{2} \biggl[ 1 - E_{\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{ \lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr] \biggr\} \\ &{}+ c_{4} \biggl[ \frac{ ( 1 - \alpha ) }{1 - \lambda ( 1 - \alpha ) ^{2}} - \frac{\sqrt{\lambda } ( 1 - \alpha ) ^{2}}{B ( \alpha ) ( B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2} ) } \\ &{}\times \biggl[ 1 - E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{ \lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr] \\ &{}+ \frac{\sqrt{\lambda } ( 1 - \alpha ) ^{2}}{B ( \alpha ) ( B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2} ) } \biggl[ 1 - E_{\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr] \\ &{}- \frac{ ( 1 - \alpha ) }{2B ( \alpha ) ( B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) ) } \biggl[ 1 - E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr] \\ &{}- \frac{ ( 1 - \alpha ) }{2B ( \alpha ) ( B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) ) } \biggl[ 1 - E_{\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x ^{\alpha } \biggr) \biggr] \\ &{}+ \alpha \biggl( \frac{1}{ - 2B ( \alpha ) \sqrt{ \lambda }} \biggl\{ 1 - E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x ^{\alpha } \biggr) \biggr\} \\ &{} + \frac{1}{2B ( \alpha ) \sqrt{ \lambda }} \biggl\{ 1 - E_{\alpha } \biggl( \frac{ - \alpha \sqrt{ \lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr\} \biggr) \biggr] \\ &{}- \biggl[ \frac{\delta ( x ) }{B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2}} \\ &{}+ \frac{\lambda \alpha ( 1 - \alpha ) }{B ( \alpha ) ( B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2} ) } \biggl[ \frac{x^{\alpha - 1}}{B ( \alpha ) - \sqrt{ \lambda } ( 1 - \alpha ) }E_{\alpha,\alpha } \biggl( \frac{ \alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{} + \frac{x^{\alpha - 1}}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }E _{\alpha,\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr] \\ &{}+ \frac{\lambda \alpha^{2}}{B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2}} \biggl[ \frac{x^{\alpha - 1}}{2\alpha \sqrt{ \lambda } B ( \alpha ) }E_{\alpha,\alpha } \biggl( \frac{ \alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{} - \frac{x^{\alpha - 1}}{2 \alpha \sqrt{\lambda } B ( \alpha ) }E_{\alpha,\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{ \lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr] \\ &{}+ \frac{\alpha ( 1 - \alpha ) }{B ( \alpha ) } \biggl[ \frac{x^{\alpha - 1}}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }E_{\alpha,\alpha } \biggl( \frac{\alpha \sqrt{ \lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{} + \frac{x^{\alpha - 1}}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }E_{ \alpha,\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr] \\ &{} + \alpha \biggl( \frac{x^{\alpha - 1}}{2\sqrt{\lambda } B ( \alpha ) }E_{\alpha,\alpha } \biggl( \frac{\alpha \sqrt{ \lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{} - \frac{x^{\alpha - 1}}{2\sqrt{ \lambda } B ( \alpha ) }E_{\alpha,\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr) \biggr] *q(x)f(x). \end{aligned}$$

(29)

Proof

Proof is straightforward from the proof of Theorem 16. □

Theorem 18

Let us consider the fractional Sturm–Liouville initial value problem with Mittag-Leffler kernel:

$$\begin{aligned}& ^{AB}L_{3}f ={}_{\hspace{9pt}0}^{ABR}D^{\alpha } \bigl( {}_{\hspace{9pt}0}^{ABC}D^{\alpha } f ( x ) \bigr) + q ( x ) f ( x ) = \lambda f ( x ),\quad x \in [ 0, 1 ] , \end{aligned}$$

(30)

$$\begin{aligned}& f ( 0 ) = c_{4}, \end{aligned}$$

(31)

where $0 < \alpha < 1$, $q ( x )$ is a real-valued continuous function on $[ 0, 1 ]$. Then the representation of solution of problem (30)–(31) is as follows: $\lambda \ne \{ 0, 1 \}$,

$$\begin{aligned} f ( x,\lambda ) =& c_{4} \biggl[ \frac{1}{B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2}} \\ &{}+ \frac{\sqrt{\lambda } ( 1 - \alpha ) }{B ( \alpha ) ( B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2} ) } \biggl\{ E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x ^{\alpha } \biggr) \\ &{} - E_{\alpha } \biggl( \frac{ - \alpha \sqrt{ \lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr\} \\ &{}+ \frac{1}{B ( \alpha ) ( B ( \alpha ) + \sqrt{ \lambda } ( 1 - \alpha ) ) } \biggl\{ - \frac{1}{2} \biggl( 1 - E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr) \biggr\} \\ &{}- \frac{1}{B ( \alpha ) ( B ( \alpha ) - \sqrt{ \lambda } ( 1 - \alpha ) ) } \biggl\{ - \frac{1}{2} \biggl( 1 - E_{\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x ^{\alpha } \biggr) \biggr) \biggr\} \\ &{}+ \frac{ ( 1 - \alpha ) }{\sqrt{\lambda } B ( \alpha ) } \biggl\{ E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) - E_{\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x ^{\alpha } \biggr) \biggr\} \\ &{} + \frac{1}{\lambda B ( \alpha ) } \biggl\{ \frac{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }{ - 2} \biggl[ 1 - E_{\alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr] \\ &{} - \frac{B ( \alpha ) + \sqrt{ \lambda } ( 1 - \alpha ) }{2} \biggl[ 1 - E_{\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{ \lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr] \biggr\} \biggr] \\ &{} - \biggl[ \frac{\delta ( x ) }{B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2}} \\ &{}+ \frac{\lambda \alpha ( 1 - \alpha ) }{B ( \alpha ) ( B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2} ) } \biggl[ \frac{x^{\alpha - 1}}{B ( \alpha ) - \sqrt{ \lambda } ( 1 - \alpha ) }E_{\alpha,\alpha } \biggl( \frac{ \alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{} + \frac{x^{\alpha - 1}}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }E _{\alpha,\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr] \\ &{}+ \frac{\lambda \alpha^{2}}{B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2}} \biggl[ \frac{x^{\alpha - 1}}{2\alpha \sqrt{ \lambda } B ( \alpha ) }E_{\alpha,\alpha } \biggl( \frac{ \alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{} - \frac{x^{\alpha - 1}}{2 \alpha \sqrt{\lambda } B ( \alpha ) }E_{\alpha,\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{ \lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr] \\ &{}+ \frac{\alpha ( 1 - \alpha ) }{B ( \alpha ) } \biggl[ \frac{x^{\alpha - 1}}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }E_{\alpha,\alpha } \biggl( \frac{\alpha \sqrt{ \lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{} + \frac{x^{\alpha - 1}}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }E_{ \alpha,\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr] \\ &{} + \alpha \biggl( \frac{x^{\alpha - 1}}{2\sqrt{\lambda } B ( \alpha ) }E_{\alpha,\alpha } \biggl( \frac{\alpha \sqrt{ \lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{} - \frac{x^{\alpha - 1}}{2\sqrt{ \lambda } B ( \alpha ) }E_{\alpha,\alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr) \biggr] *q(x)f(x). \end{aligned}$$

(32)

Proof

Proof is straightforward from the proof of Theorem 16. □

Theorem 19

Let us consider the fractional Sturm–Liouville initial value problem with Mittag-Leffler kernel:

$$ ^{AB}L_{4}f ={}_{\hspace{9pt}0}^{ABR}D^{\alpha } \bigl( {}_{\hspace{9pt}0}^{ABR}D^{\alpha } f ( x ) \bigr) + q ( x ) f ( x ) = \lambda f ( x ),\quad x \in [ 0, 1 ] , $$

(33)

where $0 < \alpha < 1$, $q ( x )$ is a real-valued continuous function on $[ 0, 1 ]$. Then the representation of solution of equation (33) is as follows: $\lambda \ne \{ 0, 1 \}$,

$$\begin{aligned} f ( x, \lambda ) =& \biggl[ \frac{\delta ( x ) }{B ^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2}} \\ &{}+ \frac{\lambda \alpha ( 1 - \alpha ) }{B ( \alpha ) ( B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2} ) } \biggl[ \frac{x^{\alpha - 1}}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }E_{ \alpha, \alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \\ &{} + \frac{x^{\alpha - 1}}{B ( \alpha ) + \sqrt{ \lambda } ( 1 - \alpha ) }E_{\alpha, \alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr] \\ &{}+ \frac{\sqrt{\lambda } \alpha }{B^{2} ( \alpha ) - \lambda ( 1 - \alpha ) ^{2}} \biggl[ \frac{x^{\alpha - 1}}{2B ( \alpha ) }E_{\alpha, \alpha } \biggl( \frac{\alpha \sqrt{ \lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{}- \frac{x^{\alpha - 1}}{2B ( \alpha ) }E_{\alpha, \alpha } \biggl( \frac{ - \alpha \sqrt{ \lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr] \\ &{}+ \frac{\alpha ( 1 - \alpha ) }{B ( \alpha ) } \biggl[ \frac{x^{\alpha - 1}}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }E_{\alpha, \alpha } \biggl( \frac{\alpha \sqrt{\lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{} + \frac{x^{\alpha - 1}}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }E_{ \alpha, \alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{ \alpha } \biggr) \biggr] \\ &{} + \alpha \biggl[ \frac{x^{\alpha - 1}}{2\sqrt{\lambda } B ( \alpha ) }E_{\alpha, \alpha } \biggl( \frac{\alpha \sqrt{ \lambda }}{B ( \alpha ) - \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \\ &{} - \frac{x^{\alpha - 1}}{2\sqrt{ \lambda } B ( \alpha ) }E_{\alpha, \alpha } \biggl( \frac{ - \alpha \sqrt{\lambda }}{B ( \alpha ) + \sqrt{\lambda } ( 1 - \alpha ) }x^{\alpha } \biggr) \biggr] \biggr] * q ( x ) f ( x ). \end{aligned}$$

(34)

Proof

Proof is straightforward from the proof of Theorem 16. □

4 Conclusion

In this study, we have considered fractional Sturm–Liouville (S–L) problems within non-singular operators. A fractional S–L problem with exponential and Mittag-Leffler kernels is given with different versions in the Riemann–Liouville and Caputo sense. Also, we obtain the representation of solutions for S–L problems by the Laplace transform and find analytical solutions of the problems. We analyze solutions of these different versions and display them by simulation under different potentials, different orders, and different eigenvalues. However, we compare the solutions of the problem with these different versions, and we also compare the solutions of the problem with exponential and Mittag-Leffler kernels together by simulation.

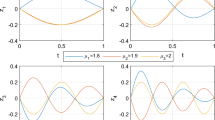
We compare the eigenfunctions of problems (12)–(13), (19)–(20), and (16)–(17) under different orders, and we observe that the eigenfunctions of the problems converge to each other as x increases in Fig. 1, Fig. 2, and Fig. 3. We compare the eigenfunctions of problems (12)–(13), (19)–(20), and (16)–(17) with each other, and we observe that the eigenfunctions of the problems converge to each other as x increases in Fig. 4. We compare the eigenfunctions of problem (12)–(13) with different orders, different domains, different potential functions, and different eigenvalues in Fig. 5, Fig. 6, Fig. 7, and Fig. 8.

Figure 1

Comparions of eigenfunctions for the problem (12), (13) under different orders $\lambda = 36$, $c_{1} = - 1$, $q = 0$

Figure 2

Comparions of eigenfunctions for the problem (19), (20) under different orders $\lambda = 36$, $c_{2} = - 1$, $q = 0$

Figure 3

Comparions of eigenfunctions for the problem (16), (17) under different orders $\lambda = 36$, $c_{1} = c_{2} = - 1$, $q = 0$

Figure 4

Comparions of eigenfunctions for the problems (19), (20)—(12), (13)—(16), (17) $\lambda = 36$, $c_{1} = c_{2} = - 1$, $q = 0$, $\alpha = 0.4$

Figure 5

Comparions of eigenfunctions for the problem (12), (13) under different orders $c_{1} = - 1$, $q = 0$, $x = 1$

Figure 6

Comparions of eigenfunctions for the problem (12), (13) under different domains $c _{1} = - 1$, $\alpha = 0.4$, $q = 0$

Figure 7

Comparions of eigenfunctions for the problem (12), (13) under different eigenvalues $c_{1} = - 1$, $\alpha = 0.3$, $q = 0$

Figure 8

Comparions of eigenfunctions for the problem (12), (13) under different potentials $c_{1} = - 1$, $\lambda = 36$, $\alpha = 0.3$

We compare the eigenfunctions of problems (24)–(25), (30)–(31), and (27)–(28) under different orders, and we observe that the eigenfunctions of the problems converge to each other as x increases in Fig. 9, Fig. 10, and Fig. 11. We compare the eigenfunctions of problems (24)–(25), (30)–(31), and (27)–(28) with each other in Fig. 12. We compare the eigenfunctions of problem (24)–(25) with different orders, different eigenvalues, different domains, and different potential functions in Fig. 13, Fig. 14, Fig. 15, and Fig. 16.

Figure 9

Comparions of eigenfunctions for the problem (24), (25) under different orders $\lambda = 36$, $c_{3} = - 1$, $q = 0$

Figure 10

Comparions of eigenfunctions for the problem (30), (31) under different orders $\lambda = 36$, $c_{4} = - 1$, $q = 0$

Figure 11

Comparions of eigenfunctions for the problem (27), (28) under different orders $\lambda = 36$, $c_{3} = c_{4} = - 1$, $q = 0$

Figure 12

Comparions of eigenfunctions for the problem (30), (31)—(24), (25)—(27), (28) $\lambda = 36$, $\alpha = 0.4$, $c_{3} = c_{4} = - 1$, $q = 0$

Figure 13

Comparions of eigenfunctions for the problem (24), (25) under different orders $c_{3} = 1$, $q = 0$, $x = 0.5$

Figure 14

Comparions of eigenfunctions for the problem (24), (25) under different eigenvalues $\alpha = 0.4$, $c_{3} = - 1$, $q = 0$

Figure 15

Comparions of eigenfunctions for the problem (24), (25) under different domains $\alpha = 0.4$, $c _{3} = 1$, $q = 0$

Figure 16

Comparions of eigenfunctions for the problem (24), (25) under different potentials $\lambda = 36$, $\alpha = 0.3$, $c_{3} = - 1$

Eigenvalues of problem (24)–(25) corresponding to some specific eigenfunctions are given with different orders in Table 1 and Table 2. Finally, we compare the eigenfunctions of problems (12)–(13) and (24)–(25) with different orders in Fig. 17, Fig. 18, and Fig. 19.

Figure 17

Comparison of eigenfunctions for the problem (12), (13)—(24), (25) $\alpha = 0.3$, $\lambda = 36$, $c_{1} = c_{3} = - 1$, $q = 0$

Figure 18

Comparison of eigenfunctions for the problem (12), (13)—(24), (25) $\alpha = 0.4$, $\lambda = 36$, $c_{1} = c_{3} = - 1$, $q = 0$

Figure 19

Comparison of eigenfunctions for the problem (12), (13)—(24), (25) $\alpha = 0.5$, $\lambda = 36$, $c_{1} = c_{3} = - 1$, $q = 0$

Table 1 Numerical approximations to the first four eigenvalues of problem (24)–(25) according to $E_{\delta, \theta } ( z) =\sum_{k = 0}^{750}\frac{z^{k}}{\Gamma ( \delta k + \theta ) }$. Eigenvalues correspond to eigenfunction $f ( 1 )$

Table 2 Numerical approximations to the first four eigenvalues of problem (24)–(25) according to $E_{\delta, \theta } ( z) =\sum_{k = 0}^{750}\frac{z^{k}}{\Gamma ( \delta k + \theta ) }$. Eigenvalues correspond to eigenfunction $f ( 0.5 )$

Generally, in this study, we consider fractional SL problems with different versions of new non-singular fractional operators with different versions, i.e., Caputo–Caputo, Caputo–Riemann, Riemann–Caputo, and Riemann–Riemann. We have obtained the representation of solutions of these different versions, we simulate these solutions with graphics and evaluate the solutions by means of graphics.

Also, we analyze advantages and disadvantages of these different versions. We have called SL problems (12)–(13) and (24)–(25) with Caputo–Riemann non-singular operators ${}^{CF}L_{1}$ and ${}^{AB}L_{1}$ respectively, problems (16)–(17) and (27)–(28) with Caputo–Caputo non-singular operators ${}^{CF}L_{2}$ and ${}^{AB}L_{2}$ respectively, problems (19)–(20) and (30)–(31) with Riemann–Caputo non-singular operators ${}^{CF}L_{3}$ and ${}^{AB}L_{3}$ respectively, equations (22) and (33) with Riemann–Riemann non-singular operators ${}^{CF}L_{4}$ and ${}^{AB}L_{4}$ respectively. Problems (12)–(13) and (24)–(25) have one initial condition and this initial condition has fractional order. Problems (16)–(17) and (27)–(28) have two initial conditions, one is fractional and one is integer order. Hence, problems (16)–(17) and (27)–(28) are more suitable in view of proving the existence and uniqueness results. Problems (19)–(20) and (30)–(31) have one initial condition and this initial condition has integer order. Equations (22) and (33) have no initial condition, thus this solution has only a nontrivial solution while $q ( x )$ is not a constant.

We can observe that the eigenfunctions of problems (12)–(13), (16)–(17), and (19)–(20) converge to each other as x increases in Fig. 4, additionally the eigenfunctions of problems (24)–(25), (27)–(28), and (30)–(31) show paralellism to each other in Fig. 12, and accordingly, the eigenfunctions may coincide with each other if the initial conditions are changed.

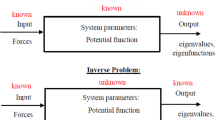
This paper may give an idea for determining the most suitable choice for defining inverse problems in fractional spectral theory.