Dynamic behaviors of a turbidostat model with Tissiet functional response and discrete delay

Abstract

In this paper, dynamic behaviors of a turbidostat model with Tissiet functional response, linear variable yield and time delay are investigated. The existence and boundedness of solutions, the local asymptotic stability of its equilibria and the phenomenon of Hopf bifurcation for this system are considered. Using the Liapunov–LaSalle invariance principle, we show that the washout equilibrium is global asymptotic stability for any time delay. Furthermore, based on some knowledge of limit set, we show the necessary and sufficient conditions of permanent of the turbidostat model. Finally, numerical simulations are offered to support our results.

1 Introduction

The turbidostat is an important laboratory apparatus used to culture the microorganisms continuously. It is of both mathematical and ecological interest since its applicability in microbiology and population biology. Therefore, the study of the turbidostat model has been one of the hottest subjects investigated by many mathematical and theoretical biologists [1–7].

Dynamical behaviors of ecological systems may be affected by many factors such as time delay, variable yield and functional response. It is well known that the time delay occurs naturally in daily life and makes ecological systems have more complex dynamic behaviors. Therefore, ecological systems with time delay have been investigated in recent years (discrete delays [8–15], neutral delays [16, 17] and impulsive delay [18]). Taking the time delay as a parameter, the stability of the equilibrium may be changed and periodic solutions may occur as the time delay varies. So it is also necessary to consider the impact of the time delay in turbidostat model.

Chemostat models not only with constant yield but also with variable yield [19–24] are considered. Since actual experiments show that the constant yield cannot explain the oscillatory phenomenon in the chemostat, and the greater the nutrient concentrate is the lower the consuming rate is. However, mostly for the turbidostat model we assume that the yield term is a constant. Based on the facts, a variable yield should be considered for the turbidostat model and the model with variable yield will have more complicated dynamic behaviors than that with constant yield.

Furthermore, the functional response also has an important impact on the behavior of biological dynamical systems [25–29]. We note the fact that, in biology, very high nutrient concentration may inhibit the growth of microorganisms actually, and the microorganisms will die eventually as the nutrient concentration increasing unlimitedly. So the Tissiet functional response $\mu(S)= \frac{\mu_{m}Se^{-\frac{S}{k_{i}}}}{k_{m}+S}$ is introduced, where $\mu_{m}$, $k_{m}$ and $k_{i}$ are positive constants.

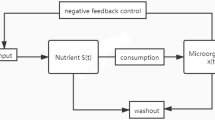
Based on the above biological phenomenon, in this paper, we consider the combined effect of time delay due to the digestion, linear variable yield and Tissiet functional response as the following system:

$$ \textstyle\begin{cases} \frac{\mathrm{d}x(t)}{\mathrm{d}t}=x(t) ( \frac{\mu_{m}S(t-\tau )}{k_{m}+S(t-\tau)}e^{-\frac{S(t-\tau)}{k_{i}}}-(d+kx(t)) ),\\ \frac{\mathrm{d}S(t)}{\mathrm{d}t}=(S^{0}-S(t))(d+kx(t))- \frac{\mu _{m}S(t)}{k_{m}+S(t)}e^{-\frac{S(t)}{k_{i}}}\frac{x(t)}{A+BS(t)}, \end{cases} $$

(1.1)

where $x(t)$ and $S(t)$ represent the concentration of microorganism and nutrient at time t, respectively. $S^{0}>0$ presents the input concentration of the nutrient. $A+BS(t)$ $(A>0,B>0)$ is the linear variable yield. $\tau\geq0$ is the delay of digestion, and $d+kx(t)$ $(d>0, k>0)$ is the dilution rate of the turbidostat.

For the sake of simplicity, we usually set

$$x(t)=S^{0}\bar{x}(t), \qquad S(t)=S^{0}y(t), \qquad k= \frac{\bar{k}}{S^{0}}, \qquad k_{m}=aS^{0}, \qquad k_{i}= \frac{S^{0}}{b},\qquad B= \frac{S^{0}}{C}. $$

The bars of $x(t)$ and k are dropped, and system (1.1) becomes

$$ \textstyle\begin{cases} \frac{\mathrm{d}x(t)}{\mathrm{d}t}=x(t) ( \frac{\mu_{m}y(t-\tau )}{a+y(t-\tau)}e^{-by(t-\tau)}-(d+kx(t)) ),\\ \frac{\mathrm{d}y(t)}{\mathrm{d}t}=(1-y(t))(d+kx(t))- \frac{\mu _{m}y(t)}{a+y(t)}e^{-by(t)}\frac{x(t)}{A+Cy(t)}, \end{cases} $$

(1.2)

with initial value conditions

$$x(t)=\varphi_{1}(t)\geq0,\qquad y(t)=\varphi_{2}(t)\geq0, \quad t\in[-\tau,0], $$

where $\varphi_{1}(t)$, $\varphi_{2}(t)$ are continuous functions on $[-\tau,0]$. By a biological meaning, we further assume that $\varphi_{i}(0)>0$ for $i=1,2$.

The organization of this paper is as follows. In next section, we analyze the existence and boundedness of solutions of (1.2) with the initial condition. In Sect. 3, the existence, local stability of the equilibriums and the existence of the local Hopf bifurcation are considered. Using the Liapunov–LaSalle invariance principle, we in Sect. 4 discuss the global asymptotic stability of the washout equilibrium of (1.2). In Sect. 5, the permanence of (1.2) is discussed by some analytic techniques on limit sets of differential dynamical systems. Finally, some discussions and numerical simulations are given to illustrate the theoretical analysis in Sect. 6.

2 Existence and boundedness of solutions

In the section, we investigate the existence and boundedness of solutions of (1.2) with the initial condition. The following theorem is achieved.

Theorem 2.1

The solution $(x(t), y(t))$ of system (1.2) with the initial condition exists and is positive on $[0, +\infty)$. Furthermore,

$$\limsup_{t\rightarrow+\infty}x(t)\leq \frac{\mu_{m}}{k},\qquad \limsup _{t\rightarrow+\infty} y(t) \leq1, \qquad \liminf_{t\rightarrow+\infty} y(t) \geq v_{1}, $$

where $v_{1}= \frac{akdA}{akdA+\mu_{m}^{2}}$.

Proof

From the theory of local existence of solutions of functional differential equations, we see that $(x(t), y(t))$ is existent on $[0, e)$ for some positive constant e. We first show that $x(t)>0$ for any $t\in[0, e)$. From the first equation of (1.2) and $\varphi_{1}(0)>0$, we have

$$x(t)=x(0)e^{ \int_{0}^{t}\frac{\mu_{m}y(t-\tau)}{a+y(t-\tau)}e^{-by(t-\tau )}-(d+kx(t))\,\mathrm{d}t}>0, \quad\mbox{for any } t\in[0, e). $$

We further show that $y(t)>0$ for any $t\in[0, e)$. In fact, if not so, by the continuity of $y(t)$ and $\varphi_{2}(0)\geq0$, then there is $t_{1}\geq0$ such that

$$y(t_{1})=0,\qquad\dot{y}(t_{1})\leq0 \quad\mbox{and}\quad y(t)\geq0\quad (-\tau\leq t\leq t_{1}), $$

where $\dot{y}(t_{1})$ denotes the right-hand derivative, if $t_{1}=0$. From the second equation of (1.2) and $x(t)>0$ for $t\in[0, e)$, we see that

$$\dot{y}(t_{1})=\bigl(1-y(t_{1})\bigr) \bigl(d+kx(t_{1})\bigr)- \frac{\mu _{m}y(t_{1})}{a+y(t_{1})}e^{-by(t_{1})} \frac{x(t_{1})}{A+Cy(t_{1})}=d+kx(t_{1})>0, $$

which contradicts $\dot{y}(t_{1})\leq0$. This shows that $y(t)>0$ for any $t\in[0, e)$.

In the following, we will show that $x(t)$ and $y(t)$ are bounded on $[0, e)$. In fact, from the non-negative of $x(t)$ and $y(t)$ on $[-\tau, e)$ and system (1.2), we see that for any $t\in[0, e)$

$$ \textstyle\begin{cases} \frac{\mathrm{d}x(t)}{\mathrm{d}t}\leq x(t)(\mu_{m}-kx(t)),\\ \frac{\mathrm{d}y(t)}{\mathrm{d}t}\leq (1-y(t))(d+kx(t)). \end{cases} $$

(2.1)

Since the solution $u(t)$ of the following equation:

$$\frac{\mathrm{d}u(t)}{\mathrm{d}t}= u(t) \bigl(\mu_{m}-ku(t)\bigr) $$

is existent on $[0, +\infty)$ with the initial condition $u(t)=\varphi_{1}(t)\geq0$ for $t\in[-\tau,0]$, from the comparison principle $x(t)\leq u(t)$ for any $t\in[0, e)$ the maximum of $d+kx(t)$ for $t\in[0, e)$ exists, it is denoted by M. Hence, we obtain

$$ \textstyle\begin{cases} \frac{\mathrm{d}x(t)}{\mathrm{d}t}\leq x(t)(\mu_{m}-kx(t)),\\ \frac{\mathrm{d}y(t)}{\mathrm{d}t}\leq M(1-y(t)). \end{cases} $$

(2.2)

Similarly, from the solution $v(t)$ of the following equation:

$$\frac{\mathrm{d}v(t)}{\mathrm{d}t}= M\bigl(1-v(t)\bigr) $$

is existent on $[0, +\infty)$ with the initial condition $v(t)=\varphi_{2}(t)\geq0$ for $t\in[-\tau,0]$, $y(t)\leq v(t)$ for any $t\in[0, e)$. Hence, we see that the solution $(x(t), y(t))$ is bounded on $[0, e)$.

Thus, from the theory of continuation of solutions for functional differential equations, we see that $(x(t), y(t))$ is existent and positive on $[0, +\infty)$. Further, from (2.2), we have

$$\limsup_{t\rightarrow+\infty}x(t)\leq \frac{\mu_{m}}{k},\qquad \limsup_{t\rightarrow+\infty} y(t) \leq1. $$

For sufficiently large T, $t>T$, it is easy to see that from system (1.2)

$$\frac{\mathrm{d}y(t)}{\mathrm{d}t}\geq d\bigl(1-y(t)\bigr)- \frac{\mu _{m}^{2}y(t)}{akA}=d-\biggl(d+ \frac{\mu_{m}^{2}}{akA}\biggr)y(t), $$

which implies

$$\liminf_{t\rightarrow+\infty} y(t)\geq v_{1}, $$

where $v_{1}= \frac{akdA}{akdA+\mu_{m}^{2}}$.

The proof of Theorem 2.1 is thus completed. □

3 Local asymptotic stability of equilibriums and Hopf bifurcations

In this section, we will investigate the existence and local stability of the equilibriums of system (1.2) and Hopf bifurcations are induced by delay.

First, we define the subset

$$G=\bigl\{ \varphi=(\varphi_{1}, \varphi_{2})\in C | \varphi_{1}\geq0, v_{1}\leq \varphi_{2} \leq1\bigr\} $$

and show that G is a positively invariant set with respect to (1.2).

For any $\varphi=(\varphi_{1}, \varphi_{2})\in G$, let $(x(t), y(t))$ be the solution of (1.2) with the initial function φ, we see that $(x(t), y(t))$ is positive on $[0, +\infty)$ from Theorem 2.1. We show $y(t)\leq1$ for any $t\geq0$. In fact, if there is a $t_{2}>0$ such that $y(t_{2})> 1$, from the Lagrange mean value theorem, we see that $\dot{y}(t_{3})>0$ and $y(t_{3})=1$ for some $t_{3} \in(0, t_{2})$. From the second equation of (1.2), we see that

$$\frac{\mathrm{d}y(t_{3})}{\mathrm{d}t}=\bigl(1-y(t_{3})\bigr) \bigl(d+kx(t_{3}) \bigr)- \frac{\mu _{m}y(t_{3})}{a+y(t_{3})}e^{-by(t_{3})}\frac{x(t_{3})}{A+Cy(t_{3})}< 0, $$

which contradicts $\dot{y}(t_{3})>0$.

We further show that $y(t)\geq v_{1}$ for any $t\geq0$. If not so, there must be $t_{4}\geq0$ such that $y(t_{4})=v_{1}$, $y(t)\geq v_{1}$ for all $t\in[-\tau, t_{4}]$ and $\dot{y}(t_{4})\leq0$. From the second equation of (1.2), we see that

$$\begin{aligned} \frac{\mathrm{d}y(t_{4})}{\mathrm{d}t}&=\bigl(1-y(t_{4})\bigr) \bigl(d+kx(t_{4}) \bigr)- \frac{\mu _{m}y(t_{4})}{a+y(t_{4})}e^{-by(t_{4})}\frac{x(t_{4})}{A+Cy(t_{4})} \\ &>d(1-v_{1})- \frac{\mu_{m}^{2}v_{1}}{akA} \\ &=d-v_{1} \frac{\mu_{m}^{2}+akdA}{akdA}=0, \end{aligned}$$

which contradicts $\dot{y}(t_{4})\leq0$.

Therefore, G is a positively invariant set with respect to (1.2). It is enough to consider system (1.2) on G.

Next, we will consider the existence of the equilibriums of (1.2).

From the right part of (1.2), we see that (1.2) always has a washout equilibrium $E_{0}=(0, 1)$. As far as the positive equilibrium is concerned, the analysis of the equation $\frac{\mu_{m}y}{a+y}e^{-by}-k(1-y)(A+Cy)-d=0$ is needed. We define

$$f(y)=\mu_{m}ye^{-by}-k(1-y) (A+Cy) (a+y)-d(a+y), $$

then accordingly we have

$$\begin{aligned} &f'(y)=\mu_{m}e^{-by}-\mu_{m}bye^{-by}+3kCy^{2}+2k(aC+A-C)y-Ak+ak(A-C)-d, \\ &f''(y)=-2\mu_{m}be^{-by}+ \mu_{m}b^{2}ye^{-by}+6kCy+2k(aC+A-C), \\ &f'''(y)=3\mu_{m}b^{2}e^{-by}- \mu_{m}b^{3}ye^{-by}+6kC, \\ &f''''(y)= \mu_{m}b^{3}e^{-by}(by-4). \end{aligned}$$

Notice that

$$\begin{aligned} &f(0)=-ad-akA< 0,\qquad f(1)=\mu_{m}e^{-b}-d-ad, \\ &f'(0)=\mu_{m}+Ak(a-1)+akC-d,\qquad f''(0)=-2 \mu_{m}b+2k(aC+A-C), \\ &f'''(0)=3\mu_{m}b^{2}+6kC>0, \qquad f'''(1)=\mu_{m}b^{2}(3-b)e^{-b}+6kC, \\ &f''''(0)=-4 \mu_{m}b^{3}< 0,\qquad f''''(1)= \mu_{m}b^{3}(b-4)e^{-b}. \end{aligned}$$

For convenience, we assume that

$$\begin{aligned} &(\mathrm{H}_{1})\quad b< 4, \qquad f'''(1)>0, \qquad f''(0)>0 \quad\mbox{and}\quad f'(0)>0; \\ &(\mathrm{H}_{2})\quad \frac{\mu_{m}e^{-b}}{1+a}\leq d; \\ &(\mathrm{H}_{3})\quad \frac{\mu_{m}e^{-b}}{1+a}> d. \end{aligned}$$

Hence, we have the following results.

Theorem 3.1

• (1) If $(\mathrm{H}_{1})$ and $(\mathrm{H}_{2})$ hold, then there is no root for $f(y)=0$ on $[0, 1]$, i.e., system (1.2) only has the washout equilibrium $E_{0}=(0, 1)$.

• (2) If $(\mathrm{H}_{1})$ and $(\mathrm{H}_{3})$ hold, then there is a positive root for $f(y)=0$ on $[0, 1]$, denoted by $y^{*}$, i.e., system (1.2) has a unique positive equilibrium $E^{*}=(x^{*}, y^{*})$, where $x^{*}=(1-y^{*})(A+Cy^{*})$.

In the following, we will discuss the locally asymptotical stability of the washout equilibrium $E_{0}=(0, 1)$ of system (1.2).

Theorem 3.2

If $\frac{\mu_{m}e^{-b}}{1+a}< d$, then $E_{0}$ is locally asymptotically stable; If $\frac{\mu_{m}e^{-b}}{1+a}= d$, then the trivial solution of the linearized system of (1.2) about $E_{0}$ is stable; if $\frac{\mu_{m}e^{-b}}{1+a}> d$, then $E_{0}$ is unstable.

Proof

Let $y_{1}(t)=y(t)-1$ and rewrite $y_{1}(t)$ as $y(t)$. We obtain the linear system

$$ \textstyle\begin{cases} \frac{\mathrm{d}x(t)}{\mathrm{d}t}= ( \frac{\mu_{m}e^{-b}}{1+a}-d)x(t),\\ \frac{\mathrm{d}y(t)}{\mathrm{d}t}= - \frac{\mu_{m}e^{-b}}{(1+a)(A+C)}x(t)-dy(t). \end{cases} $$

(3.1)

The following characteristic equation can be obtained from (3.1):

$$ (\lambda+d) \biggl(\lambda- \frac{\mu_{m}e^{-b}}{1+a}+d\biggr)=0. $$

(3.2)

It is obvious that (3.2) has a negative root $\lambda_{1}=-d$. We will further study the sign of the root $\lambda_{2}= \frac{\mu_{m}e^{-b}}{1+a}-d$.

If $\frac{\mu_{m}e^{-b}}{1+a}< d$, then $\lambda_{2}<0$. Hence, $E_{0}$ is locally asymptotically stable.

If $\frac{\mu_{m}e^{-b}}{1+a}= d$, then $\lambda_{2}=0$. Hence, we see that the trivial solution of the linearized system of (1.2) about $E_{0}$ is stable.

If $\frac{\mu_{m}e^{-b}}{1+a}> d$, then $\lambda_{2}>0$. Hence, $E_{0}$ is unstable.

The proof of Theorem 3.2 is completed. □

To consider the local stability of $E^{*}$ and the existence of Hopf bifurcations, we set

$$\begin{aligned} &M=-kx^{*},\qquad N= \frac{\mu_{m}e^{-by^{*}}x^{*}(a-aby^{*}-by^{*^{2}})}{(a+y^{*})^{2}},\qquad P= \frac{-d}{A+Cy^{*}}, \\ &Q=-d-kx^{*}- \frac{\mu _{m}e^{-by^{*}}x^{*}(-bCy^{*^{3}}-(abC+Ab+C)y^{*^{2}}-Aaby^{*}+Aa)}{((a+y^{*})(A+Cy^{*}))^{2}}, \end{aligned}$$

and make the following assumptions:

$$\begin{aligned} &(\mathrm{H}_{4})\quad Q+M< 0, MQ-PN>0; \\ &(\mathrm{H}_{5})\quad MQ+PN< 0. \end{aligned}$$

Theorem 3.3

If $(\mathrm{H}_{4})$ and $(\mathrm{H}_{5})$ hold, then $E^{*}$ is locally asymptotically stable for $\tau<\tau_{0}$; $E^{*}$ is unstable for $\tau>\tau_{0}$; Hopf bifurcation occurs when $\tau=\tau_{j}$, $j=0,1,2,\ldots$ , that is, a family of periodic solutions bifurcate from the positive equilibrium $E^{*}$ as τ passes through the critical values $\tau_{j}$, $j=0,1,2,\ldots$ .

Proof

Let $\bar{x}(t)=x(t)-x^{*}$, $\bar{y}(t)=y(t)-y^{*}$ and drop the bars, then we obtain the linear system

$$ \textstyle\begin{cases} \frac{\mathrm{d}x(t)}{\mathrm{d}t}= Mx(t)+Ny(t-\tau),\\ \frac{\mathrm{d}y(t)}{\mathrm{d}t}= Px(t)+Qy(t). \end{cases} $$

(3.3)

The following characteristic equation can be achieved from (3.3):

$$ \lambda^{2}-(Q+M)\lambda-PNe^{-\lambda\tau}+MQ=0. $$

(3.4)

When $\tau=0$, (3.4) becomes

$$ \lambda^{2}-(Q+M)\lambda+MQ-PN=0. $$

(3.5)

According to the Routh–Hurwitz criterion, one can see that (3.5) always has two roots with negative real parts when $(\mathrm{H}_{4})$ holds.

Now for $\tau>0$, suppose that $\lambda=iw$ ($w>0$) is a root of (3.4) for some τ, then we have

$$-w^{2}-(Q+M)wi+MQ-PNe^{-iw\tau}=0. $$

Separating the real and imaginary parts, we obtain

$$ \textstyle\begin{cases} -w^{2}+MQ-PN\cos w\tau=0,\\ -(Q+M)w+PN\sin w\tau=0, \end{cases} $$

(3.6)

which implies the following equation:

$$ w^{4}+\bigl(Q^{2}+M^{2} \bigr)w^{2}+(MQ)^{2}-(PN)^{2}=0. $$

(3.7)

It is easy to see that when $(\mathrm{H}_{5})$ holds, (3.7) has only one positive real root,

$$w_{0}=\sqrt{\frac{-(Q^{2}+M^{2})+\sqrt{(Q^{2}+M^{2})^{2}-4((MQ)^{2}-(PN)^{2})}}{2}}. $$

By substituting $w_{0}$ into (3.6) and solving for τ, we can obtain

$$ \tau_{j}= \frac{1}{w_{0}}\biggl(\arccos\biggl( \frac{-w_{0}^{2}+MQ}{PN}\biggr)+2j\pi\biggr),\quad j=0,1,2,\ldots. $$

(3.8)

Thus, when $\tau=\tau_{j}$, the characteristic equation (3.4) has a pair of purely imaginary roots $\pm iw_{0}$.

Let $\lambda(\tau)=\alpha(\tau)+i\beta(\tau)$ be the root of (3.4) near $\tau=\tau_{j}$ satisfying $\alpha(\tau_{j})=0$ and $\beta(\tau_{j})=w_{0}$. Next, we will prove the transversality condition of a Hopf bifurcation.

Differentiating (3.4) with respect to τ, we have

$$ \biggl( \frac{\mathrm{d}\lambda}{\mathrm{d}\tau} \biggr)^{-1}= \frac{2\lambda -(Q+M)}{-PNe^{-\lambda\tau}\lambda}- \frac{\tau}{\lambda}, $$

(3.9)

which together with (3.4) leads to

$$ \begin{aligned}[b] \operatorname{sign} \biggl\{ \operatorname{Re} \biggl( \frac{\mathrm{d}\lambda}{\mathrm {d}\tau} \biggr)_{\tau=\tau_{j}} \biggr\} &=\operatorname{sign} \biggl\{ \operatorname{Re} \biggl( \frac{\mathrm{d}\lambda}{\mathrm {d}\tau} \biggr)^{-1}_{\tau=\tau_{j}} \biggr\} \\ &=\operatorname{sign} \biggl\{ \operatorname{Re} \biggl( \frac{Q+M-2\lambda}{\lambda(\lambda ^{2}-(Q+M)\lambda+QM)} \biggr)_{\tau=\tau_{j}} \biggr\} \\ &=\operatorname{sign} \biggl\{ \frac {Q^{2}+M^{2}+2w_{0}^{2}}{(Q+M)^{2}w_{0}^{2}+(QM-w_{0}^{2})^{2}} \biggr\} \\ &=1. \end{aligned} $$

(3.10)

Hence, if $(\mathrm{H}_{5})$ holds, then there is a Hopf bifurcation at $\tau=\tau_{j}$. Therefore, if $(\mathrm{H}_{4})$ and $(\mathrm{H}_{5})$ hold, then $E^{*}$ is locally asymptotically stable for $\tau<\tau_{0}$, $E^{*}$ is unstable for $\tau>\tau_{0}$ and there is a periodic solution around $E^{*}$ for $\tau=\tau_{j}$, $j=1,2,\ldots$ .

The proof of Theorem 3.3 is completed. □

4 Global asymptotic stability analysis of $E_{0}$

In Sect. 3, we have studied the local stability of $E_{0}$. In this section, we will analyze the global asymptotic stability of $E_{0}$ by the Liapunov–LaSalle invariance principle. We obtain the following theorem.

Theorem 4.1

For any time delay τ, if $(\mathrm{H}_{1})$ holds, then the washout equilibrium $E_{0}$ is globally asymptotically stable for $\frac{\mu _{m}e^{-b}}{1+a}< d$, and globally attractive for $\frac{\mu _{m}e^{-b}}{1+a}= d$.

Proof

We have shown that $G=\{\varphi=(\varphi_{1}, \varphi_{2})\in C | \varphi_{1}\geq0, v_{1}\leq\varphi_{2} \leq1\}$ is a positively invariant set with respect to (1.2).

Consider the function V on G as follows:

$$ V(x, y)= e^{V_{1}}, $$

(4.1)

where $V_{1}=-y(t)+ \int_{0}^{t}d(1-y(t)-\frac{x(t)}{A+Cy(t)})\,\mathrm{d}t$. It is clear that $V(x, y)$ is continuous on G. Its derivative along the solution of (1.2) satisfies

$$ \begin{aligned}[b] \dot{V}(x, y)|_{\text{(1.2)}}={}&e^{V_{1}} \biggl(-\dot{y}(t)+d\biggl(1-y(t)-\frac {x(t)}{A+Cy(t)}\biggr)\biggr) \\ ={}&e^{V_{1}}\biggl(-\bigl(1-y(t)\bigr) \bigl(d+kx(t)\bigr)+ \frac{\mu_{m}y(t)}{a+y(t)}e^{-by(t)}\frac {x(t)}{A+Cy(t)} \\ &{}+d\biggl(1-y(t)-\frac{x(t)}{A+Cy(t)}\biggr)\biggr) \\ ={}&e^{V_{1}} \frac{x(t)}{(a+y(t))(A+Cy(t))}\bigl(\mu_{m}y(t)e^{-by(t)} \\ &{}-k\bigl(1-y(t)\bigr) \bigl(a+y(t)\bigr) \bigl(A+Cy(t)\bigr)-d\bigl(a+y(t) \bigr)\bigr) \\ ={}&e^{V_{1}} \frac{x(t)}{(a+y(t))(A+Cy(t))}f\bigl(y(t)\bigr). \end{aligned} $$

(4.2)

Since (1.2) has a unique equilibrium $E_{0}$, we have $f(y)\leq0$ for any $y\in[0, 1]$. Hence, for any $t\geq0$

$$\dot{V}(x, y)|_{\text{(1.2)}}\leq0. $$

This implies that $V(x, y)$ is a Liapunov function of (1.2) on G.

Define the subset E of G as $E=\{(x(t), y(t))\in G \mid \dot{V}(x, y)|_{\text{(1.2)}}=0 \}$. From (4.2), we see that

$$E=\bigl\{ \bigl(x(t), y(t)\bigr)\in G \mid x(t)=0 \mbox{ or } f\bigl(y(t) \bigr)=0 \bigr\} . $$

Let M be the largest invariant set of (1.2) in E. Since $E_{0}=(0, 1)\in M$, M is not empty. We discuss the following two cases, respectively.

(i) If $\frac{\mu_{m}e^{-b}}{1+a}< d$, then $f(y(t))<0$ on $[0, 1]$. Hence,

$$E=\bigl\{ \bigl(x(t), y(t)\bigr)\in G \mid x(t)=0 \bigr\} . $$

Let $(x(t), y(t))\in M\subset E$ be the solution of (1.2). We have $x(t)\equiv0$ for any $t\in R$. From the second equation of system (1.2), we see that $\dot{y}(t)=d(1-y(t))$ for any $t\in R$. Since $y(t)\rightarrow1$ as $t\rightarrow+\infty$, we have $y(t)\equiv1$ for any $t\in R$. Therefore,

$$M=\bigl\{ (0, 1)\bigr\} =\{E_{0}\}. $$

By the Liapunov–LaSalle invariance principle, we see that $E_{0}$ is globally attractive. From Theorem 3.2, we see that $E_{0}$ is globally asymptotically stable.

(ii) If $\frac{\mu_{m}e^{-b}}{1+a}= d$, then we have $f(y)=0$ for $y=1$. Hence,

$$E=\bigl\{ \bigl(x(t), y(t)\bigr)\in G \mid x(t)=0 \mbox{ or } y(t)=1 \bigr\} . $$

If $y(t)=1$ for some $t\in R$, from the invariance of G, the function $y(t)$ takes local maximum at t. Hence, it must see that $\dot{y}(t)=0$. From the second equation of system (1.2), we see that

$$\dot{y}(t)=\bigl(1-y(t)\bigr) \bigl(d+kx(t)\bigr)- \frac{\mu_{m}y(t)}{a+y(t)}e^{-by(t)} \frac {x(t)}{A+Cy(t)}=0. $$

Since $y(t)=1$, we see that $x(t)=0$. Therefore, it has $x(t)\equiv 0$ for any $t\in R$. From the proof of case (i), one also has $M=\{(0, 1)\}=\{E_{0}\}$. Thus, from the Liapunov–LaSalle invariance principle, we see that $E_{0}$ is globally attractive, again.

The proof of Theorem 4.1 is completed. □

5 Permanence

In this section, we will use the same method as [30] to prove the permanence of (1.2). We have the following theorem.

Theorem 5.1

Under the condition $(\mathrm{H}_{1})$, for any time delay τ, $(\mathrm{H}_{3})$ is the necessary and sufficient condition for the permanence of (1.2).

Proof

If $(\mathrm{H}_{3})$ is not valid, then the washout equilibrium $E_{0}$ of (1.2) is globally asymptotically stable or globally attractive. Thus, we only need to prove the sufficiency. From the definition of permanence, we need to prove

$$ \liminf_{t\rightarrow+\infty}x(t)\geq v_{2}, $$

(5.1)

where $v_{2}$ is some positive constant which does not depend on the initial function φ. The proof is divided into two steps.

In a first step, we will prove

$$ \liminf_{t\rightarrow+\infty}x(t)> 0. $$

(5.2)

Since we have the invariance of G, it is enough to consider the solution $(x(t), y(t))$ $(t\geq0)$ with the initial function $\varphi\in G$. From the above discussion, we see that the omega limit set $\omega(\varphi)$ of $(x(t), y(t))$ $(t\geq0)$ is nonempty, compact, invariant and $\omega(\varphi)\subset G$.

If $\liminf_{t\rightarrow+\infty}x(t)= 0$, we will show that there is a contradiction.

In fact, since $\liminf_{t\rightarrow+\infty}x(t)= 0$, we see that there exists a positive time sequence $\{t_{n}\}$: $t_{n}\rightarrow+\infty$ as $n\rightarrow+\infty$ such that

$$\lim_{t_{n}\rightarrow+\infty}x(t_{n})= 0,\qquad\dot{x}(t_{n}) \leq0,\qquad x(t)\geq x(t_{n}) \quad(t_{n}-\tau\leq t \leq t_{n}). $$

By Theorem 2.1, the solution $(x(t), y(t))$ is bounded for any $t\geq0$. From (1.2), the solution $(x(t), y(t))$ is uniformly continuous for any $t\geq0$. Hence, by Ascoli’s theorem, there is a subsequence of $\{t_{n}\}$, still denoted by $\{t_{n}\}$, such that

$$\lim_{t_{n}\rightarrow+\infty}\bigl(x(t_{n}), y(t_{n}) \bigr)= \bigl(\bar{x}(t), \bar{y}(t)\bigr) $$

uniformly on R in the wider sense. From the invariance of G and Theorem 4.1, we see that $(\bar{x}(t), \bar{y}(t))\in G$ for any $t\in R$, and that, for any $\tau\in R$, the function $(\bar{x}(t+\tau), \bar{y}(t+\tau))$ of t is the solution of (1.2) with the initial function $(\bar{x}_{\tau}, \bar{y}_{\tau})$. Here we note that $\bar{x}(0)=0$ and $v_{1}\leq \bar{y}(t)\leq1$ for $t\in R$.

We claim that $(\bar{x}(t), \bar{y}(t))=(0, 1)$ for all $t\in R$. In fact, if $\varphi_{1}(0)>0$, then we see that the solution $(x(t), y(t))$ of (1.2) exists and $x(t)>0$ and $y(t)>0$ for all $t\geq0$. Hence, from $\bar{x}(0)=0$, we further see that $\bar{x}(t)=0$ for any $t<0$. Thus, from (1.2), we see that $\bar{x}(t)\equiv0$ for any $t \in R$ and that $\bar{y}'(t))=d(1-\bar{y}(t))$ for any $t \geq\tau$. Thus,

$$\bar{y}(t)=\bar{y}(0)e^{-dt}+1-e^{-dt} \quad(t \geq\tau). $$

From the arbitrariness of τ, we see that

$$\bar{y}(t)=1+\bigl(\bar{y}(0)-1\bigr)e^{-dt}. $$

From Theorem 2.1, we know that $\bar{y}(t)$ is bounded for any $t\in R$. Thus, we have $\bar{y}(0)=1$, which implies $\bar{y}(t)=1$ for any $t\in R$. From system (1.2) and the invariance of G, we see that $(\bar{x}(t), \bar{y}(t))=(0, 1)$ for any $t\in R$. Thus, the above claim holds.

Specially, we see that

$$\begin{aligned} &\lim_{n\rightarrow+\infty}x(t_{n})=\bar{x}(0)=0, \\ & \lim _{n\rightarrow+\infty}y(t_{n}-\tau)=\bar{y}(-\tau)=1, \\ &\lim_{n\rightarrow+\infty}\frac{\mu_{m}y(t_{n}-\tau)}{a+y(t_{n}-\tau )}e^{-by(t_{n}-\tau)}= \frac{\mu_{m}e^{-b}}{a+1}>d. \end{aligned}$$

For sufficiently small $\epsilon>0$ and sufficiently large n, we have

$$\frac{\mu_{m}y(t_{n}-\tau)}{a+y(t_{n}-\tau)}e^{-by(t_{n}-\tau)}-kx(t_{n})> \frac {\mu_{m}e^{-b}}{a+1}- \epsilon>d. $$

Hence,

$$\begin{aligned} \dot{x}(t_{n})&=\biggl( \frac{\mu_{m}y(t_{n}-\tau)}{a+y(t_{n}-\tau)}e^{-by(t_{n}-\tau )}-d-kx(t_{n}) \biggr)x(t_{n}) \\ &>\biggl( \frac{\mu_{m}e^{-b}}{a+1}-\epsilon-d\biggr)x(t_{n})>0, \end{aligned}$$

which contradicts $\dot{x}(t_{n})\leq0$.

The proof of $\liminf_{t\rightarrow+\infty}x(t)> 0$ is completed.

In a second step, we will prove

$$\liminf_{t\rightarrow+\infty}x(t)\geq v_{2}. $$

For any initial functions sequence $\{\varphi_{n}\}=\{(\varphi_{1}^{(n)}, \varphi_{2}^{(n)})\}\subset G$, let $(x^{(n)}(t), y^{(n)}(t))$ be the solution of (1.2) with the initial function $\varphi_{n}$. Let $\omega_{n}(\varphi_{n})$ be the omega limit set of $(x^{(n)}(t), y^{(n)}(t))$. We see that there is some compact and invariant set $\omega^{*} \subset G$ such that $dist(\omega_{n}(\varphi_{n}), \omega^{*})\rightarrow0$ as $n\rightarrow +\infty$. Here, $dist(\omega_{n}(\varphi_{n}), \omega^{*})$ means Hausdorff distance.

If (5.1) does not hold, for some initial function sequence $\{\varphi_{n}\}=\{(\varphi_{1}^{(n)}, \varphi_{2}^{(n)})\}\subset G$ such that $\varphi_{1}^{(n)}(0)>0$, we see that there is some $\bar{\varphi}=(\bar{\varphi}_{1}, \bar{\varphi}_{2})\in\omega^{*}$ such that $\bar{\varphi}_{1}(\theta_{0})=0$ for some $\theta_{0}\in[-\tau, 0]$. Now, let $(\bar{x}(t), \bar{y}(t))$ be the solution of (1.2) with the initial function φ̄. Then, from the invariance of $\omega^{*}$, we see that $(\bar{x}_{t}, \bar{y}_{t})\in\omega^{*}$ for any $t\in R$. From $\bar{\varphi}_{1}(\theta_{0})=0$ and the positivity of all solutions, we easily see that $\bar{x}(t)=0$ for all $t\leq\theta_{0}$. Thus, from (1.2), we have $\bar{\varphi}_{1}(\theta)=0$ $(-\tau\leq \theta\leq0)$ and $\bar{x}(t)=0$ $(t\in R)$. This implies that $\bar{x}(t)=0$, $\bar{y}(t)=h(t)$ for all $t\in R$, where $h(t)=1+(\bar{\varphi}_{2}(0)-1)e^{-dt}$.

If $\bar{\varphi}_{2}(0)<1$, we see that the negative semi-orbit $(\bar{x}_{t}, \bar{y}_{t})$ $(t\leq0)$ is unbounded. This is a contradiction.

If $\bar{\varphi}_{2}(0)=1$, we see that $\bar{x}(t)=0$, $\bar{y}(t)=1$ for any $t\in R$. This shows that $\bar{\varphi}=(0, 1)=E_{0}\in\omega^{*}$. We will show that $E_{0}$ is isolated. That is, there exists some neighborhood U of $E_{0}$ in G such that $E_{0}$ is the largest invariant set in U. In fact, we choose

$$U=\bigl\{ \varphi\mid\varphi=(\varphi_{1}, \varphi_{2})\in \bar{G}, \Vert \varphi -E_{0} \Vert < \epsilon\bigr\} , $$

for some sufficiently small positive constant ϵ and $\epsilon< \frac{\mu_{m}e^{-b}-d(a+1)}{\mu_{m}e^{-b}-d}$. We shall show that $E_{0}$ is the largest invariant set in U for some ϵ.

If not, for any sufficiently small ϵ, there exists some invariant set W $(W\subset U)$ such that $W\setminus E_{0}$ is not empty. Let $\varphi=(\varphi_{1}, \varphi_{2})\in W\setminus E_{0}$ and $(x_{t}, y_{t})$ be the solution of (1.2) with the initial function φ. Then, $(x_{t}, y_{t})\in W$ for all $t\in R$.

If $\varphi_{1}(0)=0$, by the invariance of W and Theorem 2.1, we also have the contradiction that $\varphi=E_{0}$ or that the negative semi-orbit $(x_{t}, y_{t})$ $t<0$ of (1.2) through φ is unbounded.

If $\varphi_{1}(0)>0$, from Theorem 2.1, we have $x(t)>0$ for all $t\geq0$. Now, let us consider the following continuous function:

$$ P(t)=x(t)+\rho \int_{0}^{t} kx^{2}(t)\,\mathrm{d}t. $$

(5.3)

for some constant $\rho>1$. Since $(x_{t}, y_{t})\in W$ for all $t\in R$, we have $1-\epsilon\leq y(t) \leq1$ for all $t\in R$. The time derivative of $P(t)$ along the solution $(x(t), y(t))$ satisfies

$$ \begin{aligned}[b] \dot{P}(t)&=\dot{x}(t)+\rho kx^{2}(t) \\ &=x(t) \biggl( \frac{\mu_{m}y(t-\tau)}{a+y(t-\tau)}e^{-by(t-\tau )}-\bigl(d+kx(t)\bigr) \biggr)+ \rho kx^{2}(t) \\ &=(\rho-1) \bigl(d+kx(t)\bigr)x(t)+x(t) \biggl( \frac{\mu_{m}y(t-\tau)}{a+y(t-\tau )}e^{-by(t-\tau)}-d \rho\biggr) \\ &\geq (\rho-1) \bigl(d+kx(t)\bigr)x(t)+x(t) \biggl( \frac{\mu_{m}e^{-b}(1-\epsilon)}{a+1-\epsilon }-d\rho \biggr). \end{aligned} $$

(5.4)

Since $\epsilon< \frac{\mu_{m}e^{-b}-d(a+1)}{\mu_{m}e^{-b}-d}$ and $\frac{\mu_{m}e^{-b}}{a+1}>d$, we see that $\frac{\mu_{m}e^{-b}(1-\epsilon)}{a+1-\epsilon}>d$. We can choose $\rho>1$ such that $1<\rho< \frac{\mu_{m}e^{-b}(1-\epsilon)}{d(a+1-\epsilon)}$. From (5.2), for some constant η and all large $t\geq t_{5}>0$, we see that $x(t)\geq\eta>0$. Thus, from (5.4)

$$ \dot{P}(t)\geq(\rho-1) \bigl(d+kx(t)\bigr)x(t)>0. $$

(5.5)

Thus, $P(t)\rightarrow+\infty$ as $t\rightarrow+\infty$. This is a contradiction to Theorem 2.1. We see that $E_{0}$ is isolated.

It is easy to see that the semigroup defined by the solution of (1.2) satisfies the conditions of Lemma 4.3 in [31] with $M=E_{0}$. Thus, from the lemma, we see that there is some $\xi=(\xi_{1}, \xi_{2})$ such that $\xi\in\omega^{*} \cap(W^{s}(E_{0}) \setminus E_{0})$. Here, $W^{s}(E_{0})$ is the stable set of $E_{0}$.

If $\xi_{1}(0)=0$, by the invariance of M and Theorem 2.1, we have the contradiction that $\xi=E_{0}$ or that the negative semi-orbit $(\tilde{x}_{t}, \tilde{y}_{t})$ $(t<0)$ of (1.2) through ξ is unbounded.

If $\xi_{1}(0)>0$, by Theorem 2.1, we see that $\tilde{x}(t)>0$, $\tilde{y}(t)>0$ for any $t>0$. From $\xi\in \omega^{*} \cap(W^{s}(E_{0}) \setminus E_{0})$, we have $\lim_{t\rightarrow+\infty}\tilde{x}(t)=0$, $\lim_{t\rightarrow+\infty}\tilde{y}(t)=1$, which is a contradiction to (5.2). This shows that (5.1) holds. Hence, (1.2) is permanent.

The proof of Theorem 5.1 is completed. □

6 Discussion and numerical simulation

We have studied a turbidostat model with Tissiet functional response, linear variable yield and time delay in this paper. Using comparison principle and some knowledge of functional differential equations, we obtain the global existence and boundedness of solutions of (1.2). Furthermore, based on the Liapunov–LaSalle invariance principle, we also obtain the global attraction and global asymptotic stability of the washout equilibrium of (1.2). The results tell us that the time delay is harmless for the local and global stability of the washout equilibrium of (1.2). However, the stability of the positive equilibrium will be changed and Hopf bifurcations will occur with the time delay varying. Finally, we show that the system is permanent if and only if the positive equilibrium $E^{*}$ exists. Unfortunately, in this paper, we only consider one of the cases of the existence of the positive equilibriums. The other cases shall be left as future work.

In the section, we present numerical simulation to illustrate the analytical results. By setting $a=1.2$, $\mu_{m}=2.5$, $b=0.1$, $d=0.2$, $k=0.5$, $A=0.2$ and $C=1.8$, we obtain the following specific example of system (1.2):

$$ \textstyle\begin{cases} \frac{\mathrm{d}x(t)}{\mathrm{d}t}=x(t) ( \frac{2.5y(t-\tau )}{1.2+y(t-\tau)}e^{-0.1y(t-\tau)}-(0.2+0.5x(t)) ),\\ \frac{\mathrm{d}y(t)}{\mathrm{d}t}=(1-y(t))(0.2+0.5x(t))- \frac {2.5y(t)}{1.2+y(t)}e^{-0.1y(t)}\frac{x(t)}{0.2+1.8y(t)}. \end{cases} $$

(6.1)

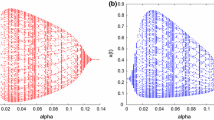
It is easy to see that the conditions $(\mathrm{H}_{1})$ and $(\mathrm{H}_{3})$ hold. Thus, system (6.1) has a positive equilibrium $E^{*}=(x^{*}, y^{*})=(0.5, 0.27)$. Through a simple calculation, conditions $(\mathrm{H}_{4})$ and $(\mathrm{H}_{5})$ hold, we have $w_{0}\doteq0.206$, $\tau_{0}\doteq10.1$ and $\operatorname{Re}\{ ( \frac{\mathrm{d}\lambda}{\mathrm{d}\tau} )^{-1}_{\lambda=iw_{0}}\}=12.42>0$. By Theorem 3.3, the positive equilibrium $E^{*}$ is asymptotically stable when $\tau=9$ $<\tau_{0}$ (see Fig. 1). The positive equilibrium $E^{*}$ is unstable and a Hopf bifurcation occurs, i.e., a bifurcating periodic solution occurs from $E^{*}$ when $\tau=11$ $>\tau_{0}$ (see Fig. 2).

Figure 1

The positive equilibrium $E^{*}=(0.5, 0.27)$ of (6.1) is asymptotically stable when $\tau=9 <\tau_{0}\doteq 10.1$. Here $(x(0), y(0))=(0.2,0.4)$

Figure 2

The positive equilibrium $E^{*}=(0.5, 0.27)$ of (6.1) is unstable and a bifurcating periodic solution occurs from $E^{*}$ when $\tau=11 >\tau_{0}\doteq 10.1$. Here $(x(0), y(0))=(0.2,0.4)$