1 Introduction

During the last decade, many scholars [1–39] proposed various single or multiple species modeling. Such topics as the existence and stability of the equilibrium, the existence, uniqueness, and stability of the periodic solution or almost periodic solution, the persistence and extinction of the system have been extensively investigated, and many interesting results have been obtained. It brings to our attention that all the models are based on a single species model, while a logistic model is one of the basic single species models, it is the cornerstone of the mathematics biology. On the other hand, the harvest of populations is one of the human purposes to achieve the economic interests. Already, there are many scholars investigating the dynamic behaviors of the population models incorporating the harvesting, see [3, 4, 7, 28–31] and the references cited therein.

The classical single species logistic equation is as follows:

$$ \dot{x}(t)=x(t) \bigl(r-ax(t) \bigr), $$
(1.1)

where \(x(t)\) is the density of the species at time t, r represents the intrinsic growth rate. \(a=\frac{r}{K}\) is usually referred to as the density dependent rate, the positive constant K is the environmental saturation level or carrying capacity. Traditionally, one may assume that the harvest rate \(h(t)\) is a constant h or under the catch-per-unit effort hypothesis \(Ex(t)\); consequently, the logistic equation with harvesting takes the form [3, 4]:

$$ \dot{x}(t)=x(t) \bigl(r-ax(t) \bigr)-h $$
(1.2)

or

$$\dot{x}(t)=x(t) \bigl(r-ax(t) \bigr)-Ex(t), $$

where E denotes the harvesting effort. Two types of solution behavior may be seen in system (1.2). If \(h< r^{2}/(4a)\), the harvesting is subcritical and solutions either tend to a positive limiting value as \(t\rightarrow\infty\), or, depending on the value of initial value, may tend to zero in finite time. If \(h>r^{2}/(4a)\), the harvesting is supercritical and solutions always tend to zero in finite time.

A more realistic harvesting term would be small for small value of x and would incorporate a saturation effect for enough large x; one option is to replace h in (1.2) with a Holling type-II functional response.

$$ h(t)=\frac{\eta Ex(t)}{\mu E+\nu x(t)}, $$
(1.3)

where η, E, μ, ν are positive parameters that are used for the catchability coefficient of the species, the effort devoted to their nonselective harvesting, each proportional to the radio of the stock-level to the catch-rate at higher levels of effort and each proportional to the radio of the effort level to the catch-rate at higher stock-levels. One could refer to [5–7] for more detailed information on term (1.3). As \(E\rightarrow\infty\), the limiting value of \(h(t)\) becomes a function of x only and \(h(t)\rightarrow(\eta/\mu)x\). When \(x\rightarrow\infty\), \(h(t)\rightarrow(\eta/\nu)E\). One can easily observe that the catch-rate function in (1.3) embodies saturation efforts with respect to the effort level as well as stocking abundance. Term (1.3) can be translated into another form as follows:

$$h(t)=\frac{\gamma x(t)}{\alpha+\beta x(t)}, $$

where \(\alpha=\mu\), \(\beta=\nu/E\), and \(\gamma=\eta\) are positive parameters that are used for the species saturation constant, another saturation constant, and the effects of harvest rate, respectively. Obviously, if \(\beta=0\), then the above term degenerates to linear capture [4].

It is often the case that harvesting occurs at fixed moments every year, which brings about short-term rapid changes for the densities of the species. Impulsive differential systems are suitable for the mathematical simulation of this evolutionary process ([3–14, 28–39]). In this paper, we propose the following autonomous logistic model with regular harvest pulse:

$$ \begin{gathered} \dot{x}(t)=x(t) \bigl(r-ax(t) \bigr),\quad t \neq t_{k}, \\ x\bigl(t^{+}_{k}\bigr)= \biggl(1- \frac{\gamma}{\alpha+\beta x(t_{k})} \biggr)x(t_{k}),\quad t=t_{k}, \end{gathered} $$
(1.4)

together with the initial condition

$${x}(0)>0. $$

It is assumed that the impulsive points satisfy \(0=t_{0}< t_{1}=t_{0}+\theta<\cdots<t_{k}=t_{0}+k\theta<\cdots\) with \(\lim_{t\rightarrow+\infty}t_{k}=+\infty\), that is, the harvests are regular. And it is necessary to satisfy the relationship \(0\leq \gamma<\min\{\alpha,1\}\) for biological reality (\(x(t_{k}^{+})>0\), \(k=1,2,\ldots \)), i.e., the harvesting is proportional to the current density of species x. There are some particular forms on system (1.4). System (1.4) with \(\beta=\gamma=0\), \(\alpha\neq0\) is reduced to the logistic equation 1.1. System (1.4) with \(\alpha=1\), \(\beta=0\) is reduced to the linear impulsive logistic equation [2]:

$$ \begin{gathered}\dot{x}(t)=x(t) \bigl(r-ax(t) \bigr),\quad t \neq t_{k}, \\ x\bigl(t^{+}_{k}\bigr)= (1-\gamma )x(t_{k}),\quad t=t_{k}. \end{gathered} $$
(1.5)

In [2], by applying the comparison theorem and constructing some suitable Lyapunov functionals, the authors discussed the permanence and global attractivity of system (1.5), but they did not discuss the extinction property of system (1.5). System (1.4) with \(\theta=0\) is reduced to the logistic equation with Holling type-II harvesting [7]:

$$ \dot{x}(t)=x(t) \bigl(r-ax(t) \bigr)-\frac{\gamma x(t)}{\alpha+\beta x(t)}. $$
(1.6)

For system (1.4), an interesting question is the following: Are the dynamical behaviors of system (1.4) similar to or quite different from those of system (1.5) and system (1.6)? It is generally known that the ecological system will be destroyed with the high capturing intensity or high frequency capture. In order to ensure the economic benefits and sustainable population development, should we control the level of capture strength and cycle?

The paper is organized as follows. In Sect. 2, some sufficient conditions for the existence and global attractivity of system (1.4) are derived; also, under some conditions, the system may admit a unique positive periodic solution. In Sect. 3, we investigate the extinction property of system (1.4). In Sect. 4, several numeric simulations are carried out to illustrate the feasibility of the main results. We end this paper with a brief discussion.

2 Permanence and global attractivity

Theorem 2.1

Assume that

$$ r\theta-\ln\xi>0 $$
(2.1)

holds, then for any positive solution \(x(t)\) of system (1.4),

$$m\leq\liminf_{t\rightarrow+\infty}x(t)\leq\limsup_{t\rightarrow +\infty}x(t) \leq M, $$

where

$$M=\frac{r}{a},\qquad m=\frac{r\theta-\ln\xi}{a\theta\xi},\qquad \xi=\frac {\alpha+\beta M}{\alpha-\gamma}. $$

Proof

Let \(y(t)=1/x(t)\), from \(\gamma\geq0\) we have

$$ \begin{gathered} \dot{y}(t)=-ry(t)+a,\quad t\neq t_{k}, \\ \begin{aligned}y\bigl(t^{+}_{k}\bigr)&= \frac{\alpha y(t_{k})+\beta}{\alpha y(t_{k})+\beta -\gamma y(t_{k})}y(t_{k}) \\ &\geq y(t_{k}), \quad t=t_{k}.\end{aligned} \end{gathered} $$
(2.2)

Applying the comparison theorem and from [8] page 19, for any \(T>0\), we obtain

$$\begin{aligned} y(t)&\geq e^{-r(t-T)}y(T)+a \int_{T}^{t}e^{-r(t-s)}\,ds \\ &=e^{-r(t-T)}y(T)+ \frac{a}{r} \bigl(1-e^{-r(t-T)} \bigr), \end{aligned} $$

which implies that

$$\liminf_{t\rightarrow+\infty}y(t)\geq\frac{a}{r}. $$

Consequently,

$$ \limsup_{t\rightarrow+\infty}x(t)\leq\frac{r}{a} \stackrel { \mathrm{def}}{=}M. $$
(2.3)

From (2.1), there exists enough small positive \(\varepsilon_{1}>0\) such that

$$ \zeta_{\varepsilon_{1}} e^{-r\theta}< 1, $$
(2.4)

where \(\zeta_{\varepsilon_{1}}=\frac{\alpha+\beta(M+\varepsilon _{1})}{\alpha-\gamma}\geq1\). For this \(\varepsilon_{1}\), from (2.3), there exists enough large \(T_{1}>0\) such that

$$1/y(t)=x(t)< M+\varepsilon_{1} \quad{\text{for }} t\geq T_{1}. $$

Furthermore, from system (1.4), \(\beta\geq0\), and the above inequality, it is easy to obtain

$$ \begin{gathered} \dot{y}(t)=-ry(t)+a,\quad t\neq t_{k}, \\ \begin{aligned}y \bigl(t^{+}_{k}\bigr)&= \frac{\alpha y(t_{k})+\beta}{\alpha y(t_{k})+\beta-\gamma y(t_{k})}y(t_{k}) \\ &\leq\frac{\alpha+\beta/y(t_{k})}{\alpha-\gamma}y(t_{k}) \\ &\leq\frac{\alpha+\beta(M+\varepsilon_{1})}{\alpha-\gamma }y(t_{k}) \\ &=\zeta_{\varepsilon_{1}} y(t_{k}),\quad t=t_{k}. \end{aligned} \end{gathered} $$
(2.5)

Note that \([Y]\) represents the maximum integer not greater than the real number Y. According to the comparison theorem and [8], for any \(T>0\), we obtain

$$ \begin{aligned}[b] y(t)&\leq \biggl(\prod_{T\leq t_{k}< t} \zeta_{\varepsilon_{1}} \biggr) e^{-r(t-T)}y(T)+a \int_{T}^{t} \biggl(\prod _{s\leq t_{k}< t}\zeta _{\varepsilon_{1}} \biggr)e^{-r(t-s)}\,ds \\ &\leq\zeta_{\varepsilon_{1}}^{[\frac{t-T}{\theta }]}e^{-r(t-T)}y(T)+\frac{a\theta\zeta_{\varepsilon_{1}}}{r\theta -\ln\zeta_{\varepsilon_{1}}} \bigl(1-\zeta_{\varepsilon _{1}}^{[\frac{t-T}{\theta}]}e^{-r(t-T)} \bigr). \end{aligned} $$
(2.6)

In particular, if \(t=T+k\theta\), then from (2.6) it follows that

$$y(T+k\theta)\leq\bigl(\zeta_{\varepsilon_{1}}e^{-r\theta }\bigr)^{k}y(T)+ \frac{a\theta\zeta_{\varepsilon_{1}}}{r\theta-\ln\zeta _{\varepsilon_{1}}} \bigl(1-\bigl(\zeta_{\varepsilon_{1}}e^{-r\theta } \bigr)^{k} \bigr) \quad{\text{for }} k\in N. $$

From this inequality and (2.4), and letting \(\varepsilon _{1}\rightarrow0\), we obtain

$$\limsup_{k\rightarrow+\infty}y(T+k\theta)\leq\frac{a\theta\xi }{r\theta-\ln\xi}, $$

where \(\xi=\frac{\alpha+\beta M}{\alpha-\gamma}\).

For \(T+k\theta\leq t< T+(k+1)\theta\), we have

$$\zeta_{\varepsilon_{1}}^{k}\leq\zeta_{\varepsilon_{1}}^{[\frac {t-T}{\theta}]}\leq \zeta_{\varepsilon_{1}}^{k+1},\qquad e^{-r(k+1)\theta }\leq e^{-r(t-T)}\leq e^{-rk\theta}. $$

From inequality (2.6) we obtain

$$\begin{gathered} y(t)\leq\zeta_{\varepsilon_{1}}\bigl(\zeta_{\varepsilon_{1}}e^{-r\theta } \bigr)^{k}y(T)+\frac{a\theta\zeta_{\varepsilon_{1}}}{r\theta-\ln\zeta _{\varepsilon_{1}}} \bigl(1-e^{-r\theta}\bigl( \zeta_{\varepsilon _{1}}e^{-r\theta}\bigr)^{k} \bigr) \\\quad{\text{for }} k\in N, T+k\theta \leq t< T+(k+1)\theta.\end{gathered} $$

Clearly, let \(\varepsilon_{1}\rightarrow0\), we have

$$\limsup_{k\rightarrow+\infty}y(t)\leq\frac{a\theta\xi}{r\theta -\ln\xi} \quad{\text{for }} T+k\theta\leq t< T+(k+1)\theta. $$

Therefore,

$$\liminf_{t\rightarrow+\infty}x(t)\geq\frac{r\theta-\ln\xi}{ a\theta\xi} \stackrel{ \mathrm{def}}{=}m. $$

This proof of Theorem 2.1 is completed. □

Remark 2.1

When \(\beta=\gamma=0\), system (1.4) is reduced to the logistic equation (1.1). In view of \(r>0\), we have

$$\xi=\frac{\alpha+\beta M}{\alpha-\gamma}=1 $$

and

$$r\theta-\ln\xi=r\theta>0. $$

It follows from Theorem 2.1 that

$$r/a\leq\liminf_{t\rightarrow+\infty}x(t)\leq\limsup_{t\rightarrow +\infty}x(t) \leq r/a, $$

that is \(\lim_{t\rightarrow+\infty}x(t)=r/a\). Therefore, our result generalizes the simple dynamics of the traditional logistic equation.

Remark 2.2

When \(\alpha=1\) and \(\beta=0\), system (1.4) is reduced to the linear impulsive logistic equation (1.5). In view of \(r>0\), \(0\leq\gamma<1\), one obtains

$$\xi=\frac{\alpha+\beta M}{\alpha-\gamma}=\frac{1}{1-\gamma}. $$

Moreover, if the inequality

$$r\theta-\ln\xi=r\theta+\ln(1-\gamma)>0 $$

holds, it follows from Theorem 2.1 that

$$\frac{ (r\theta+\ln(1-\gamma) )(1-\gamma)}{a\theta}\leq \liminf_{t\rightarrow+\infty}x(t)\leq\limsup _{t\rightarrow+\infty }x(t)\leq r/a, $$

which generalizes the simple dynamics of the linear impulsive logistic equation.

Theorem 2.2

If condition (2.1) holds, then system (1.4) has at least one θ-periodic solution \(x(t)\), for which \(x(0)>0\).

Proof

Owing to r, a and α, β, γ are positive constants, the impulsive system (1.4) is periodic.

Suppose that there is a positive θ-periodic solution \(x(t)\) of (1.4) with \(x(0^{+})=x_{0}>0\). For \(t\in(0,\theta]\), we have

$$x(t)=\frac{x_{0}}{e(t)+b(t)x_{0}}, $$

where

$$e(t)=e^{-rt},\qquad b(t)=\frac{1-e^{-rt}}{r/a}. $$

Then

$$\begin{gathered} x(\theta)=\frac{x_{0}}{e(\theta)+b(\theta)x_{0}}, \\ x_{0}=x(\theta)-\frac{\gamma x(\theta)}{\alpha+\beta x(\theta)}.\end{gathered} $$

From the condition \(x(\theta^{+})=x_{0}\), we obtain

$$x(\theta)=\frac{x(\theta^{+})}{e(\theta)+b(\theta)x(\theta^{+})}, $$

consequently

$$x\bigl(\theta^{+}\bigr)=\frac{x(\theta)e(\theta)}{1-b(\theta)x(\theta)}. $$

Let

$$ \begin{aligned}[b] g \bigl(x(\theta) \bigr)&\equiv x\bigl( \theta^{+}\bigr)-x(\theta) \\ &= \frac{x(\theta)e(\theta)}{1-b(\theta)x(\theta)}-x(\theta) \\ &= \frac{x(\theta) (e(\theta)-1+b(\theta)x(\theta) )}{1-b(\theta)x(\theta)} \\ &= \frac{-\gamma x(\theta)}{\alpha+\beta x(\theta)}. \end{aligned} $$
(2.7)

Since \(g(x)\geq-x\) for \(x\in [0,1/b(\theta) )\) and \(\frac {-\gamma x}{\alpha+\beta x}\geq-x\) for \(x\geq0\), equation (2.7) has a positive solution only in the interval \(x\in [0,1/b(\theta) )\). Suppose that equation (2.7) has a positive solution \(x(\theta)\) and denote by \(\pi(t)\) the corresponding positive θ-periodic solution of equation (1.4) for which

$$\pi\bigl(0^{+}\bigr)=x_{0}=\frac{e(\theta)x(\theta)}{1-b(\theta)x(\theta)},\qquad \pi( \theta)=x(\theta), $$

and

$$\pi(t)=\frac{x_{0}}{e(t)+b(t)x_{0}} \quad{\text{for }} t\in (0,\theta]. $$

From

$$x_{0}=x(\theta)-\frac{\gamma x(\theta)}{\alpha+\beta x(\theta)}, $$

we have

$$\begin{aligned} x(\theta)&= \frac{x_{0}}{e(\theta)+b(\theta)x_{0}} \\ &= \frac{x(\theta)- \frac{\gamma x(\theta)}{\alpha+\beta x(\theta )}}{ e(\theta)+b(\theta) (x(\theta)- \frac{\gamma x(\theta )}{\alpha+\beta x(\theta)} )}, \end{aligned} $$

that is,

$$ \beta b(\theta)x^{2}(\theta)+ \bigl(\beta e(\theta )+\alpha b(\theta)- \gamma b(\theta)-\beta \bigr)x(\theta)+ \bigl(\alpha e(\theta)-\alpha+\gamma \bigr)=0. $$
(2.8)

We declare that under assumption (2.1), equation (2.8) admits a positive solution.

When \(\beta=0\), equation (2.8) has a positive solution

$$x(\theta)=\frac{\alpha (1-e(\theta) )-\gamma}{(\alpha -\gamma)b(\theta)}. $$

When \(\beta\neq0\), because of

$$\ln\frac{\alpha}{\alpha-\gamma}\leq\ln\frac{\alpha+\beta M}{\alpha-\gamma}, $$

from (2.1), we have

$$r\theta-\ln\frac{\alpha}{\alpha-\gamma}\geq r\theta-\ln\xi>0. $$

It is easy to see that

$$\begin{gathered} \gamma< \alpha \bigl(1-e(\theta) \bigr), \\ \gamma-\alpha+\alpha e(\theta)< 0,\end{gathered} $$

hence,

$$\Delta> B^{2}, $$

where \(B=\beta e(\theta)+\alpha b(\theta)-\gamma b(\theta)-\beta\), \(\Delta=B^{2}-4\beta b(\theta) (\alpha e(\theta)-\alpha+\gamma )\).

That is,

$$-B+\sqrt{\Delta}>0. $$

Then equation (2.8) has a positive solution

$$x(\theta)=\frac{-B+\sqrt{\Delta}}{2\beta b(\theta)}. $$

Therefore, when \(\beta=0\), set

$$x_{0}=\frac{\alpha-\alpha e(\theta)-\gamma}{\alpha b(\theta)}; $$

when \(\beta\neq0\), set

$$x_{0}=\frac{(-B+\sqrt{\Delta})e(\theta)}{2\beta b(\theta)-b(\theta )(-B+\sqrt{\Delta})}. $$

Consequently, system (1.4) has at least one positive θ-period solution

$$\pi(t)=\frac{x_{0}}{e(t)+b(t)x_{0}} $$

for which \(x(0)>0\).

The proof of Theorem 2.2 is completed. □

Theorem 2.3

If condition (2.1) holds and assume that

$$ \Phi_{0}e^{-am\theta}< 1, $$
(2.9)

where

$$\Phi_{0}=\frac{\alpha+\beta(m+2M)-\gamma}{\alpha+\beta m-\gamma}, $$

then for any two positive solutions \(x(t)\) and \(x^{*}(t)\) of system (1.4), \(\lim_{t\rightarrow+\infty} (x(t)-x^{*}(t) )=0\).

Proof

From (2.9) and the expression of \(\Phi_{0}\), we could choose \(\varepsilon>0\) small enough. Without loss of generality, we may assume that \(\varepsilon<\frac{1}{2}m\) such that

$$ \Phi_{\varepsilon}e^{-a(m-\varepsilon)\theta }< 1, $$
(2.10)

where \(\Phi_{\varepsilon}=\frac{\alpha+\beta(m+2M+\varepsilon )-\gamma}{\alpha+\beta(m-\varepsilon)-\gamma}\geq1\). For this ε, from Theorem 2.1, there exists enough large \(T>0\) such that

$$m-\varepsilon< x(t)< M+\varepsilon,\qquad m-\varepsilon < x^{*}(t)< M+ \varepsilon\quad{\text{for }} t\geq T. $$

Now, we will prove that \(x(t)\) is globally attractive.

Using the mean value theorem, we can obtain

$$\frac{1}{M+\varepsilon}\big|x(t)-x^{*}(t)\big|< \big|\ln x(t)-\ln x^{*}(t)\big|< \frac {1}{m-\varepsilon}\big|x(t)-x^{*}(t)\big|. $$

Let

$$V(t)=\big|\ln x(t)-\ln x^{*}(t)\big|, $$

then

$$\begin{aligned} \dot{V}(t)&=\operatorname{sgn} \bigl(x(t)-x^{*}(t) \bigr) \bigl(r-ax(t)-r+ax^{*}(t) \bigr) \\ &\leq-a\big|x(t)-x^{*}(t)\big| \\ &\leq-a(m-\varepsilon)\big|\ln x(t)-\ln x^{*}(t)\big| \\ &=-a(m-\varepsilon)V(t)\quad{\text{for }} t\geq T, t\neq t_{k}. \end{aligned} $$

Using the mean value theorem, we can easily check that

$$\begin{aligned} V\bigl(t_{k}^{+}\bigr)={}& \bigl\vert \ln x\bigl(t_{k}^{+}\bigr)-\ln x^{*} \bigl(t_{k}^{+}\bigr) \bigr\vert \\ ={}& \biggl\vert \ln \biggl[ \biggl(1- \frac{\gamma}{\alpha+\beta x(t_{k})} \biggr)x(t_{k}) \biggr]-\ln \biggl[ \biggl(1- \frac{\gamma }{\alpha+\beta x^{*}(t_{k})} \biggr)x^{*}(t_{k}) \biggr] \biggr\vert \\ ={}& \biggl\vert \ln\frac{\alpha+\beta x(t_{k})-\gamma}{\alpha+\beta x(t_{k})}-\ln\frac{\alpha+\beta x^{*}(t_{k})-\gamma}{\alpha+\beta x^{*}(t_{k})}+\ln x(t_{k})-\ln x^{*}(t_{k}) \biggr\vert \\ \leq{}& \bigl\vert \ln x(t_{k})-\ln x^{*}(t_{k}) \bigr\vert + \biggl\vert \ln\frac {\alpha+\beta x(t_{k})-\gamma}{\alpha+\beta x(t_{k})}-\ln\frac {\alpha+\beta x^{*}(t_{k})-\gamma}{\alpha+\beta x^{*}(t_{k})} \biggr\vert \\ ={}& \bigl\vert \ln x(t_{k})-\ln x^{*}(t_{k}) \bigr\vert +\big|\ln \bigl(\alpha +\beta x(t_{k})-\gamma \bigr)-\ln \bigl(\alpha+\beta x(t_{k}) \bigr) \\ &-\ln \bigl(\alpha+\beta x^{*}(t_{k})-\gamma \bigr)+\ln \bigl(\alpha +\beta x^{*}(t_{k}) \bigr) \big| \\ \leq{}& \bigl\vert \ln x(t_{k})-\ln x^{*}(t_{k}) \bigr\vert + \bigl\vert \ln \bigl(\alpha+\beta x(t_{k})-\gamma \bigr)-\ln \bigl(\alpha+\beta x^{*}(t_{k})-\gamma \bigr) \bigr\vert \\ &+ \bigl\vert \ln \bigl(\alpha+\beta x(t_{k}) \bigr)-\ln \bigl( \alpha+\beta x^{*}(t_{k}) \bigr) \bigr\vert \\ \leq{}& \bigl\vert \ln x(t_{k})-\ln x^{*}(t_{k}) \bigr\vert + \frac{\beta }{\alpha+\beta(m-\varepsilon)-\gamma} \bigl\vert x(t_{k})-x \bigl(t_{k}^{*}\bigr) \bigr\vert \\ &+ \frac{\beta}{\alpha+\beta(m-\varepsilon)} \bigl\vert x(t_{k})-x\bigl(t_{k}^{*} \bigr) \bigr\vert \\ \leq{}& \bigl\vert \ln x(t_{k})-\ln x^{*}(t_{k}) \bigr\vert + \frac{\beta (M+\varepsilon)}{\alpha+\beta(m-\varepsilon)-\gamma} \bigl\vert \ln x(t_{k})-\ln x \bigl(t_{k}^{*}\bigr) \bigr\vert \\ &+ \frac{\beta(M+\varepsilon)}{\alpha+\beta(m-\varepsilon)} \bigl\vert \ln x(t_{k})-\ln x \bigl(t_{k}^{*}\bigr) \bigr\vert \\ \leq{}& \biggl(1+ \frac{2\beta(M+\varepsilon)}{\alpha+\beta (m-\varepsilon)-\gamma} \biggr)V(t_{k}) \\ ={}& \frac{\alpha+\beta(m+2M+\varepsilon)-\gamma}{\alpha+\beta (m-\varepsilon)-\gamma}V(t_{k}) \\ ={}&\Phi_{\varepsilon} V(t_{k}) \quad{\text{for }} t=t_{k}. \end{aligned}$$

According to the impulsive differential inequality in [8], for any \(T>0\), it follows that

$$ \begin{aligned}[b] V(t)&\leq \biggl(\prod_{T\leq t_{k}< t} \Phi_{\varepsilon} \biggr)e^{-a(m-\varepsilon)(t-T)}V(T) \\ &= \Phi_{\varepsilon}^{ [\frac{t-T}{\theta} ]}e^{-a(m-\varepsilon)(t-T)}V(T) \quad{\text{for }} t \geq T. \end{aligned} $$
(2.11)

In particular, if \(t=T+k\theta\), then from (2.11) it follows that

$$V(T+k\theta)\leq\bigl(\Phi_{\varepsilon}e^{-a(m-\varepsilon)\theta }\bigr)^{k}V(T) \quad{\text{for }} k\in N. $$

From this inequality and (2.10), we obtain

$$V(T+k\theta)\rightarrow0 \quad{\text{as }} k\rightarrow+\infty. $$

For \(T+k\theta\leq t< T+(k+1)\theta\), we have

$$\Phi_{\varepsilon}^{[\frac{t-T}{\theta}]}\leq\Phi_{\varepsilon }^{k+1},\qquad e^{-a(m-\varepsilon)(t-T)}\leq e^{-a(m-\varepsilon)k\theta}. $$

From inequality (2.11) we obtain

$$V(t)\leq\Phi_{\varepsilon}\bigl(\Phi_{\varepsilon}e^{-a(m-\varepsilon )\theta} \bigr)^{k}V(T),\quad{\text{for }} k\in N, T+k\theta\leq t< T+(k+1) \theta. $$

Clearly, from (2.10) we have

$$V(t)\rightarrow0 \quad{\text{as }} k\rightarrow+\infty, {\text{for }} T+k\theta \leq t< T+(k+1)\theta. $$

Therefore,

$$V(t)\rightarrow0 \quad{\text{as }} t\rightarrow+\infty. $$

That shows

$$\lim_{t\rightarrow+\infty} \bigl(x(t)-x^{*}(t) \bigr)=0. $$

This proof of Theorem 2.3 is completed. □

As a direct corollary of Theorems 2.2 and 2.3, we have the following.

Theorem 2.4

If conditions (2.1) and (2.9) hold, then system (1.4) has a unique θ-periodic solution \(x(t)\), which is globally attractive.

3 Extinction

In this section, we give the following result which indicates that species \(x(t)\) will be driven to extinction.

Theorem 3.1

If the assumption

$$ r\theta-\ln\delta< 0 $$
(3.1)

holds, then the species x will be driven to extinction, that is, for any positive solution \(x(t)\) of system (1.4), \(x(t)\rightarrow0\) as \(t\rightarrow+\infty\).

Here,

$$\delta=\frac{\alpha+\beta M}{\alpha+\beta M-\gamma}. $$

Proof

Let \(y(t)=1/x(t)\), from \(\alpha-\gamma>0\), we have

$$\begin{gathered} \dot{y}(t)=-ry(t)+a,\quad t\neq t_{k}, \\ \begin{aligned} y\bigl(t^{+}_{k}\bigr)&= \frac{\alpha+\beta/y(t_{k})}{\alpha+\beta /y(t_{k})-\gamma}y(t_{k}) \\ &\geq\frac{\alpha+\beta(M+\varepsilon)}{\alpha+\beta (M+\varepsilon)-\gamma}y(t_{k}),\quad t=t_{k}. \end{aligned} \end{gathered} $$

Let \(\varepsilon\rightarrow0\), we have

$$ \begin{gathered} \dot{y}(t)=-ry(t)+a, \quad t\neq t_{k}, \\ y\bigl(t^{+}_{k}\bigr)\geq\delta y(t_{k}), \quad t=t_{k}, \end{gathered} $$
(3.2)

where \(\delta=\frac{\alpha+\beta M}{\alpha+\beta M-\gamma}>1\).

Condition (3.1) is equivalent to

$$\frac{\delta^{\frac{1}{\theta}}}{e^{r}}>1. $$

From (3.2), applying the comparison theorem and the theory of impulsive differential inequality [8], we get

$$\begin{aligned} y(t)&\geq \biggl(\prod_{0\leq t_{k}< t} \delta \biggr)e^{-rt}y(0)+a \int_{0}^{t} \biggl(\prod _{s\leq t_{k}< t}\delta \biggr)e^{-r(t-s)}\, ds \\ &\geq\delta^{\frac{t}{\theta}-1}e^{-rt}y(0)+a \int_{0}^{t}\delta ^{\frac{t-s}{\theta}-1}e^{-r(t-s)} \,ds \\ &=\delta^{-1} \biggl(\frac{\delta^{\frac{1}{\theta}}}{e^{r}} \biggr)^{t}y(0)+ \frac{a\theta}{\delta(\ln\delta-r\theta)} \biggl[ \biggl(\frac{\delta^{\frac{1}{\theta}}}{e^{r}} \biggr)^{t}-1 \biggr]\rightarrow+\infty \quad{\text{as }} t\rightarrow+\infty. \end{aligned} $$

Consequently,

$$x(t)\rightarrow0 \quad{\text{as }} t\rightarrow+\infty. $$

This proof of Theorem 3.1 is completed. □

As a direct corollary of Theorem 3.1, we have the following.

Corollary 3.1

Assume \(\beta=\gamma=0\), in this case, system (1.4) degenerates to system (1.1). Assume further that \(r<0\), then any positive solution \(x(t)\) of system (1.1)

$$x(t)\rightarrow0 \quad{\textit{as }} t\rightarrow+\infty. $$

That is, the species x will be driven to extinction when the intrinsic growth rate is negative.

Corollary 3.2

Assume that \(\alpha=1\) and \(\beta=0\), in this case, system (1.4) is reduced to the linear impulsive logistic equation (1.5). Assume further that

$$r\theta+\ln(1-\gamma)< 0, $$

then the species x will be driven to extinction in system (1.5).

Remark 3.1

Noting that the authors in [2] did not investigate the extinction property of system (1.5), Corollary 3.2 supplements and complements the main results of [2].

4 Numeric simulations

Example 4.1

Consider system (1.4) with the following coefficients: \(r=3\), \(a=2\), \(\theta=1\).

When \(\alpha=1\) and \(\beta=\gamma=0\), system (1.4) is reduced to the traditional logistic equation (1.1). It follows from Remark 2.1 that

$$\lim_{t\rightarrow+\infty}x(t)=r/a=3/2=1.5. $$

When \(\alpha=1\), \(\beta=0\), and \(\gamma=0.5\), system (1.4) is reduced to the linear impulsive logistic equation (1.5). One obtains that

$$\begin{gathered} \xi=\frac{\alpha+\beta M}{\alpha-\gamma}=\frac{1}{1-\gamma}=2, \\ r\theta-\ln\xi=3\times1-\ln2\approx2.3069>0.\end{gathered} $$

It follows from Remark 2.2 that

$$\begin{aligned} m&= \frac{ (r\theta+\ln(1-\gamma) )(1-\gamma)}{a\theta} \\ &= \frac{ (3\times1+\ln(1-0.5) )(1-0.5)}{2\times 1}\approx0.5767 \\ &\leq\liminf_{t\rightarrow+\infty}x(t)\leq\limsup_{t\rightarrow +\infty}x(t) \\ &\leq M=\frac{r}{a}=1.5. \end{aligned} $$

Moreover,

$$\begin{gathered} \Phi_{0}=\frac{\alpha+\beta(m+2M)-\gamma}{\alpha+\beta m-\gamma }=\frac{1-0.5}{1-0.5}=1, \\ \Phi_{0}e^{-am\theta}\approx1\times e^{-2\times0.5767\times 1} \approx0.3156< 1.\end{gathered} $$

It follows from Theorem 2.4 that system (1.4) has a unique globally attractive positive 1-periodic solution.

When \(\alpha=1\), \(\beta=0.2\), and \(\gamma=0.5\), it is easy to obtain

$$\begin{gathered} \xi=\frac{\alpha+\beta M}{\alpha-\gamma}=\frac{1+0.2\times 1.5}{1-0.5}=2.6, \\ r\theta-\ln\xi=3\times1-\ln2.6\approx2.0445>0.\end{gathered} $$

From Theorem 2.1, one has

$$\begin{aligned} m&= \frac{r\theta-\ln\xi}{a\theta\xi} \\ &= \frac{3\times1-\ln2.6}{2\times1\times2.6}\approx0.3932 \\ &\leq\liminf_{t\rightarrow+\infty}x(t)\leq\limsup_{t\rightarrow +\infty}x(t) \\ &\leq M=\frac{r}{a}=1.5, \end{aligned} $$

and

$$\begin{gathered} \Phi_{0}=\frac{\alpha+\beta(m+2M)-\gamma}{\alpha+\beta m-\gamma }\approx\frac{1+0.2\times(0.3932+2\times1.5)-0.5}{1+0.2\times 0.3932-0.5}\approx2.0369, \\ \Phi_{0}e^{-am\theta}\approx2.0369\times e^{-2\times0.3932\times 1} \approx0.9278< 1.\end{gathered} $$

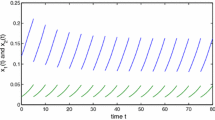
From Theorem 2.4, then system (1.4) has a unique globally attractive positive 1-periodic solution. Numeric simulation (Fig. 1) supports these findings.

Figure 1
figure 1

Dynamic behaviors of the species \(x(t)\) in system (1.4) with the initial conditions \(x(0)=0.4\), \(x(0)=0.8\), \(x(0)=1.8\), respectively

Full size image

Example 4.2

Consider system (1.4) with the following coefficients: \(r=3\), \(a=2\), \(\theta=0.05\).

When \(\alpha=1\) and \(\beta=\gamma=0\) in system (1.4) (i.e., system (1.1)), it follows from Remark 2.1 that

$$\lim_{t\rightarrow+\infty}x(t)=1.5. $$

When \(\alpha=1\), \(\gamma=0.5\), and \(\beta=0\) in system (1.4) (i.e., system (1.5)), one has

$$r\theta+\ln(1-\gamma)\approx-0.5431< 0. $$

The condition of Corollary 3.2 holds. It follows from Corollary 3.2 that the species of system (1.5) will be driven to extinction.

When \(\alpha=1\), \(\beta=1\), and \(\gamma=0.5\), by simple computation, we have

$$\delta=\frac{\alpha+\beta M}{\alpha+\beta M-\gamma}=1.25, $$

and so

$$r\theta-\ln\delta\approx-0.0731< 0, $$

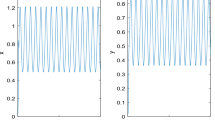
that is, the condition of Theorem 3.1 holds. It follows from Theorem 3.1 that the species of system (1.4) will be driven to extinction. Numeric simulation (Fig. 2) supports these findings.

Figure 2
figure 2

Dynamic behaviors of the species \(x(t)\) in system (1.4) with the initial conditions \(x(0)=0.4\), \(x(0)=0.8\), \(x(0)=1.8\), respectively

Full size image

Remark 4.1

For fixed values of r, a and α, β, γ (i.e., the population nature coefficients and capture intensity are fixed), if the harvesting cycle

$$\theta< \frac{1}{r}\ln\frac{\alpha}{\alpha-\gamma}, $$

then, from Theorem 3.1, the species x will be driven to extinction in system (1.4), that is, too intensive harvesting could lead to the extinction of the species.

If the harvesting cycle satisfies

$$\theta>\frac{1}{r}\ln\frac{\alpha a+\beta r}{a(\alpha-\gamma)}, $$

then, from Theorem 2.1, system (1.4) is permanent. That is, the period of harvesting is one of the essential factors leading to the extinction or permanence of the species.

All the analytical calculations are performed in detail in Appendix A.1.

Example 4.3

Take \(r=3\), \(a=2\), \(\alpha=1\), \(\beta=0.2\), \(\gamma=0.5\).

Through simple computation, one can see that when \(\theta=0.05\) in system (1.4),

$$\begin{gathered} \delta=1.625, \\ r\theta-\ln\delta\approx-0.3355< 0,\end{gathered} $$

then from Theorem 3.1, the species x will be driven to extinction.

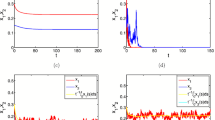
Similarly, if \(\theta=0.02\) and \(\theta=0.01\), the species x will be driven to extinction. Numeric simulation (Fig. 3) supports this finding.

Figure 3
figure 3

Dynamic behaviors of the species \(x(t)\) in system (1.4) with the initial conditions \(x(0)=0.2\), \(x(0)=0.4\), \(x(0)=0.6\), respectively

Full size image

When \(\theta=1\) in system (1.4), one has

$$M=1.5,\qquad\xi=2.6,\qquad r\theta-\ln\xi\approx2.0455>0, $$

then from Theorem 2.1,

$$\begin{gathered} m\approx0.3932, \\ 0.3932\leq\liminf_{t\rightarrow+\infty}x(t)\leq\limsup_{t\rightarrow+\infty}x(t) \leq1.5.\end{gathered} $$

Similarly, if \(\theta=1.3\) and \(\theta=2\), system (1.4) is permanent. Numeric simulation (Fig. 4) supports this finding.

Figure 4
figure 4

Dynamic behaviors of the species \(x(t)\) in system (1.4) with the initial conditions \(x(0)=0.6\), \(x(0)=1.2\), \(x(0)=1.6\), respectively

Full size image

When \(\theta=0\), from [7], we can obtain that system (1.4) has a globally stable positive equilibrium. Numeric simulation (Fig. 5) supports this finding.

Figure 5
figure 5

Dynamic behaviors of the species \(x(t)\) in system (1.4) with the initial conditions \(x(0)=0.6\), \(x(0)=1.2\), \(x(0)=1.8\), respectively

Full size image

Figure 3, Fig. 4, and Fig. 5 exhibit the effect of harvesting cycle θ. One could easily see that if θ is large enough (\(\theta>\frac{1}{r}\ln\frac{\alpha a+\beta r}{a(\alpha-\gamma )} \)), then (2.1) holds; and consequently, species x is permanent. With the increase in θ, the density of species x is increasing accordingly. If θ is small enough such that \(\theta<\frac{1}{r}\ln\frac{\alpha}{\alpha-\gamma}\), then (3.1) holds, and the species will be driven to extinction. That is, the harvesting cycle can change the persistence and extinction property of the system.

Remark 4.2

For fixed values of r, a and α, β, θ (i.e., the population nature coefficients and harvesting cycle are fixed), if the capture intensity

$$\gamma>\alpha-\frac{\alpha}{e^{r\theta}}, $$

then, from Theorem 3.1, the species x will be driven to extinction in system (1.4), that is, this harvesting cycle cannot be sustained.

If the capture intensity

$$\gamma< \alpha-\frac{\alpha a+\beta r}{ae^{r\theta}}, $$

then, from Theorem 2.1, system (1.4) is permanent, that is, this harvesting cycle can be sustained.

All the analytical calculations are performed in detail in Appendix A.2.

Example 4.4

Take \(r=3\), \(a=2\), \(\alpha=1\), \(\beta=0.2\).

Through simple computation, one can see that when \(\gamma=0.5\), \(\theta=1\) in system (1.4), then from Theorem 2.1,

$$0.3932\leq\liminf_{t\rightarrow+\infty}x(t)\leq\limsup_{t\rightarrow+\infty}x(t) \leq1.5. $$

Similarly, if \(\gamma=0.2\) and \(\gamma=0.1\), system (1.4) is permanent. Numeric simulation (Fig. 6) supports this finding.

Figure 6
figure 6

Dynamic behaviors of the species \(x(t)\) in system (1.4) with the initial conditions \(x(0)=1\), \(x(0)=1.3\), \(x(0)=1.6\), respectively

Full size image

When \(\gamma=0.5\), \(\theta=0.05\) in system (1.4),

$$\delta=1.625,\qquad r\theta-\ln\delta\approx-0.3355< 0, $$

then, from Theorem 3.1, the species x will be driven to extinction.

Similarly, if \(\gamma=0.6\) and \(\gamma=0.8\), the species x will be driven to extinction. Numeric simulation (Fig. 7) supports this finding.

Figure 7
figure 7

Dynamic behaviors of the species \(x(t)\) in system (1.4) with the initial conditions \(x(0)=0.2\), \(x(0)=0.4\), \(x(0)=0.6\), respectively

Full size image

Numerical simulations (Fig. 6, Fig. 7) show that if γ is small enough (\(\gamma<\alpha-\frac{\alpha a+\beta r}{ae^{r\theta }} \)), such that (2.1) holds, then the species is permanent. For the fixed θ, as γ gradually decreases, the density of species x is increasing accordingly. If γ is large enough such that \(\gamma>\alpha-\frac{\alpha}{e^{r\theta}}\), then (3.1) holds, the species will be driven to extinction. From this point, the capture intensity γ plays a negative effect on the persistence property of the system. Also, for the fixed θ, as γ is increasing gradually, the time for the species to be extinct becomes shorter.

5 Discussion

In this paper, a logistic model incorporating nonlinear impulsive Holling type-II harvesting is proposed and studied.

Based on the theoretical analysis and numerical simulations, we show that different parameter relationships may result in different dynamical behaviors of the system. From Remarks 4.1 and 4.2, sufficiently small value of θ and sufficiently large value of γ will cause the extinction of the species. Furthermore, high capture frequency θ (Fig. 3) and high capture intensity γ (Fig. 7) accelerate the speed of extinction. If the value of θ is large enough and the value of γ is small enough, the species is permanent (Figs. 4 and 6). Furthermore, with the increase in the harvesting cycle and the decrease in the capture intensity, the density of species x is increasing.

To sum up, to ensure the permanence of the specie, we could increase the period between the capture or decrease the capture strength.

At the end of the paper, we would like to mention that we assume that θ is a positive constant in system (1.4), that is, for all \(k\in Z^{+}\), \(t_{k}-t_{k-1}=\theta\). What would happen if we assume that \(t_{k}\) is a periodic sequence or an almost periodic sequence? We leave this for future investigation.