Abstract
In this paper, we study a Lotka-Volterra prey-predator system with feedback control. We establish sufficient conditions under which a unique positive equilibrium is globally stable. Further, we show that a suitable feedback control on predator species can make prey species that is on the brink of extinction become globally stable, but under the conditions of small feedback control on predator, the prey species still extinct, whereas the predator species is stable at certain values. Several examples are presented to show the feasibility of the main results.
Similar content being viewed by others
1 Introduction
A famous prey-predator system with discrete delays can be defined by
where \(x_{1}(t)\) is the prey population density at time t, \(x_{2}(t)\) is the predator population density at time t, \(r_{1}\) is the intrinsic growth rate of prey, \(r_{2}\) is the intrinsic growth rate for predator species, \(a_{ii}\) for \(i=1,2\) are intraspecific competition rates, and \(a_{ij}\) for \(i\neq j\), \(i,j=1,2\) are interspecific competition rates for prey and predator species, \(\tau_{1}\) is the time of catching prey, and \(\tau_{2}\) is maturation delay of predator.
The dynamical behavior of prey-predator system such as (1.1) has been investigated by many authors, and many excellent results concerned with permanence, extinction and persistence or uniform persistence, global stability, and almost periodic solutions are obtained (see, for example, [1–18]). In all prey-predator systems, there is a common competition between prey and predator species, and in general this competition is one sided, that is, the loss occurs only in the prey populations. In some cases, poor natural environment leads to a decrease in the birth rate of the prey population. Meanwhile, with the large predatory, the prey population is less and less and then tends to zero. Recently, many scholars have done research on the ecosystem with feedback controls (see [19–26] and the references therein). In particular, Gopalsamy and Weng [22] introduced a feedback control variable into a two-species competitive system and discussed the existence of the globally attractive positive equilibrium of the system with feedback controls. Hu et al. [26] considered the extinction of a nonautonomous Lotka-Volterra competitive system with pure delays and feedback controls, and by simulation they found that suitable feedback control variables can transform extinct species into permanent. Therefore, a natural and important question is that whether a proper control only on the predator population can make the extinct prey species become permanent, and the prey-predator can coexist in a certain pattern.
Motivated by the above work, in this paper, we consider the following predator-prey Lotka-Volterra delay system with feedback control:
where \(u(t)\) is the indirect control variable, \(r_{i}>0\), \(\tau_{i}\geq0\), \(a_{ij}>0\), \(i,j=1,2\), \(\tau=\max\{\tau_{1},\tau_{2}\}\), \(c>0\), \(e>0\), \(d>0\),
where \(\phi_{i}(\theta)\) (\(i=1,2\)) and \(\psi({\theta})\) are nonnegative and bounded continuous functions on \([-\tau,0]\).
The aim of this paper is, by using the method of multiple Lyapunov functionals [22, 24] and by developing a new analysis technique [26], to obtain sufficient conditions under which a unique positive equilibrium is globally stable.
This paper is organized as follows. In the next section, as preliminaries, some assumptions and lemmas are introduced. In Section 3, the main results of this paper are stated and proved. Finally, several examples together with their numerical simulations show the feasibility of the main results and the considerable effects of feedback controls to extinction of prey species.
2 Preliminaries
Throughout this paper, we introduce the following hypotheses:
By the method of Lyapunov functions (see [22, 26–29]), one can show that if the coefficients of system (1.1) satisfy (H1), then system (1.1) possesses a unique positive equilibrium \((\bar{x}_{1}, \bar{x}_{2})=(\frac {r_{1}a_{22}-r_{2}a_{12}}{a_{11}a_{22}+a_{12}{a_{21}}},\frac {r_{2}a_{11}+r_{1}a_{21}}{a_{11}a_{22}+a_{12}{a_{21}}})\), which is globally attractive, that is, all positive solutions of system (1.1) satisfy
If the coefficients of system (1.1) satisfy (H2), then system (1.1) is extinct, that is, all positive solutions of system (1.1) satisfy
Now, we state the following lemmas, which are useful in the proof of the main results.
Lemma 2.1
Suppose that assumption (H3) holds. It is not difficult to verity that system (1.2) has a unique positive equilibrium
Lemma 2.2
Let \((x_{1}(t), x_{2}(t),u(t))^{T}\) be a solution of system (1.2) with initial condition (1.3). Then \((x_{1}(t), x_{2}(t),u(t))^{T}\) is positive and bounded for all \(t\geq0\).
Proof
Obviously, the solution \((x_{1}(t), x_{2}(t),u(t))^{T}\) of system (1.2) with initial condition (1.3) is positive for all \(t\geq 0\). By the first equation of system (1.2) we have
By a standard comparison principle and basic ODE theory it follows that \(\limsup_{t\rightarrow \infty}x(t)\leq\frac{r_{1}}{a_{11}}\). Hence, for any \(\varepsilon_{1}>0\) sufficiently small, there exists \(T_{1}>0\) such that \(x_{1}(t)\leq\frac{r_{1}}{a_{11}}+\varepsilon_{1}\), \(t>T_{1}\). By the second equation of system (1.2) we have
which implies that \(\limsup_{t\rightarrow\infty}x_{2}(t)\leq \frac{r_{2}+a_{21}(\frac{r_{1}}{a_{11}}+\varepsilon_{1})}{a_{22}}\). Setting \(\varepsilon_{1}\rightarrow0\), it follows that \(\limsup_{t\rightarrow\infty}x_{2}(t)\leq \frac{r_{2}a_{11}+r_{1}a_{21}}{a_{11}a_{22}}\). Therefore, for any \(\varepsilon_{2}>0\) small enough, there exists \(T>T_{1}+\tau_{2}>0\) such that \(x_{2}(t)\leq \frac{r_{2}a_{11}+r_{1}a_{21}}{a_{11}a_{22}}+\varepsilon_{2}\), \(t>T\). By the third equation of system (1.2),
which means that \(\limsup_{t\rightarrow\infty}u(t)\leq \frac{d}{e}(\frac{r_{2}a_{11}+r_{1}a_{21}}{a_{11}a_{22}}+\varepsilon_{2})\). Letting \(\varepsilon_{2}\rightarrow0\), it follows that \(\limsup_{t\rightarrow\infty}u(t)\leq \frac{d}{e}\frac{r_{2}a_{11}+r_{1}a_{21}}{a_{11}a_{22}}\). This completes the proof of Lemma 2.2. □
3 Main results
Now, we give our main results.
Theorem 3.1
Let \((x_{1}(t), x_{2}(t),u(t))^{T}\) be a solution of system (1.2). If condition (H1) or (H3) holds, then the unique positive equilibrium of system (1.2) is globally asymptotically stable, that is,
Proof
Define a Lyapunov function as follows:
where \(\eta_{1}=1\), and \(\eta_{2}\) is a positive constant to be determined.
Note that system (1.2) can be rewritten as
Calculating the derivative of \(V_{1}(t)\) along the solution \((x_{1}(t), x_{2}(t),u(t))^{T}\) of system (1.2), we have
By the inequality \(ab\leq\frac{\theta}{2}a^{2}+\frac{1}{2\theta}b^{2}\), \(\theta>0\), from (3.2) it follows that
Let
Calculating the derivative of \(V_{2}(t)\), we obtain
Define \(V(t)=V_{1}(t)+V_{2}(t)\). It follows from (3.3) and (3.4) that
Denote \(\delta_{1}=a_{11}-\frac{a_{12}}{2\theta_{1}}-\frac{\eta _{2}a_{21}}{2\theta_{2}}\) and \(\delta_{2}=a_{22}\eta_{2}-\frac{a_{12}\theta_{1}}{2}-\frac{\eta _{2}a_{21}\theta_{2}}{2}\).
Then taking \(\eta_{2}=\frac{a_{12}}{a_{21}}\) and \(\theta_{1}=\theta_{2}=\frac{a_{11}a_{22}+a_{12}a_{21}}{2a_{11}a_{21}}\), we have
Then, (H1) or (H3) shows that \(\delta_{i}>0\), \(i=1,2\). It is easy to see that
Therefore, \(V(t)\) is nonincreasing. By Lemma 2.2, \(\dot{x}_{i}(t)\), \(i=1,2\), are bounded. So \(\vert x_{i}(t)-x_{i}^{*} \vert \), \(i=1,2\), are uniformly continuous on \([0, +\infty)\). Integrating both sides of (3.7) on the interval \([T,t)\), we have
It follows from Lemma 2.2 and the initial condition \(\phi_{i}\) that \(x_{i}(t)\), \(i=1,2\), are bounded for \(t\in R\), that is, there exists \(M>0\) such that \(0< x_{i}(t)< M\), \(i=1,2\), \(t\in R\). Obviously, \(V_{1}(T)\) is bounded, and
Therefore
From this inequality it follows that \((x_{i}(s)-x_{i}^{*})^{2}\in L^{1}[0,+\infty)\), \(i=1,2\). By Barbalat’s lemma (see [30]) we conclude that
and therefore
By the third equation of system (1.2) we have
This completes the proof of Theorem 3.1. □
Corollary 3.1
Let \((x_{1}(t), x_{2}(t),u(t))^{T}\) be a solution of system (1.2). If condition (H5) holds, then the unique positive equilibrium of system (1.2) is globally asymptotically stable, that is,
Proof
(H5) implies (H3), so system (1.2) has a positive globally asymptotically stable equilibrium. □
Remark 3.1
If (H1) holds, then systems (1.1) and (1.2) are globally stable. Theorem 3.1 implies that the feedback control keeps the property of stability of system (1.2) but only changes the position of the unique positive equilibrium. That is, feedback control of system (1.2) leads to the number of the prey population increased (\(x_{1}^{*}=\frac {e(r_{1}a_{22}-r_{2}a_{12})+r_{1}cd}{e(a_{11}a_{22}+a_{12}{a_{21})+cda_{11}}}>\bar {x}_{1}=\frac{r_{1}a_{22}-r_{2}a_{12}}{a_{11}a_{22}+a_{12}{a_{21}}}\)) and the number of the predator population decreased (\(x_{2}^{*}= \frac {e(r_{2}a_{11}+{r_{1}}a_{21})}{e(a_{11}a_{22}+a_{12}{a_{21}})+cda_{11}}<\bar {x}_{2}=\frac{r_{2}a_{11}+r_{1}a_{21}}{a_{11}a_{22}+a_{12}{a_{21}}}\)).
Remark 3.2
If (H2) holds, system (1.1) is extinct. (H5) implies (H2), and system (1.2) has a unique positive equilibrium, which is globally asymptotically stable. Theorem 3.1 implies that the proper feedback control on predator species can change extinct prey species to be permanent.
Theorem 3.2
Assume that (H4) holds. Let \((x_{1}(t), x_{2}(t),u(t))^{T}\) be a solution of system (1.2). Then
Proof
Condition (H4) implies that
By (3.9) we can choose positive constants \(\alpha>0\), \(\beta>0\), \(\gamma>0\) such that
and
Thus there exists \(\delta>0\) such that
Consider a Lyapunov functional of the form
Calculating the derivative of V along the solution of system (1.2), we have
From inequalities (3.10) and (3.11) we obtain
Integrating this inequality from 0 to t, we have
By similar arguments as in the proof of Theorem 3.1, there exists \(M>0\) such that \(0< x_{i}(t)< M\), \(i=1,2\), \(t\in R\). So
On the other hand,
Combining inequalities (3.12), (3.13), and (3.14), we have
Inequality (3.15) means that
where \(\lambda= [M^{\beta}\exp(\beta a_{21}M\tau+\alpha a_{12}M\tau) V(0) ]^{\frac{1}{\alpha}}\). Hence, we obtain that
This completes the proof of Theorem 3.2. □
Theorem 3.3
If condition (H4) holds, then the equilibrium \((x_{1}^{**}, x_{2}^{**}, u^{**})=(0,\frac{er_{2}}{e a_{22}+cd}, \frac{dr_{2}}{e a_{22}+cd})\) of system (1.2) is globally asymptotically stable, that is,
Proof
Let \((x_{1}(t), x_{2}(t),u(t))^{T}\) be a solution of system (1.2). It follows from Theorem 3.2 that \(\lim_{t\rightarrow\infty}x_{1}(t)=0\), and it is easy to obtain that system (1.2) has an equilibrium \((x_{1}^{**}, x_{2}^{**}, u^{**})=(0,\frac{er_{2}}{e a_{22}+cd}, \frac{dr_{2}}{e a_{22}+cd})\). Therefore, we only need to verify
As before, we define a Lyapunov function as follows:
Calculating the derivative of \(V_{1}(t)\) along the solution of system (1.2), we obtain that
Let
Calculating the derivative of \(V_{2}(t)\) along the solution of system (1.2), we have
Define
It follows from (3.17) and (3.18) that
Integrating both sides of (3.19) on the interval \([T, t)\), we obtain
Obviously, \(V_{1}(t)\) is bounded, and
By (H5) it follows Theorem 3.2 that \(\int_{0}^{+\infty} x_{1}(s)\,ds<+\infty\), and so \(\int_{T}^{t} x_{1}(s)\,ds<+\infty\). Hence, we have
Similarly to the analysis of the proof of Theorem 3.1, by Barbalat’s lemma (see [30]) we have
that is,
This completes the proof of Theorem 3.3. □
Remark 3.3
By comparative analysis of (H3) and (H4) note that when the feedback control repression \(\frac{cd}{e}\) remains small, feedback control on predator species has no influence on the extinction of system (1.2).
4 Examples
In this section, we give examples to illustrate the results obtained.
Example 4.1
We consider the following equations:
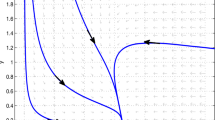
Consider the initial conditions \((x_{1}(\theta),x_{2}(\theta))^{T}=(0.3, 0.2)^{T}\) and \((1, 0.8)^{T}\) for all \(\theta\in[-3,0] \) and \(t \in[0,100]\). Obviously, \(\frac{r_{1}}{r_{2}}=\frac{2}{1}>\frac{a_{12}}{a_{22}}=\frac {4}{3}\), \(\frac{a_{11}}{a_{21}}=\frac{3}{2}>\frac {a_{12}}{a_{22}}=\frac{4}{3} \). Then condition (H1) holds, and there exists a unique positive equilibrium \((x_{1}^{*}, x_{2}^{*})=(\frac{2}{17},\frac{7}{17})\), which is globally asymptotically stable (see Figure 1).
Dynamic behavior of model ( 4.1 ) with the initial value \(\pmb{(x_{1},x_{2})=(0.3,0.2)\mbox{ and }(1,0.8)}\) .
Example 4.2
We introduce feedback control to the predator species of system (4.1):
Consider the initial conditions \((x_{1}(\theta),x_{2}(\theta), u(\theta))^{T}=(0.3, 0.2, 0.3)^{T}\) and \((1, 0.8, 1)^{T}\) for all \(\theta\in[-3,0]\) and \(t \in[0,100]\). For system (4.1), condition (H1) holds; then system (4.2) has a unique positive equilibrium \((x_{1}^{*}, x_{2}^{*}, u^{*})=(\frac{4}{13},\frac{7}{26},\frac{21}{104} )\), which is globally asymptotically stable. Therefore, the feedback control variable can change the position of equilibrium and retain the stable property (Figure 2).
Dynamic behavior of model ( 4.2 ) with the initial value \(\pmb{(x_{1},x_{2},u)=(0.3,0.2,0.3)\mbox{ and }(1,0.8,1)}\) .
Example 4.3
We consider the equation
Consider the initial conditions \((x_{1}(\theta),x_{2}(\theta))^{T}=(0.3, 0.2)^{T}\) and \((1, 0.8)^{T}\) for all \(\theta\in[-3,0]\) and \(t \in[0,100]\). It is easy to see that \(\frac{r_{1}}{r_{2}}=\frac{4}{3}<\frac{a_{12}}{a_{22}}=\frac{3}{2}\), so that condition (H2) holds. Then system (4.3) has an equilibrium \((x_{1}^{**}, x_{2}^{**})=(0,\frac{3}{2})\), which means that the prey species will be extinct whereas the predator species will be globally asymptotically stable (see Figure 3).
Dynamic behavior of model ( 4.3 ) with the initial value \(\pmb{(x_{1},x_{2})=(0.3,0.2)\mbox{ and }(1,0.8)}\) .
Example 4.4
We append the proper feedback control variables only to the predator species of (4.3):
Consider the initial conditions \((x_{1}(\theta),x_{2}(\theta), u(\theta))^{T}=(0.3, 0.2, 0.3)^{T}\) and \((1, 0.8, 1)^{T}\) for all \(\theta\in[-3,0]\) and \(t \in[0,100]\). By calculation, \(\frac{r_{1}}{r_{2}}=\frac{4}{3}\), \(\frac{a_{12}}{a_{22}+\frac{cd}{e}}=\frac{3}{5}\), \(\frac{a_{11}}{a_{21}}=\frac{2}{1}\), \(\frac{a_{12}}{a_{22}}=\frac{3}{2}\). \(\frac{a_{12}}{a_{22}+\frac{cd}{e}}<\frac{r_{1}}{r_{2}}<\frac {a_{12}}{a_{22}}<\frac{a_{11}}{a_{21}}\), so that condition (H3) or (H5) holds. Therefore, system (4.4) has a unique positive equilibrium \((x_{1}^{*}, x_{2}^{*}, u^{*})=(\frac{11}{13},\frac{10}{13},\frac{15}{26} )\), which is globally asymptotically stable.
The result shows that the proper feedback control on predator species can change extinct prey species to be permanent, and the label shows that the number of the prey species has increased, however, is larger than that of the predator species (see Figure 4).
Dynamic behavior of model ( 4.4 ) with the initial value \(\pmb{(x_{1},x_{2},u)=(0.3,0.2,0.3)\mbox{ and }(1,0.8,1)}\) .
Example 4.5
Finally, we consider the system
Consider the initial conditions \((x_{1}(\theta),x_{2}(\theta), u(\theta))^{T}=(0.3, 0.2, 0.3)^{T}\) and \((1, 0.8, 1)^{T}\) for all \(\theta\in[-3,0]\) and \(t \in[0,100]\), so that condition (H4) holds. System (4.5) has an equilibrium \((x_{1}^{**}, x_{2}^{**}, u^{**})=(0,\frac{3}{5},\frac{9}{20} )\), which shows that the prey species is extinct whereas the predator species still has a positive equilibrium, which is globally asymptotically stable (see Figure 5).
Dynamic behavior of model ( 4.5 ) with the initial value \(\pmb{(x_{1},x_{2},u)=(0.3,0.2,0.3)\mbox{ and }(1,0.8,1)}\) .
References
Saito, Y, Hara, T, Ma, W: Necessary and sufficient conditions for permanence and global stability of a Lotka-Volterra system with two delays. J. Math. Anal. Appl. 236, 534-556 (1999)
Xu, R, Chen, LS: Persistence and global stability for a delayed nonautonomous predator-prey system without dominating instantaneous negative feedback. J. Math. Anal. Appl. 262, 50-61 (2001)
Muroya, Y: Permanence and global stability in a Lotka-Volterra predator-prey system with delays. Appl. Math. Lett. 16, 1245-1250 (2003)
Song, X, Chen, L: Persistence and global stability for nonautonomous predator-prey system with diffusion and time delay. Comput. Math. Appl. 35, 33-40 (1998)
Cui, J: The effect of dispersal on permanence in a predator-prey population growth model. Comput. Math. Appl. 44, 1085-1097 (2002)
Chen, FD, Chen, LJ, Xie, XD: On a Leslie-Gower predator-prey model incorporating a prey refuge. Nonlinear Anal., Real World Appl. 10, 2905-2908 (2009)
Chen, FD, Ma, ZZ, Zhang, HY: Global asymptotical stability of the positive equilibrium of the Lotka-Volterra prey-predator model incorporating a constant number of prey refuges. Nonlinear Anal., Real World Appl. 13, 2790-2793 (2012)
Chen, FD, Xie, X, Miao, Z, Pu, L: Extinction in two species nonautonomous nonlinear competitive system. Appl. Math. Comput. 274, 119-124 (2016)
Ahmad, S, Stamova, IM: Partial persistence and extinction in N-dimensional competitive systems. Nonlinear Anal. 60, 821-836 (2005)
Zu, L, Jiang, DQ, O’Regan, D, Ge, B: Periodic solution for a non-autonomous Lotka-Volterra predator-prey modal with random perturbation. J. Math. Anal. Appl. 430, 428-437 (2015)
Li, Z, Chen, FD, He, MX: Permanence and global attractivity of a periodic predator-prey system with mutual interference and impulses. Commun. Nonlinear Sci. Numer. Simul. 17, 444-453 (2012)
Teng, ZD, Yu, YH: The extinction in nonautonomous prey-predator Lotka-Volterra systems. Acta Math. Appl. Sin. 15(4), 401-408 (1999)
Gomez, L, Ortega, R: The periodic predator-prey Lotka-Volterra models. Adv. Differ. Equ. 1, 403-423 (1996)
Kuang, Y: Delay Differential Equations with Applications in Population Dynamics. Academic Press, New York (1993)
Hou, Z: Vanishing components in autonomous competitive Lotka-Volterra systems. J. Math. Anal. Appl. 359, 302-310 (2009)
Kar, TK, Ghorai, A: Dynamic behaviour of a delayed predator-prey model with harvesting. Appl. Math. Comput. 217, 9085-9104 (2011)
Jana, S, Kar, TK: A mathematical study of a prey-predator model in relevance to pest control. Nonlinear Dyn. 74, 667-683 (2013)
Liu, M, Mandal, PS: Dynamical behavior of a one-prey two-predator model with random perturbations. Commun. Nonlinear Sci. Numer. Simul. 28, 123-137 (2015)
Huo, HF, Li, WT: Positive periodic solutions of a class of delay differential system with feedback control. Appl. Math. Comput. 148, 35-46 (2004)
Muroya, Y: Global stability of a delayed nonlinear Lotka-Volterra system with feedback controls and patch structure. Appl. Math. Comput. 239, 60-73 (2014)
Weng, PX: Existence and global stability of positive periodic solution of periodic integrodifferential systems with feedback controls. Comput. Math. Appl. 40, 747-759 (2000)
Gopalsamy, K, Weng, PX: Global attractivity in a competition system with feedback controls. Comput. Math. Appl. 45, 665-676 (2003)
Shi, CL, Li, Z, Chen, FD: Extinction in nonautonomous Lotka-Volterra competitive system with infinite delay and feedback controls. Nonlinear Anal., Real World Appl. 13, 2214-2226 (2012)
Li, Z, Han, M, Chen, FD: Influence of feedback controls on an autonomous Lotka-Volterra competitive system with infinite delays. Nonlinear Anal., Real World Appl. 14, 402-413 (2013)
Nie, LF, Teng, ZD, Hu, L, Peng, JG: Permanence and stability in non-autonomous predator-prey Lotka-Volterra system with feedback controls. Comput. Math. Appl. 58, 436-448 (2009)
Hu, HX, Teng, ZD, Gao, SJ: Extinction in a nonautonomous Lotka-Volterra competitive system with pure-delays and feedback controls. Nonlinear Anal., Real World Appl. 10, 2508-2520 (2009)
Zeeman, ML: Extinction in competitive Lotka-Volterra systems. Proc. Am. Math. Soc. 123, 87-96 (1995)
Liu, SQ, Chen, LS, Luo, GL, Jiang, YL: Asymptotic behaviors of competitive Lotka-Volterra system with stage structure. J. Math. Anal. Appl. 271, 124-138 (2002)
He, M, Chen, F, Li, Z: Permanence and global attractivity of an impulsive delay logistic model. Appl. Math. Lett. 62, 92-100 (2016)
Gopalsamy, K: Stability and Oscillations in Delay Different Equations of Population Dynamics. Kluwer Academic, Dordrecht (1992)
Acknowledgements
This work is supported by the National Natural Science Foundation of Fujian Province (2015J01012) and the Foundation of Fujian Education Bureau (JA13361).
Author information
Authors and Affiliations
Contributions
All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shi, C., Chen, X. & Wang, Y. Feedback control effect on the Lotka-Volterra prey-predator system with discrete delays. Adv Differ Equ 2017, 373 (2017). https://doi.org/10.1186/s13662-017-1410-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-017-1410-0