1 Introduction

In wireless communication systems, a major challenge is to overcome the effect of small-scale fading cased by Doppler spread and multi-path propagation. Cooperative communication strategies, e.g., distributed beamforming strategies, distributed STC strategies and relay selection strategies, can be used to mitigate these effects. By using the latter strategies, the destination terminal receives many copies of the same information signal from several paths with different amplitudes and phases which improves the overall system performance of the whole network in terms of BER and data rate. Making use of relay nodes in cooperative communication networks is attractive, especially if there is no direct link among the communicating terminals. Relays can jointly process the received information symbol vectors before broadcasting the resulting signal vector to the communicating terminals by sharing their antennas and forming a virtual antenna array to offer a substantial spatial diversity gain. In other words, relay nodes increase the number of independent paths resulting in increasing the number of received copies of the same information signal at the destination to improve the diversity gain. By doing this, the reliability and throughput of the whole system can improve. Recently, several wireless cooperative communication strategies using either one-way or two-way relaying protocols are suggested to offer extra coding or diversity gain and improve the whole system performance in terms of BER and data rate of the wireless cooperative communication networks [1–7].

Some strategies are implemented assuming perfect channel state information (CSI) at all nodes to be used in case of slow fading channels [7–12]. Other strategies were considered the case of perfect or partial CSI at the receiving antennas only [2, 13]. Recent approaches have also been implemented based on the assumption of no CSI at both the transmitting and the receiving antennas such as the non-coherent strategies and differential strategies, e.g., differential chaos shift keying (DCSK), [2–6, 14–21]. The latter strategies overcome the overhead involved with channel estimation, however, they suffer from low BER performance, low spectral efficiency, and a comparably high latency and decoding complexity for more than two transmit antennas due to unavailable CSI at any node.

In two-way relaying strategies, two terminals communicate with each other through many relays in a bi-directional fashion [2–7]. According to the number of time slots required for exchanging the symbols between the communicating terminals, two-way relaying protocols can be categorized into three classes: the four-phase protocols, the three-phase protocols, and the two-phase protocols. The cooperative diversity strategies performed according to the two- and the three-phase protocols reduce the transmission period from four phases to three or two phases, thus resulting in higher spectral efficiency. Therefore, the cooperative diversity strategies performed according to the two- and the three-phase protocols outperform the conventional strategies using those performed according to the four-phase protocols due to the increase in the achievable rate associated with the former strategies [2–4, 14].

In order to offer more coding gain and improve the overall system performance for a two-way relay network, network coding is performed. Network coding schemes can be classified into two categories based on the number of time slots required for exchanging the symbols between the communicating terminals: (i) direct network coding, (ii) analog network coding or physical-layer network coding. In the first category, two terminals send their information symbols to relay nodes during the first two time slots. During the third time slot, relay nodes decode the information symbols of the two terminals and then combine them into a single information symbol before broadcasting the resulting signal back to the terminals [3, 8, 12]. In the second category, the communicating terminals send their symbols simultaneously to the relays to reduce the number of time slots required for transmitting the information symbols of the communicating terminals from three time slots to two time slots, thus resulting in higher spectral efficiency. However, analog network coding or physical-layer network coding requires accurate synchronization and suffers from high decoding complexity at the relays [2, 8, 12]. In this paper, both networking coding schemes are used.

In the normal wireless communication strategies, relay nodes can forward the received information symbol vectors on orthogonal channels or process the received signal vectors using orthogonal strategies, e.g., orthogonal STC strategy [13], before broadcasting them to enjoy the highest coding and diversity gain without increasing the decoding complexity. Relay nodes can also process the received information symbol vectors using non-orthogonal strategies before forwarding them. However, these strategies suffer from high decoding complexity. As an alternative to the previous wireless communication strategies, relay selection strategies in non-orthogonal wireless cooperative communication networks can be performed [8–10] to have the highest diversity gain and use a symbol-wise decoder which enjoys a linear decoding complexity. Recently, many novel one- and two-relay selection strategies are suggested [8–12]. Some strategies choose one relay among several relay nodes distributed randomly among the communicating terminals based on either the measured signal to noise ratio (SNR) or the achievable throughput [9, 10]. Other strategies choose one or two relay nodes according to a certain criterion, e.g., the max-min criterion or the double-max criterion [9, 12]. It has recently been proven that double-relay selection strategies enjoy higher performance than that of the single-relay strategies [8, 9, 12, 14]. In this paper, novel dual-relay selection strategy based STC using the two- and the three-phase protocol is proposed. In addition to that, the concept of network coding is applied at relays to combine the symbols of the communicating terminals in one symbol of the same constellation in order not to waste power for broadcasting redundant information and hence offer additional coding gain. In this work, we offer also analytical approximation of the BER performance for the proposed strategy where the simulation results match perfectly the analytical ones. From the simulation results, the proposed strategy shows a substantially improved BER performance as compared to the current ones.

2 System model

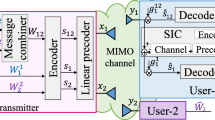
In this paper, we consider a conventional centralized half-duplex wireless cooperative communication network similarly as in [8–12, 15]. The considered wireless cooperative communication network consisting of (R+2) single-antenna nodes. Two of them act as communicating terminals, i.e., \(\mathcal {T}_{1}\) and \(\mathcal {T}_{2}\), and R nodes are utilized as relay nodes. The relays are randomly distributed between the terminals to process the received signal vectors before broadcasting the resulting signal vector to the destination terminals as shown in Fig. 1. Note that, in a centralized network, a centralized node, i.e., a single central server, has all CSI for the whole network and handles all major processes such as applying the proposed strategy to select the optimal two relays and informing them in order to apply space time coding. Note that CSI is available also at the receiving nodes to decode the information symbols. Further, let us consider the extended block Rayleigh fading channel model, for which in the two- and the three-phase scheme the channels are assumed to remain approximately constant over two and three phases, respectively, and to slowly change outside the respective period. Remark that the considered Rayleigh fading channel model is a commonly used fading model that reasonably describes the channel observed in environments with several scattering objects and no line of sight. All channels between the communicating terminals and relay nodes are assumed to be reciprocal. Let us denote the link from \(\mathcal {T}_{1}\) to \(\mathcal {R}_{r}\) and from \(\mathcal {T}_{2}\) to \(\mathcal {R}_{r}\) as fr and gr, respectively. The average transmitted power of the communicating terminal and relay nodes \(\mathcal {T}_{1}, \mathcal {T}_{2}, \mathcal {R}_{1},\ldots,\mathcal {R}_{R}\) are \(P_{\mathcal {T}_{1}}, P_{\mathcal {T}_{2}}, P_{\mathcal {R}_{1}},\ldots,P_{\mathcal {R}_{R}}\), respectively. Throughout this work, ⊕,|·|,⌊·⌋,(·)∗,mod(a,b),∥·∥,[a]i,IT,σ2, and E{·} denote the exclusive OR (XOR) operation, the absolute value, the floor operation which rounds toward zero, the complex conjugate, the remainder of the division of a by b, the Frobenius norm, the ith element of a vector a, the T×T identity matrix, the noise variance, and the statistical expectation, respectively.

Fig. 1
figure 1

Two-way wireless relay network with (R+2) nodes

Full size image

3 Two-phase bi-directional relay selection strategy

In this strategy, communicating terminals exchange their information signals via two time slots. In the first time slot of this strategy, both communicating terminals, i.e., \(\mathcal {T}_{1}\) and \(\mathcal {T}_{2}\), broadcast their information signal vectors, i.e., \(\textbf {s}_{\mathcal {T}_{1}}\) and \(\textbf {s}_{\mathcal {T}_{2}}\). Therefore, the rth relay \(\mathcal {R}_{r}\) receives

$$ \mathbf{y}_{\mathcal{R},r}=\sqrt {2 P_{\mathcal{T}_{1}}}~f_{r}~\mathbf{s}_{\mathcal{T}_{1}}+ \sqrt{2 P_{\mathcal{T}_{2}}}~g_{r}~\mathbf{s}_{\mathcal{T}_{2}}+ \mathbf{n}_{\mathcal{R},r} $$
(1)

where \([\textbf {s}_{\mathcal {T}_{1}}]_{i}\in \mathcal {S}_{\mathcal {T}_{1}}, [\textbf {s}_{\mathcal {T}_{2}}]_{i}\in \mathcal {S}_{\mathcal {T}_{2}}, \mathrm {E}\left \{{|[\textbf {s}_{\mathcal {T}_{1}}]_{i}|^{2}}\right \}=1, \mathrm {E}\left \{ {|[\textbf {s}_{\mathcal {T}_{2}}]_{i}|^{2}}\right \}=1, \mathcal {S}_{\mathcal {T}_{1}}\) and \(\mathcal {S}_{\mathcal {T}_{2}}\) denote two, possibly different, constellations, and \(\textbf {n}_{\mathcal {R},r}\) is the noise signal vector received at the rth relay \(\mathcal {R}_{r}\) during the first time slot. The rth relay \(\mathcal {R}_{r}\) decodes the received information symbol vector using the following maximum likelihood (ML) decoder

$$\begin{array}{@{}rcl@{}} \arg\min_{\mathbf{s}_{\mathcal{T}_{1}}, \mathbf{s}_{\mathcal{T}_{2}}} \left\| \textbf{y}_{\mathcal{R},r} - \left(\sqrt {2 P_{\mathcal{T}_{1}}} f_{r} \mathbf{s}_{\mathcal{T}_{1}} + \sqrt{2 P_{\mathcal{T}_{2}}} g_{r} \mathbf{s}_{\mathcal{T}_{2}} \right) \right\|. \end{array} $$
(2)

To improve the overall system performance, the rth relay \(\mathcal {R}_{r}\) performs digital network coding by combining the decoded information signal vectors of both terminals, \(\tilde {\textbf {s}}_{\mathcal {T}_{1},r}\) and \(\tilde {\textbf {s}}_{\mathcal {T}_{2},r}\), in one vector in order not to broadcast known symbols to the communicating terminals, such that

$$ {\mathbf{s}}_{\mathcal{R},r}=\mathcal{F}(\tilde{\mathbf{s}}_{\mathcal{T}_{1},r},\tilde{\mathbf{s}}_{\mathcal{T}_{2},r}) $$
(3)

where \(\mathcal {F}(\cdot,\cdot)\) denotes a function used for combining the information symbols. Many functions have recently been suggested, e.g., modular arithmetic (MA) function [2]. Remark that \({\textbf {s}}_{\mathcal {R},r}\in \mathcal {S}_{\mathcal {R}}\) where \(\mathcal {S}_{\mathcal {R}}\) denotes the constellation of the information symbols from relay nodes and \(|\mathcal {S}_{\mathcal {R}}|=\max \{|\mathcal {S}_{\mathcal {T}_{1}}|,|\mathcal {S}_{\mathcal {T}_{2}}|\}\). Let us consider the jth entry s of a constellation \(\mathcal {S}\) as \(\mathcal {S}(j)\) where \(j \in \{0,1,\ldots,|\mathcal {S}|-1\}\) and the inverse as \(\mathcal {S}^{-1}(s)=j\). Let define \(\textbf {k}_{\mathcal {T}_{1}}\) and \(\textbf {k}_{\mathcal {T}_{2}}\) as \(\mathcal {S}_{\mathcal {T}_{1}}({\textbf {k}_{\mathcal {T}_{1}}})={\textbf {s}}_{\mathcal {T}_{1}}\) and \(\mathcal {S}_{\mathcal {T}_{2}}({\textbf {k}_{\mathcal {T}_{2}}})={\textbf {s}}_{\mathcal {T}_{2}}\), the MA function can be expressed as \(\mathcal {F}_\text{m}({\textbf {s}}_{\mathcal {T}_{1}},{\textbf {s}}_{\mathcal {T}_{2}})= \mathcal {S}_{\mathcal {R}}(\text {mod}(\mathcal {S}^{-1}_{\mathcal {T}_{1}}({\textbf {s}}_{\mathcal {T}_{1}})+ \mathcal {S}^{-1}_{\mathcal {T}_{2}}({\textbf {s}}_{\mathcal {T}_{2}}),|\mathcal {S}_{\mathcal {R}}|))= \mathcal {S}_{\mathcal {R}}({\text {mod}(\textbf {k}_{\mathcal {T}_{1}}+\textbf {k}_{\mathcal {T}_{2}},|\mathcal {S}_{\mathcal {R}}|)})\). The XOR function proposed in [1] and the function suggested in [2] can also be applied to combine the information signal vectors. In the suggested strategy, two relays, the ath relay \(\mathcal {R}_{a}\) and the bth relay \(\mathcal {R}_{b}\), are selected among R relay nodes according to a dual relay selection method. The first relay, i.e., the ath relay \(\mathcal {R}_{a}\), is selected among R relay nodes using max-min criterion which is the optimal single-relay selection method [8–10, 12]. The second relay, i.e., the bth relay \(\mathcal {R}_{b}\), is selected among (R−1) relay nodes, after excluding the ath relay \(\mathcal {R}_{a}\), using also max-min criterion, where

$$\begin{array}{@{}rcl@{}} a &=& \arg \max_{a} \min ({|f_{a}|}, {|g_{a}|}), \\ b &=& \arg \max_{b} \min ({|f_{b}|}, {|g_{b}|}), b\neq a. \end{array} $$
(4)

We observe that the suggested method chooses two relays, i.e., \(\mathcal {R}_{a}\) and \(\mathcal {R}_{b}\), according to the max-min selection criterion. The first relay, i.e., \(\mathcal {R}_{a}\), is chosen among R relay nodes based on the max-min selection criterion which is the optimal single-relay selection method in both directions [10] while the second relay, i.e., \(\mathcal {R}_{b}\), is chosen among R−1 relay nodes based also on the optimal single-relay selection method, i.e., max-min selection criterion [10]. In the following, we consider the received vectors at the second terminal \(\mathcal {T}_{2}\). The received vectors at the first terminal \(\mathcal {T}_{1}\) can be reconstructed correspondingly. Thus, during the first time slot, the selected single-antenna relays, i.e., \(\mathcal {R}_{a}\) and \(\mathcal {R}_{b}\), decode the information symbol vector of the first and the second terminal before combining them into a single vector. During the second time slot, the antenna of the first relay, i.e., \(\mathcal {R}_{a}\), and the antenna of the second relay, i.e., \(\mathcal {R}_{b}\), perform orthogonal STC using the following 2×2 Alamouti STC matrices

$$\begin{array}{@{}rcl@{}} \mathbf{A}_{a} &=& \left[ {\begin{array}{*{20}c} {1} & {0} \\ { 0} & { 1} \\ \end{array}} \right],\quad \mathbf{A}_{b} = \left[ {\begin{array}{*{20}c} {0} & {1} \\ { -1} & { 0} \\ \end{array}} \right], \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} \breve{\mathbf{s}}_{\mathcal{R},a}&=&{\mathbf{s}}_{\mathcal{R},a},\quad \quad \quad \breve{\mathbf{s}}_{\mathcal{R},b}=({\mathbf{s}}_{\mathcal{R},b})^{*} \end{array} $$
(6)

before broadcasting the output signal vector to the destinations. Thus, the second terminal \(\mathcal {T}_{2}\) receives the following signal vector

$$\begin{array}{@{}rcl@{}} \mathbf{y}_{\mathcal{T}_{2}}=\sqrt{P_{\mathcal{R}_{a}}}g_{a}\mathbf{A}_{a}\breve{\mathbf{s}}_{ \mathcal{R},a} + \sqrt{P_{\mathcal{R}_{b}}}g_{b}\mathbf{A}_{b}\breve{\mathbf{s}}_{ \mathcal{R},b} +\mathbf{n}_{\mathcal{T}_{2}} \end{array} $$
(7)

where \(\textbf {n}_{\mathcal {T}_{2}}\) stands for noise signal vector at the second terminal \(\mathcal {T}_{2}\). Let us consider the case of error-free decoding on all relay nodes i.e., \({\textbf {s}}_{\mathcal {R},a}={\textbf {s}}_{\mathcal {R},b}={\textbf {s}}_{\mathcal {R}}\). Therefore, the ML decoder of the second terminal \(\mathcal {T}_{2}\) can be expresses as

$$ \hat{\mathbf{s}}_{\mathcal{R},\mathcal{T}_{2}}=\arg\min_{{\mathbf{s}}_{\mathcal{R}}}\left\| \mathbf{y}_{\mathcal{T}_{2}} - \sum_{r=\{a,b\}}\sqrt{P_{\mathcal{R}_{r}}}g_{r}\mathbf{A}_{r}\breve{\mathbf{s}}_{\mathcal{R}} \right\|. $$
(8)

The second terminal \(\mathcal {T}_{2}\) reconstructs the information signal vector \(\hat {\textbf {s}}_{\mathcal {T}_{1}}\) by using its own transmitted information symbol vector \({\textbf {s}}_{\mathcal {T}_{2}}\) and by inverting the combination function \(\mathcal {F}\) (expressed as \(\mathcal {F}^{-1}\)), i.e., \(\hat {\textbf {s}}_{\mathcal {T}_{1}}=\mathcal {F}^{-1}(\hat {\textbf {s}}_{\mathcal { R},\mathcal {T}_{2}}, {\textbf {s}}_{\mathcal {T}_{2}})\). When MA function is performed on the relay nodes, \(\hat {\textbf {k}}_{\mathcal {R},\mathcal {T}_{2}}\) can be expressed as \(\mathcal {S}_{\mathcal {R}}(\hat {\textbf {k}}_{\mathcal {R},\mathcal {T}_{2}})=\hat {\textbf {s}}_{\mathcal {R},\mathcal {T}_{2}}\); therefore, the second terminal \(\mathcal {T}_{2}\) decodes the information signals of the first terminal \(\mathcal {T}_{1}\) by using \(\hat {\textbf {s}}_{\mathcal {T}_{1}}=\mathcal {F}_\text{m}^{-1}(\hat {\textbf {s}}_{\mathcal {R},\mathcal {T}_{2}},\textbf {s}_{\mathcal {T}_{2}})=\mathcal {S}_{\mathcal {T}_{1}}({\text{mod}(\hat {\textbf {k}}_{\mathcal {R},\mathcal {T}_{2}}-\textbf {k}_{\mathcal {T}_{2}},|\mathcal {S}_{\mathcal {T}_{1}}|)})\) where \(\mathcal {F}_{\mathrm {m}}^{-1}\) stands for the inverse of the MA function.

4 Three-phase bi-directional relay selection strategy

In this part, three-phase protocol is performed. In the first two time slots, both terminals, \(\mathcal {T}_{1}\) and \(\mathcal {T}_{2}\), transmit their information symbol vectors, \(\textbf {s}_{\mathcal {T}_{1}}\) and \(\textbf {s}_{\mathcal {T}_{2}}\), such that the rth relay \(\mathcal {R}_{r}\) receives

$$ \mathbf{y}_{\mathcal{R}_{1},r}=\sqrt{3P_{\mathcal{T}_{1}}}~f_{r}~\mathbf{s}_{\mathcal{T}_{1}} + \mathbf{n}_{\mathcal{R}_{1},r} $$
(9)
$$ \mathbf{y}_{\mathcal{R}_{2},r}=\sqrt{3P_{\mathcal{T}_{2}}}~g_{r}~\mathbf{s}_{\mathcal{T}_{2}} + \mathbf{n}_{\mathcal{R}_{2},r} $$
(10)

where \(\textbf {n}_{\mathcal {R}_{1},r}\) and \(\textbf {n}_{\mathcal {R}_{2},r}\) denote as the noise signal vectors received at the rth relay \(\mathcal {R}_{r}\) in the first and the second time-slot, respectively. Similarly as in Section 3 and using (9) and (10), the rth relay \(\mathcal {R}_{r}\) decodes the information symbol vectors of the first and the second terminal, \(\mathcal {T}_{1}\) and \(\mathcal {T}_{2}\), using the following ML decoders

$$\begin{array}{@{}rcl@{}} \hat{\mathbf{s}}_{\mathcal{T}_{1},r} &=& \arg\min_{\mathbf{s}_{\mathcal{T}_{1}}} \left\| \mathbf{y}_{\mathcal{R}_{1},r} - \sqrt {3P_{\mathcal{T}_{1}}} f_{r} \mathbf{s}_{\mathcal{T}_{1}} \right\|, \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} \hat{\mathbf{s}}_{\mathcal{T}_{2},r} &=& \arg\min_{\mathbf{s}_{\mathcal{T}_{2}}} \left\| \mathbf{y}_{\mathcal{R}_{2},r}- \sqrt {3P_{\mathcal{T}_{2}}} g_{r} \mathbf{s}_{\mathcal{T}_{2}} \right\|. \end{array} $$
(12)

We observe from the previous equations, i.e., (11) and (12), that the relay decoding complexity is very low where a symbol-wise decoder, that enjoys a linear decoding complexity, can be applied to decode the information symbols. However, the relay decoders of the proposed strategy using the two-phase relaying protocol, explained in Section 3, suffer from high decoding complexity which increases quadratically with the increase of the constellation size. Similar to Section 3, the decoded symbol vectors, \(\tilde {\textbf {s}}_{\mathcal {T}_{1},r}\) and \(\tilde {\textbf {s}}_{\mathcal {T}_{2},r}\), of the first terminal \(\mathcal {T}_{1}\) and the second terminal \(\mathcal {T}_{2}\) are combined in a single symbol vector as follows

$$ {\mathbf{s}}_{\mathcal{R},r}=\mathcal{F}(\tilde{\mathbf{s}}_{\mathcal{T}_{1},r},\tilde{\mathbf{s}}_{ \mathcal{T}_{2},r}). $$
(13)

Similar to Section 3, the relays, \(\mathcal {R}_{a}\) and \(\mathcal {R}_{b}\), are chosen according to the suggested dual relay-selection criterion given in (4). The selected relays, \(\mathcal {R}_{a}\) and \(\mathcal {R}_{b}\), perform orthogonal STC technique using Almouti scheme in order to improve the diversity and coding gain without adding extra decoding complexity, where the information symbol vectors of the selected relays, \({\textbf {s}}_{\mathcal {R},a}\) and \(({\textbf {s}}_{\mathcal {R},b})^{*}\) given in (13), are encoded using the 2×2 Alamouti STC matrices, Aa and Ab, defined in (5) before sending the combined symbol vector to both terminals during the third time-slot. Thus, the second terminal \(\mathcal {T}_{2}\) receives

$$\begin{array}{@{}rcl@{}} \mathbf{y}_{\mathcal{T}_{2}}=\sqrt{P_{\mathcal{R}_{a}}} g_{a} \mathbf{A}_{a} {\mathbf{s}}_{ \mathcal{R},a} + \sqrt{P_{\mathcal{R}_{b}}}g_{b} \mathbf{A}_{b} ({\mathbf{s}}_{ \mathcal{R},b})^{*} +\mathbf{n}_{\mathcal{T}_{2}} \end{array} $$
(14)

where \(\textbf {n}_{\mathcal {T}_{2}}\) stands for the noise signal vector received at the second terminal \(\mathcal {T}_{2}\) in the third time slot. Similar to Section 3, the ML decoder given in (8) is performed to recover the information vector at the second terminal \(\mathcal {T}_{2}\). Remark that the second terminal \(\mathcal {T}_{2}\) can recover the information symbol vector via a symbol-by-symbol decoder which enjoys a linear decoding complexity instead of applying the ML decoder given in (8). The second terminal \(\mathcal {T}_{2}\) uses the knowledge of its own information vector \({\textbf {s}}_{\mathcal {T}_{2}}\) and the inverse of the combination function, i.e., \(\mathcal {F}^{-1}\), in order to reconstruct the information symbol vector of the first terminal \(\hat {\textbf {s}}_{\mathcal {T}_{1}}\), i.e., \(\hat {\textbf {s}}_{\mathcal {T}_{1}}=\mathcal {F}^{-1}(\hat {\textbf {s}}_{\mathcal { R},\mathcal {T}_{2}}, {\textbf {s}}_{\mathcal {T}_{2}})\).

5 BER performance analysis

In this section, let us derive the theoretical BER performance of the suggested strategy using BPSK modulation according to the assumptions in Section 2 and assuming that all relays are ideal similar to [2, 9, 12]. Based on the previous assumptions, the strategies that use the two-phase and the three-phase protocol enjoy the same BER performance. In the derivations of the average BER performance, we consider that the noise signals are drawn from independent and identically distributed Gaussian random variables having zero mean and covariance σ2IT. The suggested relay- selection strategy defined in (4) selects the ath and bth relay with \(P_{\mathcal {R}_{a}}=P_{\mathcal {R}_{b}}=P_{\mathcal {R}}\). Let us rearrange \(\gamma _{r}^{\mathcal {T}_{t}}\), r=1,⋯,R,t=1,2 in ascending order, where \(\gamma _{1}^{\mathcal {T}_{t}} \le \gamma _{2}^{\mathcal {T}_{t}}\le \cdots \le \gamma _{R}^{\mathcal {T}_{t}}\) and denote \(w_{1}^{\mathcal {T}_{t}}=\gamma _{1}^{\mathcal {T}_{t}}\) and \( w_{l}^{\mathcal {T}_{t}}=\gamma _{l}^{\mathcal {T}_{t}}-\gamma _{(l-1)}^{\mathcal {T}_{t}}\) for l=2,⋯,R. Note that \(\gamma _{r}^{\mathcal {T}_{1}}=\gamma |f_{r}|^{2}\), \(\gamma _{r}^{\mathcal {T}_{2}}=\gamma |g_{r}|^{2}\), and \(\gamma =P_{\mathcal {R}}/\sigma ^{2}\) denote the SNR of the link between \(\mathcal {R}_{r}\) and \({\mathcal {T}_{1}}\), the SNR of the link between \(\mathcal {R}_{r}\) and \({\mathcal {T}_{2}}\), and the mean SNR at the rth relay \(\mathcal {R}_{r}\), respectively. The independent factors, wl for l=1,⋯,R, have probability distribution function, expressed as [9, 10, 12]

$$\begin{array}{@{}rcl@{}} f_{w_{l}}(w_{l})= \frac{R-l-1}{\gamma} \exp\left(- \frac{R-l-1}{\gamma} w_{l} \right). \end{array} $$
(15)

In this work, the ath relay \(\mathcal {R}_{a}\) is chosen out of R relays based on the max-min relay selection method explained in (4), such that ga and fa are the link between the ath relay \(\mathcal {R}_{a}\) and \({\mathcal {T}_{2}}\) with \(\gamma _{\lfloor R/2\rfloor }^{{\mathcal {T}_{2}}}\) and the link between \(\mathcal {R}_{a}\) and \({\mathcal {T}_{1}}\) with \(\gamma _{u_{1}}^{{\mathcal {T}_{1}}}\) where \(\gamma _{u_{1}}^{{\mathcal {T}_{1}}}\ge \gamma _{\lfloor R/2\rfloor }^{{\mathcal {T}_{2}}}\) and u1 could be any uth greater than ⌊R/2⌋, i.e., u=⌊R/2⌋+1,⋯,R. After selecting the ath relay \(\mathcal {R}_{a}\), the bth relay \(\mathcal {R}_{b}\) is chosen out of R−1 relays based on the max-min relay selection method explained in (4), such that gb and fb are the link between the bth relay \(\mathcal {R}_{b}\) and \({\mathcal {T}_{2}}\) with \(\gamma _{\lfloor (R-1)/2\rfloor }^{{\mathcal {T}_{2}}}\) and the link between \(\mathcal {R}_{b}\) and \({\mathcal {T}_{1}}\) with \(\gamma _{u_{2}}^{{\mathcal {T}_{1}}}\) where \(\gamma _{u_{1}}^{{\mathcal {T}_{1}}}\ge \gamma _{\lfloor (R-1)/2\rfloor }^{{\mathcal {T}_{2}}}\) and u2 could be any uth greater than ⌊(R−1)/2⌋, i.e., u=⌊(R−1)/2⌋+1,⋯,R. Let us first consider that \(\gamma _{u_{1}}^{{\mathcal {T}_{t}}}\ge \gamma _{u_{2}}^{{\mathcal {T}_{t}}}\ge \gamma _{\lfloor R/2\rfloor }^{{\mathcal {T}_{t}}}\ge \gamma _{\lfloor (R-1)/2\rfloor }^{{\mathcal {T}_{t}}}, t={1,2}\). The average BER for the suggested double-relay selection strategy can be written as

$$\begin{array}{@{}rcl@{}} P(\gamma)&\,=\,& \frac{1}{4} \mathrm{E}\left\{\!{Q\left(\sqrt{\gamma_{\lfloor R/2\rfloor}^{\mathcal{T}_{2}}\,+\,\gamma_{\lfloor (R-1)/2\rfloor}^{\mathcal{T}_{2}}} \right) \!\,+\, \!Q \left(\sqrt{\gamma_{u_{1}}^{\mathcal{T}_{1}}\,+\,\gamma_{u_{2}}^{\mathcal{T}_{1}}} \right)}\right\} \\ &\,+\,& \frac{1}{4} \mathrm{E}\left\{{Q\left(\sqrt{\gamma_{\lfloor R/2\rfloor}^{\mathcal{T}_{2}}\,+\,\gamma_{u_{2}}^{\mathcal{T}_{2}}} \right) \!\,+\,\! Q \left(\!\sqrt{\gamma_{\lfloor (R-1)/2\rfloor}^{\mathcal{T}_{1}}\,+\,\gamma_{u_{1}}^{\mathcal{T}_{1}}} \right)}\right\}\\ &\,=\,& \frac{1}{4}(T_{1}+T_{2}+T_{3}+T_{4}). \end{array} $$
(16)

We can observe that Eq. 16 contains four terms where the first one T1 could be found via the moment-generation function (MGF), such that

$$ {\begin{aligned} Q_{1}\!&=\!\gamma_{\lfloor R/2\rfloor}^{\mathcal{T}_{2}}\,+\,\gamma_{\lfloor (R-1)/2\rfloor}^{\mathcal{T}_{2}} \,=\,\!\! \sum_{i=1}^{\lfloor (R-1)/2\rfloor} \!\!w_{i} \,+\,\! \sum_{i=1}^{\lfloor R/2\rfloor} \! w_{i} \!\,=\, 2 \!\!\sum_{i=1}^{\lfloor (R-1)/2\rfloor} \\&\quad w_{i} \,+\,\!\!\!\! \sum_{i={\lfloor (R-1)/2\rfloor}+1}^{\lfloor R/2\rfloor} \!\!\!\!\!\!\!\! w_{i}. \end{aligned}} $$
(17)

Making use of (17), the MGF of Q1 can be given by [12, 22]

$$ {{} \begin{aligned} M_{Q_{1}}(s)&=\int_{0}^{\infty} \!\!\!\!\!\cdots \!\!\int_{0}^{\infty} \left(\prod_{i=1}^{R} f_{w_{i}} (w_{i})\right) \exp({sQ}_{1}) {dw}_{1} \cdots {dw}_{R}\\ & \quad= \prod_{i=1}^{\lfloor (R-1)/2\rfloor} \!\!\!\!\int_{0}^{\infty} f_{w_{i}} (w_{i}) \exp(2 s w_{i}) {dw}_{i}\\&\quad \prod_{i=\lfloor (R-1)/2\rfloor+1}^{\lfloor R/2\rfloor} \int_{0}^{\infty} \!\!\!\!f_{w_{i}} (w_{i}) \exp(s w_{i}) {dw}_{i}\\ & \quad= \frac{{\lfloor R/2\rfloor}! (-1)^{\lfloor R/2\rfloor}}{2^{\lfloor (R-1)/2\rfloor} \gamma^{{\lfloor R/2\rfloor}}} \prod_{i=1}^{\lfloor (R-1)/2\rfloor} \frac{1}{s-\frac{{\lfloor R/2\rfloor}-i+1}{2 \gamma}}\\& \prod_{i=\lfloor (R-1)/2\rfloor+1}^{{\lfloor R/2\rfloor}} \frac{1}{s-\frac{{\lfloor R/2\rfloor}-i+1}{\gamma}}. \end{aligned}} $$
(18)

Eq. 18, after using partial fraction expansion method, can be given by

$${{}\begin{aligned} & M_{Q_{1}}(s)\,=\, \frac{{\lfloor R/2\rfloor}! (-1)^{\lfloor R/2\rfloor}}{2^{\lfloor (R-1)/2\rfloor} \gamma^{\lfloor R/2\rfloor}}\\ & \quad \sum_{i=1}^{\lfloor (R-1)/2\rfloor} \!\!\!\!\! \frac{1}{\left(s-\frac{{\lfloor R/2\rfloor}-i+1}{2 \gamma}\right)\!\! \prod\limits_{\substack{j=1\\j\ne i}}^{\lfloor R/2\rfloor}\!\!{\left(\frac{{\lfloor R/2\rfloor}-i+1}{2 \gamma} - \frac{{\lfloor R/2\rfloor}-j+1}{2 \gamma} \right)}}\\ &\times \sum_{p=\lfloor (R-1)/2\rfloor+1}^{{\lfloor R/2\rfloor}}\\& \quad\frac{1}{\left(s-\frac{{\lfloor R/2\rfloor}-p+1}{\gamma}\right) \prod\limits_{\substack{r=\lfloor (R-1)/2\rfloor+1\\ j\ne p}}^{{\lfloor R/2\rfloor}} {\left(\frac{{\lfloor R/2\rfloor}-p+1}{\gamma} - \frac{{\lfloor R/2\rfloor}-r+1}{\gamma} \right)}}\\ &= \frac{{\lfloor R/2\rfloor}! (-1)^{\lfloor R/2\rfloor}}{2 \gamma^{2}} \sum_{i=1}^{\lfloor (R-1)/2\rfloor}\\ \end{aligned}} $$
$$ {\begin{aligned} &\quad \sum_{p=\lfloor (R-1)/2\rfloor+1}^{{\lfloor R/2\rfloor}} \frac{1}{\prod\limits_{\substack{j=1\\j\ne i}}^{\lfloor (R-1)/2\rfloor} (j-i) \prod\limits_{\substack{r=\lfloor (R-1)/2\rfloor+1 \\r\ne p}}^{{\lfloor R/2\rfloor}} (r-p)}\\ &\times \frac{1}{\left(s-\frac{{\lfloor R/2\rfloor}-i+1}{2 \gamma}\right) \left(s-\frac{{\lfloor R/2\rfloor}-p+1}{\gamma}\right) }. \end{aligned}} $$
(19)

Thus, T1 in (16) can be expressed using (19) as [12, 22]

$$\begin{array}{@{}rcl@{}} && \!\!\!\! T_{1} = \frac{1}{2\pi} \int_{0}^{\pi/2} M_{Q_{1}}\left(\frac{-1}{2 \sin^{2}(\phi)}\right) d\phi. \end{array} $$
(20)

Making use of (19) and (20), T1 in (16) is given by

$$ {{} \begin{aligned} & T_{1} \,=\, \frac{{\lfloor R/2\rfloor}! (-1)^{\lfloor R/2\rfloor}}{4 \gamma^{2}} \sum_{i=1}^{\lfloor (R-1)/2\rfloor} \sum_{p=\lfloor (R-1)/2\rfloor+1}^{{\lfloor R/2\rfloor}}\\&\quad \times \frac{1}{\prod\limits_{\substack{j=1\\j\ne i}}^{\lfloor (R-1)/2\rfloor} (j-i) \!\!\!\prod\limits_{\substack{r=\lfloor (R-1)/2\rfloor+1 \\r\ne p}}^{{\lfloor R/2\rfloor}}(r-p)}\\ &\!\times\! \frac{1}{\pi}\int_{0}^{\pi/2}\!\!\!\!\!\!\!\frac{1}{ \left(\frac{1}{2 \sin^{2}(\phi)} + \frac{{\lfloor R/2\rfloor}-i+1}{2 \gamma} \right) \left(\frac{1}{2 \sin^{2}(\phi)} + \frac{{\lfloor R/2\rfloor}-p+1}{\gamma} \right)} d\phi. \end{aligned}} $$
(21)

Similarly as in the previous Eqs. 17–(21) and by considering u1≥u2 and making use of the MGF of \(Q_{2}=\gamma _{u_{1}}^{\mathcal {T}_{1}}+\gamma _{u_{2}}^{\mathcal {T}_{1}}\), the second term T2 could also be found as follows

$$ {{} \begin{aligned} Q_{2}=\gamma_{u_{1}}^{\mathcal{T}_{1}}+\gamma_{u_{2}}^{\mathcal{T}_{1}} = \sum_{i=1}^{u_{1}} w_{i} + \sum_{i=1}^{u_{2}} w_{i} = 2 \sum_{i=1}^{u_{2}} w_{i} \!\!+ \!\!\!\!\!\sum_{i=u_{2}+1}^{u_{1}} w_{i}. \end{aligned}} $$
(22)

Making use of (22), the MGF of Q2 can be given by

$$\begin{array}{@{}rcl@{}} M_{Q_{2}}(s)\!\!\!\!&=&\!\!\!\! \!\! \int_{0}^{\infty} \!\!\!\! \cdots \!\!\int_{0}^{\infty} \left(\prod_{i=1}^{R} f_{w_{i}} (w_{i})\right) \exp({sQ}_{2}) {dw}_{1} \cdots {dw}_{R}\\ && \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\,=\, \prod_{i=1}^{u_{2}} \! \int_{0}^{\infty} \!\!\!\!\! f_{w_{i}} (w_{i}) \exp(2 s w_{i}) {dw}_{i} \!\!\!\! \prod_{i=u_{2}+1}^{u_{1}} \! \int_{0}^{\infty} \!\!\!\! f_{w_{i}} (w_{i}) \exp(s w_{i}) {dw}_{i}\\ && \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\,=\, \frac{u_{1}! (-1)^{u_{1}}}{2^{u_{2}} \gamma^{u_{1}}} \prod_{i=1}^{u_{2}} \frac{1}{s-\frac{{u_{1}}-i+1}{2 \gamma} } \prod_{i=u_{2}+1}^{u_{1}} \frac{1}{s-\frac{u_{1}-i+1}{\gamma}}. \end{array} $$
(23)

Similarly as in the previous Eq. 18, (23) is given using partial fraction expansion by

$$\begin{array}{@{}rcl@{}} && \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! M_{Q_{2}}(s)\,=\, \frac{u_{1}! (-1)^{u_{1}}}{2 \gamma^{2}} \sum_{i=1}^{u_{2}} \sum_{p=u_{2}+1}^{u_{1}} \frac{1}{\prod\limits_{\substack{j=1\\j\ne i}}^{u_{2}} (j-i) \prod\limits_{\substack{r=u_{2}+1 \\r\ne p}}^{u_{1}} (r-p)}\\ &\times& \!\!\!\! \frac{1}{\left(s-\frac{u_{1}-i+1}{2 \gamma}\right) \left(s-\frac{u_{1}-p+1}{\gamma}\right) }. \end{array} $$
(24)

Similarly as in (20), the second term T2 can be expressed using the MGF as

$$\begin{array}{@{}rcl@{}} && \!\!\!\! T_{2}= \frac{1}{2\pi} \int_{0}^{\pi/2} M_{Q_{2}}\left(\frac{-1}{2 \sin^{2}(\phi)}\right) d\phi. \end{array} $$
(25)

Making use of (24) and (25), T2 in (16) is given by

$$\begin{array}{@{}rcl@{}} && \!\!\!\!\!\!\!\!\!\!\!\!\!\!\! T_{2}= \frac{u_{1}! (-1)^{u_{1}}}{4 \gamma^{2}} \sum_{i=1}^{u_{2}} \sum_{p=u_{2}+1}^{u_{1}} \frac{1}{\prod\limits_{\substack{j=1\\j\ne i}}^{u_{2}} (j-i) \prod\limits_{\substack{r=u_{2}+1 \\r\ne p}}^{u_{1}} (r-p)}\\ &\!\!\!\!\!\!\!\!\!\!\!\!\times& \!\!\!\!\!\!\!\!\! \frac{1}{\pi}\!\int_{0}^{\pi/2}\!\!\!\!\!\!\!\!\!\!\frac{1}{ \left(\frac{1}{2 \sin^{2}(\phi)} + \frac{u_{1}-i+1}{2 \gamma} \right) \left(\frac{1}{2 \sin^{2}(\phi)} + \frac{u_{1}-p+1}{\gamma} \right)} d\phi. \end{array} $$
(26)

Similarly as in the previous Eqs. 17–(21), and by considering u2≥⌊R/2⌋ and making use of the MGF of \(Q_{3}=\gamma _{u_{2}}^{\mathcal {T}_{2}}+\gamma _{{\lfloor R/2\rfloor }}^{\mathcal {T}_{2}}\), the third term T3 could also be found as follows

$$ {{} \begin{aligned} Q_{3}\!\,=\,\gamma_{u_{2}}^{\mathcal{T}_{2}}\,+\,\gamma_{{\lfloor R/2\rfloor}}^{\mathcal{T}_{2}} \,=\,\! \sum_{i=1}^{u_{2}} w_{i} \,+\,\!\! \sum_{i=1}^{{\lfloor R/2\rfloor}} w_{i} \,=\, 2 \sum_{i=1}^{{\lfloor R/2\rfloor}} w_{i} \!\,+\,\!\!\ \sum_{i={\lfloor R/2\rfloor}+1}^{u_{2}} w_{i}. \end{aligned}} $$
(27)

Making use of (27), the MGF of Q3 can be given by

$$ {{}\begin{aligned} M_{Q_{3}}(s)&=\int_{0}^{\infty} \cdots \!\!\int_{0}^{\infty} \left(\prod_{i=1}^{R} f_{w_{i}} (w_{i})\right) \exp({sQ}_{2}) {dw}_{1} \cdots {dw}_{R}\\ & = \prod_{i=1}^{{\lfloor R/2\rfloor}} \! \int_{0}^{\infty} f_{w_{i}} (w_{i}) \exp(2 s w_{i}) {dw}_{i}\\ &\quad \times \prod_{i={\lfloor R/2\rfloor}+1}^{u_{2}} \! \int_{0}^{\infty} f_{w_{i}} (w_{i}) \exp(s w_{i}) {dw}_{i}\\ & =\! \frac{u_{2}! (-1)^{u_{2}}}{2^{{\lfloor R/2\rfloor}} \gamma^{u_{2}}} \prod_{i=1}^{{\lfloor R/2\rfloor}} \frac{1}{s\,-\,\frac{{u_{2}}-i+1}{2 \gamma} } \prod_{i={\lfloor R/2\rfloor}+1}^{u_{2}} \frac{1}{s-\frac{u_{2}-i+1}{\gamma}}. \end{aligned}} $$
(28)

Similarly as in the previous Eq. 18, (28) is given using partial fraction expansion by

$$ {{}\begin{aligned} & M_{Q_{3}}(s)\,=\, \frac{u_{2}! (-1)^{u_{2}}}{2 \gamma^{2}} \sum_{i=1}^{{\lfloor R/2\rfloor}} \sum_{p={\lfloor R/2\rfloor}+1}^{u_{2}} \frac{1}{\prod\limits_{\substack{j=1\\j\ne i}}^{{\lfloor R/2\rfloor}} (j-i) \prod\limits_{\substack{r={\lfloor R/2\rfloor}+1 \\r\ne p}}^{u_{2}} (r-p)}\\ &\times \frac{1}{\left(s-\frac{u_{2}-i+1}{2 \gamma}\right) \left(s-\frac{u_{2}-p+1}{\gamma}\right) }. \end{aligned}} $$
(29)

Similarly as in (20), the third term T3 can be expressed using the MGF as

$$\begin{array}{@{}rcl@{}} && \!\!\!\! T_{3}= \frac{1}{2\pi} \int_{0}^{\pi/2} M_{Q_{3}}\left(\frac{-1}{2 \sin^{2}(\phi)}\right) d\phi. \end{array} $$
(30)

Making use of (29) and (30), T3 in (16) is given by

$$\begin{array}{@{}rcl@{}} && \!\!\!\!\!\!\!\!\!\!\!T_{3}= \frac{u_{2}! (-1)^{u_{2}}}{4 \gamma^{2}} \sum_{i=1}^{{\lfloor R/2\rfloor}} \sum_{p={\lfloor R/2\rfloor}+1}^{u_{2}} \frac{1}{\prod\limits_{\substack{j=1\\j\ne i}}^{{\lfloor R/2\rfloor}} (j-i) \prod\limits_{\substack{r={\lfloor R/2\rfloor}+1 \\r\ne p}}^{u_{2}} (r-p)}\\ &\!\!\times& \frac{1}{\pi}\!\int_{0}^{\pi/2}\!\!\!\!\!\!\!\!\!\!\frac{1}{ \left(\frac{1}{2 \sin^{2}(\phi)} + \frac{u_{2}-i+1}{2 \gamma} \right) \left(\frac{1}{2 \sin^{2}(\phi)} + \frac{u_{2}-p+1}{\gamma} \right)} d\phi. \end{array} $$
(31)

Similarly as in the previous equations, (17)–(21), and considering u1≥⌊(R−1)/2⌋, and making use of the MGF of \(Q_{4}=\gamma _{u_{1}}^{\mathcal {T}_{1}}+\gamma _{{\lfloor (R-1)/2\rfloor }}^{\mathcal {T}_{1}}\), the forth term T4 could also be found as follows

$$ {\begin{aligned} Q_{4}&=\gamma_{u_{1}}^{\mathcal{T}_{1}}+\gamma_{{\lfloor (R-1)/2\rfloor}}^{\mathcal{T}_{1}} = \sum_{i=1}^{u_{1}} w_{i} + \sum_{i=1}^{{\lfloor (R-1)/2\rfloor}}\\&\quad w_{i} = 2 \sum_{i=1}^{{\lfloor (R-1)/2\rfloor}} w_{i} \!\!+ \!\!\!\!\!\sum_{i=u_{2}+1}^{u_{1}} w_{i}. \end{aligned}} $$
(32)

Making use of (32), the MGF of Q4 can be given by

$$ {{}\begin{aligned} M_{Q_{4}}(s)&= \int_{0}^{\infty} \!\!\!\! \cdots \!\!\int_{0}^{\infty} \left(\prod_{i=1}^{R} f_{w_{i}} (w_{i})\right) \exp({sQ}_{2}) {dw}_{1} \cdots {dw}_{R}\\ & = \prod_{i=1}^{{\lfloor (R-1)/2\rfloor}} \! \int_{0}^{\infty} \!\!\!\!\! f_{w_{i}} (w_{i}) \exp(2 s w_{i}) {dw}_{i}\\ &\quad \prod_{i={\lfloor (R-1)/2\rfloor}+1}^{u_{1}} \! \int_{0}^{\infty} \!\!\!\! f_{w_{i}} (w_{i}) \exp(s w_{i}) {dw}_{i}\\ & =\! \frac{u_{1}! (-1)^{u_{1}}}{2^{{\lfloor (R-1)/2\rfloor}} \gamma^{u_{1}}} \prod_{i=1}^{{\lfloor (R-1)/2\rfloor}} \frac{1}{s-\frac{{u_{1}}-i+1}{2 \gamma} }\\&\quad \prod_{i={\lfloor (R-1)/2\rfloor}+1}^{u_{1}} \frac{1}{s-\frac{u_{1}-i+1}{\gamma}}. \end{aligned}} $$
(33)

Similarly as in the previous Eq. 18, (33) is given using partial fraction expansion by

$$ {{}\begin{aligned} M_{Q_{4}}(s)&= \frac{u_{1}! (-1)^{u_{1}}}{2 \gamma^{2}} \sum_{i=1}^{{\lfloor (R-1)/2\rfloor}} \sum_{p={\lfloor (R-1)/2\rfloor}+1}^{u_{1}}\\ &\quad \frac{1}{\prod\limits_{\substack{j=1\\j\ne i}}^{{\lfloor (R-1)/2\rfloor}} (j-i) \prod\limits_{\substack{r={\lfloor (R-1)/2\rfloor}+1 \\r\ne p}}^{u_{1}} (r-p)}\\ &\quad \times \frac{1}{\left(s-\frac{u_{1}-i+1}{2 \gamma}\right) \left(s-\frac{u_{1}-p+1}{\gamma}\right) }. \end{aligned}} $$
(34)

Similarly as in (20), the fourth term T4 can be expressed using the MGF as

$$\begin{array}{@{}rcl@{}} && \!\!\!\! T_{4}= \frac{1}{2\pi} \int_{0}^{\pi/2} M_{Q_{4}}\left(\frac{-1}{2 \sin^{2}(\phi)}\right) d\phi. \end{array} $$
(35)

Making use of (34) and (35), T4 in (16) is given by

$$ {{}\begin{aligned} & T_{4}= \frac{u_{1}! (-1)^{u_{1}}}{4 \gamma^{2}} \sum_{i=1}^{{\lfloor (R-1)/2\rfloor}} \sum_{p={\lfloor (R-1)/2\rfloor}+1}^{u_{1}}\\ &\quad\quad\frac{1}{\prod\limits_{\substack{j=1\\j\ne i}}^{{\lfloor (R-1)/2\rfloor}} (j-i) \prod\limits_{\substack{r={\lfloor (R-1)/2\rfloor}+1 \\r\ne p}}^{u_{1}} (r-p)}\\ &\quad \times \frac{1}{\pi}\!\int_{0}^{\pi/2}\frac{1}{ \left(\frac{1}{2 \sin^{2}(\phi)} + \frac{u_{1}-i+1}{2 \gamma} \right) \left(\frac{1}{2 \sin^{2}(\phi)} + \frac{u_{1}-p+1}{\gamma} \right)} d\phi. \end{aligned}} $$

Making use of the Eqs. 21, (26), (31), (36), and (16), the average BER for the suggested double-relay selection strategy can be expressed as

$$ P(\gamma)= \frac{1}{4}(T_{1} + T_{2} + T_{3} + T_{4}). $$
(36)

6 Methods/experimental

In the simulation results, let us consider a wireless cooperative communication network consisting of (R+2) single-antenna nodes, two of them act as communicating terminals and R of them act as relay nodes. The communicating terminals use the relay nodes to exchange their symbol vectors. In this simulations, we consider the case of R={2,4,6} relay nodes with a power distribution \(P_{\mathcal {T}_{1}}=P_{\mathcal {T}_{2}}=\sum \limits _{r=m,n} P_{\mathcal {R}_{r}}\). To fairly compare the performance in terms of BER of the suggested and current strategies, the same average power, i.e., \(P_{T}= P_{\mathcal {T}_{1}}+P_{\mathcal {T}_{2}}+\sum \limits _{r=m,n} P_{\mathcal {R}_{r}}\) where \(P_{\mathcal {R}_{m}}=P_{\mathcal {R}_{n}}\), and data rate are assumed. The following abbreviations “SRS,” “DRS,” “2-phase,” “3-phase,” and “Proposed” denote the single-relay selection strategy suggested in [10], the double-relay selection strategy suggested in [9], the strategy that performs the two-phase relaying protocol, the strategy that performs the three-phase relaying protocol, and the suggested strategy, respectively.

7 Simulation results and discussion

In Fig. 2, let us consider wireless cooperative networks with R={2,4,6} relay nodes using BPSK constellation and assuming no direct link available between the first terminal \(\mathcal {T}_{1}\) and the second terminal \(\mathcal {T}_{2}\). In this figure, we compare the simulated performance of the suggested strategy in terms of BER with the theoretical BER performance attained from Eq. 36 in Section 5. From Fig. 2, we observe that the simulated performance of the suggested strategy in terms of BER is very close to the theoretical BER performance attained from Eq. 36 in Section 5.

Fig. 2
figure 2

Theoretical and simulated BER performance versus SNR for the suggested strategy with R = 2,R = 4, and R = 6

Full size image

In Figs. 3 and 4, let us consider wireless cooperative networks with R = {2,4} relay nodes using 4-QAM constellation and R = {2,4,6} relay nodes using 8-QAM constellation, respectively, and assuming no direct link available between the first terminal \(\mathcal {T}_{1}\) and the second terminal \(\mathcal {T}_{2}\). In the latter figures, we compare the suggested strategy that performs the three-phase relaying protocol with the double-relay selection strategy that performs the three-phase relaying protocol suggested in [9] and the single-relay selection strategy that performs the three-phase relaying protocol suggested in [10]. In Figs. 3 and 4, it can be observed that the suggested strategy that uses the three-phase relaying protocol outperforms the current state-of-the-art strategies that perform the same relaying protocol.

Fig. 3
figure 3

BER versus SNR for several single and dual relay selection strategies using the three-phase relaying protocol with R = {2,4} and 4-QAM modulation

Full size image
Fig. 4
figure 4

BER versus SNR for several single and dual relay selection strategies using the three-phase relaying protocol with 8-QAM modulation and R = 2,R = 4, and R = 6

Full size image

In Fig. 5, we consider a wireless cooperative communication network with R={2,4} relay nodes and assume that there is no direct link between the first terminal \(\mathcal {T}_{1}\) and the second terminal \(\mathcal {T}_{2}\). In Fig. 5, the performance in terms of BER at the first terminal \(\mathcal {T}_{1}\) is shown with respect to the SNR with a bit rate of 1 bit per channel use (bpcu), respectively, where the suggested strategy that performs the two- and the three-phase relaying protocol using 4-QAM and 8-QAM constellation, respectively, has been compared with the double-relay selection strategy that performs the two- and the three-phase relaying protocol suggested in [9] using 4-QAM and 8-QAM constellation, respectively and the single-relay selection strategy that performs the two- and three-phase relaying protocol suggested in [10] using 4-QAM and 8-QAM constellation, respectively. In Fig. 5, the strategy that performs the two-phase relaying protocol outperforms those which use the three-phase relaying protocol due to the increase of the symbol rate as discussed in Section 3. We also observe that the suggested strategy that performs the two- and the three-phase relaying protocol outperforms the current state-of-the-art strategies that perform the same relaying protocol. From all simulation figures related to theoretical and simulated results, we can also observe that the proposed strategy enjoys full diversity order, especially at high SNR values.

Fig. 5
figure 5

BER versus SNR for several single and dual relay selection strategies using the two and three-phase relaying protocol with a rate of 1 bpcu and R = 4

Full size image

8 Conclusion

In this work, we suggested a new dual-relay selection strategy according to orthogonal space time coding using the two-phase two-way relaying protocol and the three-phase two-way relaying protocol with its performance analysis. In the suggested strategy, two relays have been chosen according to the suggested dual relay selection criterion. The chosen relay nodes perform the concept of digital network coding to further improve the coding gain by combining the information symbol vectors of both terminals in a single vector in order not to send known symbols to the communicating terminals. Since an orthogonal space time coding technique, i.e., Alamouti scheme, is performed on the wireless cooperative network, a symbol-wise decoder, which enjoys a linear decoding complexity, can be used to recover the information vectors.