1 Introduction

With the rapid development of wireless communication technology, the problem of information security transmission in wireless networks is becoming more and more important. In recent years, physical layer security technology has become a research hotspot in the field of information security, because it does not rely on data encryption and encapsulation but has the absolute security of information transmission [1, 2]. For an additive noise-degraded wiretap channel, the security capacity CS is CS = CM − CE; the CM and CE are the main channel and wiretap channel capacity respectively. Wyner [3] has done an earlier research work in this area. His research shows that the source node and destination node can exchange secret information at a non-zero rate without stealing information from an eavesdropper. However, when the channel condition between the source node and its destination node is worse than that between the source node and the eavesdropper, the secrecy capacity of the source node and its destination node can be zero. Early wireless communication is mainly point-to-point communication. The wireless communication nodes are basically single-antenna configurations with a single function. These characteristics make the actual security capacity zero.

The physical layer security technology uses the characteristics of randomness, time variability, and reciprocity of wireless channels. It can make sure that both sides of legitimate communication cannot be wiretapped to any information in the presence of the eavesdropper [3]. Now, the rapid progress of wireless communication physical layer technology has promoted the emergence of a new form of eavesdropping channel. For example, the antenna array eavesdropper channel [4, 5], orthogonal frequency division multiplexing (OFDM) wiretap channel [6,7,8], and relay cooperative eavesdropping channel [9,10,11] can all get effective secrecy capacity. According to reference [4], when the degree of freedom of artificial noise is greater than that of the eavesdropper receiving signal, the eavesdropper cannot separate secret information and artificial noise from the received signal, and the artificial noise method can achieve a certain secrecy speed. Reference [5] has studied how to introduce the idea of frequency diversity array into an OFDM transmitter and to form effective physical layer secure communication capacity in free space. Reference [6] studied the maximum achievable secrecy rate of the OFDM system through reasonable power allocation. Reference [7] took the max-min fairness criterion of confidentiality rate as an optimization objective and studies how to allocate channels and power among multiple users in a cellular network downlink based on OFDM technology in the presence of an eavesdropper node. The literature in [8] studied the power allocation problem for the wireless users in the downlink of the OFDM system to consider the energy collection and the secret information decoding process. In reference [9], the author studied the physical layer security of the relay network model with multiple relay nodes. With the goal of maximizing the security rate, several different cooperative mechanisms were proposed. Reference [10] studied how to use cooperative nodes to send blocking signals to suppress information disclosure of an eavesdropper. Under the scenario of multiple relay nodes and multiple eavesdropping nodes, the relay adopts decode and forward technology; reference [11] first adopts the finite rate feedback scheme to study the resource allocation of the wireless source node.

When the channel quality between the legitimate users is inferior to the eavesdropping channel, the effective safe transmission rate cannot be obtained. Therefore, the cooperative interference mechanism is proposed, which reduces the quality of the eavesdropping channel by means of artificial interference and destroys the listening ability of the eavesdropping node. In reference [9], the cooperative jamming schemes for improving the physical layer security rate of wireless communication through cooperative nodes are studied. In reference [12], it studied how to use cooperative relay nodes to improve the physical layer security rate of wireless communication by combining decode and forward and cooperative jamming. The literature in [13] discussed the main technology and difficulties in the physical layer security of the OFDM communication system. In that paper, the OFDM beamforming was briefly introduced, and the robustness was also reviewed in the presence of noise and multipath fading. Then, the robustness of OFDM beamforming technology under various noise jamming attacks was discussed. Finally, the latest jamming attack techniques were explored and some potential anti-jamming attacks to improve the robustness and reliability were pointed out. On the basis of reference [14], in reference [15], the time domain artificial noise generation technology for the physical layer security in the multiple input and multiple output (MIMO) OFDM system was studied. It extends the limitation that the number of sender antennas must be less than the number of legitimate receiver antennas in application. In an OFDM technology access network where exist a source node, multiple untrusted nodes, and a friendly interference node, reference [16] studied how to interfere with friendly nodes or improve the sum of secrecy rates or improve the fairness of the whole system.

However, the wireless collaboration nodes in the heterogeneous wireless network are selfish and need an incentive mechanism to ensure their participation in collaboration. A game-based cooperative scheme can motivate the selfish relay nodes to participate in the cooperative [17,18,19,20]. Han and Zhang [17, 18] respectively analyze the system game performance of two cooperative interference nodes and the game performance of multi-user shared single cooperative interference node system. In view of the high requirement of communication quality among legitimate communication users and the limited energy of cooperative nodes, multiple collaboration nodes are required to interfere with the service. In order to allocate the compensation and improve the energy efficiency of the cooperative node, a scheme of energy efficiency optimal power allocation based on a Stackelberg game was proposed. The scheme used a two-tier game strategy, the first layer game determines the optimal payment compensation, and the second layer game is used for compensation allocation and power adjustment among the cooperative nodes. Reference [19] proposed a scheme for optimal energy efficiency compensation and power allocation based on a Stackelberg game theory. The two-level game model proved that there exists a global optimal energy efficiency only and gives a closed form solution of the optimal power allocation scheme. Reference [20] studied sub-carrier allocation and cooperative partner selection based on the Nash bargaining game for physical layer security in OFDM wireless networks.

This paper studies the cooperation of multiple cooperative jamming nodes in a heterogeneous wireless network environment, forming virtual beamforming, which helps to secure information transmission between source node and destination nodes, and to prevent an eavesdropper node from eavesdropping on useful information. For example, in the heterogeneous network environment where wireless sensor network and wireless fidelity (WiFi) network coexist, the wireless sensor networks often need to communicate important information through WiFi network. The joint points connecting the wireless sensor network and the WiFi network are crucial. There are many trusted wireless sensor nodes around them, which can be used to collaborate and interfere in the process of important information interaction to prevent malicious nodes from eavesdropping. Similar situations will also occur in other wireless communication networks such as cellular networks.

In addition, in order to encourage potential trusted wireless nodes to participate in collaboration and optimize the allocation of overall energy consumption, on the one hand, the source node needs a paid use of the power consumed by the cooperative jamming node; on the other hand, the jamming nodes involved in cooperation can reasonably price the power cost and adjust the market price dynamically according to the importance of their own energy, which depends on the number of nodes involved in cooperation, the channel state information of the node itself, and the relative relationship between the node and the source node, the destination node, and the eavesdropper node. Therefore, the cooperation relationship between source node and cooperative nodes is modeled as a Stackelberg game, and the competition and cooperation relationship among all cooperative jamming nodes is modeled as a non-cooperative game.

The contents of this paper are organized as follows: the second part is the system model, the third part is the game modeling, the fourth part is the power allocation strategy and the power price dynamic adjustment program, the fifth part is the simulation, and the sixth part is the summary of this paper.

2 System model

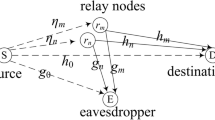
In Fig. 1, there is a source node and destination node pair, which communication is helped by N jamming nodes (J i , i∈N, N = {1,2,…,N}) with the existence of an eavesdropper E. The eavesdropping node is always eavesdropping on the information sent by the source node. When the quality of the eavesdropping channel between the source node and the eavesdropping node is weaker than the quality of the main channel, the two parties of the legitimate communication can realize the physical layer security communication. When the main channel quality is weaker than the eavesdropper channel, in order to ensure the security of transmission information, it is necessary to request some cooperative jamming nodes to assist in sending artificial interference signals to destroy the quality of the eavesdropper channel, so as to create a secure communication environment. Here, N cooperative interference node J1,…,J N are equipped with a omnidirectional single antenna to transmit and receive data and jointly implement beamforming interference eavesdropping node.

Fig. 1
figure 1

The system model for cooperative transmission with terminals S transmitting information to destination D

Full size image

The whole communication process includes two parts for the cooperation scene of jamming nodes. First, the source node sends the signal to the destination node with power Ps. Meanwhile, the information will also be eavesdropped by the eavesdropping node. The channel gain of link S → D and S → E is |h0|2 and |g0|2, respectively. The second is that all jamming nodes are combined to send an artificial interference signal with power PJ. The weight vector of all the cooperative nodes to transmit interference signals is wJ(N × 1), h(N × 1) represents the channel vector between the N jamming nodes and the destination node, and g(N × 1) represents the channel vector between the N jamming nodes and the eavesdropping node, defining R h  = hh† and R g  = gg†. In addition, it is assumed that all communication channels are ergodic, flat fading, and semi-static. It is assumed that the source node can obtain the instantaneous channel information of each communication channel and the noise power at the eavesdropping node and the destination node are σ2. In this paper, the variables are expressed in the following form. The black body capitals represent the matrix, while the black body lowercase letter represents the column vector. The conjugate, transposition, and conjugate transposition of the matrix are expressed by three markers, (·)∗, (·)T, and (·)† respectively.

In the recommended scheme, the N trusted relay nodes transmit the human interference signals completely independent of the source node, and the purpose is to confuse the eavesdropping nodes. This can help the secure communication between the source node and its destination node. The cooperative jamming nodes that participate in the cooperative transmission are transmitting to the human interference signal according to the weight, which are expressed as the vector z. In this way, the signal received at the destination can be expressed as follows

$$ {y}_d=\sqrt{P_s}{h}_0x+{\mathbf{h}}^{\dagger }{\mathbf{w}}_Jz+{n}_d $$
(1)

And the signals received at the eavesdropping node can be

$$ {y}_e=\sqrt{P_s}{g}_0x+{\mathbf{g}}^{\dagger }{\mathbf{w}}_Jz+{n}_e $$
(2)

where n d and n e represent the noise signals received at the destination node and the eavesdropping node, respectively.

Furthermore, the information rates that can be obtained at the destination node and the eavesdropping node are expressed as R d and R e respectively, which are expressed as follows

$$ {R}_d=\frac{1}{2}\log \left(1+\frac{P_s{\left|{h}_0\right|}^2}{\sigma^2+{\mathbf{w}}_J^{\dagger }{\mathbf{R}}_h{\mathbf{w}}_J}\right) $$
(3)
$$ {R}_e=\frac{1}{2}\log \left(1+\frac{P_s{\left|{g}_0\right|}^2}{\sigma^2+{\mathbf{w}}_J^{\dagger }{\mathbf{R}}_g{\mathbf{w}}_J}\right) $$
(4)

As a result, in the presence of an eavesdropping node, the secrecy rate that can be obtained at the destination node is shown as follows

$$ {R}_s=\max \left\{0,{R}_d-{R}_e\right\} $$
(5)

In this paper, discussed only is R d  > R e , so the above formula can be further expressed as

$$ {R}_s=\frac{1}{2}\log \left(\frac{\sigma^2+{P}_s{\left|{h}_0\right|}^2+{\mathbf{w}}_J^{\dagger }{\mathbf{R}}_h{\mathbf{w}}_J}{\sigma^2+{\mathbf{w}}_J^{\dagger }{\mathbf{R}}_h{\mathbf{w}}_J}\right)\left(\frac{\sigma^2+{\mathbf{w}}_J^{\dagger }{\mathbf{R}}_g{\mathbf{w}}_J}{\sigma^2+{P}_s{\left|{g}_0\right|}^2+{\mathbf{w}}_J^{\dagger }{\mathbf{R}}_g{\mathbf{w}}_J}\right) $$
(6)

3 Problem description and game modeling

In practical applications, the demand for the secrecy rate of user link needs to be guaranteed. Assuming that the user’s secrecy rate requirement is \( {R}_s^0 \), the user link secrecy rate demand will be satisfied when \( {R}_s\ge {R}_s^0 \) is satisfied. As a result, the key problem is to be built to minimize the payment of the source node under the constraints of \( {R}_s\ge {R}_s^0 \).

It is obvious that the nodes in the wireless collaboration network belong to different individuals and are selfish. As a result, the source nodes need to take measures to encourage possible collaboration nodes to participate in collaboration and interfere with eavesdropping in eavesdropping nodes. At the same time, the source node needs to select the most beneficial collaboration nodes for themselves. According to the behavior characteristics of the source node and the cooperative node, the distributed resource allocation scheme based on game theory is used to analyze.

For the source node, it can be regarded as a buyer whose purpose is to use as small as possible to achieve link secrecy rate requirements. Suppose that Us represents the payment of the source node and Us is defined as a linear function of the transmission power. It is expressed as follows:

$$ {U}_s={v}_s{P}_s+\sum \limits_{m=1}^M{v}_{J_m}{P}_{J_m} $$
(7)

where vs and \( {v}_{J_m} \) respectively represent the power price of the source node S and the cooperative jamming node J m , and \( {P}_{J_m} \) represents the power purchased by the source node to the cooperative jamming node J m to interfere with the eavesdropping node.

By combining the transmission power of the source node and the transmission power of the cooperative interference node, each source node always minimizes the payment of its own. As a result, the optimization problem for the source node can be expressed as the following formula:

$$ \underset{R_s\ge {R}_s^0}{\min }{U}_s={v}_s{P}_s+\sum \limits_{m=1}^N{v}_{J_m}{P}_{J_m} $$
(8)

where \( \mathbf{P}=\left\{{P}_s,{P}_{J_1},{P}_{J_2},\dots \dots {P}_{J_N}\right\} \) is a power vector, and

$$ {R}_s\left(\mathbf{P}\right)=\frac{1}{2}\log \left(\frac{\sigma^2+{P}_s{\left|{h}_0\right|}^2+{\mathbf{w}}_J^{\dagger }{\mathbf{R}}_h{\mathbf{w}}_J}{\sigma^2+{\mathbf{w}}_J^{\dagger }{\mathbf{R}}_h{\mathbf{w}}_J}\right)\left(\frac{\sigma^2+{\mathbf{w}}_J^{\dagger }{\mathbf{R}}_g{\mathbf{w}}_J}{\sigma^2+{P}_s{\left|{g}_0\right|}^2+{\mathbf{w}}_J^{\dagger }{\mathbf{R}}_g{\mathbf{w}}_J}\right) $$
(9)

For cooperative jamming nodes, they can be considered as sellers. The goal is not only to satisfy the payment that the source nodes give them to participate in collaboration, but also to gain as much extra benefits as possible by competing with each other. Then, the utility function of the cooperative jamming node J m can be defined as

$$ {U}_{J_m}=\left({v}_{J_m}-{c}_{J_m}\right){P}_{J_m} $$
(10)

where \( {c}_{J_m} \) is the power cost of the cooperative jamming node J m . As a result, the optimization problem for the revenue of cooperative jamming nodes can be expressed as

$$ \underset{0<{P}_{J_m}\le {P}_{\mathrm{max}}}{\max }{U}_{J_m},m=1,2,\dots, M $$
(11)

In the above network models, in order to maximize their profits, each cooperative jamming node needs not only to compete with other jamming nodes, but also to compete with the source node. For the source node, it will optimize the power allocation between the source node and the various jamming nodes based on the power price provided by the cooperative jamming node. For each of the jamming nodes, they must provide the optimal power price to maximize the utility. Between all the jamming nodes, they compete with each other by constantly adjusting their power prices. As a result, the source node can be regarded as the main party of the game, and the jamming node is regarded as a slave. Therefore, there is a Stackelberg game between the source node and the jamming nodes, while all the jamming nodes are non-cooperative games [21].

Lemma 1: Order \( {\mathbf{w}}_J^{\dagger}\mathbf{g}=\mu \), and \( {\mathbf{w}}_J^{\dagger}\mathbf{h}=0 \). The solution of the following problem [9]

$$ \min {\mathbf{w}}_J^{\dagger }{\mathbf{w}}_J $$
(12)

can be expressed as

$$ {\mathbf{w}}_J=\mu \left[\mathbf{g}\kern0.5em \mathbf{h}\right]{\left[\begin{array}{cc}{\mathbf{g}}^{\dagger}\mathbf{g}& {\mathbf{g}}^{\dagger}\mathbf{h}\\ {}{\mathbf{h}}^{\dagger}\mathbf{g}& {\mathbf{h}}^{\dagger}\mathbf{h}\end{array}\right]}^{-1}\left[\begin{array}{c}1\\ {}0\end{array}\right] $$
(13)

4 The power and price selection method

4.1 Power allocation method

We first fix P s and find the weights that minimize the payment of the source node to the jamming nodes. Then, we find the value of P s that minimizes the overall payment. In practical applications, it is difficult to obtain the global information of malicious eavesdropping nodes. In addition, it is noted that the problem (8) is the product of two correlated generalized eigenvector problems, which is generally quite difficult. In order to simplify the analysis, we will add a constraint to completely eliminate the interference signals at the destination, i.e.,

$$ {\mathbf{w}}_J^{\dagger}\mathbf{h}=0 $$
(14)

Thus, the optimization problem of Eq. (8) can be expressed as

$$ {\displaystyle \begin{array}{l}\underset{R_s\ge {R}_s^0}{\min }{U}_s={v}_s{P}_s+\sum \limits_{m=1}^M{v}_{J_m}{P}_{J_m}\\ {} st\Big\{\begin{array}{l}{\mathbf{w}}_J^{\dagger}\mathbf{h}=0\\ {}{\mathbf{w}}_J^{\dagger}\mathbf{g}=\mu \end{array}\operatorname{}\end{array}} $$
(15)

where \( \mu =\sqrt{\frac{P_s{\left|{g}_0\right|}^2}{4^{-{R}_s^0}\left(1+{P}_s{\left|{h}_0\right|}^2/{\sigma}^2\right)-1}-{\sigma}^2}. \)

Under the assumption that P s is a constant value, the optimal power allocation of the jamming nodes involved in the cooperation is obtained. In order to solve the optimization problem of Eq. (15), let \( \tilde{\mathbf{h}}=\left\{\frac{h_{J_1}}{\sqrt{v_{J_1}}},\frac{h_{J_2}}{\sqrt{v_{J_2}}},\dots \dots, \frac{h_{J_N}}{\sqrt{v_{J_N}}}\right\} \), \( \tilde{\mathbf{g}}=\left\{\frac{g_{J_1}}{\sqrt{v_{J_1}}},\frac{g_{J_2}}{\sqrt{v_{J_2}}},\dots \dots, \frac{g_{J_N}}{\sqrt{v_{J_N}}}\right\} \) and \( {\tilde{\mathbf{w}}}_J=\left(\sqrt{v_{J_1}}{w}_{J_1},\sqrt{v_{J_2}}{w}_{J_2},\dots \dots, \sqrt{v_{J_N}}{w}_{J_N}\right) \). Then, the optimization problem of Eq. (15) can be further transformed into

$$ {\displaystyle \begin{array}{l}\underset{R_s\ge {R}_s^0}{\min }{U}_s={v}_s{P}_s+{\overset{\sim }{\mathbf{w}}}_J^{\dagger }{\overset{\sim }{\mathbf{w}}}_J\\ {} st\Big\{\begin{array}{l}{\overset{\sim }{\mathbf{w}}}_J^{\dagger}\overset{\sim }{\mathbf{h}}=0\\ {}{\overset{\sim }{\mathbf{w}}}_J^{\dagger}\overset{\sim }{\mathbf{g}}=\mu \end{array}\operatorname{}\end{array}} $$
(16)

From the above formula, it can be seen that \( {\tilde{\mathbf{w}}}_J^{\dagger}\tilde{\mathbf{g}} \) is a positive real number.

According to Lemma 1, \( {\left\Vert {\tilde{\mathbf{w}}}_J\right\Vert}^2 \) can be first expressed as a function of μ2:

$$ {\tilde{\mathbf{w}}}_J=\frac{\mu \left({\tilde{\mathbf{h}}}^{\dagger}\tilde{\mathbf{h}}\tilde{\mathbf{g}}-{\tilde{\mathbf{h}}}^{\dagger}\tilde{\mathbf{g}}\tilde{\mathbf{h}}\right)}{{\mathbf{g}}^{\dagger}\mathbf{g}\left({\mathbf{h}}^{\dagger}\mathbf{h}\right)-{\mathbf{g}}^{\dagger}\mathbf{h}\left({\mathbf{h}}^{\dagger}\mathbf{g}\right)} $$
(17)

Therefore, it can be further obtained

$$ {\left\Vert {\tilde{\mathbf{w}}}_J\right\Vert}^2={k}_0{\mu}^2 $$
(18)
$$ {P}_{J_m}={\left\Vert {w}_{J_m}\right\Vert}^2=\frac{\mu^2{k}_{m1}}{{\left\Vert {k}_{m2}{v}_{J_m}+{k}_{m3}\right\Vert}^2} $$
(19)

where the expressions of k0, km1, km2, and km3 are as follows

$$ {k}_0={\left\Vert \frac{\left({\tilde{\mathbf{h}}}^{\dagger}\tilde{\mathbf{h}}\tilde{\mathbf{g}}-{\tilde{\mathbf{h}}}^{\dagger}\tilde{\mathbf{g}}\tilde{\mathbf{h}}\right)}{{\mathbf{g}}^{\dagger}\mathbf{g}\left({\mathbf{h}}^{\dagger}\mathbf{h}\right)-{\mathbf{g}}^{\dagger}\mathbf{h}\left({\mathbf{h}}^{\dagger}\mathbf{g}\right)}\right\Vert}^2 $$
(20)
$$ \left\{\begin{array}{l}{k}_{m1}={\mu}^2{\left\Vert {g}_{J_m}\sum \limits_{i=1,i\ne m}^N\frac{h_{J_i}^{\dagger }{h}_{J_i}}{v_{J_i}}-{h}_{J_m}\sum \limits_{i=1,i\ne m}^N\frac{h_{J_i}^{\dagger }{g}_{J_i}}{v_{J_i}}\right\Vert}^2\\ {}{k}_{m2}=\sum \limits_{i=1,i\ne m}^N\frac{g_{J_i}^{\dagger }{g}_{J_i}}{v_{J_i}}\sum \limits_{i=1,i\ne m}^N\frac{h_{J_i}^{\dagger }{h}_{J_i}}{v_{J_i}}-{\left(\sum \limits_{i=1,i\ne m}^N\frac{h_{J_i}^{\dagger }{g}_{J_i}}{v_{J_i}}\right)}^2\\ {}{k}_{m3}=\sum \limits_{i=1,i\ne m}^N\left(\frac{h_{J_m}^{\dagger }{h}_{J_m}{g}_{J_i}^{\dagger }{g}_{J_i}}{v_{J_i}}+\frac{g_{J_m}^{\dagger }{g}_{J_m}{h}_{J_i}^{\dagger }{h}_{J_i}}{v_{J_i}}-\frac{2{h}_{J_m}^{\dagger }{g}_{J_m}{h}_{J_i}^{\dagger }{g}_{J_i}}{v_{J_i}}\right)\end{array}\right. $$
(21)

Therefore, Eq. (16) is further expressed as the following form with P s as a variable

$$ \underset{R_s\ge {R}_s^0}{\min }{U}_s={v}_s{P}_s+\frac{k_0{P}_s{\left|{g}_0\right|}^2}{4^{-{R}_s^0}\left(1+{P}_s{\left|{h}_0\right|}^2/{\sigma}^2\right)-1}-{k}_0{\sigma}^2 $$
(22)

Equation (22) is the convex function of P s , and there is a unique optimal solution. To obtain the first derivative of P s and to make it zero, the optimal solution of P s is obtained

$$ {P}_s^{\ast }=\frac{\sqrt{\left(1-{4}^{-{R}_s^0}\right){k}_0{\left|{g}_0\right|}^2}}{4^{-{R}_s^0}{\left|{h}_0\right|}^2/{\sigma}^2}\frac{1}{\sqrt{v_s}}+\frac{1-{4}^{-{R}_s^0}}{4^{-{R}_s^0}{\left|{h}_0\right|}^2/{\sigma}^2} $$
(23)

It can be seen that the power of the source node decreases with the increase of the power cost v s of the source node. However, the source node power value P s will not be lower than the second half \( \frac{1-{4}^{-{R}_s^0}}{4^{-{R}_s^0}{\left|{h}_0\right|}^2/{\sigma}^2} \) of the above formula on the right side. It is equivalent to the minimum power consumption of the source node in order to achieve the secret rate \( {R}_s^0 \) without the presence of the eavesdropping node.

4.2 Power price method for jamming nodes

In this section, we will discuss the power price strategy of the jamming nodes. To replace the \( {P}_{J_m} \) into Eq. (19), it can be obtained

$$ \underset{0<{P}_m\le {P}_{\mathrm{max}}}{\max }{U}_{J_m}=\left({v}_{J_m}-{c}_{J_m}\right){P}_{J_m}^{\ast },m=1,2,\dots, M $$
(24)

It is noted that Eq. (24) is a non-cooperative game between the cooperative jamming nodes, and there is a tradeoff between the utility \( {U}_{J_m} \) and the energy price \( {v}_{J_m} \) of the interference nodes. If the jamming node J m has good channel conditions and its energy price is relatively low, the source node will ask for more cooperative power from the jamming node J m , so that \( {U}_{J_m} \) will increase with \( {v}_{J_m} \) growth. When \( {v}_{J_m} \) grows to more than one value, it is no longer useful for the source node to select it to participate, even if the channel of J m is dominant. In this way, J m will reduce \( {v}_{J_m} \), and \( {U}_{J_m} \) also decreases. Therefore, every jamming node J m is required to dynamically give the optimal power price which changes with the channel condition. Because the source node will only choose the most favorable jamming nodes, the optimal price will also be influenced by other jamming nodes. In addition, when the power cost of cooperative jamming node is increased (for example, the energy of the node itself is reduced, the request of cooperation is increased, the maximum power limit value, and so on), the starting point of cooperative node’s cooperation and power price will rise.

Property 1: When the power price of the source node and other cooperative jamming nodes are fixed, the equilibrium point of utility function \( {U}_{J_m} \) of every cooperative jamming node exists and unique.

Proof: from the above formula, Eq. (19) shows that

$$ {P}_{J_m}=\frac{\mu^2{k}_{m1}}{{\left({k}_{m2}{v}_{J_m}+{k}_{m3}\right)}^2} $$
(25)

Then, substituting the above equation into the utility function of the interference node, it can be obtained.

$$ \underset{0<{P}_m\le {P}_{\mathrm{max}}}{\max }{U}_{J_m}=\frac{\left({v}_{J_m}-{c}_{J_m}\right){k}_{m1}{\mu}^2}{{\left({k}_{m2}{v}_{J_m}+{k}_{m3}\right)}^2},m=1,2,\dots, M $$
(26)

Taking the first order derivative of \( {U}_{J_m} \) to \( {v}_{J_m} \), it can be obtained.

$$ \frac{\partial {U}_{J_m}}{\partial {v}_{J_m}}=\frac{\mu^2{k}_{m1}\left({k}_{m3}+2{k}_{m2}{c}_{J_m}-{k}_{m2}{v}_{J_m}\right)}{{\left({k}_{m2}{v}_{J_m}+{k}_{m3}\right)}^3} $$
(27)

Then, taking the two order derivation of the objective function \( {U}_{J_m} \) to \( {v}_{J_m} \), it can be further obtained.

$$ \frac{\partial^2{U}_{J_m}}{\partial {v}_{J_m}^2}=\frac{2{k}_{m2}{k}_{m1}{\mu}^2\left({k}_{m2}{v}_{J_m}-2{k}_{m3}-3{k}_{m2}{c}_{J_m}\right)}{{\left({k}_{m2}{v}_{J_m}+{k}_{m3}\right)}^4} $$
(28)

Through the first derivative \( \partial {U}_{J_m}/\partial {v}_{J_m} \) and the two order derivations \( {\partial}^2{U}_{J_m}/\partial {v}_{J_m}^2 \) of the above, we can analyze it piecewise.

(1) When \( 0<{v}_{J_m}<3{c}_{J_m}+2{k}_{m3}/{k}_{m2} \), \( {\partial}^2{U}_{J_m}/\partial {v}_{J_m}^2 \) is always less than zero. This shows that \( {U}_{J_m}\left(0<{v}_{J_m}<3{c}_{J_m}+2{k}_{m3}/{k}_{m2}\right) \) is a concave function, and there is a unique maximum value.

(2)When \( {v}_{J_m}\ge 3{c}_{J_m}+2{k}_{m3}/{k}_{m2} \), \( \partial {U}_{J_m}/\partial {v}_{J_m} \) is always less than zero. This explanation decreases with the increase of \( {U}_{J_m}\left({v}_{J_m}\ge 3{c}_{J_m}+\frac{2{k}_{m3}}{k_{m2}}\right) \).

Therefore, the maximum value of \( {U}_{J_m}\left({v}_{J_m}>{c}_{J_m}\right) \) exists and is unique, and the Property 1 is proved.

According to the above analysis, we need to take the derivative of \( {U}_{J_m} \) to \( {v}_{J_m} \) and make it equal to zero, and it can be obtained.

$$ \frac{\partial {U}_{J_m}}{\partial {v}_{J_m}}={P}_{J_m}^{\ast }+\left({v}_{J_m}-{c}_{J_m}\right)\frac{\partial {P}_{J_m}^{\ast }}{\partial {v}_{J_m}}=0 $$
(29)

After solving all these equations about \( {v}_{J_m} \), the optimal price of all the jamming nodes can be obtained in theory, which can be expressed as

$$ {v}_{J_m}^{\ast }={v}_{J_m}^{\ast}\left({\sigma}^2,{G}_{sd},{G}_{sJ_m},{G}_{J_md},\left\{{G}_{sJ_n}\right\},\left\{{G}_{J_nd}\right\},\left\{{v}_{J_n}\right\}\right),n\ne m $$
(30)

Solving Eq. (29), it can be obtained

$$ {v}_{J_m}=2{c}_{J_m}+\frac{k_{m3}}{k_{m2}} $$
(31)

It is important to note that the value of \( {v}_{J_m} \) calculated by the upper type is obtained when the power of the source node and the power price of other relay nodes are given. So, the result of the upper calculation is not optimal. The value of the optimal \( {v}_{J_m} \) to meet the requirements of a certain precision can be recursively obtained by the gradient method. The steps are as follows: (1) The calculation of the initial price \( {v}_{J_m}(0)=2{c}_{J_m}+\frac{k_{m3}}{k_{m2}} \) by (31); (2) with Eq. (24) to calculate \( {U}_{J_m}\left({v}_{J_m}(n)\right) \) and \( {U}_{J_m}\left({v}_{J_m}(n)+\Delta \right) \) (when the cost is \( {c}_{J_m}=1 \), the step size Δ is generally 0.01); (3) the price update formula is\( {v}_{J_m}\left(n+1\right)={v}_{J_m}(n)+\lambda \left[{U}_{J_m}\left({v}_{J_m}(n)+\Delta \right)-{U}_{J_m}\left({v}_{J_m}(n)\right)\right] \); (4) repeat (2) and (3) until \( \left|{v}_{J_m}\left(n+1\right)-{v}_{J_m}(n)\right| \) is less than the stop value.

In heterogeneous wireless networks, each node is often able to obtain only local channel state information. Therefore, it is difficult to provide the optimal value directly, whether it is the power allocation by the source nodes or the pricing of the power price of the cooperative jamming nodes. In this case, it is necessary for the source node to cooperate with all the cooperative jamming nodes through “the power pricing of each jamming node → the power allocation → the power pricing of each jamming node → the power allocation of source node.” After several rounds, it converges to the optimal value while meeting the error requirement.

5 Simulation and result

In this part, the dynamic power allocation, price dynamic pricing, cost price change, and convergence are simulated. The same system setting as reference [9] is used in this paper, where the source node, the destination node, and the eavesdropping node are placed in a straight line. In order to illustrate the effect of distance (the effect of distance is used to represent the change of wireless channel environment), the channel model between any two nodes is set as a line-of-sight transmission channel model. The path gain is expressed as d−c/2eiθ, where d represents the distance between any two nodes (unit: meter), c = 3.5 represents the exponential factor of the path loss, and θ is a random phase that is evenly distributed between [0, 2π].

In the following simulation, it is assumed that the distance between the cooperative jamming nodes is negligible relative to the distance from source node, destination node, and eavesdropping node. The distance between the cooperative jamming nodes and the source node, the destination node, and the eavesdropping node can be approximately regarded as the same. The source node and the destination node are fixed in the two-dimensional coordinate system at the point S (0, 0) and point D (100, 0),respectively(unit: meter). The noise in the channel is additive Gauss white noise, and the noise power is 10−9 W. The next simulation in this paper has carried out 1000 Monte Carlo independent experiments and then averages to get the average results.

Figure 2 describes that the benefit \( {U}_{J_1} \) of the cooperative jamming node J1 is a curve with the change of its power price \( {v}_{J_1} \). It can be seen from the diagram that the maximum value of the revenue \( {U}_{J_1} \) exists only.

Fig. 2
figure 2

The revenue \( {U}_{J_1} \) of J1 varies with its power price \( {v}_{J_1} \) (There are 5 cooperative jamming nodes)

Full size image

In Figs. 3 and 4, the cooperative jamming node power price and utility function with recursion times and the convergence of the situation are described (The cooperative interference is at coordinate (30, 5), and the eavesdropping node is at coordinate (50, 0)). As it can be seen from the chart after five rounds of the dynamic adjustment of pricing power and power allocation, the power price and the utility function of each node can quickly converge.

Fig. 3
figure 3

The power price of the cooperative jamming nodes vs the recursion times

Full size image
Fig. 4
figure 4

The utility function vs the recursion times

Full size image

Figure 5 describes a curve that the power price \( {v}_{J_1} \) of a cooperative jamming node J1 changes dynamically as its position changes, and Fig. 6 describes a curve of dynamic changes in the revenue \( {U}_{J_1} \) of a cooperative jamming node J1 with its location (The location of the cooperative jamming node moves along the straight line from the coordinate point (10, 5) to the coordinate point (90, 5), and the eavesdropping node is fixed at the coordinate point (50, 0)). When the jamming nodes are in different positions and their channel conditions are different, the optimal power price will be adjusted dynamically. As it can be seen from the above two figures, the highest power price does not deserve the highest income. The income of the jamming node is determined by its power price and the power consumed by it. Only the power price of the jamming node is appropriate, and the source node is willing to assign it more power to participate in the collaboration. The jamming nodes also gain the most benefit because of their reasonable choice.

Fig. 5
figure 5

The power price \( {v}_{J_1} \) of cooperative jamming node vs its position change

Full size image
Fig. 6
figure 6

The revenue \( {U}_{J_1} \) of cooperative jamming node vs its position change

Full size image

Figure 7 describes the total payment US of the source node changing along with the location of the cooperative jamming node (the cooperative jamming node moves along the straight line from the coordinate point (10, 5) to the coordinate point (90, 5), and the eavesdropping node is fixed at the coordinate point (50, 0)). As you can see from Fig. 7, the total payment of the source node is the lowest when the cooperative jamming node is nearest to the eavesdropper node. This is because the cooperative jamming node has the best effect on the eavesdropping node when the distance from the eavesdropping node is nearest and the power consumption is the lowest.

Fig. 7
figure 7

The source node total payment US vs the location change of cooperative jamming nodes

Full size image

Figure 8 describes the total payment US of the source node changing along with the location of the eavesdropping node (the eavesdropping node moves along the straight line from the coordinate point (20, 0) to the coordinate point (90, 0)). The five simulation curves above correspond to the situation where the cooperative jamming nodes are located at the coordinate points (30, 5), (40, 5), (50, 5), (60, 5), and (70, 5), respectively. It can be seen from the figure that the total payment of the source node is the lowest when the eavesdropping node is nearest to the cooperative jamming node. And the closer the distance from the source node to the cooperative jamming node, the lower the maximum value of each curve (the source node total payment US).

Fig. 8
figure 8

The source node total payment US vs the location change of the eavesdropping node

Full size image

Combining with the previous analysis, when the information of the channel state of the eavesdropping node is known, it is most favorable to select the cooperative jamming node closest to the eavesdropping node; when the channel state information of the eavesdropping node is unknown, it is necessary to consider the worst case, that is, the best choice is to choose the cooperative jamming node closest to the source node.

Figure 9 is a curve that increases the power price V1 of a cooperative jamming node J1 as its cost price c1 increases. This is due to the higher cost price of the cooperative jamming node, and it is bound to increase the power price in order to obtain the same income. From the simulation results, the curve approximated linearly.

Fig. 9
figure 9

The curve of the change in the price of power with the cost price

Full size image

Figure 10 describes the curve that the total payment US of the source node varies with the number of cooperative jamming nodes. The eavesdropping node is fixed at the coordinate point (50, 0), and the three simulation curves above correspond to the situation where the jamming nodes are located at the coordinate points (30, 5), (50, 5), and (70, 5) respectively. It can be seen that the total payment US of the source node decreases with the increase of the number of the cooperative jamming nodes. This is due to the increase of the number of cooperation nodes, which will lead to more intense competition among the cooperative nodes, resulting in lower power price of the cooperative jamming node. This inevitably reduces the cost that the source node seeks for collaboration. Therefore, the source nodes always want more cooperative jamming nodes to participate in cooperative jamming in order to reduce the total cost of payment. However, from Fig. 9, it can be seen that when the number of jamming nodes involved in cooperative jamming transmission reaches five, the total payment US of the source node will decrease slowly with the increase of the number of nodes involved in cooperative jamming. In practice, the participation of more nodes in collaboration will bring more complex communication overhead of channel state information. Therefore, it is not necessary for source nodes to seek more than six interference nodes to participate in the cooperative jamming transmission.

Fig. 10
figure 10

The total payment US of the source node vs the number of cooperative jamming nodes

Full size image

In a word, the following conclusions can be obtained from the above simulations. The cooperative jamming nodes are competitive and cooperative. They dynamically optimize their own power price independently according to the network environment change (including channel characteristics, competition intensity, and energy status). Correspondingly, the source node can also optimize the power allocation according to the power pricing of the cooperative node, channel characteristics and its energy status, so as to improve the dynamic adaptability of the physical layer security rate.

6 Conclusions

In a heterogeneous wireless network environment, this paper studied, in the presence of an eavesdropping node, the source node and destination node cooperating to intercept the eavesdropping nodes through trusted jamming nodes, so as to achieve the physical layer secure communication. In order to encourage the potential nodes to participate in cooperation and interfere with the eavesdropping of malicious nodes, the relationship between the source node and the cooperative interference node was modeled as a Stackelberg game in this paper. The jamming power consumed by the cooperative jamming nodes was paid according to the market price, and the power allocation solution under the market price was given. At the same time, the competition relationship among the jamming nodes involved in cooperative jamming was modeled as a non-cooperative game. Each jamming node dynamically adjusts the power cost price and market price independently based on its own channel characteristics, surplus energy, and consumed power. In a word, through the joint optimization of these two games, the power pricing and power allocation can be dynamically optimized according to the change of channel characteristics and competition intensity.

In this paper, the following several cases were simulated. First, the simulation of the dynamic power allocation and the dynamic power pricing of each cooperative jamming node shows that the power allocation and the market price would soon reach the optimum value after more than five rounds of dynamic adjustment. And it had good convergence. Secondly, the dynamic changes of the location of the cooperative jamming node and the eavesdropping node were simulated respectively, and the results illustrated the cooperative node selection idea under different circumstances. Finally, it could be seen that the total payment US of the source node decreases with the increase in the number of participating cooperative jamming nodes. However, when the number of nodes involved in cooperative jamming transmission reaches five, the total payment US of the source node will decrease slowly as the number of cooperative jamming nodes increases, which is of guiding significance for the selection of the number of cooperative jamming nodes.