Abstract
Intra-vehicular wireless sensor network (IVWSN) enables the integration of the wireless sensor network technology into the vehicle architecture through either eliminating the wires between the existing sensors and the corresponding electronic controller units (ECUs) or empowering new sensor technologies that are not currently implemented due to technical limitations. Ultra-wideband (UWB) has been determined to be the most appropriate technology for IVWSNs since it provides energy efficiency through the low duty-cycle operation and high reliability by exploiting the large bandwidth. In this paper, we propose a time variation model for UWB-based IVWSN-based on the extensive amount of data collected from the transmitter and receiver antennas at various locations and separation distances beneath the chassis of a vehicle moving at different speeds on different types of roads. We adopt the commonly used Saleh-Valenzuela (SV) model to represent the clustering phenomenon in the received power delay profiles (PDPs). The proposed novel time variation model then determines the time evolution of the PDPs by representing the changes in their cluster breakpoints, slopes, and break point amplitudes with the auto-regressive integrated moving average (ARIMA) model. ARIMA(5,1,0) has been demonstrated to fit the breakpoint, cluster slope, and breakpoint amplitude sequences collected at different vehicle speeds with different transmitter and receiver locations on asphalt and stone roads by using Box-Jenkins procedure. This model is validated with diagnostic checking. The absolute values of the model coefficients are observed to be mostly larger on asphalt road than their counterparts on the stone road while exhibiting no dependence on the vehicle speed nor the location of transmitter and receiver antennas.
Similar content being viewed by others
1 Introduction
Intra-vehicular wireless sensor network (IVWSN) is a specific type of wireless sensor network between the vehicle sensors and their corresponding ECUs deployed with the purpose of either eliminating the currently existing wires or enabling new sensor technologies that cannot be integrated into the vehicle using wired means. The elimination of the wires provides savings in part, assembly and maintenance cost together with fuel efficiency whereas new sensor technologies enable new vehicle applications. The full adoption of a IVWSN requires providing the same performance and reliability as the wired equivalent that has been tested for a long time with vehicles on the road. The first IVWSN examples are therefore expected to be in the integration of either new sensor technologies such as intelligent tire [1] or some sensor technologies for non-critical vehicle applications such as park sensors and steering-wheel angle sensors. Proving the robustness of these applications on the vehicle will then pave the way for the usage of IVWSN in more critical vehicle applications such as the transmission of automotive speed data from the wheel speed sensors to the ECU in an antilock braking system [2].
Among various modulation techniques investigated for IVWSN, ultra-wideband (UWB) has been demonstrated to be the most suitable satisfying the high-reliability requirement of vehicle control systems and the strict energy-efficiency requirement of the sensor nodes at short distance and low cost [3–5]. The vast literature on UWB channel measurement campaigns performed in such locations as indoor [6–8], outdoor [9, 10], around the human body [11, 12], industrial environments [13], vehicle-to-vehicle, and vehicle-to-roadside [14–17] cannot be applied to the IVWSNs since the intra-vehicular environment is very different containing a large number of metal reflectors and operating at extreme temperatures.
Although the locations of the transmitter and receiver within the vehicle do not change over a short time scale in IVWSN, the movement of the vehicle generates small variations in the sensor locations due to vibrations and considerable changes in the environment such as road conditions and nearby vehicles. The development of an efficient UWB communication system for IVWSNs therefore requires introducing these time variations into the channel model. A time-varying channel model allows optimizing system performance and robustness under realistic radio propagation conditions. The time variations of the wireless channel can also be used in the design of channel estimation algorithms and rake receivers. The UWB channel models developed for different parts of the vehicle, including engine compartment [3, 4, 18], beneath the chassis [3, 4, 19, 20], passenger compartment [21–26], and trunk [27], all aim to represent the average behavior and the variations around the average behavior of the UWB channel without adopting time-series analysis. Even when these works collect data on the vehicle moving on the road, they still consider the distribution of the power delay profiles (PDPs) around their average value without considering the ordering of the data in time. Such modeling therefore does not allow the regeneration of the successive PDPs. Time-series analysis on the other hand models the data as an ordered sequence of values. Embedding this ordering into the model allows the representation of the temporal variations in the channel.
The goal of this paper is to provide the time-variation model for the UWB channel beneath the chassis of a vehicle by employing time-series analysis on the data collected from the vehicle moving at different speeds on different types of roads with transmitter and receiver antennas at different locations and separation distances. Previous work on the modeling of the temporal variations in the UWB channel mostly focus on the representation of the non-stationary attenuation due to obstructing people [28–31] and movement of a receiver along a linear trajectory at a constant velocity [32] in indoor environment. The models describing non-stationary attenuation due to obstructing people however cannot be applied to the beneath the chassis channel. Only [29, 33] additionally model small-scale signal variations due to scattered propagation paths in indoor environment but again by focusing on the distribution of the variations around the average PDP without considering their ordering in time. The original contributions of the paper are as follows:
-
We employ auto-regressive integrated moving average (ARIMA) model to determine the time evolution of the parameters of the modified Saleh-Valenzuela (SV) model derived for the beneath the chassis UWB channel [20]. ARIMA model is a flexible tool that provides a good understanding of trends, correlation, and forecasting in time series. The modified SV model aims to generate the clustering phenomenon in the PDP by statistically determining its parameters including cluster arrival times, cluster amplitude, and ray amplitude decay rate. The ARIMA model is then used to determine the time evolution of the PDPs by representing the changes in the time series of these parameters. This is the first work to propose a time-varying UWB channel model based on the time series analysis employing ARIMA model on the SV model parameters, allowing the regeneration of successive PDPs.
-
We validate the proposed ARIMA model on the SV model parameters as a time-varying UWB channel model beneath the chassis of the vehicle based on the analysis of the residuals between generated and observed values and the sensitivity of the model parameters to different vehicle speeds, road types, and distances and locations of transmitter and receiver antennas. This is the first work to analyze the validity of a time variation model across a wide range of scenarios.
The rest of the paper is organized as follows: Section 2 provides the experimental setup. Section 3 presents the data processing required to derive the coefficients of the ARIMA model. This includes deriving the PDP corresponding to each received pulse, determining the parameters of the modified SV model based on the separation of the PDP into clusters, and generating the ARIMA model corresponding to the time series of the parameters of the SV model. Section 4 provides and analyzes the coefficients of the ARIMA model at different vehicle speeds, road types, locations, and separation distances of transmitter and receiver antennas. Finally, Section 5 concludes the paper and gives the future work.
2 Experiment setup
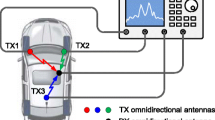
The data measurements are conducted in the time domain by using Picosecond Pulse Labs 3500D impulse generator and Agilent DSO91304 Infiniium high performance oscilloscope, as shown in Fig. 1. The impulse generator is used to periodically generate an ultra short pulse of 75 ps width and peak amplitude of 8 V corresponding to a bandwidth of 13.3 GHz. The repetition rate is set to 1 kHz. The generated pulse is sent to the transmitter antenna via low-loss coaxial cables. The UWB antennas used are roughly the size of a playing card and display an omnidirectional pattern having a near perfect circular polar antenna pattern in azimuth plane and vertical-slice-of-a-bagel shape in elevation plane with the beamwidth of 36.37°. The transmitter and receiver antennas are placed beneath the chassis of a commercial vehicle Fiat Linea, as seen in Fig. 2. These antennas provide good impedance matching with return loss less than −10 dB for the frequency range 3.1–10.6 GHz. Since the antennas act as filters and limit the signal bandwidth in their application range, the frequency range of our model is 3.1–10.6 GHz. The propagation medium of transmitted signals consists of air, asphalt surface, and chassis, which is a metal surface. Dielectric properties of air, asphalt, and metals exhibit a steady behavior over the frequency of interest, as demonstrated in [34], [35], and [36], respectively.
The receive antenna is connected to the oscilloscope via low-loss coaxial cables. The oscilloscope is used to record the received signal. The segmented memory feature of the digital oscilloscope is used to increase the number of pulses that can be captured with the limited memory: The oscilloscope stores information only during the active periods so that the memory is not used during the inactive periods. We capture 1024 successive pulses by sampling 200 ns long signal at 40 G samples/s for each pulse. The output of the impulse generator is also connected to the trigger input of the oscilloscope via another low-loss cable for synchronization. The distance between the antennas and the road is around 20 cm. The data was collected at low vehicular traffic on asphalt and stone roads within the Koc University campus on mostly sunny or cloudy days. We have chosen Koc University campus to have full control on the speed of the vehicle and road conditions. On the other hand, we have chosen sunny or cloudy days to avoid the damage of the antennas on the wet roads. Moreover, we have collected the data over roads without any impulsive interference, which is ensured as a result of measuring the signals in the data collection environment without any pulses transmitted. We have also checked the collected data to guarantee that there is no impulsive interfering noise other than white noise. The collected data are provided in [37].
3 ARIMA-based time variation model
ARIMA model is used to represent the variation of the subsequent received pulses over time in relation to each other. Since each received pulse is a noisy time domain signal itself, first, the PDP associated with the received pulse is separated into clusters to determine the parameters of the modified SV model. The time evolution of the PDPs are then represented by the time evolution of each parameter of the SV model separately by using ARIMA model. The outline of the algorithm is given in Fig. 3. Next, we provide the procedures followed for the derivation of the PDP associated with the received signal, estimation of the SV model parameters corresponding to the PDP, and estimation of the ARIMA model coefficients corresponding to each parameter of the SV model in Sections 3.1, 3.2, and 3.3, respectively.
3.1 Derivation of PDP
The received signal at the oscilloscope corresponding to each transmitted pulse is first clipped from the beginning and end to extract the signal part with significant energy. As an example, Fig. 4 shows the received signal corresponding to the pulse transmission from 25-cm distance beneath the chassis of the vehicle moving on the stone road at 20 km/h. The signal part with significant energy is determined by identifying the time interval with starting point as the first zero crossing prior to the peak, around 35 ns and end point as 60 ns after which the received energy is at the noise floor. Following the clipping, the signal is passed through the low pass filter to smooth out the noise. The resulting signal, denoted by y(t), is then processed to eliminate the effect of the cables and antennas. The signal representing the response of the cables and antennas is collected by locating the antennas at 2-cm separation distance in an open area to prevent the effect of reflections on the channel impulse response and denoted by x(t) (we have also located the antennas at 1-m separation distance for the representation of the response of the cables and antennas to verify the effects of mutual coupling and near-field antenna are negligible on the final derived parameters). Assuming that y(t) is the sum of attenuated and delayed copies of x(t), CLEAN algorithm is used to derive the channel impulse response through deconvolution [38].
The CLEAN algorithm is a serial interference cancellation algorithm. The algorithm first finds the largest attenuated and delayed copy of x(t) contributing to y(t) by determining the correlation of the received signal y(t) with x(t) and identifying the highest peak in that correlation. The contribution of the identified contribution is then subtracted from the total signal. The process continues with the resulting cleaned up signal. At the ith iteration, the correlation of the cleaned up signal y(t) and x(t) is calculated. The value and delay index of the peak correlation are then recorded as K i and τ i , respectively. y(t) is then updated by subtracting the effect of the ith path signal, i.e., K i x(t−τ i ), from y(t). This process continues until the energy of the updated y(t) drops under a certain threshold. The value of the threshold is found to be 0.001 by trial and error so that we can obtain a nice PDP. Figure 5 shows the deconvolution output of the received signal in Fig. 4.
PDP corresponding to the pulse transmission from 25-cm distance beneath the chassis of the vehicle moving on the stone road at 20 km/h (Fig. 4)
3.2 Estimation of SV model parameters
In the PDPs recorded beneath the chassis, the multipath signals arrive in the form of clusters. The arrival time of the PDP clusters is determined by using the automatic clustering algorithm [39] and validated by visual inspection. Based on the assumption that the slope changes at the beginning of each cluster, automatic clustering algorithm identifies the change points of the partial slopes of the PDP. The clustering is exemplified for the PDP corresponding to the pulse transmission from 25-cm distance beneath the chassis of the vehicle moving on the stone road at 20 km/h in Fig. 5.
The clustering behavior in the PDPs has been modeled by using the modified SV model in [20]. SV model describes the impulse response as
where a l,k and θ l,k are the gain and phase of the kth component in the lth cluster, respectively; T l is the delay of the lth cluster; τ l,k is the delay of the kth multipath component in the lth cluster relative to the l-th cluster arrival time T l ; K is the number of the multipath components within a cluster; and L is the number of clusters. The phases θ l,k are uniformly distributed in the range [ 0,2π].
Similar to the PDP in Fig. 5, we observed that 99 % of the PDPs beneath the chassis fit three cluster SV models with root-mean-square error (rmse) below 4.51 dB. The histogram of rmse is shown in Fig. 6. Therefore, the list of the parameters of the SV model that will be used in the time series analysis include the cluster breakpoints, slopes, and breakpoint amplitudes representing these three clusters as given in Table 1.
3.3 Estimation of ARIMA model coefficients for SV parameter sequences
3.3.1 Description of ARIMA model
ARIMA models are the most general class of models for understanding and forecasting a possibly non-stationary time series.
ARIMA (p,d,q) is mathematically described as
where d is the degree of differencing; θ 0 is the deterministic trend term; B and its superscript represent shift operator and the amount of shift to be applied, respectively, as
Φ p (B) and Θ q (B) are AR and MA operators with degrees of p and q, respectively, and given as
and
where ϕ i and θ i represent the ith AR and MA coefficients, respectively; and a t is zero mean white Gaussian error term with standard deviation σ a .
3.3.2 Determination of ARIMA model coefficients
Box-Jenkins procedure is widely used to determine the coefficients of the ARIMA model corresponding to time series data [40, 41]. The summary of the procedure is given as a flowchart in Fig. 7. The description of each step of the procedure is given next.
3.3.3 Convert time series data to a stationary process
The stationarity of the process is determined by using Dickey-Fuller test. In this test, the existence of a unit root in the AR model corresponds to the non-stationarity of the model. The test provides a p value, which is used whether to reject or accept the null hypothesis of the existence of the unit root (the p value is the probability of obtaining a test statistic result at least as extreme or as close to the one that was actually observed, assuming that the null hypothesis is true. A researcher will often reject the null hypothesis when the p value turns out to be less than a predetermined significance level, often 0.05 or 0.01).
If the time-series data is stationary, we can skip this step. Otherwise, it must be reduced to a stationary process. Generally, there are two types of reasons for the non-stationarity of time series: non-constant mean and variance. If the mean is not constant, the time series can be reduced to stationary process by applying differencing. The number of differencing operations is denoted by d in the ARIMA model given in Eq. (2). Although theoretically there is no limit on the number of differencing operations, applying it more than twice is not recommended. On the other hand, if the variance is not constant, then power transformation should be applied to the original data to make the time series stationary. If the power transformation is needed, it should be performed before differencing.
3.3.4 Examine the ACF and PACF
Autocorrelation function (ACF) measures the similarity between the observations as a function of the time lag whereas partial autocorrelation function (PACF) is defined as the correlation between Z t and Z t+k after the linear dependence of the lags [ t+1,t+k−1] is removed.
ACF and PACF are used in predicting the orders of the ARIMA model. The AR order p and MA order q are predicted by the visual inspection of PACF and ACF, respectively. If PACF or ACF exhibits either exponential or damped sinusoidal behavior, then no order is assigned to p or q, respectively. On the other hand, if either PACF or ACF cuts off at a certain lag, then the cutting lag is assigned as the value of p or q, respectively.
3.3.5 Estimate the coefficients of the ARIMA model
The coefficients of the ARIMA model are determined by using maximum likelihood estimation.
The maximization of the exact likelihood function should be determined numerically. Here, we use Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm to iteratively solve the resulting unconstrained nonlinear optimization problem [18, 42]. The accuracy of the calculated coefficients is checked by using their p values. If a p value is larger than the significance level of 0.05, then this coefficient is omitted.
3.3.6 Diagnostic check
Diagnostic check aims to determine the suitability of the selected ARIMA model by checking whether the distribution of the residuals between the generated and observed data is white Gaussian. Whiteness of the residuals is measured by using Ljung-Box test on the ACF whereas their normality is tested by using chi-square test. The Ljung-Box test is a type of statistical test of whether the ACF of a time series except the zero lag is different from zero. Instead of testing randomness at each distinct lag, it tests the overall randomness based on a number of lags. The null hypothesis in this test is the whiteness of the residuals. Chi-square test is a statistical hypothesis test used to determine whether there is a significant difference between two distributions. The null hypothesis used in this test is the normality of the residuals. A researcher will often accept the null hypothesis when the p value turns out to be greater than a predetermined significance level, often 0.05 or 0.01.
4 ARIMA model analysis results
The ARIMA model is determined for the time series data of B 1, B 2, S 1, S 2, S 3, X1, X 2 at vehicle speeds of 20, 40, and 60 km/h on asphalt and stone roads for the transmit and receive antennas at 25, 50, and 100 cm distance in different locations beneath the chassis by following the procedure given in Section 3. The main results are summarized as follows:
-
ARIMA(5,1,0) consistently fits the data collected over different types of roads, speeds, antenna locations, and antenna separation distances. The suitability of the selected ARIMA model is tested by checking whether the distribution of the residuals between the generated and observed data is white and Gaussian based on Ljung-Box and chi-square tests, respectively, as explained in detail in Section 3.3. Since all the p values of Ljung-Box and chi-square tests are greater than 0.1, the residuals are white Gaussian with 90 % confidence. This confirms ARIMA(5,1,0) model. Table 2 shows the ARIMA model coefficients for the parameters of the PDPs collected on asphalt road for the transmit and receive antennas at 25-cm distance as an example.
Table 2 ARIMA model coefficients for the parameters of the PDPs collected on asphalt road for the transmit and receive antennas at 25 cm distance -
The absolute values of the ARIMA coefficients are mostly larger on asphalt road than their counterparts on the stone road whereas the standard deviation of the innovation is larger on stone road than the asphalt road. Although this trend is not seen very clearly on all of the results, considering that this holds for the majority of the data, we conclude that the absolute value of the ARIMA coefficients decreases as the roughness of the road increases. Smaller absolute value of the coefficients means lower partial correlation between delayed elements of the time series. If the experiment was conducted on a perfectly smooth road, the consecutive PDPs would be very similar to each other resulting in the highest correlation between the delayed elements of the time series. As the roughness of the road increases, the shape of the PDPs are distorted in a random manner, decreasing their correlation to the previously received PDPs with increasing power of the innovation component. The general trend of the model coefficients as a function of the road roughness is exemplified for the ARIMA model coefficient ϕ 1 on different types of roads under various scenarios in Fig. 8.
-
There is no trend in the variation of the absolute values of the ARIMA model coefficients with vehicle speed, antenna locations, and antenna separation distances, as exemplified for the ARIMA model coefficient ϕ 1 under various scenarios in Figs. 9, 10, 11 and 12. The main reason for this behavior is the independence of the ARIMA model coefficients from the values of the SV model parameters. As the distance between the transmitter and receiver antennas and the location of these antennas vary, the shape of the PDP hence the corresponding SV model parameters change. However, the time variation of these parameters only depends on the variation of the environment around the transmitter and receiver therefore exhibits similar behavior independent of the distance and location. Likewise, as the vehicle speed increases, the distance the vehicle travels between the PDPs increases. Unless the vehicle stays at the same location, the variation in the environment depends on the random changes in the road, independent of the speed.
Fig. 10 Fig. 11
5 Conclusions
We build a time variation model for the beneath the chassis UWB channel. The clustering phenomenon in the PDPs collected beneath the chassis of the vehicle has been previously represented by using modified SV model. We propose a novel ARIMA-based time variation model for the time series data corresponding to the parameters of the SV model including cluster arrival times, cluster amplitudes, and ray amplitude decay rates. ARIMA(5,1,0) has been demonstrated to fit the time series of all the SV parameters corresponding to the data collected at different vehicle speeds and locations of transmitter and receiver antennas at different separation distances on asphalt and stone roads. The absolute values of the ARIMA model coefficients are demonstrated to be mostly larger on asphalt road than their counterparts on the stone road. On the other hand, these coefficients do not exhibit any dependency on vehicle speed, antenna locations and antenna separation distances. We are planning to investigate the usage of smaller channel bandwidth on the time variation of the channel as future work.
References
SC Ergen, A Sangiovanni-Vincentelli, X Sun, R Tebano, S Alalusi, G Audisio, M Sabatini, The tire as an intelligent sensor. IEEE Trans. Computer-Aided Design Integr. Circuits Syst.28(7), 941–955 (2009).
W Niu, J Li, S Liu, T Talty, in IEEE Milcom. Intra-vehicle ultra-wideband communication testbed (IEEE, 2007), pp. 1–6.
W Niu, J Li, T Talty, in IEEE Globecom. Intra-vehicle UWB channel measurements and statistical analysis (IEEE, 2008), pp. 1–5.
W Niu, J Li, T Talty, Ultra-wideband channel modeling for intravehicle environment. EURASIP J. Wirel. Commun. Netw. - Special issue on wireless access in vehicular environments, 1–12 (2009). http://jwcn.eurasipjournals.springeropen.com/articles/10.1155/2009/806209.
W Niu, J Li, T Talty, in IEEE Milcom. Intra-vehicle UWB channels in moving and stationary scenarios (IEEE, 2009), pp. 1–6.
A Saleh, RA Valenzuela, A statistical model for indoor multipath propagation. IEEE J. Selected Areas Commun.5(2), 128–137 (1987).
D Cassioli, MZ Win, AF Molisch, The ultra-wide bandwidth indoor channel: from statistical model to simulations. IEEE J. Selected Areas Commun.20(6), 1247–1257 (2002).
SS Ghassemzadeh, LJ Greenstein, T Sveinsson, A Kavcic, V Tarokh, UWB delay profile models for residential and commercial indoor environments. IEEE Trans. Vehic. Technol.54(4), 1235–1244 (2005).
JY Lee, UWB channel modeling in roadway and indoor parking environments. IEEE Trans. Vehic. Technol.59(7), 3171–3180 (2010).
AF Molisch, D Cassioli, C-C Chong, S Emami, A Fort, B Kannan, J Karedal, J Kunisch, K Siwiak, M Z.Win, A comprehensive standardized model for ultrawideband propagation channels. IEEE Trans. Antennas Propag.54(11), 3151–3166 (2006).
Y Chen, J Teo, JY Lai, E Gunawan, KS Low, CB Soh, PB Rapajic, Cooperative communications in ultra-wideband wireless body area networks: channel modeling and system diversity analysis. IEEE J. Selected Areas Commun.27(1), 5–16 (2009).
A Fort, J Ryckaert, C Desset, P Doncker, P Wambacq, L Biesen, Ultra-wideband channel model for communication around the human body. IEEE J. Selected Areas Commun.24(4), 927–933 (2006).
J Karedal, S Wyne, P Almers, F Tufvesson, AF Molisch, A measurement-based statistical model for industrial ultra-wideband channels. IEEE Trans. Wireless Commun.6(8), 3028–3037 (2007).
J Karedal, N Czink, A Paier, F Tufvesson, AF Molisch, Path loss modeling for vehicle-to-vehicle communications. IEEE Trans. Vehic. Technol.60(1), 323–328 (2011).
L Cheng, BE Henty, DD Stancil, F Bai, P Mudalige, Mobile vehicle-to-vehicle narrow-band channel measurement and characterization of the 5.9 GHz dedicated short range communication (DSRC) frequency band. IEEE J. Selected Areas Commun.25(8), 1501–1516 (2007).
O Renaudin, V-M Kolmonen, P Vainikainen, C Oestges, Non-stationary narrowband MIMO inter-vehicle channel characterization in the 5-GHz band. IEEE Trans. Vehic. Technol.59(4), 2007–2015 (2010).
I Sen, DW Matolak, Vehicle-to-vehicle channel models for the 5-GHz band. IEEE Trans. Intell. Transportation Syst.9(2), 235–245 (2008).
U Demir, CU Bas, SC Ergen, Engine compartment UWB channel model for intra-vehicular wireless sensor networks. IEEE Trans. Vehic. Technol.63(6), 2497–2505 (2015).
CU Bas, SC Ergen, in IEEE Wireless Communications and Networking Conference (WCNC). Ultra-wideband channel model for intra-vehicular wireless sensor networks (IEEE, 2012), pp. 42–47.
CU Bas, SC Ergen, Ultra-wideband channel model for intra-vehicular wireless sensor networks beneath the chassis: from statistical model to simulations. IEEE Trans. Vehic. Technol.62(1), 14–25 (2013).
PC Richardson, W Xiang, W Stark, Modeling of ultra-wideband channels within vehicles. IEEE J. Selected Areas Commun.24(4), 906–912 (2006).
T Tsuboil, J Yamada, N Yamauchi, M Nakagawa, T Maruyama, in International Conference on Intelligent Transportation Systems. UWB radio propagation inside vehicle environments (IEEE, 2007), pp. 1–5.
IJG Zuazola, JMH Elmirghani, JC Batchelor, High-speed ultra-wide band in-car wireless channel measurements. IET Commun.3(7), 1115–1123 (2009).
J Blumenstein, A Prokes, T Mikulasek, R Marsalek, T Zemen, C Mecklenbrauker, Measurements of ultra wide band in-vehicle channel - statistical description and TOA positioning feasibility study. EURASIP J. Wireless Commun. Netw.104:, 1–10 (2015). December 2015.
J Blumenstein, T Mikulasek, R Marsalek, A Chandra, A Prokes, T Zemen, C Mecklenbrauker, in IEEE Vehicular Networking Conference (VNC). In-vehicle UWB channel measurement, model and spatial stationarity (IEEE, 2014), pp. 77–80.
M Schack, J Jemai, R Piesiewicz, R Geise, I Schmidt, T Kurner, in IEEE Vehicular Technology Conference (VTC). Measurements and analysis of an in-car UWB channel (IEEE, 2008), pp. 459–463.
W Xiang, in IEEE Vehicular Technology Conference (VTC). A vehicular ultra-wideband channel model for future wireless intra-vehicle communications (IVC) systems (IEEE, 2007), pp. 2159–2163.
S He, X Dong, in IEEE Vehicular Technology Conference Fall. The temporal variation of indoor ultra-wideband channel (IEEE, 2009), pp. 1–5.
P Pagani, P Pajusco, Characterization and modeling of temporal variations on an ultrawideband radio link. IEEE Trans. Antennas Propagation. 54(11), 3198–3206 (2006).
UG Schuster, H Bolcskei, Ultrawideband channel modeling on the basis of information-theoretic criteria. IEEE Trans. Wireless Commun.6(7), 2464–2475 (2007).
R Zhang, L Cai, A packet-level model for UWB channel with people shadowing process based on angular spectrum analysis. IEEE Trans. Wireless Commun.8(8), 4048–4055 (2009).
J Tsao, D Porrat, D Tse, Prediction and modeling for the time-evolving ultra-wideband channel. IEEE J. Selected Topics Signal Process.1(3), 340–356 (2007).
J Kunisch, J Pamp, in IEEE Conference on Ultra Wideband Systems and Technologies. An ultra-wideband space-variant multipath indoor radio channel model (IEEE, 2003), pp. 290–294.
Dielectric Properties. http://www.itis.ethz.ch/virtual-population/tissue-properties/database/dielectric-properties/. Accessed 11 June 2016.
EJ Jaselskis, J Grigas, A Brilingas, Dielectric properties of asphalt pavement. J. Mater. Civil Eng.15(5), 427–434 (2003).
DB Tanner, Optical effects in solids. Department of Physics, University of Florida (2013).
ARIMA Based Time Variation Model for Beneath the Chassis UWB Channel. https://bitbucket.org/utkuDe/arima_data/wiki/Home. Accessed 17 July 2016.
Y Chen, et al., Cooperative communications in ultra-wideband wireless body area networks: Channel modeling and system diversity analysis. IEEE J. Selected Areas Commun.27(1), 5–16 (2009).
M Corrigan, A Walton, W Niu, J Li, T Talty, in IEEE Radio and Wireless Symposium (RWS). Automatic UWB Clusters Identification (IEEE, 2009), pp. 376–379.
WWS Wei, Time Series Analysis: Univariate and Multivariate Methods (2nd Edition) (Pearson, USA, 2006).
GEP Box, G Jenkins, Time Series Analysis: Forecasting and Control (Holden-Day, San Francisco, 1970).
Gretl User’s Guide. http://gretl.sourceforge.net/gretl-help/gretl-guide.pdf. Accessed 17 July 2016.
Acknowledgements
We would like to thank Prof. Ibrahim Akduman and his group for providing the UWB antennas, and Seyhan Ucar for collecting the experimental data used to derive the antenna patterns.
This work is supported by Marie Curie Reintegration Grant on Intra Vehicular Wireless Sensor Networks, PIRG06-GA-2009-256441. Sinem Coleri Ergen also acknowledges support from Bilim Akademisi - The Science Academy, Turkey under the BAGEP program, and the financial support by the Turkish Academy of Sciences (TUBA) within the Young Scientist Award Program (GEBIP).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Demir, U., Ergen, S.C. ARIMA-based time variation model for beneath the chassis UWB channel. J Wireless Com Network 2016, 178 (2016). https://doi.org/10.1186/s13638-016-0676-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-016-0676-3