Abstract
This paper considers spectrum utilization, the probability of detection in cognitive radio (CR) model based on cooperative spectrum sensing with both simultaneous adaptive sensing and transmission at a transmitting secondary user (TSU), and the bit error rate (BER) detection with variation checking at a receiving user (RSU). In this paper, a novel detecting model is proposed in the being considered scenario for the full-duplex TSU’s simultaneous sensing and transmitting. A spectrum sensing scheme with an adaptive sensing window is designed to improve the spectrum utilization with a high SNR. At RSU, the BER variation is used further to detect whether a PU is active or not. Data fusion based on the proposed adaptive sensing scheme and the BER detection is processed for better decison on the spectrum holes. Simulation results show that (1) simultaneous spectrum sensing with an adaptive window improves the spectrum utilization compared with a periodical sensing and (2) cooperative spectrum sensing with the BER-assisted detection improves the probability of detection and spectrum utilization compared with the single simultaneous sensing at TSU.
Similar content being viewed by others
1 Introduction
Cognitive radio (CR) is an important strategy to enhance spectrum efficiency, allowing the secondary user (SU) to utilize the licensed spectrum of the primary user (PU) when PU is inactive. This kind of time slot is called as a spectrum hole [1, 2]. CR has two important functionalities: spectrum sensing and adaption [1]. Energy detection is conventionally used for spectrum sensing [3]. Traditionally, SU firstly detects the spectrum band using energy collection periodically. If a spectrum hole is found, SU will immediately utilize this time interval to transmit data by upconverting to the PU’s frequency band. Once SU senses the activity of PU, it will immediately stop transmitting and give the spectrum back to PU. Then SU keeps detecting the spectrum in its own period till the coming of next spectrum hole.
Different from the model described above where SU executes sensing only when it does not transmit data [4, 5], a couple of full-duplex spectrum sensing schemes have been proposed in which the SU can simultaneously implement transmitting and sensing whether PU is active or not. Researchers present a new design paradigm for future CR by exploring the full-duplex techniques to achieve the simultaneous spectrum sensing and data transmission in [6], published in a magazine to explore key research directions, and proposed an adaptive scheme to improve SUs’ throughput by switching between the “Listen-and-Talk” and “Listen-before-Talk” protocols in [7]. Non-time-slotted CR has been investigated in [8] and [9] and the full duplex spectrum sensing scheme is presented for non-time-slotted cognitive radio networks in [8]. Afifi and Krunz [10] exploits self-interference suppression for improved spectrum awareness/efficiency in simultaneous transmit-and-receive mode. Results in [11] show the performance of antenna for the full-duplex transmission in CR. The possibility of extending full-duplex designs to support multiple input, multiple output (MIMO) systems using commodity hardware has been discussed in [12]. Tsakalaki et al. [13] describes the basic design challenges and hardware requirements that restrain CRs from simultaneously and continuously sensing the spectrum while transmitting in the same frequency band.
This paper also considers the full-duplex spectrum sensing and utilization in CR. The being considered CR in this paper consists of two SUs. One SU transmits data and another SU receives the data. The SU which is used to transmit the data is called TSU while the one receiving the data is called RSU. Both TSU and RSU are radio transceivers. In this paper, a novel detecting algorithm is proposed by combining an adaptive sensing in TSU and the BER detection in RSU, where a dedicated line is required for the transmission of the result of BER detection to the TSU and data fusion is processed in the TSU. The difference of our algorithm from the existing full-duplex cognitive radio lies in the adaptiveness of the sensing window, the feedback of BER detection and the data fusion of the sensing in TSU and the BER detection in RSU. One point to be noted is that we ignore the overhead effect in this paper because the data is less and negligible. The corresponding probability of detection as well as the false alarm are provided, on the basis of which the utilization of spectrum holes is mathematically derived. With the proposed spectrum detecting algorithm, a spectrum sensing scheme with an adaptive sensing window is designed to improve the spectrum utilization. Several schemes based on the adaptive sensing window have been proposed in literature [14, 15]. In this paper, the novel detection algorithm is followed by an adaptive spectrum sensing algorithm to provide an improved CR. Furthermore, in order to enhance the overall detection accuracy, this paper feeds back the detection results based on the estimated bit error rate (BER) by RSU to TSU. By data fusion, this information is combined with the detection algorithm using an adaptive sensing window at TSU. The combined detection algorithm provides a better probability of detection and consequently a higher spectrum hole utilization. Although there is a trade-off between spectrum sensing and data transmission, it is also important to improve its spectrum utilization [16].
The rest of this chapter is organized as follows. Section 1 mentions the problems associated with recent developments in spectrum sensing. Section 2 describes the system model and the spectrum sensing procedure that is proposed in our novel P2P cognitive radio. Section 3 shows the energy detection algorithm at TSU and derives its corresponding probability of detection as well as false alarm, spectrum utilization and our proposed adaptive sensing algorithm. Section 4 describes the detection algorithm that is based on estimating the BER at RSU. Section 5 gives the derivations of spectrum utilization under periodical sensing, simultaneously sensing with fixed window and adaptive window, as well as cooperative sensing with simultaneous sensing and BER detection. Simulation results are reported in Section 6 followed by a conclusion in Section 7.
2 Problem statement
Most existing spectrum-sensing technologies have two main problems. First, at TSU, periodical spectrum sensing cannot determine the periodical duration of spectrum sensing. Here, we consider simultaneous spectrum sensing and transmitting. Secondly, spectrum sensing at TSU often brings miss-detection of PU signals when PU becomes a hidden node compared to TSU. Thus, we propose a novel BER-assisted detection to improve the spectrum sensing.
2.1 Simultaneous sensing/transmitting at full-duplex TSU
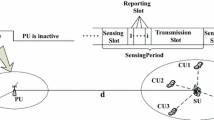
In the majority of existing spectrum-sensing technologies, spectrum sensing at TSU is executed periodically without the transmission of SU signals. However, this periodical sensing exists a problem when selecting its periodical duration. As shown in Fig. 1, if the duration is too long, the SU signal can represent interference to the PU signal. It is obvious that this interference will decrease when the periodical duration decreases. However, if the periodical duration is too short, it will cost more time to execute spectrum sensing instead of transmitting SU signals which will decrease the utilization of spectrum holes. In order to overcome this problem, we propose a solution to execute spectrum sensing while transmitting SU signals. When SU detects the existence of a spectrum hole, it transmits its signal over the licensed channel. Meanwhile, it will start to detect whether PU is active or not in order to minimize interfering with the SU signal. TSU in cognitive radio is a full-duplex system which can transmit data while simultaneously perform spectrum sensing.
2.2 Assisting detection based on BER At SU receiver
We have proposed the concept of cooperative spectrum sensing between TSU and RSU based on estimating the BER at RSU. This is useful because a PU transmitter sometimes becomes a hidden node compared to TSU which means that TSU cannot detect the existence of PU. There are two kinds of hidden nodes. The two cases are shown below.
2.2.1 Case I: TSU is out of the transmitting range of a PU transmitter
In Fig. 2, when TSU is out of the transmitting range of a PU transmitter, the TSU cannot detect the presence of PU no matter whether PU is active or not. TSU will continue to transmit data to its receiver. However, if RSU is in the transmitting range of a PU transmitter while hidden from it, the transmission between TSU and RSU can bring serious interference to PU.
2.2.2 Case II: PU signal is hidden from TSU
As shown in Fig. 3, the energy of the PU signal at TSU is lower than the minimum detection threshold possibly due to the existence of obstructions between TSU and PU. Thus, it is difficult to detect the existence of PU if the spectrum sensing only happens at TSU. In this case, there will still exist serious interference between RSU and PU when RSU is close to PU and there is no obstruction between them.
From the two cases above, one can notice that it is necessary to assist spectrum sensing at TSU with additional spectrum sensing at RSU based on BER measurement. If the BER at RSU is large enough, the presence of PU is detected even if the received energy of PU at TSU is below the detection threshold.
3 System model
Spectrum sensing and transmitting at TSU in cognitive radio could be represented as shown in Fig. 4. Denote h 0, h 1, h 2, ⋯, h m−1 as spectrum holes, i.e., PU is inactive and the spectrum is idle during these time slots. The time duration of spectrum hole h i is represented by D i , 0≤i≤m−1, which is also the time interval between two adjacent transmissions by PU. In each spectrum hole, the TSU first senses whether the spectrum is being used or not. If the spectrum is unoccupied, the TSU borrows it to transmit data while simultaneously sense the start of a PU transmission. Therefore, the process consists of two stages: “sensing” only, followed by “transmitting and sensing”, as shown in Fig. 4. S i denotes the duration that TSU takes to sense the spectrum before it can find a spectrum hole, and T i represents the duration that TSU executes simultaneously sensing and transmitting. Spectrum sensing includes both spectrum sensing at TSU by energy detection and spectrum sensing at RSU by BER estimation. The whole procedure of SU spectrum sensing and signal transmission can be summarized as follows:
-
Step I: TSU senses the PU spectrum by energy detection.
-
Step II: If TSU finds a spectrum hole, it awaits sensing of a spectrum hole at RSU by BER estimation. If not, it continues spectrum sensing by energy detection alone at TSU.
-
Step III: If RSU also detects the existence of a spectrum hole, TSU starts to transmit data. At the same time, it continues to sense the spectrum band to detect when PU becomes active.
-
Step IV: If TSU finds out that PU is active either by itself or with the help of RSU, it stops transmitting at once and goes back to Step I.
In the following section, we discuss spectrum sensing at TSU based on energy detection and at RSU based on BER estimation.
4 Energy detection at TSU
The block diagram corresponding to spectrum sensing using energy detection at TSU is shown in Fig. 5. The received signal is sampled to obtain a discrete time signal as shown in Fig. 6. Then, the system estimates the energy of the sampled signal during a sensing window. The length of the sensing window W can be a fixed value or a variable value. By comparing the threshold with the estimated energy, the system can conclude whether PU is active or not.
4.1 The energy detection algorithm and corresponding probability of detection at TSU
At the ith “sensing” stage, S i in Fig. 4, the sensing signal at TSU can be expressed as:
where y(n), 0≤n≤N−1, denotes the received signal at TSU, N is the number of samples, α p(n) denotes the PU signal at TSU, v(n) denotes the AWGN with zero mean and variance σ 2, α represents the channel gain between PU transmitter and TSU which depends on their relative positions and surrounding environment. Hypothesis H 0 indicates that PU is inactive while hypothesis H 1 indicates that PU is active.
At the ith “transmitting and sensing” stage, T i in Fig. 4, the sensing signal at TSU can be expressed as:
where y(n), p(n) and s(n), 0≤n≤N−1, have the same definition as the ones corresponding to the sensing stage, and s(n) denotes the received SU signal after going through the interference cancellation module in Fig. 7. Hypothesis H 2 indicates that PU is inactive while hypothesis H 3 indicates that PU is active. Without loss of generality, it is assumed that p(n), s(n) and v(n) are all independent from each other.
The test statistic for energy detection under the four hypotheses, H 0 though H 3, can be expressed as
where y(n) is the TSU’s sensing signal as given in Eqs. (1) and (2), and W is the length of the sensing window, i.e., the number of baseband samples used for each detection decision. It can be described as:
where f s is the sampling frequency at TSU and τ is the duration of W. In order to estimate the energy, TSU estimates the energy for a time duration τ, which corresponds to f s τ baseband samples.
Based on the theory described in [16], it is easily shown that the test statistic follows a normal distribution:
where \(\gamma _{1} = \frac {\alpha ^{2}{\sigma _{p}^{2}}}{\sigma ^{2}}\) is the SNR under hypothesis H 1, \(\alpha ^{2}{\sigma _{p}^{2}}\) denotes the power of the received PU’s signal, \(\gamma _{2} = \frac {{\sigma _{s}^{2}}}{\sigma ^{2}}\) is the SNR under H 2, \({\sigma _{s}^{2}}\) denotes the power of the received SU’s signal, and γ 3 is the SNR under H 3, which can be obtained as \(\gamma _{3} = \frac {{\sigma _{s}^{2}}+\alpha ^{2}{\sigma _{p}^{2}}}{\sigma ^{2}}=\gamma _{1}+\gamma _{2}\).
Based on Eqs. (5) and (6), at the “sensing” stage, the probability of detection \(P_{d_{1}}\) and of false alarm \(P_{f_{1}}\) can be obtained as
where λ 1 is the assumed threshold value which needs to be selected appropriately and Q(·) represents the Q-Function.
Similarly, at the “sensing and transmitting” stage, the probability of detection \(P_{d_{2}}\) and of false alarm \(P_{f_{2}}\) can be obtained as
where λ 2 is the assumed threshold value to be selected appropriately. In the selection of thresholds, we hope to strike a balance between decreasing the probability of false-alarm and increasing the probability of detection. The threshold values λ 1 and λ 2 are constrained by the equations below:
where \(P_{m_{1}}\) is the probability of miss-detection in hypothesis H 1 while \(P_{m_{2}}\) is the probability of miss-detection in hypothesis H 3. θ is a factor which is used to describe the relationship between the miss-detection and the false alarm. It is called control factor. If θ is greater than 1, it means the probability of miss-detection is selected to be lower than the probability of false alarm. If θ is less than 1, it means the probability of miss-detection is selected to be greater than the probability of false alarm. If θ=1, it means the probability of false alarm and the probability of miss-detection are selected to be the same. According to [14] and [17], we assume θ=1 and substitute Eqs. (7)–(10) into (11). Then, we have
From Eq. (12), it is concluded that the threshold values λ 1 and λ 2 depend on σ 2 and on the SNRs: γ 1, γ 2 and γ 3, but not on the length of the sensing window W.
4.2 Discussion of power attenuation between PU and TSU
In this section, we discuss the power attenuation between PU and TSU according to the channel gain α between them. As previously discussed, we have known that p(n) denotes the amplitude of the PU signal at PU while α p(n) represents the amplitude of the PU signal at the detection end (TSU). Thus, we can derive the transmitting power at the PU transmitter and its received power at TSU, i.e.,
where ρ pu represents the transmitting power at PU while ρ su represents the received power at TSU. The relationship between ρ pu and ρ su is as follows:
where α depends on the transmission channel which can include path-loss and shadow fading. According to a traditional radio channel model, the equation to describe the fading of a radio signal can be expressed in a log scale (dB) as:
where z pu and z su represents the position of PU and TSU, respectively; ∥z pu−z su∥ is the Euclidean distance which represents the relative distance, d,between PU and TSU while ρ su (d B) and ρ pu (d B) represents ρ su and ρ pu in dB g 1/10 is called the fading constant, which is related to shadow fading such as the position of obstructions in the transmission while g 2/10 is a factor which depends on the transmission environment and is referred to as path loss exponent. From Eq. (16), the channel gain α can be expressed as:
From Eqs. (15) and (17), one can express α 2 as:
where \(PL\left (d \right)=d^{{g_{2}}/{10}} \) and \(\varphi =10^{-{g_{1}}/{10}}\phantom {\dot {i}\!}\). When the distance d becomes large, the value of α 2decreases. For Case I in Fig. 2, the path loss P L(d) is large when TSU is out of the transmission range of PU transmitter. Thus, the power gain α 2 decreases to the point that TSU cannot detect the presence of PU. In Fig. 3, the value of φ is small because of obstructions between PU and TSU. Thus, the power gain α 2 is too small for PU signal to be detected.
4.3 Antenna cancellation technique in duplex TSU at P2P cognitive radio
In the P2P cognitive radio, because of the power attenuation over the radio channel between PU and TSU, the power of the transmitted signal s(n) at TSU, i.e., from its own transmit antenna, is much larger than the received signal at TSU from PU α p(n). This makes it difficult to realize a full duplex operation at TSU because of this large power difference. It is highly possible that TSU cannot detect the energy of the weak received PU signal unless special care is undertaken. One way is to decrease such a power difference by making α p(n) and s(n) of the same order of magnitude.
According to [18], a technique called antenna cancellation can be used for full-duplex operation. It combines the existing RF interference cancellation with digital baseband cancellation to reduce self-interference. Self-interference cancellation aims at decreasing the power difference between α p(n) and s(n). In Fig. 7, the value of s(n) is decreased to the same energy level as α p(n) using antenna cancellation technique. Thus, a full-duplex operation is enabled and TSU is able to detect the presence of PU while it is transmitting signals. In other words, once the energy α p(n) is close to that of s(n), transmitting will not affect the detection of PU.
4.4 Spectrum sensing with adaptive window
In this section, we introduce the concept of an adaptive sensing window as applied to spectrum sensing based on energy detection, where the length of the sensing window, W, varies from W max to W min . Denote as W max the maximum allowed length of the sensing window. If W>W max , there is no performance improvement. Denote as W min the minimum allowed length of the sensing window. If W<W min , TSU cannot detect the PU signal due to an insufficient energy collection. In order to obtain a better sensing performance, the adaptive sensing algorithm is designed as follows:
-
Step I: initialization - Let W=W max so that TSU can detect a real spectrum hole with high probability.
-
Step II: active PU - If W>W min , assign W=W−W min to reduce the possibility of missing spectrum holes with a small duration; if W≤W min , assign W=W min .
-
Step III: inactive PU - Assign W=W max to enhance the probability of detecting the coming PU.
The state transition diagram in Fig. 8 can be used to represent the change in the value of W with the state transition as a function of hypothesis H 0 to H 3. The flowchart of the adaptive sensing algorithm is shown in Algorithm 1. In this algorithm, we denote wcounter as a counter to keep track of the number of consecutive windows with an active PU and denote C as the number of consecutive windows after which the length of the sensing window is decreased by W min .

5 BER assisting detection at RSU
5.1 Novel TSU and RSU modules
In order to accomplish the proposed BER-assisted spectrum detection scheme, a new TSU architecture as well as a new receiver architecture is proposed based on using a dedicated control channel.
5.1.1 Proposed architecture for TSU
The proposed TSU architecture consists of three components as shown in Fig. 9. As previously discussed, one component is used to sense PU’s activities, the second is used to transmit data by using the idle PU channel while the last is used to exchange control information via a dedicated channel. The first component is used to estimate the energy of the received signal and to decide whether the PU channel is occupied or idle. This decision, as indicated by the dotted line in Fig. 9 controls a key “K1”; if the PU channel is idle, TSU starts to transmit data using the PU channel; otherwise, TSU does not transmit. The dedicated control channel is used for transmitting the training sequence and for receiving the probability of detection based on BER estimation.
5.1.2 Proposed architecture for RSU
The corresponding RSU architecture consists of two components as shown in Fig. 10. The first component is used to receive the signal transmitted from TSU via the PU channel. The second component is the dedicated control channel which is used for receiving the training sequence and for transmitting the estimated BER via a dedicated control channel. The BER is estimated using data sequences transmitted over the PU channel. These data sequences consist of useful information.
5.2 Modulation assumption
Without loss of generality, BPSK is assumed to be the modulation scheme for both TSU and PU. For analysis simplification, a perfect receiving process is considered and thus the continuous-time RF-received signal can be expressed as
where \(AP_{1}(t) = \left \{\begin {array}{lcr} -A && \text {Sending a bit ``0''} \\ A && \text {Sending a bit ``1''} \end {array} \right.\) for TSU signal,
while \(AP_{1}(t) = \left \{\begin {array}{lcr} -B && \text {Sending a bit ``0''} \\ B && \text {Sending a bit ``1''} \end {array} \right.\) for PU signal, where A and B are determined by their own transmit power and their propagation attenuation, f c is the carrier frequency and v(t) is the continuous-time white Gaussian noise with its discrete form v(n) in Eq. (1), with a zero mean and a variance σ 2. It is also assumed that the probability of transmitting a bit “0” or “1” is equal for both TSU and PU, and that coherent detection is used at RSU.
5.3 BER with/without a PU signal
Without a PU signal, the BER is the well known BPSK expression given in [19], which is re-written here for convenience
where the optimal decision threshold T=0 is used.
On the other hand, when PU is active, the received signal at RSU can be expressed as
where \(AP_{2}(t) = \left \{\begin {array}{lcr} -A \pm B && \text {when TSU sends a} ``0'' \\ A \pm B && \text {when TSU sends a} ``1'' \end {array} \right.\).
The received signal after coherent detection is
where v c (t) and v s (t) are, respectively, the in-phase component and quadrature component of v(t), a random process with a variance of σ 2. After the low-pass filter, the received signal can be obtained as
The probability of error is derived below based on the probabilities in Eqs. (24) and (25). By choosing the decision threshold value as T=0, the probability of error decision when transmitting a bit “0”, \(\hat {P}_{e0}\), is given by
and the probability of error decision when transmitting a bit ‘1’, \(\hat {P}_{e1}\), is given by
Therefore, the overall BER can be obtained as
5.4 Detection algorithm and probability of detection at RSU
Usually, a reliable communication system has a relatively low BER, e.g., lower than 10−3 level, [19], so \(Q\left (\frac {A}{\sigma }\right)\) in Eq. (20) must be small. By looking at the Q-function table, \(\frac {1}{2} \left [Q\left (\frac {A+B}{\sigma }\right) + Q\left (\frac {A-B}{\sigma }\right) \right ]\) in Eq. (26) is much higher than \(Q\left (\frac {A}{\sigma }\right)\) in Eq. (20). So, intuitively, the change of BER could be used for detecting the spectrum hole.
5.4.1 Method I
From Eqs. (20) and (26), one can conclude that BER estimation follows a nonnegative distribution with mean of \(Q\left (\frac {A}{\sigma }\right)\) for the case when PU is inactive and \(\frac {1}{2} \left [Q\left (\frac {A+B}{\sigma }\right) + Q\left (\frac {A-B}{\sigma }\right) \right ]\) for the case when PU is active. However, the variance is unknown and is represented by \({\sigma ^{2}_{b}} \) for both cases. Denote T as the threshold: if the BER measurement is greater than T, it says that PU is active; otherwise, it says that PU is inactive. The optimal threshold, T, must be selected in such a way that the minimum probability of decision error is reached. The probability of decision error P fT can be represented by
By calculating \(\frac {dP_{fT}}{dT}=0\), one can solve for the optimal threshold value T op , which corresponds to the minimum probability of decision error. A good approximation of the optimal threshold value is \(T_{op}=\frac {P_{e}+\hat {P}_{e}}{2}\), due to the low variance for this kind of measurements. As such, the probability of detection and the probability of false alarm as defined in Section II can be represented by
One must note that a higher \(\hat {P}_{e}\) leads to a larger probability of detection \(P_{d_{3}}\) and a smaller probability of false alarm \(P_{f_{3}}\).This makes sense because a higher \(\hat {P}_{e}\) results in a bigger difference with P e . It should be noted that when \(\hat {P}_{e} >> P_{e}\), the optimal threshold value \(T\approx \frac {\hat {P}_{e}}{2}\).
5.4.2 Method II
This algorithm is proposed by considering the ratio between the BER in Eq. (20) and the BER in Eq. (26), as a way to provide an obvious distinction between the two cases: inactive PU and active PU. The ratio of the real measurements of BER on P e also follows a nonnegative distribution. The mean is obviously 1 for the case when PU is inactive and \(\frac {Q\left (\frac {A+B}{\sigma }\right) + Q\left (\frac {A-B}{\sigma }\right)}{2Q\left (\frac {A}{\sigma }\right)}\) for the case when PU is active. The variance can be represented by \(\hat {\sigma }^{2}_{b} =\frac {{\sigma ^{2}_{b}}}{{P^{2}_{e}}} \) for both cases. The optimal threshold corresponding to the minimum probability of decision error, which can be calculated as
Once again, by calculating \(\frac {d\hat {P}_{fT}}{dT}=0\), the optimal threshold value can be found, which can be approximated as \(T=\frac {P_{e}+\hat {P}_{e}}{2P_{e}}\) due to the low variance for this kind of measurements. As such, the probability of detection and false alarm as defined in Section II can be represented by
which show the same performance as Method I.
5.5 Probability of detection based on a cooperative scheme between TSU and RSU
When TSU receives the BER which is estimated at RSU, it will make the final decision of whether PU is active or not based on a threshold. Here, we can obtain the probability of detection based on such a cooperation between TSU and RSU. The condition for cooperative detection is that the spectrum hole is firstly detected at TSU. If PU is sensed by TSU, the training sequence will not be transmitted to RSU.
In hypothesis H 1 and hypothesis H 3, the probability of cooperative detection is the combination of two probabilities. The first is the probability of detection at TSU which we have already discussed in the previous section. The second is the probability when PU is detected at RSU though not at TSU. Thus, the probability of cooperative detection in hypothesis H 1 and H 3 can be expressed as follows:
Here, \(P_{d_{1}}^{coop}\) denotes the probability of cooperative detection in hypothesis H 1 while \(P_{d_{2}}^{coop}\) represents the probability of cooperative detection in hypothesis H 2. Because the probability of detection at TSU and the probability of detection at RSU are relatively independent, Eqs. (33) and (34) can be expressed as follows:
In Eqs. (35) and (36), \(P_{d_{1}}\) represents the probability of detection in hypothesis H 1 at TSU while \(P_{d_{2}}\) is the probability of detection in hypothesis H 3 at TSU. \(P_{d_{3}}\) denotes the probability of detection based on BER estimation at RSU. All of these parameters have been discussed in the previous sections.
By the same principle, we can obtain the probabilities of false alarm \(P_{f_{1}}^{coop}\) and \(P_{f_{2}}^{coop}\) under hypothesis H 0 and H 2 which are the probabilities that PU is detected though it is actually inactive.
According to the derivation from Eqs. (33)–(38), we can show that the new spectrum sensing scheme improves the probability of detection. It decreases the interference from SU. However, it also brings an increase in the probability of false alarm which might decrease the spectrum utilization.
6 Spectrum utilization
6.1 Case I: ideally no noise or negligible noise
In order to measure spectrum utilization, and compare it to the traditional periodical sensing, it is necessary firstly to figure out how much time the “sensing” stage occupies and how much time the “transmitting” stage occupies during transmission. In our new full duplex TSU, it is also necessary to estimate the durations of the “sensing” stage “transmitting and sensing”. Assuming that D H is the total duration of the spectrum holes in an observation interval, such as in Fig. 4, it can be written as \(D_{H} = \sum _{i=0}^{N_{H}-1} D_{i}\), where N H denotes the number of holes in the observation interval, and D i , indicates the time duration of the i th spectrum hole h i . Denoting \({T_{H}^{d}}\) as the total duration of the data transmission (i.e., the“transmitting ” stage in periodical sensing and the “transmitting and sensing” stage both at TSU) of all detected spectrum holes in an observation interval, it can be written as \({T_{H}^{d}} = \sum _{i=0}^{{N_{H}^{d}} - 1} T_{i}\), where \({N_{H}^{d}}\) denotes the total number of spectrum holes detected by SU during the observation interval, while T i , indicates the duration of the real data transmitting stage for the i th spectrum hole h i . Denote η as the utilization of the spectrum holes. Spectrum utilization, η, can thus be calculated as
6.1.1 Ideally no noise or negligible noise in periodical spectrum sensing
In the traditional periodical spectrum sensing, the duration of a spectrum hole, D i , which can be regarded as a random variable, as in [16], follows an exponential distribution with an assumed mean μ. Its cumulative distribution function (CDF) can therefore be given as
and its probability density function (PDF) can be described as
In addition, T i can also be regarded as a random variable, since:
where f sens is the frequency of periodical spectrum sensing. It is a fixed value for a CR spectrum sensing system. N i is the sensing instants in the ith spectrum hole.
In order to compute the CDF of T i , for an arbitrary T, we have
Therefore, its CDF and PDF can be obtained, respectively, as
Furthermore, we have the expectation of T i :
One must note that f sens W≤1 because the sensing period \(\frac {1}{f_{sens}}\) is always greater or equal to the length W of the sensing window. It is therefore reasonable to assume that when the sensing frequency f sens increases, the duration of data transmission decreases.
If there is no noise or negligible noise, each valid spectrum hole is assumed to be detected. So, Eq. (39) can be written as
where \(\bar {T}_{H}^{d} = \bar {T}\) and \(\bar {D}_{H} = \mu \). So spectrum utilization η period in an ideal periodical spectrum sensing system is obtained as:
where W is a fixed value when the licensed channel is sensed by a sensing window with a fixed sized. In Eq. (47), one can conclude that the utilization of the spectrum decreases when the size of the sensing window becomes larger. This result makes sense because the wasted time when the spectrum is not used is equal to the size of the sensing window during the sensing stage.
6.1.2 Ideally no noise or negligible noise when sensing and transmitting at the same time
Similar to traditional periodical spectrum sensing, the duration D i of a spectrum hole, at a full duplex TSU, can be regarded as a random variable foll an exponential distribution with an assumed mean μ whose cumulative distribution function (CDF) and probability density function (PDF) are shown in Eqs. (40) and (41).
Similarly, T i can also be regarded as a random variable, indicating the duration of the “sensing and transmitting ” stage. In each spectrum hole, data transmission always happens except during the first spectrum sensing window. Thus, the transmission duration can be described as:
In order to compute the CDF of T i , for an arbitrary T, we have
Therefore, its CDF and PDF can be obtained, respectively, as
Furthermore, we have the expectation of T i as
If there is no noise or negligible noise, each valid spectrum hole is assumed to be detected. So, Eq. (39) can be written as
where \(\bar {T}_{H}^{d} = \bar {T}\) and \(\bar {D}_{H} = \mu \). In Eq. (52), W represents the size of the first sensing window in one spectrum hole. The utilization of the spectrum also decreases when the size of the sensing window W becomes larger. The size of the first sensing window is adaptive and changeable. Its range, W adaptive should be W min <W adaptive <W max . The aim of having an adaptive window is to decrease W and improve spectrum utilization. It regulates the trade-off between the probability of detection and spectrum utilization because the probability of detection increases with W, while spectrum utilization decreases with W.
6.2 Case II: noisy environment
In general, there is non-negligible noise which increases the probability of false alarms. False alarms cause spectrum holes not to be used. Thus, spectrum utilization is affected by the probability of false alarm.
First, when spectrum sensing is carried out only at TSU, spectrum utilization in Eq. (39) can be expressed as
where \({T}_{i}^{loss}\) denotes the wasted durations in the ith spectrum hole h i which are caused by false alarms while \(\bar {D}_{H} = \mu \), \(\bar {T}_{H}^{d} = \bar {T}-\bar {T}^{loss}\), \(\bar {T}^{loss}\) is defined as the expected value of the wasted spectrum duration \(E\{T_{i}^{loss} \}\) in ith spectrum hole.
6.2.1 Noisy environment in periodical spectrum sensing
In a periodical spectrum sensing scheme, \(E\left \{T_{i}^{loss} \right \}\) comes entirely from false-alarms during the “sensing” stage. It can be expressed as the expected value \(E\left \{T_{i}^{loss} \left | \text {sensing stage} \right.\right \}\) of all wasted durations in one period of spectrum sensing which denotes as \(\bar {W}_{loss}\):
where \(\bar {N}\) is the expected value of the number of spectrum sensing times in each spectrum hole. According to Eq. (42), we can obtain the expression below:
Thus, the expected value of the number of spectrum sensing times in each spectrum hole \(\bar {N} \) is:
When spectrum sensing is only based on energy detection at TSU, \(E\{T_{i}^{loss} | \text {sensing stage} \}\) depends on the probability of false alarm \(P_{f_{1}}\). at TSU. It can be derived as follows:
Here, W is the size of the spectrum sensing window. Its value is W=W max . This is because, in our adaptive window algorithm the size of the sensing window does not change when PU is inactive.
According to Eqs. (55) and (56), \(E\{T_{i}^{loss} \}\) is expressed as:
Then, according to Eqs. (57) and (58), we can derive the utilization of the spectrum \(\eta ^{period}_{noise}\) in a periodical spectrum sensing system in a noisy environment as:
From Eq. (59), one can conclude that spectrum utilization \(\eta ^{period}_{noise}\) decreases when the probability of false-alarm \(P_{f_{1}}\) increases. On the other hand, the utilization \(\eta ^{period}_{noise}\) becomes lower when the size of the sensing window W becomes larger which implies that Eq. (59) makes sense.
6.2.2 Noisy environment when sensing and transmitting at the same time
When sensing and transmitting at the same time in a full duplex TSU, the expected value of the wasted durations \(\bar {T}^{loss}_{duplex}\) in each spectrum hole consists of two components. The first is the expected value of the wasted spectrum durations during the sensing stage. The other one is the wasted spectrum durations during the transmitting and sensing stage. In other words, we have
where N duplex represents the number of sensing times in transmitting and sensing stage. In Eq. (60), \(E\{T_{i}^{loss} | \text {sensing stage} \}\) is the expected value of the wasted spectrum durations during the spectrum sensing in the sensing stage. Its expression is shown in Eq. (57). The sensing stage occurs once at the beginning of the spectrum hole.
In Eq. (60), \(E\left \{T_{i}^{loss} \left | \text {sensing and transmitting stage}\right.\right \}\) denotes the expected value of the wasted spectrum durations during the transmitting and sensing stage.
Similar to Eq. (57), we can obtain the expected value of the wasted spectrum durations during the transmitting and sensing stage as:
By comparing Eq. (57) with Eq. (61), one can see that the only difference between \(E\left \{T_{i}^{loss} \left | \text {sensing stage} \right.\right \}\) and \(E\{T_{i}^{loss} | \text {transmitting and sensing stage}\}\) is that the probability of false alarm in hypothesis H 0 is different from the corresponding false alarm in H 2.
In addition, in order to derive the utilization of a spectrum hole, we need to know n duplex since the average duration of the “transmitting and sensing” stage \(\bar {T}\) is
Thus, \(\bar N_{duplex}\) can be expressed as:
In Eq. (62), the duration of the “transmitting and sensing” stage includes the wasted durations in both the sensing stage and the transmitting and sensing’ stage as well as the used spectrum in hypothesis H 2. From Eq. (63), we can obtain the following:
We substitute Eqs. (51) and (64) into Eq. (53), to obtain an expression for the spectrum utilization \(\eta _{noise}^{duplex}\):
In Eq. (65), when the probabilities of false alarm \(P_{f_{1}}\) and \(P_{f_{2}}\) increase, the utilization \(\eta _{noise}^{duplex}\) becomes smaller. On the other hand, the utilization η also becomes lower when the size of the sensing window W becomes larger. Thus, we can conclude that Eq. (65) makes senses.
6.3 Spectrum utilization in cooperative spectrum sensing between TSU and RSU
Next, we introduce the utilization of a spectrum hole when we use our new spectrum sensing scheme, i.e., when we combine BER estimation with energy detection to realize spectrum sensing. When we use the new spectrum sensing method, all relevant expressions are the same as Eqs. (60)–(65) except that we use \(P_{f_{1}}^{coop}\) and \(P_{f_{2}}^{coop}\) to replace the original \(P_{f_{1}}\) and \(P_{f_{2}}\). Moreover, the duration of the “transmitting and sensing” stage not only includes the wasted duration as well as the used spectrum in hypothesis H 2, but also includes the length of the training sequence which is used in BER estimation. So Eq. (62) can be rewritten as:
Here, \(\bar {W_{ts}}\) is the expected value of the length of the training sequence and W ts is the length of training sequence in each estimation of BER. Thus, the number of sensing times \(\bar N_{coop}\) can be expressed as:
Then \(\bar {T}^{loss}\) can be expressed according to Eqs. (66) and (67) as
Finally, it is easy to derive the utilization of the spectrum \(\eta _{noise}^{coop} \) as
From Eqs. (68) and (69), we can conclude that the utilization of the spectrum depends on the probability of cooperative false-alarm \(P_{f_{2}}^{coop}\). The loss of spectrum \(\bar {T}^{loss}\) becomes larger when the cooperative probability of false-alarm at the “transmitting and sensing” stage \(P_{f_{2}}^{coop}\) increases. This is reasonable because the “transmitting and sensing” stage occupies most of the spectrum hole for a CR full duplex system. If \(P_{f_{2}}^{coop}\) increases, it implies that the CR transmitter will spend more time on spectrum sensing instead of sensing and transmitting. In other words, some of the spectrum hole is missed without transmitting data at TSU. Thus, it is reasonable to assume that the utilization of the spectrum \(\eta _{noise}^{coop}\) decreases with the increase in \(P_{f_{2}}^{coop}\) in Eq. (69).
In addition, according to Eqs. (68) and (69), we can also conclude that spectrum utilization \(\eta _{noise}^{coop}\) is larger when the training sequence W ts that is used in BER estimation has a larger duration. However, it is possible that the longer length of the training sequence causes interference to PU especially at the end of a spectrum hole when PU might become active.
7 Numerical analysis and simulation results
7.1 Parameters
7.1.1 Basic parameters for the simulation
In this section, the proposed spectrum sensing at TSU is simulated using Matlab 2014b in a 64 bit computer with a core i7 and 8 GB RAM in order to demonstrate our proposed theory. The duration of a spectrum hole, which is also called appearance duration, follows an exponential distribution with a mean of μ=30000 samples. The arrival rate of a spectrum hole follows a Poisson distribution with an average arrival rate ε=20000 samples intervals. From [14], the maximum allowed length of the sensing window W max is 1000 samples. The minimum allowed length of sensing window W min is 100 samples. The number of consecutive windows after which the length, C, of the sensing window is decreased by W min , is set as 1, 2, or 5. In BER detection, the size of training sequence W ts is also 1000 samples. The RF parameters which include the bandwidth of the channel B, the thermal noise spectrum density V(f), the noise factor of the receiver NF and the variance of AWGN σ 2 are all shown in Table 1.
7.1.2 Parameters for performance evaluation
The probability of detection P d of a spectrum hole is an important factor when evaluating the performance of the proposed spectrum sensing algorithm. It is used to weigh the ability for TSU to avoid interfering with PU when PU is active. It is necessary to measure P d at TSU and RSU. That is why we need to obtain the probability of cooperative detection as well.
On the other hand, the probability of false alarm detection P f is another important factor when PU is inactive. It affects the utilization of the spectrum η, which is another parameter when evaluating the performance of the proposed system. The utilization of the spectrum is also another parameter that plays a fundamental role in a CR system.
7.2 Probability of detection
In the simulations, we examine the probability of detection at TSU first. As previously discussed, there exist two kinds of probabilities of detection and probabilities of false alarm: \(P_{d_{1}}\), \(P_{f_{1}}\) at “sensing" stage and \(P_{d_{2}}\), \(P_{f_{2}}\) at “sensing and transmitting” stage. Because the selection of the detection thresholds λ 1 and λ 2 is based on Eq. (12), the value of \(P_{d_{1}}\) and of \(P_{d_{2}}\) increase while the value of \(P_{f_{1}}\) and \(P_{f_{2}}\) decrease. Thus, when we evaluate the detection performance at TSU, we must examine the probability of detection \(P_{d_{1}}\) and \(P_{d_{2}}\) instead of \(P_{d_{1}}\), \(P_{d_{2}}\), \(P_{f_{1}}\), and \(P_{f_{2}}\).
According to Eq. (7), \(P_{d_{1}}\) depends on the SNR γ 1, the variance of the AWGN σ 2 and the length of the sensing window W. σ 2 is a constant in Table 1. The SNR γ 1 depends on the PU transmitting power \({\sigma _{p}^{2}}\) and factors which affect the channel gain α such as the transmission distance d, and shadow fading φ in Eqs. (17) and (18). In our simulations, we evaluate the performance of CR for an SNR range from −20 to 10 dB. The length of the sensing window W is regarded as a constant when the spectrum sensing work has a fixed window. The length of a fixed window is between W min and W max . If spectrum sensing with an adaptive window as in Algorithm 1 is applied, the length of the sensing window will be a variable changing from W max to W min . The simulation results on the probability of detection, \(P_{d_{1}}\), in Eq. (7) vs. SNR, γ 1, are shown in Fig. 11. It makes sense that the probability of detection, \(P_{d_{1}}\), is always larger when W=W max than when W=W min . The reason is obvious: more energy is collected with a larger window, which has a higher probability to be greater than the preset threshold. When spectrum sensing uses an adaptive window, the average length of the sensing window for each sensing interval is between W max and W min . It depends on the value of C in Algorithm 1. The average W for each sensing interval becomes smaller as C becomes larger. Thus, when C increases, it is reasonable to assume that the probability of detection P d1 decreases. There is a gap between the simulation result and the corresponding theoretical result. Based on our analysis, the number of iteration should be the reason for this gap. Especially when the SNR is low, it requires a large iteration to precisely find out the exact probability of detection. When the SNR is high, it shows a better consistence between the simulation and the theoretical result. Overall speaking, the simulation result approximately matches the derived theory (similar issue occurs again for the following simulation results).
Because a larger window leads to a better detection, for hypotheses H 2/H 3, the largest window W=W max is used to attain the best detection. Under this condition, the probability of detection, \(P_{d_{1}}\), in Eq. (7) for hypotheses H 0/H 1 is compared with the probability of detection, \(P_{d_{2}}\), in Eq. (9) for hypotheses H 2/H 3. Four cases are considered: \(\frac {\gamma _{2}}{\gamma _{1}}=0.5,1,2,4\) with various transmitting power. When \(\frac {\gamma _{2}}{\gamma _{1}}\) is greater than 1, it implies that the power of the SU signal is larger than the power of the PU signal. Fig. 12 shows the probability of detection versus SNR γ 1. As seen, \(P_{d_{1}}\) is always larger than the corresponding \(P_{d_{2}}\) especially when the TSU signal is larger than the PU signal. It is reasonable to assume that the PU signal is difficult to detect when the TSU signal is too large to exceed the PU signal. It also explains why we need to apply antenna cancellation techniques as previously discussed. It is reasonable to regard \(P_{d_{1}}\) as an approximation of \(P_{d_{2}}\) when the PU signal α p(n) and the SU signal s(n) are within the same or close order of magnitude. However, because both are based on energy detection, \(P_{d_{1}}\) and \(P_{d_{2}}\) are both imperfect when the SNR is relatively low. Thus, our proposed cooperative detection model provides a more precise detection. It requires detection at RSU which assists TSU in spectrum sensing.
From Section 4.4, the detection results at TSU depend on BER estimation using training sequences at RSU as well as using the optimal threshold which is a function of the difference between the theoretical BER P e when PU is inactive and \(\hat P_{e}\) when PU is active. When the difference between P e and \(\hat P_{e}\) is large, it is easier to judge whether PU is active or not. From Eqs. (20) and (26), P e and \(\hat P_{e}\) are related to \(\frac {A}{\sigma }\) and \(\frac {B}{\sigma }\). Because the variance of the AWGN σ 2 is a fixed value, P e and \(\hat P_{e}\) depend on the relationship between the two signal amplitudes A and B. Here, we denote \(n=\frac {B}{A}\) as the ratio between the PU signal amplitude B and the SU signal amplitude A. The difference between P e and \(\hat P_{e}\) vs. SNR are shown in Fig. 13. The difference between P e and \(\hat P_{e}\) increases with the increase in n. This is reasonable because in this case PU adds more interference to the training sequence which causes bit errors when its transmitting power is large. In addition, when n is fixed, the difference between P e and \(\hat P_{e}\) also increases with the increase in SNR because the interference from the PU signal is much larger than the effect of the AWGN. From Fig. 13, P e and \(\hat P_{e}\) are always very close if n=0.25. In order to obtain a better detection based on BER estimation, we select n=0.5,1,2 by transmitting power control signals.
According to our simulations, the probability of detection \(P_{d_{3}}\) based on BER estimation vs. SNR with different values of n=0.5,1,2 is shown in Fig. 14.
In Fig. 14, increasing n implies that the power of the PU signal becomes larger relative to that of the TSU signal. In this case, PU is easier to be detected which causes \(P_{d_{3}}\) to increase. Actually, the ratio n between the PU signal power and the SU signal power can influence the experiment substantially. From Fig. 14, the simulation results are better than theory. This is reasonable because the theoretical results are based on statistical assumptions while each instant of BER detection is carried out in a discrete and independent fashion in the simulations. When n decreases from 2 to 0.5. The difference between the simulation results and the theory becomes smaller. Regular power control technology can force A=B. In the next simulation, we assume that the power of the SU signal is the same as the power of the PU signal. By comparing \(P_{d_{3}}\) in Fig. 14 with \(P_{d_{1}}\) and \(P_{d_{2}}\) in Fig. 12, one can see that the detection \(P_{d_{3}}\) at RSU is greater than the detection at TSU in theory when A≥B It is helpful when a missed detection occurs at TSU such as in case I and case II in section 1.2.
So far, we have discussed the values of \(P_{d_{1}}\), \(P_{d_{2}}\), and \(P_{d_{3}}\) vs. SNR. The probability of cooperative detection under hypothesis H 1, \(P_{d_{1}}^{coop}\) and the probability of cooperative detection under hypothesis H 3, \(P_{d_{2}}^{coop}\) are presented in Fig. 15 using theoretical analysis from Eq. (35), Eq. (36), and practical simulation. They are to be compared with the probability of detection \(P_{d_{1}}\) and \(P_{d_{2}}\). From Fig. 15, it is obvious that the performance of detection is improved using cooperative spectrum sensing between TSU and RSU, especially when the SNR is low. For instance, at an SNR = −20 dB, cooperative detection increases the probability of detection to around 77 from around 55 %. The probability of detection can be increased because a missed detection at TSU is compensated by the detection at RSU. When PU is not detected at TSU, there still exists a good probability for TSU to detect PU at RSU. Thus, the proposed cooperative detection at both ends of SU overcomes the shortcoming of energy detection and improves the performance of detection when the SNR is low. In addition, experimental results are better than the results obtained from theory because the theoretical result are based on statistical assumptions while each instant of spectrum sensing is carried out in a discrete and independent fashion in the simulations. The experimental results can not be fully described by theoretical analysis.
7.3 Probability of false alarm
False alarm happens when hypotheses H 0 or H 3 are selected even though PU is inactive. It directly affects the utilization of the spectrum. When the probability of false alarm is high, a number of spectrum holes are missed by TSU. For this reason, we discuss the probability of false alarm before discussing the utilization of the spectrum. As in previous sections, the selection of the detection thresholds λ 1 and λ 2 is based on Eq. (12). According to Eqs. (37) and (38), the probabilities of false alarm \(P_{f_{1}}^{coop}\) and \(P_{f_{2}}^{coop}\) cannot be expressed by \(P_{d_{1}}^{coop}\) and \(P_{d_{2}}^{coop}\) directly even though they depend on \(P_{f_{1}}\) and \(P_{f_{2}}\). In Fig. 16, we compare \(P_{f_{1}}^{coop}\) and \(P_{f_{2}}^{coop}\), with \(P_{f_{1}}\) and \(P_{f_{2}}\) which shows that the probability of false alarm increases when the cooperative spectrum sensing is applied, especially when the SNR is low. Compared with \(P_{f_{1}}\) and \(P_{f_{2}}\), the total probability of false alarm \(P_{f_{1}}^{coop}\) and \(P_{f_{2}}^{coop}\) are greater because of the additional probability of false alarm \(P_{f_{3}}\) at RSU. The simulation results are better than the theory because the simulation results for \(P_{d_{1}}\), \(P_{d_{2}}\) and \(P_{d_{3}}\) are relatively higher than theory while \(P_{f_{1}}\), \(P_{f_{2}}\), and \(P_{f_{3}}\) are relatively lower.
7.4 Spectrum utilization
In this section, we discuss the spectrum utilization by periodical spectrum sensing at TSU, simultaneously sensing/transmitting, and cooperative spectrum between TSU and RSU.
7.4.1 Simulation results for periodical sensing and simultaneous sensing
We first compare our proposed simultaneous sensing/transmitting with the traditional periodical sensing. For both cases, the sensing window is fixed. Its value is either W max or W min . In periodical sensing, the ratio of the sensing window size W to the sensing period can be represented as f sens W. The value of f sens W is selected to be \(\frac {2}{3}\). Figure 17 indicates that the utilization of the spectrum \(\eta _{noise}^{duplex}\) is always higher than \(\eta _{noise}^{period}\) in both simulation and theory. This is reasonable because the spectrum hole is not used to transmit data in each instance of periodical spectrum sensing while our proposed model can sense and transmit data at the same time. The duration of the wasted spectrum hole are shown as the blue blocks in Fig. 1. One can show that the simultaneous sensing/transmitting algorithm wastes less spectrum hole durations than periodical spectrum sensing.
When the SNR is relatively low (e.g., the SNR is from −20 to −5 dB), in either of the two spectrum sensing algorithms, the utilization of spectrum becomes higher with the increase of W from W min to W max . This is reasonable because the probability of false alarm decreases and the probability of detection increases when W increases.
When the SNR is greater than 0 dB, the spectrum utilization of periodical sensing \(\eta _{noise}^{period}\) becomes a constant value equal to 60 % regardless whether W is W max or W min . In this case, the probability of false alarm is always 0 and the probability of detection is always 1 no matter how large the sensing window W is. \(\eta _{noise}^{period}\) depends on the ratio of sensing window size to sensing period f sens W which is a constant.
For a fixed SNR greater than 0 dB, the spectrum utilization of simultaneous sensing/transmitting \(\eta _{noise}^{duplex}\) depends on the duration of the only sensing stage. Figure 18 shows the spectrum holes before TSU senses and uses them in the simulation, and the usage of this spectrum after TSU senses and utilizes the spectrum holes. In each spectrum hole, the tiny white space shown in Fig. 18b is the only sensing stage which is at the beginning of each spectrum hole. The value of its duration depends on the corresponding size of the sensing window W. When W is larger, the spectrum utilization becomes lower. Thus, the energy detection with W=W max has the lowest utilization. Its bigger step causes more missing usage of the spectrum holes. Therefore, its spectrum utilization with high SNR cannot come close to 100 % (96.72 % from simulation). Conversely, energy detection with W=W min leads to an approximate 100 % (99.67 % from simulation) hole utilization. It shortens the sensing duration. Hence, in order to obtain a high spectrum utilization at high SNR, we use the adaptive window algorithm to assist with simultaneous sensing at TSU.
7.4.2 Simulation on simultaneous sensing with adaptive window
Figure 19 indicates the comparison of spectrum utilization between sensing with a fixed window and sensing with an adaptive window. When C is reduced from 5 to 1, the sensing duration becomes smaller and the spectrum utilization becomes larger at high SNR. The best performance is obtained when C=1. In this case, the spectrum utilization improves from 96.72 % to 99.6 %.
Once again, the simulation results are better than theory because the expected value of the wasted duration \(T_{i}^{loss}\) in Eqs. (57) and (61) is larger than the one we obtain in the simulations. This is because it is less possible for false alarm to occur twice or more. The wasted duration in the simulations is mostly W or 2W which is less than \(E\left \{T_{i}^{loss} \left | \text {sensing stage} \right.\right \}\) and \(E\left \{T_{i}^{loss} \left | \text {sensing stage and transmitting stage} \right.\right \}\).
7.4.3 Simulation on cooperative spectrum sensing
Figure 19, indicates that the spectrum utilization is improved by using an adaptive window. In this case, spectrum utilization approaches 100 % when the SNR is between −5 and 10 dB. However, the spectrum utilization is still low when the SNR is between −20 and −10 dB. It is because we use energy detection to implement spectrum sensing at TSU. Energy detection has a poor detection performance when the SNR is low(i.e., it causes the increase of the probability of false alarm and the decrease of the probability of detection). In order to improve the probability of detection and consequently spectrum utilization, cooperative spectrum with BER estimation is introduced.
In the simulations, Fig. 20 indicates that spectrum utilization at low SNR is improved when the BER is considered as part of spectrum detection. For instance, at an SNR=−20dB, the proposed “adaptive sensing + BER” algorithm increases spectrum utilization from around 44 % to around 48 % using either a fixed or an adaptive sensing window in the simulations and increases spectrum utilization from around 37 % to around 43 % in theory. Its spectrum utilization is greater than the periodical spectrum sensing.This is reasonable because, at low SNR, the BER detection uses the PU channel to transmit a training sequence. On one hand, the training sequence is used for PU detection in order to improve the probability of detection and decrease the probability of false alarm. On the other hand, the training sequence occupies the spectrum hole, which increases the spectrum utilization.
8 Conclusions
In this paper, a cooperative spectrum sensing between TSU and RSU is implemented in CR. Our novel adaptive spectrum sensing scheme improves the spectrum utilization. Both the theoretical analysis and simulations show that the usage of an adaptive window improves the spectrum utilization from 96.72 to 99.6 %. Furthermore, BER-assisted detection greatly helps the adaptive spectrum sensing. Simulation results demonstrate that cooperative spectrum sensing can offer a better performance. It increases the utilization of the spectrum from around 44 % to around 48 % in the simulations and increases spectrum utilization from around 37 % to around 43 % in theory when SNR is −20dB.
References
W Krenik, A Wyglinski, L Doyle, Guest editorial-cognitive radios for dynamic spectrum access. IEEE Commun. Mag. 5(45), 64–65 (2007).
S Haykin, Cognitive radio: brain-empowered wireless communications. Selected Areas Commun. IEEE J. 23(2), 201–220 (2005).
JE Salt, HH Nguyen, Performance prediction for energy detection of unknown signals. Vehicular Technol. IEEE Trans. 57(6), 3900–3904 (2008).
W Cheng, X Zhang, H Zhang, Full duplex wireless communications for cognitive radio networks (2011). arXiv preprint arXiv:1105.0034.
W Afifi, M Krunz, in Dynamic Spectrum Access Networks (DYSPAN), 2014 IEEE International Symposium On. Adaptive transmission-reception-sensing strategy for cognitive radios with full-duplex capabilities, IEEE, Tyson’s Corner, Virginia, USA, (2014), pp. 149–160.
Y Liao, L Song, Z Han, Y Li, Full duplex cognitive radio: a new design paradigm for enhancing spectrum usage. Commun. Mag. IEEE. 53(5), 138–145 (2015).
Y Liao, T Wang, L Song, Z Han, in Global Communications Conference (GLOBECOM), 2014 IEEE. Listen-and-talk: full-duplex cognitive radio networks, IEEE, Austin, USA, (2014), pp. 3068–3073.
W Cheng, X Zhang, H Zhang, in MILITARY COMMUNICATIONS CONFERENCE, 2011-MILCOM 2011. Full duplex spectrum sensing in non-time-slotted cognitive radio networks, IEEE, Baltimore, USA, (2011), pp. 1029–1034.
W Cheng, X Zhang, H Zhang, in Proceedings of the 3rd ACM Workshop on Cognitive Radio Networks. Imperfect full duplex spectrum sensing in cognitive radio networks (ACMNew York, USA, 2011), pp. 1–6.
W Afifi, M Krunz, in INFOCOM, 2013 Proceedings IEEE. Exploiting self-interference suppression for improved spectrum awareness/efficiency in cognitive radio systems, IEEE, Turin, Italy, (2013), pp. 1258–1266.
E Ahmed, A Eltawil, A Sabharwal, in Antennas and Propagation Society International Symposium (APSURSI), 2012 IEEE. Simultaneous transmit and sense for cognitive radios using full-duplex: A first study, IEEE, Memphis, USA, (2012), pp. 1–2.
JI Choi, S-K Hong, M Jain, S Katti, P Levis, J Mehlman, in Signals, Systems and Computers (ASILOMAR), 2012 Conference Record of the Forty Sixth Asilomar Conference On. Beyond full duplex wireless, IEEE, Pacific Grove, California, USA, (2012), pp. 40–44.
E Tsakalaki, ON Alrabadi, A Tatomirescu, E De Carvalho, GF Pedersen, Concurrent communication and sensing in cognitive radio devices: challenges and an enabling solution. Antennas Propag. IEEE Trans. 62(3), 1125–1137 (2014).
D Treeumnuk, DC Popescu, in Communications (ICC), 2012 IEEE International Conference On. Energy detector with adaptive sensing window for improved spectrum utilization in dynamic cognitive radio systems, IEEE, Ottawa, Canada, (2012), pp. 1528–1532.
TS Shehata, M El-Tanany, in Information Theory, 2009. CWIT 2009. 11th Canadian Workshop On. A novel adaptive structure of the energy detector applied to cognitive radio networks, IEEE, Ottawa, Canada, (2009), pp. 95–98.
Y-C Liang, Y Zeng, EC Peh, AT Hoang, Sensing-throughput tradeoff for cognitive radio networks. Wireless Commun. IEEE Trans. 7(4), 1326–1337 (2008).
DR Joshi, DC Popescu, O Dobre, et al, Gradient-based threshold adaptation for energy detector in cognitive radio systems. Commun. Lett. IEEE. 15(1), 19–21 (2011).
JI Choi, M Jain, K Srinivasan, P Levis, S Katti, in Proceedings of the Sixteenth Annual International Conference on Mobile Computing and Networking. Achieving single channel, full duplex wireless communication, ACM, New York, USA (ACMNew York, USA, 2010), pp. 1–12.
TT Ha, Theory and Design of Digital Communication Systems (ACM, New York, 2010).
Y Lu, D Wang, M Fattouche, in Personal, Indoor, and Mobile Radio Communication (PIMRC), 2014 IEEE 25th Annual International Symposium On. Novel spectrum sensing scheme in cognitive radio by simultaneously sensing/transmitting at full-duplex tx and ber measurements at rx, IEEE, Pittsburg, USA, (2014), pp. 638–642.
Acknowledgements
A short version of this paper was presented in IEEE PIMRC 2014 [20].
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lu, Y., Wang, D. & Fattouche, M. Cooperative spectrum-sensing algorithm in cognitive radio by simultaneous sensing and BER measurements. J Wireless Com Network 2016, 136 (2016). https://doi.org/10.1186/s13638-016-0635-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-016-0635-z