1 Introduction

Audios in a realistic environment are typically composed of different sound sources. Yet humans have no problem in organizing the elements into their sources to recognize the acoustic environment. This process is called auditory scene analysis [1]. Studies in the central auditory system [2–4] have inspired numerous hypotheses and models concerning the separation of audio elements. One prominent hypothesis that underlies most investigations is that audio elements are segregated whenever they activate well-separated populations of auditory neurons that are selective to frequency [5, 6], which emphasizes the audio distinction on the frequency dimension. At the same time, other studies [7, 8] also suggest that auditory scenes are essentially dynamic, containing many fast-changing, relatively brief acoustic events. Therefore an essential aspect of auditory scene analysis is the linking over time [9].

Problems inherent to auditory scene analysis are similar to those found in visual scene analysis. However, the time and frequency characteristic of a spectrogram makes it very different from natural images. For example in Fig. 1, (a) and (b) are two audio fragments randomly selected from an audio of “cafe” scene. We first calculate the average energy distribution of the two examples in the frequency direction, which is shown in (c). And then the temporal coherence of salient audio elements in each frequency bin is measured as (d). It is obvious that the energy distribution and temporal coherence vary tremendously in different frequency bins, but are similar in the same frequency bin of different spectrograms. Thus for audio signals, the spectrogram structure is not equivalent in time and frequency direction. In this paper, we propose a novel network structure to learn the energy distribution and temporal coherence in different frequency bins.

Fig. 1
figure 1

Spectrogram examples of “cafe” scene. a, b Two audio fragments randomly selected from “cafe” scene. c The average energy distribution of the two examples in frequency direction. d The temporal coherence of the two examples in different frequency bins

Full size image

1.1 Related work

For audio separation [10, 11] and recognition [12, 13] tasks, the time and frequency analysis is usually implemented using well designed filter banks.

Filter banks are traditionally composed of finite or infinite response filters in principle [14], but the stability of the filters is usually difficult to be guaranteed. For simplicity, filter banks on STFT spectrogram have been investigated for a long time [15]. In this case, the time resolution is determined by the frameshift in the STFT procedure and the frequency resolution is modelled by the frequency response of the filter banks. Frequency filter banks can be parameterized in the frequency domain with filter centre, bandwidth, gain and shapes [16]. If these parameters are learnable, deep neural networks (DNNs) can be utilized to learn them discriminatively [17–19]. These frequency filter banks are usually used to model the frequency selectivity of the auditory system, but cannot represent the temporal coherence of audio elements.

DNNs are often used as classifiers when the inputs are dynamic acoustic features such as filter bank-based cepstral features and Mel-frequency cepstral coefficients [20, 21]. When the input to DNNs is a magnitude spectrogram, time-frequency structure of the spectrogram can be learned. Neural networks organized into a two-dimensional space have been proposed to model the time and frequency organization of audio elements by Wang and Chang [22]. They utilized two-dimensional Gaussian lateral connectivity and global inhibition to parameterize the network, where the two dimensions correspond to frequency and time respectively. In this model, time is converted into a spatial dimension, temporal coherence can take place in auditory organization much like in visual organization where an object is naturally represented in spatial dimensions. However, these two dimensions are not equivalent in a spectrogram according to our analysis. And what is more, the parameters of the network are set empirically and not learnable, which is still significantly dependent on domain knowledge and modelling skill.

In recent years, neural networks with special structures such as convolutional neural network (CNN) [23, 24] and long short-term memory (LSTM) [25, 26] have been used to extract the long-term information of audios. But in both network structures, the temporal coherence is considered to be the same in different frequency bins, which is in contradiction with Fig. 1.

1.2 Contribution of this paper

As shown in Fig. 1, when perceptual frequency scale is utilized to map the linear frequency domain to the nonlinear perceptual frequency domain [27], the major concern comes to be how to model the energy distribution and temporal coherence in different frequency bins.

To obtain better time and frequency analysis results, we divide the audio processing procedure into two stages. In the first stage, traditional frequency filter banks are implemented on STFT spectrogram to extract frequency features. Without loss of generality, the parameters of the frequency filter banks are set experimentally. In the second stage, a novel long-term filter bank spanning several frames is constructed in each frequency bin. The long-term filter banks proposed here can be implemented by neural networks and trained jointly with the target of the specific task.

The major contributions are summarized as follows:

  • Toeplitz matrix motivated long-term filter banks: Unlike filter banks in frequency domain, our proposal of long-term filter banks spreads over the time dimension. They can be parameterized with the time duration and shape constraints. For each frequency bin, the time duration is different, but for each frame, the filter shape is constant. This mechanism can be implemented using a Toeplitz matrix motivated network.

  • Spectrogram reconstruction from filter bank coefficients: Consistent with the audio processing procedure, we also divide the reconstruction procedure into two stages. The first stage is a dual inverse process of the long-term filter banks and the second stage is a dual inverse process of the frequency filter banks. This paper investigates the spectrogram reconstruction problem using an elaborate neural network.

This paper is organized as follows. The next section describes the detailed mechanism of the long-term filter banks and the spectrogram reconstruction method. Then network structures used in our proposed method are introduced in Section 3. Section 4 conducts several experiments to show the performance of long-term filter banks regarding source separation and audio scene classification. Finally, we conclude our paper and give directions for future work in Section 5.

2 Long-term filter banks

For generality, we consider in this section a long-term filter bank learning framework based on neural networks as Fig. 2.

Fig. 2
figure 2

Long-term filter banks learning framework. The left part of the framework is the feature analysis procedure including STFT, frequency filter banks and long-term filter banks. The right part is the application examples of the extracted feature map, such as audio scene classification and audio source separation. Long-term filter banks in the feature analysis procedure and the back-end application modules are stacked into a deep neural network

Full size image

The input audio signal is first transformed to a sequence of vectors using STFT [28]; the STFT result can be represented as X1...T={x1,x2,...,x T }. T is determined by the frame shift in STFT, the dimension of each vector x can be labelled as N, which is determined by the frame length.

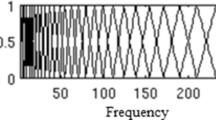
The frequency filter banks can be simplified as a linear transformation \(\boldsymbol {y}_{t}=\left \{\boldsymbol {f}_{1}^{T}\boldsymbol {x}_{t},\boldsymbol {f}_{2}^{T}\boldsymbol {x}_{t},...,\boldsymbol {f}_{m}^{T}\boldsymbol {x}_{t}\right \}\), where f k is the weights of the k-th frequency filter. In the history of auditory frequency filter banks [29], the rounded exponential family [30] and the gammatone family [31] are the most widely used families. We use the simplest form of these two families, triangular shape for the rounded exponential family and Gaussian shape for the gammatone family. For triangular filter banks, the bandwidth is 50% overlapped between neighbouring filters. For Gaussian filter banks, the bandwidth is 4σ, where σ represents the standard deviation in the Gaussian function. These two types of frequency filter banks are the baselines in this paper, respectively named TriFB and GaussFB. The triangular and gaussian examples distributed uniformly in the Mel-frequency scale [32] can be seen in Fig. 3.

Fig. 3
figure 3

Shape of frequency filter banks. a The triangular filter banks. b The gaussian filter banks

Full size image

When the number of frequency filters is equal to m, the long-term filter banks can be parameterized by m linear transformations. The parameters will be labelled as θ and discussed in the following part of this section in detail.

The back-end processing modules vary from different applications. For audio scene classification task, they will be deep convolutional neural networks followed by a softmax layer to convert the feature maps to the corresponding categories. However, for audio source separation task, the modules will be composed by a binary gating layer and some spectrogram reconstruction layers. We define them as nonlinear functions f γ . The long-term filter bank parameters θ can be trained jointly with the back-end parameters γ using back propagation method [33] in neural networks.

2.1 Toeplitz motivation

The long-term filter banks in our proposed method are used to extract the energy distribution and temporal coherence in different frequency bins which have been discussed in Section 1. As shown in Fig. 4, the long-term filter banks can be implemented by a series of filters with different time durations. If the output of the frequency filter banks is y t , and the long-term filter banks are parameterized as W={w1,w2,...,w m }, the operation of the long-term filter banks can be mathematically represented as Eq. 1. T is the length of the STFT output, m is the dimension of y t , which also represents the number of frequency bins, w k is a set of T positive weights to represent the time duration and shape of the k-th filter. In Fig. 4 for example, w k is a rectangular window with individual width, each row of the spectrogram is convolved by the corresponding filter.

$$ z_{t,k}=\sum_{i=1}^{T}y_{i,k}*w_{k,i-t}, 1\le k\le m $$
(1)
Fig. 4
figure 4

Model architecture of long-term filter banks. Each row of the spectrogram is convolved by a filter bank with individual width. In this sketch map, time durations of the filter banks in the highest four frequency bins are 3, 2, 1 and 2 frames

Full size image

As a matter of fact, the operation in Eq. 1 is a series of one-dimensional convolutions along time axis. We rewrite it using the Toeplitz matrix [34] for simplicity. In Eq. 2, the tensor \(\vec {\boldsymbol {S}}=\{\boldsymbol {S}_{1},\boldsymbol {S}_{2},...,\boldsymbol {S}_{m}\}\) represents the linear transformation form of long-term filter banks in each frequency bin. z k in Eq. 2 is equivalent to {z1,k,z2,k,...,zT,k} in Eq. 1. In this case, long-term filter banks can be represented as a simple form of tensor operation, which can be easily implemented by a Toeplitz motivated network layer. According to [35], Toeplitz networks are mathematically tractable and can be easily computed.

$$\begin{array}{*{20}l} &\boldsymbol{z}_{k}=\boldsymbol{\hat{y}}_{k}\boldsymbol{S}_{k}, 1\le k\le m \\ &\boldsymbol{\hat{y}}_{k}=\left\{\boldsymbol{y}_{1,k},\boldsymbol{y}_{2,k},...,\boldsymbol{y}_{T,k}\right\}\\ &\boldsymbol{S}_{k}= \left[\begin{array}{cccc} w_{k,0} & w_{k,-1} & \cdots & w_{k,1-T} \\ w_{k,1} & w_{k,0} & \cdots & w_{k,2-T} \\ \vdots & \vdots & \ddots & \vdots \\ w_{k,T-1} & w_{k,T-2} & \cdots & w_{k,0} \\ \end{array}\right] \end{array} $$
(2)

2.2 Shape constraint

If W is totally independent, S k is a dense Toeplitz matrix, which means that the time duration of the filter in each frequency bin is T. This assumption is unreasonable especially when T is extremely large. The long-term correlation should be limited to a certain range according to our intuition. Inspired by traditional frequency filter banks, we attempt to use the parameterized window shape to limit the time duration of long-term filter banks.

In Fig. 4, rectangular shapes with time durations of 3, 2, 1 and 2 frames are utilized as an interpretation. From the theory of frequency filter banks, triangular and gaussian shapes are also commonly used options. However, rectangular and triangular shapes are not differentiable and unable to be incorporated into a scheme of a back-propagation algorithm. Thus in this paper, the shape of long-term filter banks is constrained using the Gaussian function as Eq. 3. The time duration of long-term filter banks is limited by σ k , the strength of each frequency bin is reconstructed by α k , the total number of parameters reduces from 2mT in Eq. 2 to 2m in Eq. 3.

$$ w_{k,t}=\alpha_{k}\cdot exp\left(-\frac{t^{2}}{\sigma_{k}^{2}}\right), 1\le k\le m $$
(3)

When we initialize the parameters α k and σ k randomly, we believe that the learning will be well behaved, which is the so-called “no bad local minim” hypothesis [36]. However, a different view presented in [37] is that the underlying easiness of optimizing deep networks is rather tightly connected to the intrinsic characteristics of the data these models are run on. Thus for us, the initialization of parameters is a tricky problem, especially when α k and σ k have clear physical meanings.

If σ k in Eq. 3 is initialized with a value larger than 1.0, the corresponding S k is approximately equal to a k-tridiagonal Toeplitz matrix [38], where k is less than 3. Thus, if the totally independent W is initialized with an identity matrix, similar results with limited time durations should be obtained. Whether it is the Gaussian shape-constrained algorithm as Eq. 3 or is the totally independent W in Eq. 2, the initialization of parameters is important and intractable when adapting to different tasks. More details will be discussed and tested in Section 4.

2.3 Spectrogram reconstruction

In our proposal of learning framework as Fig. 2, STFT spectrogram is transformed into subband coefficients after frequency filter banks and long-term filter banks. The dimension of subband coefficients z t is usually much less than x t to reduce computational cost and extract significant features. In this case, the subband coefficients are incomplete, perfect spectrogram reconstruction from subband coefficients is impossible.

The spectrogram vector x t is firstly transformed using frequency filter banks described at the beginning of this section. Then long-term filter banks work as Eq. 2 to get the subband coefficients. Thus the process of the conversion from spectrogram vector to filter subband coefficients and the dual reconversion can be represented as Eq. 4. The operation of frequency filter banks f1 can be simplified as a singular matrix F where the number of rows is much less than columns. The reconversion process \(f_{1}^{-1}\) is approximately the Moore-Penrose pseudoinverse [39] of F; this module can be easily implemented using a fully connected network layer. However, the tensor operation of long-term filter banks f2 is much more intractable.

$$\begin{array}{*{20}l} \boldsymbol{z}_{t}=f_{2}(f_{1}(\boldsymbol{x}_{t})) \end{array} $$
$$\begin{array}{*{20}l} \boldsymbol{x}_{t}=f_{1}^{-1}\left(f_{2}^{-1}(\boldsymbol{z}_{t})\right) \end{array} $$
(4)

Without regard to the special structure of Toeplitz matrix, \(f_{2}^{-1}\) can be mathematically represented as Eq. 5. S k is a nonsingular matrix which has been defined in Eq. 2. In general, \(\boldsymbol {S}_{k}^{-1}\) is another nonsingular matrix R k which can be learned using a fully connected network layer independently. There are m frequency bins in total, so m parallel fully connected network layers are needed and the number of parameters is mT2.

$$ \boldsymbol{y}_{k}=\boldsymbol{z}_{k}\boldsymbol{S}_{k}^{-1}, 1\le k\le m $$
(5)

However, considering that S k is a Toeplitz matrix, R k can be represented in a simple way [40]. R k is given by Eq. 6, where A k , B k , \(\hat {\boldsymbol {A}}_{k}\) and \(\hat {\boldsymbol {B}}_{k}\) all are lower triangular Toeplitz matrices given by Eq. 7.

$$ \boldsymbol{R}_{k}=\frac{1}{a_{1}}\left(\boldsymbol{A}_{k}\boldsymbol{B}_{k}^{T}-\hat{\boldsymbol{B}}_{k}\hat{\boldsymbol{A}}_{k}^{T}\right) $$
(6)
$$\begin{array}{*{20}l} &\boldsymbol{A}_{k}= \left(\setlength{\arraycolsep}{2pt} \renewcommand{\arraystretch}{0.8} \begin{array}{cccc} a_{1} & 0 & \cdots & 0 \\ a_{2} & a_{1} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ a_{n} & a_{n-1} & \cdots & a_{1} \\ \end{array}\right), \hat{\boldsymbol{A}}_{k}= \left(\begin{array}{cccc} 0 & \cdots & 0 & 0 \\ a_{n} & \cdots & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots \\ a_{2} & \cdots & a_{n} & 0 \\ \end{array} \right)\\ &\boldsymbol{B}_{k}= \left(\setlength{\arraycolsep}{2pt} \renewcommand{\arraystretch}{0.8} \begin{array}{cccc} b_{n} & 0 & \cdots & 0 \\ b_{n-1} & b_{n} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ b_{1} & b_{2} & \cdots & b_{n} \\ \end{array}\right), \hat{\boldsymbol{B}}_{k}= \left(\begin{array}{cccc} 0 & \cdots & 0 & 0 \\ b_{1} & \cdots & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots \\ b_{n-1} & \cdots & b_{1} & 0 \\ \end{array} \right) \end{array} $$
(7)

Note that a and b can also be regarded as the solutions of two linear systems, which can be learned using a fully connected neural work layer. In this case, the number of parameters reduces from mT2 to 2mT.

In conclusion, the spectrogram reconstruction procedure can be implemented using a two-layer neural network. When the first layer is implemented as Eq. 5, the total number of parameters is mN+mT2. While when the first layer is represented as Eq. 6, the total number is mN+2mT. Experiments in Section 4.1 will show the difference between these two methods.

3 Training the models

As described in Section 2, the long-term filter banks we proposed here can be integrated into a neural network (NN) structure. The parameters of the models are learned jointly with the target of the specific task. In this section, we introduce two NN-based structures respectively for audio source separation and audio scene classification tasks.

3.1 Audio source separation

In Fig. 5a, the procedures of STFT and frequency filter banks in Fig. 2 are excluded from the NN structure because they are implemented empirically and have no parameters. The NN structure for audio source separation task is divided into four steps, in which three steps have been discussed in Section 2. The layers of long-term filter banks and inverse of long-term filter banks are implemented respectively as Eqs. 2 and 5, which can be denoted as h1 and h2. The reconstruction layer is constructed using a fully connected layer and can be denoted as h4.

Fig. 5
figure 5

NN-based structures with proposed method. a The NN structure for audio source separation task. b The NN structure for audio scene classification task

Full size image

We attempt the audio separation from an audio mixture using a simple masking method [41], which can be represented as the binary gating layer in Eq. 8 and denoted as h3. The output of this layer is a linear projection modulated by the gates g t . These gates multiply each element of the matrix Z and control the information passed on in the hierarchy. Stacking these four layers on the top of input Y gives a representation of the separated clean spectrogram \(\hat {\boldsymbol {X}}=h_{4}\circ h_{3}\circ h_{2}\circ h_{1}(\boldsymbol {Y})\).

$$ \begin{array}{l} g_{ti}=sigmoid\left(\sum_{j=1}^{N}z_{tj}v_{ji}\right) \\ o_{ti}=z_{ti}g_{ti} \\ \end{array} $$
(8)

Neural networks are trained on a frame error (FE) minimization criterion and the corresponding weights are adjusted to minimize the error squares over the whole training data set. The error of the mapping is given by Eq. 9, where x t is the targeted clean spectrogram and \(\hat {\boldsymbol {x}}_{t}\) is the corresponding separated representation. As commonly used, L2-regularization is typically chosen to impose a penalty on the complexity of the mapping, which is the λ term in Eq. 9. However, when the layer of long-term filter banks is implemented by Eq. 3, the elements of w1 have definitude physical meanings. Thus, L2-regularization is operated only on the upper three layers in this model. In this case, the network in Fig. 5a can be optimized by the back-propagation method.

$$ \epsilon=\sum_{t=1}^{T}\parallel \boldsymbol{x}_{t}-\hat{\boldsymbol{x}}_{t}\parallel^{2}+\lambda \sum_{l=2}^{4}\parallel \boldsymbol{w}_{l}\parallel^{2} $$
(9)

3.2 Audio scene classification

In early pattern recognition studies [42], the input is first converted into some features, which are usually defined empirically by experts and believed to be identified with the recognition targets. In Fig. 5b, a feature extraction structure including the long-term filter banks is proposed to systematically train the overall recognizer in a manner consistent with the minimization of recognition errors.

The NN structure for audio scene classification task can also be divided into four steps, where the first layer of long-term filter banks is implemented using Eq. 2. The convolutional layer and the pooling layer are conducted using the network structure described in [43]. In general, let zi:i+j refer to the concatenation of frames after long-term filter banks z i ,zi+1,...zi+j. The convolution operation involves a filter w∈Rhm, which is applied to a window of h frames to produce a new feature. For example, a feature c i is generated from a window of frames zi:i+h−1 by Eq. 10, where b∈R is a bias term and f is a non-linear function. This filter is applied to each possible window of frames to produce a feature map c=[c1,c2,...cT−h+1]. Then a max-overtime pooling operation [44] over the feature map is applied and the maximum value \(\hat {c}=\text {max}(\boldsymbol {c})\) is taken as the feature corresponding to this filter. Thus one feature is extracted using one filter. This model uses multiple filters with varying window sizes to obtain multiple features.

$$ c_{i}=f(\boldsymbol{w}\cdot \boldsymbol{z}_{i:i+h-1}+b) $$
(10)

The features extracted from the convolutional and pooling layers are then passed to a fully connected softmax layer to output the probability distribution over categories. The classification loss of this model is given by Eq. 11, where n is the number of audios, k is the number of categories, y is the category labels and p is the probability distribution produced by the NN structure. In this case, the network in Fig. 5b can be optimized by the back-propagation method.

$$ \epsilon=\sum_{i=1}^{n}\sum_{j=1}^{k}y_{i,j}\cdot log(p_{i,j})+\lambda \sum_{l=2}^{4}\parallel \boldsymbol{w}_{l}\parallel^{2} $$
(11)

4 Experiments

To illustrate the properties and performance of long-term filter banks proposed in this paper, we conduct two groups of experiments respectively on audio source separation and audio scene classification. To achieve a fair comparison with traditional frequency filter banks, all experiments conducted in this section utilize the same settings and structures except for the items listed below.

  • Models: The models tested in this section are different from each other in two aspects. The variants of frequency filter banks include TriFB and GaussFB, as described in Section 2. For long-term filter banks, Gaussian shape-constrained filters introduced in Section 2.2 are named GaussLTFB and totally independent filters are named FullLTFB. The baseline of our experiments has no long-term filter banks, which is labelled as Null. The initials of the names are used to differentiate models. For example, when TriFB and FullLTFB are used in the model, the model is named TriFB-FullLTFB.

  • Initialization: When we use totally independent filters as the long-term filter banks, two initialization methods discussed in Section 2.2 are tested in this section. When the parameters are initialized randomly, the method is named Random, while when the parameters are initialized using an identity matrix, the method is named Identity.

  • Reconstruction: When the spectrogram reconstruction is implemented as Eq. 5, the method is named Re_inv, while when the reconstruction is implemented as Eq. 6, the method is named Re_toep.

In all experiments, the audio signal is first transformed using short-time Fourier transform with a frame length of 1024 and a frameshift of 220. The number of frequency filters is set to be 64; the detailed settings of NN structures are shown in Fig. 5. All parameters in the neural network are trained jointly using Adam [45] optimizer; the learning rate is initialized with 0.001.

4.1 Audio source separation

In this experiment, we investigate the application of long-term filter banks in audio source separation task using the MIR-1K dataset [46]. The dataset consists of 1000 song clips recorded at a sample rate of 16kHz, with durations ranging from 4 to 13 s. The dataset is then utilized with 4 training/testing splits. In each split, 700 of the examples are randomly selected for training and the others for testing. We use the mean average accuracy over the 4 splits as the evaluation criterion. In order to achieve a fair comparison, we use this dataset to create 3 sets of mixtures. For each clip, we mix the vocal and music track under various conditions, where the energy ratio between music and voice takes 0.1, 1 and 10 respectively.

We first test our methods on the outputs of frequency filter banks. In this case, the combination of classical frequency filter banks and our proposed temporal filter banks work as two-dimensional filter banks on magnitude spectrograms. Classical CNN models can learn two-dimensional filters on spectrograms directly. Thus we introduce a 1-layer CNN model as a comparison. The CNN model is implemented as [22], but the convolutional layer here is composed of learnable parameters, instead of constant Gaussian lateral connectivity in [22]. This convolution layer works as a two-dimensional filter whose size is set to be 5×5, the outputs of this layer is then processed as Fig. 5a. We use the NN model in [47] and the one-layer CNN model as our baseline models. For our proposed long-term filter banks, we test two variant modules: GaussLTFB and FullLTFB which have been defined at the beginning of Section 4. For FullLTFB situation, two initialization methods discussed in Section 2.2 are tested respectively. The three variant modules GaussLTFB, FullLTFB-Random and FullLTFB-Identity can be utilized on two types of frequency filter banks TriFB and GaussFB respectively, thus a total of six long-term filter banks related experiments are conducted in this part.

Table 1 shows the results of these experiments. From the results, we can get conclusions as follows. First, the best results in the table are obtained using long-term filter banks, which demonstrates the effectiveness of our proposal, especially when the energy of interference is larger than music. As an example, when we use gaussian frequency filter banks and the energy ratio between music and voice is 1, the reconstruction error is reduced by relatively 6.7% by using Gaussian shape-constrained long-term filter banks. Second, totally independent filters are severely influenced by the initialization. When the parameters are initialized using an identity matrix, the performance is close to the Gaussian shape-constrained filters in this task. However, when the parameters are initialized randomly, the reconstruction error seems to be unable to converge effectively. This result has to do with the task itself, which will be further tested in Section 4.3. Then, the one-layer CNN model improves the performance only when the energy ratio between music and voice is 0.1, this can be attributed to the local sensitivity of reconstruction task. As a matter of fact, the time durations of long-term filter banks in most frequency bins we learned here are 1. Thus, the convolution size 5×5 is too large. Finally, Toeplitz inversion motivated reconstruction algorithm performs much better than the direct inverse matrix algorithm. When the direct inverse matrix algorithm is utilized, the performance of our proposal of long-term filter banks becomes even worse than the frequency filter banks.

Table 1 Reconstruction error of audio source separation using frequency filter banks as input
Full size table

We now test our methods on magnitude spectrograms as described in [47]. In this situation, long-term filter banks are used as one-dimensional filter banks to extract temporal information. The size of magnitude spectrograms is 513×128. The settings of NN structures in Fig. 5a are modified correspondingly to adapt to this size. We also use the NN model in [47] and the 1-layer CNN model as our baseline models. The three variant modules GaussLTFB, FullLTFB-Random and FullLTFB-Identity are utilized on magnitude spectrograms directly in this part.

The results of these experiments are shown in Table 2. Compared with the results in Table 1, all the conclusions above remain unchanged. When the energy ratio between music and voice is 1, the reconstruction error is reduced by relatively 5.0% by using Gaussian shape-constrained long-term filter banks, this effect is less obvious than the result in Table 1. This is because that the information of magnitude spectrograms is too rich, so the performance of the simplest NN model is also good. But when the energy of interference is larger than music, the effectiveness of our long-term filter banks is obvious.

Table 2 Reconstruction error of audio source separation using magnitude spectrograms as input
Full size table

A direct perspective of the separation results can be seen in Fig. 6. The figure shows the clean music spectrogram (a), mixed spectrogram (b) and the separated spectrogram (c–e) when the energy ratio is 1. For this example, (c) is the separated spectrogram from GaussFB-Null which has been defined at the beginning of this section, (d) is the separated spectrogram from GaussFB-GaussLTFB and (e) is the separated spectrogram from GaussFB-FullLTFB. When compared with (c), the results of our proposal of long-term filter banks (d) and (e) show significant temporal coherence in each frequency bin, which is more approximate to the clean music spectrogram in (a).

Fig. 6
figure 6

Reconstructed spectrogram of audio source separation task. The clean music spectrogram in a is randomly selected from the dataset. b The corresponding music and vocal mixture. c–e The reconstructed music spectrograms from the mixture spectrogram using different configurations

Full size image

4.2 Audio scene classification

In this section, we apply the long-term filter banks to the audio scene classification task. We employ LITIS ROUEN dataset [48] and DCASE2016 dataset [49] to conduct acoustic scene classification experiments.

Details of these datasets are listed as follows.

  • LITIS ROUEN dataset: This is the largest publicly available dataset for ASC to the best of our knowledge. The dataset contains about 1500 min of acoustic scene recordings belonging to 19 classes. Each audio recording is divided into 30-s examples without overlapping, thus obtain 3026 examples in total. The sampling frequency of the audio is 22,050 Hz. The dataset is provided with 20 training/testing splits. In each split, 80% of the examples are kept for training and the other 20% for testing. We use the mean average accuracy over the 20 splits as the evaluation criterion.

  • DCASE2016 dataset: The dataset is released as Task 1 of the DCASE2016 challenge. We use the development data in this paper. The development data contains about 585 min of acoustic scene recordings belonging to 15 classes. Each audio recording is divided into 30-s examples without overlapping, thus obtain 1170 examples in total. The sampling frequency of the audio is 44,100 Hz. The dataset is divided into fourfold. Our experiments obey this setting, and the average performance will be reported.

For both datasets, the examples are 30 s long. In the data preprocessing step, we first divide the 30-s examples into 1-s clips with 50% overlap. Then each clip is processed using neural networks as Fig. 5b. The classification results of all these clips will be averaged to get an ensemble result for the 30-s examples. The size of audio spectrograms is 64×128. For CNN structure in Fig. 5b, the window sizes of convolutional layers are 64×2×64, 64×3×64 and 64×4×64, the fully connected layers are 196×128×19(15). For DCASE2016 dataset, we use dropout rate of 0.5. For all these methods, the learning rate is 0.001, l2 weight is 1e−4, training is done using the Adam [45] update method and is stopped after 100 training epochs. In order to compute the results for each training-test split, we use the classification error over all classes. The final classification error is its average value over all splits.

We begin with experiments where we train different neural network models without long-term filter banks on both datasets. As described at the beginning of Section 4, our baseline systems take the outputs of frequency filter banks as input. TriFB and GaussFB are placed in the frequency domain to integrate the frequency information. Classical CNN models have the ability to learn two-dimensional filters on the spectrum directly. We introduce two CNN structures as a comparison. The first CNN model is implemented as [50], which has multiple convolutional layers, pooling layers, and fully connected layers. The window size of convolutional kernels are 5×5, the pooling size is 3, the output channels are [8, 16, 23], the fully connected layers are 196×128×19(15). Another CNN structure is the same as the one-layer CNN model described in Section 4.1, the outputs of this model is then processed as Fig. 5b.

The results of these experiments are shown in Table 3. Comparing with other CNN related works, our baseline models on both datasets achieve gains in accuracy. On LITIS Rouen dataset, recurrent neural network (RNN) [26] performs better than our baseline models, because of the powerful sequence modelling capabilities of RNN. DNN model in [51] is the best-performing single model on both datasets, this can be attributed to the lack of training data and the stability of Constant Q-transform (CQT) [52] feature representations. On DCASE2016 dataset, only DNN model using CQT features performs better than our baseline models. Classical CNN model with three layers performs almost the same as [24] on LITIS Rouen dataset, but gets a rapid deterioration of performance on DCASE2016 dataset. This can also be attributed to the lack of training data, especially on DCASE2016 dataset. CNN model with one convolutional layer performs a little better, but still worse than our baseline models. These results show that the time-frequency structure of the spectrum is difficult to be learned using two-dimensional convolution kernels in classical CNN models. For the two baseline models, GaussFB performs better than TriFB on both datasets, because of that Gaussian frequency filter banks can extract more global information. In conclusion, the results of our baseline models are in line with expectations on both datasets.

Table 3 Average performance comparison with related works on LITIS Rouen dataset and DCASE2016 dataset
Full size table

We now test our long-term filter banks on both datasets. We also test three variant modules in this part: GaussLTFB, FullLTFB-Random and FullLTFB-Identity. These three variant modules can be injected into neural networks directly as Fig. 5b.

Table 4 is the performance comparison on both datasets. Models with GaussLTFB module perform consistently better than the corresponding baseline models. Although the performance fluctuates for different variants, the performance gain is obvious. For FullLTFB situation, random initialization obtains performance gain on both datasets, but identity initialization degrades the performance on DCASE2016 dataset. This can be attributed that in classification tasks, we need to extract a global representation of all frames, more details will be discussed in Section 4.3. On LITIS Rouen dataset, TriFB-GaussLTFB model performs significantly better than the state-of-the-art result in [51] and obtains 2.82% on classification error. On DCASE2016 dataset, GaussFB-FullLTFB model with random initialization reduces the classification error by relatively 6.5% and reaches the performance of DNN model using CQT features in [51], meaning that the long-term filter banks make up for the lack of feature extractions.

Table 4 Average performance comparison using different configurations on LITIS Rouen dataset and DCASE2016 dataset
Full size table

Validation curves on both datasets are shown in Fig. 7. After 100 training epochs, experiments on DCASE2016 dataset encounter overfitting problem; experiments on LITIS ROUEN dataset have almost converged. Figure 7c, e shows that the performance of classical CNN model is significantly worse than models with only the frequency filter banks, which is consistent with the results in Table 3. The performance of one-layer CNN model is between TriFB and GaussFB models on both datasets. Figure 7a–e shows consistent results with Table 4.

Fig. 7
figure 7

Validation curves on LITIS ROUEN dataset and DCASE2016 dataset. a, b The proposed methods on LITIS ROUEN dataset. d, e The proposed methods on DCASE2016 dataset. c The classical CNN nodels on LITIS ROUEN dataset. f The classical CNN nodels on DCASE2016 dataset

Full size image

4.3 Reconstruction vs classification

In the experiment of audio source separation task, when the parameters of totally independent long-term filter banks are initialized randomly, the result seems to be unable to converge effectively. However, it is completely the opposite in audio scene classification task.

Figure 8 is an explanation of the unconformity between the above two tasks. Figure 8a, b is the filters learned on MIR-1K dataset. At low frequencies, the time duration of filters are almost equal to 1, only at very high frequencies, the time durations become large. But for Fig. 8c, d which is learned on DCASE2016 dataset, the time duration is much larger. It is intuitive that in audio source separation task, the time duration of the filters is much smaller than in audio scene classification task, especially at low frequencies. When the parameters of totally independent long-term filter banks are initialized randomly, the implicit assumption is that the time durations of the filters is as large as the number of all frames, which is not applicable. In reconstruction related tasks, for example, the long-term correlation is much more limited because our goal is to reconstruct the spectrogram frame by frame. However, in classification tasks, we need to extract a global representation of all frames, which is exactly in line with our hypothesis.

Fig. 8
figure 8

Time durations of long-term filter banks in different tasks. a, b The long-term filters learned on MIR-1K dataset. c, d The long-term filters learned on DCASE2016 dataset

Full size image

5 Conclusions

A novel framework of filter banks that can extract long-term time and frequency correlation is proposed in this paper. The new filters are constructed after traditional frequency filters and can be implemented using Toeplitz matrix motivated neural networks. Gaussian shape constraint is introduced to limit the time duration of the filters, especially in reconstruction-related tasks. Then a spectrogram reconstruction method using the Toeplitz matrix inversion is implemented using neural networks. The spectrogram reconstruction error in audio source separation task is reduced by relatively 6.7% and the classification error in audio scene classification task is reduced by relatively 6.5%. This paper provides a practical and complete framework to learn long-term filter banks for different tasks.

The former frequency filter banks are somehow interrelated with the long-term filter banks. Combining the idea of these two types of filter banks, future work will be an investigation on two-dimensional filter banks.