A robust fusion estimation with unknown cross-covariance in distributed systems

Abstract

An efficient robust fusion estimation (RFE) for distributed fusion system without knowledge of the cross-covariances of sensor estimation errors is suggested. With the hypothesis that the object lying in the intersection of some ellipsoids related to sensor estimations, the robust fusion estimation is designed to be a minimax problem, which is solved by proposing a novel relaxation strategy. Some properties of the RFE are discussed, and numerical simulations are also present to compare the tracking performance of RFE with that of the centralized fusion and CI method. The numerical examples show that the average tracking performance of RFE is slightly better than that of the CI method, and the performance degradation of RFE is acceptable compared with the centralized fusion.

1 Introduce

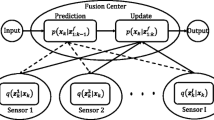
In recent years, multisensor information fusion has received significant attention for both military and civilian applications. The fusion center integrates information from multiple sensors to achieve improved accuracies and system survivability than could be achieved by the use of a single sensor alone. If the communication channel and processor bandwidth are not constrained, then all observations from local sensors can be transmitted to a central processor for fusing. In this case, there is no preprocessing in each sensor, and the local sensors only act as simple observers. Therefore, the multisensor fusion system can be viewed as a single sensor system in nature, and conventional optimal methods can be implemented (see [20]). Such a multisensor fusion is called the centralized fusion. Clearly, the centralized fusion has the best performance since all observations are used. However, in many practical applications, processing all sensor measurements at a single location is sometimes infeasible due to communication or reliability constraints. So one may require that a preprocessing is performed at the individual sensors and a compressed sensor data is transmitted to the fusion center. Accordingly, we call this multisensor fusion the distributed fusion or decentralized fusion. In a distributed fusion system, the sensors will form sensor tracks from the measurements and communicate the tracks with other sensors or processors. The tracks are then associated and the estimates of associated tracks are fused in the fusion center. Many distributed fusion architectures have been proposed over the years.

With the assumption that the cross-covariance of the errors of local estimators is known, Bar-Shalom and Campo proposed a track-to-track fusion for two-sensor distributed estimation systems. The analysis of the optimality of the fusion formulae is given in [2]. For the system with l local sensors, the fusion equations presented in [8] and [10] use the fusion center’s one-step prediction as well as the l sensors’ state estimates and their one-step predictions to obtain a final fusion. Moreover, they proved rigorously that the presented fusion formulae can be converted equivalently from the corresponding centralized Kalman filtering. Recently, the best linear unbiased estimation (BLUE) (see, e.g., [12, 18]) was proposed, and a general version of the linear minimum variance of estimation fusion rule is derived. The above two estimation fusion methods turn into the special cases of BLUE fusion method with some appropriate assumptions. The BLUE fusion method relies on two assumptions: (1) the local estimators are unbiased; (2) the error covariance matrix of the sensor estimates at each time is known. The cross-covariance of estimation errors is the key to optimally fuse the sensor estimates in the distributed estimation systems, but it is very difficult to realize in many practical applications.

Over the last three decades, many works have been performed to design different appropriate distributed fusion estimations with unknown cross-covariance of estimation errors. Considering a distributed fusion system, when there exist some uncertainties in state equation or sensor observation equations, some researchers seek to design robust distributed fusion estimation by modeling the uncertainties appropriately (including deterministic and stochastic uncertainties, see [5, 6], and references therein). When the state equation and sensor observation equations are unavailable, and only the sensors estimators are given, the well-known covariance intersection (CI) filter (see [7, 11, 13]) is designed to fuse sensor estimates without cross-covariance of sensor estimators. The objective of CI filter is to obtain a consistent estimation of the covariance matrix when two estimates are linearly combined, where “consistent” means the estimated covariance is always an “upper-bound” (in the positive-definite sense) of the true covariance. The CI filter is more robust than the linear combination algorithm and provides a bound on the estimation accuracy. Therefore, the CI algorithm has been widely applied in the area of distributed estimation. However, the CI method has some obviously disadvantages: (1) it designs the estimator to be linear form of local sensor estimates; (2) the parameter to be optimized is a scalar although the estimated state may be a multiple dimensional vector.

Recently, different strategies are proposed to fuse sensor estimators without complete knowledge of the cross-covariance matrix. A formulation is proposed in [9] to restrict the set of possible cross-covariance matrices, then an optimal robust fusion method is presented in the minimax sense via semi-definite programming. The work in [1] provides a deeper insight into the suboptimality of the covariance intersection fusion of multiple estimates under unknown correlations. In reference [17], the authors generalize the covariance intersection algorithm for distributed estimation and information fusion of random vectors.

In this paper, inspired by the idea of set-membership filtering, which seeks to compute a compact feasible set in which the true state or parameter lies (see [4, 14]), we consider the problem to fuse local estimates by directly maximizing the estimation error on some set given by the prior knowledge, then select the optimal estimation to minimize it. Compared with the works in references [1, 9, 17], all the methods are presented to fuse sensor estimators with unknown cross-correlation. However, the strategies employed to design robust fusion estimation are different. In [1, 9, 17], the authors seek to design the upper bound of the cross-covariance, then robust fusion estimations are proposed based on different optimization methods. In this paper, we suppose that the true state lies in a compact feasible set, then we model it as a non-convex optimization problem with the minimax strategy, and propose a novel relaxation strategy to approximatively solve the non-convex problem. The prominent merits of the presented robust optimal fusion estimation (RFE) includes (1) instead of optimizing the trace of the estimation error covariance, we directly minimize the estimation error; (2) the fused estimator is a non-linear combination of local estimators; (3) the presented methods can be used to fusion multiple sensors directly; (4) the average tracking performance of the RFE is slightly better than that of the CI filter in our simulations.

This paper is organized as follows. A brief introduction of the CI filter are given in Section 2. Then the RFE is proposed in Section 3, and some properties the RFE are also discussed. Section 4 provided a number of simulations to show the performances of the presented method. Finally, Section 5 gives a conclusion.

2 The CI filter

The CI filter provides a mechanism for fusing two estimates of the mean value of a random variable when the correlation between the estimation errors is unknown. The following notations are followed from [7]. Let c^∗∈R^n×1 be the mean of some random variable to be estimated. Two sources of information are available: estimate a∈R^n×1 and estimate b∈R^n×1. Define their estimation errors as

$$\tilde{a}=a-c^{*},\ \ \tilde{b}=b-c^{*},$$

and suppose

$$E(\tilde{a})=0, E(\tilde{b})=0, E\left(\tilde{a}\tilde{a}^{T}\right)=\tilde{P}_{aa}, E\left(\tilde{b}\tilde{b}^{T}\right)=\tilde{P}_{bb}.$$

The true values of $\tilde {P}_{aa}$ and $\tilde {P}_{bb}$ may be unknown, but some consistent estimates P_aa∈R^n×n and P_bb∈R^n×n of $\tilde {P}_{aa}$ and $\tilde {P}_{bb}$ are obtainable respectively with properties

$$P_{aa}\succeq \tilde{P}_{aa},\ \ P_{bb}\succeq \tilde{P}_{bb}, $$

where the notation “ A≽B” means that the matrix A−B is positive semi-definite. The cross-covariance between the two estimation $E\left (\tilde {a}\tilde {b}^{T}\right)=\tilde {P}_{ab}$ is also unknown.

Firstly, the CI method proposes a linear unbiased estimator

$$c = K_{1}a+K_{2}b, $$

where K₁,K₂∈R^n×n,K₁+K₂=I. Let $\tilde {c}=c-c^{*}$, then the covariance of $\tilde {c}$ is

$$\begin{array}{@{}rcl@{}} \tilde{P}_{cc} &&= E\left(\tilde{c}\tilde{c}^{T}\right)\\ &&= K_{1}\tilde{P}_{aa}K_{1}^{T}+K_{2}\tilde{P}_{bb}K_{2}^{T}+K_{1}\tilde{P}_{ab}K_{2}^{T} +K_{2}\tilde{P}_{aa}^{T}K_{1}^{T}. \end{array} $$

Secondly, it tries to find a consistent estimator P_cc of $\tilde {P}_{cc}$, such that $P_{cc}\succeq \tilde {P}_{cc}$. It is easy to find a kind of consistent estimators in following form

$$P_{cc}=(1+\gamma)K_{1}P_{aa}K_{1}^{T}+\left(1+\frac{1}{\gamma}K_{2}P_{bb}K_{2}^{T}\right),\quad \gamma>0.$$

Finally, the CI estimator is derived by minimizing the trace of P_cc which is given as follows.

Theorem 1

(Theorem 2 in [7]) There exists ω∈[0,1] such that

$$\sqrt{\text{Tr}\left(K_{1}P_{aa}K_{1}^{T}\right)}+\sqrt{\text{Tr}\left(K_{2}P_{bb}K_{2}^{T}\right)},\quad K_{1}+K_{2}=I,$$

is minimized by

$$\begin{array}{@{}rcl@{}} &&P_{cc}= \left(\omega P_{aa}^{-1} + (1 - \omega) P_{bb}^{-1}\right)^{-1},\\ &&K_{1}= \omega P_{cc} P_{aa}^{-1}, K_{2}=\omega P_{cc}P_{bb}^{-1}. \end{array} $$

Therefore, the CI estimator is $a\omega P_{cc}P_{aa}^{-1}+b\omega P_{cc}P_{bb}^{-1}$.

3 The robust fusion estimation

In a distributed system with l sensors, let x_k∈Rⁿ is a deterministic parameter vector to be estimated. Suppose $\hat {x}_{k}^{(i)},i=1,\ldots, l$ are sensor estimators of x_k at time k, and we have the prior information that the state x_k lies in the non-empty intersection of l ellipsoids $S_{k}^{(i)}$defined by

$${}S_{k}^{(i)}\,=\,\left\{\!x_{k}:\left(\!x_{k}-\hat{x}_{k}^{(i)}\!\right)^{T} \!\bar{P}_{k}^{(i)}\left(x_{k}-\hat{x}_{k}^{(i)}\right)\leq a_{i},i=1,\ldots,l\right\},$$

where $P_{k}^{(i)}$ are some known positive semi-definite matrices, and a_i is a positive scalar. It is easy to standardize the ellipsoids as

$$S_{k}^{(i)}=\{x_{k}:(x_{k}-\hat{x}_{k}^{(i)})^{T} P_{k}^{(i)}(x_{k}-\hat{x}_{k}^{(i)})\leq 1,i=1,\ldots,l\}.$$

When the fusion central receives l sensor estimators and the ellipsoids $S_{k}^{(i)},i=1,\ldots, l$, they should be fused to obtain optimal fusion estimation. Therefore, we first maximize the estimation error over the intersection of $S_{k}^{(i)}$, then choose the fusion estimate $\hat {x}_{k}$ to minimize the estimation error. Finally, the fusion estimation is designed to solve the following minimax problem:

$$\begin{array}{@{}rcl@{}} &&\min_{\hat{x}_{k}}\max_{x_{k}\in \bigcap_{i=1}^{l}S_{k}^{(i)}}\|x_{k}-\hat{x}_{k}\|_{2}^{2}. \end{array} $$

(1)

Generally speaking, problem (1) is an NP-hard problem when l≥2. In the sequel, we seek for approximation solution of problem (1) by designing a convex relaxation strategy.

The following lemmas are necessary for further derivation.

Lemma 1

(see [15]) Let X be an symmetric matrix partitioned as

$$X=\left(\begin{array}{cc} X_{1} & X_{2} \\ X_{2}' & X_{3} \\ \end{array} \right). $$

Then X>0 if and only if $X_{3}-X_{2}'X_{1}^{-1}X_{2}>0$. Furthermore, if X₁>0, then X≥0 if and only if $X_{3}-X_{2}'X_{1}^{-1}X_{2}\geq 0$.

Lemma 2

Let ε,γ_i be non-negative scalars, z and B_i be any compatible vector and Hermitian matrices, i=1,…,l. Then the following inequality holds for any vector y and scalar t

$$\begin{array}{@{}rcl@{}} \epsilon t^{2} + \sum_{i = 1}^{l} \gamma_{i} y^{T} B_{i} y - (y^{T} y - 2 t y^{T} z) \geq 0, \end{array} $$

(2)

if and only if

$$\begin{array}{@{}rcl@{}} \left(\begin{array}{cc} \epsilon & z^{T} \\ z & \sum\limits_{i = 1}^{l}\gamma_{i} B_{i} - I\\ \end{array} \right)\geq 0. \end{array} $$

(3)

Furthermore, if (2) or (3) holds, then

$$ {\begin{aligned} \max_{y, t} &\left\{y^{T} y - 2t y^{T} z : y^{T} B_{i} y \leq 1, i = 1, \ldots, l, t^{2} \leq 1\right\} \\ &\quad\leq \epsilon + \sum_{i = 1}^{l}\gamma_{i}. \end{aligned}} $$

(4)

Proof

Note that (3) is equivalent to

$$\left(\begin{array}{c} t \\ y \\ \end{array} \right)^{T} \left(\begin{array}{cc} \epsilon & z^{T} \\ z & \sum\limits_{i = 1}^{l} \gamma_{i} B_{i} - I \\ \end{array} \right) \left(\begin{array}{c} t \\ y \\ \end{array} \right) \geq 0 $$

holds for any vector y and scalar t, which implies the equivalence between (2) and (3). At the same time, from (2),

$$\begin{array}{@{}rcl@{}} y^{T} y - 2t y^{T} z \leq \epsilon t^{2} + \sum_{i = 1}^{l} \gamma_{i} y^{T} B_{i} y. \end{array} $$

Obviously,

$${{} \begin{aligned} \max_{y, t} &\left\{\epsilon t^{2} + \sum_{i = 1}^{l} \gamma_{i} y^{T} B_{i} y: y^{T} B_{i} y \leq 1, i = 1, \ldots, l, t^{2} \leq 1\right\} \\&\quad\leq \epsilon + \sum_{i = 1}^{l} \gamma_{i}. \end{aligned}} $$

Therefore, (4) follows from (2).

A positive semi-definite relaxation of problem (1) is presented in the following theorem, which can be solved by some efficient semidefinite programming solvers such as SeDuMi (see [16]). □

Theorem 2

The positive semi-definite relaxation of the optimal problem (1) is

$$\begin{array}{@{}rcl@{}}{} &&\min_{\epsilon \geq 0,\gamma_{i}\geq 0, \tau\geq 0, \hat{x}_{k},\alpha_{k}^{(i)}} \tau\\ && {}s.t.\left(\begin{array}{ccc} \epsilon & 0 & \left(\sum_{i=1}^{l}\alpha_{k}^{(i)}\hat{x}_{k}^{(i)}-\hat{x}_{k}\right)^{T} \\ 0 & \sum_{i=1}^{l}\gamma_{i} Q_{k}^{(i)} & \left(\sum_{i=1}^{l}\alpha_{k}^{(i)}A_{k}^{(i)}\right)^{T} \\ \sum_{i=1}^{l}\alpha_{k}^{(i)}\hat{x}_{k}^{(i)}-\hat{x}_{k} & \sum_{i=1}^{l}\alpha_{k}^{(i)}A_{k}^{(i)} & I \\ \end{array} \right)\!\geq\! 0~~ \\ &&{\text{and}}~~~~~~~~ \epsilon+\sum_{i=1}^{l}\gamma_{i}\leq \tau,\sum_{i=1}^{l}\alpha_{k}^{(i)}=1, \end{array} $$

(5)

where $A_{k}^{(i)}=(0,\ldots,I\ldots,0)_{n\times nl}, Q_{k}^{(i)}=\left (A_{k}^{(i)}\right)^{T} P_{k}^{(i)}A_{k}^{(i)}, i=1,\ldots,l$. The optimal fusion estimation $\hat {x}_{k}$ is given by the solution of the SDP problem (5).

Proof

Note that problem (1) is the same as

$$\begin{array}{@{}rcl@{}} &&\min_{\hat{x}_{k},\tau>0}\tau \\ &&s.t. ~\|x_{k}-\hat{x}_{k}\|_{2}^{2}\leq \tau ~~ {\text{and}} \\ &&~~\left(x_{k}-\hat{x}_{k}^{(i)}\right)^{T} P_{k}^{(i)}\left(x_{k}-\hat{x}_{k}^{(i)}\right)\leq 1,i=1,\ldots,l. \end{array} $$

(6)

Denoted by

$$\begin{array}{*{20}l} {}\eta_{k}^{(i)}&=x_{k}-\hat{x}_{k}^{(i)},\eta_{k}=\left(\begin{array}{c} \eta_{k}^{(1)} \\ \ldots \\ \eta_{k}^{(l)} \\ \end{array} \right),\\ A_{k}^{(i)}&=(0,\ldots,I\ldots,0)_{n\times nl},i=1,\ldots,l, \end{array} $$

then $\eta _{k}^{(i)}=A_{k}^{(i)}\eta _{k},i=1,\ldots,l$. For any real scalars $\alpha _{k}^{(i)},i=1,\ldots, l$ satisfy $\sum \limits _{i=1}^{l}\alpha _{k}^{(i)}=1$, let

$$\zeta_{k}=\sum_{i=1}^{l} \alpha_{k}^{(i)}\hat{x}_{k}^{(i)}.$$

Note that the ζ_k is not the linear combination of local estimator $\hat {x}_{k}^{(i)}$, unless the $\alpha _{k}^{(i)}$ is independent of local estimators $\hat {x}_{k}^{(i)}$. In fact, the $\alpha _{k}^{(i)}$ is given by the optimal problem (1), thus it is not independent of $\hat {x}_{k}^{(i)}$. Therefore, problem (6) is the same as

$$\begin{array}{@{}rcl@{}} &&\min_{\hat{x}_{k},\tau>0}\tau \\ &&s.t. ~\|x_{k}-\zeta_{k}+\zeta_{k}-\hat{x}_{k}\|_{2}^{2}\leq \tau ~~ {\text{and}} \\ &&~~\eta_{k}^{T} \left(A_{k}^{(i)}\right)^{T}P_{k}^{(i)}A_{k}^{(i)}\eta_{k}\leq 1,i=1,\ldots,l. \end{array} $$

(7)

Let $\beta _{k}=\zeta _{k}-\hat {x}_{k}, Q_{k}^{(i)}=(A_{k}^{(i)})^{T} P_{k}^{(i)}A_{k}^{(i)}$, so $x_{k}-\zeta _{k}=\sum _{i=1}^{l}\alpha _{k}^{(i)}A_{k}^{(i)}\eta _{k}$. Denote $A_{k}=\sum _{i=1}^{l}\alpha _{k}^{(i)}A_{k}^{(i)}$, then problem (7) is equivalent to

$$\begin{array}{@{}rcl@{}} &&\min_{\hat{x}_{k},\tau>0}\tau \\ &&s.t. ~\|A_{k}\eta_{k}+\beta_{k}\|_{2}^{2}\leq \tau ~~ {\text{and}} \\ &&~~\eta_{k}^{T}Q_{k}^{(i)}\eta_{k}\leq 1,i=1,\ldots,l. \end{array} $$

(8)

Considering the constrains of problem (8), it is the same as

$$\max_{\eta_{k}}\{\|A_{k}\eta_{k}+\beta_{k}\|_{2}^{2}:\eta_{k}^{T}Q_{k}^{(i)}\eta_{k}\leq 1,i=1,\ldots,l\}\leq \tau.$$

Equivalently,

$${}\begin{aligned} \max_{\eta_{k},t}\left\{\|A_{k}t\eta_{k}+\beta_{k}\|_{2}^{2}:\eta_{k}^{T}Q_{k}^{(i)}\eta_{k}\leq 1,i=1,\ldots,l,t^{2}\leq 1\right\}\leq \tau, \end{aligned} $$

which can be reformulated to

$$\begin{array}{*{20}l} &\max_{\eta_{k},t}\left\{(A_{k}\eta_{k})^{T} A_{k}\eta_{k}+2t(A_{k}\eta_{k})^{T}\beta_{k}:\eta_{k}^{T}Q_{k}^{(i)}\eta_{k}\right.\\ &\qquad\left.\leq 1,i=1,\ldots,l,t^{2}\leq 1{\vphantom{Q_{k}^{(i)}}}\right\}\\ &\qquad\leq \tau-\beta_{k}^{T}\beta_{k}. \end{array} $$

(9)

From Lemma 2, for non-negative scalars γ,γ_i,i=1,…,l, the constrains

$$\begin{array}{@{}rcl@{}} \left(\begin{array}{cc} \gamma & -\beta_{k}^{T}A_{k} \\ -(\beta_{k}^{T}A_{k})^{T} & \sum_{i=1}^{l}\gamma_{i} Q_{k}^{(i)}-A_{k}^{T}A_{k} \\ \end{array} \right)\geq 0 \end{array} $$

(10)

and

$$\begin{array}{@{}rcl@{}} && \gamma +\sum_{i=1}^{l}\gamma_{i}\leq \tau-\beta_{k}^{T}\beta_{k} \end{array} $$

are sufficient for (9) holding. Let $\epsilon =\gamma +\beta _{k}^{T}\beta _{k}$, then (10) can be rewritten as

$$\begin{array}{@{}rcl@{}} \left(\begin{array}{cc} \epsilon & 0 \\ 0 & \sum_{i=1}^{l}\gamma_{i}Q_{k}^{(i)} \\ \end{array} \right)- \left(\begin{array}{cc} \beta_{k}^{T}\beta_{k} & \beta_{k}^{T}A_{k} \\ (\beta_{k}^{T}A_{k})^{T} & A_{k}^{T}A_{k} \\ \end{array} \right) \geq 0. \end{array} $$

From Lemma 1, which is equivalent to

$$\begin{array}{@{}rcl@{}} &&\left(\begin{array}{ccc} \epsilon & 0 & \beta_{k}^{T} \\ 0 & \sum_{i=1}^{l}\gamma_{i}Q_{k}^{(i)} & A_{k}^{T} \\ \beta_{k} & A_{k} & I \\ \end{array} \right)\geq 0. \end{array} $$

Therefore, we can relax the problem (8) to be the following SDP problem:

$$\begin{array}{@{}rcl@{}} &&\min_{\epsilon \geq 0,\gamma_{i}\geq 0, \tau\geq 0, \beta_{k},\alpha_{k}^{(i)}} \tau\\ && s.t.\left(\begin{array}{ccc} \epsilon & 0 & \beta_{k}^{T} \\ 0 & \sum_{i=1}^{l}\gamma_{i}Q_{k}^{(i)} & A_{k}^{T} \\ \beta_{k} & A_{k} & I \\ \end{array} \right)\geq 0~~ {\text{and}}\\ &&~~~~~~~~\epsilon+\sum_{i=1}^{l}\gamma_{i}\leq \tau,\sum_{i=1}^{l}\alpha_{k}^{(i)}=1 \end{array} $$

which is equivalent to

$$\begin{array}{@{}rcl@{}} &&\min_{\epsilon \geq 0,\gamma_{i}\geq 0, \tau\geq 0, \hat{x}_{k},\alpha_{k}^{(i)}} \tau\\ && s.t.\left(\begin{array}{ccc} \epsilon & 0 & (\sum_{i=1}^{l}\alpha_{k}^{(i)}\hat{x}_{k}^{(i)}-\hat{x}_{k})^{T} \\ 0 & \sum_{i=1}^{l}\gamma_{i}Q_{k}^{(i)} & (\sum_{i=1}^{l}\alpha_{k}^{(i)}A_{k}^{(i)})^{T} \\ \sum_{i=1}^{l}\alpha_{k}^{(i)}\hat{x}_{k}^{(i)}-\hat{x}_{k} & \sum_{i=1}^{l}\alpha_{k}^{(i)}A_{k}^{(i)} & I \\ \end{array} \right)\geq 0\\ &&{\text{and}}\ \epsilon+\sum_{i=1}^{l}\gamma_{i}\leq \tau,\sum_{i=1}^{l}\alpha_{k}^{(i)}=1. \end{array} $$

Then, we finish the proof from the equivalence between the problem (8) and problem (1). □

Remark 1

Theorem 2 gives a approximate solution of problem (1), and the approximation is exactly when l=1 (see [3]). Furthermore, the proof of the Theorem 2 does not require the positive semi-definite of P_k, so we can only require the P_k to be Hermitian if problem (5) is of sense.

Just like the idea of weighted least squares estimation, we can generalize the result by introducing a positive semi-definite weight-valued matrix W_k, and replace problem (1) by

$$\begin{array}{@{}rcl@{}} &&\min_{\hat{x}_{k}}\max_{x_{k}\in \bigcap_{i=1}^{l}S_{k}^{(i)}}\|x_{k}-\hat{x}_{k}\|_{W_{k}}, \end{array} $$

(11)

where $\|x_{k}-\hat {x}_{k}\|_{W_{k}}=(x_{k}-\hat {x}_{k})^{T}W_{k}(x_{k}-\hat {x}_{k})$.

Obviously, it is of sense to introduce weight matrix W_k if one wants to give different punishments to the estimation error in different dimension. Then, problem (1) is a special of problem (11) by taking W_k=I. Similar to the proof of Theorem 2, we can derived the positive semi-definite relaxation of problem (11).

Colloary 1

The positive semi-definite relaxation of optimal problem (11) is

$$ {{} \begin{aligned} &{}\min_{\epsilon \geq 0,\gamma_{i}\geq 0, \tau\geq 0, \hat{x}_{k},\alpha_{k}^{(i)}} \tau\\ &{} s.t.\left(\!\! \begin{array}{ccc} \epsilon & \!0 & \!\!\!\left(\sum_{i=1}^{l}\alpha_{k}^{(i)}\hat{x}_{k}^{(i)}-\hat{x}_{k}\right)^{T}W_{k}^{\frac{T}{2}} \\ 0 & \sum_{i=1}^{l}\gamma_{i}Q_{k}^{(i)} & \!\left(\sum_{i=1}^{l}\alpha_{k}^{(i)}A_{k}^{(i)}\right)^{T}W_{k}^{\frac{T}{2}} \\ W_{k}^{\frac{1}{2}}\left(\sum_{i=1}^{l}\alpha_{k}^{(i)}\hat{x}_{k}^{(i)}-\hat{x}_{k}\right) & W_{k}^{\frac{1}{2}}\left(\sum_{i=1}^{l}\alpha_{k}^{(i)}A_{k}^{(i)}\right) & I \\ \end{array} \! \!\right)\\ &{}\geq 0\ and~~~~~~~~ \epsilon+\sum_{i=1}^{l}\gamma_{i}\leq \tau,\sum_{i=1}^{l}\alpha_{k}^{(i)}=1, \end{aligned}} $$

(12)

where $A_{k}^{(i)}, Q_{k}^{(i)}$ is defined as in Theorem 2. The optimal fusion estimation $\hat {x}_{k}$ is given by the solution of the SDP (12).

Theorem 2 provides a way to fusion sensor estimates when the prior knowledge $x_{k}\in \bigcap _{i=1}^{l}S_{k}^{(i)}$ is available. With appropriate assumption, the feasible and unique of the solution to problem (1) can be derived.

Proposition 1

Suppose the set $\bigcap _{i=1}^{l}S_{k}^{(i)}$ has non-empty inner point, then the optimal fusion estimation given by problem (1) is feasible and unique.

Proof

Note that problem (1) can be rewritten as

$$\begin{array}{@{}rcl@{}} &&\min_{\hat{x}_{k}}\left\{\|\hat{x}_{k}\|_{2}^{2}+\max_{x\in \bigcap_{i=1}^{l} S_{k}^{(i)}}\left(-2x_{k}^{T}\hat{x}_{k}+\|x_{k}\|_{2}^{2}\right)\right\}, \end{array} $$

thus $\max _{x_{k}\in \bigcap _{i=1}^{l} S_{k}^{(i)}}\left (-2x_{k}^{T}\hat {x}_{k}+\|x_{k}\|_{2}^{2}\right)$ is convex in $\hat {x}_{k}$. Therefore, $\|\hat {x}_{k}\|_{2}^{2}+\max _{x_{k}\in \bigcap _{i=1}^{l}S_{k}^{(i)}}\left (-2x_{k}^{T}\hat {x}_{k}+\|x_{k}\|_{2}^{2}\right)$ is strictly convex in $\hat {x}_{k}$, which implies the solution of problem (1) is feasible and unique.

In the sequel, some properties of RFE are considered. □

Theorem 3

Suppose that there is one $P_{k}^{(i)}>0$, then the feasible solution set of problem (5) is always non-empty, thus the solution of problem (5) always exists.

Proof

Without loss of generality, suppose $P_{k}^{(l)}>0$, note that problem (5) is the same as

$$\begin{array}{@{}rcl@{}} &&{}\min_{\epsilon \geq 0,\gamma_{i}\geq 0, \tau\geq 0, \hat{x}_{k},\alpha_{k}^{(i)}} \tau\\ &&{}\left(\! \begin{array}{ccc} \epsilon & 0 & (\sum_{i=1}^{l-1}\alpha_{k}^{(i)}(\hat{x}_{k}^{(i)}-\hat{x}_{k}^{(l)})+\hat{x}_{k}^{(l)}-\hat{x}_{k})^{T} \\ 0 & \sum_{i=1}^{l}\gamma_{i}Q_{k}^{(i)} & (\sum_{i=1}^{l-1}\alpha_{k}^{(i)}(A_{k}^{(i)}-A_{k}^{(l)})+A_{k}^{(l)})^{T} \\ \sum_{i=1}^{l-1}\alpha_{k}^{(i)}(\hat{x}_{k}^{(i)}-\hat{x}_{k}^{(l)})+\hat{x}_{k}^{(l)}-\hat{x}_{k} & \sum_{i=1}^{l-1}\alpha_{k}^{(i)}(A_{k}^{(i)}-A_{k}^{(l)})+A_{k}^{(l)} & I \\ \end{array}\!\! \right)\!\geq\! 0\\ &&~~~~~~~~ and~~\epsilon+\sum_{i=1}^{l}\gamma_{i}\leq \tau. \end{array} $$

Let $\alpha _{k}^{(i)}=0, i=1,\ldots,l-1$, and $\hat {x}_{k}=\hat {x}_{k}^{(l)}$, then the matrix constrain is

$$\begin{array}{@{}rcl@{}} &&\left(\begin{array}{ccc} \epsilon & 0 & 0 \\ 0 & \sum_{i=1}^{l}\gamma_{i}Q_{k}^{(i)} & (A_{k}^{(l)})^{T} \\ 0 & A_{k}^{(l)} & I \\ \end{array} \right)\geq 0, \end{array} $$

equivalently,

$$\begin{array}{@{}rcl@{}} &&\left(\begin{array}{ccccc} \varepsilon & 0 & \ldots & 0 &0 \\ 0 & \gamma_{1}P_{k}^{(1)} & \ldots &0 & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & \gamma_{l}P_{k}^{(l)} & I \\ 0 & 0 & \ldots & I & I \\ \end{array} \right)\geq 0 \end{array} $$

(13)

Note that $P_{k}^{(i)}\!\geq 0,i=1,\ldots,l-1$, and $P_{k}^{(l)}>0$, then (13) always holds by taking large enough γ_l. In other words, the feasible solution set of problem (5) is always non-empty, thus the positive semi-definite relaxation solution exists. □

Proposition 2

Suppose $P_{k}^{(i)}>0, i=1,\cdots,l$, then each local estimate $\hat {x}_{k}^{(i)}$ is a feasible fusion estimations of problem (5). In other words, the fusion estimation $\hat {x}_{k}$ always has better tracking performance than that of local estimates $\hat {x}_{k}^{(i)}$.

Proof

Suppose $P_{k}^{(l)}>0$, from the proof of Theorem 3, there exist appropriate ε, $\alpha _{k}^{(i)}, \gamma _{i},i=1,\cdots,l$ and τ, such that $(\epsilon,\gamma _{i},\tau,\hat {x}_{k}^{(l)}, \alpha _{k}^{(i)})$ is a feasible solution of problem (5). Therefore, the local estimate $\hat {x}_{k}^{(l)}$ is a feasible fusion estimation. The proofs of local estimates $\hat {x}_{k}^{(i)}, i=1, \cdots, l-1$ are similar. □

4 Simulations

Considering that both RFE and CI method seek for fusing local estimates with unknown cross-covariance, and the knowledge of state and sensor observation equations is not unavailable in the design of the fusion estimation. Therefore, some comparisons between the RFE and CI method are provided to analyze the tracking performance of the proposed method. Furthermore, the centralized fusion is also employed to show the performance degradation of the proposed method.

Simulation 1: The simulations were done for a dynamic system modeled as an object moving in a helical trajectory at constant speed with process and measurement noises. Let the system equation be

$$x_{k+1}=F_{k} x_{k}+v_{k}, $$

where v_k is the Gaussian noise with zero mean and covariance matrix

$$R_{v_{k}}=\left(\begin{array}{cc} 5 & 1 \\ 1 & 5 \\ \end{array} \right), $$

and x_k is a deterministic parameter vector with initial state x₀=(1,0), and

$$F_{k}=\left(\begin{array}{cc} {\text{cos}}(\pi/150) & 3 {\text{sin}}(\pi/150) \\ -3 {\text{sin}}(\pi/150) & {\text{cos}}(\pi/150) \\ \end{array} \right). $$

At time k, two sensors estimate x_k in the plane from observations $y_{k}^{(i)}$ respectively, which are related through the linear model

$$y_{k}^{(i)}=H_{i}x_{k}+w_{k}^{(i)}, \quad i=1, 2, $$

where $w_{k}^{(i)}$ is Gaussian noise with zero mean and covariance matric $R_{w_{k}^{(i)}}$ is

$$R_{w_{k}^{(i)}}=\left(\begin{array}{cc} 5 & 1 \\ 1 & 5 \\ \end{array} \right),\quad i=1,2, $$

and the measurement matrices H_i (i=1,2) are also constant and given by

$$H_{1}=\left(\begin{array}{cc} 2 & 1 \\ -1 & 2 \\ \end{array} \right),\quad H_{2}=\left(\begin{array}{cc} 2 & 1.5 \\ -1.5 & 2 \\ \end{array} \right) $$

To obtain the local estimation $\hat {x}_{k}^{(i)}$ and their covariance matrices $C_{k}^{(i)}~(i=1,2)$ of x_k at every step, Kalman filter is employed to each sensor.

Then, the CI and RFE methods are applied to fuse the local estimations by taking a_i=8 and $\bar {P}_{k}^{(i)}=(C_{k}^{(i)})^{-1}$ for i=1,2. Using Monte Carlo method of 50 runs, the absolute track errors in x-axis and y-axis are given in Figs. 1, 2, 3, and 4.

Fig. 1

The absolute tracking errors of CI method in x-axis with a_i=8

Fig. 2

The absolute tracking errors of RFE in x-axis with a_i=8

Fig. 3

The absolute tracking errors of CI method in y-axis with a_i=8

Fig. 4

The absolute tracking errors of RFE in y-axis with a_i=8

From Figs. 1 and 2, the average tracking performance of FRE is comparable to that of CI method. The average absolute tracking errors of RFE and CI method in x-axis are 0.080 and 0.094, respectively. For the average tracking performance in y-axis, the case is similar. As shown in Figs. 3 and 4, the average absolute tracking errors are 0.083 and 0.072 respectively.

In order to derive a clearer comparison of average tracking performance, we evaluate the tracking performance of an algorithm by estimating the second moments of the tracking errors $E_{k}^{2}$, which is presented in [19], and given by

$$E_{k}^{2}=\frac{1}{k}\sum\limits_{i=1}^{k}\|\hat{x}_{i}-x_{i}\|^{2}. $$

using Monte Carlo method of 50 runs, the second moments of the tracking errors of CI and RFE are given in Fig. 5.

Fig. 5

The comparison of the second moments of the tracking errors with a_i=8

It can be observed from Fig. 5, the RFE has smaller second moments of the tracking errors.

Therefore, compared with the CI method, the average tracking performance of RFE is slightly better than that of CI method.

More comparisons are present in the following with different a_i.

From Figs. 6, 7, 8, and 9, for a_i=10,i=1,2, the average absolute tracking errors of CI method and RFE in x-axis are 0.092 and 0.078, and the average absolute tracking errors in y-axis are 0.077 and 0.067, respectively.

Fig. 6

The absolute tracking errors of CI method in x-axis with a_i=10

Fig. 7

The absolute tracking errors of RFE in x-axis with a_i=10

Fig. 8

The absolute tracking errors in of CI method in y-axis with a_i=10

Fig. 9

The absolute tracking errors of RFE in y-axis with a_i=10

Let a_i=12,i=1,2, as shown in Figs. 10, 11, 12, and 13, the average absolute tracking errors of CI method and RFE in x-axis are 0.089 and 0.072, and the average absolute tracking errors in y-axis are 0.079 and 0.067, respectively.

Fig. 10

The absolute tracking errors of CI method in x-axis with a_i=12

Fig. 11

The absolute tracking errors of RFE in x-axis with a_i=12

Fig. 12

The absolute tracking errors in of CI method in y-axis with a_i=12

Fig. 13

The absolute tracking errors of RFE in y-axis with a_i=12

It can be observed from Figs. 14, 15, 16, and 17, as a_i=14,i=1,2, the average absolute tracking errors of CI method and RFE in x-axis are 0.097 and 0.083, and the average absolute tracking errors in y-axis are 0.078 and 0.068, respectively.

Fig. 14

The absolute tracking errors of CI method in x-axis with a_i=14

Fig. 15

The absolute tracking errors of RFE in x-axis with a_i=14

Fig. 16

The absolute tracking errors in of CI method in y-axis with a_i=14

Fig. 17

The absolute tracking errors of RFE in y-axis with a_i=14

As shown in Figs. 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, and 17, when a_i varied from 8 to 14, both the tracking performance of RFE and CI method are degraded. However, the average absolute tracking errors of RFE are always slightly better than that of CI method.

In the sequel, the performance of the proposed method is verified under different cross-correlation levels. To assure that the levels of cross-correlation varies in steady state for the above tracking problem, let

$$\begin{array}{@{}rcl@{}} &&R_{w_{k}^{(i)}}=\left(\begin{array}{cc} 5 & u_{k}^{(i)} \\ u_{k}^{(i)} & 5 \\ \end{array} \right),\quad i=1,2, \end{array} $$

where $u_{k}^{(i)},i=1,2$ are sampled from the sets {0.5,1,1.5} and {1.5,2,2.5} in equal probability respectively. The parameters a_i,i=1,2 are taken as a₁=8 and a₂=10. After 50 Monte Carlo runs, the comparisons of the absolute track errors in x-axis and y-axis are given in Figs. 18, 19, 20, and 21.

Fig. 18

The absolute tracking errors of CI method in x-axis with varied cross-correlation

Fig. 19

The absolute tracking errors of RFE in x-axis with varied cross-correlation

Fig. 20

The absolute tracking errors of CI method in y-axis with varied cross-correlation

Fig. 21

The absolute tracking errors of RFE in y-axis with varied cross-correlation

As shown in Figs. 18, 19, 20, and 21, the average absolute tracking errors of CI method and RFE in x-axis are 0.4337 and 0.4175, and the average absolute tracking errors in y-axis are 0.6360 and 0.5362, respectively.

Simulation 2: In the following, the RFE is employed to fuse three sensor estimators, and the centralized fusion is used to show the performance degradation of RFE.

The object dynamics equation and the first two sensor measurement equations are the same as given in simulation 1. The third sensor measurement equation is $y_{k}^{(3)}=H_{3}x_{k}+w_{k}^{(3)}$, where $w_{k}^{(3)}$ is Gaussian noise with zero mean and covariance matric $R_{w_{k}^{(3)}}$ is

$$R_{w_{k}^{(3)}}=\left(\begin{array}{cc} 4 & 1.5 \\ 1.5 & 4 \\ \end{array} \right), $$

and the measurement matrices

$$H_{3}=\left(\begin{array}{cc} 3 & -2 \\ 1 & 2 \\ \end{array} \right). $$

With 50 Monte Carlo simulations, the average absolute tracking errors of the RFE and centralized fusion are presented in Figs. 22, 23, 24, and 25.

Fig. 22

The absolute tracking errors of the centralized fusion in x-axis with a_i=10

Fig. 23

The absolute tracking errors of RFE in x-axis with a_i=10

Fig. 24

The absolute tracking errors of the centralized fusion in y-axis with a_i=10

Fig. 25

The absolute tracking errors of RFE in y-axis with a_i=10

It can be observed from Figs. 22, 23, 24, and 25, the absolute tracking errors of RFE are larger than that of the centralized fusion. The average absolute tracking errors of the RFE and centralized fusion in x-axis are 0.071 and 0.054, and the average absolute tracking errors in y-axis are 0.056 and 0.049. Considering that the centralized fusion utilizes complete information of system and observation equations, the performance degradation of RFE is acceptable.

The second moments of the tracking errors of RFE and the centralized fusion are given in Fig. 26.

Fig. 26

The comparison of the second moments of the tracking errors

As shown in Fig. 26, after 30 steps, the tracking performance of both method become stable, and the second moments of the tracking errors of RFE is about 0.005 larger than that of the centralized fusion.

5 Conclusion

A robust fusion estimation in distributed systems are derived in this paper which minimizes the worst-case estimation errors on some given parameter set. Compared with the BLUE fusion, the RFE tracks well without the information of the cross-covariance between sensor estimates. At the same time, simulation example shows that the tracking performance of RFE is comparable to that of the CI filter.