1 Introduction

Magnesium alloy sheets have low density, good thermal conductivity, high specific strength and stiffness, desirable damping properties, and excellent electromagnetic shielding. Therefore they are widely used in the aviation, aerospace [1], automobile [2], high-speed rail, and electronics industries [3]. Consequently, magnesium alloy sheets have become the most promising non-ferrous metal material in the world today [4,5,6]. In the rolling process of magnesium alloy sheets, the roll temperature has a large influence on plate quality [7]. When the roll temperature is too low, the edges crack and surface cracking of the plate occurs. When the roll temperature is too high, the roll can become stuck [8, 9]. There is an urgent need to make an important breakthrough in the accurate control of roll temperature.

In recent years, the traditional methods for heating the roll have included the induction heating method, resistance wire heating method, and flame heating method [10, 11]. These traditional methods suffer from long heating times and uneven heating, therefore a new model using circular fluid flow to control roll temperature has been designed. This method heats and cools the roll using two tanks. The roll temperature can be controlled by adjusting the velocity and temperature of the fluid. A high precision heat transfer model (between the magnesium alloy sheet and roll) has been built, and the regulation strategy of roll temperature is given, meaning the roll temperature can be controlled within a reasonable range at any time. Therefore, this study can solve the existing problems of large crown, serious wave-shapes, and stuck rolls caused by inaccurate roll temperature control. This will significantly increase the finished production rate of the magnesium alloy sheets.

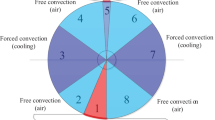
Heat transfer in the rolling process of magnesium alloy sheet is complex [12]. It includes deformation heat, friction heat, thermal radiation, convective heat transfer within the air between the magnesium alloy sheet and roll, and heat transfer between fluid and the roll [13,14,15]. These are indicated by the arrows in Figure 1. The temperature field in the rolling process is divided into two stages because of the complexity: single coupled heat transfer between the fluid and roll, and coupled heat transfer factors of the rolling process. The first stage is studied in this paper (the second stage will be studied later), then an experiment and modifications to the model are conducted. An experimental roll (D = 320 mm, L = 350 mm) is the chosen object to establish a fluid-solid coupled model of the fluid heating transfer roll. The roll temperature is studied for different times and velocities when fluid is heating the roll. The results are both an important and significant guide for controlling the roll temperature in the rolling process.

Figure 1
figure 1

Heat transfer in the process of magnesium alloy sheet rolling

Full size image

2 Design of the Roll Structure Using Fluid Heat Transfer

The thermostat oil holes on the roll were designed to force the fluid to flow cyclically through the oil holes, as shown in Figure 2. To prevent a problems caused by insufficient bending stiffness, the roll bending strength reduced rate (M) was less than 8% when the roll was designed. The roll bending rigidity before drilling is \(E\frac{{\uppi D^{4} }}{64},\) the smallest roll bending rigidity after drilling is \(E\frac{{\uppi D^{4} - 2n\uppi d_{0}^{4} - 16\uppi Qs^{2} d_{0}^{2} }}{64},\) the roll stiffness reduction is \(E\left( {\frac{{2n\uppi d_{0}^{4} }}{64} - Q\frac{{\uppi s^{2} d_{0}^{2} }}{4}} \right),\) and the roll bending strength reduced rate is \(M = \frac{{(2nd_{0}^{2} + 16Qs^{2} )d_{0}^{2} }}{{D^{4} }} \times 100\% \le 8\% .\)

Figure 2
figure 2

Thermal fluid heating work roll diagram

Full size image

Here, E is the modulus of elasticity of the roll (Pa); d0 is the diameter of thermostat oil hole (m); D is the diameter of the roll (m); s is the distance between the center of the thermostat hole and cross-sectional center of the roll (m); n is half the number of thermostat oil holes (the thermostat oil hole number is even). \(Q = \hbox{min} \left[ {\sum\limits_{k = 0}^{k = 2n - 1} {\left( {\sin \left( {x + \frac{\uppi}{n}k} \right)} \right)^{2} } } \right]\) (k is an integer, x is a real number and satisfies \(- \frac{\pi }{n} \le x \le \frac{\pi }{n},\) and the Q value can be obtained by mathematical software (MATLAB).

With the roll as the research object, the diameter of the thermostat hole is d0 = 0.02 m, the distance between the center of the thermostat hole and the cross-sectional center of the roll was s = 0.12 m, the number of thermostat oil holes was 8, and the roll bending strength reduced rate was 4.528%. This met the requirements. The two directions of the roll cross section in Figure 2 are shown in Figure 3(a) and (b). Fluid flows from oil hole 1, passed through oil holes 2‒7, then finally flowed from oil hole 8.

Figure 3
figure 3

Work roll cross section diagram

Full size image

3 Establishment of the Analytical Model for Heat Transfer

The most accurate method for solving heat conduction is by mathematical analysis. However, the analysis can only solve the simple problem of heat conduction, whereas many of the complex thermal problems can only be obtained by numerical calculations using the finite difference method [16,17,18,19].

3.1 Hypothetical Condition

  1. (1)

    The model of the fluid heat transfer roll is three-dimensional. The temperature is transmitted from the inner surface of the oil hole in the radial direction (the temperature difference in the circumferential direction can be neglected), so the model can be simplified as two-dimensional. This means the heat transfer is along the radial and axial directions, and the roll temperature field changes with time and position. Therefore, the model of the fluid heat transfer roll was simplified to a two-dimensional unsteady heat conduction model of a hollow cylinder.

  2. (2)

    The physical property parameters of the roll and the fluid are not changed with time.

  3. (3)

    The boundary conditions of fluid heat transfer, the roll inner and outer walls, and the outside are considered as the third boundary condition.

3.2 Calculation of Heating Transfer Process

The temperature distribution on the hollow cylinder T(r, t) changes with the time t and position r, the initial temperature distribution is T(r, 0) = T(r), r1 is the radius of the thermostat oil hole, and r2 is the closest distance from the thermostat oil hole center to the roll surface: \(r_{1} = \frac{{d_{0} }}{2} = 0.01\;{\text{m}},\) r2 = 0.04 m, and r1 < r < r2, as shown in Figure 3.

$$\frac{{\partial^{2} T(r,t)}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T(r,t)}{\partial r} = \frac{1}{a}\frac{\partial T(r,t)}{\partial t},{\kern 1pt} \quad r_{1} < r < r_{2} ,t > 0,{\kern 1pt}$$
(1a)
$$T(r,0) = T(r),{\kern 1pt} {\kern 1pt} \quad {\kern 1pt} r_{1} \le r \le r_{2} ,t = 0,{\kern 1pt}$$
(1b)
$$- \lambda \frac{\partial T(r,t)}{\partial r} + h_{1} T(r,t) = f_{1} ,{\kern 1pt} {\kern 1pt} \quad {\kern 1pt} r = r_{1} ,t > 0,{\kern 1pt} {\kern 1pt}$$
(1c)
$$\lambda \frac{\partial T(r,t)}{\partial r} + h_{2} T(r,t) = f_{2} ,{\kern 1pt} \quad r = r_{2} ,t > 0,{\kern 1pt}$$
(1d)

where \(a = \frac{\lambda }{\rho c};\) f1 = h1tf1; f2 = h2tf2. h1 is the heat transfer coefficient of the fluid and inner wall of the roll (W/(m2·°C)); h2 is the heat transfer coefficient of the roll outer wall and the outside (W/(m2·°C)); λ is the thermal conductivity of the roll (W/m·°C)); ρ is the density of the roll (kg/m3); c is the specific heat capacity of the roll (kJ/kg); a is the thermal diffusivity of the roll (m2/s); tf1 is the temperature of the fluid (°C); and tf2 is the outside temperature (°C).

The area (r, t) is divided into the grid of step Δr, Δt, as shown in Figure 4. Then there are:

$$r = j\Delta r{\kern 1pt} ,{\kern 1pt} {\kern 1pt} \quad j = 0,1,2,\ldots,N{\kern 1pt} ,{\kern 1pt} \quad {\kern 1pt} L = r_{2} - r_{1} = N\Delta r,$$
(2)
$$t = n\Delta t,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} n = 0,1,2,3,\ldots$$
(3)
Figure 4
figure 4

Grid of step length for Δr, Δt in area (r, t)

Full size image

The temperature can be expressed as

$$T(r,t) = T(j\Delta r,n\Delta t) \equiv T_{j}^{n} .$$
(4)

Using the boundary conditions r = r1 and r = r2, respectively for the forward difference and backward difference gives

$$- \lambda \frac{{T_{1}^{n + 1} - T_{0}^{n + 1} }}{\Delta r} + h_{1} T_{0}^{n + 1} = f_{1} ,$$
(5)
$$\lambda \frac{{T_{N}^{n + 1} - T_{N - 1}^{n + 1} }}{\Delta r} + h_{2} T_{N}^{n + 1} = f_{2} .$$
(6)

The terms \(T_{0}^{n + 1}\) and \(T_{N}^{n + 1}\) are determined by rearranging

$$\begin{array}{*{20}c} {T_{0}^{n + 1} = \frac{1}{{1 + (h_{1} \Delta r/\lambda )}}\left( {T_{1}^{n + 1} + \frac{{f_{1} \Delta r}}{\lambda }} \right),} \\ {n = 0,1,2,\ldots,{\kern 1pt} {\kern 1pt} \quad j = 0,} \\ \end{array} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$$
(7)
$$\begin{array}{*{20}c} {T_{N}^{n + 1} = \frac{1}{{1 + (h_{2} \Delta r/\lambda )}}\left( {T_{N - 1}^{n + 1} + \frac{{f_{2} \Delta r}}{\lambda }} \right),} \\ {n = 0,1,2,\ldots,{\kern 1pt} \quad j = N,} \\ \end{array} {\kern 1pt} {\kern 1pt} {\kern 1pt}$$
(8)

Its magnitude of truncation error is Δr, and Eq. (1a) is differentially calculated to give

$$\frac{{T_{j - 1}^{n} - 2T_{j}^{n} + T_{j + 1}^{n} }}{{(\Delta r)^{2} }} + \frac{1}{r}\frac{{T_{j + 1}^{n} - T_{j - 1}^{n} }}{2\Delta r} = \frac{1}{a}\frac{{T_{j}^{n + 1} - T_{j}^{n} }}{\Delta t}.$$
(9)

Which combines with Eq. (2) to give

$$\begin{array}{*{20}c} {T_{j}^{n + 1} = (1 - \frac{1}{2j})mT_{j - 1}^{n} + (1 - 2m)T_{j}^{n} + (1 + \frac{1}{2j})mT_{j + 1}^{n} ,} \\ {j = 1,2,3,\ldots,N - 1,{\kern 1pt} \quad n = 0,1,2\ldots} \\ \end{array}$$
(10)

where \(m = \frac{a\Delta t}{{(\Delta r)^{2} }}.\)

Its magnitude of truncation error is (Δr)2 + (Δt), the right side of Eq. (10) includes \(T_{0}^{n}\) when j = 1 and \(T_{N}^{n}\) when j = N − 1. These temperatures can be calculated by Eqs. (7) and (8), the superscript n + 1 in place of n, and then the resulting \(T_{0}^{n}\) and \(T_{N}^{n}\) put into Eq. (10). The results are summarized as follows:

$$T_{0}^{n + 1} = \frac{1}{{\beta_{1} }}(T_{1}^{n + 1} + \gamma_{1} ){\kern 1pt} ,{\kern 1pt} {\kern 1pt} \quad j = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$$
(11)
$$T_{1}^{n + 1} = \left( {1 - 2m + \frac{m}{{2\beta_{1} }}} \right)T_{1}^{n} + \frac{3}{2}mT_{2}^{n} + \frac{{m\gamma_{1} }}{{2\beta_{1} }}{\kern 1pt} ,{\kern 1pt} \quad j = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$$
(12a)
$$\begin{array}{*{20}ll} & {T_{j}^{n + 1} = \left( {1 - \frac{1}{2j}} \right)mT_{j - 1}^{n} + \left( {1 - 2m} \right)T_{j}^{n} + \left( {1 + \frac{1}{2j}} \right)mT_{j + 1}^{n} ,{\kern 1pt} {\kern 1pt} } \\ & \quad {j = 2,\ldots,N - 2,} \\ \end{array} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$$
(12b)
$$\begin{aligned} & T_{{N - 1}}^{{n + 1}} = \frac{{2N - 3}}{{2N - 2}}mT_{{N - 2}}^{n} + (1 - 2m + \frac{m}{{\beta _{2} }}\frac{{2N - 1}}{{2N - 2}})T_{{N - 1}}^{n} \\ & \quad \quad + \frac{{m\gamma _{2} }}{{\beta _{2} }}\frac{{2N - 1}}{{2N - 2}}{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \quad j = N - 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} \\ \end{aligned}$$
(12c)
$$T_{N}^{n + 1} = \frac{1}{{\beta_{2} }}\left( {T_{N - 1}^{n + 1} + \gamma_{2} } \right),{\kern 1pt} \quad j = N{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$$
(13)

where n = 0, 1, 2,… and \(\beta_{i} = 1 + \frac{{h_{i} \Delta r}}{\lambda },\) \(\gamma_{i} = \frac{{f_{i} \Delta r}}{\lambda },\) and i = 1 or 2.

The initial condition is

$$T_{j}^{0} = T(j\Delta r) \equiv T(r),{\kern 1pt} \quad {\kern 1pt} j = 0,1,2,\ldots,N.{\kern 1pt} {\kern 1pt} {\kern 1pt}$$
(14)

Equations (11) to (14) give the finite difference expression of the heat conduction equation. The solving method for this is described below.

Equation (12) provides N − 1 algebraic equations to solve the N − 1 unknown nodal temperatures: \(T_{1}^{n + 1} ,\;T_{2}^{n + 1} , \ldots ,T_{N - 1}^{n + 1} .\) Due to the use of explicit form these equations are not coupled, and may be calculated separately. Calculation is started with n = 0, \(T_{1}^{1} ,\;T_{2}^{1} , \ldots ,T_{N - 1}^{1}\) and are determined according to Eq. (12), then the temperature values are found when n = 1,2,…. As \(T_{1}^{n + 1}\) and \(T_{N - 1}^{n + 1}\) can be obtained by Eq. (12), then the boundary surface temperature \(T_{0}^{n + 1}\) and \(T_{N}^{n + 1}\) can be calculated respectively according to Eqs. (11) and (13).

Once a and Δr are determined, the time step Δt will be limited by the stability criterion:

$$m \equiv \frac{a\Delta t}{{(\Delta r)^{2} }} \le \frac{1}{2}{\kern 1pt} {\kern 1pt} {\kern 1pt} .$$
(15)

3.3 Calculation of the Heat Transfer Coefficient

When the size of the hole and type of fluid are determined, the heat transfer coefficient between the fluid and the inner wall is related to the temperature and velocity of the fluid. In this paper, the heat conducting fluid was L-QD330, and the initial temperature of the fluid was 300 °C. In the following section the effect of fluid velocity on heat transfer coefficient will be studied. The faster the fluid the greater the heat transfer coefficient, but the flow resistance will increase when the velocity increases, and damage to the equipment will increase. To protect the equipment and reduce pipe wear, the velocity was controlled within a reasonable range.

The temperature \(t^{\prime}_{f}\) = 300 °C was used as a qualitative temperature to calculate the Reynolds number, then the calculation was checked. Table 1 describes the physical property parameters of the heat conducting fluid L-QD330.

Table 1 Physical property parameters of heat conducting fluid L-QD330
Full size table

The Reynolds number of the heat conducting fluid is \(Re_{f} = \frac{{u_{m} d}}{{v_{f} }},\) the Pr number is \(Pr_{{_{f} }} = \frac{{c\rho v_{f} }}{\lambda }\) [20, 21], the Nu number is \(Nu_{f} = 0.027Re_{f}^{0.8} Pr_{f}^{1/3} \left( {\frac{{u_{f} }}{{u_{w} }}} \right)^{0.25} ,\) and when Re > 104 the fluid flow regime is turbulent [22, 23]. Therefore, the heat transfer coefficient is \(h_{1} = \frac{{\lambda Nu_{f} }}{d},\) where

$$h_{1} = 0.027\frac{{u_{m}^{0.8} c^{1/3} \rho^{1/3} \lambda^{2/3} }}{{v_{w}^{0.25} v_{f}^{13/60} d^{0.2} }}.$$
(16)

The fluid heat release per unit time is equal to the enthalpy difference of import and export, therefore, \(\overline{M} c\left( {t^{\prime}_{f} - t^{\prime\prime}_{f} } \right) = h_{1}\uppi dl\left[ {\frac{1}{2}\left( {t^{\prime}_{f} + t^{\prime\prime}_{f}} \right) - t{}_{w}} \right],\) whose simplification is

$$t^{\prime\prime}_{f} = \frac{{h_{1}\uppi dl\left( {t_{w} - \frac{1}{2}t^{\prime}_{f} } \right) + \overline{M} ct^{\prime}_{f} }}{{\overline{M} c + \frac{1}{2}h_{1}\uppi dl}},$$
(17)

where um is the velocity of the fluid (m/s); vf is the kinematic viscosity of the fluid (m2/s); c is the specific heat of the fluid (kJ/kg); ρ is the density of the fluid (kg/m3); λ is the thermal conductivity of the fluid (W/m·°C); uf and uw are the fluid dynamic viscosities under fluid temperature tf and wall temperature tw as characterization temperature (Pa·s); \(t^{\prime\prime}_{f}\) is the fluid export temperature when \(t^{\prime}_{f}\) is the qualitative temperature, and \(\overline{M} = \rho \frac{{\uppi d^{2} }}{4}u_{m}\) is the traffic quality of the fluid.

The export temperature \(t^{\prime\prime}_{f}\) is calculated, then input to \(t^{\prime\prime\prime}_{f} = \frac{1}{2}\left( {t^{\prime}_{f} + t^{\prime\prime}_{f} } \right),\) so the average temperature of the fluid in the whole pipe can be obtained. Then this can be re-checked as a qualitative temperature, and iterated until the difference between the calculated outlet temperature and the previous outlet temperature is less than 1%. Table 2 indicates the heat transfer coefficient and average fluid temperature of the respective velocities after calculation.

Table 2 Heat transfer coefficient and the average fluid temperature of the respective velocities after calculation
Full size table

The heat transfers between the roll and the outside are mainly natural convection heat transfer and thermal radiation in air. The natural convection heat transfer coefficient of the outside is:

$$h^{\prime}_{2} = 0.53\lambda \left[ {\frac{{gPr (T - t_{f2} )}}{{v^{2} l(t_{m} + 273)}}} \right]^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}} ,$$
(18)

where \(t_{m} = \frac{{T + t_{f2} }}{2}.\)

The heat transfer coefficient when the roll radiates is [18, 19]:

$$h^{\prime\prime}_{2} = \sigma \varepsilon \left[ {\left( {T + 273} \right)^{2} + (t_{f2} + 273)^{2} } \right]\left[ {(T + 273) + (t_{f2} + 273)} \right]$$
(19)

The heat transfer coefficient between the roll and the outside is:

$$h_{2} = h^{\prime}_{2} + h^{\prime\prime}_{2} .$$

Where λ, v, and Pr are the heat conductivity coefficient (W/m °C), the kinematic viscosity (W/m °C), and the Pr number of the outside when the temperature is tm, respectively. Further, T is the average temperature of the roll (°C); σ is 5.669 × 10−8, ε is the emissivity of the roll, and tf2 is the outside temperature (20 °C).

The heat transfer coefficient (h1) is calculated in the ideal circumstances of a constant wall temperature. In fact, the wall temperature gradually increased, the temperature and physical parameters of the fluid were always changing, and the heat transfer coefficient reduced. Therefore we needed to correct the calculated values. Table 3 describes the heat transfer coefficient of the respective velocities after the experiment. Calculation and experimental results are shown in Figure 5. The heat transfer coefficient was corrected, and the fitting equation is shown as Eq. (20). The heat transfer coefficient has more influence than the fluid temperature on the heat transfer process, so the temperature of the fluid is the average calculating value.

Table 3 Heat transfer coefficient of the respective velocities after the experiment
Full size table
Figure 5
figure 5

The calculated and simulation values of the heat transfer coefficient: a v = 0.3 m/s; b v = 0.5 m/s; c v = 0.7 m/s; d v = 0.9 m/s; e v = 1.1 m/s

Full size image

Equations (11)‒(14) were programmed by C++, the correction heat transfer coefficients h1 and h2 were generated into the equation at various velocities, and then the roll temperature was calculated under various velocities over time.

$$\begin{aligned} \left\{ {\begin{array}{*{20}l} {h_{1} = 3009.96\exp ( - t/2.54) + 6.42,} \hfill \\ {h_{1} = 440.29,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}c} {t \le 6\;\hbox{min} ,} \\ {t > 6\;\hbox{min} ,} \\ \end{array} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} v = 0.3\;{\text{m/s}}, \hfill \\ \left\{ {\begin{array}{*{20}l} {h_{1} = 4404.15\exp ( - t/1.62) + 114.52,} \hfill \\ {h_{1} = 433.25,} \hfill \\ \end{array} } \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}c} {t \le 5\;\hbox{min} ,} \\ {t > 5\;\hbox{min} ,} \\ \end{array} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} v = 0.5\;{\text{m/s}}, \hfill \\ \left\{ {\begin{array}{*{20}l} {h_{1} = 4940.27\exp ( - t/1.45) + 84.16,} \hfill \\ {h_{1} = 508.20,} \hfill \\ \end{array} } \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}c} {t \le 4\;\hbox{min} ,} \\ {t > 4\;\hbox{min} ,} \\ \end{array} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} v = 0.7\;{\text{m/s}}, \hfill \\ \left\{ {\begin{array}{*{20}l} {h_{1} = 6554.64\exp ( - t/1.57) - 180.69,} \hfill \\ {h_{1} = 491.74,} \hfill \\ \end{array} } \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}c} {t \le 4\;\hbox{min} ,} \\ {t > 4\;\hbox{min} ,} \\ \end{array} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} v = 0.9\;{\text{m/s}}, \hfill \\ \left\{ {\begin{array}{*{20}l} {h_{1} = 5784.70\exp ( - t/1.49) - 154.57,} \hfill \\ {h_{1} = 396.19,} \hfill \\ \end{array} } \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}c} {t \le 4\;\hbox{min} ,} \\ {t > 4\;\hbox{min} ,} \\ \end{array} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} v = 1.1\;{\text{m/s}}. \hfill \\ \end{aligned}$$
(20)

4 Discussion of Numerical Simulation and Results

4.1 Numerical Simulation

Depending on the size of the roll (and the designed value of the thermostat hole), the model of the roll was built by finite element software (Pro-E), as shown in Figure 6(a). The established model was imported into Workbench for gridding, and the grid type was set to Tetra. Considering the time and accuracy of the calculation, it was determined that the maximum value of the grid was 5−3 mm, and the minimum value was 5−4 mm. Due to the viscosity of the heat conduction oil during the flow process, five layers of fluid boundary layer were set up, and the growth rate was 1.1, as shown in Figure 6(b). The heat transfer model was set as transient, the temperature unit was K, the fluid flow state was set to turbulent state, and the roll parameters were set as shown in Table 4. The initial temperature of the roll was 20 °C, and the heat transfer process of the velocity at 0.3, 0.5, 0.7, 0.9 and 1.1 m/s were numerically simulated.

Figure 6
figure 6

Three-dimensional model diagram of the work roll

Full size image
Table 4 Physical property parameters of the fluid and roll
Full size table

4.2 Results Analysis of Numerical Simulation

The heat transfer process under different velocities was simulated, and the temperature values of a, b, c, d and the temperature field of the roll were obtained, as shown in Figures 7, 8. This shows that the fluid heats the outside along the thermostat hole progressive layers. On the roll surface, four points (a, b, c, and d) were measured, and the fluid flowed through the thermostat hole successively at the four points, as shown in Figure 3(a). The temperature at point c was measured to compare with the calculated temperature. Each temperature point on the roll surface increased with time, but the rate of increase reduced. The temperature difference between the points did not vary with the change of time and velocity after three minutes. The temperature difference value between import and export was approximately 30 °C. There was also a temperature difference along the axial direction of the roll. The temperature difference at the first oil hole on the roll surface (import) was bigger (up to 27 °C), and the temperature difference for the rest of the roll surface was small (approximately 5 °C). The nearest hole warmed the quickest, the furthest the hole warmed the slowest, and it decreased with the reduced trend of the slope.

Figure 7
figure 7

Temperature simulation value of the point a, b, c, and d, and the roll temperature field (after 10 min): a v = 0.3 m/s; b v = 0.5 m/s; c v = 0.7 m/s; d v = 0.9 m/s

Full size image
Figure 8
figure 8

Temperature simulation value of the point a, b, c, and d, and the roll temperature field (after 10 min): v = 1.1 m/s

Full size image

The relationship between temperature of point c and time (under different velocities) is shown in Figure 9. The greater the velocity, the faster the heat transferred, the temperature of points on the roll increased quicker, but the rate of the rise decreased.

Figure 9
figure 9

Simulation temperature curve of point c under different velocities

Full size image

The optimum roll temperature range was 160−250 °C for the rolling process of magnesium alloy. The time (t) and the pressure difference (ΔP) between the import and export (when the roll was heated from room temperature to 200 °C under different velocities) are shown in Table 5. The trend of the change is shown in Figure 10. The fluid velocity changed from 0.3 to 1.1 m/s, t reduced from 34.4 to 15.5 minutes, the pressure increased from 0.03 to 0.32 MPa, the heating time shortened, and the velocity increased to a certain value. Further, the heat transfer increase rate decreased, but the pressure became larger and the flow resistance increased. The relationships between velocity (v), time (t), and the pressure difference (ΔP) between the import and exports were fitted as in Eqs. (21) and (22). In the actual production, the best velocity was selected according to the required heating time, and whether different equipment could withstand the pressure.

$$t = 46.29\exp ( - v/0.39) + 12.65,$$
(21)
$$\Delta P = 4.01\exp (v/0.5) - 4.16.$$
(22)
Table 5 Time and pressure values up to 200 °C under different velocities
Full size table
Figure 10
figure 10

Time and pressure values when the roll surface temperature was heated to 200 °C under different velocities

Full size image

4.3 Results Analysis of Theoretical Calculations

The roll surface temperature field (obtained by the above calculation method under different velocities with time) is shown in Figure 11. The greater the velocity is, the faster the heat transfer. The roll temperature was consistent with the simulation results.

Figure 11
figure 11

Calculated temperature curve under different velocities

Full size image

4.4 Comparative Analysis of Theoretical and Numerical Data

Calculation and simulation results of the roll temperature field are compared in Figure 12. The error was 1.8%–12.3%, which indicates the validity of the model of heat transfer theory. Temperature values of the import and export was approximately 30 °C, the difference and the influence on the magnesium alloy sheet were both bigger, therefore the fluid reverse flowed, then after a period of time it positive flowed to balance the temperature of the roll surface.

Figure 12
figure 12

Heat transfer coefficient comparison of the calculation and simulation results

Full size image

5 Heat Transfer after Reverse Flow of Fluid

A study of the temperature required for points on the roll surface to reach equilibrium is necessary, as the required roll temperatures will vary depending on the rolling conditions. From the above results, when the velocity was 1.1 m/s, the heat transfer was optimum, so the process of fluid reverse flow after forward flow for different times was simulated under this velocity. The temperature of the points and the temperature field of the roll are shown in Figure 13, 14. The equilibrium time and equilibrium temperature (when point temperatures reached the same value under different velocities) are shown in Table 6.

Figure 13
figure 13

Temperature value of the points a, b, c, and d under different forward flow times: a t = 3 min; b t = 5 min; c t = 7 min; d t = 9 min

Full size image
Figure 14
figure 14

Temperature value of the points a, b, c, and d under different forward flow times: t = 11 min

Full size image
Table 6 Equilibrium time and equilibration temperature after different flowing times
Full size table

The results showed that the equilibrium time was substantially constant when the positive fluid flow was longer, but the equilibrium temperature increased with the velocity increase. After the reverse flow of fluid, the export temperature of the roll increased, but the length of this area range was less than 1/5 of the length of the roll, and the temperature difference (between the surface area of the hole and the surface area of non-holes) did not exceed 8 °C. The axial temperature difference at the roll import was approximately 18 °C, the high temperature zone was concentrated at 1/8 of the roll body length, and the temperature of other positions was uniform. The surface temperature for the remaining 7/8 of the roll surface was even more uniform. As the roll surface temperature difference was small, the rolling process could be carried out.

When the relationship between the fluid flowing time (t) and equilibrium temperature (T) is fitted we get:

$$T = - 5400.7 + 5605.1\exp \left[ {\frac{ - 0.5(t - 12.6)}{70.8}} \right]^{2} .$$
(23)

Therefore we can determine the fluid flowing time according to the required roll temperature to obtain a more accurate roll temperature value.

6 Conclusions

  1. (1)

    The theoretical calculation results and numerical simulation results of heat transfer between the fluid and roll were compared (the error was 1.8%‒12.3%). This showed that the heat transfer theoretical model could forecast and regulate roll temperature when magnesium alloy sheets are rolled.

  2. (2)

    Compared with the traditional heating method, the method of heating the surface temperature of the roll with the fluid reduced the heating time, and the temperature distribution of the roll surface was more uniform. However, the temperature difference between import and export was bigger. The lager the velocity, the faster the heat transfer, but the rate of increase decreased.

  3. (3)

    The method of fluid reverse flowing after a period of positive flowing was used to balance the temperature difference between import and export. The longer the time of fluid flow, the time required to reach equilibrium was constant (approximately four minutes). When the fluid forward flow time was longer, the equilibrium temperature was higher. The more accurate roll temperature can be obtained by reasonably determining the time of forward flow of fluid.