1 Introduction

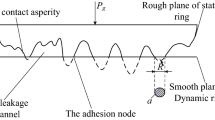
Face contact is an important physical reality in a number of research fields [1,2,3]. In the field of face seals, for contacting face seals, face contact is inevitable during the opened operation. For non-contacting face seals such as spiral groove gas face seals as shown in Figure 1, they should possess a proper gas film thickness to avert face contact during the opened operation. Even so, face contact does occur during the startup and shutdown operations [4], and is also a risk from disturbances during the opened operation [5]. Therefore, it is imperative to choose an adequate asperity contact model in the analyses of face seals. With respect to asperity contact, Greenwood and Williamson (GW model) [6] have done a pioneering work, developing an elastic contact model between rough surfaces. McCool [7] and Bhushan [8] added asperity slope and curvature to capture rough surfaces. Chang et al. [9] proposed the CEB elastic-plastic contact model based on volume conservation during plastic deformation to improve the GW model. Kogut and Etsion (KE model) [10, 11] developed a finite element method to investigate the contact between a deformable spherical asperity and a rigid flat, showing dimensionless contact load and contact area over the increase in the interference range from purely elastic through elastic-plastic to fully plastic contact.

Figure 1
figure 1

Schematic of a typical spiral groove face seal

Full size image

However, Sayles and Thomas [12] revealed that many engineered surfaces have the multi-scale characteristic. Bhushan et al. [13] found that statistical parameters depend strongly on the resolution of measuring instruments, and are not unique for a surface because of the multi-scale characteristic. It leads to the result that measurements with different resolutions and scanning lengths wouldn’t yield unique statistical parameters for a surface. Moreover, statistical contact models overlook the fact that the curvature radius of an asperity is a function of asperity size, and surely assume a constant curvature radius for all asperities. Majumdar and Bhushan [14] used the Weierstrass-Mandelbrot (WM) function to develop the first fractal contact model for real rough surfaces where the assumption of variable curvature radius was adopted. This fractal contact model has been of interest to many researchers, and has been applied to various applications. Wang and Komvopoulos [15, 16] researched the interfacial temperature factor in the fractal contact. Komvopoulos and Yan [17] generated a three-dimensional fractal surface by the WM function and introduced it into the contact model. Sahoo and Chowdhury [18, 19] analyzed the friction and the wear of fractal surfaces. Ciavarella et al. [20] investigated the elastic contact stiffness and the contact resistance of fractal surfaces. Kogut and Jackson [21] used both statistical and fractal approaches to characterize simulated surfaces, and obtained substantial differences between the two. Morag and Etsion (ME model) [22] argued that a single asperity transferring from plastic to elastic when the load increases and the contact area becomes larger in the MB model is in contrast with classical contact mechanics. They suggested the real deformation is an independent parameter ranging from zero to full interference, and thus developed a revised elastic-plastic contact model with respect to a single fractal asperity.

Face contact can affect sealing performance, such as dynamic behavior, thermodynamics, friction, wear. The dynamics of face seals has been an active area since the works by Etsion [23,24,25]. In the aspect of gas face seals, direct numerical method [26,27,28,29,30] is detailed but computationally intensive, whilst semi-analytical method including perturbation method [31,32,33,34] and step jump method [35], on the other hand, is a more practical and efficient alternative but intensively depends on small displacement precondition. Before the introduction of asperity contact, stability and tracking have been used to illustrate the potential menace of face contact. Variables such as minimum film thickness, axial relative displacement and angular transmissibility are regarded as the indirect evaluation indexes of face contact. With the development of simulation, asperity contact models have been involved to directly gauge their influence on sealing dynamic performance. Harp and Salant [36] developed an axial dynamic model including the Abbott-Firestone plastic asperity contact model. Green [37] researched the transient performance of coned gas face seals during the startup operation by using the CEB model. Ruan [38] also used the CEB model to investigate the transient performance of spiral groove gas face seals during the startup and shutdown operations.

The above dynamic works all used the statistical contact models, while the fractal contact theory has not been applied. The present study is an attempt to involve the fractal theory in the dynamic research of gas face seals. And a comparison of dynamic performance between statistical and fractal approaches is performed. The widely used, original contact models (i.e., the MB and the CEB models) are selected, respectively, as the representatives of fractal and statistical asperity contact models accounting for excluding extra factors (such as the impact of work hardening, the influence of neighboring asperities, the introduction of new bi-Gaussian stratified surface parameters [39,40,41,42,43,44,45], the revision of contact mechanic in ME model) involved in advanced statistical or fractal models.

2 Model

2.1 MB Model

In the MB model, the surface profile z(x), as shown in Figure 2, is random, multiscale and statistically self-affine. The WM function is used to describe the surface profile. Its power spectrum is [14]

$$S(\omega ) = \frac{{G^{2(D - 1)} }}{2\ln \gamma } \cdot \frac{1}{{\omega^{(5 - 2D)} }},$$
(1)

where S is the power spectrum, ω is the frequency that is the reciprocal of the wavelength of roughness, D is the fractal dimension, G is the fractal roughness parameter, γ determines the frequency spectrum of surface roughness where γ = 1.5 is found to be a suitable value for high spectral density and phase randomization [46]. In a log-log plot of S(ω) ~ ω, the power law behavior of Eq. (1) transforms into a straight line. The slope kp is related to the fractal dimension D and the intercept Bp is related to the fractal roughness parameter G. In practical experiments, one needs to obtain the power spectrum of a real surface profile in a log-log plot. If the relation is linear and kp satisfies (− 3, − 1), it reveals the real surface profile owns fractal characteristic. Then, D and G can be calculated referring to kp and Bp.

Figure 2
figure 2

Multi-scale and statistical self-affine nature of surfaces

Full size image

The critical contact area of an asperity is [14]

$$a_{\text{c}} = \frac{{G^{2} }}{{({{KH} \mathord{\left/ {\vphantom {{KH} {2E}}} \right. \kern-0pt} {2E}})^{{{2 \mathord{\left/ {\vphantom {2 {D - 1}}} \right. \kern-0pt} {D - 1}}}} }},$$
(2)

where E is the Hertz elastic modulus, H is the hardness of softer material, and the maximum contact pressure coefficient K = 0.454 + 0.41υ (υ is the Poisson ratio). If the area of a contact spot a < ac, the asperity is in plastic contact; if a > ac, the asperity is in elastic contact. The total contact load between a rough surface and a smooth plate Pc is [14]

$$P_{\text{c}} = \frac{{4\sqrt\uppi EG^{D - 1} }}{3}\int_{{a_{\text{c}} }}^{{a_{\text{l}} }} {n(a)a^{{{{(3 - D)} \mathord{\left/ {\vphantom {{(3 - D)} 2}} \right. \kern-0pt} 2}}} } {\text{d}}a + KH\int_{0}^{{a_{c} }} {n(a)a{\text{d}}a} ,$$
(3)

where the first term corresponds to elastic deformation and the second term corresponds to plastic deformation. al is the area of the largest contact spot. n(a) is the size-distribution of a [14]:

$$n(a) = \frac{D}{2} \cdot \frac{{a_{l}^{{{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0pt} 2}}} }}{{a^{{{D \mathord{\left/ {\vphantom {D {2 + 1}}} \right. \kern-0pt} {2 + 1}}}} }}.$$
(4)

The real contact area Ar is [14]

$$A_{\text{r}} = \int_{0}^{{a_{l} }} {n(a)a{\text{d}}a = \frac{D}{2 - D}} a_{\text{l}} .$$
(5)

If al < ac, the elastic and plastic deformation can be simply rendered as [14]

$$\begin{aligned} A_{\text{re}} = 0, \hfill \\ A_{\text{rp}} = A_{\text{r}} = \frac{D}{2 - D}a_{\text{l}} . \hfill \\ \end{aligned}$$
(6)

If al > ac, the elastic and plastic deformation can be calculated as [14]

$$\begin{aligned} A_{\text{re}} & = \int_{{a_{\text{c}} }}^{{a_{\text{l}} }} {n(a)a{\text{d}}a = \frac{D}{2 - D}(a_{\text{l}} - a_{\text{l}}^{{{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0pt} 2}}} a_{\text{c}}^{{{{(2 - D)} \mathord{\left/ {\vphantom {{(2 - D)} 2}} \right. \kern-0pt} 2}}} )} , \hfill \\ A_{\text{rp}} & = \int_{0}^{{a_{\text{c}} }} {n(a)a{\text{d}}a = \frac{D}{2 - D}a_{\text{l}}^{{{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0pt} 2}}} a_{\text{c}}^{{{{(2 - D)} \mathord{\left/ {\vphantom {{(2 - D)} 2}} \right. \kern-0pt} 2}}} } . \hfill \\ \end{aligned}$$
(7)

2.2 Application of MB Model in Sealing Dynamics

The dynamic schematic of the two mated rings and the geometry of the rotor are depicted in Figure 3. A total of N spiral grooves are processed on the rotor at a depth of δg. The ratio of groove width to the land width is captured by λ = Wg/(Wg + Wl), and the ratio of groove length to the dam length is characterized by β = (rg − ri)/(ro − ri). α is the spiral angle varying from 0 to 180°. ro, ri and rg are outer radius, inner radius and the boundary between groove region and dam region. The gas film thickness of any point (x, y) on the stator h(x, y) is given by h(x, y) = c + <δg>, where c is the central gas film thickness between the coupling rings, and <δg> indicates a δg-deep groove in the groove region. Considering the stiffness and damping properties of springs and the secondary seal, the 1D axial dynamic equation is rendered by [27, 35]

$$m\ddot{c} + c_{\text{sz}} \dot{c} + k_{\text{sz}} c = - F_{\text{closing}} + F_{\text{g}} + F_{\text{c}} ,$$
(8)

where m is the stator mass. ksz is the stiffness of springs. csz is the damping of flexible support. Fclosing is the total load of the pressure-drop-generated fluid load and the spring support load at equilibrium. Fclosing is applied on the back of the stator, balancing the gas film opening load Fg and the face contact load Fc. Fg can be obtained by integrating the gas film pressure p over the nominal sealing area An, rendered as \(F_{g} = \int_{{A_{n} }} {p{\text{d}}A}\). The gas pressure distribution p is governed by the lubrication equation. Assuming the gas flow is ideal and isothermal, and the effect of surface texture is ignored, the compressible Reynolds equation is adopted as [36,37,38]

Figure 3
figure 3

Dynamic schematic of the two mated rings and the geometry of the rotor

Full size image
$$\nabla \cdot \left[ {ph^{3} \nabla p - 6\mu \varOmega rph\varvec{i}_{\uptheta} } \right] - 12\mu \frac{\partial (ph)}{\partial t} = 0,$$
(9)

where μ is the gas viscosity, r is the radius, iθ is the unit vector in θ direction, and Ω is the shaft speed. The boundary conditions to Eq. (9) are

$$p(r = r_{\text{i}} ) = p_{\text{i}} ,\;\;\;p(r = r_{\text{o}} ) = p_{\text{o}} .$$
(10)

For a given gas face seal, the film thickness h measured from the mean plane of asperity height is easily obtained. Majumdar and Bhushan [14] proposed that if the asperity height of a surface follows a Gaussian distribution, h respects the relation as below

$$\frac{{A_{\text{r}} }}{{A_{\text{n}} }} = \frac{1}{\sqrt 2 \pi }\int_{{{h \mathord{\left/ {\vphantom {h \sigma }} \right. \kern-0pt} \sigma }}}^{\infty } {{{e}}^{{{{ - x^{2} } \mathord{\left/ {\vphantom {{ - x^{2} } 2}} \right. \kern-0pt} 2}}} } {\text{d}}x.$$
(11)

Then Eq. (11) can be deduced as

$$\begin{aligned} \frac{{A_{\text{r}} }}{{A_{\text{n}} }} & = \frac{1}{{\sqrt\uppi }}(\frac{1}{{\sqrt {2\uppi} }}\int_{ - \infty }^{\infty } {{{e}}^{{ - {{x^{2} } \mathord{\left/ {\vphantom {{x^{2} } 2}} \right. \kern-0pt} 2}}} } {\text{d}}x - \frac{1}{{\sqrt {2\uppi} }}\int_{ - \infty }^{{{h \mathord{\left/ {\vphantom {h \sigma }} \right. \kern-0pt} \sigma }}} {{{e}}^{{ - {{x^{2} } \mathord{\left/ {\vphantom {{x^{2} } 2}} \right. \kern-0pt} 2}}} } {\text{d}}x) \hfill \\ & = \frac{1}{{\sqrt\uppi }}(1 - \frac{1}{{\sqrt {2\uppi} }}\int_{ - \infty }^{{{h \mathord{\left/ {\vphantom {h \sigma }} \right. \kern-0pt} \sigma }}} {{{e}}^{{ - {{x^{2} } \mathord{\left/ {\vphantom {{x^{2} } 2}} \right. \kern-0pt} 2}}} } {\text{d}}x) \hfill \\ \end{aligned}$$
(12)

The value of \({{\int_{ - \infty }^{{{h \mathord{\left/ {\vphantom {h \sigma }} \right. \kern-0pt} \sigma }}} {{{e}}^{{ - {{x^{2} } \mathord{\left/ {\vphantom {{x^{2} } 2}} \right. \kern-0pt} 2}}} } {\text{d}}x} \mathord{\left/ {\vphantom {{\int_{ - \infty }^{{{h \mathord{\left/ {\vphantom {h \sigma }} \right. \kern-0pt} \sigma }}} {{\text{e}}^{{ - {{x^{2} } \mathord{\left/ {\vphantom {{x^{2} } 2}} \right. \kern-0pt} 2}}} } {\text{d}}x} {\sqrt {2\uppi} }}} \right. \kern-0pt} {\sqrt {2\uppi} }}\) can be calculated by using an error function erf

$$\frac{1}{{\sqrt {2\uppi} }}\int_{ - \infty }^{{{h \mathord{\left/ {\vphantom {h \sigma }} \right. \kern-0pt} \sigma }}} {{{e}}^{{{{ - x^{2} } \mathord{\left/ {\vphantom {{ - x^{2} } 2}} \right. \kern-0pt} 2}}} } {\text{d}}x \approx {\text{erf}}(\frac{h}{\sigma }) = \frac{1}{{1 + {{e}}^{{ - 1.668{h \mathord{\left/ {\vphantom {h \sigma }} \right. \kern-0pt} \sigma }}} }}.$$
(13)

Therefore, the value of Eq. (11) finally becomes

$$\frac{{A_{\text{r}} }}{{A_{\text{n}} }} = \frac{1}{{\sqrt\uppi }}(1 - \frac{1}{{1 + {{e}}^{{{{ - 1.668h} \mathord{\left/ {\vphantom {{ - 1.668h} \sigma }} \right. \kern-0pt} \sigma }}} }}).$$
(14)

The relation between h and al can be obtained from Eqs. (5) and (14)

$$a_{\text{l}} = \frac{{(2 - D)A_{\text{n}} }}{{D\sqrt\uppi }}(1 - \frac{1}{{1 + {{e}}^{{{{ - 1.668h} \mathord{\left/ {\vphantom {{ - 1.668h} \sigma }} \right. \kern-0pt} \sigma }}} }}).$$
(15)

Therefore, for a gas face seal, if h is known, al can be calculated according to Eq. (15). Substituting n(a) from Eq. (4) in Eq. (3), Pc finally becomes

$$P_{\text{c}} = \left\{ {\begin{array}{*{20}ll} \begin{aligned} \frac{{4\sqrt\uppi EDG^{D - 1} a_{\text{l}}^{{{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0pt} 2}}} }}{3(3 - 2D)}\left[ {a_{\text{l}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2} - D}} - a_{\text{c}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2} - D}} } \right] + \frac{{KHDa_{\text{l}}^{{{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0pt} 2}}} }}{2 - D}a_{\text{c}}^{{1 - {D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0pt} 2}}} , \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;D \ne 1.5, \hfill \\ \end{aligned} \\ \begin{aligned} \sqrt\uppi G^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} Ea_{\text{l}}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}}} \ln \frac{{a_{\text{l}} }}{{a_{\text{c}} }} + 3KHa_{\text{l}}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}}} a_{\text{c}}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}} ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;D = 1.5. \hfill \\ \end{aligned} \\ \end{array} } \right.$$
(16)

Note the special condition that if al < ac, all the contact spots are in plastic contact and Pc can be simplified as

$$Pc = \frac{KHDa1}{2 - D}.$$
(17)

Then, the resulting Pc can be used in the sealing dynamics to take the place of Fc in Eq. (8).

All in all, the calculation scheme can be summarized as Figure 4.

Figure 4
figure 4

Calculation scheme

Full size image

3 Results and Discussion

3.1 Test of Fractal Characteristic in Gas Face Seals

As not all rough surfaces own fractal characteristic [46], the precondition for using the MB model in gas face seals is to determine whether the surface of sealing rings own fractal characteristic. Ganti and Bhushan [47] proposed that for an isotropic fractal surface, the study of a section provides complete information about the surface because the fractal dimension D of the rough profile and that of the surface Ds are related as D = Ds + 1, and the profile and surface spectral densities are also related. Therefore, a surface can be characterized by fractal parameters D and G. Here, structure–function method [47] is adopted to analyze the properties of surface profiles. In the structure–function method, structure function S(τ) is defined as

$$S(\tau ) = \left\langle {\left[ {z(x + \tau ) - z(x)} \right]^{2} } \right\rangle = \int_{ - \infty }^{\infty } {S(\omega )} ({{e}}^{{{\text{j}}\omega \tau }} - 1){\text{d}}\omega ,$$
(18)

where τ is an increment of x, and <·> means the space average. Substituting S(ω) from Eq. (1) in Eq. (18) and integrating to yield

$$S(\tau ) = CG^{2(D - 1)} \tau^{4 - 2D} ,$$
(19)

where

$$C = \frac{{\varGamma (2D - 3)\sin \left[ {{{(2D - 3)\uppi} \mathord{\left/ {\vphantom {{(2D - 3)\uppi} 2}} \right. \kern-0pt} 2}} \right]}}{(4 - 2D)\ln \gamma },$$

and Γ is the Gamma function. As the structure function also follows a power law relation, Eq. (19) will transform into a line in the log-log plot of S(τ) ~ τ. If its slope ks satisfies the interval of (0, 2), it reveals that the real surface owns fractal characteristic. Then, the fractal dimension D and the fractal roughness parameter G can be calculated by

$$k_{\text{s}} = 4 - 2D,$$
(20)
$$B_{\text{s}} = \lg CG^{2(D - 1)} ,$$
(21)

where Bs is the intercept.

The surface of an isotropic carbon-graphite ring, serving in an industrial spiral gas-face-seal product, is tested by the Talysuf surface topography measurement system. Three rough profiles spaced 120° apart are tested from inner radius to outer radius. The corresponding log-log plot of S(τ) ~ τ is displayed in Figure 5. The slopes of these three profiles are, respectively, 1.5933, 1.5905 and 1.5823, satisfying the interval of (0, 2) and verifying that the measured surface owns fractal characteristic. Therefore, the MB model can be used in this typical gas face seal. Using Eqs. (20) and (21), the fractal dimension D of the three profiles are, respectively, 1.2034, 1.2048 and 1.2089, and the fractal roughness parameter G are 2.9961 × 10−13 m, 2.1073 × 10−13 m and 3.5568 × 10−13 m, respectively.

Figure 5
figure 5

Results of structure-function method for three rough profiles

Full size image

3.2 Comparison of Steady-state and Transient Sealing Performance

Since face contact occurs under low-speed conditions such as the startup and shutdown operations, and may take place during disturbances [4, 5], the following dynamic simulation is classified into two groups: the steady-state response under low-speed conditions and the transient response to disturbances. Here, the typical operation condition parameter, pressure drop, is taken as the variable. The organized simulation cases are listed in Table 1. Table 2 illustrates the parameters of a spiral groove gas face seal. Table 3 shows the parameters of the CEB and the MB models with respect to the above three profiles. The total contact load of the CEB model is calculated by [9, 48]

Table 1 Simulation cases
Full size table
Table 2 Fundamental parameters of a gas face seal
Full size table
Table 3 Parameters of the CEB and the MB models for three profiles
Full size table
$$\begin{aligned} P_{\text{c}} &= \eta A_{\text{n}} E\frac{4}{3}R^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \int_{{h - y_{\text{s}} }}^{{h - y_{\text{s}} + \omega_{c} }} {(z - h} + y_{s} )^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} \phi (z){\text{d}}z \\ & \quad+ \, \eta A_{\text{n}} E\uppi RK\frac{H}{E}\int_{{h - y_{\text{s}} + \omega_{\text{c}} }}^{\infty } {\left[ {2(z - h + y_{\text{s}} ) - \omega_{\text{c}} } \right]\phi (z){\text{d}}z} , \\ \end{aligned}$$
(22)

where R is the mean summit radius, ys is the distance between the mean of summit height and that of asperity height, ωc is the critical elastic deformation of an asperity, and ϕ is the distribution function of summit height which is assumed to respect a Gaussian distribution. Note that the surface parameters used in the CEB model, as shown in Table 3 and Eq. (22), are calculated referring to Eqs. (A4, A9–A13) in the appendix of Ref. [48] based on three variables m0, m2 and m4. In Ref. [48], m0, m2 and m4 are, respectively, defined as

$$\begin{aligned} m_{0} & = {\text{avg}}[z^{2} (x)], \\ m_{2} & = {\text{avg}}[(\frac{{{\text{d}}z(x)}}{{{\text{d}}x}})^{2} ], \\ m_{4} & = {\text{avg}}[(\frac{{{\text{d}}^{2} z(x)}}{{{\text{d}}x^{2} }})^{2} ]. \\ \end{aligned}$$
(23)

Figure 6(a) displays the dimensionless contact area A *r as a function of the dimensionless contact load P *c using the MB and the CEB approaches, where P *c  = Pc/(AnE) and A *r  = Ar/An. The contact area obtained by the CEB model is greater than that obtained by the MB model at the same contact load. The deviation between the two is in the same order of magnitude with the results of simulated surfaces in Figure 2 of Ref. [21]. It can be seen that the results obtained by the CEB model have fine distinctions, while those obtained by the MB model are overlapped. It is because that the dimensionless critical area of the asperity a *c (a *c  = ac/An) in the MB model is about 10−1 under current fractal parameters. When P *c increases from 10−7 to 10−3, the dimensionless largest area a *l (a *l  = al/An) in the MB model increases from about 10−6 to 10−2. In the MB model, it means that all the contact spots are smaller than the critical contact area, leading to full plastic contact. Thus, only the second term of Eq. (16) for plastic contact is available, and the distinction of G in Table 3 is not involved. One may wonder the explanation about the full plastic deformation, yet this phenomenon has also occurred in the case with D = 1.1 in Figure 10 of Ref. [14], and explained by Majumdar and Bhushan that the load-area relation and the fraction of the contact area in elastic and plastic deformation are quite sensitive to fractal parameters [14]. This difference between the MB and the CEB approaches shows that the two approaches have distinctions in contact mechanism and end face damage regardless of the degree of distinctions in dynamic performance including film thickness, leakage rate and face contact load. Figure 6(b) shows the dimensionless gas film thickness h/σ as a function of the dimensionless contact load P *c . It is obvious that the gas film thickness of the CEB model is smaller than that of the MB model at the same contact load. When P *c is about 10−7, the face contact load is too small to be considered. By this, h/σ is about 4.0 in the CEB model and 6.6 in the MB model. It means that if h/σ was in the interval of (4.0, 6.6), the MB model would provide a face contact load in the dynamic analysis whilst the CEB model would not. Therefore, it can be expected that there will be an apparent difference between the two approaches in the occurrence of face contact, which will be shown in the subsequent simulation under low-speed conditions.

Figure 6
figure 6

Dimensionless contact area and gas film thickness as a function of the dimensionless contact load using the MB and the CEB approaches. a dimensionless contact area; b dimensionless gas film thickness

Full size image

Profile 3 is selected to gauge the differences of sealing performance between the MB and the CEB approaches. A whole-ring numerical model is established for the dynamic analyses of a spiral groove gas face seal with a flexibly mounted stator using the finite element method. In regards to the accuracy and stability of a complex dynamic system, a very fine mesh and a very small time step would be ideal. Yet, a balance should be struck between accuracy and computing time. After experiments, it is determined that a time step of 1 × 10−6 s with a 3160-finite element mesh is adopted. The simulation is carried out on a 2.3 GHz workstation.

Figure 7 shows the differences of steady-state performance using the MB and the CEB approaches under different pressure drops where the shaft speed Ω maintains at 31.4 rad/s. The leakage rate Qi is r = (ri + rg)/2 referring to the relationship

$$\frac{{M_{\text{gas}} }}{{R_{\text{gas}} T_{\text{gas}} }}\oint {\frac{{ph^{3} }}{12\mu }(\frac{\partial p}{\partial x}\frac{x}{{\sqrt {x^{2} + y^{2} } }} + \frac{\partial p}{\partial y}\frac{y}{{\sqrt {x^{2} + y^{2} } }})} {\text{d}}l.$$

Mgas is the molar mass set to 29 g/mol, Rgas is the gas constant set to 8.314 J mol−1 K−1, and Tgas is gas temperature set to 293 K. There is no difference under the non-pressure-drop condition (po = pi = 0.1 MPa) because the gas film opening load Fg are able to balance the closing load Fclosing at equilibrium and the face contact load Fc is zero. When po increases in Figure 7(b), Fc transforms into a non-zero value and its proportion in the total opening load rises. The larger the proportion of Fc, the more apparently the deviations display in the central film thickness at equilibrium and face contact load. However, after po reaching 5 MPa, the deviations of the two approaches in the central film thickness at equilibrium and face contact load start to decrease because the proportion of Fc obtained by the MB model starts to decrease, accounting for Fg becoming the dominant component of the total opening load again. The deviation in leakage rate still increases monotonically because the leakage rate is related to not only the film thickness but also the pressure drop. Moreover, it should be emphasized that before po arriving at 1 MPa, Fc obtained by the MB model starts to transform into a value of 40 N whilst Fc obtained by the CEB model is still maintains at nearly zero, which is in accordance with the prediction in Figure 6(b). It is concluded that the two approaches will induce differences in terms of the occurrence and the level of face contact.

Figure 7
figure 7

Steady-state performance under different pressure drops where the shaft speed Ω maintains at 31.4 rad/s using the MB and the CEB approaches. a central film thickness at equilibrium c0 and leakage rate at inner radius Qi; b face contact load Fc and its proportion in the total opening load

Full size image

Figure 8 illustrates the differences of transient performance using the MB and the CEB approaches during a fluctuation of pressure drop (i.e., po, instantaneously, raises from 1 to 2 MPa at 0.01 s) where shaft speed Ω maintains at 104.7 rad/s. The value of 104.7 rad/s is large enough to guarantee the completely opened state of the two mated rings. From the simulation case without the contact model, it can be seen that the fluctuation of pressure drop induces oscillations in the central film thickness and leakage rate. After coupling the contact model, face contact occurs. In Figure 8(b), the face contact load obtained by the MB model is greater than that obtained by the CEB model at the same film thickness under current sealing parameters, which is in accordance with Figure 6(b). When c decreases with an instantaneous increase of po, Fc obtained by the MB model occurs earlier and is greater at the same film thickness than that obtained by the CEB model. These lead to a result that the stator in the MB approach returns to a stable state faster and its oscillation amplitude is smaller. Moreover, though the distinctions of the two approaches about the oscillation amplitude and oscillation time are tiny in terms of film thickness and leakage rate, the distinction in the face contact load is apparent. A greater face contact load obtained by the MB model indicates that the surface of the seal would undergo much more severe wear during the fluctuation. Therefore, here, the dynamics using the CEB model will offer a more optimistic consideration of face wear than the dynamics using the MB model.

Figure 8
figure 8

Transient performance during a fluctuation of pressure drop where shaft speed Ω maintains at 104.7 rad/s using the MB and the CEB approaches. a central film thickness c; b face contact load Fc; c leakage rate at inner radius Qi

Full size image

To sum up, the MB and the CEB approaches induce different steady-state and transient performance in the dynamic simulation. In particular, under current sealing parameters, even if the distinctions of the two approaches in film thickness and leakage rate are tiny, the two approaches will induce apparent differences in the occurrence and the level of face contact, which affect contact mechanism and end face damage. In addition, since not all surfaces own fractal characteristic, it should be emphasized that the use of the MB model in other types of seals or other fields has an extra limitation.

3.3 Investigation of Fractal Characteristic

Adhesive wear is a significant physical phenomenon in the dynamic analyses of gas face seals for its effect on the end face damage and service life. As adhesive wear is more easily caused by plastic deformation, it is better to raise the proportion of elastic deformation in the face contact. In the MB model, a feasible approach to raise the proportion of elastic deformation is to control the fractal parameters D and G. Therefore, a parametric investigation of D and G is performed. Note that the present study focuses on the influence of D and G on the proportion of elastic deformation. The detailed approach to realize the control of D and G should be researched in the manufacture-process field.

The dimensionless form of total contact load in the MB model is rendered as [14]

$$P_{c}^{*} = \left\{ \begin{aligned} &\frac{{4\sqrt\uppi }}{3}G^{*D - 1} g_{1} A_{\text{r}}^{{*{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0pt} 2}}} \left[ \begin{aligned} (\frac{2 - D}{D})^{{{{(1 - D)} \mathord{\left/ {\vphantom {{(1 - D)} 2}} \right. \kern-0pt} 2}}} A_{\text{r}}^{{*{{(3 - 2D)} \mathord{\left/ {\vphantom {{(3 - 2D)} 2}} \right. \kern-0pt} 2}}} \hfill \\ - a_{\text{c}}^{{*{{(3 - 2D)} \mathord{\left/ {\vphantom {{(3 - 2D)} 2}} \right. \kern-0pt} 2}}} \hfill \\ \end{aligned} \right]\; \hfill \\ & + \,\frac{KH}{E}g_{2} A_{\text{r}}^{{*{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0pt} 2}}} a_{\text{c}}^{{*{{(2 - D)} \mathord{\left/ {\vphantom {{(2 - D)} 2}} \right. \kern-0pt} 2}}} , \hfill \\ & \quad \quad a_{\text{l}} > a_{\text{c}} \;\text {and}\;D \ne 1.5, \hfill \\ & \sqrt\uppi G^{{*{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} (\frac{{A_{\text{r}}^{*} }}{3})^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}}} \ln \frac{{A_{\text{r}}^{*} }}{{3a_{\text{c}}^{*} }} + \frac{3KH}{4E}(\frac{{A_{\text{r}}^{*} }}{3})^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}}} a_{\text{c}}^{{*{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}} , \hfill \\ & \quad \quad a_{l} > a_{\text{c}} \;\text {and}\;D = 1.5, \hfill \\ &\frac{KH}{E}A_{\text{r}}^{*} ,\quad a_{\text{l}} < a_{\text{c}} , \hfill \\ \end{aligned} \right.$$
(24)

where

$$\begin{aligned} G^{*} & = \frac{G}{{\sqrt {A_{\text{n}} } }}, \hfill \\ a_{\text{c}}^{*} & = \frac{{G^{*2} }}{{({{KH} \mathord{\left/ {\vphantom {{KH} {2E}}} \right. \kern-0pt} {2E}})^{{{2 \mathord{\left/ {\vphantom {2 {(D - 1)}}} \right. \kern-0pt} {(D - 1)}}}} }}, \hfill \\ g_{1} & = \frac{D}{3 - 2D}(\frac{2 - D}{D})^{{{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0pt} 2}}} , \hfill \\ g_{2} & = (\frac{D}{2 - D})^{{{{(2 - D)} \mathord{\left/ {\vphantom {{(2 - D)} 2}} \right. \kern-0pt} 2}}} . \hfill \\ \end{aligned}$$
(25)

Therefore, the proportion of elastic deformation can be deduced from Eqs. (2), (5), (7), (24) and (25)

$$\frac{{A_{\text{re}} }}{{A_{\text{r}} }} = 1 - \left[ {\frac{{DG^{*2} }}{{(2 - D)(\frac{KH}{2E})^{{{2 \mathord{\left/ {\vphantom {2 {(D - 1)}}} \right. \kern-0pt} {(D - 1)}}}} A_{\text{r}}^{*} }}} \right]^{{{{(2 - D)} \mathord{\left/ {\vphantom {{(2 - D)} 2}} \right. \kern-0pt} 2}}} .$$
(26)

The values of D and G* are assumed within a common range, and other material properties are still selected from Table 2. Figure 9(a) shows the influence of D on the asperity contact where G* maintains at 10−10. The case with D = 1.5 has the greatest proportion of elastic contact area at the same A *r . In the MB model, contact spots will be in plastic deformation when a < ac. When D increases from 1.3 to 1.5, ac decreases according to Eq. (2). It leads to the result that more and more contact spots transform from plastic deformation into elastic deformation. However, after D reaching 1.5, the positive effect caused by the decrease of ac is surpassed by the negative effect caused by the refining of surface topography, leading to more spots in plastic deformation. With respect to the above negative effect, Majumdar and Bhushan [14] found that with the increase of D, the number of contact spots below the critical size increases and the contribution of these contact spots to the total contact area is significant. Figure 9(b) shows the influence of G* on the asperity contact when D maintains at 1.5. It can be seen that the proportion of elastic contact area increases as G* decreases because ac decreases with a decrease of G* according to Eq. (2). Since ac decreases, a large amount of contact spots transform from plastic deformation into elastic deformation. It is concluded that a proper D (nearly 1.5) and a small G are helpful for maximizing the proportion of elastic deformation.

Figure 9
figure 9

Transient influence of parameter D and G* on the proportion of elastic deformation. a investigation of D (G* = 10−10); b investigation of G* (D = 1.5)

Full size image

4 Conclusions

  1. (1)

    Fractal asperity contact model can provide an asperity contact load out of the influence of measuring instruments or sample length for its scale-independence. It also uses an assumption of variable curvature radius. The MB fractal contact model is selected as the representative of fractal contact models in the attempt of incorporating the fractal theory into the dynamic research of gas face seals.

  2. (2)

    Structure-Function method is adopted to process the surface profiles of a typical carbon-graphite ring which is an industrial product, proving the MB model can be utilized in the typical gas face seals.

  3. (3)

    The CEB statistical model is selected to compare with the MB model to gauge the differences of the two approaches in dynamic performance. The MB and the CEB approaches will induce differences in terms of the occurrence and the level of face contact. Although the distinctions in film thickness and leakage rate may be tiny, the distinctions in contact mechanism and end face damage are apparent. The CEB approach offers a more optimistic consideration of face contact.

  4. (4)

    An investigation of fractal parameters D and G is performed to explore a feasible approach to raise the proportion of elastic deformation to weaken adhesive wear in the sealing dynamic performance.