Abstract
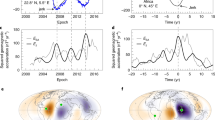
Rapid changes in the magnetic field characterised by an abrupt change in the secular variation have been named “secular variation impulses” or “geomagnetic jerks”. Three of these events, around 1968, 1978 and 1990, occurred during the time-span covered by the comprehensive model CM4 (Sabaka et al., 2002, 2004). This model, providing the best temporal resolution between 1960 and 2002 as well as a fine separation of the different magnetic sources, can be used to study rapid phenomena of internal origin. In order to analyse these events all over the globe, synthetic time series were obtained from the CM4 model between 1960–2002. Geomagnetic jerks are detected here as a rapid movement of the zero isoline of the second field derivative. Analysis of the area swept out by this isoline as a function of time allows us to map the spatial extent of jerks though time, and to identify an event around 1985 that is localized in the Pacific area. At the core surface, we compute the fluid flows under the frozen-flux and tangentially geostrophic assumptions. The flows do not exhibit any special pattern at jerk times, but instead show a smooth temporal evolution over the whole time period. However, the mean amplitude of the dynamical pressure associated with these flows present maxima at each jerk occurrence and helps to confirm the identification of a jerk in 1985.
Article PDF
Similar content being viewed by others
References
Achache, J., V. Courtillot, J. Ducruix, and J.-L. Le Mouël, The late 1960’s secular variation impulse: Further constraints on deep mantle conductivity, Phys. Earth Planet. Inter., 23, 72–75, 1980.
Alexandrescu, M., D. Gibert, G. Hulot, J.-L. Le Mouël, and G. Saracco, Detection of geomagnetic jerks using wavelet analysis, J. Geophys. Res., 100(B7), 12557–12572, 1995.
Alexandrescu, M., D. Gibert, G. Hulot, J.-L. Le Mouël, and G. Saracco, Worldwide wavelet analysis of geomagnetic jerks, J. Geophys. Res., 101, 21975–21994, 1996.
Alldredge, L. R., A discussion of impulses and jerks in the geomagnetic Field, J. Geophys. Res., 89, 4403–4412, 1984.
Alldredge, L. R., More on the alleged 1970 geomagnetic jerk, Phys. Earth Planet. Inter., 39, 255–264, 1985.
Amit, H. and P. Olson, Helical core flow from geomagnetic secular variation, Phys. Earth Planet. Inter., 147, 1–25, 2004.
Backus, G. E., Application of mantle filter theory to the magnetic jerk of 1969, Geophys. J. R. Astron. Soc, 74, 713–746, 1983.
Backus, G. E. and J.-L. Le Mouël, The region on the core-mantle boundary where a geostrophic velocity field can be determined from frozen flux magnetic data, Geophys. J. R. Astr. Soc, 85, 617–628, 1986.
Backus, G. E. and J.-L. Le Mouël, The region on the core-mantle boundary where a geostrophic velocity field can be determined from frozen-flux magnetic data-Addendum, Geophys. J. R. Astron. Soc, 88, 321–322, 1987.
Backus, G. E., R. H. Estes, D. Chinn, and R. A. Langel, Comparing the jerk with other global models of the geomagnetic Field from 1960 to 1978, J. Geophys. Res., 92, 3615–3622, 1987.
Bellanger, E., J.-L. Le Mouël, M. Mandea, and S. Labrosse, Chandler Wobble and geomagnetic Jerks, Phys. Earth Planet. Inter., 124, 95–103, 2001.
Blakely, R., Potential theory in gravity and magnetic applications, Cambridge University Press, 1995.
Bloxham, J., On the consequences of strong stable stratification at the top of the Earth’s outer core, Geophys. Res. Lett., 17, 2081–2084, 1990.
Bloxham, J., S. Zatman, and M. Dumberry, The origin of geomagnetic jerks, Nature, 420, 65–68, 2002.
Chambodut, A., Le champ magnétique terrestre: structures spatiales et variations temporelles vues par les Ondelettes, Ph.D. thesis, Institut de Physique du Globe de Paris, 2004.
Chambodut, A. and M. Mandea, Evidence for geomagnetic jerks in comprehensive models, Earth Planets Space, 57, 139–149, 2005.
Courtillot, V., J. Ducruix, and J.-L. Le Mouël, Surune accélération récente de la variation séculaire du champ magnétique terrestre, C. R. Hebd. Séances Acad. Sci., ser. D, 287, 1095–1098, 1978.
Courtillot, V. and J.-L. Le Mouël, Comment on “discussion of impulses and jerks in the geomagnetic field” by L. R. Alldredge, J. Geophys. Res., 90, 6897–6898, 1985.
Courtillot, V., J.-L. Le Mouël, and J. Ducruix, On Backus’ mantle filter theory and the 1969 geomagnetic impulse, Geophys. J. Roy. Astron. Soc, 78, 619–624, 1984.
Davis, R. and K. Whaler, Velocity fields at the Earth’s core surface from 1900 to 1980 using the frozen-flux approximation and steady velocity assumption, Geophys. Astrophys. Fluid Dynamics, 67, 241–258, 1993.
Davis, R. and K. Whaler, The 1969 geomagnetic impulse and spin-up of the Earth’s liquid core, Phys. Earth Planet. Inter., 103, 181–194, 1997.
De Michelis, P., L. Cafarella, and A. Meloni, Worldwide character of the 1991 geomagnetic jerk, Geophys. Res. Lett., 25, 377–380, 1998.
Eymin, C, Etude des mouvements à la surface du noyau terrestre: du 17ème au 21ème siècle, Ph.D. thesis, Université Paris VI, 2004.
Eymin, C. and G. Hulot, On core surface flows inferred from satellite magnetic data, Phys. Earth Planet. Inter., 152, 200–220, 2005.
Gavoret, J., D. Gibert, M. Menvielle, and J.-L. Le Mouël, Long-term variations of the external and internal components of the Earth’s magnetic field, J. Geophys. Res., 91, 4787–4796, 1986.
Gire, C, Sur la variation séculaire du champ magnétique terrestre et les mouvements des couches externes du noyau fluide, Ph.D. thesis, University of Paris 7, 1985.
Gire, C, J.-L. Le Mouël, and T. Madden, Motions of the core surface derived by SV data, Geophys. J. R. Astron. Soc, 84, 1–29, 1986.
Gire, C. and J.-L. Le Mouël, Tangentially geostrophic flow at core-mantle boundary compatible with the observed geomagnetic secular variation: The large-scale component of the flow, Phys. Earth Planet. Inter., 59, 259–287, 1990.
Golovkov, V P., T. I. Zvereva, and A. O. Simonyan, Common features and differences between jerks of 1947, 1958 and 1969, Geophys. Astrophys. Fluid Dyn., 49, 81–96, 1989.
Gubbins, D., Finding core motions from magnetic observations, Phil. Trans. R. Soc. Lond., A306, 247–254, 1982.
Gubbins, D., Geomagnetic field analysis — II. Secular variation consistent with a perfectly conducting core, Geophys. J. Roy. Astron. Soc, 77, 753–766, 1984.
Hills, R. G., Convection in the Earth’s mantle due to viscous shear at the core-mantle interface and due to large-scale buoyancy, Ph.D. thesis, New Mexico State University, Las Cruces, 1979.
Holme, R. and K. Whaler, Steady core flow in an azimuthally drifting reference frame, Geophys. J. Int., 145, 560–569, 2001.
Hulot, G., M. Le Huy, and J.-L. Le Mouël, Secousses (jerks) de la variation séculaire et mouvements dans le noyau terrestre, C. R. Acad. Sci., 317, 333–341, 1993.
Jackson, A., Time-dependency of tangentially geostrophic core surface motions, Phys. Earth Planet. Inter., 103, 293–311, 1997.
Jackson, A., A. Jonkers, and M. Walker, Four centuries of geomagnetic secular variation from historical records, Phil. Trans. R. Soc. Lond., 358, 957–990, 2000.
Jault, D., Variation séculaire du champ géomagnétique et fluctuations de la longueur du jour, Ph.D. thesis, Universite Paris VII, 1990.
Le Huy, M., M. Mandea, G. Hulot, and J. Le Mouël, On the characteristics of successive geomagnetic jerks, Earth Planets Space, 50, 723–732, 1998.
Le Huy, M., M. Mandea, J.-L. Le Mouël, and A. Pais, Time evolution of the fluid flow at the top of the core—Geomagnetic jerks, Earth Planets Space, 52, 163–173, 2000.
Le Mouël, J.-L., Outer-core geostrophic flow and secular variation of Earth’s geomagnetic field, Nature, 311, 734–735, 1984.
Le Mouël, J.-L., C. Gire, and T. Madden, Motions at the core surface in the geostrophic approximation, Phys. Earth planet. Inter., 39, 270–287, 1985.
Macmillan, S., A geomagnetic jerk for the early 1990’s, Earth Planet. Sci. Lett., 137, 189–192, 1996.
Malin, S. and B. Hodder, Was the 1970 geomagnetic jerk of internal or external origin?, Nature, 296, 726–728, 1982.
Malin, S., B. Hodder, and D. Barraclough, Geomagnetic variation: a jerk in 1970, in 75th Anniversary Volume ofEbro Observatory, edited by J. O. Cardus, 239–256, Ebro Obs., Tarragona, Spain, 1983.
Mandea, M., E. Bellanger, and J.-L. Le Mouël, A geomagnetic jerk for the end of the 20th century?, Earth Planets Space Letters, 183, 369–373, 2000.
Mandea Alexandrescu, M., D. Gibert, J.-L. Le Mouël, G. Hulot, and G. Saracco, An estimate of average lower mantle conductivity by wavelet analysis of geomagnetic jerks, J. Geophys. Res., 104, 17735–17745, 1999.
McLeod, M., On the geomagnetic jerk of 1969, J. Geophys. Res., 90 (B6), 0148–0227, 1985.
Menke, W, Geophysical data analysis: Discrete inverse theory, Academic Press, 1984.
Nagao, H., T. Iyemori, T. Higuchi, S. Nakano, and T. Araki, Local time features of geomagnetic jerks, EarthPlanets Space, 54, 119–131, 2002.
Nagao, H., T. Iyemori, T. Higuchi, and T. Araki, Lower mantle conductivity anomalies estimated from geomagnetic jerks, J. Geophys. Res., 108, 2254, 2003.
Olsen, N. and M. Mandea, Investigation of a secular variation impulse using satellite data: The 2003 geomagnetic jerk, Earth Planet. Sci. Lett., 255, 94–105, doi:10.1016/j.epsl.2006.12.008, 2007.
Pais, A. and G. Hulot, Length of day decade variations, torsional oscillations and inner core superrotation: Evidence from recovered core surface zonal flows, Phys. Earth Planet. Inter, 118, 291–316, 2000.
Pais, M. A., O. Oliveira, and F. Nogueira, Non-uniqueness of inverted CMB flows and deviations from tangential geostrophy, J. Geophys. Res, 109, B08105-1-B08105-20, 2004.
Roberts, P. H. and S. Scott, On the analysis of the secular variation: 1. A hydromagnetic constraint: theory, J. Geomagn. Geoelectr., 17, 137–151, 1965.
Sabaka, T, N. Olsen, and R. A. Langel, A comprehensive model of the quiet-time, near-Earth magnetic field: phase 3, Geophys. J. Int., 151, 32–68, 2002.
Sabaka, T., N. Olsen, and M. Purucker, Extending Comprehensive Models of the Earth’s Magnetic Field with Ørsted and CHAMP data, Geophys. J. Int., 159, 521–547, doi: 10.1111/j.1365246X.2004.02,421.x, 2004.
Voorhies, C. V, Magnetic Location of Earth’s Core-Mantle Boundary and Estimates of the Adjacent Fluid Motion, Ph.D. thesis, University of Colorado, 1984.
Voorhies, C. V, Steady flows at the top of Earth’s core derived from geomagnetic field models, J. Geophys. Res., 91, 12 444–12 466, 1986.
Voorhies, C. V, Coupling an Inviscid Core to an Electrically Insulating Mantle, J. Geomagn. Geoelectr., 43, 131–156, 1991.
Voorhies, C. V, Time-varying fluid-flow a the top of Earth’s core derived from definitive geomagnetic reference field models, J. Geophys. Res., 100, 10,029–10,039, 1995.
Voorhies, C. V, Narrow-scale flow and a weak field by the top of Earth’s core: Evidence from Ørsted, Magsat, and secular variation, J. Geophys. Res., 109, B03106, doi:10.1029/2003JB002833, 2004a.
Voorhies, C. V, Correction to Narrow-scale flow and a weak field by the top of Earth’s core: Evidence from rsted, Magsat, and secular variation, J. Geophys. Res., 109, B08103, doi:10.1029/2004JB003289, 2004b.
Voorhies, C. V and G. E. Backus, Steady flows at the top of the core from geomagnetic-field models the steady motions theorem, Geophys. Astrophys. Fluid Dyn., 32, 163–173, 1985.
Waddington, R., D. Gubbins, and D. Barber, Geomagnetic field analysis—5. Determining steady core-surface flows directly from geomagnetic observations, Geophys. J. Int., 122, 326–350, 1995.
Wessel, P. and W. H. F. Smith, Free software helps map and display data, Eos Trans. AGU, 72, 1991.
Whaler, K. A., Does the whole of the Earth’s core convect?, Nature, 287, 528–530, 1980.
Author information
Authors and Affiliations
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chambodut, A., Eymin, C. & Mandea, M. Geomagnetic jerks from the Earth’s surface to the top of the core. Earth Planet Sp 59, 675–684 (2007). https://doi.org/10.1186/BF03352730
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1186/BF03352730