Abstract
Blind identification of MIMO FIR systems has widely received attentions in various fields of wireless data communications. Here, we use Particle Swarm Optimization (PSO) as the update mechanism of the well-known inverse filtering approach and we show its good performance compared to original method. Specially, the proposed method is shown to be more robust against lower SNR scenarios or in cases with smaller lengths of available data records. Also, a modified version of PSO is presented which further improves the robustness and preciseness of PSO algorithm. However the most important promise of the modified version is its drastically faster convergence compared to standard implementation of PSO.
Similar content being viewed by others
1. Introduction
This paper addresses the problem of blind identification of multi-input-multi-output (MIMO) channels in the general scenario, where all of the  observed signals
observed signals  are considered to be convolutive mixtures of
are considered to be convolutive mixtures of  unknown, yet statistically independent sources
unknown, yet statistically independent sources  .This is often the case in typical echoic environments, where each sensor captures not only the direct contributions from each source, but also several reflected versions of the original signals with totally different propagation delays. The blindness here means that we have no prior knowledge about the MIMO system and no training data is available. The
.This is often the case in typical echoic environments, where each sensor captures not only the direct contributions from each source, but also several reflected versions of the original signals with totally different propagation delays. The blindness here means that we have no prior knowledge about the MIMO system and no training data is available. The  th observed mixture can be written as
th observed mixture can be written as

Here  is additive white Guassian noise and
is additive white Guassian noise and  are tap weight coefficients of channel impulse response from
are tap weight coefficients of channel impulse response from  th source to the
th source to the  th sensor. Each subchannel of the MIMO system can be written in
th sensor. Each subchannel of the MIMO system can be written in  domain as
domain as  .
.
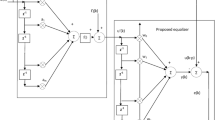
Inverse filtering approach [1] consists of an iterative solution, which recursively extracts sources from the mixture one by one and then following the estimation of experienced channel by any extracted source, and reconstructs this signal as it was originally observed on each sensor. Now, after reduction of reconstructed sources from sensor measurements, the same procedure can be used for extraction of remaining sources. The source extraction step is down by the steepest descent maximization of a class of cumulant-based cost functions with respect to coefficients of equalizer filters. However, this optimization strategy is prone to being trapped in local maxima, especially in lower SNR scenarios or when the available data record is too small [1].
An alternative to this gradient-based optimization is a structured stochastic search of the objective function space. These types of global searches are structure independent because a gradient is not calculated and the adaptive filter structure does not directly influence the parameter updates. Due to this property these types of algorithms are potentially capable of globally optimizing any class of objective functions [2]. Particle Swarm Optimization (PSO) is one of these stochastic structured search algorithms that have recently gained popularity for optimization problems.
This paper investigates the application of PSO technique in source extraction step of the above-mentioned procedure for mutually independent, zero mean i.i.d binary sequences. It should be noted that although [3] has addressed the same subject, but its update equation seems more like a heuristic method which employs a random weighted addition of gradients based on second-order statistics and prediction methods, while PSO is defined as cooperative random search of particles toward their current global and local best points in search space according to some fitness function [4] as it will be discussed in Section 3.1 and simple multiplication of update equation by a random number (as in [3]) does not represent the essence of global random search suggested by PSO.
In this paper, after studying the suitability of standard PSO for blind identification problem, we propose a modified version which finds its initial direction according to original gradient-based method in [1]. In fact the promised random search of PSO will be limited to smaller local areas with the most probability of maximizing the cost function. Also we modify the original fitness function used in [1, 3] by two supportive performance indexes in order to reduce the probability of algorithm failures which are the result of complete ignorance of original objective function about the existence of additive noise.
2. Iterative Source Extraction and Channel Estimation
In this section, we provide a detailed description of inverse filtering approach. Note that here we neglect the presence of noise  in (1). Consider that a
in (1). Consider that a  row vector
row vector  , with its
, with its  th element
th element  , operates on observed data vector
, operates on observed data vector  to construct equalizer output as
to construct equalizer output as

Here 
 are elements of the overall impulse response from
are elements of the overall impulse response from  th source to equalizer output:
th source to equalizer output:

Based on third- and fourth- order cumulant of equalizer output, [1] introduced a set of objective functions  as
as

Here  is
is  th order cumulant of the equalizer output. The following upper bound has derived in [1] for
th order cumulant of the equalizer output. The following upper bound has derived in [1] for 

Here,  . Equality of (5) holds when the overall transfer function becomes
. Equality of (5) holds when the overall transfer function becomes

So the maximization of  with respect to equalizer coefficients
with respect to equalizer coefficients  leads to extraction of one of the sources on equalizer output up to a scaled and delayed version as
leads to extraction of one of the sources on equalizer output up to a scaled and delayed version as

This separation criteria, however, has the weakness of complete ignorance about the presence of noise. Authors in [1] have developed their theoretical proof about suitability of the above-mentioned objective function based on the assumption that the noise  in (1) is negligible. This is the reason for poor performance of their proposed iterative, batch, steepest descent method
in (1) is negligible. This is the reason for poor performance of their proposed iterative, batch, steepest descent method  optimization at lower SNRs.
optimization at lower SNRs.
If we consider the presence of noise  in (1), the addition of the term
in (1), the addition of the term  to
to  of (2) will destruct the validity of theoretical proof in [1]. In fact when noise is dominant in sensor measurements, cooperation of this noise with equalizer coefficients may build up new fake maxima into
of (2) will destruct the validity of theoretical proof in [1]. In fact when noise is dominant in sensor measurements, cooperation of this noise with equalizer coefficients may build up new fake maxima into  regardless of overall impulse response
regardless of overall impulse response  and in this new maximum, separation point of (6) is no longer achievable.
and in this new maximum, separation point of (6) is no longer achievable.
However it is obvious that (6) would still provide local maximum for  and separation would be met if we could somehow control the algorithm from trapping into these new maximum as it will be explained in Section 3.2.
and separation would be met if we could somehow control the algorithm from trapping into these new maximum as it will be explained in Section 3.2.
After extraction of each source, the estimated signal can be used for estimation of the experienced channel by that signal through its way to each sensor:

Now, the third step is to reconstruct the extracted source as it was originally observed on each sensor in order to suppress its contribution from sensor observations:

Hereafter, the same procedure can be used for extraction of remaining sources and then estimating the SIMO channel experienced by any one of them.
3. Particle Swarm Optimization
3.1. PSO Principles
Particle swarm optimization [2] is a stochastic, population-based evolutionary algorithm for problem solving in complex multidimensional parameter spaces. It is a kind of swarm intelligence that is based on social-psychological principles.
A multidimensional optimization problem is given, along with an objective function to evaluate the fitness of each candidate point in parameter space; the swarm is typically modeled by particles in this multidimensional space that have a position and a velocity. After the definition of a random population of individuals (particles) as candidate solutions, they fly through hyperspace of parameters with the aid of two essential reasoning capabilities: their memory of their own best local position and knowledge of the global or their neighborhood's best [5].
PSO begins by initializing a random swarm of  particles
particles  , each having
, each having  parameters. At each iteration, the fitness of each particle is evaluated according to selected fitness function. The fittest experienced position of each particle is stored and progressively replaced as
parameters. At each iteration, the fitness of each particle is evaluated according to selected fitness function. The fittest experienced position of each particle is stored and progressively replaced as  along with a single most globally fit particle (
along with a single most globally fit particle ( as fitter locations are encountered during algorithm iterations. The parameters of each particle in the swarm are updated at each iteration
as fitter locations are encountered during algorithm iterations. The parameters of each particle in the swarm are updated at each iteration  according to a velocity vector as [6]
according to a velocity vector as [6]


Here,  is the velocity vector of particle
is the velocity vector of particle  ,
,  is a random value,
is a random value,  are acceleration coefficients toward
are acceleration coefficients toward  and
and  and
and  is the inertia weight.
is the inertia weight.
In fact, the trajectory of each particle is determined by random superposition of its previous velocity with the location of local and global best particles found by far. As new  are encountered during the update process, all other particles begin to swarm toward this new
are encountered during the update process, all other particles begin to swarm toward this new  , continuing their random search along the way. The optimization is terminated when all of the particles have converged to
, continuing their random search along the way. The optimization is terminated when all of the particles have converged to  or a sufficient condition of fitness function met:
or a sufficient condition of fitness function met:
3.2. Implementation of PSO for Source Extraction
We propose to use PSO as optimization method for maximization of  with respect to coefficients of parallel equalizers (
with respect to coefficients of parallel equalizers ( ,
,  ,
,  ) as
) as  dimensional particles.
dimensional particles.
Clearly  of (4) seems a reasonable choice of fitness function since in the absence of noise, its maximization provides pure separation of the source
of (4) seems a reasonable choice of fitness function since in the absence of noise, its maximization provides pure separation of the source  at multichannel equalizer output. But as it is mentioned in Section 2 this objective function fails in low SNR scenarios and would have several fake maxima with respect to equalizer coefficients. Also the steepest gradient method of [1] has shown poor performance in cases with limited number of available data samples.
at multichannel equalizer output. But as it is mentioned in Section 2 this objective function fails in low SNR scenarios and would have several fake maxima with respect to equalizer coefficients. Also the steepest gradient method of [1] has shown poor performance in cases with limited number of available data samples.
The simplicity of PSO suggests that we can easily combine several objective functions for further evaluation of the true level of fitness of a candidate particle in order to stay aside from the trap of fake global maxima in the case of noisy and smaller length records of data. For instance, since we expect complete deconvolution of extracted source at each iteration, a simple choice is to evaluate the level of correlation between successive samples of equalizer output. It is clear that there will be no time dependency between successive samples at ideal point of separation and deconvolution as in (5). It allows us to exploit signal correlations at nonzero lags as in [7]. Specifically we expect the following cost function to converge to zero when the true separation met.

Also we can use histogram of equalizer output as a clue for leading particles toward desired solution. For the assumed equiprobable sequence of  we expect the histogram of the equalized output to have a form like Figure 1 which shows the histogram of one of the successfully extracted sources in high SNR scenario. In lower SNR cases, when algorithms fails this histogram finds irregular Gaussian like shapes as in Figure 2. Two important differences between these two histograms exist: first, the concentration of histogram in Figure 2 around zero and second, the existence of infrequent extreme deviations as few points which are larger than 2.
we expect the histogram of the equalized output to have a form like Figure 1 which shows the histogram of one of the successfully extracted sources in high SNR scenario. In lower SNR cases, when algorithms fails this histogram finds irregular Gaussian like shapes as in Figure 2. Two important differences between these two histograms exist: first, the concentration of histogram in Figure 2 around zero and second, the existence of infrequent extreme deviations as few points which are larger than 2.
Then as another measure of fitness, we can use the frequency of occurrence of samples with very small absolute values (smaller than 0.2 e.g.,) or with values larger than 2 as fitness parameter  . Here by frequency of occurrence we mean the number of occurrences. Now, our overall fitness function of particles
. Here by frequency of occurrence we mean the number of occurrences. Now, our overall fitness function of particles  is defined as
is defined as

Here  ,
,  are approximately small coefficients and their selection has some effects on the convergence speed and robustness of the algorithms. In this new fitness function,
are approximately small coefficients and their selection has some effects on the convergence speed and robustness of the algorithms. In this new fitness function,  and
and  have comparable values as their weight should be adjusted by
have comparable values as their weight should be adjusted by  and
and  .
.  has very large modulus values which is desirable because it should strictly reject any particle with undesired histogram shape in the tails. Note that we can not apply this objective function to original gradient based method since the disapproval of a new equalizer coefficient set is equal to termination of algorithm run and it may causes the algorithm to stock near the initialization point, even in high SNR scenarios.
has very large modulus values which is desirable because it should strictly reject any particle with undesired histogram shape in the tails. Note that we can not apply this objective function to original gradient based method since the disapproval of a new equalizer coefficient set is equal to termination of algorithm run and it may causes the algorithm to stock near the initialization point, even in high SNR scenarios.
As it will be shown in Section 4, although this combination of three different cost functions improves the performance of PSO algorithm in noisy scenarios, it also has restricted the approval of new global and local best particles to some extent and it may slow down the search for optimum vector of parameters even in high SNR cases. So there will be a tradeoff between convergence speed and probability of algorithm failures in noisy environments.
In Practice, one general weakness of PSO is that its local search is not guaranteed convergent and based on the selected swarm size and its initialization; it may converge in a local non-optimal solution. Also, the relatively slower rate of convergence of combined fitness function (13) requires larger swarm sizes and more iterations of algorithm. Hence, some modifications in original position update (11) have introduced using a similar approach suggested in [2]. We modify (11) as follos hybrid update equation:

Here,  is a small constant about 0.25 and
is a small constant about 0.25 and  ,
,  are two constants that may dynamically change during the algorithm. The added
are two constants that may dynamically change during the algorithm. The added  term is the gradient of
term is the gradient of  w.r.t multichannel equalizer coefficients. Further details about derivation of this gradient are just the same as the steepest descent method of [1]. In our implementation we have used larger starting
w.r.t multichannel equalizer coefficients. Further details about derivation of this gradient are just the same as the steepest descent method of [1]. In our implementation we have used larger starting  and after few iterations set
and after few iterations set  . With this choice, we are able to use the gradient as initial fast direction of swarm toward desired point in search space. Later when the swarm finds its way toward desired solution, we set
. With this choice, we are able to use the gradient as initial fast direction of swarm toward desired point in search space. Later when the swarm finds its way toward desired solution, we set  in order to let random cooperative search of swarm perform its fine tuning of equalizer coefficients. Clearly the relation
in order to let random cooperative search of swarm perform its fine tuning of equalizer coefficients. Clearly the relation  must be hold. The exact values of these two will not seriously affect the results, since the PSO will adjust the initial direction of the gradient anyhow. For example a good initial choice would be
must be hold. The exact values of these two will not seriously affect the results, since the PSO will adjust the initial direction of the gradient anyhow. For example a good initial choice would be  . These values will be changed into
. These values will be changed into  after 10 iterations.
after 10 iterations.
From now on, we will refer to this modified version of PSO as hybrid PSO.
4. Simulation Results
In this section we compare performance of the proposed hybrid PSO of (14) with the steepest gradient method of [1] for the source extraction step of the well-known inverse filtering approach. Since the comparison with [3] was impossible due to its abstruse presentation of update equations we compare our proposed modified version with standard implementation of PSO (as in (11)) in terms of computational complexity, fidelity, and robustness against noise. We chose  as objective function of steepest gradient algorithm and used (13) as fitness function of PSO. A
as objective function of steepest gradient algorithm and used (13) as fitness function of PSO. A  transfer function
transfer function  was chosen as
was chosen as

Inputs  of MIMO system are mutually independent, zero mean i.i.d., binary sequences taking values
of MIMO system are mutually independent, zero mean i.i.d., binary sequences taking values  with probability 0.5 each. The normalized fourth-order cumulant is
with probability 0.5 each. The normalized fourth-order cumulant is  in this case.
in this case.
In the first simulation, the equalizer length was chosen to be 15  . For the purpose of impulse response estimation and extracted signal cancellation,
. For the purpose of impulse response estimation and extracted signal cancellation,  was estimated for
was estimated for  . The possible permutation and scaling ambiguities in this estimation were solved by imposing proper normalization, and some shifting and alignments as in [1].
. The possible permutation and scaling ambiguities in this estimation were solved by imposing proper normalization, and some shifting and alignments as in [1].
The performance index used for evaluation of  monte carlo runs is normalized mean square error (NMSE) which can be written for each subchannel
monte carlo runs is normalized mean square error (NMSE) which can be written for each subchannel  as
as

In which  denotes the estimate of the
denotes the estimate of the  th subchannel in
th subchannel in  th Monte Carlo runs. The overall NMSE is:
th Monte Carlo runs. The overall NMSE is:

The parameters for PSO and hybrid PSO algorithms were chosen according to the tradeoff between convergence speed and algorithm runtime. A population of 100 particles is used with the maximum of 400 allowable iterations for PSO and 60 iterations for hybrid PSO.  and
and  of (13) are set to 0.3 and
of (13) are set to 0.3 and  ,
,  and
and  of (10) are all set to 1.
of (10) are all set to 1.  of (14) was chosen to be 0.2 at the start of simulation (
of (14) was chosen to be 0.2 at the start of simulation ( ) in order to force the swarm in desired direction. After about 30 iterations,
) in order to force the swarm in desired direction. After about 30 iterations,  was set to 0.8 (
was set to 0.8 ( ) so the cooperative random local search (around the global maximum) of the directed swarm begins.
) so the cooperative random local search (around the global maximum) of the directed swarm begins.
Figure 3 shows the results for 30 Monte Carlo runs of these three algorithms for several SNRs. The moderate improvement of about 5 dB at lower SNRs can be seen in Figure 3. However as the SNR increases these entire three algorithms exhibit approximately the same very good performance of less than  .
.
As it was mentioned previously, the steepest gradient approach has difficulties coping with smaller lengths of available data records. In order to evaluate our proposed algorithm under such conditions, another simulation was done with different number of available observed samples. 30 Monte Carlo simulations were run at  for data sample sizes of 200 to 1000 and the results are presented in Figure 4. It can be seen that the significant improvement of about 5 dB has achieved by proposed hybrid PSO algorithm for
for data sample sizes of 200 to 1000 and the results are presented in Figure 4. It can be seen that the significant improvement of about 5 dB has achieved by proposed hybrid PSO algorithm for  . Although, in the case of
. Although, in the case of  . The standard PSO algorithm is the only method with acceptable performance of less than
. The standard PSO algorithm is the only method with acceptable performance of less than  . The poor performance of hybrid method is due to primary effect of gradient term in (14). Since this gradient has gone in a wrong direction (just like we expect from complete failure of steepest gradient approach), its justification to PSO decreases the probability of even random convergences of PSO search to separation point.
. The poor performance of hybrid method is due to primary effect of gradient term in (14). Since this gradient has gone in a wrong direction (just like we expect from complete failure of steepest gradient approach), its justification to PSO decreases the probability of even random convergences of PSO search to separation point.
It is interesting to note the stability of PSO method, specially the hybrid PSO. If we define the NMSEs of larger than  as algorithm failures, even in low noise scenarios, there exists the possibility of failure for steepest gradient approach. For instance, in
as algorithm failures, even in low noise scenarios, there exists the possibility of failure for steepest gradient approach. For instance, in  , although the mean NMSE of 100 Monte Carlo runs are approximately the same, but 3 complete failures have met (10%). Table 1, summarizes the standard deviation of NMSE in the case of
, although the mean NMSE of 100 Monte Carlo runs are approximately the same, but 3 complete failures have met (10%). Table 1, summarizes the standard deviation of NMSE in the case of  and
and  , for these methods.
, for these methods.
 ,
,  ).
).In final comparison of PSO and proposed hybrid PSO, the speed of convergence and computational complexity of these two must be studied. Simulation results show that for hybrid PSO, usually a small population of less than 30 particles is enough to very fine convergence of the swarm to the global optimal point; however it takes more than hundreds of iterations for even large populations of more than 100 particles for standard PSO. So, the very fast convergence and the preciseness of optimization are two most important promises of hybrid PSO.
In order to study the effect of  and
and  of (13) in the identification quality, another experiment was done. In this experiment, the quotient of
of (13) in the identification quality, another experiment was done. In this experiment, the quotient of  and
and  is the parameter under study. The simulation results for 50 Monte Carlo simulations with
is the parameter under study. The simulation results for 50 Monte Carlo simulations with  are presented in Figure 2. It can be seen that the best results are met by
are presented in Figure 2. It can be seen that the best results are met by  .
.
Finally, it should be mentioned that our implementation of both PSO and hybrid PSO was the simplest possible approach in order to keep computational complexity and algorithm run time as close as possible to steepest gradient approach. However, it is always possible to further improve PSO algorithms by employing larger population of swarms and more number of allowable iterations with the cost of more computational complexity. Also the performance of any PSO algorithm can be further improved by strategically selecting the starting positions of the particles [8].
5. Conclusion
Two different realizations of Particle Swarm Optimization for source extraction step of well known inverse filtering MIMO identification approach were studied. They both show satisfying results as the original steepest descent method in noise-free scenarios. However, they achieved moderate improvement in lower SNRs and smaller data lengths.
Also the Hybrid PSO algorithm exhibited significant improvement in convergence speed compared to standard PSO, while the initial population of particles was kept smaller. This was the main advantage of hybrid PSO over standard PSO beside the fact that Hybrid PSO was the most precise method with the least probability of complete failure.
References
Tugnait JK: Identification and deconvolution of multichannel linear non-Gaussian processes using higher order statistics and inverse filter criteria. IEEE Transactions on Signal Processing 1997, 45(3):658-672. 10.1109/78.558482
Kennedy J, Eberhart RC: Particle swarm optimization. Proceedings of IEEE International Conference on Neural Networks, November 1995, Perth, Australia 4: 1942-1948.
Song T, Xu J, Zhang K: Blind MIMO channel identification using particle swarm algorithm. Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM '07), September 2007, Shanghai, China 444-447.
Krusienski DJ, Jenkins WK: A particle swarm optimization-least mean squares algorithm for adaptive filtering. Proceedings of the 8th Asilomar Conference on Signals, Systems and Computers, November 2004, Pacific Grove, Ca, USA 1: 241-245.
Krusienski DJ, Jenkins WK: The application of particle swarm optimization to adaptive IIR phase equalization. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '04), May 2004, Montreal, Canada 2: 693-696.
Das S, Abraham A: Synergy of particle swarm optimization with evolutionary algorithms for intelligent search and optimization. Proceedings of IEEE International Congress on Evolutionary Computation, 2006 1: 84-88.
Tugnait JK: On blind separation of convolutive mixtures of independent linear signals in unknown additive noise. IEEE Transactions on Signal Processing 1998, 46(11):3109-3111. 10.1109/78.726826
Richards M, Ventura D: Choosing a starting configuration for particle swarm optimization. Proceedings of IEEE International Conference on Neural Networks, July 2004, Budapest, Hungary 3: 2309-2312.
Acknowledgment
We gratefully acknowledge partial financial support of this research by the French Institut national de recherche en informatique et en automatique (INRIABordeaux SudOuest).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Khanagha, V., Khanagha, A. & Tabataba Vakili, V. Modified Particle Swarm Optimization for Blind Deconvolution and Identification of Multichannel FIR Filters. EURASIP J. Adv. Signal Process. 2010, 716862 (2010). https://doi.org/10.1155/2010/716862
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/716862