Abstract
It is known that in the field of learning theory based on reproducing kernel Hilbert spaces the upper bounds estimate for a  -functional is needed. In the present paper, the upper bounds for the
-functional is needed. In the present paper, the upper bounds for the  -functional on the unit sphere are estimated with spherical harmonics approximation. The results show that convergence rate of the
-functional on the unit sphere are estimated with spherical harmonics approximation. The results show that convergence rate of the  -functional depends upon the smoothness of both the approximated function and the reproducing kernels.
-functional depends upon the smoothness of both the approximated function and the reproducing kernels.
Similar content being viewed by others
1. Introduction
It is known that the goal of learning theory is to approximate a function (or some function features) from data samples.
Let  be a compact subset of
be a compact subset of  -dimensional Euclidean spaces
-dimensional Euclidean spaces  ,
,  . Then, learning theory is to find a function
. Then, learning theory is to find a function  related the input
related the input  to the output
to the output  (see [1–3]). The function
(see [1–3]). The function  is determined by a probability distribution
is determined by a probability distribution  on
on  where
where  is the marginal distribution on
is the marginal distribution on  and
and  is the condition probability of
is the condition probability of  for a given
for a given 
Generally, the distribution  is known only through a set of sample
is known only through a set of sample  independently drawn according to
independently drawn according to  . Given a sample
. Given a sample  , the regression problem based on Support Vector Machine (SVM) learning is to find a function
, the regression problem based on Support Vector Machine (SVM) learning is to find a function  such that
such that  is a good estimate of
is a good estimate of  when a new input
when a new input  is provided. The binary classification problem based on SVM learning is to find a function
is provided. The binary classification problem based on SVM learning is to find a function  which divides
which divides  into two parts. Here
into two parts. Here  is often induced by a real-valued function
is often induced by a real-valued function  with the form of
with the form of  where
where  if
if  , otherwise,
, otherwise,  . The functions
. The functions  are often generated from the following Tikhonov regularization scheme (see, e.g., [4–9]) associated with a reproducing kernel Hilbert space (RKHS)
are often generated from the following Tikhonov regularization scheme (see, e.g., [4–9]) associated with a reproducing kernel Hilbert space (RKHS)  (defined below) and a sample
(defined below) and a sample  :
:

where  is a positive constant called the regularization parameter and
is a positive constant called the regularization parameter and  (
( ) called
) called  -norm SVM loss.
-norm SVM loss.
In addition, the Tikhonov regularization scheme involving offset  (see, e.g., [4, 10, 11]) can be presented below with a similar way to (1.1)
(see, e.g., [4, 10, 11]) can be presented below with a similar way to (1.1)

We are in a position to define reproducing kernel Hilbert space. A function  is called a Mercer kernel if it is continuous, symmetric, and positive semidefinite, that is, for any finite set of distinct points
is called a Mercer kernel if it is continuous, symmetric, and positive semidefinite, that is, for any finite set of distinct points  , the matrix
, the matrix  is positive semidefinite.
is positive semidefinite.
The reproducing kernel Hilbert space (RKHS)  (see [12]) associated with the Mercer kernel
(see [12]) associated with the Mercer kernel  is defined to be the closure of the linear span of the set of functions
is defined to be the closure of the linear span of the set of functions  with the inner product
with the inner product  satisfying
satisfying  and the reproducing property
and the reproducing property

If  , then
, then  . Denote
. Denote  as the space of continuous function on
as the space of continuous function on  with the norm
with the norm  . Let
. Let  Then the reproducing property tells that
Then the reproducing property tells that

It is easy to see that  is a subset of
is a subset of  We say that
We say that  is a universal kernel if for any compact subset
is a universal kernel if for any compact subset  is dense in
is dense in  (see [13, Page 2652]).
(see [13, Page 2652]).
Let  be a given discrete set of finite points. Then, we may define an RKHS
be a given discrete set of finite points. Then, we may define an RKHS  by the linear span of the set of functions
by the linear span of the set of functions  . Then, it is easy to see that
. Then, it is easy to see that  and for any
and for any  there holds
there holds 
Define  and
and  where the minimum is taken over all measurable functions. Then, to estimate the explicit learning rate, one needs to estimate the regularization errors (see, e.g., [4, 7, 9, 14])
where the minimum is taken over all measurable functions. Then, to estimate the explicit learning rate, one needs to estimate the regularization errors (see, e.g., [4, 7, 9, 14])


The convergence rate of (1.5) is controlled by the  -functional (see, e.g., [9])
-functional (see, e.g., [9])

and (1.6) is controlled by another  -functional (see, e.g., [4])
-functional (see, e.g., [4])

where  with
with

We notice that, on one hand, the  -functionals (1.7) and (1.8) are the modifications of the
-functionals (1.7) and (1.8) are the modifications of the  -functional of interpolation theory (see [15]) since the interpolation relation (1.4). On the other hand, they are different from the usual
-functional of interpolation theory (see [15]) since the interpolation relation (1.4). On the other hand, they are different from the usual  -functionals (see e.g., [16–30]) since the term
-functionals (see e.g., [16–30]) since the term  However, they have some similar point. For example, if
However, they have some similar point. For example, if  is a universal kernel,
is a universal kernel,  is dense in
is dense in  (see e.g., [31]). Moreover, some classical function spaces such as the polynomial spaces (see [2, 32]) and even some Sobolev spaces may be regarded as RKHS (see e.g., [33]).
(see e.g., [31]). Moreover, some classical function spaces such as the polynomial spaces (see [2, 32]) and even some Sobolev spaces may be regarded as RKHS (see e.g., [33]).
In learning theory we often require  and
and  for some
for some  (see e.g., [1, 7, 14]). Many results on this topic have been achieved. With the weighted Durrmeyer operators [8, 9] showed the decay by taking
(see e.g., [1, 7, 14]). Many results on this topic have been achieved. With the weighted Durrmeyer operators [8, 9] showed the decay by taking  to be the algebraic polynomials kernels on
to be the algebraic polynomials kernels on  or on the simplex in
or on the simplex in  .
.
However, in general case, the convergence of  -functional (1.8) should also be considered since the offset often has influences on the solution of the learning algorithms (see e.g., [6, 11]). Hence, the purpose of this paper is twofold. One is to provide the convergence rates of (1.7) and (1.8) when
-functional (1.8) should also be considered since the offset often has influences on the solution of the learning algorithms (see e.g., [6, 11]). Hence, the purpose of this paper is twofold. One is to provide the convergence rates of (1.7) and (1.8) when  is a general Mercer kernel on the unit sphere
is a general Mercer kernel on the unit sphere  and
and  The other is how to construct functions of the type of
The other is how to construct functions of the type of

to obtain the convergence rate of (1.8). The translation networks constructed in [34–37] have the form of (1.10) and the zonal networks constructed in [38, 39] have the form of (1.10) with  . So the methods used by these references may be used here to estimate the convergence rates of (1.7) and (1.8) if one can bound the term
. So the methods used by these references may be used here to estimate the convergence rates of (1.7) and (1.8) if one can bound the term 
In the present paper, we shall give the convergence rate of (1.7) and (1.8) for a general kernel defined on the unit sphere  and
and  with
with  being the usual Lebesgue measure on
being the usual Lebesgue measure on  . If there is a distortion between
. If there is a distortion between  and
and  the convergence rate of (1.7)-(1.8) in the general case may be obtained according to the way used by [1, 8].
the convergence rate of (1.7)-(1.8) in the general case may be obtained according to the way used by [1, 8].
The rest of this paper is organized as follows. In Section 2, we shall restate some notations on spherical harmonics and present the main results. Some useful lemmas dealing with the approximation order for the de la Vallée means of the spherical harmonics, the Gauss integral formula, the Marcinkiewicz-Zygmund with respect to the scattered data obtained by G. Brown and F. Dai and a result on the zonal networks approximation provided by H. N. Mhaskar will be given in Section 3. A kind of weighted norm estimate for the Mercer kernel matrices on the unit sphere will be given in Lemma 3.8. Our main results are proved in the last section.
Throughout the paper, we shall write  if there exists a constant
if there exists a constant  such that
such that  . We write
. We write  if
if  and
and  .
.
2. Notations and Results
To state the results of this paper, we need some notations and results on spherical harmonics.
2.1. Notations
For integers  ,
,  , the class of all one variable algebraic polynomials of degree
, the class of all one variable algebraic polynomials of degree  defined on
defined on  is denoted by
is denoted by  , the class of all spherical harmonics of degree
, the class of all spherical harmonics of degree  will be denoted by
will be denoted by  , and the class of all spherical harmonics of degree
, and the class of all spherical harmonics of degree  will be denoted by
will be denoted by  . The dimension of
. The dimension of  is given by (see [40, Page 65])
is given by (see [40, Page 65])

and that of  is
is  One has the following well-known addition formula (see [41, Page 10, Theorem
One has the following well-known addition formula (see [41, Page 10, Theorem  ]):
]):

where  is the degree-
is the degree- generalized Legendre polynomial. The Legendre polynomials are normalized so that
generalized Legendre polynomial. The Legendre polynomials are normalized so that  and satisfy the orthogonality relations
and satisfy the orthogonality relations

Define  and
and  by taking
by taking  to be the usual volume element of
to be the usual volume element of  and the Jacobi weights functions
and the Jacobi weights functions  ,
,  ,
,  , respectively. For any
, respectively. For any  we have the following relation (see [42, Page 312]):
we have the following relation (see [42, Page 312]):

The orthogonal projections  of a function
of a function  on
on  are defined by (see e.g., [43])
are defined by (see e.g., [43])

where  denotes the inner product of
denotes the inner product of  and
and  .
.
2.2. Main Results
Let  satisfy
satisfy  and
and  . Define
. Define

Then, by [44, Chapter 17] we know that  is positive semidefinite on
is positive semidefinite on  and the right of (2.6) is convergence absolutely and uniformly since
and the right of (2.6) is convergence absolutely and uniformly since  . Therefore,
. Therefore,  is a Mercer kernel on
is a Mercer kernel on  By [13, Theorem
By [13, Theorem  ] we know that
] we know that  is a universal kernel on
is a universal kernel on  . We suppose that there is a constant
. We suppose that there is a constant  depending only on
depending only on  such for any
such for any 

Given a finite set  , we denote by
, we denote by  the cardinality of
the cardinality of  . For
. For  and
and  we say that a finite subset
we say that a finite subset  is an
is an  -covering of
-covering of  if
if

where  with
with  being the geodesic distance between
being the geodesic distance between  and
and  .
.
Let  be an integer,
be an integer,  a sequence of real numbers. Define forward difference operators by
a sequence of real numbers. Define forward difference operators by  ,
,  ,
, 

We say a finite subset  is a subset of interpolatory type if for any real numbers
is a subset of interpolatory type if for any real numbers  there is a
there is a  such that
such that  ,
,  This kind of subsets may be found from [45, 46].
This kind of subsets may be found from [45, 46].
Let  be the set of all sequence
be the set of all sequence  for which
for which  and
and  the set of all sequence
the set of all sequence  for which
for which 
Let  be a real number,
be a real number,  Then, we say
Then, we say  if there is a function
if there is a function  such that
such that

We now give the results of this paper.
Theorem 2.1.
If there is a constant  depending only on
depending only on  such that
such that  is a subset of interpolatory type and a
is a subset of interpolatory type and a  -covering of
-covering of  satisfying
satisfying  with
with  and
and  being a given positive integer.
being a given positive integer.  is an integer.
is an integer.  is a real number such that there is
is a real number such that there is  and
and  ,
,  satisfies
satisfies  and
and  .
.  is the reproducing kernel space reproduced by
is the reproducing kernel space reproduced by  and the kernel (2.6).
and the kernel (2.6).  . Then there is a constant
. Then there is a constant  depending only on
depending only on  and
and  and a function
and a function  with
with  and
and  a constant such that
a constant such that


The functions  satisfying the conditions of Theorem 2.1 may be found in [39, Page 357].
satisfying the conditions of Theorem 2.1 may be found in [39, Page 357].
Corollary 2.2.
Under the conditions of Theorem 2.1. If  , then
, then

Corollary 2.2 shows that the convergence rate of the  -functional (1.8) is controlled by the smoothness of both the reproducing kernels and the approximated function
-functional (1.8) is controlled by the smoothness of both the reproducing kernels and the approximated function  .
.
Theorem 2.3.
If there is a constant  depending only on
depending only on  such that
such that  is a subset of interpolatory type and a
is a subset of interpolatory type and a  -covering of
-covering of  satisfying
satisfying  with
with  and
and  being a given positive integer.
being a given positive integer.  is the reproducing kernel space reproducing by
is the reproducing kernel space reproducing by  and the kernel (2.6) with
and the kernel (2.6) with  satisfying
satisfying  and
and  Then, for
Then, for  and
and  there holds
there holds

where 
3. Some Lemmas
To prove Theorems 2.1 and 2.3, we need some lemmas. The first one is about the Gauss integral formula and Marcinkiewicz inequalities.
There exist constants  depending only on
depending only on  such that for any positive integer
such that for any positive integer  and any
and any  -covering
-covering  of
of  satisfying
satisfying  , there exists a set of real numbers
, there exists a set of real numbers  ,
,  such that
such that

for any  and for
and for 

where  the constants of equivalence depending only on
the constants of equivalence depending only on  ,
,  ,
,  , and
, and  when
when  is small. Here one employs the slight abuse of notation that
is small. Here one employs the slight abuse of notation that 
The second lemma we shall use is the Nikolskii inequality for the spherical harmonics.
Lemma 3.2 (see [38, 45, 49, 51, 52]).
If  ,
,  , then one has the following Nikolskii inequality:
, then one has the following Nikolskii inequality:

where the constant  depends only on
depends only on  .
.
We now restate the general approximation frame of the Cesàro means and de la Vallée Poussin means provided by Dai and Ditzian (see [53]).
Lemma 3.3.
Let  be a positive measure on
be a positive measure on  .
.  is a sequence of finite-dimensional spaces satisfying the following:
is a sequence of finite-dimensional spaces satisfying the following:
(I) .
.
(II) is orthogonal to
is orthogonal to  (in
(in  ) when
) when 
(III) is dense in
is dense in  for all
for all  .
.
(IV) is the collection of the constants.
is the collection of the constants.
The Cesàro means  of
of  is given by
is given by

for  , where
, where

and  is an orthogonal base of
is an orthogonal base of  in
in  One sets,for a given
One sets,for a given  ,
,  and
and  if there exists
if there exists  such that
such that 
Let  be defined as
be defined as  for
for  and
and  for
for  and is a nonegative and nonincrease function.
and is a nonegative and nonincrease function.  are the de la Vallée Poussin means defined as
are the de la Vallée Poussin means defined as

Then,  If for some
If for some  ,
,  ,
,  then,
then,  and
and

Lemma 3.3 makes the following Lemma 3.4.
Lemma 3.4.
Let  be the function defined as in Lemma 3.3. Define two kinds of operators, respectively, by
be the function defined as in Lemma 3.3. Define two kinds of operators, respectively, by

Then,  for any
for any  and
and  for any
for any  . Moreover,
. Moreover,


where for  one defines
one defines

Proof.
By [54, Lemma  ] we know
] we know  for some
for some  . Hence, (3.9) holds by (3.7). By [19, Theorem
. Hence, (3.9) holds by (3.7). By [19, Theorem  ] we know
] we know  for
for  Hence, (3.10) holds by (3.7).
Hence, (3.10) holds by (3.7).
Let  be a finite set. Then we call
be a finite set. Then we call  an M-Z quadrature measure of order
an M-Z quadrature measure of order  if (3.1) and (3.2) hold for
if (3.1) and (3.2) hold for  By this definition one knows the finite set
By this definition one knows the finite set  in Lemma 3.1 is an M-Z quadrature measure of order
in Lemma 3.1 is an M-Z quadrature measure of order  .
.
Define an operator as

Then, we have the following results.
Lemma 3.5 (see [39]).
For a given integer  let
let  be an M-Z quadrature measure of order
be an M-Z quadrature measure of order  ,
,  ,
,  an integer,
an integer,  ,
,  , where
, where  satisfies
satisfies  which satisfies
which satisfies  if
if  and
and  if
if  .
.  defined in Lemma 3.3 is a nonnegative and non-increasing function. Let
defined in Lemma 3.3 is a nonnegative and non-increasing function. Let  satisfy
satisfy  . Then, for
. Then, for  ,
,  , where
, where  consists of
consists of  for which the derivative of order
for which the derivative of order  ; that is,
; that is,  , belongs to
, belongs to  . Then, there is an operator
. Then, there is an operator  such that
such that
(i)(see [39, Proposition  , (b)]).
, (b)]).  for
for 


where 
(ii)(see [39, Theorem  ]). Moreover, if one adds an assumption that
]). Moreover, if one adds an assumption that  then, there are constants
then, there are constants  and
and  such that
such that

and for 

Lemma 3.6 (see e.g., [29, Page 230]).
Let  . Then,
. Then,

Following Lemma 3.7 deals with the orthogonality of the Legendre polynomials 
Lemma 3.7.
For the generalized Legendre polynomials  one has
one has

Proof.
It may be obtained by (2.2).
Lemma 3.8.
Let  satisfy (2.7) for
satisfy (2.7) for  and
and  .
.  is a finite set satisfying the conditions of Theorem 2.1. Then, there is a constant
is a finite set satisfying the conditions of Theorem 2.1. Then, there is a constant  depending only on
depending only on  such that
such that

Proof.
Define a matrix by  , where
, where  with
with  and
and  Then,
Then,

By the Parseval equality we have

Let  satisfy
satisfy  ,
,  . Then, by (3.1)
. Then, by (3.1)

Hence,  . On the other hand, since
. On the other hand, since  ,
,  , we have for any
, we have for any  that
that

It follows for  that
that

Define  . Then, (3.24), (3.10), the Cauchy inequality, and the fact
. Then, (3.24), (3.10), the Cauchy inequality, and the fact  make
make

It follows that

Equation (3.2) thus holds.
4. Proof of the Main Results
We now show Theorems 2.1 and 2.3, respectively.
Proof of Theorem 2.1.
Lemma  in [39] gave the following results.
in [39] gave the following results.
Let ,
, ,
, be an integer, and a sequence of real numbers such
be an integer, and a sequence of real numbers such  . Then, there exists
. Then, there exists  such that
such that  ,
,
Since  and
and  we have a
we have a  such that
such that  Hence,
Hence,  and
and

and for  there holds for
there holds for  that
that

It follows for  that
that

On the other hand, since

where for  , we have by (4.3)
, we have by (4.3)

Hence, above equation and (3.1)-(3.2) makes

where  ,
,  Define
Define

Then, we know  and by (3.9)
and by (3.9)

where

It follows by (3.9) that

On the other hand, by the definition of  and (3.14) we have for
and (3.14) we have for  that
that

where  denotes the operator
denotes the operator  of Lemma 3.5 for
of Lemma 3.5 for  Hence,
Hence,

Equation (3.2) and the definition of  make
make

The Hölder inequality, the  of Lemma 3.5, and the fact that
of Lemma 3.5, and the fact that  make
make  . Therefore,
. Therefore,

Take  then
then

Equations (3.2), (3.17), (3.16), and the Cauchy inequality make

Let  be the Gamma function. Then, it is well known that
be the Gamma function. Then, it is well known that  Therefore,
Therefore,

Hence,

Equations (4.14) and (4.4) make

and hence

Since  , we have (2.11) by (4.20). Equation (2.12) follows by (4.3), (4.4), and (3.19).
, we have (2.11) by (4.20). Equation (2.12) follows by (4.3), (4.4), and (3.19).
Proof of Corollary 2.2.
By (2.11)-(2.12) one has

Proof of Theorem 2.3.
Take the place of  in Lemma 3.5 with
in Lemma 3.5 with  denote still by
denote still by  the operator
the operator  in Lemma 3.5 with
in Lemma 3.5 with  and
and

then,  and by (3.15)
and by (3.15)  In this case,
In this case,

Since  is a spherical harmonics of order
is a spherical harmonics of order  , we know by
, we know by  of Lemma 3.5 that
of Lemma 3.5 that  are also spherical harmonics of order
are also spherical harmonics of order  Then, (3.2),
Then, (3.2),  of Lemma 3.5, (3.3), and (3.16) make
of Lemma 3.5, (3.3), and (3.16) make

Hence, (3.19) and above equation make  . Equation (2.14) follows by (3.15).
. Equation (2.14) follows by (3.15).
References
Cucker F, Smale S: On the mathematical foundations of learning. Bulletin of the American Mathematical Society 2002, 39(1):1–49.
Cucker F, Zhou D-X: Learning Theory: An Approximation Theory Viewpoint, Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press, Cambridge, Mass, USA; 2007:xii+224.
Vapnik VN: Statistical Learning Theory, Adaptive and Learning Systems for Signal Processing, Communications, and Control. John Wiley & Sons, New York, NY, USA; 1998:xxvi+736.
Chen DR, Wu Q, Ying YM, Zhou DX: Support vector machine soft margin classifier: error analysis. Journal of Machine Learning and Research 2004, 5: 1143–1175.
Evgeniou T, Pontil M, Poggio T: Regularization networks and support vector machines. Advances in Computational Mathematics 2000, 13(1):1–50. 10.1023/A:1018946025316
Li Y, Liu Y, Zhu J: Quantile regression in reproducing kernel Hilbert spaces. Journal of the American Statistical Association 2007, 102(477):255–268. 10.1198/016214506000000979
Tong H, Chen D-R, Peng L: Analysis of support vector machines regression. Foundations of Computational Mathematics 2009, 9(2):243–257. 10.1007/s10208-008-9026-0
Tong H, Chen D-R, Peng L: Learning rates for regularized classifiers using multivariate polynomial kernels. Journal of Complexity 2008, 24(5–6):619–631. 10.1016/j.jco.2008.05.008
Zhou D-X, Jetter K: Approximation with polynomial kernels and SVM classifiers. Advances in Computational Mathematics 2006, 25(1–3):323–344.
Chen D, Xiang D-H: The consistency of multicategory support vector machines. Advances in Computational Mathematics 2006, 24(1–4):155–169.
De Vito E, Rosasco L, Caponnetto A, Piana M, Verri A: Some properties of regularized kernel methods. Journal of Machine Learning Research 2004, 5: 1363–1390.
Aronszajn N: Theory of reproducing kernels. Transactions of the American Mathematical Society 1950, 68: 337–404. 10.1090/S0002-9947-1950-0051437-7
Micchelli CA, Xu Y, Zhang H: Universal kernels. Journal of Machine Learning Research 2006, 7: 2651–2667.
Wu Q, Ying Y, Zhou D-X: Multi-kernel regularized classifiers. Journal of Complexity 2007, 23(1):108–134. 10.1016/j.jco.2006.06.007
Bergh J, Löfström J: Interpolation Spaces. Springer, New York, NY, USA; 1976.
Berens H, Lorentz GG: Inverse theorems for Bernstein polynomials. Indiana University Mathematics Journal 1972, 21(8):693–708. 10.1512/iumj.1972.21.21054
Berens H, Li LQ: The Peetre -moduli and best approximation on the sphere. Acta Mathematica Sinica 1995, 38(5):589–599.
Berens H, Xu Y:
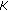 -moduli, moduli of smoothness, and Bernstein polynomials on a simplex. Indagationes Mathematicae 1991, 2(4):411–421. 10.1016/0019-3577(91)90027-5
-moduli, moduli of smoothness, and Bernstein polynomials on a simplex. Indagationes Mathematicae 1991, 2(4):411–421. 10.1016/0019-3577(91)90027-5Chen W, Ditzian Z: Best approximation and -functionals. Acta Mathematica Hungarica 1997, 75(3):165–208. 10.1023/A:1006543020828
Chen W, Ditzian Z: Best polynomial and Durrmeyer approximation in . Indagationes Mathematicae 1991, 2(4):437–452. 10.1016/0019-3577(91)90029-7
Dai F, Ditzian Z: Jackson inequality for Banach spaces on the sphere. Acta Mathematica Hungarica 2008, 118(1–2):171–195. 10.1007/s10474-007-6206-3
Ditzian Z, Zhou X: Optimal approximation class for multivariate Bernstein operators. Pacific Journal of Mathematics 1993, 158(1):93–120.
Ditzian Z, Runovskii K: Averages and -functionals related to the Laplacian. Journal of Approximation Theory 1999, 97(1):113–139. 10.1006/jath.1997.3262
Ditzian Z: A measure of smoothness related to the Laplacian. Transactions of the American Mathematical Society 1991, 326(1):407–422. 10.2307/2001870
Ditzian Z, Totik V: Moduli of Smoothness, Springer Series in Computational Mathematics. Volume 9. Springer, New York, NY, USA; 1987:x+227.
Ditzian Z: Approximation on Banach spaces of functions on the sphere. Journal of Approximation Theory 2006, 140(1):31–45. 10.1016/j.jat.2005.11.013
Ditzian Z: Fractional derivatives and best approximation. Acta Mathematica Hungarica 1998, 81(4):323–348. 10.1023/A:1006554907440
Schumaker LL: Spline Functions: Basic Theory. John Wiley & Sons, New York, NY, USA; 1981:xiv+553. Pure and Applied Mathematics Pure and Applied Mathematics
Wang KY, Li LQ: Harmonic Analysis and Approximation on the Unit Sphere. Science Press, Beijing, China; 2000.
Xu Y: Approximation by means of -harmonic polynomials on the unit sphere. Advances in Computational Mathematics 2004, 21(1–2):37–58.
Smale S, Zhou D-X: Estimating the approximation error in learning theory. Analysis and Applications 2003, 1(1):17–41. 10.1142/S0219530503000089
Sheng B: Estimates of the norm of the Mercer kernel matrices with discrete orthogonal transforms. Acta Mathematica Hungarica 2009, 122(4):339–355. 10.1007/s10474-008-8037-2
Loustau S: Aggregation of SVM classifiers using Sobolev spaces. Journal of Machine Learning Research 2008, 9: 1559–1582.
Mhaskar HN, Micchelli CA: Degree of approximation by neural and translation networks with a single hidden layer. Advances in Applied Mathematics 1995, 16(2):151–183. 10.1006/aama.1995.1008
Sheng BH: Approximation of periodic functions by spherical translation networks. Acta Mathematica Sinica. Chinese Series 2007, 50(1):55–62.
Sheng B: On the degree of approximation by spherical translations. Acta Mathematicae Applicatae Sinica. English Series 2006, 22(4):671–680. 10.1007/s10255-006-0341-4
Sheng B, Wang J, Zhou S: A way of constructing spherical zonal translation network operators with linear bounded operators. Taiwanese Journal of Mathematics 2008, 12(1):77–92.
Mhaskar HN, Narcowich FJ, Ward JD: Approximation properties of zonal function networks using scattered data on the sphere. Advances in Computational Mathematics 1999, 11(2–3):121–137.
Mhaskar HN: Weighted quadrature formulas and approximation by zonal function networks on the sphere. Journal of Complexity 2006, 22(3):348–370. 10.1016/j.jco.2005.10.003
Groemer H: Geometric Applications of Fourier Series and Spherical Harmonics, Encyclopedia of Mathematics and Its Applications. Volume 61. Cambridge University Press, Cambridge, Mass, USA; 1996:xii+329.
Müller C: Spherical Harmonics, Lecture Notes in Mathematics. Volume 17. Springer, Berlin, Germany; 1966:iv+45.
Lu SZ, Wang KY: Bochner-Riesz Means. Beijing Normal University Press, Beijing, China; 1988.
Wang Y, Cao F: The direct and converse inequalities for jackson-type operators on spherical cap. Journal of Inequalities and Applications 2009, 2009:-16.
Wendland H: Scattered Data Approximation, Cambridge Monographs on Applied and Computational Mathematics. Volume 17. Cambridge University Press, Cambridge, Mass, USA; 2005:x+336.
Mhaskar HN, Narcowich FJ, Sivakumar N, Ward JD: Approximation with interpolatory constraints. Proceedings of the American Mathematical Society 2002, 130(5):1355–1364. 10.1090/S0002-9939-01-06240-2
Narcowich FJ, Ward JD: Scattered data interpolation on spheres: error estimates and locally supported basis functions. SIAM Journal on Mathematical Analysis 2002, 33(6):1393–1410. 10.1137/S0036141001395054
Brown G, Dai F: Approximation of smooth functions on compact two-point homogeneous spaces. Journal of Functional Analysis 2005, 220(2):401–423. 10.1016/j.jfa.2004.10.005
Brown G, Feng D, Sheng SY: Kolmogorov width of classes of smooth functions on the sphere . Journal of Complexity 2002, 18(4):1001–1023. 10.1006/jcom.2002.0656
Dai F: Multivariate polynomial inequalities with respect to doubling weights and weights. Journal of Functional Analysis 2006, 235(1):137–170. 10.1016/j.jfa.2005.09.009
Mhaskar HN, Narcowich FJ, Ward JD: Spherical Marcinkiewicz-Zygmund inequalities and positive quadrature. Mathematics of Computation 2001, 70(235):1113–1130.
Belinsky E, Dai F, Ditzian Z: Multivariate approximating averages. Journal of Approximation Theory 2003, 125(1):85–105. 10.1016/j.jat.2003.09.005
Kamzolov AI: Approximation of functions on the sphere . Serdica 1984, 10(1):3–10.
Dai F, Ditzian Z: Cesàro summability and Marchaud inequality. Constructive Approximation 2007, 25(1):73–88. 10.1007/s00365-005-0623-8
Dai F: Some equivalence theorems with -functionals. Journal of Approximation Theory 2003, 121(1):143–157. 10.1016/S0021-9045(02)00059-X
Acknowledgments
This work is supported by the National NSF (10871226) of China. The authors thank the reviewers for giving very valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sheng, BH., Xiang, DH. The Convergence Rate for a 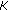 -Functional in Learning Theory.
J Inequal Appl 2010, 249507 (2010). https://doi.org/10.1155/2010/249507
-Functional in Learning Theory.
J Inequal Appl 2010, 249507 (2010). https://doi.org/10.1155/2010/249507
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/249507




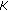 -moduli, moduli of smoothness, and Bernstein polynomials on a simplex. Indagationes Mathematicae 1991, 2(4):411–421. 10.1016/0019-3577(91)90027-5
-moduli, moduli of smoothness, and Bernstein polynomials on a simplex. Indagationes Mathematicae 1991, 2(4):411–421. 10.1016/0019-3577(91)90027-5