Abstract
In this paper, we establish two different existence results of solutions for a nonlocal elliptic equations with nonlinear boundary condition. The first one is based on Galerkin method, and gives a priori estimate. The second one is based on Mountain Pass Lemma.
Similar content being viewed by others
1. Introduction
In this paper, we deal with the following elliptic equation with nonlinear boundary condition:

where  is a bounded domain in
is a bounded domain in  with smooth boundary
with smooth boundary  ,
,  ,
,  is the outer unite normal derivative,
is the outer unite normal derivative,  is continuous,
is continuous,  ,
,  are Carathéodory functions.
are Carathéodory functions.
For (1.1), if the nonlocal term  is replaced by
is replaced by  , then the equation
, then the equation

is related to the stationary analog of the Kirchhoff equation:

where  . It was proposed by Kirchhoff [1] as an extension of the classical D'Alembert wave equations for free vibrations of elastic strings. The Kirchhoff model takes into account the length changes of the string produced by transverse vibrations. Equation (1.3) received much attention and an abstract framework to the problem was proposed after the work [2]. Some interesting and further results can be found in [3, 4] and the references therein. In addition, (1.2) has important physical and biological background. There are many authors who pay more attention to this equation. In particularly, authors concerned with the existence of solutions for (1.2) with zero Dirichlet boundary condition via Galerkin method, and built the variational frame in [5, 6]. More recently, Perera and Zhang obtained solutions of a class of nonlocal quasilinear elliptic boundary value problems using the variational methods, invariant sets of descent flow, Yang index, and critical groups [7, 8].
. It was proposed by Kirchhoff [1] as an extension of the classical D'Alembert wave equations for free vibrations of elastic strings. The Kirchhoff model takes into account the length changes of the string produced by transverse vibrations. Equation (1.3) received much attention and an abstract framework to the problem was proposed after the work [2]. Some interesting and further results can be found in [3, 4] and the references therein. In addition, (1.2) has important physical and biological background. There are many authors who pay more attention to this equation. In particularly, authors concerned with the existence of solutions for (1.2) with zero Dirichlet boundary condition via Galerkin method, and built the variational frame in [5, 6]. More recently, Perera and Zhang obtained solutions of a class of nonlocal quasilinear elliptic boundary value problems using the variational methods, invariant sets of descent flow, Yang index, and critical groups [7, 8].
If the nonlocal term  is replaced by
is replaced by  , then the equation
, then the equation

arises in numerous physical models such as systems of particles in thermodynamical equilibrium via gravitational (Coulomb) potential, 2-D fully turbulent behavior of real flow, thermal runaway in Ohmic Heating, shear bands in metal deformed under high strain rates, among others. Because of its importance, in [9, 10], the authors similarly studied the existence of solution for (1.4) with zero Dirichlet boundary condition.
On the other hand, elliptic equations with nonlinear boundary conditions have become rather an active area of research; see [11–15] and reference therein. Those references present necessary and sufficient conditions of solutions of elliptic equations with nonlinear boundary conditions. In [13], the authors study the elliptic equation

with the nonlinear boundary condition

They obtain various existence results applying coincidence degree theory and the method of upper and lower solutions.
Inspired by the above references, we deal with the existence of solutions for elliptic equation (1.1) with nonlinear boundary condition based on Galerkin method and the Mountain Pass Lemma.
The paper is organized as follows. In Section 2, we will give the existence of solution for (1.1) via Galerkin method. In Section 3, we will study the solution for (1.1) using the Mountain Pass Lemma.
2. Existence
In this section, we state and prove the main theorem via Galerkin method when  is bounded.
is bounded.
For convenience, we give the following hypotheses.
(H1)A typical assumption for  is that there exists an
is that there exists an  such that
such that  , for all
, for all 
(H2) For all  , assume that the functions
, assume that the functions  ,
,  satisfying
satisfying

where  are constants,
are constants,  ,
,  .
.
(H3) The function  is not identically zero.
is not identically zero.
Let  be endowed with norm
be endowed with norm  . Then
. Then  is a Banach space.
is a Banach space.
A function  is a weak solution of (1.1) if
is a weak solution of (1.1) if

for all  .
.
Lemma 2.1.
Suppose that  is a continuous function such that
is a continuous function such that  on
on  , where
, where  is the usual inner product in
is the usual inner product in  and
and  its related norm. Then, there exists
its related norm. Then, there exists  such that
such that  .
.
Lemma 2.2 (see [16]).
Let  be a domain in
be a domain in  satisfying the uniform
satisfying the uniform  -regularity condition, and suppose that there exists a simple
-regularity condition, and suppose that there exists a simple  -extension operator
-extension operator  for
for  . Also suppose that
. Also suppose that  and
and  . Then
. Then

If  , then the embedding still holds for
, then the embedding still holds for  . Moreover, if
. Moreover, if  , then the embedding is compact.
, then the embedding is compact.
Theorem 2.3.
Assume that (H1)–(H3) hold. In addition, we suppose that
(H4)there exist constants  such that
such that  ,
,  ,
,  with
with

Then problem (1.1) has at least one weak solution. Besides, any solution  satisfies the estimate
satisfies the estimate

Proof.
Let  be different complete orthonormal systems for
be different complete orthonormal systems for  and set
and set

Then  is isometric to
is isometric to  . Then, each
. Then, each  is uniquely associated to
is uniquely associated to  by the relation
by the relation  . Since
. Since  are, respectively, orthonormal in
are, respectively, orthonormal in  , we get
, we get  .
.
We search for solutions  of the approximate problem
of the approximate problem

To solve this algebraic system we define the operator 

By condition (H2), the growth of function  is subcritical, so
is subcritical, so  defines a continuous Nemytskii mapping
defines a continuous Nemytskii mapping  . Similarly, we also define a continuous mapping
. Similarly, we also define a continuous mapping  .
.
From the continuity of  and
and  , with respect to
, with respect to  , we denote that
, we denote that  is continuous. Therefore, from (H1), (H2), (H4) and Hölder's inequality, we note that
is continuous. Therefore, from (H1), (H2), (H4) and Hölder's inequality, we note that 

On the other hand, by Lemma 2.2, we have

where  is constant.
is constant.
From (2.9) and (2.10), we can prove that

This shows that there exists  , depending only on
, depending only on  , such that
, such that  if
if  . Then system (2.7) has a solution
. Then system (2.7) has a solution  satisfying
satisfying

From this bound estimate, going to a subsequence if necessary, there are  and
and  such that
such that

Besides, since  ,
,  compactly and the mapping
compactly and the mapping  is, respectively, continuous
is, respectively, continuous  and
and 

Then fixing  in (2.7) and letting
in (2.7) and letting  , we conclude that
, we conclude that

From the completeness of  , identity holds with
, identity holds with  replaced by any
replaced by any  . In particularly, when
. In particularly, when  , we get
, we get

On the other hand, let  in (2.7) and passing to the limit, we get
in (2.7) and passing to the limit, we get

Then we conclude that  , which shows that
, which shows that  is a solution of (1.1). Finally, if
is a solution of (1.1). Finally, if  is any solution of (1.1) and
is any solution of (1.1) and  is nontrivial, then
is nontrivial, then

The proof is complete.
3. Variational Method
In this section, we consider the following problem:

where  are constants, and
are constants, and  are defined in (H2).
are defined in (H2).
The nontrivial solution of (3.1) comes from the Mountain Pass Lemma in [17].
Lemma 3.1 (Mountain Pass Lemma).
Let  be a Banach space and let
be a Banach space and let  satisfy the Palais-Smale condition. Suppose also that
satisfy the Palais-Smale condition. Suppose also that
(i)
-
(ii)
there exist constants
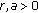 such that
such that 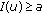 , if
, if 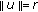 ,
, -
(iii)
there exists an element
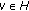 with
with 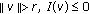 .
.
Define  . Then
. Then

is a critical value of  .
.
Theorem 3.2.
Assume the conditions (H1)–(H3) hold. In addition, the function  satisfies
satisfies
(H5)there exist  with
with  and
and  , such that
, such that  ,
,  , where
, where  .
.
Then (3.1) has a nontrivial solution.
Proof.
The weak solutions of (3.1) are critical points of the functional  defined by
defined by

where  .
.
Let us check the  condition. Let
condition. Let  , we have
, we have

Let  be a Palais-Smale sequence in
be a Palais-Smale sequence in  , that is,
, that is,  and
and  and assume the contradiction that
and assume the contradiction that  , then, from (H1), (H5), we have
, then, from (H1), (H5), we have

where  . Then by the Sobolev embedding theorem and Lemma 2.2, we can select
. Then by the Sobolev embedding theorem and Lemma 2.2, we can select  such that
such that

which is a contradiction with  . Hence
. Hence  is bounded in
is bounded in  . So
. So  admits a weakly convergence subsequence. From (H2), all the growth of
admits a weakly convergence subsequence. From (H2), all the growth of  is subcritical, so the standard argument shows that
is subcritical, so the standard argument shows that  admits a strongly convergence subsequence.
admits a strongly convergence subsequence.
Next we will verify the hypotheses of Lemma 3.1. By Hölder's inequality, Sobolev embedding theorem, and Lemma 2.2, we have

So we obtain

Let  , we get
, we get

Let  , then we take
, then we take  such that
such that  , when
, when  is sufficient small.
is sufficient small.
So for  and
and  small enough, then we have
small enough, then we have  for all
for all  .
.
On the other hand, take  with
with  for
for  , we have
, we have

Since  , we obtain
, we obtain  when
when  .
.
Let  , with
, with  large enough, we have
large enough, we have  and
and  . So by the Mountain Pass Lemma and (H3), we have a nontrivial solution
. So by the Mountain Pass Lemma and (H3), we have a nontrivial solution  for (3.1). The proof is complete.
for (3.1). The proof is complete.
References
Kirchhoff G: Mechanik. Teubner, Leipzig, Germany; 1883.
Lions J-L: On some questions in boundary value problems of mathematical physics. In Contemporary Developments in Continuum Mechanics and Partial Differential Equations (Proc. Internat. Sympos., Inst. Mat., Univ. Fed. Rio de Janeiro, Rio de Janeiro, 1977), North-Holland Mathematics Studies. Volume 30. Edited by: de la Penha G, Medeiros LA. North-Holland, Amsterdam, The Netherlands; 1978:284–346.
Arosio A, Panizzi S: On the well-posedness of the Kirchhoff string. Transactions of the American Mathematical Society 1996, 348(1):305–330. 10.1090/S0002-9947-96-01532-2
Ono K: On global solutions and blow-up solutions of nonlinear Kirchhoff strings with nonlinear dissipation. Journal of Mathematical Analysis and Applications 1997, 216(1):321–342. 10.1006/jmaa.1997.5697
Aives CO, Corrêa FJSA, Ma TF: Positive solutions for a quasilinear elliptic equation of Kirchhoff type. Computers & Mathematics with Applications 2005, 49(1):85–93. 10.1016/j.camwa.2005.01.008
Ma TF: Remarks on an elliptic equation of Kirchhoff type. Nonlinear Analysis: Theory, Methods & Applications 2005, 63(5–7):e1967-e1977.
Perera K, Zhang Z: Nontrivial solutions of Kirchhoff-type problems via the Yang index. Journal of Differential Equations 2006, 221(1):246–255. 10.1016/j.jde.2005.03.006
Zhang Z, Perera K: Sign changing solutions of Kirchhoff type problems via invariant sets of descent flow. Journal of Mathematical Analysis and Applications 2006, 317(2):456–463. 10.1016/j.jmaa.2005.06.102
Stańczy R: Nonlocal elliptic equations. Nonlinear Analysis: Theory, Methods & Applications 2001, 47(5):3579–3584. 10.1016/S0362-546X(01)00478-3
Corrêa FJSA, de Morais Filho DC: On a class of nonlocal elliptic problems via Galerkin method. Journal of Mathematical Analysis and Applications 2005, 310(1):177–187. 10.1016/j.jmaa.2005.01.052
Bonder JF, Rossi JD: Existence results for the
 -Laplacian with nonlinear boundary conditions. Journal of Mathematical Analysis and Applications 2001, 263(1):195–223. 10.1006/jmaa.2001.7609
-Laplacian with nonlinear boundary conditions. Journal of Mathematical Analysis and Applications 2001, 263(1):195–223. 10.1006/jmaa.2001.7609Chaïb K: Necessary and sufficient conditions of existence for a system involving the
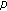 -Laplacian
-Laplacian 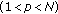 . Journal of Differential Equations 2003, 189(2):513–525. 10.1016/S0022-0396(02)00094-3
. Journal of Differential Equations 2003, 189(2):513–525. 10.1016/S0022-0396(02)00094-3Amster P, Mariani MC, Méndez O: Nonlinear boundary conditions for elliptic equations. Electronic Journal of Differential Equations 2005, 2005(144):1–8.
Song S-Z, Tang C-L: Resonance problems for the
 -Laplacian with a nonlinear boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(9):2007–2021. 10.1016/j.na.2005.07.035
-Laplacian with a nonlinear boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(9):2007–2021. 10.1016/j.na.2005.07.035Zhao J-H, Zhao P-H: Existence of infinitely many weak solutions for the
 -Laplacian with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(4):1343–1355. 10.1016/j.na.2007.06.036
-Laplacian with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(4):1343–1355. 10.1016/j.na.2007.06.036Adams RA, Fournier JJF: Sobolev Spaces. Academic Press, Amsterdam, The Netherlands; 2003.
Evans LC: Partial Differential Equations. American Mathematical Society, Providence, RI, USA; 1998.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, F., An, Y. Existence of Nontrivial Solution for a Nonlocal Elliptic Equation with Nonlinear Boundary Condition. Bound Value Probl 2009, 540360 (2009). https://doi.org/10.1155/2009/540360
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/540360



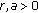 such that
such that 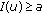 , if
, if 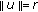 ,
,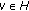 with
with 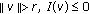 .
. -Laplacian with nonlinear boundary conditions. Journal of Mathematical Analysis and Applications 2001, 263(1):195–223. 10.1006/jmaa.2001.7609
-Laplacian with nonlinear boundary conditions. Journal of Mathematical Analysis and Applications 2001, 263(1):195–223. 10.1006/jmaa.2001.7609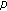 -Laplacian
-Laplacian 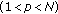 . Journal of Differential Equations 2003, 189(2):513–525. 10.1016/S0022-0396(02)00094-3
. Journal of Differential Equations 2003, 189(2):513–525. 10.1016/S0022-0396(02)00094-3 -Laplacian with a nonlinear boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(9):2007–2021. 10.1016/j.na.2005.07.035
-Laplacian with a nonlinear boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(9):2007–2021. 10.1016/j.na.2005.07.035 -Laplacian with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(4):1343–1355. 10.1016/j.na.2007.06.036
-Laplacian with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(4):1343–1355. 10.1016/j.na.2007.06.036