Abstract
Global behaviors and optimal harvesting of a class of impulsive periodic logistic single-species system with continuous periodic control strategy is investigated. Four new sufficient conditions that guarantee the exponential stability of the impulsive evolution operator introduced by us are given. By virtue of exponential stability of the impulsive evolution operator, we present the existence, uniqueness and global asymptotical stability of periodic solutions. Further, the existence result of periodic optimal controls for a Bolza problem is given. At last, an academic example is given for demonstration.
Similar content being viewed by others
1. Introduction
In population dynamics, the optimal management of renewable resources has been one of the interesting research topics. The optimal exploitation of renewable resources, which has direct effect on their sustainable development, has been paid much attention [1–3]. However, it is always hoped that we can achieve sustainability at a high level of productivity and good economic profit, and this requires scientific and effective management of the resources.
Single-species resource management model, which is described by the impulsive periodic logistic equations on finite-dimensional spaces, has been investigated extensively, no matter how the harvesting occurs, continuously [1, 4] or impulsively [5–7]. However, the associated single-species resource management model on infinite-dimensional spaces has not been investigated extensively.
Since the end of last century, many authors including Professors Nieto and Hernández pay great attention on impulsive differential systems. We refer the readers to [8–22]. Particulary, Doctor Ahmed investigated optimal control problems [23, 24] for impulsive systems on infinite-dimensional spaces. We also gave a series of results [25–34] for the first-order (second-order) semilinear impulsive systems, integral-differential impulsive system, strongly nonlinear impulsive systems and their optimal control problems. Recently, we have investigated linear impulsive periodic system on infinite-dimensional spaces. Some results [35–37] including the existence of periodic  -mild solutions and alternative theorem, criteria of Massera type, asymptotical stability and robustness against perturbation for a linear impulsive periodic system are established.
-mild solutions and alternative theorem, criteria of Massera type, asymptotical stability and robustness against perturbation for a linear impulsive periodic system are established.
Herein, we devote to studying global behaviors and optimal harvesting of the generalized logistic single-species system with continuous periodic control strategy and periodic impulsive perturbations:

On infinite-dimensional spaces, where  denotes the population number of isolated species at time
denotes the population number of isolated species at time  and location
and location  ,
,  is a bounded domain and
is a bounded domain and  , operator
, operator  . The coefficients
. The coefficients  ,
,  are sufficiently smooth functions of
are sufficiently smooth functions of  in
in  , where
, where  ,
,  and
and  ,
,  . Denoting
. Denoting  ,
,  , then
, then  =
=  .
.  is related to the periodic change of the resources maintaining the evolution of the population and the periodic control policy
is related to the periodic change of the resources maintaining the evolution of the population and the periodic control policy  , where
, where  is a suitable admissible control set. Time sequence
is a suitable admissible control set. Time sequence  and
and  as
as  ,
,  denote mutation of the isolate species at time
denote mutation of the isolate species at time  where
where  .
.
Suppose  is a Banach space and
is a Banach space and  is a separable reflexive Banach space. The objective functional is given by
is a separable reflexive Banach space. The objective functional is given by

where  is Borel measurable,
is Borel measurable,  is continuous, and nonnegative and
is continuous, and nonnegative and  denotes the
denotes the  -periodic
-periodic  -mild solution of system (1.1) at location
-mild solution of system (1.1) at location  and corresponding to the control
and corresponding to the control  . The Bolza problem (
. The Bolza problem ( ) is to find
) is to find  such that
such that  for all
for all 
Suppose that  ,
,  ,
,  and
and  is the least positive constant such that there are
is the least positive constant such that there are  s in the interval
s in the interval  and
and  where
where  ,
,  . The first equation of system (1.1) describes the variation of the population number
. The first equation of system (1.1) describes the variation of the population number  of the species in periodically continuous controlled changing environment. The second equation of system (1.1) shows that the species are isolated. The third equation of system (1.1) reflects the possibility of impulsive effects on the population.
of the species in periodically continuous controlled changing environment. The second equation of system (1.1) shows that the species are isolated. The third equation of system (1.1) reflects the possibility of impulsive effects on the population.
Let  satisfy some properties (such as strongly elliptic) in
satisfy some properties (such as strongly elliptic) in  and set
and set  (such as
(such as  . For every
. For every  define
define  ,
,  is the infinitesimal generator of a
is the infinitesimal generator of a  -semigroup
-semigroup  on the Banach space
on the Banach space  (such as
(such as  ). Define x
). Define x
 ,
,  and
and  then system (1.1) can be abstracted into the following controlled system:
then system (1.1) can be abstracted into the following controlled system:

On the Banach space  , and the associated objective functional
, and the associated objective functional

where  denotes the
denotes the  -periodic
-periodic  -mild solution of system (1.3) corresponding to the control
-mild solution of system (1.3) corresponding to the control  . The Bolza problem (P) is to find
. The Bolza problem (P) is to find  such that
such that  for all
for all  The investigation of the system (1.3) cannot only be used to discuss the system (1.1), but also provide a foundation for research of the optimal control problems for semilinear impulsive periodic systems. The aim of this paper is to give some new sufficient conditions which will guarantee the existence, uniqueness, and global asymptotical stability of periodic
The investigation of the system (1.3) cannot only be used to discuss the system (1.1), but also provide a foundation for research of the optimal control problems for semilinear impulsive periodic systems. The aim of this paper is to give some new sufficient conditions which will guarantee the existence, uniqueness, and global asymptotical stability of periodic  -mild solutions for system (1.3) and study the optimal control problems arising in the system (1.3).
-mild solutions for system (1.3) and study the optimal control problems arising in the system (1.3).
The paper is organized as follows. In Section 2, the properties of the impulsive evolution operator  are collected. Four new sufficient conditions that guarantee the exponential stability of the
are collected. Four new sufficient conditions that guarantee the exponential stability of the  are given. In Section 3, the existence, uniqueness, and global asymptotical stability of
are given. In Section 3, the existence, uniqueness, and global asymptotical stability of  -periodic
-periodic  -mild solution for system (1.3) is obtained. In Section 4, the existence result of periodic optimal controls for the Bolza problem (P) is presented. At last, an academic example is given to demonstrate our result.
-mild solution for system (1.3) is obtained. In Section 4, the existence result of periodic optimal controls for the Bolza problem (P) is presented. At last, an academic example is given to demonstrate our result.
2. Impulsive Periodic Evolution Operator and It's Stability
Let  be a Banach space,
be a Banach space,  denotes the space of linear operators on
denotes the space of linear operators on  ;
;  denotes the space of bounded linear operators on
denotes the space of bounded linear operators on  .
.  is the Banach space with the usual supremum norm. Denote
is the Banach space with the usual supremum norm. Denote  and define
and define  is continuous at
is continuous at  ,
,  is continuous from left and has right-hand limits at
is continuous from left and has right-hand limits at  and
and  .
.
Set

It can be seen that endowed with the norm  ,
,  is a Banach space.
is a Banach space.
In order to investigate periodic solutions, we introduce the following two spaces:

Set

It can be seen that endowed with the norm  ,
,  is a Banach space.
is a Banach space.
We introduce assumption [H1].
[H1.1]: is the infinitesimal generator of a
is the infinitesimal generator of a  -semigroup
-semigroup  on
on  with domain
with domain  .
.
[H1.2]:There exists  such that
such that  where
where  .
.
[H1.3]:For each  ,
,  ,
,  .
.
Under the assumption [H1], consider

and the associated Cauchy problem

For every  ,
,  is an invariant subspace of
is an invariant subspace of  , using ([38, Theorem 5.2.2, page 144]), step by step, one can verify that the Cauchy problem (2.5) has a unique classical solution
, using ([38, Theorem 5.2.2, page 144]), step by step, one can verify that the Cauchy problem (2.5) has a unique classical solution  represented by
represented by  , where
, where  given by
given by

The operator  is called impulsive evolution operator associated with
is called impulsive evolution operator associated with  and
and  .
.
The following lemma on the properties of the impulsive evolution operator  associated with
associated with  and
and  is widely used in this paper.
is widely used in this paper.
Lemma 2.1.
Let assumption [H1] hold. The impulsive evolution operator
hold. The impulsive evolution operator  has the following properties.
has the following properties.
(1)For  ,
,  , there exists a
, there exists a  such that
such that 
(2)For  ,
,  ,
,  .
.
(3)For  ,
,  ,
,  .
.
(4)For  ,
,  ,
,  .
.
(5)For  , there exits
, there exits  ,
,  such that
such that

Proof.
-
(1)
By assumption [H1.1], there exists a constant
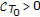 such that
such that 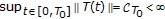 . Using assumption [H1.3], it is obvious that
. Using assumption [H1.3], it is obvious that 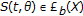 , for
, for  . (2) By the definition of
. (2) By the definition of 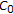 -semigroup and the construction of
-semigroup and the construction of 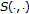 , one can verify the result immediately. (3) By assumptions [H1.2], [H1.3], and elementary computation, it is easy to obtain the result. (4) For
, one can verify the result immediately. (3) By assumptions [H1.2], [H1.3], and elementary computation, it is easy to obtain the result. (4) For 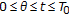 ,
, 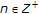 , by virtue of (3) again and again, we arrive at
, by virtue of (3) again and again, we arrive at 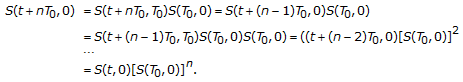 (2.8)
(2.8)
-
(5)
Without loss of generality, for
 ,
,  (2.9)
(2.9)
This completes the proof.
In order to study the asymptotical properties of periodic solutions, it is necessary to discuss the exponential stability of the impulsive evolution operator  . We first give the definition of exponential stable for
. We first give the definition of exponential stable for  .
.
Definition 2.2.
 ,
,  is called exponentially stable if there exist
is called exponentially stable if there exist  and
and  such that
such that

Assumption [H2]:  is exponentially stable, that is, there exist
is exponentially stable, that is, there exist  and
and  such that
such that

An important criteria for exponential stability of a  -semigroup is collected here.
-semigroup is collected here.
Lemma 2.3 (see [38, Lemma 7.2.1]).
Let be a
be a  -semigroup on
-semigroup on  , and let
, and let  be its infinitesimal generator. Then the following assertions are equivalent:
be its infinitesimal generator. Then the following assertions are equivalent:
(1) is exponentially stable.
is exponentially stable.
(2)For every  there exits a positive constants
there exits a positive constants  such that
such that

Next, four sufficient conditions that guarantee the exponential stability of impulsive evolution operator  are given.
are given.
Lemma 2.4.
Assumptions [H1]  and [H2]
and [H2] hold. There exists
hold. There exists  such that
such that

Then,  is exponentially stable.
is exponentially stable.
Proof.
Without loss of generality, for  , we have
, we have

Suppose  and let
and let  Then,
Then,

Let  and
and  , then we obtain
, then we obtain 
Lemma 2.5.
Assume that assumption [H1] holds. Suppose
holds. Suppose

If there exists  such that
such that

for  where
where

Then,  is exponentially stable.
is exponentially stable.
Proof.
It comes from (2.17) that

Further,

where  is denoted the number of impulsive points in
is denoted the number of impulsive points in  .
.
For  , by (2.16), we obtain the following two inequalities:
, by (2.16), we obtain the following two inequalities:

This implies

that is,

Then,

Thus, we obtain

By (5) of Lemma 2.1, let  ,
,  ,
, 
Lemma 2.6.
Assume that assumption [H1] holds. The limit
holds. The limit

Suppose there exists such that
such that

Then,  is exponentially stable.
is exponentially stable.
Proof.
Let  with
with  . It comes from
. It comes from

that there exits a  enough small such that
enough small such that

that is,

From (2.27), we know that

Then, we have

Hence,

Here, we only need to choose  small enough such that
small enough such that  , by (5) of Lemma 2.1 again, let
, by (5) of Lemma 2.1 again, let  ,
,  , we have
, we have 
Lemma 2.7.
Assume that assumption [H1] holds. For some
holds. For some  ,
,  ,
,

Imply the exponential stability of .
.
Proof.
It comes from the continuity of  , the inequality
, the inequality

and the boundedness of  ,
,  are convergent, that
are convergent, that  for every
for every  and fixed
and fixed  . This shows that
. This shows that  is bounded for each
is bounded for each  and fixed
and fixed  and hence, by virtue of uniform boundedness principle, there exists a constant
and hence, by virtue of uniform boundedness principle, there exists a constant  such that
such that  for all
for all  . Let
. Let  denote the operator given by
denote the operator given by  ,
,  and
and  is fixed. Clearly,
is fixed. Clearly,  is defined every where on
is defined every where on  and by assumption it maps
and by assumption it maps  and it is a closed operator. Hence, by closed graph theorem, it is a bounded linear operator from
and it is a closed operator. Hence, by closed graph theorem, it is a bounded linear operator from  to
to  . Thus, there exits a constant
. Thus, there exits a constant  such that
such that  for all
for all  and
and  ,
,  is fixed.
is fixed.
Let  ,
,  and
and  and define
and define  as
as

Then,

and hence,

Thus, for  ,
,

where  . Fix
. Fix  . Then, for any
. Then, for any  we can write
we can write  for some
for some  and
and  and we have
and we have

where  and
and  . Since
. Since  , this shows that our result.
, this shows that our result.
3. Periodic Solutions and Global Asymptotical Stability
Consider the following controlled system:

and the associated Cauchy problem

In addition to assumption [H1], we make the following assumptions:
[H3]: is measurable and
is measurable and  for
for  .
.
[H4]:For each  , there exists
, there exists  and
and  ,
,  .
.
[H5]: has bounded, closed, and convex values and is graph measurable,
has bounded, closed, and convex values and is graph measurable,  and
and  are bounded, where
are bounded, where  is a separable reflexive Banach space.
is a separable reflexive Banach space.
[H6]:Operator  and
and  , for
, for  . Obviously,
. Obviously,  .
.
Denote the set of admissible controls

Obviously,  and
and  ,
,  is bounded, convex, and closed.
is bounded, convex, and closed.
We introduce  -mild solution of Cauchy problem (3.2) and
-mild solution of Cauchy problem (3.2) and  -periodic
-periodic  -mild solution of system (3.1).
-mild solution of system (3.1).
Definition 3.1.
A function  , for finite interval
, for finite interval  , is said to be a
, is said to be a  -mild solution of the Cauchy problem (3.2) corresponding to the initial value
-mild solution of the Cauchy problem (3.2) corresponding to the initial value  and
and  if
if  is given by
is given by

A function  is said to be a
is said to be a  -periodic
-periodic  -mild solution of system (3.1) if it is a
-mild solution of system (3.1) if it is a  -mild solution of Cauchy problem (3.2) corresponding to some
-mild solution of Cauchy problem (3.2) corresponding to some  and
and  for
for  .
.
Theorem 3.2 .A.
Assumptions [H1], [H3], [H4], [H5], and [H6] hold. Suppose
hold. Suppose  is exponentially stable, for every
is exponentially stable, for every  , system (3.1) has a unique
, system (3.1) has a unique  -periodic
-periodic  -mild solution:
-mild solution:

where  ,
,

Further,

is a bounded linear operator and

where  and
and  .
.
Further, for arbitrary , the
, the  -mild solution
-mild solution  of the Cauchy problem (3.2) corresponding to the initial value
of the Cauchy problem (3.2) corresponding to the initial value  and control
and control  , satisfies the following inequality:
, satisfies the following inequality:

where  is the
is the  -periodic
-periodic  -mild solution of system (3.1),
-mild solution of system (3.1),  is not dependent on
is not dependent on  ,
,  ,
,  , and
, and  . That is,
. That is,  can be approximated to the
can be approximated to the  -periodic
-periodic  -mild solution
-mild solution  according to exponential decreasing speed.
according to exponential decreasing speed.
Proof.
Consider the operator  . By (4) of Lemma 2.1 and the stability of
. By (4) of Lemma 2.1 and the stability of  , we have
, we have

Thus,  . Obviously, the series
. Obviously, the series  is convergent, thus operator
is convergent, thus operator  . It comes from
. It comes from  that
that  It is well known that system (3.1) has a periodic
It is well known that system (3.1) has a periodic  -mild solution if and only if
-mild solution if and only if  . Since
. Since  is invertible, we can uniquely solve
is invertible, we can uniquely solve

Let  , where
, where

Note that

it is not difficult to verify that the  -mild solution of the Cauchy problem (3.2) corresponding to initial value
-mild solution of the Cauchy problem (3.2) corresponding to initial value  given by
given by

is just the unique  -periodic of system (3.1).
-periodic of system (3.1).
It is obvious that  is linear. Next, verify the estimation (3.8). In fact, for
is linear. Next, verify the estimation (3.8). In fact, for  ,
,

On the other hand,

Let  , next the estimation (3.8) is verified.
, next the estimation (3.8) is verified.
System (3.1) has a unique  -periodic
-periodic  -mild solution
-mild solution  given by (3.5) and (3.6). The
given by (3.5) and (3.6). The  -mild solution
-mild solution  of the Cauchy problem (3.2) corresponding to initial value
of the Cauchy problem (3.2) corresponding to initial value  and control
and control  can be given by (3.4). Then,
can be given by (3.4). Then,

Let  , one can obtain (3.9) immediately.
, one can obtain (3.9) immediately.
Definition 3.3.
The  -periodic
-periodic  -mild solution
-mild solution  of the system (3.1) is said to be globally asymptotically stable in the sense that
of the system (3.1) is said to be globally asymptotically stable in the sense that

where  is any
is any  -mild solutions of the Cauchy problem (3.2) corresponding to initial value
-mild solutions of the Cauchy problem (3.2) corresponding to initial value  and control
and control  .
.
By Theorem 3.2 and the stability of the impulsive evolution operator  in Section 2, one can obtain the following results.
in Section 2, one can obtain the following results.
Corollary 3.A.
Under the assumptions of Theorem 3.2 , the system ( 3.1 ) has a unique -periodic
-periodic  -mild solution
-mild solution  which is globally asymptotically stable.
which is globally asymptotically stable.
4. Existence of Periodic Optimal Harvesting Policy
In this section, we discuss existence of periodic optimal harvesting policy, that is, periodic optimal controls for optimal control problems arising in systems governed by linear impulsive periodic system on Banach space.
By the  -periodic
-periodic  -mild solution expression of system (3.1) given in Theorem 3.2, one can obtain the result.
-mild solution expression of system (3.1) given in Theorem 3.2, one can obtain the result.
Theorem 4.A.
Under the assumptions of Theorem 3.2 , the -periodic
-periodic  -mild solution of system (3.1) continuously depends on the control on
-mild solution of system (3.1) continuously depends on the control on  , that is, let
, that is, let  be
be  -periodic
-periodic  -mild solution of system (3.1) corresponding to
-mild solution of system (3.1) corresponding to  . There exists constant
. There exists constant  such that
such that

Proof.
Since  and
and  are the
are the  -periodic
-periodic  -mild solution corresponding to
-mild solution corresponding to  and
and  , respectively, then we have
, respectively, then we have

where

Further,

where  . This completes the proof.
. This completes the proof.
Lemma 4.A.
Suppose is a strong continuous operator. The operator
is a strong continuous operator. The operator  , given by
, given by

is strongly continuous.
Proof.
Without loss of generality, for  ,
,

By virtue of strong continuity of  , boundedness of
, boundedness of  ,
,  ,
,  is strongly continuous.
is strongly continuous.
Let  denote the
denote the  -periodic
-periodic  -mild solution of system (3.1) corresponding to the control
-mild solution of system (3.1) corresponding to the control  , we consider the Bolza problem (P).
, we consider the Bolza problem (P).
Find  such that
such that  for all
for all  , where
, where

We introduce the following assumption on  and
and  .
.
Assumption [H7].
[H7.1] The functional
The functional  is Borel measurable.
is Borel measurable.
[H7.2]
 is sequentially lower semicontinuous on
is sequentially lower semicontinuous on  for almost all
for almost all  .
.
[H7.3]
 is convex on
is convex on  for each
for each  and almost all
and almost all  .
.
[H7.4] There exist constants
There exist constants  ,
,  ,
,  is nonnegative and
is nonnegative and  such that
such that

[H7.5] The functional
The functional  is continuous and nonnegative.
is continuous and nonnegative.
Now we can give the following results on existence of periodic optimal controls for Bolza problem (P).
Theorem 4.B.
Suppose C is a strong continuous operator and assumption [H7] holds. Under the assumptions of Theorem 3.2, the problem (P) has a unique solution.
holds. Under the assumptions of Theorem 3.2, the problem (P) has a unique solution.
Proof.
If  there is nothing to prove.
there is nothing to prove.
We assume that  By assumption [H7], we have
By assumption [H7], we have

where  is a constant. Hence
is a constant. Hence  .
.
By the definition of infimum there exists a sequence  , such that
, such that 
Since  is bounded in
is bounded in  , there exists a subsequence, relabeled as
, there exists a subsequence, relabeled as  , and
, and  such that
such that  weakly convergence in
weakly convergence in  and
and  Because of
Because of  is the closed and convex set, thanks to the Mazur lemma,
is the closed and convex set, thanks to the Mazur lemma,  . Suppose
. Suppose  and
and  are the
are the  -periodic
-periodic  -mild solution of system (3.1) corresponding to
-mild solution of system (3.1) corresponding to  (
( ) and
) and  , respectively, then
, respectively, then  and
and  can be given by
can be given by

where

Define

then by Lemma 4.2, we have

as  weakly convergence in
weakly convergence in  .
.
Next, we show that

In fact, for  , we have
, we have

By elementary computation, we arrive at

Consider the time interval  , similarly we obtain
, similarly we obtain

In general, given any  ,
,  and the
and the  ,
,  , prior to the jump at time
, prior to the jump at time  , we immediately follow the jump as
, we immediately follow the jump as

the associated interval  , we also similarly obtain
, we also similarly obtain

Step by step, we repeat the procedures till the time interval is exhausted. Let  ,
,  ,
,  ,
,  ,
,  ,
,  , thus we obtain
, thus we obtain

that is,

with strongly convergence as  .
.
Since  , using the assumption [H7]
, using the assumption [H7] and Balder's theorem, we can obtain
and Balder's theorem, we can obtain

This shows that  attains its minimum at
attains its minimum at  . This completes the proof.
. This completes the proof.
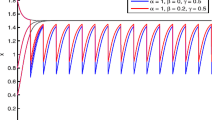
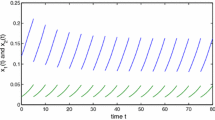
5. Example
Last, an academic example is given to illustrate our theory.
Let  and consider the following population evolution equation with impulses:
and consider the following population evolution equation with impulses:

where  denotes time,
denotes time,  denotes age,
denotes age,  is called age density function,
is called age density function,  and
and  are positive constants,
are positive constants,  is a bounded measurable function, that is,
is a bounded measurable function, that is,  .
.  denotes the age-specific death rate,
denotes the age-specific death rate,  denotes the age density of migrants, and
denotes the age density of migrants, and  denotes the control. The admissible control set
denotes the control. The admissible control set  .
.
A linear operator  defined on
defined on  by
by

where the domain of  is given by
is given by

By the fact that the operator  is an infinitesimal generator of a
is an infinitesimal generator of a  -semigroup (see [39, Example 2.21]) and [38, Theorem 4.2.1], then
-semigroup (see [39, Example 2.21]) and [38, Theorem 4.2.1], then  is an infinitesimal generator of a
is an infinitesimal generator of a  -semigroup since the operator
-semigroup since the operator  is bounded.
is bounded.
Now let us consider the following operators family:

It is not difficult to verify that  defines a
defines a  -semigroup and
-semigroup and  is just the infinitesimal generator of the
is just the infinitesimal generator of the  -semigroup
-semigroup  . Since
. Since  , then there exits a constant
, then there exits a constant  such that
such that  a.e.
a.e.  . For an arbitrary function
. For an arbitrary function  , by using the expression (5.4) of the semigroup
, by using the expression (5.4) of the semigroup  , the following inequality holds:
, the following inequality holds:

Hence, Lemma 2.3 leads to the exponential stability of  . That is, there exist
. That is, there exist  and
and  such that
such that 
Let

Define  ,
,  ,
,  ,
,  ,
,  . Thus system (5.1) can be rewritten as
. Thus system (5.1) can be rewritten as

with the cost function

By Lemma 2.4, for  ,
,  is exponentially stable. Now, all the assumptions are met in Theorems 3.2 and 4.3, our results can be used to system (5.1). Thus, system (5.1) has a unique
is exponentially stable. Now, all the assumptions are met in Theorems 3.2 and 4.3, our results can be used to system (5.1). Thus, system (5.1) has a unique  -periodic
-periodic  -mild solution
-mild solution  which is globally asymptotically stable and there exists a periodic control
which is globally asymptotically stable and there exists a periodic control  such that
such that  for all
for all 
The results show that the optimal population level is truly the periodic solution of the considered system, and hence, it is globally asymptotically stable. Meanwhile, it implies that we can achieve sustainability at a high level of productivity and good economic profit by virtue of scientific, effective, and continuous management of the resources.
References
Clark CW: Mathematical Bioeconomics: The Optimal Management of Renewable Resources, Pure and Applied Mathematics. John Wiley & Sons, New York, NY, USA; 1976:xi+352.
Song X, Chen L: Optimal harvesting and stability for a two-species competitive system with stage structure. Mathematical Biosciences 2001,170(2):173-186. 10.1016/S0025-5564(00)00068-7
Marzollo R (Ed): Periodic Optimization. Springer, New York, NY, USA; 1972.
Fan M, Wang K: Optimal harvesting policy for single population with periodic coefficients. Mathematical Biosciences 1998,152(2):165-177. 10.1016/S0025-5564(98)10024-X
Bainov DD, Simeonov PS: Impulsive Differential Equations: Periodic Solutions and Applications, Pitman Monographs and Surveys in Pure and Applied Mathematics. Volume 66. Longman Scientific & Technical, Harlow, UK; 1993:x+228.
Xiao YN, Cheng DZ, Qin HS: Optimal impulsive control in periodic ecosystem. Systems & Control Letters 2006,55(7):558-565. 10.1016/j.sysconle.2005.12.003
Lakshmikantham V, Bainov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Teaneck, NJ, USA; 1989:xii+273.
Nieto JJ: An abstract monotone iterative technique. Nonlinear Analysis: Theory, Methods & Applications 1997,28(12):1923-1933. 10.1016/S0362-546X(97)89710-6
Yan J, Zhao A, Nieto JJ: Existence and global attractivity of positive periodic solution of periodic single-species impulsive Lotka-Volterra systems. Mathematical and Computer Modelling 2004,40(5-6):509-518. 10.1016/j.mcm.2003.12.011
Jiao J-J, Chen L-S, Nieto JJ, Angela T: Permanence and global attractivity of stage-structured predator-prey model with continuous harvesting on predator and impulsive stocking on prey. Applied Mathematics and Mechanics 2008,29(5):653-663. 10.1007/s10483-008-0509-x
Zeng G, Wang F, Nieto JJ: Complexity of a delayed predator-prey model with impulsive harvest and Holling type II functional response. Advances in Complex Systems 2008,11(1):77-97. 10.1142/S0219525908001519
Wang W, Shen J, Nieto JJ: Permanence and periodic solution of predator-prey system with Holling type functional response and impulses. Discrete Dynamics in Nature and Society 2007, 2007:-15.
Zhang H, Chen L, Nieto JJ: A delayed epidemic model with stage-structure and pulses for pest management strategy. Nonlinear Analysis: Real World Applications 2008,9(4):1714-1726. 10.1016/j.nonrwa.2007.05.004
Ahmad B, Nieto JJ: Existence and approximation of solutions for a class of nonlinear impulsive functional differential equations with anti-periodic boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008,69(10):3291-3298. 10.1016/j.na.2007.09.018
Jiang D, Yang Y, Chu J, O'Regan D: The monotone method for Neumann functional differential equations with upper and lower solutions in the reverse order. Nonlinear Analysis: Theory, Methods & Applications 2007,67(10):2815-2828. 10.1016/j.na.2006.09.042
Li Y: Global exponential stability of BAM neural networks with delays and impulses. Chaos, Solitons & Fractals 2005,24(1):279-285.
De la Sen M: Stability of impulsive time-varying systems and compactness of the operators mapping the input space into the state and output spaces. Journal of Mathematical Analysis and Applications 2006,321(2):621-650. 10.1016/j.jmaa.2005.08.038
Yu L, Zhang J, Liao Y, Ding J: Parameter estimation error bounds for Hammerstein nonlinear finite impulsive response models. Applied Mathematics and Computation 2008,202(2):472-480. 10.1016/j.amc.2008.01.002
Jankowski T: Positive solutions to second order four-point boundary value problems for impulsive differential equations. Applied Mathematics and Computation 2008,202(2):550-561. 10.1016/j.amc.2008.02.040
Hernández EM, Pierri M, Goncalves G: Existence results for an impulsive abstract partial differential equation with state-dependent delay. Computers & Mathematics with Applications 2006,52(3-4):411-420. 10.1016/j.camwa.2006.03.022
Hernández EM, Rabello M, Henríquez HR: Existence of solutions for impulsive partial neutral functional differential equations. Journal of Mathematical Analysis and Applications 2007,331(2):1135-1158. 10.1016/j.jmaa.2006.09.043
Hernández EM, Sakthivel R, Aki ST: Existence results for impulsive evolution differential equations with state-dependent delay. Electronic Journal of Differential Equations 2008,2008(28):1-11.
Ahmed NU: Some remarks on the dynamics of impulsive systems in Banach spaces. Dynamics of Continuous, Discrete and Impulsive Systems. Series A 2001,8(2):261-274.
Ahmed NU, Teo KL, Hou SH: Nonlinear impulsive systems on infinite dimensional spaces. Nonlinear Analysis: Theory, Methods & Applications 2003,54(5):907-925. 10.1016/S0362-546X(03)00117-2
Xiang X, Ahmed NU: Existence of periodic solutions of semilinear evolution equations with time lags. Nonlinear Analysis: Theory, Methods & Applications 1992,18(11):1063-1070. 10.1016/0362-546X(92)90195-K
Xiang X: Optimal control for a class of strongly nonlinear evolution equations with constraints. Nonlinear Analysis: Theory, Methods & Applications 2001,47(1):57-66. 10.1016/S0362-546X(01)00156-0
Sattayatham P, Tangmanee S, Wei W: On periodic solutions of nonlinear evolution equations in Banach spaces. Journal of Mathematical Analysis and Applications 2002,276(1):98-108. 10.1016/S0022-247X(02)00378-5
Xiang X, Wei W, Jiang Y: Strongly nonlinear impulsive system and necessary conditions of optimality. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2005,12(6):811-824.
Wei W, Xiang X: Necessary conditions of optimal control for a class of strongly nonlinear impulsive equations in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2005,63(5–7):53-63.
Wei W, Xiang X, Peng Y: Nonlinear impulsive integro-differential equations of mixed type and optimal controls. Optimization 2006,55(1-2):141-156. 10.1080/02331930500530401
Xiang X, Wei W: Mild solution for a class of nonlinear impulsive evolution inclusions on Banach space. Southeast Asian Bulletin of Mathematics 2006,30(2):367-376.
Yu X, Xiang X, Wei W: Solution bundle for a class of impulsive differential inclusions on Banach spaces. Journal of Mathematical Analysis and Applications 2007,327(1):220-232. 10.1016/j.jmaa.2006.03.075
Peng Y, Xiang X, Wei W: Nonlinear impulsive integro-differential equations of mixed type with time-varying generating operators and optimal controls. Dynamic Systems and Applications 2007,16(3):481-496.
Peng Y, Xiang X: Second order nonlinear impulsive time-variant systems with unbounded perturbation and optimal controls. Journal of Industrial and Management Optimization 2008,4(1):17-32.
Wang J: Linear impulsive periodic system on Banach spaces. Proceedings of the 4th International Conference on Impulsive and Hybrid Dynamical Systems, July 2007, Nanning, China 5: 20-25.
Wang J, Xiang X, Wei W: Linear impulsive periodic system with time-varying generating operators on Banach space. Advances in Difference Equations 2007, 2007:-16.
Wang J, Xiang X, Wei W, Chen Q:Existence and global asymptotical stability of periodic solution for the
 -periodic logistic system with time-varying generating operators and
-periodic logistic system with time-varying generating operators and  -periodic impulsive perturbations on Banach spaces Discrete Dynamics in Nature and Society 2008, 2008:-16.
-periodic impulsive perturbations on Banach spaces Discrete Dynamics in Nature and Society 2008, 2008:-16.Ahmed NU: Semigroup Theory with Applications to Systems and Control, Pitman Research Notes in Mathematics Series. Volume 246. Longman Scientific & Technical, Harlow, UK; 1991:x+282.
Luo Z-H, Guo B-Z, Morgül O: Stability and Stabilization of Infinite Dimensional Systems with Applications, Communications and Control Engineering Series. Springer, London, UK; 1999:xiv+403.
Acknowledgments
This work is supported by Natural Science Foundation of Guizhou Province Education Department (no. 2007008). This work is also supported by the undergraduate carve out project of Department of Guiyang Science and Technology (2008, no. 15-2).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, J., Xiang, X. & Wei, W. Global Behaviors and Optimal Harvesting of a Class of Impulsive Periodic Logistic Single-Species System with Continuous Periodic Control Strategy. Bound Value Probl 2008, 192353 (2009). https://doi.org/10.1155/2008/192353
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/192353



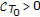 such that
such that 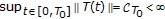 . Using assumption [H1.3], it is obvious that
. Using assumption [H1.3], it is obvious that 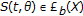 , for
, for  . (2) By the definition of
. (2) By the definition of 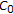 -semigroup and the construction of
-semigroup and the construction of 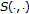 , one can verify the result immediately. (3) By assumptions [H1.2], [H1.3], and elementary computation, it is easy to obtain the result. (4) For
, one can verify the result immediately. (3) By assumptions [H1.2], [H1.3], and elementary computation, it is easy to obtain the result. (4) For 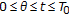 ,
, 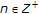 , by virtue of (3) again and again, we arrive at
, by virtue of (3) again and again, we arrive at 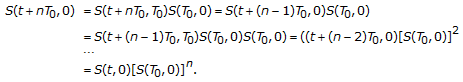
 ,
, 
 -periodic logistic system with time-varying generating operators and
-periodic logistic system with time-varying generating operators and  -periodic impulsive perturbations on Banach spaces Discrete Dynamics in Nature and Society 2008, 2008:-16.
-periodic impulsive perturbations on Banach spaces Discrete Dynamics in Nature and Society 2008, 2008:-16.