Abstract
The phasor representation is introduced to identify the characteristic of the active noise control (ANC) systems. The conventional representation, transfer function, cannot explain the fact that the performance will be degraded at some frequency for the narrowband ANC systems. This paper uses the relationship of signal phasors to illustrate geometrically the operation and the behavior of two-tap adaptive filters. In addition, the best signal basis is therefore suggested to achieve a better performance from the viewpoint of phasor synthesis. Simulation results show that the well-selected signal basis not only achieves a better convergence performance but also speeds up the convergence for narrowband ANC systems.
Similar content being viewed by others
1. Introduction
The problems of acoustic noise have received much attention during the past several decades. Traditionally, acoustic noise control uses passive techniques such as enclosures, barriers, and silencers to attenuate the undesired noise [1, 2]. These passive techniques are highly valued for their high attenuation over a broad range of frequency. However, they are relatively large in volume, expensive at cost, and ineffective at low frequencies. It has been shown that the active noise control (ANC) system [3–14] can efficiently achieve a good performance for attenuating low-frequency noise as compared to passive methods. Based on the principle of superposition, ANC system can cancel the primary (undesired) noise by generating an antinoise of equal amplitude and opposite phase.
The design concept of acoustic ANC system utilizing a microphone and of a loudspeaker to generate a canceling sound was first proposed by Leug [3]. Since the characteristics of noise source and environment are nonstationary, an ANC system should be designed adaptively to cope with these variations. A duct-type noise cancellation system based on adaptive filter theory was developed by Burgess [4] and Warnaka et al. [5]. The most commonly used adaptive approach for ANC system is the transversal filter using the least mean square (LMS) algorithm [6]. In addition, the feedforward control architecture [6–8] is usually applied to ANC systems for practical implementations. In the feedforward system, a reference microphone, which is located upstream from the secondary source, detects the incident noise waves and supplies the controller with an input signal. Alternatively, a transducer is suggested to sense the frequency of primary noise, if to place the reference microphone is difficult. The controller sends a signal, which is in antiphase with the disturbance, to the secondary source (i.e., loudspeaker) for canceling the primary noise. In addition, an error microphone-located downstream picks up the residual and supplies the controller with an error signal. The controller must accommodate itself to the variation of environment.
The single-frequency adaptive notch filter, which uses two adaptive weights and a 90° phase shift unit, was developed by Widrow and Stearns [9] for interference cancellation. Subsequently, Ziegler [10] first applied this technique to ANC systems and patented it. In addition, Kuo et al. [11] proposed a simplified single-frequency ANC system with delayed-X LMS (DXLMS) algorithm to improve the performance for the fixed-point implementation. In addition, the fact that convergence performance depends on the normalized frequency is pointed. Generally, a periodic noise contains tones at the fundamental frequency and at several harmonic frequencies of the primary noise. This type of noise can be attenuated by a filter with multiple notches [12]. If the undesired primary noise contains M sinusoids, then M two-weight adaptive filters can be connected in parallel. This parallel configuration extended to multiple-frequency ANC has also been illustrated in [6]. In practical applications, this multiple narrowband ANC controller/filter has been applied to electronic mufflers on automobiles in which the primary noise components are harmonics of the basic firing rate. Furthermore, the convergence analysis of the parallel multiple-frequency ANC system has been proposed in [12]. It is found by Kuo et al. [12] that the convergence of this direct-form ANC system is dependent on the frequency separation between two adjacent sinusoids in the reference signal. In addition, the subband scheme and phase compensation have been combined with notch filter in the recent researches [13–15].
Using the representation of transfer function [6–13], the steady state of weight vector for the ANC systems can be determined and the convergence speed can be analyzed by eigenvalue spread. However, it can not explain the fact that the performance will be degraded at some frequencies. Based on the concepts of phasor representation [16], this paper discusses the selection of reference signals in narrowband ANC systems to illustrate the effect of phase compensation in delayed-X LMS approach [11]. The different selections of signal phasor to the reference signal are considered to describe the operation of narrowband ANC systems. In addition, this paper intends to modify the structure of Kuo's FIR-type ANC filter in order to achieve a better performance. This paper is organized as follows. Section 2 briefly reviews the basic two-weight adaptive filter and the delayed two-tap adaptive filter in the single-frequency ANC systems. Besides, the solution of weight vectors will be solved by using the phasor concept. In Section 3, the signal basis is discussed and illustrated for the above-mentioned adaptive filters based on the phasor concept. In Section 4, the eigenvalue spread is discussed to compare the convergence speed for different signal basis selections. The simulations will reflect the facts and discussions. Finally, the conclusions are addressed in Section 5.
2. Two-Weight Notch Filtering for ANC System
The conventional structure of two-tap adaptive notch filter with a secondary-path estimate  is shown in Figure 1 [6–8]. The reference input is a sine wave
is shown in Figure 1 [6–8]. The reference input is a sine wave  , where
, where  is the primary noise frequency and
is the primary noise frequency and  is the normalized frequency with respect to sampling rate
is the normalized frequency with respect to sampling rate  . For the conventional adaptive notch filter, a 90° phase shifter or another cosine wave generator [17, 18] is required to produce the quadrature reference signal
. For the conventional adaptive notch filter, a 90° phase shifter or another cosine wave generator [17, 18] is required to produce the quadrature reference signal  . As illustrated in Figure 1,
. As illustrated in Figure 1,  is the residual error signal measured by the error microphone, and
is the residual error signal measured by the error microphone, and  is the primary noise to be reduced. The transfer function
is the primary noise to be reduced. The transfer function  represents the primary path from the reference microphone to the error microphone, and
represents the primary path from the reference microphone to the error microphone, and  is the secondary-path transfer function between the output of adaptive filter and the output of error microphone. The secondary signal
is the secondary-path transfer function between the output of adaptive filter and the output of error microphone. The secondary signal  is generated by filtering the reference signal
is generated by filtering the reference signal  with the adaptive filter
with the adaptive filter  and can be expressed as
and can be expressed as

where T denotes the transpose of a vector, and  is the weight vector of the adaptive filter
is the weight vector of the adaptive filter  . By using the filtered-X LMS (FXLMS) algorithm [6–8], the reference signals,
. By using the filtered-X LMS (FXLMS) algorithm [6–8], the reference signals,  and
and  , are filtered by secondary-path estimation filter
, are filtered by secondary-path estimation filter  expressed as
expressed as

where  is the impulse response of the secondary-path estimate
is the impulse response of the secondary-path estimate  , and ∗ denotes linear convolution. The adaptive filter minimizes the instantaneous squared error using the FXLMS algorithm as
, and ∗ denotes linear convolution. The adaptive filter minimizes the instantaneous squared error using the FXLMS algorithm as

where  and
and  is the step size (or convergence factor).
is the step size (or convergence factor).
Let the primary signal be  with amplitude A and phase
with amplitude A and phase  . And, assume that the phase and amplitude responses of the secondary-path
. And, assume that the phase and amplitude responses of the secondary-path  at frequency
at frequency  is
is  and A, respectively. Since the filtering of secondary-path estimate
and A, respectively. Since the filtering of secondary-path estimate  is linear, the frequencies of the output signal
is linear, the frequencies of the output signal  and the input signal
and the input signal  will be the same. To perfectly cancel the primary noise, the antinoise from the output of the adaptive filter should be set as
will be the same. To perfectly cancel the primary noise, the antinoise from the output of the adaptive filter should be set as  Therefore, the relationship
Therefore, the relationship  holds. In the following, the concept of phasor [16] is used for representing the system to solve the optimal weight solution instead of using the transfer function and control theory [6–8]. The output phasor of adaptive filter
holds. In the following, the concept of phasor [16] is used for representing the system to solve the optimal weight solution instead of using the transfer function and control theory [6–8]. The output phasor of adaptive filter  would be the linear combination of signal phasors
would be the linear combination of signal phasors  and
and  , that is,
, that is,

Therefore, the optimal weight vector is readily obtained as

which depends on the system parameter  .
.
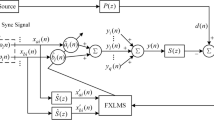
This conventional notch filtering technique requires two tables or a phase shift unit to concurrently generate the sine and cosine waveforms. This needs extra hardware or software resources for implementation. Moreover, the input signals,  , should be separately processed in order to obtain a better performance. To simplify the structure, Kuo et al. [11] replaced the 90° phase shift unit and the two individual weights by a second-order FIR filter. As shown in Figure 2, the structure does not need two quadratic reference inputs and the filter-x process is reduced. Especially, Kuo et al. inserted a delay unit located in the front of the second-order FIR filter to improve the convergence performance for considering the implementation over the finite word-length machine. This inserted delay can be called the phase compensation to the system parameter
, should be separately processed in order to obtain a better performance. To simplify the structure, Kuo et al. [11] replaced the 90° phase shift unit and the two individual weights by a second-order FIR filter. As shown in Figure 2, the structure does not need two quadratic reference inputs and the filter-x process is reduced. Especially, Kuo et al. inserted a delay unit located in the front of the second-order FIR filter to improve the convergence performance for considering the implementation over the finite word-length machine. This inserted delay can be called the phase compensation to the system parameter  . For Kuo's approach, the output phasor of adaptive filter would be the linear combination of
. For Kuo's approach, the output phasor of adaptive filter would be the linear combination of  and
and  , where D is the inserted delay. That is,
, where D is the inserted delay. That is,

Therefore, the optimal weight vector is the function of D,  and
and  shown as
shown as

To enhance the effect of delay-inserted approach, Kuo et al. compared the performance with the case of no phase-compensation ( ) for the fixed-point implementation. If no delay is inserted, that is,
) for the fixed-point implementation. If no delay is inserted, that is,  , the optimal weight vector is simplified as
, the optimal weight vector is simplified as

Kuo et al. [11] have experimented and pointed out that the delay-inserted approach can improve the convergence performance for two-tap adaptive filter in some frequency band. Based on the phasor representation, the reference signals with different phase can further improve the performance of narrowband ANC systems.
3. Signal Basis Selection
In practical applications, adaptive notch filter is usually implemented on the fixed-point hardware. Therefore, the finite precision effects play an important role on the convergence performance and speed for the adaptive filter. It is difficult to maintain the accuracy of the small coefficient and to prevent the order of magnitude of weights from overflowing simultaneously, as the ratio of two weights in the steady state is very large. When the ratio of two weights in the steady state,  , is close to one, the dynamic range of weight value in adaptive processing is fairly small [11]. Thus, the filter can be implemented on the fixed-point hardware with shorter word length, or the coefficients will have higher precision (less coefficient quantization noise) for given a word length.
, is close to one, the dynamic range of weight value in adaptive processing is fairly small [11]. Thus, the filter can be implemented on the fixed-point hardware with shorter word length, or the coefficients will have higher precision (less coefficient quantization noise) for given a word length.
Based on the concepts of signal space and phasor, the relationship of signal phasors for the above-mentioned two-weight adaptive filters is shown in Figure 3. Figure 3(a) illustrates that the combination of the signal bases (phasors),  and
and  , with the respective components in
, with the respective components in  , is able to synthesize the signal phasor
, is able to synthesize the signal phasor  . Since the weight vector
. Since the weight vector  is only the function of system parameter
is only the function of system parameter  , it is difficult to control the ratio of these two weights in steady state by the designer. Figure 4 shows that only some narrow regions in the
, it is difficult to control the ratio of these two weights in steady state by the designer. Figure 4 shows that only some narrow regions in the  -plane with specified values of
-plane with specified values of  satisfy the condition
satisfy the condition  (i.e.,
(i.e.,  ), where
), where  is a small value. If the FIR-type adaptive filter [11] is used, Figure 3(b) shows the relationship of the signal phasors
is a small value. If the FIR-type adaptive filter [11] is used, Figure 3(b) shows the relationship of the signal phasors  ,
,  and
and  , where the inserted delay
, where the inserted delay  holds. Figure 5 illustrates that the desired regions, in which the ratio of two taps satisfies
holds. Figure 5 illustrates that the desired regions, in which the ratio of two taps satisfies  (
( ), in
), in  -plane have been rearranged. We can find that there are two solutions to achieve the requirement,
-plane have been rearranged. We can find that there are two solutions to achieve the requirement,  . One solution is to translate the operation point along the vertical axis (
. One solution is to translate the operation point along the vertical axis ( -axis) by way of changing the sampling frequency. Therefore, the ratio of two weights for the optimal solution
-axis) by way of changing the sampling frequency. Therefore, the ratio of two weights for the optimal solution  can be controlled by changing the sampling frequency to design the normalized frequency
can be controlled by changing the sampling frequency to design the normalized frequency  . That is, when the system parameter
. That is, when the system parameter  and the primary noise frequency
and the primary noise frequency  are given, the designer can adjust the sampling rate
are given, the designer can adjust the sampling rate  to locate the operation point S in the desired region as shown in Figure 5. Another solution is that we can shift the operation point along the horizontal axis to locate the operation point S in the desired region by compensating the system phase
to locate the operation point S in the desired region as shown in Figure 5. Another solution is that we can shift the operation point along the horizontal axis to locate the operation point S in the desired region by compensating the system phase  .
.
If the multiple narrowband ANC systems are used, the same sampling frequency is suggested such that the synthesis noises for secondary source can therefore work concurrently. If the sampling rate has been fixed, Kuo et al. [11] suggested inserting a delay unit to control the quantity of weights. The inserted delay can compensate the system phase parameter  . This system-phase compensation can move the operation point from S to
. This system-phase compensation can move the operation point from S to  (
( ) along the
) along the  -axis, as shown in Figure 5. When the system phase has been compensated, the operation point in
-axis, as shown in Figure 5. When the system phase has been compensated, the operation point in  -plane can locate in the desired region which the ratio of two weights is close to one. Using the signal bases
-plane can locate in the desired region which the ratio of two weights is close to one. Using the signal bases  and
and  , the ratio of two weights satisfies
, the ratio of two weights satisfies

The solution to (9) is  , where k is any integer. The optimal delay D can be expressed as
, where k is any integer. The optimal delay D can be expressed as  samples, where the operation
samples, where the operation  denotes to take the nearest integer. These solutions confirm the results in [11] in which the solution is derived by transfer-function representation. Besides, since the relationship
denotes to take the nearest integer. These solutions confirm the results in [11] in which the solution is derived by transfer-function representation. Besides, since the relationship  holds, there are four solutions for delay D ; these solutions are the possible operation points,
holds, there are four solutions for delay D ; these solutions are the possible operation points,  , and
, and  , as shown in Figure 5. From the phasor point of view, the operation points
, as shown in Figure 5. From the phasor point of view, the operation points  and
and  mean that the synthesis phasor y (n) is located in the acute angle formed by basis phasors
mean that the synthesis phasor y (n) is located in the acute angle formed by basis phasors  and
and  , as shown in Figure 3(c). Therefore, the range of weights value can be efficiently used. In addition, observing Figure 5, it can be found that the area of the desired regions varies with the normalized frequencies. It means that the performance will vary with the normalized frequency. This fact also confirms the experimental results in [11]. To solve the problem that the performance depends on the normalized frequency, another signal bases should be found for the two-tap adaptive filters.
, as shown in Figure 3(c). Therefore, the range of weights value can be efficiently used. In addition, observing Figure 5, it can be found that the area of the desired regions varies with the normalized frequencies. It means that the performance will vary with the normalized frequency. This fact also confirms the experimental results in [11]. To solve the problem that the performance depends on the normalized frequency, another signal bases should be found for the two-tap adaptive filters.
In the desired signal space, the phasors  and
and  are linearly independent but not orthogonal. Based on the convergence comparison [19] according to the eigenvector and eigenvalue, the convergence speed of Kuo's FIR-type approach will be slow. To accelerate the convergence speed, the signal bases can be setup as orthogonal as possible. As shown in Figure 3(d), the near orthogonal bases
are linearly independent but not orthogonal. Based on the convergence comparison [19] according to the eigenvector and eigenvalue, the convergence speed of Kuo's FIR-type approach will be slow. To accelerate the convergence speed, the signal bases can be setup as orthogonal as possible. As shown in Figure 3(d), the near orthogonal bases  and
and  should be found to improve the performance. Based on this motivation, a new delay unit
should be found to improve the performance. Based on this motivation, a new delay unit  ,
,  is introduced as shown in Figure 6. The optimal weight vector of the proposed two-tap adaptive filter is therefore obtained as
is introduced as shown in Figure 6. The optimal weight vector of the proposed two-tap adaptive filter is therefore obtained as

such that the signal  can be represented as a linear combination of
can be represented as a linear combination of  and
and  . That is,
. That is,

Since the signal bases in the proposed two-tap adaptive filter can be controlled by the delays  and
and  , the signal bases can be setup as orthogonal as possible in order to accelerate the convergence speed and to compensate the system phase. Therefore, the delay
, the signal bases can be setup as orthogonal as possible in order to accelerate the convergence speed and to compensate the system phase. Therefore, the delay  should hold such that the signal phasor
should hold such that the signal phasor  can be approximated as close as possible to
can be approximated as close as possible to  . The ratio of two weights will be close to one when the system phase has been compensated by the delay
. The ratio of two weights will be close to one when the system phase has been compensated by the delay  . That is,
. That is,

The solution to (12) is  ,
,  . The optimal delays can therefore be found as
. The optimal delays can therefore be found as  samples. The desired regions in
samples. The desired regions in  -plane for the proposed two-tap adaptive filter are similar to that of the desired regions shown in Figure 4. Theoretically, the desired regions do not depend on the normalized frequency in theory. To achieve a better performance for fixed-point implementation, the operation point in
-plane for the proposed two-tap adaptive filter are similar to that of the desired regions shown in Figure 4. Theoretically, the desired regions do not depend on the normalized frequency in theory. To achieve a better performance for fixed-point implementation, the operation point in  -plane can be shifted to the desired area along the horizontal axis (
-plane can be shifted to the desired area along the horizontal axis ( -axis) after the delay
-axis) after the delay  is inserted.
is inserted.
4. Discussion and Simulations
The data covariance matrix for the conventional two-weight notch filter is described as [9]

It is evident that both the corresponding eigenvalues are equal to 1/2. This leads to the fact that eigenvalue spread is one; the conventional two-weight notch filter has the better performance on However, since the optimal weight

depends on the system phase parameter  , the convergence performance will depend on
, the convergence performance will depend on  . For the Kuo's FIR-type adaptive filter [11], the data covariance matrix is
. For the Kuo's FIR-type adaptive filter [11], the data covariance matrix is

The corresponding two eigenvalues are  ; the eigenvalue spread is
; the eigenvalue spread is

Since the eigenvalue spread  is larger than one, the convergence speed will be slower than the conventional two-weight notch filter. It can be found that the convergence speed will depend on the normalized frequency
is larger than one, the convergence speed will be slower than the conventional two-weight notch filter. It can be found that the convergence speed will depend on the normalized frequency  .
.
The proposed two-tap adaptive filter uses the data covariance:

The corresponding eigenvalue spread is

Using the optimal delay found in (12), the data covariance is

and the corresponding eigenvalue spread is  . Since the eigenvalue spread has been reduced from
. Since the eigenvalue spread has been reduced from  to
to  1, the proposed two-tap adaptive filter will have higher convergence speed.
1, the proposed two-tap adaptive filter will have higher convergence speed.
In the following simulations, the primary noise is set as  where
where  is a random phase and
is a random phase and  is the environmental noise with power
is the environmental noise with power  . The primary noise with frequency
. The primary noise with frequency  Hz is sampled with a fixed rate
Hz is sampled with a fixed rate  Hz. The ratio of the primary noise to environmental noise for the signal is defined as
Hz. The ratio of the primary noise to environmental noise for the signal is defined as  (dB). All the examples are simulated with
(dB). All the examples are simulated with  dB. The phase response of the secondary-path has been experimented to obtain a determined delay according to the designed sampling rate and frequency of primary noise. In addition, all input data and filter coefficients are quantized using word length of 16 bits within fraction length, and 8 bits to simulate the operation of fixed-point hardware. The temporary data is represented by 64-bit precision, and the rounding is performed only after summation. Therefore, the step size in FXLMS algorithm is
dB. The phase response of the secondary-path has been experimented to obtain a determined delay according to the designed sampling rate and frequency of primary noise. In addition, all input data and filter coefficients are quantized using word length of 16 bits within fraction length, and 8 bits to simulate the operation of fixed-point hardware. The temporary data is represented by 64-bit precision, and the rounding is performed only after summation. Therefore, the step size in FXLMS algorithm is  , which is the precision of this simulation. All the learning curves are obtained after 200 independent runs with random system parameters
, which is the precision of this simulation. All the learning curves are obtained after 200 independent runs with random system parameters  . For the frequency of primary noise
. For the frequency of primary noise  Hz, Figure 7 illustrates that Kuo's delayed two-tap adaptive filter can improve the performance of the nondelayed one, but the convergence speed is still slow. Besides, the proposed approach, which is with well-selected bases, has the fast convergence speed and the best convergence performance.
Hz, Figure 7 illustrates that Kuo's delayed two-tap adaptive filter can improve the performance of the nondelayed one, but the convergence speed is still slow. Besides, the proposed approach, which is with well-selected bases, has the fast convergence speed and the best convergence performance.
In theory, the convergence performance of the proposed approach does not depend on the normalized frequency. However, simulations could not verify this statement and it also could not be explained by the representation of transfer function. Based on the concept of phasor rotation, we can find that the location of possible synthesis phasors would have variation for each adaptation if the number of samples in a cycle is not an integer, for example,  . The phasor-location variation will be significant as the amplitude of synthesis phasors increasing and will also lead to degradation in performance. Figure 8 illustrates that Kuo's approach and the proposed approaches are degraded in performance when the frequency of primary noise is 97 Hz with the sampling rate 1000 Hz. In addition, when the normalized frequency is low, for example,
. The phasor-location variation will be significant as the amplitude of synthesis phasors increasing and will also lead to degradation in performance. Figure 8 illustrates that Kuo's approach and the proposed approaches are degraded in performance when the frequency of primary noise is 97 Hz with the sampling rate 1000 Hz. In addition, when the normalized frequency is low, for example,  Hz, the angle of signal-basis phasors is small. In this case, the phase compensation is more important for Kuo's FIR-type adaptive filter. Figure 9 illustrates that the phase compensation can greatly improve the performance for the case of low frequency for Kuo's FIR-type adaptive filter. However, the convergence speed of Kuo's two-tap adaptive filter is extremely low, since their eigenvalue spread is large; in this simulation, the eigenvalue spread is 39.8635. In addition, when the normalized frequency is close to 0.5, the eigenvalue spread of all approaches is close to 1 and the angle of the signal bases is inherently near-orthogonal. Therefore, the convergence speed for all approaches will be the same. For example, when the frequency of the primary noise is set as
Hz, the angle of signal-basis phasors is small. In this case, the phase compensation is more important for Kuo's FIR-type adaptive filter. Figure 9 illustrates that the phase compensation can greatly improve the performance for the case of low frequency for Kuo's FIR-type adaptive filter. However, the convergence speed of Kuo's two-tap adaptive filter is extremely low, since their eigenvalue spread is large; in this simulation, the eigenvalue spread is 39.8635. In addition, when the normalized frequency is close to 0.5, the eigenvalue spread of all approaches is close to 1 and the angle of the signal bases is inherently near-orthogonal. Therefore, the convergence speed for all approaches will be the same. For example, when the frequency of the primary noise is set as  Hz, all the approaches have the same convergence performance and speed as illustrated in Figure 10. Observing Figure 10, the performance of the phase-compensated and noncompensated approaches is the same, since the 16-bit fixed-point hardware with 8-bit fraction length is enough for this simulation. These experiments confirm the results presented in [11], in which their experiments found that there is no improvement for convergence performance when the normalized frequency is 0.5. Observing Figures 7–10, the proposed approach not only achieves a good performance, but also preserves the FIR adaptive filter structure.
Hz, all the approaches have the same convergence performance and speed as illustrated in Figure 10. Observing Figure 10, the performance of the phase-compensated and noncompensated approaches is the same, since the 16-bit fixed-point hardware with 8-bit fraction length is enough for this simulation. These experiments confirm the results presented in [11], in which their experiments found that there is no improvement for convergence performance when the normalized frequency is 0.5. Observing Figures 7–10, the proposed approach not only achieves a good performance, but also preserves the FIR adaptive filter structure.
5. Conclusion
In this paper, the phasor representation instead of transfer function is introduced and discussed for the narrowband ANC systems. Based on the concepts of signal basis and phasor rotation, the reference signal/phasor for two-tap adaptive filters has been modeled and well-selected. Using the representation of phasor can explain the reason why the performance of the narrowband ANC systems is degraded for some normalized frequency. In addition, to achieve a better performance, the proposed two-tap adaptive filter can choose the near-orthogonal phasors for the fixed-point hardware implementation. With the same complexity, the inserted delay in Kuo's two-tap adaptive filter can be moved back to construct the proposed approach, which would achieve a better performance.
References
Harris CM: Handbook of Acoustical Measurements and Noise Control. 3rd edition. McGraw-Hill, New York, NY, USA; 1991.
Beranek LL, Ver IL: Noise and Vibration Control Engineering: Principles and Applications. John Wiley & Sons, New York, NY, USA; 1992.
Leug P: Process of silencing sound oscillations. 1936.
Burgess JC: Active adaptive sound control in a duct: a computer simulation. The Journal of the Acoustical Society of America 1981,70(3):715-726. 10.1121/1.386908
Warnaka GE, Tichy J, Poole LA: Improvements in adaptive active attenuators. Proceedings of Inter-Noise, October 1981, Amsterdam, The Netherlands 307-310.
Kuo SM, Morgan DR: Active Noise Control Systems: Algorithms and DSP Implementations. John Wiley & Sons, New York, NY, USA; 1996.
Kuo SM, Morgan DR: Active noise control: a tutorial review. Proceedings of the IEEE 1999,87(6):943-973. 10.1109/5.763310
Nelson PA, Elliott SJ: Active Control of Sound. Academic Press, San Diego, Calif, USA; 1992.
Widrow B, Stearns SD: Adaptive Signal Processing. Prentice-Hall, Englewood Cliffs, NJ, USA; 1985.
Ziegler E Jr.: Selective active cancellation system for repetitive phenomena. 1989.
Kuo SM, Zhu S, Wang M: Development of optimum adaptive notch filter for fixed-point implementation in active noise control. Proceedings of the International Conference on Industrial Electronics, Control, Instrumentation, and Automation, November 1992, San Diego, Calif, USA 3: 1376-1378.
Kuo SM, Puvvala A, Gan WS: Convergence analysis of narrowband active noise control. Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP '06), May 2006, Toulouse, France 5: 293-296.
Kinugasa Y, Okello J, Itoh Y, Kobayashi M, Fukui Y: A new algorithm for adaptive notch filter with sub-band filtering. Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS '01), 2001, Sydney, Australia 2: 817-820.
DeBrunner V, DeBrunner L, Wang L: Sub-band adaptive filtering with delay compensation for active control. IEEE Transaction on Signal Processing 2004,52(10):2932-2937. 10.1109/TSP.2004.834340
Wang L, Swamy MNS, Ahmad MO: An efficient implementation of the delay compensation for sub-band filtered-x least-mean-square algorithm. IEEE Transactions on Circuits and Systems II 2006,53(8):748-752.
McClellan JH, Schafer RW, Yoder MA: Signal Processing First. Prentice-Hall, Upper Saddle River, NJ, USA; 2003.
Mock P:Add DTMF generation and decoding to DSP-
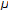 P designs. Electronic Design News 1985,30(6):205-213.
P designs. Electronic Design News 1985,30(6):205-213.Kuo SM, Gan WS: Digital Signal Processors: Architecture, Implementations and Applications. Prentice-Hall, Englewood Cliffs, NJ, USA; 2005.
Haykin S: Adaptive Filter Theory. 4th edition. Prentice-Hall, Englewood Cliffs. NJ, USA; 2000.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, FK., Chen, DH. & Jou, YD. Phasor Representation for Narrowband Active Noise Control Systems. J AUDIO SPEECH MUSIC PROC. 2008, 126859 (2008). https://doi.org/10.1155/2008/126859
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/126859







 -plane for conventional two-weight notch filter (
-plane for conventional two-weight notch filter ( ).
).
 -plane for the delayed two-taps adaptive filter (
-plane for the delayed two-taps adaptive filter ( ).
).

 .
.


 .
.

 .
.
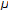 P designs. Electronic Design News 1985,30(6):205-213.
P designs. Electronic Design News 1985,30(6):205-213.