Skip to main content
SpringerLink
Log in

The interspersed spin boson lattice model

  • Regular Article
  • Published:
The European Physical Journal Special Topics Aims and scope Submit manuscript

Abstract

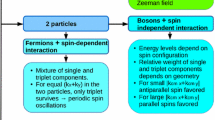
We describe a family of lattice models that support a new class of quantum magnetism characterized by correlated spin and bosonic ordering [Phys. Rev. Lett. 112, 180405 (2014)]. We explore the full phase diagram of the model using Matrix-Product-State methods. Guided by these numerical results, we describe a modified variational ansatz to improve our analytic description of the groundstate at low boson frequencies. Additionally, we introduce an experimental protocol capable of inferring the low-energy excitations of the system by means of Fano scattering spectroscopy. Finally, we discuss the implementation and characterization of this model with current circuit-QED technology.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. See I. Bloch, J. Dalibard, S. Nascimbéne, Nat. Phys. 8, 267 (2012), and references therein

    Article  Google Scholar 

  2. See R. Blatt, C.F. Roos, Nat. Phys. 8, 277 (2012), and references therein

    Article  Google Scholar 

  3. See A.A. Houck, H.E. Türeci, J. Koch, Nat. Phys. 8, 264 (2012), and references therein

    Article  Google Scholar 

  4. See P. Barthelemy, L.M.K. Vandersypen, Ann. Phys. 525, 808 (2013), and references therein

    Article  MathSciNet  Google Scholar 

  5. R.P. Feynman, Int. J. Theo. Phys. 21, 467 (1982)

    Article  MathSciNet  Google Scholar 

  6. J.I. Cirac, P. Zoller, Nat. Phys. 8, 264 (2012)

    Article  Google Scholar 

  7. J. Simon, W.S. Bakr, R. Ma, M.E. Tai, P.M. Preiss, M. Greiner, Nature 472, 307 (2011)

    Article  ADS  Google Scholar 

  8. A. Friedenauer, H. Schmitz, J.T. Glueckert, D. Porras, T. Schaetz, Nat. Phys. 4, 757 (2008)

    Article  Google Scholar 

  9. K. Kim, M.-S. Chang, S. Korenblit, R. Islam, E.E. Edwards, J.K. Freericks, G.-D. Lin, L.-M. Duan, C. Monroe, Nature 465, 590 (2010)

    Article  ADS  Google Scholar 

  10. J.W. Britton, B.C. Sawyer, A.C. Keith, C.-C.J. Wang, J.K. Freericks, H. Uys, M.J. Biercuk, J.J. Bollinger, Nature 484, 489 (2012)

    Article  ADS  Google Scholar 

  11. R. Islam, C. Senko, W.C. Campbell, S. Korenblit, J. Smith, A. Lee, E.E. Edwards, C.-C.J. Wang, J.K. Freericks, C. Monroe, Science 340, 583 (2013)

    Article  ADS  Google Scholar 

  12. P. Richerme, Z.-X. Gong, A. Lee, C. Senko, J. Smith, M. Foss-Feig, S. Michalakis, A.V. Gorshkov, C. Monroe, Nature 511, 198 (2014)

    Article  ADS  Google Scholar 

  13. P. Jurcevic, B.P. Lanyon, P. Hauke, C. Hempel, P. Zoller, R. Blatt, C.F. Roos, Nature 511, 202 (2014)

    Article  ADS  Google Scholar 

  14. S. Trotzky, P. Cheinet, S. Fölling, M. Feld, U. Schnorrberger, A.M. Rey, A. Polkovnikov, E.A. Demler, M.D. Lukin, I. Bloch, Science 319, 295 (2008)

    Article  ADS  Google Scholar 

  15. T. Fukuhara, P. Schau, M. Endres, S. Hild, M. Cheneau, I. Bloch, C. Gross, Nature 502, 76 (2013)

    Article  ADS  Google Scholar 

  16. D. Greif, T. Uehlinger, G. Jotzu, L. Tarruell, T. Esslinger, Science 340, 1307 (2013)

    Article  ADS  Google Scholar 

  17. R.A. Hart, P.M. Duarte, T.-L. Yang, X. Liu, T. Paiva, E. Khatami, R.T. Scalettar, N. Trivedi, D.A. Huse, R.G. Hulet [arXiv:1407.5932] (2014)

  18. D. Porras, J.I. Cirac, Phys. Rev. Lett. 92, 207901 (2004)

    Article  ADS  Google Scholar 

  19. A. Bermudez, M.A. Martin-Delgado, D. Porras, New J. Phys. 12, 123016 (2010)

    Article  ADS  Google Scholar 

  20. G. Zhu, S. Schmidt, J. Koch, New J. Phys. 15, 115002 (2013)

    Article  ADS  Google Scholar 

  21. C. Cormick, A. Bermudez, S.F. Huelga, M.B. Plenio, New J. Phys. 15, 073027 (2013)

    Article  ADS  Google Scholar 

  22. A. Kurcz, A. Bermudez, J.J. Garcia-Ripoll, Phys. Rev. Lett. 112, 180405 (2014)

    Article  ADS  Google Scholar 

  23. A. Leggett, S. Chakravarty, A. Dorsey, M. Fisher, A. Garg, W. Zwerger, Rev. Mod. Phys. 59, 1 (1987)

    Article  ADS  Google Scholar 

  24. A.D. Greentree, C. Tahan, J.H. Cole, L.C.L. Hollenberg, Nat. Phys. 2, 856 (2006)

    Article  Google Scholar 

  25. M.J. Hartmann, F.G.S.L. Brandao, M.B. Plenio, Nat. Phys. 2, 849 (2006)

    Article  Google Scholar 

  26. M. Schiró, M. Bordyuh, B. Öztop, H.E. Türeci, Phys. Rev. Lett. 109, 053601 (2012)

    Article  ADS  Google Scholar 

  27. M. Schiró, M. Bordyuh, B. Öztop, H.E. Türeci, J. Phys. B 46, 224021 (2013)

    Article  ADS  Google Scholar 

  28. P.A. Ivanov, S.S. Ivanov, N.V. Vitanov, A. Mering, M. Fleischhauer, K. Singer, Phys. Rev. A 80, 060301(R) (2009)

    Article  ADS  Google Scholar 

  29. P. Nevado, D. Porras, Eur. Phys. J. Special Topics 217, 29 (2013)

    Article  ADS  Google Scholar 

  30. J. Jünemann, A. Cadarso, D. Pérez-García, A. Bermudez, J.J. García-Ripoll, Phys. Rev. Lett. 111, 230404 (2013)

    Article  Google Scholar 

  31. D. Porras, P.A. Ivanov, F. Schmidt-Kaler, Phys. Rev. Lett. 108, 235701 (2012)

    Article  ADS  Google Scholar 

  32. A. Dutta, J.K. Bhattacharjee, Phys. Rev. B 64, 184106 (2001)

    Article  ADS  Google Scholar 

  33. P. Pfeuty, Ann. Phys. 57, 79 (1970)

    Article  ADS  Google Scholar 

  34. I.G. Lang, Y.A. Firsov, Zh. Eksp. Teor. Fiz. 43, 1843 (1962), (see also Y.A. Firsov, Small Polarons: Transport Phenomena, in Polarons in Advanced Materials, edited by A.S. Alexandrov (Springer Verlag, Bristol, 2007)

  35. P. Jordan, E. Wigner, Z. Physik 47, 631 (1928)

    Article  MATH  ADS  Google Scholar 

  36. N.N. Bogoliubov, Sov. Phys. JETP 7, 41 (1958)

    MathSciNet  Google Scholar 

  37. (English translation Il Nuovo Cim. 6, 794 (1958))

  38. R. Orus, G. Vidal, Phys. Rev. B 78, 155117 (2008)

    Article  ADS  Google Scholar 

  39. J.J. García-Ripoll, New J. Phys. 8, 305 (2006)

    Article  Google Scholar 

  40. F. Verstraete, V. Murg, J. Cirac, Adv. Phys. 57, 143 (2008)

    Article  ADS  Google Scholar 

  41. V.J. Emery, A. Luther, Phys. Rev. Lett. 26, 1547 (1971)

    Article  ADS  Google Scholar 

  42. R. Silbey, R.A. Harris, J. Chem. Phys. 80, 2615 (1984)

    Article  ADS  Google Scholar 

  43. R.A. Harris, R. Silbey, J. Chem. Phys. 83, 1069 (1985)

    Article  ADS  Google Scholar 

  44. S. Bera, S. Florens, H.U. Baranger, N. Roch, A. Nazir, A.W. Chin, Phys. Rev. B 89, 121108(R) (2014)

    Article  ADS  Google Scholar 

  45. S. Bera, A. Nazir, A.W. Chin, H.U. Baranger, S. Florens [arXiv:1406.4983] (2014)

  46. We define the following parameters u q = [1 2(1 + Δq/𝜖q)]1/2, v q = i[1 2(1 −Δq/𝜖q)]1/2 in terms of Δq = 2(J cosqd + h t), and 𝜖q = [Δ + (2J sinqd)2]1/2

  47. R. Kubo, J. Phys. Soc. Jpn. 12, 570 (1957)

    Article  MathSciNet  ADS  Google Scholar 

  48. H. Bruus, K. Flensberg, Many-Body Quantum Theory in Condensed Matter Physics: An Introduction (Oxford University Press, Oxford, 2004)

  49. U. Fano, Phys. Rev. 124, 1866 (1961)

    Article  MATH  ADS  Google Scholar 

  50. See A.E. Miroshnichenko, S. Flach, Y.S. Kivshar, Rev. Mod. Phys. 82, 2257 (2010), and references therein

    Article  ADS  Google Scholar 

  51. J.T. Shen, S. Fan, Opt. Lett. 30, 2001 (2005)

    Article  ADS  Google Scholar 

  52. A.E. Miroshnichenko, S.F. Mingaleev, S. Flach, Y.S. Kivshar, Phys. Rev. E 71, 036626 (2005)

    Article  MathSciNet  ADS  Google Scholar 

  53. L. Zhou, Z.R. Gong, Y.-X. Liu, C.P. Sun, F. Nori, Phys. Rev. Lett. 101, 100501 (2008)

    Article  ADS  Google Scholar 

  54. M. Biondi, S. Schmidt, G. Blatter, H.E. Türeci, Phys. Rev. A 89, 025801 (2014)

    Article  ADS  Google Scholar 

  55. The lowest higher-energy excitations are composed of two-quasiparticles with energies 𝜖(q,q′) = 𝜖(q) + 𝜖(q′). Since the system-probe coupling may connect a low-energy excitation  to these higher-energy ones, we have to impose that the process is highly off-resonant |g p|≪|𝜖(q,q′) − 𝜖(q′′)|,∀,q,q′,q′′, which amounts to the condition in the text

  56. The multi-level Fano coupling constants are g qα = g p⟨e2|𝜖(q)⟩(u qδα,+ − v qδα,−) × e iqd/√ _N, where ⟨e2| = (0,1)

  57. J.T. Shen, S. Fan, Phys. Rev. A 76, 062709 (2007)

    Article  ADS  Google Scholar 

  58. M.H. Devoret, Quantum fluctuations in electrical circuits (Les Houches, Session LXIII, 1995)

  59. B. Yurke, J.S. Denker, Phys. Rev. A 29, 1419 (1984)

    Article  MathSciNet  ADS  Google Scholar 

  60. See the Supplemental Material to [22] for a more detailed account on the microscopic circuit-QED model

  61. J. Majer, J.M. Chow, J.M. Gambetta, J. Koch, B.R. Johnson, J.A. Schreier, L. Frunzio, D.I. Schuster, A.A. Houck, A. Wallraff, A. Blais, M.H. Devoret, S.M. Girvin, R.J. Schoelkopf, Nature 449, 443 (2007)

    Article  ADS  Google Scholar 

  62. H. Paik, D.I. Schuster, L.S. Bishop, G. Kirchmair, G. Catelani, A.P. Sears, B.R. Johnson, M.J. Reagor, L. Frunzio, L.I. Glaz- man, S.M. Girvin, M.H. Devoret, R.J. Schoelkopf, Phys. Rev. Lett. 107, 240501 (2011)

    Article  ADS  Google Scholar 

  63. C. Rigetti, J.M. Gambetta, S. Poletto, B.L.T. Plourde, J.M. Chow, A.D. Corcoles, J.A. Smolin, S.T. Merkel, J.R. Rozen, G.A. Keefe, M.B. Rothwell, M.B. Ketchen, M. Steffen, Phys. Rev. B 86, 100506(R) (2012)

    Article  ADS  Google Scholar 

  64. L. Sun, A. Petrenko, Z. Leghtas, B. Vlastakis, G. Kirchmair, K.M. Sliwa, A. Narla, M. Hatridge, S. Shankar, J. Blumoff, L. Frunzio, M. Mirrahimi, M.H. Devoret, R.J. Schoelkopf, Nature 511, 444 (2014)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Instituto de Física Fundamental, IFF-CSIC, Calle Serrano 113b, 28006, Madrid, Spain

    A. Kurcz, J. J. García-Ripoll & A. Bermudez

Authors
  1. A. Kurcz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. J. García-Ripoll
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Bermudez
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kurcz, A., García-Ripoll, J.J. & Bermudez, A. The interspersed spin boson lattice model. Eur. Phys. J. Spec. Top. 224, 483–496 (2015). https://doi.org/10.1140/epjst/e2015-02378-x

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1140/epjst/e2015-02378-x

Keywords

Search

Navigation