Skip to main content
SpringerLink
Log in

On the synchronization of chains of nonlinear pendula connected by linear springs

  • Regular Article
  • Published:
The European Physical Journal Special Topics Aims and scope Submit manuscript

Abstract

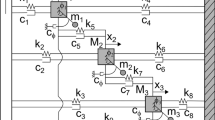
In this work the theoretical model of multidimensional physical systems, representable as chains of nonlinearly coupled chaotic pendula subjected to harmonic excitations, is formulated and its nonlinear dynamics and synchronization characteristics are studied by means of a numerical approach. Some considerations on the role of the main system parameters are drawn. Dynamic perturbations, due for example to background interactions or to intrinsic pathological imperfections of the chain, are also taken into account. Their effect is analyzed with reference to two distinct situations: uniform application to all the pendula and localized application to the extremities of the chain.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. S. Strogatz, Sync: the emerging science of spontaneous order (Hyperion, New York, 2003)

  2. A. Pikovsky, M.G. Rosenblum, J. Kurths, Synchronization: a universal concept in nonlinear science (Cambridge University Press, Cambridge, 2001)

  3. E. Fermi, J. Pasta, S. Ulam, “Studies of nonlinear problems,” Los Alamos Report LA-1940 (1955), published later in Fermi E., Pasta J. and Ulam S., Collected Papers of Enrico Fermi, edited by E. Segré (University of Chicago Press, Chicago, 1965)

  4. R. Chacón, L. Marcheggiani, Phys. Rev. E 82, 016201/1-7 (2010)

    ADS  Google Scholar 

  5. S. Boccaletti, The Synchronized Dynamics of Complex Systems (Elsevier, Amsterdam, 2008)

  6. A.H. Nayfeh, D.T. Mook, Nonlinear oscillations (John Wiley & Sons, New York, 1995)

  7. R.W. Leven, B.P. Koch, Phys. Lett. A 86, 71 (1981)

    Article  ADS  Google Scholar 

  8. W. Szemplinska-Stupnicka, E. Tyrkiel, A. Zubrzycki, Int. J. Bifurcat. Chaos 10, 2161 (2000)

    MATH  MathSciNet  Google Scholar 

  9. D. Capecchi, S.R. Bishop, Dynam. Stabil. Syst. 9, 123 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  10. M.J. Clifford, S.R. Bishop, Phys. Lett. A 201, 191 (1995)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  11. W. Szemplinska-Stupnicka, E. Tyrkiel, Int. J. Bifurcat. Chaos 12, 159 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  12. W. Szemplinska-Stupnicka, E. Tyrkiel, Nonlinear Dyn. 27, 271 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  13. X. Xu, M. Wiercigroch, M.P. Cartmell, Chaos Solitons Fract. 23, 1537 (2005)

    Article  ADS  MATH  Google Scholar 

  14. S. Lenci, E. Pavlovskaia, G. Rega, M. Wiercigroch, J. Sound Vib. 310, 243 (2008)

    Article  ADS  Google Scholar 

  15. B. Horton, J. Sieber, J.M.T. Thompson, M. Wiercigroch, Int. J. Nonlinear Mech. 46, 436 (2011)

    Article  ADS  Google Scholar 

  16. J.M. Balthazar, J.L.P. Felix, R.M.L.R.F. Brasil, Appl. Math. Comput. 164, 615 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  17. A. Najdecka, V. Vaziri, M. Wiercigroch, IUTAM Symposium on Nonlinear Dynamics for Advanced Technologies and Engineering Design, IUTAM Bookseries 32 (Springer, Aberdeen, 2013), p. 185

  18. A.O. Belyakov, Phys. Lett. A 375, 2524 (2011)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  19. C. Huygens, Christiaan Huygens’s the pendulum clock or geometrical demonstrations concerning the motion of pendula as applied to clocks, translated by Blackwell R.J., (Iowa State University Press, Ames, 1986)

  20. M. Bennett, M.F. Schatz, H. Rockwood, K. Wiesenfeld, Proc. R. Soc. Lond. A 458, 563 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  21. L.M. Pecora, T.L. Carroll, Phys. Rev. Lett. 64, 821 (1990)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  22. K. Czolczynski, P. Perlikowski, A. Stefanski, T. Kapitaniak, Int. J. Bifurcat. Chaos 22, 1 (2012)

    Article  MathSciNet  Google Scholar 

  23. K. Czolczynski, P. Perlikowski, A. Stefanski, T. Kapitaniak, Commun. Nonlinear. Numer. Simulat. 18, 386 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  24. K. Czolczynski, P. Perlikowski, A. Stefanski, T. Kapitaniak, Phys. A 388, 5013 (2009)

    Article  Google Scholar 

  25. A. Uchida, T. Sato, T. Ogawa, F. Kannari, Phys. Rev. E 58, 7249 (1998)

    Article  ADS  Google Scholar 

  26. J.M. Ottino, F.J. Muzzio, M. Tjahjadi, J.G. Franjione, S.C. Jana, H.A. Kusch, Science 257, 754 (1992)

    Article  ADS  Google Scholar 

  27. Y.V. Andreyev, Y.L. Belsky, A.S. Dmitriev, D.A. Kuminov, IEEE Trans. Neur. Networks 7, 290 (1996)

    Article  Google Scholar 

  28. W.X. Ding, H.Q. She, W. Huang, C.X. Yu, Phys. Rev. Lett. 72, 96 (1994)

    Article  ADS  Google Scholar 

  29. S.J. Schiff, K. Jerger, D.H. Duong, T. Chang, M.L. Spano, W.L. Ditto, Nature 370, 615 (1994)

    Article  ADS  Google Scholar 

  30. G.G. Gregoriou, S.J. Gotts, H. Zhou, R. Desimone, Science 324, 1207 (2009)

    Article  ADS  Google Scholar 

  31. L. Marcheggiani, S. Lenci, Meccanica 45, 531 (2010)

    Article  MATH  Google Scholar 

  32. X. Wu, J. Cai, M. Wang, Chaos Solitons Fract. 36, 121 (2008)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  33. B.A. Idowu, U.E. Vincent, A.N. Njah, Chaos Solitons Fract. 39, 2322 (2009)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  34. O.I. Olusola, U.E. Vincent, A.N. Njah, Pramana – J. Phys. 73, 1011 (2009)

    Article  ADS  Google Scholar 

  35. J.R. Dormand, P.J. Prince, J. Comp. Appl. Math. 6, 19 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  36. G. Benettin, L. Galgani, A. Giorgilli, J.M. Strelcyn, Meccanica 15, 9 (1980)

    Article  ADS  MATH  Google Scholar 

  37. A. Wolf, J.B. Swift, H.L. Swinney, J.A. Vastano, Physica D 16, 285 (1985)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  38. R. Chacón, Control of homoclinic chaos by weak periodic perturbations (World Scientific Publishing, London, 2005)

  39. S. Lenci, G. Rega, Nonlinear Dyn. 15, 391 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  40. R. Chacón, P.J. Martinez, J.A. Martinez, S. Lenci, Chaos Solitons Fract. 42, 2342 (2009)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil and Buildings Engineering, and Architecture, Polytechnic University of Marche, Ancona, Italy

    L. Marcheggiani & S. Lenci

  2. Department of Applied Physics, Faculty of Industrial Engineering, University of Extremadura, Badajoz, Spain

    R. Chacón

Authors
  1. L. Marcheggiani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Chacón
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Lenci
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Lenci.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Marcheggiani, L., Chacón, R. & Lenci, S. On the synchronization of chains of nonlinear pendula connected by linear springs. Eur. Phys. J. Spec. Top. 223, 729–756 (2014). https://doi.org/10.1140/epjst/e2014-02138-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1140/epjst/e2014-02138-6

Keywords

Search

Navigation