Skip to main content
SpringerLink
Log in

The effect of long-range dependence on modelling extremes with the generalised extreme value distribution

  • Published:
The European Physical Journal Special Topics Aims and scope Submit manuscript

Abstract

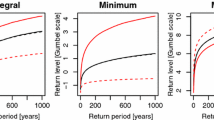
Two effects arise for the modelling of block maxima from dependent time series: a reduced rate of convergence for the block maxima probability distribution towards the generalised extreme value distribution, and an increase in uncertainty of the parameter estimates compared to independent or short range dependent records. These effects are exemplified with a simulation study using a white noise, a short-range and a long-range dependent process. The two issues raised turned out to be relatively unproblematic for short-range dependent processes. For long-range dependent processes, especially the increased parameter uncertainty poses a problem. Incautious use of standard procedures would lead to a severe underestimation of the parameter uncertainty which implies a misconception of accuracy for derived quantities, such as return levels which are frequently used for risk assessment and dimensioning of hydraulic structures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • S. Hallegatte, J. Appl. Meteorol. Climatol. 46, 1956 (2007)

  • Munich Re Group, Tech. Rep., Munich Re Group (2009)

  • J. Beirlant, Y. Goegebeur, H. Segers, J. Teugels, Statistics of Extremes: Theory and Applications (Wiley, 2004)

  • S.G. Coles, An Introduction to Statistical Modelling of Extreme Values (Springer, London, 2001)

  • P. Embrechts, C. Klüppelberger, T. Mikosch, Modelling Extremal Events for Insurance and Finance (Springer, Berlin, 1997)

  • J. Beran, Statistics for Long-Memory Processes (Chapman & Hall, 1994)

  • P.M. Robinson (ed.), Time Series with Long Memory (Oxford University Press, 2003)

  • T.A. Cohn, H.F. Lins, Geophys. Res. Lett. 32, L23402 (2005)

  • K. Fraedrich, R. Blender, Phys. Rev. Lett. 90, 108501 (2003)

    Google Scholar 

  • R.L. Smith, Long-range Dependence and Global Warming, edited by V. Barnett, P. Turkman, Statistics for the Environment (John Wiley and Sons Ltd., 1993), pp. 141–161

  • D.I. Vyushin, V.E. Fioletov, T.G. Shepherd, J. Geophys. Res. 112, D14307 (2007)

  • A. Montanari, R. Rosso, M.S. Taqqu, Water Resour. Res. 36, 1249 (2000)

    Google Scholar 

  • M. Mudelsee, Water Resour. Res. 43, W01202 (2007)

  • M. Santhanam, H. Kantz, Physica A 345, 713 (2005)

    Google Scholar 

  • A. Bunde, J.F. Eichner, S. Havlin, J.W. Kantelhart, Physica A 330, 1 (2003)

    Google Scholar 

  • E.G. Altmann, H. Kantz, Phys. Rev. E 71, 056106 (2005)

    Google Scholar 

  • R.A. Fisher, L.H.C. Tippett, Proc. Cambridge Phil. Soc. 24, 180 (1928)

    Google Scholar 

  • R.W. Katz, M.B. Parlange, C. Tebaldi, Clim. Change 60, 189 (2003)

    Google Scholar 

  • D. Maraun, H.W. Rust, T.J. Osborn, Int. J. Climatol, doi: 10.1002/joc.1811 (2009) (in press)

  • H.W. Rust, D. Maraun, T.J. Osborn, Eur. Phys. J. Special Topics 174, 99 (2009)

    Google Scholar 

  • J.R.M. Hosking, J.R. Wallis, E.F. Wood, Technometrics 27, 251 (1985)

  • R.L. Smith, Biometrika 72, 67 (1985)

  • H.W. Rust, O. Mestre, V.K.C. Venema, J. Geophys. Res. 113, D19110 (2008)

  • M.R. Leadbetter, G. Lindgren, H. Rootzén, Extremes and Related Properties of Random Sequences and Processes (Springer, New York, 1983)

  • P.J. Brockwell, R.A. Davis, Time Series: Theory and Methods (Springer, Berlin, 1991)

  • A. Montanari, R. Rosso, M.S. Taqqu, Water Resour. Res. 33, 1035 (1997)

    Google Scholar 

  • A.C. Davison, D.B. Hinkley, Bootstrap Methods and their Application (Cambridge University Press, Cambridge, 1997)

  • H.W. Rust, M. Kallache, H.-J. Schellnhuber, J. Kropp, Confidence Intervals for Flood Return Level Estimates using a Bootstrap Approach, J. Kropp, H.-J. Schellnhuber, In Extremis (Springer, Berlin, forthcoming)

  • M. Kallache, H.W. Rust, J. Kropp, Nonlin. Proc. Geophys. 2, 201 (2005)

    Google Scholar 

  • D. Maraun, H.W. Rust, J. Timmer, Nonlin. Proc. Geophys. 11, 495 (2004)

    Google Scholar 

  • R Development Core Team, R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, Vienna, 2004)

Download references

Author information

Authors and Affiliations

  1. Laboratoire des Sciences du Climat et de l’Environnement (LSCE-IPSL), Orme des Merisiers, 91191, Gif-sur-Yvette, France

    H. W. Rust

Authors
  1. H. W. Rust
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. W. Rust.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rust, H. The effect of long-range dependence on modelling extremes with the generalised extreme value distribution. Eur. Phys. J. Spec. Top. 174, 91–97 (2009). https://doi.org/10.1140/epjst/e2009-01092-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1140/epjst/e2009-01092-8

Keywords

Search

Navigation