Design study of a nonlinear electromagnetic converter using magnetic spring

Abstract

In this paper, an experimental and theoretical study for designing a nonlinear electromagnetic converter-based magnetic spring is performed. The governing equation of the converter is investigated. A special focus is given to the magnetic force acting on the moving magnet in dependence of its volume and the geometry of the two fixed magnets, i.e., disc or ring. For the developed analytical and numerical model, the same converter volume has been used for all conducted investigations. Several parameters have been studied that can be used to tune the nonlinearity behavior. Further, the coil axial position was investigated analytically and experimentally. An energy harvesting prototype consisting of an oscillating cylindrical magnet levitated between two stationary magnets is fabricated and evaluated through experiments. The open-circuit voltage obtained through the analytical model has been compared to the experiment and solutions to tune the harvester resonant frequency while maintaining its output power density were proposed.

1 Introduction

Small portable devices and wireless sensors have been receiving more and more attention in a large range of applications such as track-health monitoring systems and wireless communication devices [1]. To solve the challenging task of developing a self or longer-lasting power supply of portable electronic devices, harvesting energy from the ambient presents a good and reliable alternative. Different ambient sources can be used such as vibration [2], solar [3], and thermal gradient [4]. Though, due to its availability and its relatively high energy density compared to other sources, vibration source is a promising solution to harvest energy. To convert ambient vibration to electrical energy, two principles are mainly used which consist of the piezoelectric and the electromagnetic. However, electromagnetic energy converters are specifically interesting for some applications due to their larger current output compared to piezoelectric ones [5].

Because of the narrow frequency bandwidth of linear electromagnetic energy harvesters, introducing nonlinearity in the converter design has gained increasing interest. The challenge for the design of electromagnetic converters is especially the ability to tune its resonant frequency while maintaining a high power density. This makes the compactness of electromagnetic converter in several studies not possible due to the required bulky size for the used coil or magnets.

For an efficient vibration converter design, characterization of the dynamic response of the converter is required. This is specifically challenging in the case of levitation-based converters, which exploit magnetic repulsion to keep a moving magnet oscillating between two fixed ones at the end of a cylindrical cavity. Consequently, recent research efforts have shifted towards introducing nonlinearities into the energy harvesting system and exploiting them to broaden the frequency response to be able to harvest energy when ambient vibrations’ frequencies shift. For instance, the benefits of using a nonlinear stiffness [5, 6] or nonlinear damping [7] has been found to be relevant in the dynamics of mechanical resonators. Compared to a linear harvester, the frequency response of an electromagnetic levitation-based converter has a wider frequency bandwidth response and is mainly dependent on the nonlinear magnetic spring force [8].

Besides, a variety of electromagnetic converters based on the magnetic spring principle have been reported in the literature. In [5], the design and modeling of a magnetic spring-based energy harvesting from human motions were reported. The proposed design consists of two-disc magnets fixed to both ends of a hollow tube where a magnetic stack moves inside. The system can generate up to 10.66 mW average output power from the swing motion of the leg at a speed of 8 km/h. A novel magnetoelectric harvester device that uses magnetic forces to levitate an oscillating center magnet was proposed in [9]. The authors have investigated the potential of system nonlinearities to improve the energy harvesting capability using two outer disc magnets mechanically attached to threaded support while tuning the device resonant frequency by simply changing the spacing between the upper and lower magnets. In [10], a detailed study of vibration energy harvesting using the magnetic spring principle has been presented. Here, a similar structure was used to implement the magnetic spring nonlinear oscillators but based on two stationary ring magnets. The effect of several structure parameters to tune the harvester resonant frequency was evaluated and discussed. In another effort, in [11], the authors presented an enhanced magnetic spring-based vibration energy harvester which consists of a levitated magnet, a spring-guided magnet, and coils and is able to generate 1.97 ${\text {mW}}/{\text {cm}}^3 \,{\text {g}}^2$ at 0.4 g.

Based on the state of the art, only specific parameters are optimized such as the number of coil turns, magnet position, and output voltage. Nevertheless, several parameters are not well investigated in other research works, which influence the dynamic behavior of the converter, hence its energy outcome.

In particular, this work aims to investigate all parameters of the electromagnetic converter and study their influence at the level of the converter behavior. The study of the friction effect on the moving mass is crucial and affects the converter behavior. This includes the contact between the moving mass and the fixed part of the converter, which is investigated in this work. As well, the geometry of the magnet itself (ring or disc geometry) and its size are studied. The conducted investigations in this work include numerical, analytical, and experimental evaluation aiming to study an efficient and generic methodology for the optimization of the design of an electromagnetic converter with high power density. The paper aims to provide a detailed analysis of several design parameters, including even the size and the geometry of the used magnets due to their direct effect on the harvester performance. This work concerns also the possibility to operate in different oscillating environments such as automotive vibrating devices and industrial equipment characterized by low vibration amplitudes and frequencies. Specifically, the conceived harvester can be employed to harvest energy from vibration induced by passing trains [12].

This paper is organized as follows; in Sect. 2, the proposed harvester structure is presented. Section 3 is devoted to the analytical models of magnetic spring force and the coil-induced voltage. In Sect. 4, the influence of the magnet geometry and volume are studied through finite-element analysis. In Sect. 5, obtained results and experimental validation are presented and evaluated.

2 Harvester design

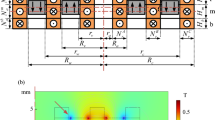
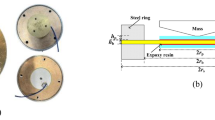
This work investigates the design of a vibration electromagnetic converter. Figure 1a shows the converter structure, which is implemented in a cavity of a $\hbox {M}14 \times 98$ mm screw and has a total volume of 12 $\hbox {cm}^3$. To ensure that the harvester has good robustness, the moving part is the inner magnet and the coil wires are placed away from that moving part. In particular, the coil wires are passing through a hole ending up to the screw head, where they are directly connected to the energy management circuit placed on the screw head. The electromagnetic vibration converter is based on the magnetic spring principle, i.e., three magnets arrangement, as depicted in Fig. 1b, c. It consists of a disc magnet levitating between two fixed rings or discs magnets due to an applied vibration source. The size of magnets and their effects on the converter response are subject of numerical and analytical investigation in this work. The levitated magnet is surrounded by a coil fixed on a thin aluminum foil. The aim of including the aluminum foil is to reduce the friction between the magnet and coil, which has an important role in the magnet dynamic behavior, hence on the converter response. The size of the levitated magnet and its position are as well investigated. For the magnet and the coil, NdFeB42 and copper are used as materials, respectively. Upon external vibration, the moving magnet moves relative to the vertical axis in the air gap between the two fixed magnets, and its kinetic energy is converted into electric energy through the coil based on Faraday’s law of induction. The system parameters are given in Table 1.

Fig. 1

Converter structure. a Prototype, b schematic with fixed disc magnets, c schematic for fixed ring magnets

Table 1 Parameters used for the converter design

3 Analytical modeling

3.1 Governing equation

The magnetic spring-based energy harvester can be modeled as a mass–spring–damping system subjected to base point excitation as shown in Fig. 2. M, C, K, z(t) and y(t) are the moving mass, the damping coefficient, the spring stiffness coefficient, the displacement of the moving mass, and the applied excitation to the system, respectively. The equation of motion is expressed by the following equation:

$$\begin{aligned} M\ddot{x}-F_{\text {c}}-F_{\text {m}}=-F(t), \end{aligned}$$

(1)

where x, $F_{\text {c}}$, $F_{\text {m}}$ and F(t) present the absolute displacement of the moving mass, the damping force, the magnetic force of the spring, and the external force due to the applied excitation, respectively. The relative displacement of the moving mass relative to the applied displacement y is defined by $z= x-y$. Equation 1 can be expressed as follows:

$$\begin{aligned} \ddot{z}+2\zeta \omega \dot{z}+\frac{F_{m}}{M}=-\ddot{y}, \end{aligned}$$

(2)

where $\zeta$ is the damping ratio, $\omega$ is the angular natural frequency, and y is the applied displacement.

Fig. 2

Vibration energy harvesting model as mass–spring system

3.2 Open-circuit voltage evaluation

The aim of this section is to evaluate the open-circuit voltage of the harvester, which is based on the presented approach in [11, 13], the magnetic vector field, $B_{\text {v}}$ caused by the moving magnet is similar to that of a point magnetic dipole. The magnetic flux, $\phi _f$, through the coil can be expressed as presented in the following equation:

$$\begin{aligned} \phi _f(t)=\frac{N}{l_c}\iiint B_{v} \psi \,{\text {d}}\psi \,{\text {d}}\theta \,{\text {d}}\kappa , \end{aligned}$$

(3)

where ($\psi$, $\theta$, $\kappa$) are the vector positions of the point of evaluation. The open-circuit voltage induced in the coil can be expressed as a function of the magnetic flux, $\phi _f$ as follows:

$$\begin{aligned} V_{\text {oc}}=-\frac{\partial \phi _f(t)}{\partial t}=-\dot{z}\frac{\partial \phi _f}{\partial z}. \end{aligned}$$

(4)

Consequently, for the system under consideration presented in Fig. 1, the open-circuit voltage is given as shown in the following equation:

$$\begin{aligned} \begin{aligned} V_{\text {oc}}&=\frac{N d_c^2 B_r^m V_{\text {m}}\dot{z}}{l_c}\left( \frac{1}{([l_c-2(z-\alpha )]^2+d_c^2)^{3/2}}\right. \\&\quad \left. -\frac{1}{([l_c+2(z-\alpha )]^2+d_c^2)^{3/2}}\right) , \end{aligned} \end{aligned}$$

(5)

where $\alpha$ is the coil axial position and $B_{\text {r}}^{\text {m}}$ is the remnant flux of the moving magnet.

3.3 Nonlinear magnetic spring

To determine the analytical expression of the magnetic spring force, the following assumptions have to be considered: (1) both the top and bottom magnets have uniform magnetization, and (2) the moving magnet is in repulsion to both fixed magnets (see Fig. 1b). The scalar magnetic potential generated by the top fixed magnet can be expressed in the form of [11, 14]

$$\begin{aligned} \begin{aligned} \chi (z)=&\frac{B_r^f}{4\mu _0}\bigg ({\sqrt{{d_{\text {out}}}^2+(2z+h-L)^2}}+{\sqrt{{d_{in}}}^2+(2z-h-L)^2} \\&- {\sqrt{{d_{\text {out}}}^2+(2z-h-L)^2}}+{\sqrt{{d_{\text {in}}}^2+(2z+h-L)^2}}\bigg ),\\ \end{aligned} \end{aligned}$$

(6)

where $B_r^f$ is the remnant flux of each of the fixed magnets. The relation between the z-component of the magnetic flux density and the scalar magnetic field potential is given by

$$\begin{aligned} \begin{aligned} B(z)=&-\mu _0\frac{\text {d}\chi (z)}{\text {d}z}. \end{aligned} \end{aligned}$$

(7)

Then, the z-component of the magnetic flux density generated by the top fixed magnet, $B_t(z)$, and the bottom one, $B_b(z)$, can be calculated as

$$\begin{aligned} \begin{aligned} B_t(z)=&\frac{B_{\text {r}}^{\text {f}}}{2} \bigg (\frac{2z-h-L}{\sqrt{{d_{\text {out}}}^2+(2z-h-H)^2}}\\&+\frac{2z+h-L}{\sqrt{{d_{\text {in}}}^2+(2z+h-L)^2}}\\&-\frac{2z+h-L}{\sqrt{{d_{\text {out}}}^2+(2z+h-L)^2}}\\&+\frac{2z-h-L}{\sqrt{{d_{\text {in}}}^2+(2z-h-L)^2}}\bigg ),\\ \end{aligned} \end{aligned}$$

(8)

$$\begin{aligned} \begin{aligned} B_b(z)=&\frac{B_r^f}{2} \bigg (\frac{2z-h+L}{\sqrt{{d_{\text {out}}}^2+(2z-h+L)^2}}\\&\quad +\frac{2z+h+L}{\sqrt{{d_{\text {in}}}^2+(2z+h+L)^2}}\\&\quad -\frac{2z+h+L}{\sqrt{{d_{\text {out}}}^2+(2z+h+L)^2}}\\&\quad +\frac{2z-h+L}{\sqrt{{d_{\text {in}}}^2+(2z-h+L)^2}}\bigg ).\\ \end{aligned} \end{aligned}$$

(9)

The total magnetic flux density from the two stationary magnets can be given by

$$\begin{aligned} \begin{aligned} B=B_{t}+ B_{b}. \end{aligned} \end{aligned}$$

(10)

The z-component of the magnetic spring force acting on the moving magnet is given by

$$\begin{aligned} \begin{aligned} F_m(z)=\varUpsilon \partial _zB(z), \end{aligned} \end{aligned}$$

(11)

where $\varUpsilon =B_{\text {r}}^m V/\mu _0$, $B_{\text {r}}^m$, and V are the magnetic dipole moment, the remnant flux density of the moving magnet and the volume of the moving magnet, respectively. Consequently, the magnetic spring force along the harvester longitudinal axis z, $F_m(z)$, can be calculated based on the following equation for ring fixed magnets and the next following equation when considering disc fixed magnets:

$$\begin{aligned} \begin{aligned} F_{m, \text {ring}}=&-\frac{B_r^f B_r^m V_m}{\mu _0}\bigg (\frac{{d_{\text {out}}}^2}{({d_{\text {out}}}^2+(2z+h-L)^2)^{3/2}}\\&\quad +\frac{{d_{\text {out}}}^2}{({d_{\text {out}}}^2+(2z+h+L)^2)^{3/2}}\\&\quad +\frac{{d_{\text {in}}}^2}{({d_{\text {in}}}^2+(2z-h-L)^2)^{3/2}}\\&\quad +\frac{{d_{\text {in}}}^2}{({d_{\text {in}}}^2+(2z-h+L)^2)^{3/2}}\\&\quad -\frac{{d_{\text {in}}}^2}{({d_{\text {in}}}^2+(2z+h-L)^2)^{3/2}}\\&\quad -\frac{{d_{\text {in}}}^2}{({d_{\text {in}}}^2+(2z+h+L)^2)^{3/2}}\\&\quad -\frac{{d_{\text {out}}}^2}{({d_{\text {out}}}^2+(2z-h-L)^2)^{3/2}}\\&\quad -\frac{b^2}{({d_{\text {out}}}^2+(2z-h+L)^2)^{3/2}}\bigg ),\\ \end{aligned} \end{aligned}$$

(12)

$$\begin{aligned} \begin{aligned} F_{m, {\text {disc}}}=&-\frac{B_{\text {r}}^{\text {f}} B_{\text {r}}^{\text {m}} V_m}{\mu _0}\bigg (\frac{{d_{\text {out}}}^2}{({d_{\text {out}}}^2+(2z+h-L)^2)^{3/2}}\\&\quad +\frac{{d_{\text {out}}}^2}{({d_{\text {out}}}^2+(2z+h+L)^2)^{3/2}}\\&\quad -\frac{{d_{\text {out}}}^2}{({d_{\text {out}}}^2+(2z-h-L)^2)^{3/2}}\\&\quad -\frac{b^2}{({d_{\text {out}}}^2+(2z-h+L)^2)^{3/2}}\bigg ).\\ \end{aligned} \end{aligned}$$

(13)

4 Finite-element modeling

In this section, the electromagnetic converter is modeled by COMSOL Multiphysics simulation platform to investigate the magnetic force acting on the moving magnet for different configurations. In particular, the length of the moving magnets and the shape of the fixed magnets (Disc or ring) are studied and results are evaluated and compared to the developed analytical model.

Fig. 3

Magnetic flux density norm. a Disc fixed magnets, b ring fixed magnets

Figure 3a, b shows the magnetic flux density norm and contour for the two different configurations. It can be seen that the magnetic strength is relatively much stronger in the case of disc magnets, which will result in a higher magnetic force amplitude acting on the moving magnet.

To further investigate the two proposed configurations, a parametric sweep study is performed by varying the position of the moving magnets in the air gap between the two fixed magnets. The effect of changing the height of the moving magnet, h, and the inner diameter of the fixed magnets, $d_{\text {in}}$ are investigated. The corresponding parameters of the magnets are given in Table 2.

Table 2 Parameters used in the numerical and analytical analyses

Fig. 4

Nonlinear magnetic spring force–displacement obtained using finite-element analysis a for disc fixed magnets (diameter = 10 mm, height = 4 mm) and a cylindrical moving magnet (diameter = 8 mm, variable h), b for ring fixed magnets ($d_{\text {out}}$ = 10 mm, $d_{\text {in}}$ = 5 mm, height = 4 mm) and a cylindrical moving magnet (diameter = 8 mm, variable h), and c for a cylindrical moving magnet (diameter = 8 mm, h = 8 mm) and for 4 mm height fixed disc or ring magnets

Finite-element simulation results are shown in Fig. 4. Figure 4a, b shows the nonlinear magnetic spring force obtained for the two configurations, disc and ring magnet ($d_{\text {in}}$ = 5 mm), respectively, in function of the position of the moving magnet in the air gap and for different moving magnet height h = 4, 8 or 12 mm.

5 Results and discussion

5.1 Magnetic force evaluation

For electromagnetic converter, especially based on magnetic spring, the magnetic spring behavior is crucial and plays an important role in the converter response. In fact, it defines the distance between the magnets to consider during the converter design. As well, it is decisive for the definition of the resonant frequency of the converter.

To this end, this section is devoted to investigating the magnetic spring force relative to several parameters. This includes the variation of the magnetic force relative to the magnet’s size, geometry, and position. This is achieved by finite-element modeling as well as compared to the analytical model. The force is calculated analytically through Eqs. 10 and 11 and based on finite-element model for a static position of the moving magnet.

The developed model is based on an axisymmetric 2D geometry comprising an air domain, 2 fixed magnets and a moving magnet. The mesh consists of triangular elements having a maximum size of 1 mm. Further, a refined mesh is defined around the moving magnet to obtain more accurate results. The number of degrees of freedom is between 3738 and 2504, depending on the position of the moving magnet.

In this study, the effect of the moving magnet thickness for 4 mm, 8 mm, and 12 mm on the magnetic force and for disc fixed magnets is studied (Fig. 4a). The results confirm the nonlinear behavior of the magnetic force, especially at high displacement. Figure 4b shows the case of using ring fixed magnets with the same variation for the moving magnet size. Figure 4c shows the comparison between both ring and discs magnets for the fixed magnets for moving magnets with a size of 8 mm of diameter and 8 mm of thickness. As it is presented, the use of ring fixed magnets instead of discs magnets leads to reducing the magnetic force level and this depends as well on the inner diameter size of the ring magnet. The numerical results obtained through the developed finite-element model are compared to the analytical model for the magnetic force evaluation.

Fig. 5

a Nonlinear magnetic spring force–displacement obtained using finite-element analysis and using the analytical model for a cylindrical moving magnet (diameter = 8 mm, height = 8 mm) and for different fixed magnets; ring ($d_{\text {in}}$ = 5 mm, $d_{\text {out}}$ = 10 mm, height = 4 mm) and disc ($d_{\text {out}}$ = 10 mm, height = 4 mm), b zoom view

The results show a good correlation between the numerical developed model and the analytical model especially at small displacement as shown in Fig. 5a. The deviation between the results obtained based on the analytical and the simulated models increases for smaller separation distances between the levitated and one of the stationary magnets as shown in Fig. 5b. This means that at a high applied acceleration, the numerical model presents an error for the prediction of the dynamic behavior of the converter and in this case the analytical model shows more adequate results. This phenomena is present for both converter model using ring or disc fixed magnets.

Fig. 6

Effect of the levitated magnet height on the converter output for 1 g of acceleration

Fig. 7

Investigation of the fixed magnets size on the converter output at 1 g of acceleration for a ring magnets with $d_{\text {out}}= 10$ mm and for different inner diameter size, b disc magnets with different $d_{\text {out}}$

5.2 Influence of geometric parameters

In the following, the effect of the levitated magnet size on the voltage output (peak to peak/2) and on the resonant frequency of the converter is investigated. As shown in Fig. 6, an evaluation for a magnet height equal to 4 mm, 8 mm, and 12 mm is conducted for 1 g of acceleration and for a frequency range from 5 to 25 Hz.

This has a direct effect on the decision for the resonant frequency of the system. In fact, increasing the moving mass does not lead to reduce systematically the resonant frequency of the system. This is especially in the case of a nonlinear converter where the stiffness has an important role, which is well shown here. As it can be seen, doubling the magnet’s height leads to shifting the resonant frequency of the harvester from   9 to 12 Hz, which presents an increase of around 30% of the resonant frequency of the system. The same for increasing three times the magnet size to 12 mm leads to an increase by 60% of the resonant frequency level of the converter. The model shows that the magnet size has an influence on the resonant frequency and this is due to its effect on the nonlinear stiffness of the converter. Further, results show an increase at the level of the output voltage, which is expected due to the constant size and coil position used for the three cases.

Fig. 8

Linear and nonlinear stiffness coefficients $k_1$ and $k_3$ relative to the outer diameter of the fixed magnet, $d_{\text {out}}$; a, b for $L=9.4$ cm and $d_{\text {in}}=0$; c), d for $L=9.4$ cm and $d_{\text {in}}=2$ cm; e, f for $L=4.7$ cm and $d_{\text {in}}=0$ cm

Fig. 9

Open-circuit output voltage in function of the outer diameter of the fixed magnet, $d_{out}$; a for $L=9.4$ cm, $d= 1$ cm and $d_{\text {in}}=0$; b for $L=9.4$ cm and $d= 1$ cm; c for $L=4.7$ cm and $d= 1$ cm

Fig. 10

a 3D design of the realized prototype, b printed prototype for the electromagnetic converter

Furthermore, the effect of the fixed magnet size is investigated. In particular, the effect of the inner ring magnet diameter, which is illustrated in Fig. 7a. The increase of the inner diameter for the ring magnet leads to reduce the stiffness strength at the level of the magnetic spring, hence shifting the frequency to a lower frequency. This is demonstrated through Fig. 7a, where doubling the inner diameter of the ring magnet leads to a 2 Hz shift. Figure 7b presents the effect of the fixed magnet size as well. In this case, the fixed magnet is evaluated as a disc magnet. As it is shown, here the stiffness has a larger effect on shifting the frequency. This is due to the effect of the magnetic force strength variation in the case of disc magnet diameter variation. In particular, the increase of the magnet size leads to an increase in the resonant frequency. Doubling the diameter size of the fixed magnet leads to a shift of the frequency by 50 %. For example, for a fixed disc magnet diameter equal to 5 mm, the resonant frequency is equal to $\sim$ 7 Hz, which can be shifted to $\sim$ 13 Hz by increasing the disc magnet size to 10 mm.

To conclude, the geometry and size of the fixed and levitated magnets have an important and decisive role in the dynamic behavior of the converter. Therefore, it is quite important to know and understand the influence of each of these parameters. This can be summarized in three main points. First, the increase of the levitated magnet height leads to the increase of the resonant frequency and has as well an effect on the converter level output. In the case of the variation of the disc fixed magnet size, the resonant frequency can be shifted and is proportional to the disc magnet size variation without varying the converter output level, since it has an influence only on the converter stiffness. Using ring fixed magnet enables to shift the resonant frequency of the converter but has limited effect in comparison to the disc fixed magnet size or the levitated magnet diameter.

Further, the effect of the geometric parameters design on the harvester behavior is investigated. In fact, the magnetic force can be defined based on curve fitting method of the results shown in the following equation:

$$\begin{aligned} F_{\text {m}}=-(k_1x+k_3x^3), \end{aligned}$$

(14)

where $k_1$ and $k_3$ are the linear and the nonlinear stiffness coefficients resulting from the polynomial expansion of the magnetic force.

Consequently, the resonant frequency can be obtained as function of $k_1$ and the mass M of the moving magnet as given in the following equation:

$$\begin{aligned} \begin{aligned} f={\sqrt{\frac{k_1}{M}}}. \end{aligned} \end{aligned}$$

(15)

In the following, the linear and nonlinear stiffness coefficients $k_1$ and $k_3$, respectively, are investigated. This includes the effect of outer and inner fixed magnet diameters $d_{\text {out}}$ and $d_{\text {in}}$, respectively, as well as the distance L separating the two stationary magnets on $k_1$ and $k_3$. Figure 8 shows the variation of the linear and nonlinear stiffness coefficients in function of $d_{out}$ (the diameter of the fixed magnet) for three different configurations:

• Disc fixed magnets where L = 9.4 cm (Fig. 8a, b)

• Ring fixed magnets where L = 9.4 cm (Fig. 8c, d)

• Disc fixed magnets where L = 4.7 cm (Fig. 8e, f)

It is worth mentioning that the same moving magnet dimensions are considered for the three configurations. Figure 9 shows the open-circuit voltage for specific values of $d_{\text {out}}$ shown in Fig. 8. It is clear that through the variation of only the outer diameter of the fixed magnet, three typical responses for the harvester are exhibited: the linear nonlinear (hardening) and nonlinear (softening) response at $d_{\text {out}}=6.03~cm$, $d_{\text {out}}=5~cm$, $d_{\text {out}}=8~cm$, respectively (Fig. 9a). The frequency response is shifted due to the variation in the outer diameter. This can be explained by Fig. 9b, where for the critical value of the diameter $d_{\text {out}}= 6.03~cm$, $k_3$ becomes 0 resulting in a linear response. Moreover, once the outer diameter $d_{\text {out}}$ is less than this critical value, $k_3$ is positive, which leads to have a hardening magnetic spring. In case the outer diameter exceeds the critical value, $k_3$ exhibits a negative value, while $k_1$ remains positive and hence the nonlinear softening behavior appears.

Furthermore, Fig. 9b shows the effect of the inner diameter size of the fixed magnet on the critical outer diameter value. In this case, by increasing the inner diameter of the magnet, the critical diameter value is decreasing from 6 cm to 3.61 cm where the linear behavior is present. Further, the resonant frequency of the harvester is shifted and decreased from 25 to 18 Hz. The same investigation is conducted to study the influence of the length L, the distance separating both fixed magnets, which have shown a shift of the critical outer diameter size as well where beyond or under it the nonlinear behavior is appearing. In fact, decreasing the L by 50% leads to a decrease of the critical outer diameter of the magnet by 50% (Fig. 9c) as well to a shift of the resonance frequency from 25 to 72 Hz. To conclude, the geometric parameters are highly decisive for the harvester response and plays a decisive role on the resonance frequency of the harvester.

5.3 Experimental model validation

The converter structure is realized based on mainly two parts. This includes the coil housing, which can be fixed in different positions aiming to investigate the coil position. Further, the second part is designed to contain the fixed magnets with free space for the moving magnet. The system design proposed in this work aims mainly to investigate most of the parameters that can influence an electromagnetic vibration converter performance including, the coil position, the magnet size, the mechanical damping for different acceleration and frequencies level. Figure 10 illustrates the proposed design for the converter.

Fig. 11

Experimental setup for the prototype validation

Fig. 12

Experimental and analytical results for the output voltage of the converter for an acceleration equal to a 0.25 g, b 0.5 g, c 0.75 g, d 1 g

The analytical model is validated through experiments by the realization of a prototype of the magnetic spring vibration converter. 3D printer (Form Lab 2) is used for the fabrication of the different parts for the converter including the coil housing and the converter housing using Clear V4 as material.

The prototype is realized in a way that the coil position can be varied to estimate the mechanical damping of the system. Disc NdFeB42 magnets of 10 mm diameter and 4 mm height are implemented to the top and bottom of the converter housing. A disc magnet of 8 mm diameter and 8 mm height is placed in the air gap in repulsive direction to the top and bottom magnet. Aiming to reduce friction for the moving magnet, an aluminum housing is added surrounding the magnet separating the magnet from the coil housing. This leads to improve the magnet movement and reduce the mechanical damping. Figure 10 shows the realized prototype for the electromagnetic nonlinear magnetic spring converter.

The experimental setup (see Fig. 11) used for experimental investigations is composed of an electrodynamic shaker (VebRobotron Type 11077), which is used to reproduce the applied harmonic vibration (Sinusoidal signals with frequencies between 8 and 25 Hz). The applied excitation is monitored using a LASER USB Shaker control system, a linear Power Amplifier (LDS LPA 100), and an acceleration sensor (ADXL 326) mounted on the moving part of the shaker. In addition, the output signal is acquired through a digital oscilloscope ($\hbox {LeCroyWaveRunner}\circledR$ 6050A). The converter is tested under harmonic signal with defined frequency and acceleration level varying between 8 to 24 Hz and 0.25 to 1g, respectively. The measurements of open-circuit voltage were conducted for different frequencies and accelerations.

Figure 12 shows the evaluation of the open-circuit voltage determined through the analytical model (Eq. 5), as well it presents the experimental results achieved under the same condition in terms of acceleration and frequencies. Results confirm that the behavior obtained through the analytical model using Eq. 5 are in good agreement with the realized experimental measurements. Further, as evaluation for the converter performance, a maximum open-circuit voltage of 0.3 V, 0.6 V, 1 V, and 1.2 V can be reached for an acceleration equal to 0.25 g, 0.5 g, 0.75 g, and 1 g with a resonant frequency at 12 Hz for a coil resistance equal to 40 $\varOmega$, respectively. The converter presents a bandwidth frequency of 6 Hz.

As discussed before, one of the parameters to evaluate and investigate is the coil position. This is presented in Fig. 13 where the analytical and experimental results are compared for an acceleration equal to 0.5 g at a resonant frequency equal to 12 Hz. As it is shown, an excellent agreement between the developed analytical model and experimental results is achieved. the behavior shows that two optima can be reached for the converter outcome, which is at $\alpha$= − 0.004 or 0.004 m. As it can be seen, at a coil position equal to 0 m, a drop of voltage is identified. This is due to the fact of magnetic flux lines cancellation passing through the coil and which needs to be avoided.

Fig. 13

Experimental and analytical results for the coil position effect on the converter output for 0.5 g at 12 Hz

6 Conclusion

The present paper explores a methodology for the design study for a nonlinear magnetic spring-based electromagnetic converter. The magnetic spring behavior is analyzed theoretically and based on finite-element analysis for different fixed magnets’ geometry. Further, the analytical model is developed to determine the harvester-induced voltage in a function of the magnet’s geometry and relative to the coil axial position. A 3D-printed prototype is fabricated for the validation of the developed model. In the system under consideration, the levitated magnet is oscillating inside an aluminum foil to minimize friction. The influence of the coil axial position was investigated experimentally, and results are evaluated and compared to the analytical model. The developed harvester shows a resonant frequency of about 12 Hz. Solutions to tune the harvester resonance were proposed by mainly changing magnet geometry while maintaining the same device dimension and its output level.