Non-Markovian quantum Otto refrigerator

Abstract

Based on a recently developed non-perturbative platform designed to simulate the full quantum dynamics of quantum thermal machines, the situation of a quantum refrigerator operating according to an Otto cycle is studied. The periodic steady-state dynamics is discussed in detail as well as the key thermodynamic quantities work, heat, and entropy. A particular benefit of the formulation is that it allows to access explicitly the work required for switching on and off the interaction with the respective thermal reservoirs in a consistent way. The domains in which the device operates in refrigerator mode are characterized.

1 Introduction

In the last decade, remarkable advances have been made in applying classical thermodynamic concepts to systems that operate at atomic scales and low temperatures [1, 2]. In this exceptionally challenging regime, quantum mechanics takes over and raises questions on how intrinsic quantum phenomena challenge our classical understanding of physics. While for thermal reservoirs, fundamental limits as the Carnot efficiency remain valid [3, 4] and fluctuation theorems equally apply to the quantum case [5,6,7], a quantum analogue of friction due to nonadiabatic finite-time coupling can be introduced [8, 9]. As opposed to the classical case, where characteristic time and length scales of thermodynamic cycles can be well separated, a microscopic description needs to address a loss of separability in the scales of the respective thermodynamic protocols, i.e., the dynamical equivalent of “valve” and “piston” operation in a machine which is not self-governed. The first experimental realizations of thermodynamic engines operating at the atomic scale employed single ions that were confined in a linear Paul trap [10, 11]. Due to the tapered geometry of such a setup, an ion can move along the gradient of a funnel-shaped potential. Thus, driving the frequency of the working medium through two isentropic processes during which the trap frequency is varied, a four-stroke Otto cycle is completed by alternate coupling to hot and cold reservoirs. Other realizations feature solid-state circuits [12] and even explore the quantum domain [13,14,15,16].

In previous theoretical work, modulations of the system-reservoir energy transfer have often been brought about by combining a modulation of the characteristic energy gap of the work medium with spectrally structured reservoirs [17,18,19]. Within a weak-coupling approximation, driving including fast modulation on the timescale of the reservoir fluctuations can bring about anti-Zeno dynamics [19]. Coherence effects thus introduced speed up energy exchange between system and reservoir, and take the dynamics beyond the paradigm of finite-time thermodynamics [20]. Likewise, modulating the system-reservoir coupling has been shown to effect a similar speedup [21]. It should be noted, however, that subjecting these couplings to explicit time dependence amounts to introducing additional transfers to/from the work reservoir. This fact is sometimes neglected in the extant literature, resulting in unrealistic figures of merit.

In a recent publication [22], we presented a non-perturbative simulation platform that allows to operate a quantum Otto cycle with harmonic/anharmonic oscillator as working medium in a fully dynamical, finite-time protocol with explicit cyclic modulation of the system-reservoir coupling. We were thereby able to observe the engine’s operation during its cyclic dynamics as an open quantum system with consecutive de-/coupling phases to/from the hot/cold reservoirs as integral parts of the net energy.

Based on an exact mapping of the Feynman–Vernon path integral formalism [23, 24] onto a Stochastic Liouville-von Neumann equation [25] that has been successfully applied in a variety of fields [26,27,28,29,30,31,32,33], this technique is especially suitable for modeling quantum thermodynamic processes at low temperatures, strong coupling, and driving as it naturally includes medium-reservoir quantum correlations and non-Markovian memory effects [34,35,36,37,38,39]. It shares the latter advantage with dynamical studies of thermal machines using hierarchical equations of motion [40], thus reaching far beyond standard weak-coupling approaches [41,42,43,44,45,46,47,48,49,50,51,52,53,54,55].

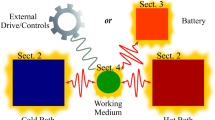
Besides the heat engine, as the most common variant of a thermal machine, a refrigerator reverses the operational principle [56]. During the cyclic operation of such a cooling machine, work is absorbed from the cold source and transferred to the hot reservoir. In this paper, we present essential dynamics and parameter regimes that allow to operate the engine cycle depicted in Fig. 1 in refrigerator mode.

Fig. 1

Top: energy–frequency diagram of a work medium in a quantum Otto refrigerator with frequency $\omega (t)$ varying around $\omega _0$. The cycle runs in alphabetical order and includes two isochore ($A\rightarrow B, C\rightarrow D$) and two isentropic strokes ($B\rightarrow C, D\rightarrow A$). Bottom: thermal contact to hot (cold) reservoirs is controlled by $\lambda _h(t)$ $[\lambda _c(t)]$ and expansion (compression) is due to $\omega (t)$. The cycle is specified by three characteristic time scales $\tau _I$, $\tau _d$, $\tau _{R}$

2 Modeling

As a microscopic, fully dynamical model to describe the four-stroke cycle of a quantum Otto refrigerator, we consider a distinct quantum system $H_{m} (t) = \frac{p^2}{2m} + V(q,t)$ (1D point particle) with coordinate q, momentum p, and mass m that is governed by a potential V(q, t). It interacts with two thermal, harmonic reservoirs $H_{c/h}$ that are characterized by their respective temperatures $T_c < T_h$. The influence of bilinear coupling to the bosonic baths leads to a global Hamiltonian of the form:

$$\begin{aligned} H(t)=H_m(t)+ H_{ c} + H_{I, c}(t) + H_{ h} + H_{I, h}(t). \end{aligned}$$

(1)

The interaction between the working medium $H_m$ and the dissipative environment is controlled by two dimensionless coupling functions $\lambda _{c/h}(t)$ (cf. Fig. 1) that vary between 1 and 0 (maximum/minimum coupling) during the four branches of the cyclic protocol. The de-/coupling stages of the cycle are implemented using sinusoidal functional segments for $\lambda _{c/h}(t)$, cf. Fig. 1b. Their explicit form strongly depends on the duration $\tau _I$ which will be discussed in the context of the characteristic cycle times later in this section. The free fluctuations of the thermal reservoirs are assumed to be Gaussian and lead to bilinear coupling terms $H_{I, c/h}(t)=-\lambda _{ c/h}(t) q\sum _k c_{k, c/h} (b_{k, c/h}^\dagger +b_{k,c/h})+\frac{1}{2} q^2 \lambda _\mathrm{c/h}^2 (t) \mu _\mathrm{c/h}$ that contain sums over bosonic modes that become infinite in the continuum limit. The renormalization coefficients $\mu _{c/h}$, related to the static reservoir response [22, 24], ensure that only the dynamical impact of the medium-reservoir coupling contributes to the microscopic dynamics. With quantum reservoir correlation functions $L_{c/h}(t-t')=\langle X_{c/h}(t) X_{c/h}(t')\rangle$ with $X_{c/h} = \sum _k c_{k, c/h} (b_{k, c/h}^\dagger +b_{k,c/h})$ as memory kernels of a non-local action functional, the effective impact of the reservoir dynamics on the dedicated system can be described as a retarded self-interaction, that is:

$$\begin{aligned} L_{c/h}(t)= & {} \frac{h}{\pi }\int _0^{\infty }\mathrm{d}\omega J_{c/h}(\omega )\left[ \coth \left( \frac{\hbar \beta _{c/h}\omega }{2}\right) \cos (\omega t) \right. \nonumber \\&\left. - i \sin \left( \omega t\right) \right] , \end{aligned}$$

(2)

with spectral distribution of reservoir modes $J_{\alpha }(\omega ), \alpha =c, h$.

This formulation can be exactly mapped onto a Stochastic Liouville–von Neumann equation (SLN) [25], an approach which remains consistent also in the regimes of strong coupling, fast driving, and low temperatures [26, 28,29,30,31,32], where master equations become unreliable or fail. In the paradigmatic case of ohmic dissipation [57], the reservoirs are not only characterized by their temperatures, but also by a coupling weighted spectral density of the form:

$$\begin{aligned} J_{\alpha }(\omega ) = \frac{m\gamma _{\alpha }\omega }{(1+\omega ^2/\omega _{\text {cut}}^2)^2}, \end{aligned}$$

(3)

up to a high-frequency cutoff $\omega _{\text {cut}}$ (significantly larger than any other frequency of the problem, including $1/\hbar \beta _{\alpha }$). The quantity $\gamma _{\alpha }$ denotes a coupling strength related to the coefficient $\eta _{\alpha }$ of classical Stokes friction $\eta _{\alpha }=m\gamma _{\alpha }$. Assuming factorizing initial conditions for the global density matrix $\rho _\mathrm{tot}$, the Feynman–Vernon path integral formulation for the reduced density operator of the medium can be converted into a highly non-trivial version of the SLN with time-dependent control of system-reservoir couplings:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\rho _{\xi }(t)= & {} \frac{1}{i \hbar }\left[ H_m(t),\rho _{\xi }\right] \nonumber \\&+ \sum _{\alpha =c,h} \left\{ \frac{i}{\hbar } \lambda _{\alpha }(t)\xi _{\alpha }(t)\left[ q,\rho _{\xi }\right] \right. \nonumber \\&- i \frac{m\gamma _{\alpha }}{2 \hbar ^2} \lambda _{\alpha }(t)\dot{\lambda }_{\alpha }(t) \left[ q^2,\rho _{\xi }\right] \nonumber \\&- i \frac{m\gamma _{\alpha }}{2\hbar ^2} \lambda _{\alpha }^2(t) \left[ q, \{p,\rho _{\xi }\}\right] \nonumber \\&\left. - \lambda _{\alpha }^2(t) \frac{m\gamma _{\alpha }}{\hbar ^2 \beta _{\alpha }} \left[ q,[q,\rho _{\xi }]\right] \right\} . \end{aligned}$$

(4)

The stochastic propagation of the reduced density in probability space is, hence, dominated by two distinct Gaussian noise sources $\xi _c(t)$ and $\xi _h(t)$ that are determined through their respective reservoir correlation function $\langle \xi _{\alpha }(t)\xi _{\alpha }(t')\rangle = \text {Re}\, L_{\alpha }(t-t') - \frac{2m\gamma _\alpha }{\beta _\alpha }\delta (t-t')$ and $\alpha =c, h$. To obtain physically meaningful results for the evolution of the reduced system, the individual stochastic trajectories need to be averaged with respect to a sufficiently large number of sample realizations $\rho (t) = \mathbb {E} [\rho _{\xi }(t)]$. We emphasize that even though the above equation is local in time, the physical density $\rho (t)$ carries the full information about the non-Markovian time evolution.

The above model contains three control parameters which will later be associated with distinct sources of work during the cycle. Both the time-dependent potential V(q, t) and time-dependent couplings $\lambda _{c/h}(t)$ are operated in alternating phases of the cycle, see Fig. 1. For simplicity, in the sequel, we consider reservoirs with equal maximal coupling rate $\gamma _\alpha \equiv \gamma$ and a single harmonic oscillator degree of freedom representing the working medium, that is:

$$\begin{aligned} V(q,t)=\frac{1}{2} m \omega ^2(t) q^2, \end{aligned}$$

(5)

with a parametric-type driving $\omega (t)$. The above formulation also allows to treat anharmonic and higher dimensional systems [22], but already the one-dimensional linear problem reveals the highly non-trivial features of the underlying dynamics. The operating principle of the quantum Otto refrigerator, as depicted in Fig. 1, includes an external modulation of the oscillation frequency $\omega (t)$ of the work medium (“piston”) and the coupling constants through the control functions $\lambda _{c/h}(t)$ (“valves”). The frequency $\omega (t)$ is varied around a center frequency $\omega _0$ between $\omega _0\pm \frac{\varDelta \omega }{2}, (\varDelta \omega >0)$ within the time $\tau _d$ during expansion and compression. The idealized cycle consists of two unitary processes (B $\rightarrow$ C and D $\rightarrow$ A) and two isochoric strokes (A $\rightarrow$ B and C $\rightarrow$ D):

• 1. The hot isochore (A $\rightarrow$ B): the working medium is in contact with the hot reservoir, heat is pumped from the system to the hot reservoir, and the frequency is kept constant (no change of volume).

• 2. Isentropic expansion (B $\rightarrow$ C): the working medium expands and produces work due to an “increase in volume” toward $\omega _0-\frac{\varDelta \omega }{2}$, ($\varDelta \omega > 0$).

• 3. The cold isochore (C $\rightarrow$ D): the working medium absorbs heat from the cold reservoir; the frequency is kept constant (no change of volume).

• 4. Isentropic compression (D $\rightarrow$ A): while isolated from both thermal reservoirs, the working medium is “compressed in volume” back toward $\omega _0+\frac{\varDelta \omega }{2}$.

The isochore branches are divided into an initial phase raising the coupling parameter $\lambda _{c/h}$ from zero to one with duration $\tau _{I}$, a relaxation phase of duration $\tau _R$, and a final phase with $\lambda _{c/h}\rightarrow 0$, also of duration $\tau _I$. During one complete cycle of the refrigerator operation, work is consumed to pump heat from the cold to the hot reservoir. The cycle adds up to $T = 4\tau _I+2\tau _d+2\tau _R$. The total simulation time covers a sufficiently large number of cycles to approach a periodic steady state (PSS) with $\rho _m(t)=\rho _m(t+T)$.

Now, we go beyond conventional treatments by including the coupling/decoupling processes as finite-time transitions between phases of the process and taking into account that modulating the thermal interaction contributes to the energy balance, see also Ref. [34]. This precludes the use of simpler formulations (e.g., master equations) which do not allow to systematically include this aspect. However, in the deep quantum regime, such effects may, on the contrary, play a crucial role as will be revealed in the sequel.

3 Periodic steady-state dynamics

In a first step, the steady-state dynamics for a quantum refrigerator cycle with harmonic work medium is shown in Fig. 2. In its initial state, the system is uncorrelated to either reservoir, in a Gibbs state with temperature $T_h$ of the hot bath. The system (work medium) approaches a periodic steady state (PSS) after a transient period of time, see Fig. 2a, characterized by fast oscillations of the second moments on time scales of order $1/\omega _0$ and cyclic modulations according to the sequence of strokes. In particular, pronounced qp-correlations are manifestations of the deviation of the finite-time operation from a mere sequence of equilibrium states. A blow-up of the PSS dynamics for one cycle is depicted in Fig. 2b. While position $\langle q^2 \rangle$ and momentum $\langle p^2 \rangle$ variances tend to approach roughly their values in thermal equilibrium values (dashed lines) toward the end of the isochores according to the respective oscillator frequencies, the oscillatory pattern survives especially during contact with the cold reservoir. These features also demonstrate the non-local dynamics in time of the reduced quantum dynamics with rapid coherent energy transfer between medium and reservoir and relatively long-lived correlations between them.

Fig. 2

Quantum dynamics for an harmonic Otto refrigerator with $\omega _0\hbar \beta _h = 1$, $\omega _0\hbar \beta _c = 1.5$. Time scales are $\omega _0\tau _I = 10$, $\omega _0\tau _{d} = 5$, $\omega _0 T = 60$ with peak reservoir coupling $\gamma /\omega _0 = 0.25$ and $\omega _\mathrm{cut}/\omega _0 = 30$. a Initially, transient dynamics settle into a periodic pattern, i.e., a PSS is approached for the variances in position, momentum and cross-correlations $\langle qp +pq \rangle$. b During a PSS cycle, the variances exhibit damped oscillations toward thermal equilibration with the respective reservoirs, while a high degree of non-equilibrated motion is maintained especially during contact with the cold reservoir

4 Heat, work, and efficiency

In a second step, we turn to the thermodynamic quantities heat and work that fully characterize the operation of a thermal machine. They can be derived from the Hamiltonian dynamics of the model according to the total energy change due to external driving:

$$\begin{aligned} \frac{d}{dt}\langle H \rangle= & {} \left\langle \frac{\partial H_m(t)}{\partial t}\right\rangle + \left\langle \frac{\partial H_{I,c}(t)}{\partial t}\right\rangle + \left\langle \frac{\partial H_{I,h}(t)}{\partial t}\right\rangle , \nonumber \\ \end{aligned}$$

(6)

with separate terms that correspond to parametric control through $\omega (t)$ and $\lambda _{c/h}(t)$. During a PSS, the microstate of the working medium as described by the reduced density $\rho _m(t)$ is restored after one iteration $\rho _m(t+T) = \rho _m(t)$. This periodic behavior continues to be apparent in the inner energy of the system and the interaction $\langle H_m(t+T)\rangle = \langle H_m(t)\rangle$ and $\langle H_{I,\alpha }(t+T)\rangle = \langle H_{I,\alpha }(t)\rangle$. The heat flux to/from the system can be decomposed into two contributions that lead to an exchange of energy with the cold and hot bath, respectively, that is:

$$\begin{aligned}&j_{Q}(t):=\text {Tr}\{H_m\dot{\rho }_\mathrm{tot}\} \nonumber \\&\quad = \underbrace{-\frac{i}{\hbar }\text {Tr}\{[H_m,H_{I,c}]\rho _\mathrm{tot}\}}_{:=j_{Q,c}(t) }\underbrace{-\frac{i}{\hbar }\text {Tr}\{[H_m,H_{I,h}]\rho _\mathrm{tot}\}}_{:=j_{Q,h}(t)}, \nonumber \\ \end{aligned}$$

(7)

so that the heat that transferred into the hot/cold reservoir over one cycle reads:

$$\begin{aligned} Q_\alpha = \int _0^T \mathrm{d}t \, j_{Q,\alpha }(t) - W_{I, \alpha }. \end{aligned}$$

(8)

Here, $W_{I, \alpha }$ denotes the work required to de-/couple the work medium from the respective thermal reservoir, that is:

$$\begin{aligned} W_{I, \alpha } = \int \limits _0^T \mathrm{d}t \left\langle \frac{\partial H_{I,\alpha }(t)}{\partial t}\right\rangle . \end{aligned}$$

(9)

The external driving leads according to Eq. (6) to another source of work, namely:

$$\begin{aligned} W_d = \int _0^T \mathrm{d}t \left\langle \frac{\partial H_m(t)}{\partial t}\right\rangle . \end{aligned}$$

(10)

More specifically, this latter work originates from driving the potential through the frequency modulation $\omega (t)$ and is either generated or consumed along the isentropic strokes. Instead, it can be shown that the total coupling work during one cycle $W_I=W_{I, c}+ W_{I, h}$ is completely dissipated into the reservoirs. A representation of the first law is, hence, verified by the per-cycle balance $W_d + W_I + Q_c + Q_h = 0$.

Fig. 3

Thermodynamic quantities of the harmonic quantum Otto refrigerator for various peak coupling strengths $\gamma /\omega _0$ at fixed hot bath $\omega _0\hbar \beta _h = 1$. The parameters of the control protocol are again $\omega _0\tau _I = 10$, $\omega _0\tau _{d} = 5$, $\omega _0 T = 60$. a Net work $W_d + W_I$ and b absorbed heat $Q_c$ from the cold reservoir

The expressions for heat transfer $Q_{\alpha }$ and the work sources $W_d$ and $W_I$ can be translated from Hamiltonian dynamics to the probabilistic framework of the SLN. This is a straightforward task if the frequency modulation of the system Hamiltonian is considered:

$$\begin{aligned} \left\langle \frac{\partial H_m(t)}{\partial t}\right\rangle = \dot{\omega }(t) \left\langle \frac{\partial H_m(t)}{\partial \omega }\right\rangle = \omega (t)\dot{\omega }(t)\langle q^2\rangle . \end{aligned}$$

(11)

As a particular benefit, the SLN approach allows to access more intricate correlations between system and reservoir degrees of freedom. An example is the heat flux $j_{Q,\alpha }(t)$, whose stochastic equivalent is found as [22]:

$$\begin{aligned} j_{Q,\alpha }(t)= & {} -\frac{i}{\hbar }\langle [H_m,H_{I,\alpha }]\rangle \nonumber \\= & {} \lambda _{\alpha }(t)\xi _{\alpha }(t)\langle p\rangle /m -\gamma _{\alpha }\lambda _{\alpha }^2(t)\langle p^2 \rangle /m \nonumber \\&+ \gamma _{\alpha }\lambda _{\alpha }^2(t) k_B T_{\alpha } \nonumber \\&- \gamma _{\alpha } \lambda _{\alpha }(t)\dot{\lambda }_{\alpha }(t)\langle qp + pq\rangle /2. \end{aligned}$$

(12)

Likewise, the energy change of the total Hamiltonian due to an explicit time-dependent system-reservoir interaction can be expressed through microscopic dynamics and stochastic force fields:

$$\begin{aligned} \left\langle \frac{\partial H_{I,\alpha }(t)}{\partial t}\right\rangle= & {} \dot{\lambda }_{\alpha }(t)\left\langle \frac{\partial H_{I,\alpha }(t)}{\partial \lambda _{\alpha }}\right\rangle \nonumber \\= & {} -\dot{\lambda }_{\alpha }(t)\xi _{\alpha }(t)\langle q \rangle + \gamma _{\alpha }\lambda _{\alpha }(t)\dot{\lambda }_{\alpha }(t) \langle qp + pq\rangle /2 \nonumber \\&+ \gamma _{\alpha }\dot{\lambda }_{\alpha }^2(t)m\langle q^2 \rangle . \end{aligned}$$

(13)

These and corresponding expressions for all relevant quantities within the stochastic formulations allow to analyze the behavior of the quantum refrigerator in detail. For this purpose, we have to operate the thermal machine in a certain regime in parameter space as we will discuss now.

In Fig. 3a, a strong coupling dependence of the net work $W_d+W_I>0$ can be seen for increased coupling strength $\gamma /\omega _0$ which always appears as consumed energy. In contrast, in (b), the dependence of the absorbed heat from the cold reservoir $Q_c$ changes its sign with growing coupling or/and with growing temperature gradient between hot and cold reservoir. Hence, to avoid that the thermodynamic cycle leaves the refrigerator regime $Q_c>0$, one roughly has to respect the cooling condition [56]:

$$\begin{aligned} \frac{\omega _h}{\omega _c} > \frac{\beta _c}{\beta _h}. \end{aligned}$$

(14)

At high temperatures and weak coupling in the quasi-stationary limit, this condition easily follows from (12) and (9): Then, only the second and the third term in $j_{Q, c}$ survive and $W_{I, c}$ is negligible. Since $\langle p^2\rangle (t)$ relaxes with coupling rate $\gamma _c$ toward the equilibrium value $\langle p^2\rangle _D\approx m/\beta _c$, one finds $Q_c\approx (\langle p^2\rangle _D-\langle p^2\rangle _C)/m$ with $\langle p^2\rangle _C\approx (\omega _c/\omega _h)m/\beta _h$. At lower temperatures, the relation still applies in the weak coupling/quasi-stationary regime but typically does not hold beyond. This is clearly seen in Fig. 3b, where $Q_c$ displays a non-monotonous behavior with increasing thermal coupling due to the growing impact of $W_{I, c}$ but also due to the coupling dependence of $\langle p^2\rangle (t)$. For a sufficiently low temperature of the cold bath, we find for the given parameter set that always $Q_c<0$ which implies that the machine consumes energy by transferring heat from the hot to the cold reservoir. Accordingly, the efficiency in the refrigerator mode defined as

$$\begin{aligned} \eta = \frac{Q_c}{W_d+W_I} \end{aligned}$$

(15)

formally becomes negative, since $W_d+W_I > 0$.

Fig. 4

Thermodynamic efficiency $\eta$ (cf. Eq. 15) for the quantum refrigerator for various peak coupling strengths $\gamma /\omega _0$, at fixed hot bath $\omega _0\hbar \beta _h = 1$ and frequency compressions $\varDelta \omega /\omega _0 = 1$ and $\varDelta \omega /\omega _0 = 0.8$ (inset, dashed). The refrigerator works efficiently for temperature differences between the hot and the cold reservoir that remain sufficiently small. For larger damping strengths, the increased coupling costs turn the refrigerator into a dissipator for $\eta < 0$

Fig. 5

The von Neumann entropy $S_{vN}(\rho _m)$ for one PSS refrigerator cycle (a) and a comparable cycle (with respect to process time scales) of a quantum Otto engine (b) is shown for various temperatures. a Refrigerator entropy for peak coupling strength $\gamma /\omega _0 = 0.25$ at fixed hot bath $\omega _0\hbar \beta _h = 1$. b Heat engine entropy for fixed cold bath inverse temperature $\omega _0\hbar \beta _c = 3$. Periods of unitary evolution of the working medium are indicated by dashed vertical lines

Figure 4 shows the effect of increased temperature spreads between hot and cold reservoir on the refrigerator’s efficiency. The thermodynamic cooling operation works quite efficiently for moderate damping $\gamma /\omega _0$ and moderate temperatures of the cold reservoir. The inset in Fig. 4 shows the effect of lowering the effective frequency modulation, i.e., the hub size of compression and expansion strokes $\varDelta \omega /\omega _0$. While for small temperature differences between hot and cold reservoir, a smaller hub size can increase the efficiency to some extent, higher temperature gradients require sufficiently large compression strokes to pump sufficient amounts of energy against the temperature gradient.

5 Von Neumann entropy—refrigerator vs. heat engine regime

In case of heat engine or refrigerator protocols with harmonic work media, the individual samples of the reduced density remain Gaussian for Gaussian initial conditions. This is a result of Gaussian transformations that always map Gaussian states onto Gaussian states [58, 59]. The von Neumann entropy of mixed states can then be derived [60] from the elements of the covariance matrix according to:

$$\begin{aligned} S_{vN}(\rho )= & {} g\left( \sqrt{\langle q^2\rangle \langle p^2\rangle -\langle qp + pq\rangle ^2/4}\right) \nonumber \\ g(x)= & {} \left( x+\frac{1}{2}\right) \log \left( x+\frac{1}{2}\right) - (x-\frac{1}{2})\log \left( x-\frac{1}{2}\right) .\nonumber \\ \end{aligned}$$

(16)

For an harmonic oscillator in thermal equilibrium weakly coupled to a thermal bath, the von Neumann entropy of the steady state is known in analytic form:

$$\begin{aligned} S_{vN} = -k_\mathrm{B} \log \left( 1-e^{-\hbar \beta \omega }\right) + \hbar \beta \omega \frac{e^{-\hbar \beta \omega }}{1-e^{-\hbar \beta \omega }}. \end{aligned}$$

(17)

In [22], it is shown how the working medium in the PSS regime of a heat engine cycle substantially deviates from a mere sequence of equilibrium states. The entropy is thereby used to indicate incomplete thermalization with the reservoirs during the isochores. Figure 5 shows the von Neumann entropy for an entire PSS cycle of a refrigerator setting (a) and for a, in terms of process time scales, corresponding heat engine (b). The von Neumann entropy $S_{vN}$ displays in both thermodynamic regimes the alternate sequences of unitary strokes and thermal contacts to reservoirs. Even with a relatively long contact time compared to $1/\gamma$, the entropy values indicate incomplete thermalization with the colder reservoir, even when the non-thermal nature of squeezing is disregarded.

6 Conclusions

In this paper, we presented a brief discussion of the quantum dynamics of a quantum refrigerator within a consistent non-perturbative formulation. This allows to monitor details of the mode of operation of the device including the periodic steady state. While we focus here on a harmonic work medium, it is straightforward to consider also nonlinear systems as shown for quantum heat engines recently [22]. The prominent role of the coupling work has been elucidated.

As a next step, the platform will be extended to implement optimal control techniques to control quantum coherences and correlations between work medium and reservoirs. This may also lead to new driving protocols beyond the known classical ones (Otto, Stirling). Furthermore, the cycle protocol could be generalized by including measurements [61].