Abstract
The linear momentum of electromagnetic radiation is proportional to the Poynting vector. However, when light interacts with a dipole, the radiation pressure generated is no longer proportional to the Poynting vector: the so-called Belinfante’s momentum or equivalently, the curl of the spin density of the light field, must be considered. In this paper, we propose an optical configuration, based on two evanescent counter-propagating waves, perpendicularly polarized, capable of detecting Belinfante’s mechanical action. The two beams interact with a high-refractive-index particle like silicon. The direction of the radiation pressure exerted on the particle, proportional only to the curl of the spin density, depends on the electric and magnetic response of the particle and changes sign at the radiation wavelengths corresponding with the Kerker conditions.
Similar content being viewed by others
1 Introduction
Radiation pressure is a direct manifestation of the existence of light linear momentum which is transferred to objects inducing scattering forces. This linear momentum density is calculated dividing the electromagnetic power per unit area by the speed of light squared. By considering the energy conservation in Maxwell equations, the power per unit area is given by the Poynting vector \(\mathbf{S}=\mathbf{E} \times \mathbf{B}/\mu _{0}\) deriving in a linear momentum given by \(<\mathbf{P}>=<\mathbf{S}>/c^2\) [1]. There are some debates related to the electromagnetic linear momentum like, for instance, the hidden momentum, the electromagnetic mass and the Abraham–Minkowski controversy [2] . In this paper, we are going to deal with the existence of the so-called virtual Belinfante’s linear momentum.
The linear momentum of light may be obtained also using classical field theories by the principle of least action. However, following this path, a different result is obtained [3]. The momentum obtained, the so-called canonical momentum \(<\mathbf{P}_o>\), is given by \(<\mathbf{P}>\) plus a new additional solenoidal contribution that we may denote as \(<-\mathbf{P}_s>\). In principle, since this new term is divergence free, it has no influence in Maxwell’s conservation laws. However, the existence of this new term implies a non-symmetric stress energy tensor and then, in order to establish a symmetric field theory, \(<-\mathbf{P}_s>\) is usually discarded [4] and light’s linear momentum is considered as \(<\mathbf{P}>=<\mathbf{P}_o>-<-\mathbf{P}_s>\). That is the reason why this solenoidal term \(<-\mathbf{P}_s>\), known as Belinfante’s momentum, is usually considered to be “virtual.”
However, this term has a fundamental importance when dealing with the radiation pressure induced by light on electric and magnetic dipoles. Light forces on dipoles are described as the sum of the gradient force and the radiation pressure or scattering force. The gradient force is proportional to the real part of the polarizability and the intensity gradient of the field, while the scattering force is proportional to the imaginary part of the polarizability and the phase gradient of the radiation [5]. Several theoretical studies have confirmed that the scattering force on a small particle is not given by the Poynting vector [6, 7], there is an extra contribution coming from the curl of the spin density of the light field [8] implying that the momentum transferred is really the orbital part of the Poynting vector [9,10,11,12,13,14]. Therefore, we may say that the momentum transferred to the particle from electromagnetic radiation is not given by \(<\mathbf{P}>\) but by \(<\mathbf{P}_o>=<\mathbf{P}>+<-\mathbf{P}_s>\).
This mechanism for momentum transfer cannot be experimentally confirmed using homogeneously distributed radiation, where \(<\mathbf{P}_s>=0\) and \(<\mathbf{P}>=<\mathbf{P}_o>\). However, if we consider an elliptically polarized, inhomogeneous field, then the curl of the spin density of the light field is different from zero [8] and the scattering force is no longer given by the full Poynting vector. By measuring the mechanical action of this kind of radiation, with a Belinfante’s momentum different from zero, we should be able to experimentally detect how the radiation pressure on a small particle is no longer proportional to the Poynting vector.
Several experimental setups have been proposed in order to detect the special mechanical action on a dipole due to the existence of a curl of the spin density different from zero. The main problem is that usually, the Poynting vector and Belinfante’s momentum are parallel and then, it is very difficult to separate both effects. We may say that there are sophisticated optical configurations, in which the action of the Poynting vector and the Belinfante’s momentum are non-parallel even within the dipolar regime [15]. The other option is to look for optical configurations with a null value of the Poynting vector. In these cases, the scattering force on a dipolar particle is only due to Belinfante’s momentum. These kinds of approaches are based on optical lattices [16, 17] and evanescent waves [18].
Recently, a different type of forces coming from the electric and magnetic dipole interaction[19] have been studied. It is possible to find optical configurations where these forces are proportional to the transverse part of the curl of the spin density of the electromagnetic radiation [20,21,22,23,24,25,26,27,28,29]. However, these transverse forces, affecting Mie particles but not Rayleigh dipoles, are not the forces that we are treating on our paper. The forces we are about to analyze come fully and solely from the transfer of the Belinfante’s momentum to a unique dipole (they show up also in configurations with a null value of the Poynting vector), are obtained from the interference between the incident and scattered fields and act separately on electric or magnetic dipoles [19]. In opposition, the transverse forces previously reported (which are zero if \(\mathbf {E} \times \mathbf {B}^{*} = 0\)) are obtained from the scattered fields, come from the interaction between the electric and magnetic dipoles and, only for particular cases, happen to be proportional to the transverse part of the Belinfante’s force. In addition, we may say that, spin dependent forces are not univocally given by the curl of the spin; it is also possible to find systems presenting interactions that depend on the spin of the electromagnetic radiation, like the chiral systems [30,31,32] or proportional to the gradient of the spin, like the magneto-optical particles [33].
In this paper, we propose and analyze a setup based on evanescent waves and on the magnetic response of dielectric particles with a large value of the refractive index . On the one hand, transverse magnetic (TM) evanescent waves have a curl of the electric spin of the light field different from zero, affecting electric dipoles, while transverse electric (TE) evanescent waves have a curl of the magnetic spin of the light field different from zero, affecting magnetic dipoles. On the other hand, high-refractive-index scatterers like silicon micro-particles behave like a magnetic or electric dipole depending on wavelength [34]. Then, if a silicon particle is illuminated with a combination of evanescent waves, the mechanical response is going to depend on wavelength and on the polarization (TE or TM) of the evanescent wave. In this paper, we use these properties to propose an optical configuration where the characteristic wavelength dependence of the radiation pressure can be only attributed to the existence of a curl of the spin density of the light field different from zero or to the “virtual” mechanical action emanating from Belinfante’s momentum.
2 The proposal
2.1 The electromagnetic fields
We are going to consider two electromagnetic fields consisting of two evanescent waves in \(z>0\) (TE (or s) and TM (or p) polarized) propagating in x and with the same amplitude. The TE field is given by:
and the TM field by:
with
being a the attenuation vector, \(\delta \) the phase difference between both waves, k the wave vector, \(n_2=\sqrt{\epsilon }\) the refractive index of the medium where the evanescent wave propagates (\(z>0\)) and \(E_{0}\) the amplitude of the y component of the electric field.
Note that
2.2 The scattering forces
Let us consider a particle that behaves like an electric and a magnetic dipole depending on wavelength. The general expression for the time-averaged scattering force on a dipole with electric and magnetic response is given at first-order approach by [19]
being \(<\mathbf{S}>=c^{2}\epsilon _{0}\mathfrak {R}(\mathbf{E} \times \mathbf{B}^{*})/2\) the time-averaged Poynting vector. \(<\mathbf{L_{s}^{e}}>=\epsilon \epsilon _{0}(\mathbf{E^{*}} \times \mathbf{E})/i 2 \omega \) and \(<\mathbf{L_{s}^{m}}>=(\mathbf{B^{*}} \times \mathbf{B})/i 2 \omega \mu _{0}\) are the time-averaged electric and magnetic spin densities of the light fields and \(\alpha _{e}^{`'}\), \(\alpha _{m}^{`'}\) are the imaginary parts of the electric and magnetic polarizabilities.
For the particular field considered, since electric field and complex conjugate of the magnetic field are parallel (see Eq. 7), \(<\mathbf {S}>=0\). On the other hand, the electric and magnetic spin densities are simply related by \(<\mathbf{L_{s}^{m}}>=-<\mathbf{L_{s}^{e}}>\):
Thus, the force is given by
which can be explicitly written as
being \(\mathbf{i}\) the unit vector in the x direction.
Note that this force is just proportional to the time-averaged value of Belinfante’s spin linear momentum density:
Since \(\mathbf{B}\) and \(\mathbf{E}^*\) are parallel, all forces coming from higher-order electric and magnetic dipoles interaction \((\alpha _{e} \alpha _{m}^{*})\) are equal to zero [19]. In the z direction, we have also forces coming from the gradient of the evanescent field intensity that may be compensated with the optical trap holding our particle over the surface.
To sum up, if the momentum transferred to the particle comes from \(<\mathbf{P}_o>=<\mathbf{P}>-<\mathbf{P}_s>\) and not from \(<\mathbf{P}>\), with this configuration, we should be able to detect that, although \(<\mathbf{S}>=0\), the force in the x direction is not zero and depends on Belinfante’s momentum and on the value of \(( \alpha _{m}^{`'}-\alpha _{e}^{`'})\).
2.3 The particle
As a probe, we propose to use a particle with tuneable electric and magnetic dipolar response depending on wavelength. For example, we can use a silicon particle, with a diameter of half a micron and radiation wavelengths ranging from 1.4 to 2 microns. For plane wave incidence, the total extinction cross section calculated from Mie theory, the extinction coming from the electric and magnetic dipoles and the sum of the contributions coming from the electric and magnetic dipoles are plotted in Fig. 1. Note how the particle can be considered just like an electric and a magnetic dipole and how, for wavelengths smaller than roughly (1700nm), the electric response dominates while, for larger wavelengths, the magnetic response is the one prevailing . At 1700nm responses (electric and magnetic) are the same and the scattering force should be zero (see equation 11).
Extinction cross section versus wavelength for a silicon particle of half a micron diameter in water. (Black) Electronic dipole contribution (\(\sigma _{e}=n_2 \omega \alpha _{e}^{''}/c\) ), (red) magnetic dipole contribution(\(\sigma _{m}=n_2 \omega \alpha _{m}^{''}/c\)), (green) electric dipole plus magnetic dipole contributions and (blue) total extinction cross section
A close analysis to the values of the polarizability reveals that, close to 1700nm, \(\alpha _{m}^{''}=\alpha _{e}^{''}\) and also, \(\alpha _{m}^{'}=-\alpha _{e}^{'}\). Then, the wavelength at which a Belinfante’s force sign change is expected, corresponds with the generalized second Kerker condition [35]. In addition, the other wavelength (close to 2000nm) with zero value of the Belinfante’s force in this configuration, corresponds to the first Kerker condition of the silicon particle \(\alpha _{m}=\alpha _{e}\). Kerker conditions have been previously proved to be important in the particular case of pulling forces [36]
2.4 Description of the experiment proposed
We consider a semi-spherical glass prism (\(n_{1}=1.55\)). The flat surface is immersed in water (\(n_2=1.33\)) and the evanescent wave in water is created by the total internal reflection in the glass–water interface. We consider the emission from a laser with a \(5\,\mathrm{mm}\) spot diameter that is split into two beams with the same intensity (\(100\,\mathrm{mW}\)) using a polarized beam splitter (see Fig. 2). Each beam is focused using a lens with \(70\,\mathrm{mm}\) focal distance. Both beams enter perpendicularly on the glass surface and, due to the reflection on the glass, the power transmitted to the prism decreases in a 0.95 factor per beam.
Since the fields (TE and TM) are induced by the total internal reflection of two plane wave with the same intensity (s-polarized and p-polarized, respectively), propagating in a medium with \(n_{1}>n_2\), the following condition on the transmission coefficients must be fulfilled \(|t_{H\perp }|/|t_{\perp }|=n_2/n_{1}\). This condition will hold as long as the incident angle (\(\theta \)) for both waves takes the value
In our case, this angle corresponds roughly to \(\theta =67^{o}\) being \(59^{o}\) the critical angle needed to obtain total internal reflection.
The attenuation and k vectors are obtained from the incident angle and the wavelength in vacuum (\(\lambda _0\)):
In order to obtain this final incident angle (\(\theta \)), we use two tilted mirrors where the beams are reflected with the proper angle [37].
Proposed experimental setup. The beam coming from an infrared non-polarized laser is split into two by a polarized beam splitter (dark blue). Both beams, s-polarized (crosses) and p-polarized (arrows) are reflected on a mirror (light blue) and focused on the same position of a glass–water interface. Two evanescent waves, TE and TM, with the same intensity and counter-propagating are generated on the water surface, inducing scattering forces on a silicon particle (yellow circle) proportional to Belinfante’s spin momentum and depending on the value of the electric and magnetic dipoles induced on the particle
2.5 The radiation pressure
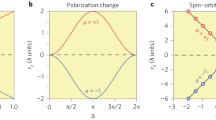
We have calculated, using equation 10, the force generated in the x direction on the half a micron diameter silicon particle as a function of wavelength. In order to ensure strong enough forces, we have considered that the spherical particle is trapped at a distance \(z=100\,nm\) from the glass surface. The expected measured force as a function of wavelength is shown in Fig. 3. For this calculation of the forces, we have considered that the power is the same for all wavelengths and we neglect possible corrections coming from the beam splitter performance. We consider the electric and magnetic polarizabilities inferred from Fig. 1. Corrections to the longitudinal scattering force felt by the electric dipole coming from the multiple scattering with the dielectric surface are only of the order of 3/1000 [38].
Note how the scattering force, coming solely from the curl of the spin density of the light field, i.e., from the spin or Belinfante’s linear momentum, should go from positive to negative, being zero at the wavelengths at which the magnitudes of the electric and magnetic dipoles are equal. This is in clear disagreement with the response expected if the scattering force comes only from the Poynting vector, which should be negligible, remaining in any case with the same orientation for every wavelength.
Force in the x direction versus wavelength (straight line for the analytic expression and circles for the results from full numerical simulations). Note how the force is negative when the electric dipole dominates and positive when the magnetic dipole prevails. The force is equal to zero close to \(1700\,\mathrm{nm}\) where the contribution from both dipoles is equal
In order to have an idea about the magnitude of the Belinfante’s force, we have calculated, on our configuration, the ratio between the curl of the spin force (\(F_{B}\)) and the standard radiation pressure force proportional to the Poynting vector (\(F_{P}\)). For TE (TM) evanescent waves and for magnetic (electric) dipoles, the ratio between these two forces is given by
which, in our case, corresponds to \(\frac{F_{B}}{F_{P}}\sim 0.3\).
2.6 Full numerical simulation
In order to corroborate this analytic prediction, we have reproduced the experiment using full numerical simulations. By solving Maxwell equations in a mesh, we obtain the electromagnetic field of the two evanescent waves and the scattering of the particle. Then, forces on the probe are calculated by integrating, on a closed surface, the flux of the Maxwell stress energy tensor. The results are plotted in Fig. 3. Note how the outcome from the simulated experiment fits the behavior obtained from the analytic expression, demonstrating that scattering forces on the particle are due to the existence of a Belinfante’s momentum, proportional to the curl of the spin density of the light field.
3 Conclusion
We have analyzed an optical configuration, based on the magnetic spin of TE evanescent waves and the electric spin of TM evanescent waves, capable of elucidating if the momentum transferred to a dipolar particle is the Poynting vector alone or the Poynting vector together with Belinfante’s momentum. The measurement is based on the electric and magnetic response of silicon particles in the infrared region of the electromagnetic spectrum. If the momentum transferred to the dipolar particle is given only by the Poynting vector, the result of the proposed experiment should be a negligible force. However, if the canonical momentum is transferred, the result should be a force coming from the curl of the spin density of the light fields (Belinfante’s momentum) depending on the difference between the magnetic and the electric response of the probe particle. In particular, for wavelengths between 1400nm and 1700nm the experiment should detect a negative displacement of the particle while, for wavelengths larger than 1700nm crossing the second Kerker condition, the particle should move in the positive direction. The full numerical simulations performed point toward the existence of a component of the radiation pressure coming from the “virtual” Belinfante’s momentum.
References
J.D. Jackson, Classical Electrodynamics (John Wiley and Sons, USA, 1962), pp. 189–194
D.J. Griffiths, Am. J. Phys. 80, 7–18 (2012)
L.D. Landau, E.M. Lifshitz., The Classical theory of fields, Fourth revised English Edition (Butterworth Heinemann) 82-87
F.J. Belinfante, Physica. 7, 449 (1940)
L. Novotny, B. Hecht., Principles of Nano-optics, second edition (Cambridge University 2012) 453-458 (2012)
J.R. Arias-Gonzalez, M. Nieto-Vesperinas, J. Opt. Soc. Am. A 20, 1201 (2003)
V. Wong, M. Ratner, Phys. Rev. B 73, 075416 (2006)
S. Albaladejo, M.I. Marqués, M. Laroche, J.J. Sáenz, Phys. Rev. Lett. 102, 113602 (2009)
M.V. Berry, J. Opt. A Pur Appl. Opt. 11, 094001 (2009)
A.Y. Bekshaev, O.V. Angelsky, S.G. Hanson, C.Y. Zenkova, Phys. Rev. A 86, 023847 (2012)
A.Y. Bekshaev, J. Opt. 15, 044004 (2013)
D.B. Ruffner, D.G. Grier, Phys. Rev. Lett. 111, 059301 (2013)
M.I. Marqués, J.J. Sáenz, Phys. Rev. Lett. 111, 059302 (2013)
A. Canaguier-Durand, A. Cuche, C. Genet, T.W. Ebbesen, Phys. Rev. A 88, 033831 (2013)
M.I. Marqués, Opt. Lett. 39, 5122 (2014)
M.I. Marqués, J.J. Sáenz., Opt. Lett. 37 (2012) 2787; 37 4470 (2012)
M.I. Marqués, J.J. Sáenz, Adv. Elect. 2, 26 (2013)
M.I. Marqués, J.J. Sáenz., Proc. SPIE 8810, Optical Trapping and Optical Micromanipulation X, 881007 (2013)
M. Nieto-Vesperinas, J.J. Sáenz, R. Gómez-Medina, and L. Chantada Opt. Express 18, 11428 (2010)
K.Y. Bliokh, A.Y. Bekshaev, F. Nori, Nat. Commun. 5, 3300 (2014)
M. Antognozzi, C.R. Bermingham, R.L. Harniman, S. Simpson, J. Senior, R. Hayward, H. Hoerber, M.R. Dennis, A.Y. Bekshaev, K.Y. Bliokh, F. Nori, Nat. Phys. 12, 731 (2016)
L. Liu, A. Di Donato, V. Ginis, S. Kheifets, A. Amirzhan, F. Capasso, Phys. Rev. Lett. 120, 223901 (2018)
A.Y. Bekshaev, K.Y. Bliokh, F. Nori, Phys. Rev. X 5, 011039 (2015)
K. Y. Bliokh, F. Nori., Phys. Rep. 592 1 (2015)
V. Svak, O. Brzobohatý, M. Šiler, P. Jákl, J. Kaňka, P. Zemánek, S.H. Simpson, Nat Commun 9, 5423 (2018)
V. Ginis, L. Liu, A. She, F. Capasso., Sci. Rep. 9 14879 (2019)
S. Sukhov, V. Kajorndejnukul, J. Broky, and A. Dogariu Optica 1, 383 (2014)
M. Neugebauer, T. Bauer, A. Aiello, and P. Banzer Phys. Rev. Lett. 114, 06390 (2015)
S. Fardad, A. Salandrino, A. Samadi, M. Heinrich, Z. Chen, N. Christodoulides. Opt Lett 41, 3615 (2016)
G. Pellegrini, M. Finazzi, M. Celebrano, L. Duò, M. A. Iatì, O. M. Maragò, Paolo . Biagioni., J. Phys. Chem. 123 28336 (2019)
S. B. Wang, C. T. Chan., Nat Commun 5 3307 (2014)
A. Hayat, J. P. Balthasar Mueller, F. Capasso., 112 13190 (2015)
S. Edelstein, R.M. Abraham-Ekeroth, P.A. Serena, J.J. Sáenz, A. García-Martín, and M. I. Marqués Physical Review Research 1, 013005 (2019)
A. García-Etxarri, R. Gómez-Medina, L.S. Froufe-Pérez, C. López, L. Chantada, F. Scheffold, J. Aizpurua, M. Nieto-Vesperinas, J.J. Sáenz, Opt. Express 19, 4815 (2011)
M. Nieto-Vesperinas, R. Gómez-Medina, J.J. Sáenz, J. Opt. Soc. Am. A 28, 54 (2011)
N. Odebo Länk, P. Johansson, M. Käll., Opt Express 26 29074 (2018)
M. Šiler, T. Čižmár, M. Šerý, P. Zemánek, Appl. Phys. B 84, 157 (2006)
P.C. Chaumet, M. Nieto-Vesperinas, Phys. Rev. B 61, 14119 (2000)
Acknowledgements
We acknowledge all the help, inspiration, teaching, knowledge, encouragement and friendship from Juan Jose Sáenz. This article is devoted to his legacy and memory. Present work has been supported by the Spanish Ministerio de Ciencia e Innovación (MELODIA PGC2018-095777-B-C21 and C-22) and UAM-CAM project (SI1/PJI/2019-00052). MIM acknowledges also financial support from the Spanish Ministerio de Ciencia e Innovación, through the “María de Maeztu” Programme for Units of Excellence in R& D (CEX2018-000805-M).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Marqués, M.I., Edelstein, S. & Serena, P.A. A proposal to measure Belinfante’s curl of the spin optical force based on the Kerker conditions. Eur. Phys. J. Plus 136, 185 (2021). https://doi.org/10.1140/epjp/s13360-021-01138-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-021-01138-z