Skip to main content
SpringerLink
Log in

Lie symmetries and dynamics of exact solutions of dissipative Zabolotskaya–Khokhlov equation in nonlinear acoustics

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

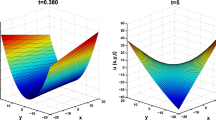
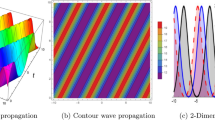
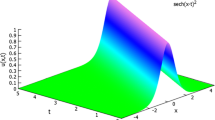
This study deals with symmetry reductions and invariant solutions of (2+1)-dimensional dissipative Zabolotskaya–Khokhlov equation. The equation governs the diffraction of sound beam propagation and describes nonlinear effects in stratified media with dissipation. The possible infinitesimal generators and commutative relation are obtained by means of the similarity transformations method. The method is based on invariance property of Lie groups, which results into the reduction in independent variables by one. Thus, twice reductions of Zabolotskaya–Khokhlov equation provide overdetermined equations, which lead to the invariant solutions under some limiting conditions. The obtained solutions are significant to explain diverse physical structures depending upon existing arbitrary functions and constants. In order to get precise insights, the numerical simulation is performed to the obtained solutions. Eventually, kink wave, parabolic, soliton and stationary profiles of the solutions are obtained.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. M. Bartuccielli, M. Pantano, T. Brugarino, Lett. Nuovo Cim. 37, 433 (1983)

    Article  Google Scholar 

  2. J.K. Hunter, SIAM J. Appl. Math. 48, 16 (1988)

    Article  Google Scholar 

  3. T. Taniuti, Wave Motion 12, 373 (1990)

    Article  MathSciNet  Google Scholar 

  4. G. Valenti, Wave Motion 12, 97 (1990)

    Article  MathSciNet  Google Scholar 

  5. G.M. Webb, G.P. Zank, J. Phys. A 23, 5465 (1990)

    Article  ADS  MathSciNet  Google Scholar 

  6. T.S. Hart, M.F. Hamilton, J. Acoust. Soc. Am. 84, 1488 (1988)

    Article  ADS  Google Scholar 

  7. P. Hariharan, M.R. Myers, R.K. Banerjee, Phys. Med. Biol. 52, 3493 (2007)

    Article  Google Scholar 

  8. M.A. Averkiou, Y.S. Lee, M.F. Hamilton, J. Acoust. Soc. Am. 94, 2883 (1993)

    ADS  Google Scholar 

  9. P.A. Clarkson, S. Hood, Eur. J. Appl. Math. 3, 381 (1992)

    Article  Google Scholar 

  10. P.N. Sionóid, A.T. Cates, Proc. R. Soc. Lond. A 447, 270 (1994)

    Google Scholar 

  11. M. Tajiri, J. Nonlinear Math. Phys. 2, 392 (1995)

    Article  ADS  MathSciNet  Google Scholar 

  12. M.H.M. Moussa, R.M.E. Shikh, Physica A 371, 335 (2006)

    Article  ADS  Google Scholar 

  13. M.S. Bruzon, M.L. Gandarias, M. Torrisi, R. Tracinà, J. Math. Phys. 50, 103504 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  14. N. Taghizadeh, M. Mirzazadeh, F. Farahrooz, Appl. Math. Model. 35, 3991 (2011)

    Article  MathSciNet  Google Scholar 

  15. B.Q. Li, S. Li, Y.L. Ma, Zeitschriftfür Naturforschung A 67, 607 (2012)

    ADS  Google Scholar 

  16. M. Kumar, R. Kumar, A. Kumar, Comput. Math. Appl. 68, 454 (2014)

    Article  MathSciNet  Google Scholar 

  17. A.M. Wazwaz, Partial Differential Equations and Solitary Waves Theory (Springer, Berlin, 2009)

    Book  Google Scholar 

  18. G.W. Bluman, J.D. Cole, Similarity Methods for Differential Equations (Springer, New York, 1974)

    Book  Google Scholar 

  19. P.J. Olver, Applications of Lie Groups to Differential Equations (Springer, New York, 1993)

    Book  Google Scholar 

  20. A.M. Wazwaz, L. Kaur, Nonlinear Dyn. 95, 2209 (2019)

    Article  Google Scholar 

  21. A.M. Wazwaz, L. Kaur, Nonlinear Dyn. 97, 83 (2019)

    Article  Google Scholar 

  22. S. Kumar, A.M. Wazwaz, D. Kumar, A. Kumar, Phys. Scr. 94, 115202 (2019)

    Article  ADS  Google Scholar 

  23. S. Kumar, D. Kumar, A.M. Wazwaz, Phys. Scr. 94, 065204 (2019)

    Article  ADS  Google Scholar 

  24. K. Sharma, R. Arora, A. Chauhan, Phys. Scr. 95, 055207 (2020)

    Article  ADS  Google Scholar 

  25. D. Kumar, S. Kumar, Eur. Phys. J. Plus 135, 162 (2020)

    Article  Google Scholar 

  26. T. Bakkyaraj, Eur. Phys. J. Plus 42, 4679 (2019)

    Google Scholar 

  27. D.V. Tanwar, A.M. Wazwaz, Phys. Scr. 95, 065220 (2020)

    Article  ADS  Google Scholar 

  28. G.G. Polat, T. Özer, J. Nonlinear Math. Phys. 27, 106 (2020)

    Article  MathSciNet  Google Scholar 

  29. M. Kumar, D.V. Tanwar, R. Kumar, Comput. Math. Appl. 75, 218 (2018)

    Article  MathSciNet  Google Scholar 

  30. M. Kumar, D.V. Tanwar, R. Kumar, Nonlinear Dyn. 94, 2547 (2018)

    Article  Google Scholar 

  31. M. Kumar, D.V. Tanwar, Commun. Nonlinear Sci. Numer. Simul. 69, 45 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  32. M. Kumar, D.V. Tanwar, Int. J. Geom. Methods Mod. Phys. 16, 1950110 (2019)

    Article  MathSciNet  Google Scholar 

  33. M. Kumar, D.V. Tanwar, Comput. Math. Appl. 76, 2535 (2018)

    Article  MathSciNet  Google Scholar 

  34. M. Kumar, D.V. Tanwar, Pramana-J. Phys. 94, 23 (2020)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Graphic Era University, Dehradun, 248002, India

    Dig Vijay Tanwar

  2. Department of Mathematics, Saint Xavier University, Chicago, IL, 60655, USA

    Abdul–Majid Wazwaz

Authors
  1. Dig Vijay Tanwar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Abdul–Majid Wazwaz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dig Vijay Tanwar.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tanwar, D.V., Wazwaz, A. Lie symmetries and dynamics of exact solutions of dissipative Zabolotskaya–Khokhlov equation in nonlinear acoustics. Eur. Phys. J. Plus 135, 520 (2020). https://doi.org/10.1140/epjp/s13360-020-00527-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-020-00527-0

Search

Navigation