Skip to main content
SpringerLink
Log in

Riemann–Hilbert approach and nonlinear dynamics in the nonlocal defocusing nonlinear Schrödinger equation

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

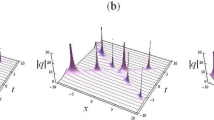
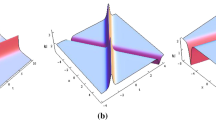
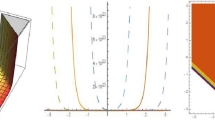
The nonlocal defocusing nonlinear Schrödinger (ND-NLS) equation is comparatively studied via the Riemann–Hilbert approach. Firstly, via spectral analysis, the spectral structure of the ND-NLS equation is investigated, which is different to those of the other three NLS-type equations, i.e., the local focusing nonlinear Schrödinger (LF-NLS) equation, the local defocusing nonlinear Schrödinger (LD-NLS) equation and the nonlocal focusing nonlinear Schrödinger (NF-NLS) equation. Secondly, by solving the Riemann–Hilbert problem corresponding to the reflectionless cases, multi-soliton solutions are obtained for the ND-NLS equation. Thirdly, we prove that, if parameters are suitably chosen, the multi-soliton solutions of the ND-NLS equation can be reduced to those of the LF-NLS equation and the LD-NLS equation, respectively. Fourthly, the multi-soliton solutions of the ND-NLS equation are demonstrated to possess repeated singularities generally, but they can also remain analytic for appropriate soliton parameters. Moreover, the multi-soliton dynamics are graphically illustrated using Mathematica symbolic computations. These results show that the solution structure and the nonlinear dynamics in the ND-NLS equation are rather different from those of the LF-NLS equation, the LD-NLS equation and the NF-NLS equation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. D.J. Benney, A.C. Newell, J. Math. Phys. 46, 133 (1967)

    MathSciNet  Google Scholar 

  2. D.J. Benney, G.J. Roskes, Stud. Appl. Math. 48, 377 (1969)

    Google Scholar 

  3. M.J. Ablowitz, H. Segur, Solitons and the Inverse Scattering Transform (SIAM, Philadelphia, 1981)

    MATH  Google Scholar 

  4. V.E. Zakharov, A.B. Shabat, Sov. Phys. JETP 34, 62 (1972)

    ADS  Google Scholar 

  5. M.J. Ablowitz, D.J. Kaup, A.C. Newell, H. Segur, Stud. Appl. Math. 53, 249 (1974)

    Google Scholar 

  6. M.J. Ablowitz, Z.H. Musslimani, Phys. Rev. Lett. 110, 064105 (2013)

    ADS  Google Scholar 

  7. M.J. Ablowitz, Z.H. Musslimani, Nonlinearity 29, 915 (2016)

    ADS  MathSciNet  Google Scholar 

  8. M.J. Ablowitz, Z.H. Musslimani, Stud. Appl. Math. 139, 7 (2017)

    MathSciNet  Google Scholar 

  9. C.M. Bender, S. Boettcher, Phys. Rev. Lett. 80, 5243 (1998)

    ADS  MathSciNet  Google Scholar 

  10. V.V. Konotop, J.K. Yang, D.A. Zezyulin, Rev. Mod. Phys. 88, 035002 (2016)

    ADS  Google Scholar 

  11. T.A. Gadzhimuradov, A.M. Agalarov, Phys. Rev. A 93, 062124 (2016)

    ADS  Google Scholar 

  12. M. Li, T. Xu, Phys. Rev. E 91, 033202 (2015)

    ADS  MathSciNet  Google Scholar 

  13. X. Huang, L.M. Ling, Eur. Phys. J. Plus 131, 148 (2016)

    ADS  Google Scholar 

  14. A. Khare, A. Saxena, J. Math. Phys. 56, 032104 (2015)

    ADS  MathSciNet  Google Scholar 

  15. T. Xu, S. Lan, M. Li, L.L. Li, G.W. Zhang, Phys. D 390, 47 (2019)

    MathSciNet  Google Scholar 

  16. J.K. Yang, Phys. Lett. A 383, 328 (2019)

    ADS  MathSciNet  Google Scholar 

  17. J.K. Yang, Nonlinear Waves in Integrable and Nonintegrable Systems (SIAM, Philadelphia, 2010)

    MATH  Google Scholar 

  18. J.K. Yang, D.J. Kaup, J. Math. Phys. 50, 023504 (2009)

    ADS  MathSciNet  Google Scholar 

  19. D.S. Wang, D.J. Zhang, J.K. Yang, J. Math. Phys. 51, 023510 (2010)

    ADS  MathSciNet  Google Scholar 

  20. B.L. Guo, L.M. Ling, J. Math. Phys. 53, 073506 (2012)

    ADS  MathSciNet  Google Scholar 

  21. B.L. Guo, N. Liu, Y.F. Wang, J. Math. Anal. Appl. 459, 145 (2018)

    MathSciNet  Google Scholar 

  22. X.G. Geng, J.P. Wu, Wave Motion 60, 62 (2016)

    MathSciNet  Google Scholar 

  23. D.S. Wang, X.L. Wang, Nonlinear Anal. RWA 41, 334 (2018)

    Google Scholar 

  24. W.X. Ma, Nonlinear Anal. RWA 47, 1 (2019)

    Google Scholar 

  25. W.X. Ma, J. Geom. Phys. 132, 45 (2018)

    ADS  MathSciNet  Google Scholar 

  26. W.X. Ma, J. Math. Anal. Appl. 471, 796 (2019)

    MathSciNet  Google Scholar 

  27. H.Q. Zhang, Z.J. Pei, W.X. Ma, Chaos Solitons Fract. 123, 429 (2019)

    ADS  Google Scholar 

  28. M.J. Ablowitz, A.S. Fokas, Complex Variables: Introduction and Applications (Cambridge University Press, Cambridge, 2003)

    MATH  Google Scholar 

  29. A.B.D. Monvel, D. Shepelsky, C. R. Math. 352, 189 (2014)

    Google Scholar 

  30. J.P. Wu, X.G. Geng, Commun. Nonlinear Sci. Numer. Simul. 53, 83 (2017)

    ADS  MathSciNet  Google Scholar 

  31. J.P. Wu, Nonlinear Dyn. 96, 789 (2019)

    Google Scholar 

  32. V.B. Matveev, M.A. Salle, Darboux Transformation and Solitons (Springer, Berlin, 1991)

    MATH  Google Scholar 

  33. Z.X. Zhou, Commun. Nonlinear Sci. Numer. Simulat. 62, 480 (2018)

    ADS  Google Scholar 

  34. R. Hirota, The Direct Methods in Soliton Theory (Cambridge University Press, Cambridge, 2004)

    MATH  Google Scholar 

  35. A.M. Wazwaz, S.A. El-Tantawy, Nonlinear Dyn. 88, 3017 (2017)

    Google Scholar 

  36. J.J.C. Nimmo, N.C. Freeman, Phys. Lett. A 95, 4 (1983)

    ADS  MathSciNet  Google Scholar 

  37. W.X. Ma, Y.C. You, Trans. Am. Math. Soc. 357, 1753 (2005)

    Google Scholar 

  38. P.A. Deift, X. Zhou, Ann. Math. 137, 295 (1993)

    MathSciNet  Google Scholar 

  39. A.S. Fokas, A Unified Approach to Boundary Value Problems (SIAM, Philadelphia, 2008)

    MATH  Google Scholar 

  40. X.G. Geng, H. Liu, J. Nonlinear Sci. 28, 739 (2018)

    ADS  MathSciNet  Google Scholar 

  41. H. Liu, X.G. Geng, B. Xue, J. Differ. Equ. 265, 5984 (2018)

    ADS  Google Scholar 

Download references

Acknowledgements

The author is very grateful to the editor and the anonymous referees for their valuable suggestions. The author would also like to thank the support by the Collaborative Innovation Center for Aviation Economy Development of Henan Province.

Author information

Authors and Affiliations

  1. School of Science, Zhengzhou University of Aeronautics, Zhengzhou, 450046, Henan, People’s Republic of China

    Jianping Wu

Authors
  1. Jianping Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jianping Wu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, J. Riemann–Hilbert approach and nonlinear dynamics in the nonlocal defocusing nonlinear Schrödinger equation. Eur. Phys. J. Plus 135, 523 (2020). https://doi.org/10.1140/epjp/s13360-020-00348-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-020-00348-1

Search

Navigation