Abstract
We clarify that the q-generalization of the simple harmonic oscillator to the Arik–Coon one leads us to obtain two different families of q-coherent states in a Fock representation space of the system. They are eigenstates of unbounded and bounded annihilation operators associated with the Arik–Coon q-oscillator. The first family satisfies the resolution of identity condition on all the complex plane and the second one on a disc in radius \(1/\sqrt{1-q}\). Their positive definite q-measures are different, but in the limit \(q\rightarrow 1\) both of them convert to the measure of well-known coherent states for the simple harmonic oscillator. The first and second families of the q-coherent states are also deformed eigenstates of the bounded and unbounded annihilation operators, respectively. Thus, it is possible to study the statistical properties of both q-coherent states via both bounded and unbounded operators. The nonclassical behaviours of interest in this article are signal-to-quantum noise ratio, sub-Poissonian photon statistics, photon antibunching, quadrature squeezing effect and bipartite entanglement for the two families of the q-coherent states, as well as Hillery-type higher-order squeezing for their corresponding photon-added states.





Similar content being viewed by others
Change history
18 June 2020
Unfortunately, after publication, we found some misprints in Eur. Phys. J. Plus (2020) 135: 253. We list them here because their number is not few.
Notes
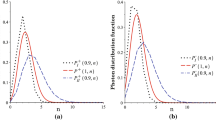
Preparing the figures of this article we have used the following approximations: \(E_{q}((1-q)|z|^2)\cong 1+\sum _{k=1}^{1000}\frac{q^{\frac{k(k-1)}{2}}{(1-q)^k|z|^{2k}}}{\Pi _{l=1}^{k}(1-q^l)}\) and \(e_{q}((1-q)|z|^2)\cong 1+\sum _{k=1}^{1000}\frac{{(1-q)^k|z|^{2k}}}{\Pi _{l=1}^{k}(1-q^l)}\).
References
E. Schrödinger, Die Naturwissenshaften 14, 664–666 (1926)
R.J. Glauber, Phys. Rev. 131, 2766–2788 (1963)
L. Mandel, Phys. Scr. T12(34), 34–42 (1986)
M. Hillery, Phys. Rev. A 36, 3796–3802 (1987)
V.V. Buzek, A. Vidiella-Barranco, P.L. Knight, Phys. Rev. A 45, 6570–6585 (1992)
A. Mann, B.C. Sanders, W.J. Munro, Phys. Rev. A 51, 989–991 (1995)
Y. Feng, A.I. Solomon, Opt. Commun. 152, 299–301 (1998)
X.G. Wang, B.C. Sanders, Sh Pan, J. Phys. A Math. Gen. 33, 7451–7467 (2000)
X. Wang, B.C. Sanders, Phys. Rev. A 65, 012303 (2001)
N. Behzadi, H. Fakhri, Eur. Phys. J. D 61, 253–259 (2011)
B.C. Sanders, J. Phys. A Math. Theor. 45, 244002 (2012)
B. C. Sanders, Forty-five years of entangled coherent states, Proceedings of the first international workshop on ECS and it’s application to QIS; T.M.Q.C. 111-113, (2013)
W.S. Chung, H. Hassanabadi, Eur. Phys. J. Plus 134, 394 (2019)
V.V. Dodonov, I.A. Malkin, V.I. Man’ko, Physica 72, 597–615 (1974)
Y. Xia, G. Guo, Phys. Lett. A 136, 281–283 (1989)
C.C. Gerry, J. Mod. Opt. 40, 1053–1071 (1993)
V. Buzek, P.L. Knight, in Quantum interference, superposition states of light and nonclassical effects, in: progress in optics, vol. 34, ed. by E. Wolf (Elsevier, Amsterdam, 1995), 1158
V.I. Man’ko, G. Marmo, E.C.G. Sudarshan, F. Zaccaria, Phys. Scr. 55, 528–541 (1997)
B. Mojaveri, A. Dehghani, R. Jafarzadeh Bahrbeig, Eur. Phys. J. Plus 133, 529 (2018)
A. Bendjeffal, A. Smida, J. Messamah et al., Eur. Phys. J. Plus 134, 330 (2019)
B. Mojaveri, A. Dehghani, R. Jafarzadeh Bahrbeig, Eur. Phys. J. Plus 134, 456 (2019)
H.P. Yuen, Phys. Rev. A 13, 2226–2243 (1976)
C.M. Caves, B.L. Schumaker, Phys. Rev. A 31, 3068–3092 (1985)
G.S. Agarwal, K. Tara, Phys. Rev. A 43, 492–497 (1991)
C. Quesne, Phys. Lett. A 288, 241–250 (2001)
A. Dehghani, B. Mojaveri, Eur. Phys. J. Plus 132, 502 (2017)
A. Anbaraki, D. Afshar, M. Jafarpour, Eur. Phys. J. Plus 133, 2 (2018)
Z.-Z. Xin, Y.-B. Duan, W. Zhang, W.-J. Qian, M. Hirayama, K. Matumoto, J. Phys. B 29, 2597–2606 (1996)
D.F. Walls, Nature 306, 141–146 (1983)
R. Loudon, P.L. Knight, J. Mod. Opt. 34, 709–759 (1987)
V. Buzek, J. Mod. Opt. 37, 303–316 (1990)
V.V. Dodonov, M.A. Man’ko, V.I. Man’ko, A. Vourdas, J. Russ. Laser Res. 28, 404–428 (2007)
X. Xu, J. Wang, H. Yuan et al., Eur. Phys. J. Plus 134, 134 (2019)
V. Buzek, P.L. Knight, Opt. Commun. 81, 331–336 (1991)
R. Loudon, The Quantum Theory of Light (Oxford University Press, New York, 2000)
X.-B. Wang, L.C. Kwek, Y. Liu, C.H. Oh, J. Phys. B At. Mol. Opt. Phys. 34, 1059–1078 (2001)
Z.-Z. Xin, Y.-B. Duan, H.-M. Zhang, M. Hirayama, K. Matumoto, J. Phys. B 29, 4493–4506 (1996)
M.S. Kim, F.A.M. de Oliveira, P.L. Knight, Phys. Rev. A 40, 2494–2503 (1989)
M. Arik, D.D. Coon, J. Math. Phys. 17, 524–527 (1976)
E.V. Damaskinskii, P.P. Kulish, J. Sov. Math. 62, 2963–2986 (1992)
A.M. Perelomov, Helv. Phys. Acta 68, 554–576 (1995)
A. Klymik, K. Schmüdgen, Quantum Groups and Their Representations (Springer, Berlin, 1997)
K.A. Penson, A.I. Solomon, J. Math. Phys. 40, 2354–2363 (1999)
C. Quesne, J. Phys. A Math. Gen. 35, 9213–9226 (2002)
C. Quesne, K.A. Penson, V.M. Tkachuk, Phys. Lett. A 313, 29–36 (2003)
H. Fakhri, A. Hashemi, Int. J. Geom. Methods Mod. Phys. 13, 1650028 (2016)
H. Fakhri, A. Hashemi, Phys. Rev. A 93, 013802 (2016)
H. Fakhri, M. Sayyah-Fard, Ann. Phys. 387, 14–28 (2017)
V.I. Man’ko, G.M. Tino, Phys. Lett. A 202, 24–27 (1995)
V.I. Man’ko, R.V. Mendes, J. Phys. A Math. Gen. 31, 6037–6044 (1998)
M. Fox, Quantum Optics—An introduction (Oxford University Press, Oxford, 2006)
H.P. Yuen, Phys. Lett. A 56, 105–106 (1976)
L. Mandel, Opt. Lett. 4, 205–207 (1979)
R.J. Glauber, Phys. Rev. Lett. 10, 84–86 (1963)
E.C.G. Sudarshan, Phys. Rev. Lett. 10, 277–279 (1963)
C.C. Gerry, P.L. Knight, Am. J. Phys. 65, 964–974 (1997)
C. Gerry, P. Knight, Introductory Quantum Optics (Cambridge University Press, Cambridge, 2005)
L. Mandel, Phys. Rev. Lett. 49, 136–138 (1982)
Y. Aharonov, L. Susskind, Phys. Rev. 155, 1428–1431 (1967)
N. Gisin, Phys. Lett. A 154, 201–202 (1991)
T.M. Duc, J. Noh, Opt. Commun. 281, 2842–2848 (2008)
S. Dey, V. Hussin, Phys. Rev. A 93, 053824 (2016)
F. Li, X. Li, D.L. Lin, T.F. George, Phys. Rev. A 45, 3133–3138 (1992)
S.L. Braunstein, A. Mann, M. Revzen, Phys. Rev. Lett. 68, 3259–3261 (1992)
Author information
Authors and Affiliations
Corresponding author
Appendix A: q-exponential functions and q-integral representations of the q-factorial
Appendix A: q-exponential functions and q-integral representations of the q-factorial
For a fixed parameter q, the two different generalizations of exponential function are defined as [42]
where \({(a;q)_n:=(1-a)(1-aq)(1-aq^2)\cdots (1-aq^{n-1})}\). The convergence regions of the q-exponential functions for \(0<q<1\) are \(|x|<\infty \) and \(|x|<1\), respectively. The relation \({e_q(x)}{E_q(-x)}=1\) and the classical limits \(\lim _{q\rightarrow 1} {e_q((1-q)x)}=exp(x)\) and \(\lim _{q\rightarrow 1}{E_q((1-q)x)}=exp(x)\) are readily derived from (A1a) and (A1b). Furthermore, in the case \(|q|<1\), there exists an infinite product expansion as follows [46]
Let us assume that f(x) and g(x) are two arbitrary and continuous functions on the real line. The symmetric and asymmetric q-derivatives \(\widetilde{D}_{q,x}\) and \(D_{q,x}\) are defined as [42]
with the following q-analogues for the Leibniz rule:
Being the inverse operations of the q-derivatives \(\widetilde{D}_{q,x}\) and \({D_{q,x}}\), the q-integrals on the intervals \([0,\infty )\) and [0, c] with c as a positive real number are defined as [41, 46]
For any nonzero complex number n, a q-number as \([n]_q:=\frac{1-q^n}{1-q}\) is associated. Also, the q-factorial is defined as \([0]_q!=1\) and \([n]_q!:=[1]_q [2]_q \cdots [n]_q\) for n as a positive integer number. For \(0<q<1\), the following infinite and finite integral representations are obtained by the above definitions for the q- and \(q^2\)-factorials, respectively [40, 41, 46, 47]
We call the attention of the reader to an important issue: quantum number introduced in [46] is symmetric, and to obtain integral relation (A6a), one should write it in terms of the asymmetric quantum number used in this article. Both of the q-integrals convert to the infinite integral representation of the ordinary factorial as \(q\rightarrow 1\).
Rights and permissions
About this article
Cite this article
Fakhri, H., Mousavi-Gharalari, S.E. Nonclassical properties of two families of q-coherent states in the Fock representation space of q-oscillator algebra. Eur. Phys. J. Plus 135, 253 (2020). https://doi.org/10.1140/epjp/s13360-020-00265-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-020-00265-3