Skip to main content
SpringerLink
Log in

Influence of prestress and periodic corrugated boundary surfaces on Rayleigh waves in an orthotropic medium over a transversely isotropic dissipative semi-infinite substrate

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract.

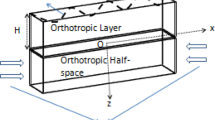
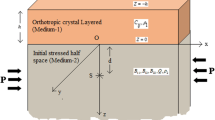
The paper environs the study of Rayleigh-type surface waves in an orthotropic crustal layer over a transversely isotropic dissipative semi-infinite medium under the effect of prestress and corrugated boundary surfaces. Separate displacement components for both media have been derived in order to characterize the dynamics of individual materials. Suitable boundary conditions have been employed upon the surface wave solutions of the elasto-dynamical equations that are taken into consideration in the light of corrugated boundary surfaces. From the real part of the sixth-order complex determinantal expression, we obtain the frequency equation for Rayleigh waves concerning the proposed earth model. Possible special cases have been envisaged and they fairly comply with the corresponding results for classical cases. Numerical computations have been performed in order to graphically demonstrate the role of the thickness of layer, prestress, corrugation parameters and dissipation on Rayleigh wave velocity. The study may be regarded as important due to its possible applications in delay line services and investigating deformation characteristics of solids as well as typical rock formations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. L. Rayleigh, Proc. London Math. Soc. 17, 4 (1885)

    Article  MathSciNet  Google Scholar 

  2. T.J. Bromwich, Proc. London Math. Soc. 30, 98 (1898)

    Article  Google Scholar 

  3. A.M. Abd-Alla, Appl. Math. Comput. 99, 61 (1999)

    MathSciNet  Google Scholar 

  4. A.M. Abd-Alla, S.M. Abo-Dahab, H.A.H. Hammad, Appl. Math. Model. 35, 2981 (2011)

    Article  MathSciNet  Google Scholar 

  5. K. Liu, Y. Liu, J. Sound Vib. 271, 1 (2004)

    Article  ADS  Google Scholar 

  6. P.C. Vinh, V.T.N. Anh, N.T.K. Linh, Waves Random Complex Media 26, 176 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  7. P.C. Vinh, V.T.N. Anh, Meccanica (2016) DOI:10.1007/s11012-016-0464-5

  8. P.C. Vinh, R.W. Ogden, Meccanica 40, 147 (2005)

    Article  MathSciNet  Google Scholar 

  9. S.K. Vishwakarma, S. Gupta, Arch. Civil Mech. Eng. 14, 181 (2014)

    Article  Google Scholar 

  10. S. Kostić, N. Vasović, M. Perc, M. Toljić, D. Nikolić, Physica A 392, 4134 (2013)

    Article  ADS  Google Scholar 

  11. S. Kostić, I. Franović, M. Perc, N. Vasović, K. Todorović, Sci. Rep. 4, 5401 (2014)

    ADS  Google Scholar 

  12. V.T. Buchwald, Q. J. Mech. Appl. Math. XIV, 293 (1961)

    Article  Google Scholar 

  13. B. Singh, J. Solid Mech. 5, 270 (2013)

    Google Scholar 

  14. B. Singh, Arc. Appl. Mech. 77, 253 (2007)

    Article  ADS  Google Scholar 

  15. J.N. Sharma, M. Pal, D. Chand, J. Sound Vib. 284, 227 (2005)

    Article  ADS  Google Scholar 

  16. A. Bucur, Acta Mech. 227, 1199 (2016)

    Article  MathSciNet  Google Scholar 

  17. S. Chiriţă, J. Elasticity 110, 185 (2013)

    Article  Google Scholar 

  18. B. Singh, R. Sindhu, J. Singh, Eng. Solid Mech. 4, 11 (2016)

    Article  Google Scholar 

  19. S. Shekhar, I.A. Parvez, Appl. Math. 4, 107 (2013)

    Article  Google Scholar 

  20. P.V. Krauzin, D.S. Goldobin, Eur. Phys. J. Plus 129, 221 (2014)

    Article  Google Scholar 

  21. K. Tanuma, C.S. Man, Y. Chen, Int. J. Eng. Sci. 92, 63 (2015)

    Article  Google Scholar 

  22. E.V. Glushkov, N.V. Glushkova, S.I. Fomenko, Acoust. Phys. 57, 230 (2011)

    Article  ADS  Google Scholar 

  23. M.A. Hayes, R.S. Rivlin, Arch. Ration. Mech. Anal. 8, 358 (1961)

    Article  Google Scholar 

  24. M. Destrade, N.H. Scott, Wave Motion 40, 347 (2004)

    Article  MathSciNet  Google Scholar 

  25. M. Destrade, M. Ottenio, A.V. Pichugin, G.A. Rogerson, Int. J. Eng. Sci. 43, 1092 (2005)

    Article  Google Scholar 

  26. R.T. Edmondson, Y.B. Fu, Int. J. Non-Linear Mech. 44, 530 (2009)

    Article  ADS  Google Scholar 

  27. P.C. Vinh, N.T.K. Linh, Meccanica 48, 2051 (2013)

    Article  MathSciNet  Google Scholar 

  28. S. Kostić, M. Perc, N. Vasović, S. Trajković, PLoS ONE 8, e82056 (2013)

    Article  ADS  Google Scholar 

  29. J.T. Kuo, J.E. Nape, Bull. Seismol. Soc. Am. 52, 807 (1962)

    Google Scholar 

  30. S.S. Singh, J. Vib. Control 17, 789 (2010)

    Article  Google Scholar 

  31. S.K. Vishwakarma, R. Xu, Appl. Math. Model. 40, 8647 (2016)

    Article  MathSciNet  Google Scholar 

  32. T. Kaur, S.K. Sharma, A.K. Singh, Meccanica 51, 2449 (2016)

    Article  MathSciNet  Google Scholar 

  33. P. Kumari, C. Modi, V.K. Sharma, Eur. Phys. J. Plus 131, 263 (2016)

    Article  Google Scholar 

  34. L. Li, P.J. Wei, X. Guo, Appl. Math. Model. 40, 8326 (2016)

    Article  MathSciNet  Google Scholar 

  35. S. Asano, Bull. Seismol. Soc. Am. 56, 201 (1966)

    Google Scholar 

  36. M.A. Biot, Mechanics of Incremental Deformations (Wiley, New York, 1965)

  37. Y.C. Fung, Foundation of Solid Mechanics (Prentice Hall of India, New Delhi, 1965)

  38. D. Gubbins, Seismology and Plate Tectonics (Cambridge University Press, Cambridge, 1990)

Download references

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Indian Institute of Technology (Indian School of Mines), Dhanbad - 826004, Jharkhand, India

    Shishir Gupta & Mostaid Ahmed

Authors
  1. Shishir Gupta
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mostaid Ahmed
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shishir Gupta.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gupta, S., Ahmed, M. Influence of prestress and periodic corrugated boundary surfaces on Rayleigh waves in an orthotropic medium over a transversely isotropic dissipative semi-infinite substrate. Eur. Phys. J. Plus 132, 8 (2017). https://doi.org/10.1140/epjp/i2017-11282-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/i2017-11282-6

Search

Navigation