Skip to main content
SpringerLink
Log in

Quasi-periodic wave solutions with asymptotic analysis to the Saweda-Kotera-Kadomtsev-Petviashvili equation

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

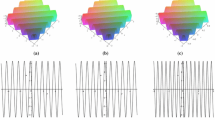
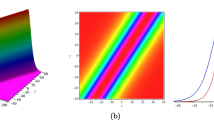
In this paper, the (2+1)-dimensional Saweda-Kotera-Kadomtsev-Petviashvili (SK-KP) equation is investigated, which can be used to describe certain situations from the fluid mechanics, ocean dynamics and plasma physics. With the aid of generalized Bell’s polynomials, the Hirota’s bilinear equation and N-soliton solution are explicitly constructed to the SK-KP equation, respectively. Based on the Riemann theta function, a direct and lucid way is presented to explicitly construct quasi-periodic wave solutions for the SK-KP equation. The two-periodic waves admit two independent spatial periods in two independent horizontal directions, which are a direct generalization of one-periodic waves. Finally, the relationships between soliton solutions and periodic wave solutions are strictly established, which implies the asymptotic behaviors of the periodic waves under a limited procedure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. G.W. Bluman, S. Kumei, Symmetries and Differential Equations (Springer-Verlag, New York, 1989).

  2. P.J. Olver, Applications of Lie Groups to Differential Equations, 2nd edition (Springer, New York, 1993).

  3. N.H. Ibragimov (Editor), CRC Handbook of Lie Group Analysis of Differential Equations, Vol. 1 (CRC Press, Boca Raton, 1994).

  4. V.B. Matveev, M.A. Salle, Darboux Transformation and Solitons (Springer, 1991).

  5. M.J. Ablowitz, P.A. Clarkson, Solitons: Nonlinear Evolution Equations and Inverse Scattering (Cambridge University Press, 1991).

  6. J.J.C. Nimmo, Darboux Transformations from Reductions of the KP Hierarchy (World Scientific, Singapore, 1995).

  7. C. Rogers, W.K. Schisf, Bäcklund and Darboux Transformations, Geometry and Modern Applications in Soliton Theory, in Cambridge Texts in Applied Mathematics (Cambridge University Press, Cambridge, 2002).

  8. R. Hirota, Direct Methods in Soliton Theory (Springer, 2004).

  9. E.D. Belokolos, A.I. Bobenko, V.Z. Enol’skii, A.R. Its, V.B. Matveev, Algebro-Geometric Aproach to Non-Linear Integrable Equations (Springer, 1994).

  10. S.P. Novikov, S.V. Manakov, L.P. Pitaevskii, V.E. Zakharov, Theory of Solitons: The Inverse Scattering Methods (Consultants Bureau, New York, 1984).

  11. P.D. Lax, Commun. Pure Appl. Math. 28, 141 (1975).

    Article  MathSciNet  MATH  Google Scholar 

  12. H.P. Mckean, P. Moerbeke, Invent Math. 30, 217 (1975).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. F. Gesztesy, H. Holden, Soliton Equations and Their Algebro-Geometric Solutions (Cambridge University Press, 2003).

  14. F. Gesztesy, H. Holden, J. Michor, G. Teschl, Soliton Equations and Their Algebro-Geometric Solutions, Vol. II, $(1+1)$-Dimensional Discrete Models, in Cambridge Studies in Advanced Mathematics, Vol. 114 (Cambridge University Press, Cambridge, 2008).

  15. Z.J. Qiao, Commun. Math. Phys. 239, 309 (2003).

    Article  ADS  MATH  Google Scholar 

  16. E.G. Amosenok, A.O. Smirnov, Lett. Math. Phys. 96, 157 (2011).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. C.W. Cao, Y.T. Wu, X.G. Geng, J. Math. Phys. 40, 3948 (1999).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. Y.C. Hon, E.G. Fan, J. Math. Phys. 46, 032701 (2005).

    Article  ADS  MathSciNet  Google Scholar 

  19. A. Nakamura, J. Phys. Soc. Jpn 48, 1365 (1980).

    Article  ADS  Google Scholar 

  20. X.B. Hu, C.X. Li, J.J.C. Nimmo, G.F. Yu, J. Phys. A 38, 195 (2005).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  21. E.G. Fan, Y.C. Hon, Phys. Rev. E 78, 036607 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  22. E.G. Fan, J. Phys. A 42, 095206 (2009).

    Article  ADS  MathSciNet  Google Scholar 

  23. E.G. Fan, Y.C. Hon, Rep. Math. Phys. 66, 355 (2010).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. W.X. Ma, R. Zhou, L. Gao, Mod. Phys. Lett. A 24, 1677 (2009).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  25. W.X. Ma, Rep. Math. Phys. 72, 41 (2013).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  26. K.W. Chow, J. Math. Phys. 36, 4125 (1995).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  27. A.M. Wazwaz, Appl. Math. Comput. 149, 103 (2004).

    Article  MathSciNet  MATH  Google Scholar 

  28. A.M. Wazwaz, Partial Differential Equations: Methods and Applications (Balkema Publishers, The Netherlands, 2002).

  29. S.F. Tian, P.L. Ma, Commun. Theor. Phys. 62, 245 (2014).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  30. S.Y. Lou, Z. Naturforsch. 53a, 251 (1998).

    ADS  Google Scholar 

  31. B. Tian, Y.T. Gao, Eur. Phys. J. B 30, 97 (1995).

    MathSciNet  MATH  Google Scholar 

  32. M. Eslami, M. Mirzazadeh, Eur. Phys. J. Plus 128, 140 (2013).

    Article  Google Scholar 

  33. M. Eslami, A. Neirameh, Eur. Phys. J. Plus 129, 54 (2014).

    Article  Google Scholar 

  34. Y. Chen, Z.Y. Yan, H.Q. Zhang, Theor. Math. Phys. 132, 970 (2002).

    Article  MathSciNet  MATH  Google Scholar 

  35. Z.Y. Yan, Appl. Math. Comput. 168, 1065 (2005).

    Article  MathSciNet  MATH  Google Scholar 

  36. E. Tala-Tebue, D.C. Tsobgni-Fozap, A. Kenfack-Jiotsa, T.C. Kofane, Eur. Phys. J. Plus 129, 136 (2014).

    Article  Google Scholar 

  37. Y. Amadou, G. Betchewe, Douvagai, M. Justin, S.Y. Doka, K.T. Crepin, Eur. Phys. J. Plus 130, 13 (2015).

    Article  Google Scholar 

  38. S.F. Tian, H.Q. Zhang, J. Math. Anal. Appl. 371, 585 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  39. S.F. Tian, H.Q. Zhang, J. Phys. A: Math. Theor. 45, 055203 (2012).

    Article  ADS  MathSciNet  Google Scholar 

  40. S.F. Tian, H.Q. Zhang, Commun. Nonlinear Sci. Numer. Simulat. 16, 173 (2011).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  41. S.F. Tian, H.Q. Zhang, Chaos Solitons Fractals 47, 27 (2013).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  42. S.F. Tian, H.Q. Zhang, Stud. Appl. Math. 132, 212 (2014).

    Article  MathSciNet  MATH  Google Scholar 

  43. E.T. Bell, Ann. Math. 35, 258 (1834).

    Article  Google Scholar 

  44. F. Lambert, I. Loris, J. Springael, Inverse Probl. 17, 1067 (2001).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  45. C. Gilson, F. Lambert, J. Nimmo, R. Willox, Proc. R. Soc. London A 452, 223 (1996).

    Article  ADS  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, China University of Mining and Technology, 221116, Xuzhou, People’s Republic of China

    Mei-Juan Xu, Shou-Fu Tian, Jian-Min Tu, Pan-Li Ma & Tian-Tian Zhang

  2. Center of Nonlinear Equations, China University of Mining and Technology, 221116, Xuzhou, People’s Republic of China

    Mei-Juan Xu, Shou-Fu Tian, Jian-Min Tu, Pan-Li Ma & Tian-Tian Zhang

Authors
  1. Mei-Juan Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shou-Fu Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jian-Min Tu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Pan-Li Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Tian-Tian Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Shou-Fu Tian or Tian-Tian Zhang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, MJ., Tian, SF., Tu, JM. et al. Quasi-periodic wave solutions with asymptotic analysis to the Saweda-Kotera-Kadomtsev-Petviashvili equation. Eur. Phys. J. Plus 130, 174 (2015). https://doi.org/10.1140/epjp/i2015-15174-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/i2015-15174-5

Search

Navigation