Skip to main content
SpringerLink
Log in

QCD ghost reconstruction of f(T) gravity in flat FRW universe

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract.

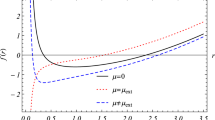
The present paper reports a reconstruction scheme for f(T) gravity based on QCD ghost dark energy. Two models of f(T) have been generated and the pressure and density contributions due to torsion have been reconstructed. Two realistic models have been obtained and the effective equations of state have been studied. Also, the squared speed of sound has been studied to examine the stability of the models.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. A.G. Riess et al., Astron. J. 116, 1009 (1998)

    Article  ADS  Google Scholar 

  2. S. Perlmutter et al., Astrophys. J. 517, 565 (1999)

    Article  ADS  Google Scholar 

  3. P.J.E. Peebles, B. Ratra, Rev. Mod. Phys. 75, 559 (2003)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  4. E.J. Copeland, M. Sami, S. Tsujikawa, Int. J. Mod. Phys. D 15, 1753 (2006)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  5. T. Padmanabhan, Curr. Sci. 88, 1057 (2005)

    ADS  Google Scholar 

  6. T. Padmanabhan, Gen. Relativ. Gravit. 40, 529 (2008)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  7. L. Amendola, S. Tsujikawa, Dark Energy: Theory and Observations (Cambridge University Press, 2010)

  8. K. Bamba, S. Capozziello, S.I. Nojiri, S.D. Odintsov, Astrophys. Space Sci. 342, 155 (2012)

    Article  ADS  Google Scholar 

  9. J. Yoo, Y. Watanabe, Int. J. Mod. Phys. D 21, 1230002 (2012)

    Article  ADS  Google Scholar 

  10. R.-G. Cai, Z.-L. Tuo, H.-B. Zhang, Q. Su, Phys. Rev. D 84, 123501 (2011)

    Article  ADS  Google Scholar 

  11. A. Pradhan, Ind. J. Phys. 88, 215 (2014)

    Article  Google Scholar 

  12. M. Sharif, A. Jawad, Ind. J Phys. 88, 529 (2014)

    Article  Google Scholar 

  13. F.R. Urban, A.R. Zhitnitsky, Phys. Lett. B 688, 9 (2010)

    Article  ADS  Google Scholar 

  14. R. Garcia-Salcedo, T. Gonzalez, I. Quiros, M. Thompson-Montero, Phys. Rev. D 88, 043008 (2013)

    Article  ADS  Google Scholar 

  15. S. Nojiri, S.D. Odintsov, Int. J. Geom. Methods Mod. Phys. 4, 115 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  16. S. Nojiri, S.D. Odintsov, M. Sasaki, Phys. Rev. D 71, 123509 (2005)

    Article  ADS  Google Scholar 

  17. M. Jamil, D. Momeni, R. Myrzakulov, Eur. Phys. J. C 72, 2137 (2012)

    Article  ADS  Google Scholar 

  18. M. Jamil, D. Momeni, R. Myrzakulov, Eur. Phys. J. C 72, 1959 (2012)

    Article  ADS  Google Scholar 

  19. K. Bamba, M. Jamil, D. Momeni, R. Myrzakulov, Astrophys. Space Sci. 344, 259 (2013)

    Article  ADS  MATH  Google Scholar 

  20. M. Jamil, D. Momeni, R. Myrzakulov, Eur. Phys. J. C 72, 2122 (2012)

    Article  ADS  Google Scholar 

  21. M. Jamil, D. Momeni, R. Myrzakulov, Eur. Phys. J. C 72, 2075 (2012)

    Article  ADS  Google Scholar 

  22. M. Jamil, D. Momeni, R. Myrzakulov, Eur. Phys. J. C 72, 2137 (2012)

    Article  ADS  Google Scholar 

  23. M. Jamil, K. Yesmakhanova, D. Momeni, R. Myrzakulov, Cent. Eur. J. Phys. 10, 1065 (2012)

    Article  Google Scholar 

  24. D. Momeni, M.R. Setare, Mod. Phys. Lett. A 26, 2889 (2011)

    Article  ADS  MATH  Google Scholar 

  25. M.J.S. Houndjo, D. Momeni, R. Myrzakulov, Int. J. Mod. Phys. D 21, 1250093 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  26. M. Jamil, D. Momeni, R. Myrzakulov, Gen. Relativ. Gravit. 45, 263 (2013)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  27. M. Jamil, D. Momeni, R. Myrzakulov, P. Rudra, J. Phys. Soc. Jpn. 81, 114004 (2012)

    Article  ADS  Google Scholar 

  28. M. Jamil, D. Momeni, R. Myrzakulov, Eur. Phys. J. C 72, 2267 (2012)

    Google Scholar 

  29. M.E. Rodrigues, M.J.S. Houndjo, D. Momeni, R. Myrzakulov, Can. J. Phys. 92, 173 (2014)

    Article  Google Scholar 

  30. M.U. Farooq, M. Jamil, D. Momeni, R. Myrzakulov, Can. J. Phys. 91, 703 (2013)

    Article  ADS  Google Scholar 

  31. M.E. Rodrigues, M.J.S. Houndjo, J. Tossa, D. Momeni, R. Myrzakulov, JCAP 11, 024 (2013)

    Article  ADS  Google Scholar 

  32. M. Jamil, K. Yesmakhanova, D. Momeni, R. Myrzakulov, Cent. Eur. J. Phys. 10, 1065 (2012)

    Article  Google Scholar 

  33. R. Myrzakulov, Eur. Phys. J. C 71, 1752 (2011)

    Article  ADS  Google Scholar 

  34. M.R. Setare, Int. J. Mod. Phys. D 12, 2219 (2008)

    Article  ADS  MathSciNet  Google Scholar 

  35. M.R. Setare, Phys. Lett. B 644, 99 (2007)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  36. M.R. Setare, Phys. Lett. B 648, 329 (2007)

    Article  ADS  MATH  Google Scholar 

  37. M.R. Setare, Phys. Lett. B 653, 116 (2007)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  38. M.R. Setare, Phys. Lett. B 654, 1 (2007)

    Article  ADS  Google Scholar 

  39. M.R. Setare, Int. J. Mod. Phys. D 18, 419 (2009)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  40. S. Chattopadhyay, A. Pasqua, Ind. J. Phys. 87, 1053 (2013)

    Article  Google Scholar 

  41. K. Bamba, R. Myrzakulov, S. Nojiri, S.D. Odintsov, Phys. Rev. D 85, 104036 (2012)

    Article  ADS  Google Scholar 

  42. M.H. Daouda, M.E. Rodrigues, M.J.S. Houndjo, Eur. Phys. J. C 72, 1893 (2012)

    Article  ADS  Google Scholar 

  43. S. Chattopadhyay, A. Pasqua, Astrophys. Space Sci. 344, 269 (2013)

    Article  ADS  Google Scholar 

  44. M. R. Setare, Int. J. Mod. Phys. D 17, 2219 (2008)

    Article  ADS  Google Scholar 

  45. A. Rozas-Fernandez, Phys. Lett. B 709, 313 (2012)

    Article  ADS  Google Scholar 

  46. S. Nojiri, S.D. Odintsov, Phys. Rev. D 72, 023003 (2005)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Application, Pailan College of Management and Technology, Bengal Pailan Park, 700 104, Kolkata, India

    Surajit Chattopadhyay

Authors
  1. Surajit Chattopadhyay
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Surajit Chattopadhyay.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chattopadhyay, S. QCD ghost reconstruction of f(T) gravity in flat FRW universe. Eur. Phys. J. Plus 129, 82 (2014). https://doi.org/10.1140/epjp/i2014-14082-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/i2014-14082-6

Keywords

Search

Navigation