Abstract.
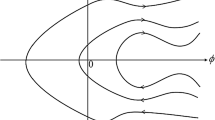
We investigate the occurrence of shear banding in nematogenic fluids under planar Couette flow, based on mesoscopic dynamical equations for the orientational order parameter and the shear stress. We focus on parameter values where the sheared homogeneous system exhibits regular oscillatory orientational dynamics, whereas the equilibrium system is either isotropic (albeit close to the isotropic-nematic transition) or deep in its nematic phase. The numerical calculations are restricted to spatial variations in shear gradient direction. We find several new types of shear-banded states characterized by regions with regular oscillatory orientational dynamics. In all cases shear banding is accompanied by a non-monotonicity of the flow curve of the homogeneous system; however, only in the case of the initially isotropic system this curve has the typical S-like shape. We also analyze the influence of different orientational boundary conditions and of the spatial correlation length.
Graphical abstract

Article PDF
Similar content being viewed by others
References
S.M. Fielding, Soft Matter 3, 1262 (2007)
J.K. Dhont, W.J. Briels, Rheol. Acta 47, 257 (2008)
M. Lopez-Gonzalez, W. Holmes, P. Callaghan, P. Photinos, Phys. Rev. Lett. 93, 268302 (2004)
J. Decruppe, R. Cressely, R. Makhloufi, E. Cappelaere, Colloid Polym. Sci. 273, 346 (1995)
L. Chen, C. Zukoski, B. Ackerson, H. Hanley, G. Straty, J. Barker, C. Glinka, Phys. Rev. Lett. 69, 688 (1992)
V. Chikkadi, D. Miedema, M. Dang, B. Nienhuis, P. Schall, Phys. Rev. Lett. 113, 208301 (2014)
J. Goveas, P. Olmsted, Eur. Phys. J. E 6, 79 (2001)
N. Spenley, X. Yuan, M. Cates, J. Phys. II 6, 551 (1996)
P. Olmsted, O. Radulescu, C.Y. Lu, J. Rheol. 44, 257 (2000)
Y.G. Tao, W. den Otter, W. Briels, Phys. Rev. Lett. 95, 237802 (2005)
M. Ripoll, P. Holmqvist, R.G. Winkler, G. Gompper, J.K.G. Dhont, M.P. Lettinga, Phys. Rev. Lett. 101, 168302 (2008)
P.D. Olmsted, C.Y.D. Lu, Phys. Rev. E 60, 4397 (1999)
R. Larson, Macromolecules 23, 3983 (1990)
O. Hess, S. Hess, Phys. A 207, 517 (1994)
G. Rienäcker, M. Kröger, S. Hess, Phys. Rev. E 66, 040702 (2002)
E.V. Alonso, A.A. Wheeler, T.J. Sluckin, Proc. R. Soc. A 459, 195 (2003)
P.D. Olmsted, P. Goldbart, Phys. Rev. A 41, 4578 (1990)
P.D. Olmsted, Ph.D. thesis, University of Illinois, Urbana-Champaign (1991)
P.D. Olmsted, P.M. Goldbart, Phys. Rev. A 46, 4966 (1992)
D.C. Roux, J.F. Berret, G. Porte, E. Peuvrel-Disdier, P. Lindner, Macromolecules 28, 1681 (1995)
M. Lettinga, Z. Dogic, H. Wang, J. Vermant, Langmuir 21, 8048 (2005)
B. Chakrabarti, M. Das, C. Dasgupta, S. Ramaswamy, A. Sood, Phys. Rev. Lett. 92, 055501 (2004)
M.G. Forest, R. Zhou, Q. Wang, Multiscale Model. Simul. 6, 858 (2007)
D. Chakraborty, C. Dasgupta, A.K. Sood, Phys. Rev. E 82, 065301 (2010)
M. Das, B. Chakrabarti, C. Dasgupta, S. Ramaswamy, A.K. Sood, Phys. Rev. E 71, 021707 (2005)
D.A. Strehober, H. Engel, S.H.L. Klapp, Phys. Rev. E 88, 012505 (2013)
H. Zhou, M.G. Forest, Q. Wang, Technical report, DTIC Document (2007)
J.K.G. Dhont, M.P. Lettinga, Z. Dogic, T.A.J. Lenstra, H. Wang, S. Rathgeber, P. Carletto, L. Willner, H. Frielinghaus, P. Lindner, Farad. Discuss. 123, 157 (2003)
P.G. de Gennes, The physics of liquid crystals (Clarendon Press, Oxford, 1993)
S. Hess, Tensors for Physics (Springer Intl., Switzerland, 2015)
R. Lugo-Frias, S.H.L. Klapp, J. Phys.: Condens. Matter (2016)
C. Oseen, Trans. Faraday Soc. 29, 883 (1933)
F.C. Frank, Discuss. Faraday Soc. 25, 19 (1958)
Y. Singh, K. Singh, Phys. Rev. A 33, 3481 (1985)
K. Singh, Y. Singh, Phys. Rev. A 34, 548 (1986)
K. Singh, Y. Singh, Phys. Rev. A 35, 3535 (1987)
G. Taylor, Proc. R. Soc. London. Ser. A, Math. Phys. Character 103, 58 (1923)
S. Hess, Z. Naturforsch. 30a, 728 (1975)
I. Pardowitz, S. Hess, Phys. A 100, 540 (1980)
S. Heidenreich, Ph.D. thesis, TU Berlin (2009)
C. Pereira-Borgmeyer, S. Hess, J. Non-Equilib. Thermodyn. 20, 359 (1995)
S. Hess, Z. Naturforsch. 31a, 1034 (1976)
S.R. De Groot, P. Mazur, Non-equilibrium thermodynamics (Dover, 1983)
R. Ganapathy, S. Majumdar, A.K. Sood, Phys. Rev. E 78, 021504 (2008)
S. Hess, M. Kröger, J. Phys.: Condens. Matter 16, S3835 (2004)
S. Hess, M. Kröger, in Computer Simulations of Liquid Crystals and Polymers (Springer Verlag, 2005) pp. 295--333
P. Kaiser, W. Wiese, S. Hess, J. Non-Equilib. Thermodyn. 17, 153 (1992)
W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery, Numerical Recipes in C, Vol. 2 (Cambridge University press, Cambridge, 1996)
G. Rienäcker, Orientational dynamics of nematic liquid crystals in a shear flow (Shaker Verlag, Aachen, 2000)
P. Sheng, Phys. Rev. A 26, 1610 (1982)
B. Jerome, Rep. Prog. Phys. 54, 391 (1991)
M. Ruths, S. Steinberg, J.N. Israelachvili, Langmuir 12, 6637 (1996)
O. Manyuhina, A.M. Cazabat, M.B. Amar, EPL 92, 16005 (2010)
O. Radulescu, P. Olmsted, J. Non-Newton. Fluid 91, 143 (2000)
J. Adams, S. Fielding, P. Olmsted, J. Non-Newton. Fluid Mech. 151, 101 (2008)
C.Y.D. Lu, P.D. Olmsted, R. Ball, Phys. Rev. Lett. 84, 642 (2000)
P.D. Olmsted, Rheol. Acta 47, 283 (2008)
K.R. Purdy, Z. Dogic, S. Fraden, A. Rühm, L. Lurio, S.G.J. Mochrie, Phys. Rev. E 67, 031708 (2003)
Z. Dogic, S. Fraden, Langmuir 16, 7820 (2000)
M. Fardin, T. Ober, V. Grenard, T. Divoux, S. Manneville, G. McKinley, S. Lerouge, Soft Matter 8, 10072 (2012)
N. Herdegen, S. Hess, Physica A 115, 281 (1982)
W. Loose, S. Hess, Phys. Rev. A 37, 2099 (1988)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lugo-Frias, R., Reinken, H. & Klapp, S.H.L. Shear banding in nematogenic fluids with oscillating orientational dynamics. Eur. Phys. J. E 39, 88 (2016). https://doi.org/10.1140/epje/i2016-16088-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epje/i2016-16088-3