1 Introduction


Thin film coatings are utilized in a wide range of applications in order to provide surface properties that the solid raw material cannot provide. These properties include among others wear resistance, easy-to-clean surfaces and barrier properties against heat or diffusion. Plasmas, and particularly atmospheric pressure plasma jets, have proven to be a very suitable tool for providing tailored coatings [1,2,3,4].

An example for a typical atmospheric pressure plasma jet, which has been proven suitable for homogeneous coatings, is the filamentary non-thermal atmospheric pressure plasma jet described by Schäfer et al. [5]. This cylindrical filamentary plasma jet exhibits different modes depending on the discharge parameters. Of particular interest are the stationary mode and the locked mode. In the stationary mode the filaments are static and do not move. Additionally, if more than one filament is present, the filaments are distributed symmetrically around the jet axis. In the locked mode, on the other hand, the filaments move around the jet axis, while still maintaining a symmetric distribution. This plasma jet was investigated in different studies and the advantages of the locked mode for the homogeneity of coatings were clearly shown [6,7,8]. The basics of both modes were investigated in detail in [9]. Recently, the locked mode was investigated in a paper of Schäfer et al. [10] where they present the same relation between the inclination of the rotating filaments and the speed of the gas flow through the plasma jet as shown in [9].

Besides a modification of the model for describing the behavior of the filaments, we present here experimentally obtained results for the validation of the model predictions regarding filament motion, for the influence of power and gas flow as well as for the transition between both modes. The dynamics of the plasma jet were examined with high-speed cameras. Furthermore, laser schlieren deflectometry was applied to measure the rotation frequency of the filaments in the locked mode for different discharge parameters. Laser schlieren deflectometry uses variations of the refractive index in the effluent of the plasma jet due to temperature variations induced by the filaments (see [11]).

2 Experimental setup

2.1 Atmospheric pressure plasma jet

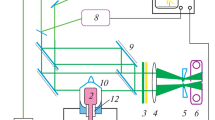
The plasma jet used and investigated in this work is shown in Fig. 1. It consists of a cylindrical glass body, inner diameter 4 mm, surrounded by two copper electrodes with a distance of 4.8 mm and an inner ceramic capillary, outer diameter 1.8 mm, for additional precursor gases, e.g., for coating purposes. The upstream electrode is rf-powered (27.12 MHz) and connected to the power supply via a matching network. The downstream electrode is grounded. Both electrodes are water-cooled. The working gas is argon. Ten of these jets are operated simultaneously next to each other with one power supply for large area treatment.

Fig. 1
figure 1

Schematic of the atmospheric pressure plasma jet. The laser for the laser schlieren deflectrometry is shown passing through the effluent

Full size image

The results presented in this work are all obtained from just one plasma jet. The plasma jets have filamentary discharges with different modes. The filaments are either stationary (stationary mode) or rotate around the plasma jet axis (locked mode). If there is more than one filament, they are distributed symmetrically around the jet axis, independent on the mode. In this work, only the modes with three filaments were considered.

2.2 Laser schlieren deflectometry

The rotation frequency of the plasma jet is investigated by the laser schlieren deflectometry described in [11]. The discharges in form of the filaments raise the temperature in the discharge volume. The temperature variations and gradients between the species from the discharge volume and their surroundings persists in the effluent. This effect leads to differences in the refractive index. A laser pointed through the effluent (Fig. 1) will be deflected due to these differences. With the plasma jet in locked mode, this deflection is periodically changing. A photodiode placed in the center of the undisturbed laser measures the deflection due to intensity variations. The shown frequencies of the deflection correspond to the rotation frequencies of the filaments multiplied by the number of filaments.

2.3 High-speed camera

High-speed video analysis of the filament dynamics was carried out with a camera IDT Motion Pro Y4 from Imaging Solutions GmbH set to 1500 fps with an exposure time of 14 µs. The transition between modes was examined with a Panasonic lumix dmc-fz100 set to 200 fps.

3 Suggestion of a simple model for the modes of the plasma jet

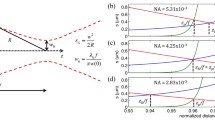
Firstly, we are assuming that the length of the filaments correlates to the input power. Correlations between the input power and the plasma volume have already been reported earlier [6, 12, 13]. Secondly, we are supposing that the attachment zone of the filament at the upstream electrode dominates the behavior of the filament. The latter assumption is supported by the fluid dynamics of plasma jets in general. The transport of plasma species and, therefore, the geometry of the plasma jet are dependent on the gas flow. Accordingly, the gas flow transports the species of the plasma filament downstream and, thereby, the energetically favorable position for the filament is defined. We now consider an inclined filament with a constant length L as shown in Fig. 2 at time t1. The plasma species move downstream together with the gas flow following the conservation of momentum (time t2). The new location of these species is the energetically favorable spot for the filament. Keeping a constant length will result in the upstream attachment point and by that the whole filament is moving sideways (time t3).

Fig. 2
figure 2

Illustration of the filament propagation between the electrodes. At time t1 the filament is located between the electrodes. The gas flow moves the plasma species downstream (time t2) and the filament moves accordingly (t3) but stays between the electrodes resulting in a sideways motion of the filament

Full size image

The velocity of the filament vF can be calculated using the velocity of the gas vgas, the distance d of the electrodes and the length of the filament L (see Fig. 3):

$$ v_{F} = v_{{{\text{gas}}}} \sqrt {\frac{{L^{2} }}{{d^{2} }} - 1} $$
Fig. 3
figure 3

Illustration for the relation between the filament movement vF, the length of the filament L and its inclination α, the distance of the electrodes d and the velocity of the gas vgas

Full size image

Consequently, the rotation frequency f is:

$$ f = \frac{{v_{{{\text{gas}}}} }}{2\pi R}\sqrt {\frac{{L^{2} }}{{d^{2} }} - 1} $$

R denotes the radius of the filament circulation, i.e., inner radius of the glass capillary in maximum.

This explanation has different consequences for the description of the plasma jet and its modes. Assuming an increasing filament length with increasing input power, starting at zero, the plasma will ignite at a certain power, sufficient for one filament with the length equal to the distance of the electrodes. This filament has no inclination and, therefore, does not move. The jet is in the stationary mode. Increasing the power further will lead to a longer filament with an inclination different from zero which will move according to the situation described above. The jet is in the locked mode. The transition from the stationary to the locked mode is described in more detail in the next section. Increasing the power even further will result in a longer filament with higher inclination and a faster rotation of the filament. At some point, the power is sufficiently high for filament length of twice the electrode distance. A second filament will form and the jet is in the stationary mode with two filaments. The process repeats itself with an increasing number of filaments for further increases of the input power.

The fundamental model was first proposed in [9]. Recently, Schäfer et al. presented the same relation connecting the rotation frequency to the gas flow and inclination of the filaments, though they start at the conservation of the temperature inside the filament [10]. However, their model starts with inclined filaments and, hence, does only explain the locked mode, whereas the model presented in this work may also explain the stationary mode and the transition between the modes. Experimentally, the succession of modes was described by Schäfer et al. [5].

4 Results and discussion

Now, the proposed model is based on the coupling of the dynamics of the plasma filaments to the gas flow. Hence, the motion of the plasma parallel to the jet axis should only depend on the gas flow and should be independent on the applied power. On the same time, an increase in the applied power should increase the frequency. For verification of the model high-speed camera investigations of the plasma jet were carried out with the camera IDT Motion Pro Y4 from Imaging Solutions GmbH. The plasma jet was operated in the locked mode with three filaments with a gas flow of 0.13 slm in the outer capillary. A sample frequency of 1500 fps was used. Figure 4 shows the filament progress for two different powers, 5.6 W and 6.6 W, with corresponding rotation frequencies of 45 Hz and 68 Hz, respectively. Despite the increase in the rotation frequency of around 50% the time ∆t between the top and the bottom part of the filament reaching the same point along the jet axis is the same.

Fig. 4
figure 4

High-speed camera images of rotating filaments at a 5.6 W and b 6.6 W. The camera was set to 1500 fps with an exposure time of 14 µs. Despite the different rotating frequencies of a 45 Hz and b 68 Hz a time difference for the filaments crossing the section shown is not discernable

Full size image

Additional analysis of the light intensities leads to the results shown in Table 1. The time difference is almost the same for all three frequencies. This shows that the plasma motion is dominated by the gas flow and independent on the applied power. Changes in the rotation frequency due to power changes are a consequence of the increased filament length and subsequent formation of additional filaments.

Table 1 Results of filament propagation investigations with the high-speed camera IDT Motion Pro Y4 from Imaging Solutions GmbH. The plasma jet was operated in the locked mode with three filaments with a gas flow of 0.13 slm in the outer and 0 slm in the inner capillary. The camera was set to 1500 fps with an exposure time of 14 µs
Full size table

The effects of the gas flow and the discharge power were investigated by laser schlieren deflectometry. During these experiments a drift of the frequency to lower numbers over time was noticed (see Fig. 5). The rotation frequency of the filaments slows down exponentially for constant power and gas flow. After about 1 h, the frequency is almost stable. Our hypothesis for this drift focusses on the matching network between the rf power supply and the plasma jet. The matching network heats up during the experiments. This changes the resonance frequency and the ratio of the power feed into the plasma also changes. With decreasing power the rotation frequency decreases as well.

Fig. 5
figure 5

Course of the frequency over time after starting the plasma jet and setting it to locked mode for three filaments. The frequency decreases exponentially for about 50 min. The measurements were done with an outer gas flow of 0.19 slm Ar, a power of 8 W and a gas flow of 0.05 slm Ar through the inner capillary

Full size image

The influence of the gas flow was investigated for a power of 7.7 W for the single jet. Because of the drift of the frequency discussed above, the jet heated up for about 100 min before the actual experiments. The results are shown in Fig. 6. The linear trend clearly confirms the expectation from the model.

Fig. 6
figure 6

Dependence of the filament frequency (three filaments) on the gas flow through the outer capillary. The trend is linear. The results were obtained with a power of 7.7 W and without a gas flow through the inner capillary after a warm up time of 100 min

Full size image

Repetitive measurements show no drift signifying that the gas flow is not influencing the drift notably. The great influence of the gas flow makes it an excellent parameter to adjust the rotation frequency to a desired value.

The influence of the gas flow was also investigated by Schäfer et al. [5]. Though the frequency also increased with increasing gas flow, the relation did not seem to be linear. However, just a few points were presented for different powers and there was no mention of a drift or the plasma source heating up before the measurements. Therefore, the drift could explain the slightly different results.

The second parameter influencing the rotation frequency is the applied power. A gas flow of 0.13 slm was used. The plasma jet was operated at 7.7 W for 130 min before the frequency was stable. Since different powers could influence the drift, the measurements were carried out with increasing powers and directly afterward repeated with decreasing powers. The results are presented in Fig. 7a. They show that the frequency increases with the power as already observed with the high-speed camera measurements. This, together with the high-speed camera measurements, supports the assumption that increasing powers lead to longer filaments and, therefore, higher filament inclinations. This is also supported by the findings of Schäfer et al. [10].

Fig. 7
figure 7

Dependence of the filament frequency (three filaments) on the applied power. The results exhibit a strong influence of the power. The results in (a) show a small hysteresis (0.13 slm outer gas flow, 0 slm inner gas flow, 130 min warm-up at 7.7 W). The results in (b) show no hysteresis at higher gas flow (0.16 slm outer gas flow, 0 slm inner gas flow, 65 min warm-up at 7.7 W). For both measurements the power was increased and after reaching the highest point decreased again

Full size image

The difference between the results in Fig. 7a from increasing and decreasing power grows during the experiments (towards smaller powers). This hysteresis indicates that there might be a stronger drift for higher powers, resulting in lower rotation frequencies going from higher to lower powers. However, further investigation with different parameters show this effect only sometimes, in particular, at low gas flow. The measurement series in Fig. 7b at higher gas flow shows no difference between the results for increasing and decreasing power. In conclusion, more investigations are necessary to explore the drift and possible influence of the plasma parameters. Furthermore, the power actually fed into the plasma is unknown, since there are different losses between the power supply and the plasma, e.g., the matching network. For a quantitative analysis of the correlation between input power and plasma frequency and filament length the determination of these losses is absolutely necessary.

Additional verification of the model can be achieved by a closer look at the transition from stationary mode to locked mode. High-speed camera image series of the transition are presented in Fig. 8. The plasma jet starts in stationary mode (first row). The length of the filaments L equals the distance d between the electrodes. Following the model, the filaments do not move, since the inclination to the jet axis is zero. With increasing power the plasma jet changes to the transition regime. First, the upstream attachment point of one of the filaments moves to the side causing a kink in the filament. This kink propagates through the filament until it moved completely to the side (second row). Afterward, the process repeats itself to the other side, restoring the symmetry. This demonstrates the increasing length of a filament with increasing power and the dependence of the filament on the upstream attachment point or rather the dependence of the downstream parts on those further upstream.

Fig. 8
figure 8

Image sequences of the transition between stationary and locked mode with three filaments. The gas flows through the capillary from top to bottom. The first row shows the stationary mode. The filaments do not move. In the second row, the right filament moves alternating to left and right. The movement starts at and is dominated by the point at the top electrode. The third row shows alternating movements of all filaments first to the right and then to the left. The last row finally shows the locked mode. All filaments move in one direction around the capillary. The images in one row have a time gap of 5 ms. The time between the rows is larger

Full size image

Further increase in power results in all filaments moving a step sideways or rotating shortly, turning around and coming back (third row). Finally, reaching the locked mode, the filaments rotate constantly along the electrodes (fourth row). The transition from locked mode to stationary mode by lowering the power follows the same steps in reversed order. This transition behavior is in good agreement with the proposed model.

5 Conclusion

A modified model for the different modes of the investigated filamentary atmospheric pressure plasma jet was proposed. The model describes both the stationary and the locked mode, in which the filaments rotate around the jet axis. Furthermore, the model can explain the transition between the modes. Experimental investigations with a high-speed camera and laser schlieren deflectometry were carried out to verify the model and its predictions. The results show clearly that the filament dynamics are dominated by the gas flow and increasing gas flow as well as power lead to rising rotation frequencies as predicted. The proposed model enhances the understanding of the physical nature of the locked mode and enables to better control the process. Future investigations need to focus on the power actually fed into the plasma and the correlation between this value and the plasma volume. Furthermore, the origin of the drift and potential influences need to be examined further.