Demonstrating quantum properties of triple photons generated by $\chi ^3$ processes

Abstract

Triple-photon generation (TPG) is based on a third-order nonlinear optical interaction, which is the most direct way to produce pure quantum three-photon states. These states can exhibit three-body quantum correlations, and their statistics cannot be reproduced by any Gaussian statistics of coherent sources or optical parametric twin-photon generator, making them potentially useful for quantum information processing tasks such as quantum state distillation, quantum error-correction and universal quantum computing. Furthermore, the generation of entangled photon pairs heralded by the detection of a third photon can be used in advanced quantum communication protocols. We made the first experimental demonstration of TPG in 2004 using a bi-stimulation scheme in a bulk KTP crystal, followed by the quantum theory. The new challenges are now to achieve a spontaneous TPG and the corresponding quantum experiments and protocols using oriented ridge KTP waveguides, which ensures both birefringence phase-matching and light confinement. The waveguides are cut by a precision dicing saw. We recently performed their characterization using third-harmonic generation measurements, which showed their good quality. A rate of about 5 triplets per second is expected when pumping a 5-cm-long waveguide with a 5-W 532 nm beam in the CW regime. Such a spontaneous TPG exhibits low rate of triple photons, which makes the certification of quantum features hard. In this article, we review our theoretical and experimental work on TPG and the associated quantum modeling. We also develop theoretical tools for the certification of quantum features of spontaneous triple-photon states.

Graphic abstract

1 Introduction

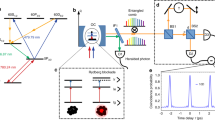
Twin photons have deeply influenced the history of nonlinear and quantum optics by their wide range of applications and the paradigmatic place they stand in generating new quantum states of light [1]. As regards triple-photon generation (TPG), the story is only starting. TPG is based on the third-order optical nonlinearity, i.e., the third-order electric susceptibility $\chi ^{(3)}$ [2, 3]: it is a process which can directly generate a 3-photon (3P) state. During TPG, three highly correlated photons at energies $\hbar \omega _1$, $\hbar \omega _2$ and $\hbar \omega _3$ are created in a nonlinear medium from the annihilation of a higher energy photon at $\hbar \omega _0$, with the energy conservation being fulfilled: $\hbar \omega _0 = \hbar \omega _1+\hbar \omega _2 + \hbar \omega _3$. Four configurations are possible regarding the level of stimulation of TPG: a stimulated TPG over three, two or one modes of the triplet that has to be generated, or the spontaneous TPG, where there is no stimulation at all. Figure 1 shows the three last cases. In the two stimulated cases, the generated photons come from the triplets as well as from the residual photons of the stimulation, as shown in Fig. 1a, b.

Fig. 1

The three schemes of generation of a 3-photon state at energies $\hbar \omega _1$, $\hbar \omega _2$ and $\hbar \omega _3$ in a third-order nonlinear medium pumped at $\hbar \omega _0$: a stimulation over two modes, at $\hbar \omega _2$ and $\hbar \omega _3$ for example; b stimulation over one mode, at $\hbar \omega _1$ for example; c no stimulation. The energy levels are described by continuous lines for the matter and a dashed line for the electromagnetic field

At the opposite, the spontaneous scheme shown in Fig. 1c allows to generate a pure 3P state, which corresponds to the third-order spontaneous parametric down conversion (SPDC). These three configurations are all interesting from the quantum point of view regarding the context of continuous or discrete variables. Indeed, these three configurations will all generate states, which exhibit quantum features such as entanglement.

In 2004, we made the first experimental demonstration of a TPG. We considered a two-photon stimulation scheme, as shown in Fig. 1a, using a phase-matched bulk KTiOPO$_4$ crystal [4]. More recently, we proposed a waveguide approach to boost the generation efficiency [5, 6]. TPG has also been an active field of research for many groups around the world [7,8,9,10,11,12,13,14,15]. This new corpus has thus opened new exciting opportunities in quantum optics.

Now we wish to overcome a new obstacle by aiming at experimentally generating the 3P state of light by mono-stimulated or spontaneous TPG. This is a real tour de force given both the low efficiency of these two configurations and the fact that the efficiency, contrary to the second-order nonlinear process, increases with the injection intensity. From this step, it will be then possible to open new avenues in quantum information. Indeed, TPG can provide a new powerful resource for advanced quantum information protocols. For example, spontaneous TPG can be considered to generate heralded two photons states, which can be used in a qubit amplifier or in a device-independent quantum key distribution protocol [16]. Our choice for the pump and 3P wavelengths is directly conditioned by this application context: $\lambda _0=532$ nm, which corresponds to the second harmonic of the Nd:YAG laser, and $\lambda _1, \lambda _2, \lambda _3$ ranging from 1500 nm to 1600 nm, that is to say in the telecom range.

This article is organized as follows: we first review our theoretical and experimental work on TPG in Sect. 2 going from bulk to waveguided configurations, followed by the review of the quantum modeling of TPG in Sect. 3 where we additionally implement an easily accessible numerical solution to this problem that has not known analytical solution. Finally, we propose new tools in order to characterize quantum features of TPG in Sect. 4, a difficult and important problem under active investigation in several international teams.

2 Triple-photon generation

2.1 Classical description

2.1.1 Theory

We are considering a practical case where the four interacting waves propagate in the same direction. The corresponding wave vectors are then written $\vec {k_i}=k_i \vec {s}$, i =(0,1,2,3), with $k_i=\frac{2\pi }{\lambda _i}n(\lambda _i)$ where $n(\lambda _i)$ is the refractive index of the wave at $\lambda _i$ in the considered direction $\vec {s}$. The electric fields are taken linearly polarized and are expressed as $\vec {E_i}=\vec {e_i}E_i(Z)expj(k_i Z)$ where $\vec {e_i}$ is the unit vector, namely the light polarization, $E_i(Z)$ the complex amplitude, and Z the spatial coordinate of the laboratory frame along $\vec {s}$.

The resolution of Maxwell equations written at each angular frequency $\omega _i$ leads to the following coupled amplitude equations [17]:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial E_{0}(Z)}{\partial Z}&=j \cdot \frac{\pi }{n\left( \lambda _{0}\right) \lambda _{0} \cos ^{2}\left( \rho _{0}\right) } \chi _{\textrm{e f f}}^{(3)} E_{1}(Z) E_{2}(Z) E_{3}(Z) \exp (-j \Delta k Z) \\ \frac{\partial E_{1}(Z)}{\partial Z}&=j \cdot \frac{\pi }{n\left( \lambda _{1}\right) \lambda _{1} \cos ^{2}\left( \rho _{1}\right) } \chi _{\textrm{e f f}}^{(3)} E_{0}(Z) E_{2}^{*}(Z) E_{3}^{*}(Z) \exp (j \Delta k Z) \\ \frac{\partial E_{2}(Z)}{\partial Z}&=j \cdot \frac{\pi }{n\left( \lambda _{2}\right) \lambda _{2} \cos ^{2}\left( \rho _{2}\right) } \chi _{\textrm{e f f}}^{(3)} E_{0}(Z) E_{1}^{*}(Z) E_{3}^{*}(Z) \exp (j \Delta k Z) \\ \frac{\partial E_{3}(Z)}{\partial Z}&=j \cdot \frac{\pi }{n\left( \lambda _{3}\right) \lambda _{3} \cos ^{2}\left( \rho _{3}\right) } \chi _{\textrm{e f f}}^{(3)} E_{0}(Z) E_{1}^{*}(Z) E_{2}^{*}(Z) \exp (j \Delta k Z). \end{aligned}\right. \end{aligned}$$

(1)

The parameter $\rho _i$, with i=(0,1,2,3), is the spatial walk-off angle in the considered direction of propagation [18]. $\chi _{\textrm{eff}}^{(3)}$ is the effective nonlinear coefficient expressed as $\chi _{\textrm{e f f}}^{(3)}=\chi ^{(3)}\left( \omega _{0}=\omega _{1}+\omega _{2}+\omega _{3}\right) {:}{:} \overrightarrow{e_{0}} \otimes \overrightarrow{e_{1}} \otimes \overrightarrow{e_{2}} \otimes \overrightarrow{e_{3}}$ where  :  :  stands for the four-rank contracted product. The parameter $\Delta k$ is defined by $\Delta k=k_0-(k_1+k_2+k_3)$: this spatial phase term corresponds to the phase mismatch between the third-order nonlinear polarization and the radiated field.

In order to maximize the derivatives $\partial E_i/\partial Z$ in Eq. (1), which corresponds to the maximization of energy exchange between the four waves, it is necessary to maximize the amplitude of $\chi _{\textrm{eff}}^{(3)}$ and to get $\Delta k=0$, i.e.,

$$\begin{aligned} \Delta k = 2 \pi \left[ \frac{n\left( \lambda _{0}\right) }{\lambda _{0}}-\left( \frac{n\left( \lambda _{1}\right) }{\lambda _{1}}+\frac{n\left( \lambda _{2}\right) }{\lambda _{2}}+\frac{n\left( \lambda _{3}\right) }{\lambda _{3}}\right) \right] =0.\nonumber \\ \end{aligned}$$

(2)

Equation 2 is called the phase-matching relation that ensures a constructive interference between the nonlinear polarization and the radiated field over the full interacting length Z. This condition also corresponds to the full momentum conservation of the photons in the quantum picture.

Then, the design of an optimal TPG requires to find a material with a high effective nonlinear coefficient, low spatial walk-off angles, and allowing phase-matching at the targeted wavelengths. We identified the biaxial crystal KTiOPO$_4$ (KTP) as the good platform, under two different technologies: a bulk crystal [4] and a ridge optical waveguide crystal [6]. Then, the strategy is to perform a birefringence phase-matching in both cases.

The phase-matching properties are calculated from the refractive indices over the full transparency range of the crystal. For bulk KTP, the best dispersion equations in the visible and near infrared of the principal refractive indices $n_j(\lambda )$, with respect to the dielectric axes, are [19]:

$$\begin{aligned} n_{j}(\lambda )=\sqrt{A_{j}+\frac{B_{j}}{\lambda ^{2}-C_{j}}-D_{j} \lambda ^{2}}. \end{aligned}$$

(3)

The dispersion coefficients are given in Table 1 for $\lambda$ given in $(\upmu \textrm{m})$.

From Eq. (3) and Table 1, we identified that angle non-critical phase-matching, i.e., $\rho _0=\rho _1=\rho _2=\rho _3=0$, is possible at a pump wavelength $\lambda _0=532\,\textrm{nm}$ when the four interacting waves propagate along the x-axis of the dielectric frame (O,x,y,z), i.e., $\vec {s}$ $\vec {O_x}$. According to Eq. 2, it means that the principle refractive indices verify $\frac{n_{y}\left( \lambda _{0}\right) }{\lambda _{0}}-\left( \frac{n_{z}\left( \lambda _{1}\right) }{\lambda _{1}}+\frac{n_{y}\left( \lambda _{2}\right) }{\lambda _{2}}+\frac{n_{z}\left( \lambda _{3}\right) }{\lambda _{3}}\right) =0$. The corresponding phase-matching curve is given in Fig. 2: it shows that the triplet $(\lambda _1, \lambda _2, \lambda _3)$ is spread over a broad continuum, from 1000 to 4500 nm, that is to say up to the infrared cutoff of KTP. This specific feature of TPG is due to the fact that there are only two coupled relations, the energy and momentum conservations, for the determination of three unknown values. Note that it is completely different from twin photon generation for which there is a unique couple of solutions for the signal and idler wavelengths once the pump wavelength and the direction of propagation are fixed. Actually, in this well-known case of second-order SPDC, there is the same number of equations as solutions to be determined. An alternative to avoid any wavelength spreading, and so any energy spreading, is to fix the value of the wavelength of at least one photon of the triplet: that can be done by stimulating at one or two of the three wavelengths, as in Fig. 1a, b, respectively. Concerning the later scheme, Fig. 2 shows that there exists a partially degenerate scenario where the two injection wavelengths are equal, i.e., $\lambda _2=\lambda _3 = 1681\,\textrm{nm}$ for $\lambda _1=1449\,\textrm{nm}$, which can be interesting from the experimental point of view as it will be seen in the next section. Note that it is also obviously possible to stimulate over the three wavelengths.

The same kind of calculations can be done in the case of ridge KTP crystals, knowing that in that case the refractive index has to be replaced by the effective index of the optical modes. For a given dimension of the square waveguide $(d\times d)$, the effective index of the fundamental guided mode is calculated using Comsol for x-, y- and z-polarized light, by considering wavelengths varying between 500 and 3000 nm. Dispersion equations giving the effective indices are retrieved by fitting those numerical data assuming a Sellmeier-like form. The best equation we found is expressed as [20]:

$$\begin{aligned} \left( n_{\textrm{e f f}}\right) _{i}= & {} \Bigg (A_{i} \times \lambda ^{B_{i}}+\frac{C_{i}}{10^{-6} \times \lambda ^{D_{i}}-E_{i}}\nonumber \\{} & {} -F_{i} \times 10^{-6} \times \lambda ^{G_{i}}\Bigg )^{H_{i}} +I_{i}, \end{aligned}$$

(4)

where the wavelength $\lambda$ is expressed in nanometer (nm). The dispersion coefficients depend on the transverse dimension of the optical waveguide and are given in Table 2 for $d \times d = 6\times 6\, \upmu \textrm{m}^2$.

Table 1 Dispersion coefficients of bulk KTP crystal at room temperature [19]

Fig. 2

TPG phase-matching curve in a bulk x-cut KTP crystal pumped at $\lambda _0=532\,\textrm{nm}$. The indices x, y and z stand for the dielectric axes of the crystal, and $\lambda _1$, $\lambda _2$ and $\lambda _3$ for the triplet wavelengths

The phase-matching curves of Fig. 3 are calculated using Eq. (4) and Table 2 . The infrared limit of 3000 nm is fixed by the range of validity of Eq. (4).

Fig. 3

TPG phase-matching curve in a ridge y-cut KTP crystal pumped at 532 nm with transverse dimension $d\times d=6\times 6 \upmu \textrm{m}^2$. The indices x, y and z stand for the dielectric axes of the crystal

Figure 3 shows that phase-matching is possible from 1000 to 3000 nm for the three triplet wavelengths. But we can expect to have a wider range, up to 4500 nm, as it is the case in Fig. 2 for bulk KTP, when using proper dispersion equations beyond 3000 nm. Figure 3 also shows that the partially degenerated configuration ($\lambda _1=1550$ nm, $\lambda _2=\lambda _3=1619$ nm) is allowed in this ridge. It is important to notice that the walk-off angle is nil along the y-axis, which ensures a perfect spatial overlap between the interacting waves.

Table 2 Dispersion coefficients at room temperature of a ridge KTP crystal with a transverse dimension $d \times d = 6\times 6\, \upmu \textrm{m}^2$ [20]

The phase-matching curves calculated for other values of transverse section $(d\times d)$ have all the same shapes and extensions. They mainly differ by the location of the intersection point corresponding to the partial degeneracy, e.g. $(\lambda _1=938$ nm, $\lambda _2=2457$ nm) for $d\times d=4\times 4\,\upmu$m$^2$ and $(\lambda _1=2456$ nm, $\lambda _2=\lambda _3=1345$ nm) for $d\times d=16 \times 16\,\upmu$m$^2$, as it is shown in Fig. 4 where it also appears that the full degeneracy ($\lambda _1=\lambda _2=\lambda _3=1596$ nm) is possible for $d\times d=6.12\times 6.12\,\upmu$m$^2$. Figure 4 shows well that the geometry of the waveguide is a fine parameter of tunability.

The system described by Eq. 1 can be analytically solved using the sn(u|m) and cn(u|m) Jacobi elliptic functions [21, 22]. Given the boundary conditions in terms of energy at the entrance of the nonlinear medium (Z=0), this resolution is only feasible if there is a stimulation at the three wavelengths of the triplet, or at two wavelengths as in the scheme described by Fig. 1a. In this latter case, the boundary conditions are: $E_{0}(Z=0) \ne 0, E_{1}(Z=0)=0, E_{2}(Z=0) \ne 0$ and $E_{3}(Z=0) \ne 0$. Knowing that the intensity is expressed as $I_{i}(Z)=\frac{n\left( \lambda _{i}\right) }{2} \sqrt{\frac{\varepsilon _{0}}{\mu _{0}}}\left| E_{i}(Z)\right| ^{2}$, it comes for the four intensities at the exit of the nonlinear medium of length $Z = L$:

$$\begin{aligned} \begin{aligned} I_{0}(L)&=\frac{I_{0}(0)\left[ \gamma _{3}+\gamma _{0}\right] c n^{2}(a L \mid 1-m)}{\gamma _{3} m s n^{2}(a L \mid 1-m)+\left[ \gamma _{3}+\gamma _{0}\right] c n^{2}(a L \mid 1-m)}\\ I_{1}(L)&=\frac{\gamma _{3} \gamma _{0} s n^{2}(a L \mid 1-m)}{\gamma _{3} m s n^{2}(a L \mid 1-m)+\left[ \gamma _{3}+\gamma _{0}\right] c n^{2}(a L \mid 1-m)}\\ I_{2}(L)&=\frac{I_{2}(0)\left[ \gamma _{3}+\gamma _{0}\right] (s n^{2}(a L \mid 1-m)+c n^{2}(a L \mid 1-m)}{\gamma _{3} m s n^{2}(a L \mid 1-m)+\left[ \gamma _{3}+\gamma _{0}\right] c n^{2}(a L \mid 1-m)}\\ I_{3}(L)&=\frac{I_{3}(0)\left[ \gamma _{3}+\gamma _{0}\right] (m\,s n^{2}(a L \mid 1-m)+c n^{2}(a L \mid 1-m))}{\gamma _{3} m s n^{2}(a L \mid 1-m)+\left[ \gamma _{3}+\gamma _{0}\right] c n^{2}(a L \mid 1-m)}, \end{aligned} \end{aligned}$$

(5)

with

$$\begin{aligned} a= & {} \frac{\Lambda }{2} \sqrt{\gamma _{3}\left( \gamma _{0}+\gamma _{2}\right) }\nonumber \\ \Lambda= & {} \sqrt{\frac{\mu _{0}}{\varepsilon _{0}}} \frac{4 \pi \chi _{\textrm{eff}}^{(3)}}{\sqrt{n\left( \lambda _{0}\right) n\left( \lambda _{1}\right) n\left( \lambda _{2}\right) n\left( \lambda _{3}\right) }} \sqrt{\frac{\lambda _{1}}{\lambda _{0} \lambda _{2} \lambda _{3}}}\nonumber \\ \gamma _{0}= & {} \frac{\lambda _{0}}{\lambda _{1}} I_{0}(0) \quad \gamma _{2}=\frac{\lambda _{2}}{\lambda _{1}} I_{2}(0) \quad \gamma _{3}=\frac{\lambda _{3}}{\lambda _{1}} I_{3}(0)\nonumber \\ m= & {} \frac{\gamma _{2}\left( \gamma _{0}+\gamma _{3}\right) }{\gamma _{3}\left( \gamma _{0}+\gamma _{2}\right) }. \end{aligned}$$

(6)

Fig. 4

Partially degenerated ($\lambda _1\ne \lambda _2=\lambda _3$) and fully degenerated ($\lambda _1=\lambda _2=\lambda _3$) TPG phase-matching curve as a function of the transverse dimension of a ridge y-cut KTP crystal pumped at 532 nm. The indices x, y and z stand for the dielectric axes of the crystal

Figure 5 gives the corresponding curves for a propagation along the x-axis of a bulk KTP crystal pumped at $\lambda _0=532$ nm. The point of partial degeneracy shown in Fig. 2, i.e., ($\lambda _1=1449$ nm, $\lambda _2=\lambda _3=1681$ nm), is taken for the calculation. In that case, the numerical values of the refractive indices are $n(\lambda _0)=n_y(\lambda _0)=1.7902$, $n(\lambda _1)=n_z(\lambda _1)=1.8182$, $n(\lambda _2)=n_y(\lambda _2)=1.7345$ and $n(\lambda _3)=n_z(\lambda _3)=1.8128$; from Eq. 3 and Table 1, the third-order nonlinear effective coefficient is $\chi _{\textrm{eff}}^{(3)}=9.0\times 10^{-22}$ m$^{2}$V$^{-2}$ using Miller’s rule from the magnitude of the third-order electric susceptibility coefficient $\chi _{yzyz}^{(3)}$ given in Ref.[23]. The incident intensities that are used are: $I_0(0)=250$ GW/cm$^2$ and $I_2(0)=I_3(0)=3.25$ GW/cm$^2$. These values correspond to the intensities considered in the experiments described in section 2.1.2.

Fig. 5

Intensities of phase-matched TPG, pumped at $\lambda _0$ and stimulated at $\lambda _2$ and $\lambda _3$, as a function of the crystal length L of a bulk x-cut KTP crystal pumped at 532 nm

Figure 5 shows well the periodic character of Jacobi elliptic functions, with several values of the crystal length for which there is the full pump depletion, i.e., $I_0(L)=0$. It is then sufficient to consider the first value, i.e., $L = 1.27$ cm, for fixing the optimal crystal length, which is suited for an experiment leading to the extremum $I_1(L=1.27$ cm$)=91.7$ GW/cm$^2$.

The generation at $\lambda _1$ and the amplification at $\lambda _2$ and $\lambda _3$ are due to the generation of 3P states. Then from the knowledge of $I_1$ assuming a Gaussian spatial and temporal shapes under the parallel beam assumption, it is easy to access to $N_{3P}$ that is the number of triple photons,

$$\begin{aligned} N_{3 P}(L)=\frac{1}{\hbar \omega _{1}}\left[ I_{1}(L)\left( \frac{\pi }{2}\right) ^{3 / 2} \frac{\tau _{1}}{2}\left( w_{1}\right) ^{2}\right] , \end{aligned}$$

(7)

where $\tau _1$ and $w_1$ are the full-width pulse duration and radius at $1/e^2$, respectively. In the example of bulk KTP, by taking $\tau _1=88$ ps and $w_1=66$ $\upmu$m for example, we obtain $N_{3P}=2.57\times 10^{15}$  triplets/pulse.

When the TPG efficiency is so weak that the pump and stimulation fields can be considered as constant over L, i.e., $E_{0}(Z) \simeq E_{0}(0) \ne 0, \quad E_{2}(Z) \simeq E_{2}(0) \ne 0 \quad$ and $\quad E_{3}(Z) \simeq E_{3}(0) \ne 0$, the integration of Eqs. 1 is immediate. For $\Delta k=0$, it leads to:

$$\begin{aligned} I_{0}(L)\simeq & {} I_{0}(0) \quad I_{2}(L) \simeq I_{2}(0) \quad I_{3}(L) \simeq I_{3}(0)\nonumber \\ I_{1}(L)\simeq & {} \frac{\mu _{0}}{\varepsilon _{0}}\left( \frac{2 \pi }{\lambda _{1}}\right) ^{2} \frac{\left( \chi _{\textrm{eff}}^{(3)} L\right) ^{2}}{n\left( \lambda _{0}\right) n\left( \lambda _{1}\right) n\left( \lambda _{2}\right) n\left( \lambda _{3}\right) }\nonumber \\{} & {} \times I_{0}(0) I_{2}(0) I_{3}(0). \end{aligned}$$

(8)

Fig. 6

Intensity generated at $\lambda _1$ by phase-matched TPG in a bulk x-cut KTP crystal pumped at 532 nm using the general modeling (red curve of Fig. 5) and the undepleted pump and stimulation approximation

The comparison of the behavior of $I_1(L)$ given in Fig. 5 with that calculated from Eq. 8 using the same boundary conditions is shown in Fig. 6.

It appears that the undepleted pump and stimulation approximation are valid below a crystal length of about 5 mm, but it underestimates the generated intensity at the level of the first maximum of the Jacobi elliptic function and it overestimates the intensity at longer interacting lengths.

2.2 Experimental demonstration of bi-stimulated triple-photon generation

An example of experimental setup of a TPG stimulated over two modes is shown in Fig. 7 [22]. The nonlinear medium was a 2-cm-long bulk KTP crystal cut along the x-axis. In order to minimize the number of stimulation beams, we choose the partially degenerated case, i.e., $\lambda _2 =\lambda _3$, the two corresponding waves being orthogonally polarized.

It was necessary to use very intense pump and stimulation beams, typically several GW/cm$^2$ because of the weakness of the amplitude of the third-order nonlinearity. This is why we used the picosecond regime. The pump beam at $\lambda _0$=532 nm was the second-harmonic of a 5 Hz picosecond Ekspla SL312-P Nd:YAG laser. The stimulation beam at $\lambda _2=\lambda _3$ was generated by a home-made optical parametric oscillator emitting at 1665 nm, which exactly corresponds to the experimental phase-matching, i.e., $(\lambda _1=1474$ nm, $\lambda _2=\lambda _3=1665$ nm), that had been determined before from the pioneer experiment thanks to a tunable source for the stimulation beam at $\lambda _2=\lambda _3$ [4]. Note that these experimental phase-matching wavelengths are very close to the calculated values, i.e., ($\lambda _1=1449$ nm, $\lambda _2=\lambda _3=1681$ nm) according to Fig. 2, the differences being due to a small inaccuracy of the refractive indices that are used for the calculation. Using a pump intensity $I_0(L=0)=250\,$GW/cm$^2$ and a stimulation intensities $I_2(L=0)=I_3(L=0)=3.25$ GW/cm$^2$, which corresponds to the intensity values taken for plotting the curves of Figs. 5 and 6, we obtained $I_1(L=2cm)=0.85$ GW/cm$^2$ at $\lambda _1=1474$ nm, which corresponds to $N_{3P}=3.7\times 10^{13}$ triplets/s according to Eq. (7) [22]. The calculation using Fig. 5 at $L=2$ cm gives $N_{3P}=6.16\times 10^{13}$ triplets/s. This small difference with the measurement has been explained by the Kerr effect due to the high intensities that are used [24]. Note also that according to Figs. 5 and 6, a crystal with the optimal length $L=1.27$ cm would lead to $I_1(L=1.27\,cm)=91.7$ GW/cm$^2$ at $\lambda _1=1474$ nm and so to $N_{3P}=2.57\times 10^{15}$  triplets/s. The triplets are mixed with residual photons at $\lambda _2$ and $\lambda _3$, their numbers corresponding simply to those at the entrance of the KTP crystal, i.e., $N_2(L=0)=N_3(L=0)=4.25\times 10^{14}$ photons/s, the number of incident pump photons being $N_0(L=0)=6.15\times 10^{15}$ photons/s.

The use of bulk KTP as described above allows the beams to be strongly confined over a limited length ranging around one centimeter. Actually, it corresponds to the typical value of the Rayleigh length associated with the focusing conditions that are considered. In order to overcome this limitation, which is a crucial point in the case of a spontaneous TPG, we proposed in 2018 to explore the feasibility of a new technology taking advantage of both birefringence phase-matching and confinement. The idea is to use ridge waveguides where the direction of propagation is along a phase-matching direction of a KTP crystal. By this way, the pump and triplet waves can exhibit the same propagation modes so that the overlap will be optimal. KTP ridge waveguides are fabricated using a technique based on precise diamond blade dicing [6]. A picture of such a waveguide is shown in Fig. 8.

Fig. 7

Experimental setup of a phase-matched TPG in a bulk x-cut KTP crystal pumped at 532 nm and stimulated at $\lambda _2 = \lambda _3 = 1665$ nm with orthogonal polarizations in the picosecond regime. The dashed lines with double arrows stand for the direction of polarization of the different interacting beams. The values of pulse durations $(\tau )$ and waist radius (w) are taken at $1/e^2$

Fig. 8

Electron microscopy image of a KTP ridge waveguide obtained using diamond blade dicing. (x, y, z) is the dielectric frame of KTP. The total length along the y-axis is equal to 8.6 mm

It is then a step index waveguide, the upper and side faces being in contact with air and the lower face being coated with a silica layer. The transverse average section was found to be of about $38\,\upmu$m$^2$, non-constant along the ridge axis: it corresponds to an average square waveguide of side $d=6.17\, \upmu$m. We performed a preliminary validation of this technology by achieving high-efficiency third-harmonic generation (THG: $\omega +\omega +\omega \rightarrow 3\omega$) in the waveguide depicted in Fig. 8 [6]. THG is particularly interesting since it is the exact reverse of TPG that is degenerated in energy, i.e.,  $3\omega \rightarrow \omega +\omega +\omega$. As a consequence, their phase-matching properties are exactly the same. But the advantage of THG is that the conversion efficiency is higher by several orders of magnitude, leading to a much easier way to study phase-matching of TPG. The experiments were carried out using a TOPAS optical parametric generator to deliver the pump beam, with a pulse duration of $15\,ps$, a repetition rate of 10Hz, and a wavelength that is tunable around 1600 nm. By measuring the third-harmonic (TH) intensity as a function of the fundamental wavelength, we found that the phase-matching was achieved at $\lambda _{\omega }=1594$ nm [6]. The calculated value is $\lambda _{\omega }=1594.2$ nm from Eq. (2), with $\lambda _0=\lambda _{3\omega }$ and $\lambda _1=\lambda _2=\lambda _3=\lambda _{\omega }$ , and using Eq. (4) and Table 1. These two values are very close and assuredly within the accuracy of measurement that is at $\pm 1$ nm. In these phase-matching conditions, we found that the TH energy conversion efficiency was $\frac{E_{3\omega }}{E_{\omega }}=3.4\,\%$ when the fundamental energy is $E_{\omega }=2\,\upmu$J [6]. The calculation gives $2.6\,\%$, which is a little bit lower than the measurement, but the two values are sufficiently close for a validation of the magnitude of the nonlinear coefficient that is excited here, i.e., $\chi _{xzxz}^{(3)}(1594\,$nm$/3)=8.0\times 10^{-22}$ m$^2$V$^{-2}$ [6]. Thus, these preliminary measurements of THG allow us to prepare at best the design of spontaneous TPG experiments in KTP ridge waveguides thanks to the validation of the dispersion equations of both the effective index and third-order nonlinear coefficient. The waveguides of the current generation are 3 cm long.

3 Quantum description

The starting point of the quantum description of triple-photon generation is the interaction Hamiltonian describing the nonlinear process, given by

$$\begin{aligned} {\hat{H}}_{nl}=i \hbar \kappa ({\hat{a}}_0{\hat{a}}^{\dagger }_1{\hat{a}}^{\dagger }_2{\hat{a}}^{\dagger }_3 - {\hat{a}}^{\dagger }_0 {\hat{a}}_1{\hat{a}}_2{\hat{a}}_3). \end{aligned}$$

(9)

where ${\hat{a}}^{\dagger }_1$, ${\hat{a}}^{\dagger }_2$ and ${\hat{a}}^{\dagger }_3$ refer to the creation operators corresponding to the three modes and ${\hat{a}}^{\dagger }_0$ the creation operator of the pump mode. The nonlinear coefficient $\kappa$ is proportional to the effective third-order nonlinear susceptibility. The evolution of the quantum system is given in the Heisenberg picture, where the operators follow

$$\begin{aligned} \frac{\textrm{d} {\hat{a}}_l }{\textrm{d} t } = \frac{i}{\hbar } [{\hat{H}}_{nl}, {\hat{a}}_l], \end{aligned}$$

(10)

which reduces to

$$\begin{aligned} \frac{\textrm{d} {\hat{a}}_l }{\textrm{d} t } = \kappa {\hat{a}}_0 {\hat{a}}^{\dagger }_m{\hat{a}}^{\dagger }_n, \end{aligned}$$

(11)

using the Hamiltonian described by Eq. (9). This set of equations is equivalent to the classical ones given in Eq. (1). However, from the quantum mechanics point of view, they have no known analytical solution. We have instead considered numerical methods using the QuTiP package [25, 26]. This approach is convenient as long as a small number of photons are considered in order to keep the computation time reasonable, due to the representation of the states and the operators in the Hilbert space of Fock states. To have a significant effect, it is thus necessary to compensate the low pumping field with a higher nonlinear interaction efficiency $\kappa$. Indeed, considering the results obtained in [23] and reported in section B, we can infer $\kappa |\alpha _0|\sim 1.75 \times 10^{-6} \ll 1$, a rather negligible value. As we are limited in the photon number used in the quantum approach, the expected effects during the interaction described by Eq. (10) will not be observed. In our approach and to gain insights on the quantum properties of TPG, we will instead consider $\kappa = 0.02$, corresponding to $\chi ^{(3)}\sim 1\times 10^{-18}$ m$^2$V$^{-2}$, a value far above the third-order nonlinearities we can reach in present materials. With this value, a pump field with an average 100 photons is sufficient to observe significant evolution of the quantum system. In the following, we will thus consider TPG evolution under Hamiltonian given by Eq. (9) with a pump field in a coherent state $|\alpha _0\rangle$, where $|\alpha _0|^2 = \langle n_0\rangle =100$. Such a coherent state has a Poisson distribution and can be expanded in the Fock-basis up to 200 with very good fidelity. As the generated modes are far weaker, we have used a Fock representation with an expansion up to 50, keeping the calculation times reasonable.

We start our analysis with the double seeding configuration, where two of the triplet modes are excited with a coherent state containing in average $\langle n\rangle =|\alpha _0|^2=5$. The quantum system is then in the initial state $|\psi _{in}\rangle = |\alpha _0,0,\alpha , \alpha \rangle$. Next, we consider the single seeding configuration $|\psi _{in}\rangle = |\alpha _0,0,0, \alpha \rangle$, and finally the spontaneous triple-photon generation for which the initial state is $|\psi _{in}\rangle = |\alpha _0,0,0,0\rangle$. Before proceeding further, it is worth noting here that the double stimulation case describes indeed a displacement operator acting on the mode which is initially in vacuum, under the assumption of a classical undepleted pump in the Hamiltonian Eq. (9). In the single stimulation case and under the classical pump approximation too, the Hamiltonian Eq. (9) reduces to the one describing the well-known spontaneous-parametric down conversion.

Fig. 9

Top: Evolution of the average photon number of the different modes under TPG. Bottom : Corresponding quadrature variances. For this analysis, $\kappa = 0.02$, $|\alpha _0|^2 = 100$, and $|\alpha |^2 = 5$

Figure 9 shows the evolution of the different modes computed numerically considering the three initial states. In the travelling wave configuration, the space evolution can be inferred from the time evolution of Eq. (10) by multiplying the time by the speed v of the propagating modes in the nonlinear material. For simplicity, we considered in our analysis that $v=1$ and we integrated Eq. (10) up to $t = 1$. It is very interesting to notice that the amplification of the mode which is initially in vacuum depends on the number of seeded modes. Indeed in the case of the double seeding configuration, at $t = 1$, the mean photon number for mode 1 is $\langle n\rangle = 1.76$, whereas it is lower, $\langle n\rangle = 0.27$, for modes 1 and 2 in the single seeding regime. These values represent the number of triple photons generated during the interaction. Indeed, we have checked that for the excited modes, the added photon number is exactly $\Delta n = 1.76$ at modes 2 and 3 for the double seeded case, and $\Delta n = 0.27$ at mode 3 for the single seeded interaction.

A similar analysis with a weaker seeding, $|\alpha |^2 = 1$, shows that the generated mean photon numbers are even smaller, indicating that the generation rate of triple photons depends not only on the strength of the pumping excitation, but also on the number and strength of the modes excited prior to the interaction. This is unlike the behavior of optical twin-photon parametric amplification. In the spontaneous configuration, the mean photon number generated is about $\langle n\rangle \simeq 0.04$, even lower, and it obviously only depends on the pump intensity and the nonlinear coefficient $\kappa$. This is the reason why, despite the fact that more than $10^{14}$ triplets are generated in the double seeded configuration as observed in [22], the spontaneous TPG emission has not yet been reported.

Figure 9 shows also the associated quantum fluctuations of the different triple-photon modes. For each mode, we have calculated the variances $\langle \Delta {\hat{q}}^2\rangle$ and $\langle \Delta {\hat{p}}^2\rangle$ of the two quadratures ${\hat{q}} = ({\hat{a}} + {\hat{a}}^{\dagger })$ and ${\hat{p}} = i({\hat{a}} - {\hat{a}}^{\dagger })$. For coherent states and vacuum, which are at the shot noise limit, the variances are $\langle \Delta {\hat{q}}^2\rangle = \langle \Delta {\hat{p}}^2\rangle = 1$. Our analysis shows that in the case of TPG, the three modes have excess noise and all the variances are greater than unity. Moreover, in the case of the double seeded interaction, the quantum fluctuations are not equally distributed, being larger along the ${\hat{q}}$ than the ${\hat{p}}$ quadrature.

Fig. 10

Left: Evolution of the average photon number of the different modes under TPG interaction when all modes are seeded and when the phase of the seeding is $\pi /2$ (blue) and $\pi /6$ (red). For this analysis, $\kappa = 0.02$, $|\alpha _0|^2 = 100$, and $|\alpha |^2 = 5$. The horizontal dashed black line indicates the initial mean photon number $|\alpha |^2 = 5$. The inset shows $\langle n\rangle$ at $t=1$ in a parametric plot as a function of the seeding phase $\psi$. The dashed black circle indicates once more the initial mean photon number $|\alpha |^2 = 5$. Right: The corresponding quadrature variances for the same seeding phase. The horizontal dashed black line shows the shot noise. The inset is the ${\hat{q}}$ and ${\hat{p}}$ variances at $t=1$ as a function of the phase of the seeding. The shot noise is highlighted by the black dashed circle

Now, we consider the case of a triple-seeded configuration where the three modes are excited by a coherent state with a mean photon number $|\alpha |^2 = 5$. In this particular situation, we should also consider the relative phase between the pump and the triple modes given by $\Delta \phi =|\psi _1+\psi _2+\psi _3-\psi _0|$. For sake of simplicity, we take $\phi _0 = 0$ and $\phi _1=\phi _2=\phi _3 = \phi$. Our analysis reveals two interesting situations: an amplification for $\phi = \pi /2, 7\pi /6$ and $11\pi /6$, where the pump photons are converted into triplets; an attenuation for $\phi = \pi /6, 5\pi /6$ and $3\pi /2$, which corresponds to a regime where the triple photons are converted back into pump photons. These behaviors are depicted in Fig. 10, representing in the left plot the evolution of mean photon number for $\phi =\pi /2$ (blue) and for $\phi =\pi /6$ (red). The inset is the mean photon number at $t=1$ as a function of the phase in a polar plot. In the plot on the right, we have reported the quantum fluctuations of the two conjugate quadratures ${\hat{q}}$ and ${\hat{p}}$. The blue curves represent the variances in the case of amplification, and the red ones correspond to the attenuation case. Like in the partially seeded configurations, the quantum fluctuations are always above the shot noise limit. Moreover, as depicted in the contour plot, they exhibit a phase dependence, similar to the one of the mean photon number. The behavior of the fully seeded TPG is comparable to the phase-sensitive twin-photon parametric interaction. It has a dependency to the relative phase between the pump and the generated modes and it exhibits noisy modes, which makes them robust against optical losses. The differences between the twin-photon and triple-photon states are related to the dependence on the seeding intensity and more importantly to the non-Gaussian nature of their statistics. This point will be addressed in the next section.

The generation of triple photons fulfills two conditions: the energy and momentum conservations, as explained in Sect. 2. In the case of spontaneous emission, where only the pump is fixed through its optical frequency $\omega _0$ and its $k_0$ wave-vector, we end up with two equations with three unknown parameters: $\omega _1$, $\omega _2$ and $\omega _3$. The system has thus an infinity of triplet solutions as already mentioned in Sect. 2.

We should thus reconsider our quantum approach by taking into account this broadband generation. A more suitable approach in this case is to consider the space evolution under the nonlinear momentum

$$\begin{aligned} {\hat{G}}_{nl}= & {} \hbar \int \int \int \textrm{d}\omega _0 \textrm{d}\omega _1 \textrm{d}\omega _2\Gamma (\omega _0,\omega _1,\omega _2)\nonumber \\{} & {} {\hat{a}}^{\dagger }_0{\hat{a}}_1{\hat{a}}_2{\hat{a}}_3 e^{-i \Delta k z} + \mathrm {H.c}, \end{aligned}$$

(12)

where

$$\begin{aligned}{} & {} \Gamma (\omega _0,\omega _1,\omega _2)\nonumber \\{} & {} =\frac{\hbar \chi ^{(3)}}{4 \epsilon _0 c^2 S} \sqrt{\frac{\omega _0 \omega _1 \omega _2 (\omega _0-\omega _1-\omega _2)}{n(\omega _0) n(\omega _1) n(\omega _2) n(\omega _0-\omega _1-\omega _2)}}, \end{aligned}$$

(13)

and $\Delta k = k(\omega _0)-k(\omega _1)-k(\omega _2)-k(\omega _0-\omega _1-\omega _2)$, where we have replaced the frequency $\omega _3$ of the third photon by $\omega _3 = \omega _0-\omega _1-\omega _2$ using the energy conservation condition. In the following, a reasonable assumption is to consider that the pump spectral bandwidth is very narrow in comparison with the bandwidth of the triple photons, especially if a CW laser is used. We can also consider that the pump is strong and undepleted and can be treated as a complex classical amplitude. We obtain the following evolution equations

$$\begin{aligned} \frac{\partial {\hat{a}}_l(\omega )}{\partial z}= & {} -i \int \textrm{d}\omega _t \Gamma (\omega _0,\omega ,\omega _t) A_0 {\hat{a}}_m^{\dagger }(\omega _t){\hat{a}}_n^{\dagger }\nonumber \\{} & {} (\omega _0-\omega -\omega _t)e^{+i \Delta k z}, \end{aligned}$$

(14)

where $A_0$ is the real amplitude of the pump electric field. Moreover, considering a weak interaction, which is reasonable for spontaneous TPG, we can solve Eq. (14) to the first-order of the Baker–Hausdorff expansion, which gives

$$\begin{aligned}{} & {} {\hat{a}}_l(\omega ,z) = {\hat{a}}_l(\omega ,0)\nonumber \\{} & {} \quad -i \int \textrm{d}\omega _t \psi (\omega _0,\omega ,\omega _t) {\hat{a}}_m^{\dagger }(\omega _t,0){\hat{a}}_n^{\dagger }(\omega _0-\omega -\omega _t,0),\nonumber \\ \end{aligned}$$

(15)

where $\psi = \Gamma (\omega _0,\omega ,\omega _t) L A_0 \textrm{sinc}(\Delta kL/2)e^{+i \Delta k L/2}$.

It is now easier to calculate the mean photon number defined as $\langle n\rangle = \langle \psi _{in}| {\hat{a}}^{\dagger }{\hat{a}} |\psi _{in}\rangle$. With the initial state in vacuum, $|\psi _{in}\rangle = |0,0,0\rangle$, we obtain:

$$\begin{aligned} \langle n_i(\omega ,L)\rangle = \int \textrm{d}\omega _t |\psi (\omega _0,\omega ,\omega _t)|^2. \end{aligned}$$

(16)

This indicates that the mean photon number at mode $i=1,2,3$ at frequency $\omega$ is the integral over all the contributions of triple photons that fulfill the phase-matching condition and the energy conservation. For example, in the KTP waveguides, these two conditions are fulfilled over almost the full transparency window of the nonlinear crystal as shown in Fig. 3. Figure 11 shows the spectral density distribution $|\psi (\omega _0,\omega ,\omega _t)|^2$ as a function of $\lambda _1$ and $\lambda _2$. It is obtained for the KTP waveguide considered in Fig. 3 and using the corresponding dispersion relations of the effective index Eq. 4.

Integrating $|\psi (\omega _0,\omega ,\omega _t)|^2$ over $\lambda _2$-axis, we obtain the mean photon number $\langle n_1(\omega ,L)\rangle$ per second as a function of $\lambda _1$. Similar calculations can be hold to compute $\langle n_2(\omega ,L)\rangle$ and $\langle n_3(\omega ,L)\rangle$. The expected mean photon number is higher than the one calculated by the single mode model described by the Hamiltonian given by Eq. (9). The total mean photon number that we expect is further estimated by integrating Eq. (16) over the full spectrum, i.e.,

$$\begin{aligned} N_{3P}(L) = \int \textrm{d}\omega \langle n_i(\omega ,L)\rangle . \end{aligned}$$

(17)

Indeed, considering the full phase-matching bandwidth of the KTP ridge waveguide as shown in Fig. 3, i.e., from 1 to 3 $\upmu$m, and a CW pump power of 5 W at 532 nm, we estimate $N_{3P}(L=5 cm) \simeq 4.9$ triplets/s. Such a pump level is a reasonable target regarding the expected improvements of the losses and surface quality of the waveguides. Note that the rate of triplets remains the same in the pulsed regime than in the CW regime if the average power is kept at the same value. But the number of triplets per pulse will depend on both the pulse duration and repetition rate. For example a pump of 5W at 532 nm with a pulse duration of 11.3 ps and a repetition rate of 88 MHz, gives $N_{3P}(L=5cm) = 4.9$ triplets/s, corresponding to $5.6\times 10^{-8}$ triplets/pulse.

4 Non-classical features of TPG

We now focus on spontaneous TPG, and we consider the non-degenerate case where the Hamiltonian is

$$\begin{aligned} {\hat{H}}_{nd}=i \xi ({\hat{a}}^{\dagger }_1{\hat{a}}^{\dagger }_2{\hat{a}}^{\dagger }_3-{\hat{a}}_1{\hat{a}}_2{\hat{a}}_3) \end{aligned}$$

(18)

and the degenerate case characterized by the following Hamiltonian:

$$\begin{aligned} {\hat{H}}_d=i \xi ({\hat{a}}^{\dagger 3}-{\hat{a}}^3). \end{aligned}$$

(19)

In both cases, we consider a pump with a high photon number so that it can be treated as a classical state. We also define $\xi =\kappa \alpha _0$ where $|\alpha _0|$ is the amplitude of the pump.

Fig. 11

Spectral density distribution $|\psi (\omega _0,\omega ,\omega _t)|^2$ as a function of the phase-matching wavelengths $\lambda _1$ and $\lambda _2$

The generation of TPG quantum states has been performed in the double-seeded configuration in [24], and in the single seeded and spontaneous cases in [15]. In those experiments, the authors show strong evidence that the states are generated by a TPG; however, the experimental demonstration of quantum features for such states remains, up to our knowledge, to be done. In this section, we develop the theoretical tools that allow to demonstrate the different quantum features of the states generated by all the possible configurations of TPG, i.e., stimulation over one, two or three modes, as well as no stimulation. We first note that all quantum features can be inferred from the density matrix of the state or equivalently from a phase space distribution. In the present case, we expect 4.9 triplets per second, which makes a full quantum tomography totally out of reach. We thus focus on tools which require a minimum information about the state but are still able to conclude about quantum features. In the first part, we focus on the states generated by the Hamiltonian (18) and propose tools to demonstrate genuine multipartite entanglement (GME) of such states using homodyne measurement. We then focus on the state generated by the Hamiltonian (19) and build tools in order to demonstrate non-classical features of such states.

4.1 Entanglement

A state is said to be GME if it cannot be written as a biseparable state for any bipartition. A general biseparable state is a mixture of states that are product states for some bipartition, i.e., a partition of all modes into two groups. Formally, it is given by:

$$\begin{aligned} \varrho _\text {bisep} = \sum _{G_1|G_2} p(G_1|G_2) \, \rho _{G_1|G_2}. \end{aligned}$$

(20)

Here, the sum runs over all 3 partitions $G_1|G_2$ of the 3 parties where $G_1\cup G_2=\{1,2,3\}$ and $G_1\cap G_2=\emptyset$. The probabilities of different partitions sum up to one, $\sum _{G_1|G_2} p(G_1|G_2)=1$, and $\rho _{G_1|G_2}$ is a separable state with respect to the partition $G_1|G_2$. We aim to demonstrate entanglement using homodyne detection, so that we define a general homodyne measurement on the mode i as ${\hat{X}}_i^{\theta }=({\hat{a}}^{\dag }e^{i\theta }+{\hat{a}}e^{-i \theta })/2$ and write ${\hat{X}}_i^{\pi /2}={\hat{p}}_i$ and ${\hat{X}}_i^{0}={\hat{q}}_i$. Our first attempt to describe the quantum properties of triple photons, especially their three-body quantum entanglement, was in 2018 [27] using the existing tools dedicated to characterize the inseparability of multi-body quantum states. Our analysis is based on P. van Loock and A. Furusawa non-separability criterion S [28], relying on the evaluation of the quantum fluctuation of the generalized quadratures

$$\begin{aligned} {\hat{u}} = \sum _{i=1}^3 h_i {\hat{p}}_i, {\hat{v}} = \sum _{i=1}^3 g_i {\hat{q}}_i, \end{aligned}$$

(21)

where $h_i$ and $g_i$ are arbitrary real numbers. Thus, the non-separability criterion is easily accessible experimentally using standard balanced homodyne detections. The criterion is defined as $S = \langle \Delta {\hat{u}}^2\rangle +\langle \Delta {\hat{v}}^2\rangle$. We can show that when $S< 2\,\textrm{min}(|h_k g_k|+|h_l g_l+h_m g_m|)$ for any permutation of $k,l,m = 1,2,3$, the triplets exhibit genuine entanglement. However, when $S>2\,(|h_k g_k|+|h_l g_l|+|h_m g_m|)$, the system is completely separable. Surprisingly, we found that the spontaneous triple photons do not exhibit three-body quantum entanglement in the continuous variable (CV) regime, always fulfilling the last inequality. Entanglement has only been predicted in the different seeded cases as depicted in Fig. 12. The different results are obtained following the analysis reported in our work [27].

Fig. 12

Evolution of the entanglement criterion S for different interactions TPG configurations. Red: fully seed TPG with a relative phase of $\pi /2$. Blue: double-seed TPG. Green: One mode seeding configuration and S calculated for the two unseeded modes. $|\alpha |^2$ is the mean photon number per second of each seeding beam

In fact, TPG is a third-order nonlinear process with non-Gaussian statistics. This statement is obvious in the degenerate case when ${\hat{a}}_1 = {\hat{a}}_2 = {\hat{a}}_3$ and the Hamiltonian (18) becomes (19). It will be shown hereafter in Fig. 16 that the Wigner function exhibits interferences and negativities, which is a clear signature of the non-Gaussian nature of the triple-photon mode a. In the non-degenerate case (Hamiltonian (18)), we have recently shown that even though the Wigner function associated with each mode looks Gaussian, the quadrature probability distribution is super-Gaussian [29]. The S criterion is thus not anymore a relevant parameter to analyze and reveal the entanglement properties of the triple-photon states. Indeed, the S criterion is based on the second-order moments, i.e.,  variances, which are sufficient to describe a Gaussian distribution. When at least one of the triplet modes is seeded, the statistics become again Gaussian, and hence, using Furusawa and Van Loock criterion, S is sufficient. The failure of the S criterion to describe the entanglement in the case of spontaneous TPG due to its super-Gaussian nature pushed us to further explore the entanglement nature of the triplet, in order to claim that the triple photons are indeed entangled despite the results based on S. Hence, we have used the logarithmic negativity defined as $E_N = \ln ||\rho ^{T_i}||$, where $\rho$ is the density matrix of the triple photons and $\rho ^{T_i}$ is its partial transpose over mode $i=1, 2$ or 3 [29, 30]. A quantum system is said to be entangled whenever $E_N>1$. Figure 13 shows the calculated $E_N$ in the case of spontaneous TPG, starting from the Hamiltonian Eq. (9) and using a numerical approach to solve the Heisenberg equation. For this simulation, we considered a coherent pump field with a mean photon number $\langle n_0\rangle = 10$. The logarithmic negativity $E_N$ increases with the nonlinear parameter $\kappa |\alpha _0|$, reaching $E_N \simeq 2$ for $\kappa |\alpha _0| = 1$, which clearly demonstrates the three-body entanglement of the triple photons. In the same figure, we have also reported the evolution of $\langle n_0\rangle$ and $\langle n_{3P}\rangle$, respectively, the pump and triplets mean photon numbers.

Fig. 13

Red: logarithmic negativity of the spontaneous TPG excited by a coherent pump with a mean photon number $|\alpha _0|^2 = 10$. Black: Evolution of the pump mean photon number. Blue: Evolution of the mean photon number of the generated triplets

Even though the logarithmic negativity has the ability to reveal the entanglement of a quantum system, it is very hard to measure in practice, as it requires a full tomography of the state. One instead can use a witness of genuine entanglement, i.e., an observable ${\hat{O}}$ such that $\langle {\hat{O}}\rangle \le 0$ for all biseparable state. As stated before, the state $|\psi _3\rangle$ associated with non-degenerate TPG has non-Gaussian entanglement, which implies that a witness of entanglement (or GME) for the state $|\psi _3\rangle$ requires at least a third-order field operator. The authors of [31] derive a non-Gaussian witness of GME, which allows the demonstration of genuine entanglement for the state $|\psi _3\rangle$. Moreover, their witness failed to detect entanglement in the seeded configuration, which highlights the difference between the two states. We briefly review their witness. The authors of [31] show that any biseparable state satisfies

$$\begin{aligned} |\langle {\hat{a}}_1{\hat{a}}_2{\hat{a}}_3\rangle |\le & {} \sqrt{\langle {\hat{n}}_1\rangle \langle {\hat{n}}_2{\hat{n}}_3\rangle }+\sqrt{\langle {\hat{n}}_2\rangle \langle {\hat{n}}_1{\hat{n}}_3\rangle }\nonumber \\{} & {} +\sqrt{\langle {\hat{n}}_3\rangle \langle {\hat{n}}_2{\hat{n}}_1\rangle } \end{aligned}$$

(22)

where ${\hat{n}}_i$ is the number operator for mode i. The state $|\psi _3\rangle$ does not satisfy (22) and is thus GME. We want to formulate a relaxation of this witness only in terms of local homodyne measurement. In order to formulate our relaxation, we first note that (22) implies that any biseparable state satisfies:

$$\begin{aligned} |\langle {\hat{a}}_1^{\dagger }{\hat{a}}_2^{\dagger }{\hat{a}}_3^{\dagger }\rangle |\le & {} \sqrt{\langle {\hat{n}}_1\rangle \langle {\hat{n}}_2{\hat{n}}_3\rangle }+\sqrt{\langle {\hat{n}}_2\rangle \langle {\hat{n}}_1{\hat{n}}_3\rangle }\nonumber \\{} & {} +\sqrt{\langle {\hat{n}}_3\rangle \langle {\hat{n}}_2{\hat{n}}_1\rangle }. \end{aligned}$$

(23)

By summing (22) and (23) and using the triangular inequality, we end up with

$$\begin{aligned} \frac{|\langle {\hat{a}}_1^{\dagger }{\hat{a}}_2^{\dagger }{\hat{a}}_3^{\dagger }\rangle +\langle {\hat{a}}_1{\hat{a}}_2{\hat{a}}_3\rangle |}{2}\le & {} \sqrt{\langle {\hat{n}}_1\rangle \langle {\hat{n}}_2{\hat{n}}_3\rangle }+\sqrt{\langle {\hat{n}}_2\rangle \langle {\hat{n}}_1{\hat{n}}_3\rangle } \nonumber \\{} & {} +\sqrt{\langle {\hat{n}}_3\rangle \langle {\hat{n}}_2{\hat{n}}_1\rangle } \end{aligned}$$

(24)

which holds for all biseparable states. Interestingly, the left-hand side of this previous equality can be measured using local homodyne measurement , i.e.,

$$\begin{aligned} {\hat{a}}_1^{\dagger }{\hat{a}}_2^{\dagger }{\hat{a}}_3^{\dagger }+ {\hat{a}}_1{\hat{a}}_2{\hat{a}}_3= & {} -2 ({\hat{X}}^{\frac{\pi }{2}}_1 {\hat{X}}^{\frac{\pi }{2}}_2 {\hat{X}}^{0}_3 + {\hat{X}}^{0}_1 {\hat{X}}^{\frac{\pi }{2}}_2 {\hat{X}}^{\frac{\pi }{2}}_3\\{} & {} + {\hat{X}}^{\frac{\pi }{2}}_1 {\hat{X}}^{0}_2 {\hat{X}}^{\frac{\pi }{2}}_3 - {\hat{X}}^{0}_1{\hat{X}}^{0}_2 {\hat{X}}^{0}_3). \end{aligned}$$

The terms ${\hat{n}}_i{\hat{n}}_j$ being hard to measure experimentally, we bound them according to

$$\begin{aligned} \forall \{i,j\} \in \{1,3\}~~\langle {\hat{n}}_i{\hat{n}}_j\rangle \le \frac{1}{2}(\langle {\hat{n}}^2_i\rangle +\langle {\hat{n}}^2_j\rangle ) \end{aligned}$$

(25)

where $\langle {\hat{n}}^2_i\rangle$ can be measured locally by combining second- and fourth-order moments of phase average field quadrature, that is to say:

$$\begin{aligned} {\hat{n}}_i^2= \frac{16}{6}\left( \int \frac{1}{2 \pi } \textrm{d}\theta \, ({\hat{X}}_i^{\theta })^4 -\frac{1}{2} \int \frac{1}{2 \pi } \textrm{d}\theta \ ({\hat{X}}_i^{\theta })^2\right) . \end{aligned}$$

(26)

We define the quantity

$$\begin{aligned} C_{i,j,k}=\sqrt{\langle {\hat{n}}_i\rangle _{\rho _{TPG}(\eta )}(\frac{1}{2}(\langle {\hat{n}}^2_j\rangle _{\rho _{TPG}(\eta )}+\langle {\hat{n}}^2_k\rangle _{\rho _{TPG}(\eta )})}\nonumber \\ \end{aligned}$$

(27)

where $\langle .\rangle _{\rho _{TPG}(\eta )}$ is the expectation value of $''.''$ on the state $\rho _{TPG}$. We can certify the presence of GME for the state $\rho _{TPG}$ if the quantity

$$\begin{aligned} w= & {} \frac{|\langle {\hat{a}}_1^{\dagger }{\hat{a}}_2^{\dagger }{\hat{a}}_3^{\dagger }\rangle _{\rho _{TPG}(\eta )}+\langle {\hat{a}}_1{\hat{a}}_2{\hat{a}}_3\rangle _{\rho _{TPG}(\eta )}|}{2}\nonumber \\{} & {} -(C_{1,2,3}+C_{2,1,3}+C_{3,2,1}) \end{aligned}$$

(28)

is positive. We plot in Fig. 14w with respect to the efficiency $\eta$. We see a violation even for low efficiency, which makes the detection of GME for the state $\rho _{TPG}$ robust against losses when homodyne detection is used.

Fig. 14

GME certification parameter w with respect to the efficiency $\eta$ for $\epsilon =\xi t_{int}=10^{-2}$

4.2 A hierarchy of quantum features for single mode of light

We focus on the degenerate state $|\psi \rangle$, which we take to be the outcoming state created by the process associated with the Hamiltonian of Eq. (19), and which we assume to be single mode. There exists a hierarchy of quantum features for a single mode of light in Fig. 15.

Fig. 15

Hierarchy of quantum features for single mode state of light

The first layer of quantum features is the non-classicality, which is defined using the Glauber– Sudarshan (GS) or P distribution [32, 33]. Any state $\rho$ can be written in terms of coherent states $|\alpha \rangle$ as follows:

$$\begin{aligned} \rho =\int \textrm{d}\alpha ^2 P(\alpha ) |\alpha \rangle \langle \alpha |. \end{aligned}$$

(29)

A state is classical if its GS distribution $P(\alpha )$ can be interpreted as a classical probability distribution [34]. Non-classicality is a necessary feature for a state to exhibit any quantum advantage, for example in quantum metrology where any advantage over classical metrology requires non-classicality.

The second layer of quantum features is quantum non-Gaussianity (QNG). A Gaussian state is by definition a state with a Gaussian Wigner function. Hudson’s theorem [35] stipulates that all non-Gaussian pure states are Wigner negative; nevertheless, it is not the case for mixed states. Any pure Gaussian state can be generated by the action of the squeezing operator ${\hat{S}}(s) = e^{{\hat{a}}^2 s^{*} - {\hat{a}}^{\dagger 2} s}$ following by displacement operator $D(\alpha )=e^{\alpha {\hat{a}}^{\dagger }-\alpha ^{*} {\hat{a}}}$ on the vacuum : $|s,\alpha \rangle =S(s)D(\alpha )|0\rangle .$ Also, any state can be written in terms of Gaussian states, i.e.,

$$\begin{aligned} \rho =\int p(\alpha ,s) |s,\alpha \rangle \langle s,\alpha |. \end{aligned}$$

(30)

A state is Gaussian if $p(\alpha ,s)$ can be interpreted as a probability distribution. Non-Gaussian quantum states are essential to a variety of quantum information processing tasks such as quantum state distillation [36], quantum error-correction [37] or quantum computational speedup [38].

The third layer of quantum features is Wigner negativity. The Wigner function is a representation of a single mode state $\rho$ in terms of the a quasi-probability distribution given as [39]:

$$\begin{aligned} W_{\rho }(\alpha )=\frac{2}{\pi }\text {Tr} (D(\alpha )(-1)^{a^{\dagger }a}D(\alpha )^\dag \, \rho ). \end{aligned}$$

(31)

Wigner negativity is arguably the strongest form of quantum feature for a single mode state and is a necessary condition to perform efficient quantum computing using CV states [40]. We plot in Fig. 16 the Wigner function of state $|\psi \rangle$ as a function of its canonical quadratures q and p.

Fig. 16

Wigner function W of the state $|\psi \rangle$ as a function of the canonical quadratures q and p. The positivity plane (colored in lighter color) divides the Wigner function axis between positive and negative values

We can observe different areas of negativities in the Wigner function, which implies that the TPG state is Wigner negative, non-Gaussian and non-classical. We note that this function is not phase-invariant, and as a consequence the presence of such negativities cannot be detected by only photon counting strategies. The reconstruction of the Wigner function requires a high number of experimental runs, which is not available in the present experiment. Witnesses of Wigner negativity can be systematically derived using hierarchy of semi-definite programs [41], but those witnesses require again a number of measurement runs that is much higher than the one available in our case, and for those reasons we proceed by focusing on non-classicality and non-Gaussianity only.

4.3 Witnessing non-classicality of the degenerate state $|\psi \rangle$

A witness of non-classicality can be represented by an observable ${\hat{W}}$ together with the maximum expectation value of ${\hat{W}}$ on a classical state. The most widely used witness of non-classicality is probably the second-order correlation function $g^2(0)$ [42] together with its classical bound 1. Several criteria that analyze matrices of moments of annihilation and creation operators have also been derived [43,44,45]. In this section, we focus on the setup of Fig. 17 and derive a witness tailored to the state $|\psi \rangle$ and that is based on photodetection events. We consider a single-mode case for the sake of clarity. The results are holding in the multimode case and, since i) the detector cannot distinguish between different modes and ii) the setup in Fig. 17 does not allow us to acquire information about the coherence terms of $|\psi \rangle ,$ then we can consider a single-mode state with the same number of photons than that of the expected multimode state in order to correctly model our experiment (see Appendix A).

In Fig. 17, an input state $\rho _i$ of the ith experimental run is split into four spatially separated modes using three balanced beam splitters and sent to four non-photon number resolving (NPNR) detectors. We do not want to make assumptions about the efficiency of the NPNR detectors, so we consider perfect detection and that any inefficiencies can be mapped into the input states $\rho _i$. A NPNR detector with unit efficiency can be modeled by a two element positive operator-valued measure (POVM) as the set $\{E_\bullet , E_\circ \}=\{\mathbbm {1}-|0\rangle \langle 0|,|0\rangle \langle 0|\}$, corresponding to the single detector events click and no click, respectively.

Fig. 17

Experimental setup consisting of three balanced beam-splitters ($t=r=1/2)$ and four detectors D1-4

The set of non-classical states is convex (29), so that the set of the different probabilities of clicks achieved by classical states is also convex, by linearity of the trace. We can thus consider a linear combination of probability operators corresponding to the events of click and no click on the detector arrangement,

$$\begin{aligned} {\hat{W}}({\theta }) = \sum c_{i}{\hat{P}}_{i}, \end{aligned}$$

(32)

where ${\hat{P}}_{i}$ are the POVM elements of the arrangement, which correspond to the event where i detectors click while the others do not click, as for example: ${\hat{P}}_{4}=E_\bullet ^{(1)}E_\bullet ^{(2)}E_\bullet ^{(3)}E_\bullet ^{(4)}=(\mathbbm {1}-|0\rangle \langle 0|)^{\otimes 4}$, and represent an event where all four detectors click. The coefficients $c_i$ are parametrized such that the vector $\textbf{c}(\theta )$ is normalized:

$$\begin{aligned} \textbf{c}({\theta }) = \begin{pmatrix} \sin {\theta _1} \\ \sin {\theta _2}\cos {\theta _1} \\ \sin {\theta _3}\cos {\theta _2}\cos {\theta _1}\\ \cos {\theta _3}\cos {\theta _2}\cos {\theta _1}, \\ \end{pmatrix}. \end{aligned}$$

(33)

The next step is to compute the maximum expectation value of the observable constructed in Eq. (32) that any classical state can achieve, i.e.,

$$\begin{aligned} w_c(\theta )=\max _{\forall ~~\rho _c}({{\textrm{Tr}}}\!\left( {\hat{W}}(\theta )\rho _c\right) ). \end{aligned}$$

(34)

We note that ${{\textrm{Tr}}}\!\left( {\hat{W}}(\theta )\rho _c\right)$ is linear in $\rho _c$, and since any arbitrary classical state can be written as a mixture of pure classical states according to Eq. (29), we find that:

$$\begin{aligned} {{\textrm{Tr}}}\!\left( {\hat{W}}(\theta )\rho _c\right)= & {} {{\textrm{Tr}}}\!\left( {\hat{W}}(\theta )\int \textrm{d}\alpha ^2 P(\alpha ) |\alpha \rangle \langle \alpha | \right) \nonumber \\= & {} \int \textrm{d}\alpha ^2 P(\alpha ){{\textrm{Tr}}}\!\left( {\hat{W}}(\theta )|\alpha \rangle \langle \alpha | \right) \nonumber \\\le & {} \big (\int \textrm{d}\alpha ^2 P(\alpha )\big )\max _{\alpha }({{\textrm{Tr}}}\!\left( {\hat{W}}(\theta )|\alpha \rangle \langle \alpha | \right) )\nonumber \\= & {} \max _{\alpha }({{\textrm{Tr}}}\!\left( {\hat{W}}(\theta )|\alpha \rangle \langle \alpha | \right) ). \end{aligned}$$

(35)

Therefore, we can conclude that the maximum of the RHS of (34) is achieved by a pure coherent state. With this simplification, we have that

$$\begin{aligned} w_c(\theta )=\max _{\forall ~~|\alpha \rangle }(\langle \alpha |{\hat{W}}({\theta })|\alpha \rangle ). \end{aligned}$$

(36)

We find that this maximization equivalent to a problem of finding the roots of a third-order polynomial (see Appendix A) and can thus be simply performed analytically. The vector ${\hat{\theta }} = (\theta _1,\theta _2,\theta _3)$ is associated with the weights of the different events defined by the operators ${\hat{P}}_i$ on the witness ${\hat{W}}$. The witness is now arranged such that if for a given state $\rho$, it exists one vector ${\hat{\theta }}$ for which $\text {Tr}({\hat{W}}({\theta })\rho )>w_c(\theta )$, then the non-classicality of the state $\rho$ can be demonstrated using the setup of Fig. 17.

In practice, the state $|\psi \rangle$ will experience losses; we then define the state

$$\begin{aligned} \rho _{TPG}(\eta )=\text {Tr}_B(U_{\eta }|\psi \rangle \langle \psi |\otimes {|0\rangle \langle 0|_B}U^{\dag }_{\eta }), \end{aligned}$$

(37)

where $U_{\eta }$ is a unitary corresponding to a beam-splitter with transmitivity $\eta$, referring to the efficiency, and the quantity $q({\theta })=\text {Tr}( \rho _{TPG}(\eta ){\hat{W}}({\theta }))-w_c({\theta })$, that will be positive when the witness can detect non-classicality for the lossy state $\rho _{TPG}(\eta ).$ In order to find the optimal witness of the state for a given efficiency, we can compute:

$$\begin{aligned} q_{\text {opt}}=\max _{{\theta }}(q({\theta })). \end{aligned}$$

(38)

We plot in Fig. 18$q_{\text {opt}}$ with respect to the overall efficiency $\eta$ of the setup for $\epsilon =\xi t=0.01$. We find that, in the present case, the optimal q is always found when $w_c(\theta )=0.$ We also find a positive $q_{\text {opt}}$ for the range of all efficiencies, which proves the detection of non-classicality of the state $|\psi \rangle$ using the setup of Fig. 17 to be robust against losses.

In the last part of this section, we turn to give an estimation of the number of experimental runs that would be necessary to estimate the quantity $W_s=\text {Tr}( \rho _{TPG}(\eta ){\hat{W}}({\theta })).$ We assume that the POVM elements ${\hat{P}}_i$ are independent quantities that are measured N times. At each run, we evaluate a random variable $X_i$, associated with ${\hat{P}}_i$, which takes the value 1 when i detectors click and $i-4$ do not click, and the value 0 otherwise. An unbiased estimator of $W_s$ after N runs is given by:

$$\begin{aligned} \bar{W_s}=\sum _{k=1}^N \sum _{i=1}^4c_i \frac{X_i^k}{N}. \end{aligned}$$

(39)

We bound the standard deviation of $\bar{W_s}$ as follows:

$$\begin{aligned} \sigma _{W_s}= \sum _{i=1}|c_i|\frac{\sigma _{X_i}}{N}, \end{aligned}$$

(40)

where $\sigma _{X_i}=\sqrt{\langle X_i\rangle (1-\langle X_i\rangle )}$ is the standard deviation of a binary variable. The number of runs that is needed to estimate the value of the witness, with a precision 3 times smaller than the distance to the classical bound, can thus be estimated by finding the number of runs $N_{opt}$ such that:

$$\begin{aligned} q_{opt}=3 \sigma _{W_s}. \end{aligned}$$

(41)

We plot $N_{opt}$ with respect to the efficiency in the inset of Fig. 19. With 4.9 triplets/s and a 5-W laser at 88 MHz, we find that 18 seconds of experiment are enough to certify the non-classicality of the state for an efficiency of 50$\%$.

Fig. 18

Optimized mean values of $q_{\text {opt}}$. The optimization is performed numerically over the set of parameter coefficients $\theta$ for a range of efficiencies $\eta$ for $\epsilon = 10^{-2}$. Inset: Number of experimental runs $N_{opt}$ necessary for certification

4.4 Demonstrating non-Gaussianity of the degenerate state $|\psi \rangle$

A witness operator ${\hat{W}}$ in the same general form of Eqs. (32–33) associated with the linear optical setup of Fig. 17 proves to be useful to the demonstration of the non-Gaussianity of the one-mode state $|\psi \rangle$ as well, meaning that, by analyzing the mean value of this operator on this state, we can assert that $|\psi \rangle$ cannot be written as a convex mixture of pure Gaussian states. Witnesses of non-Gaussianity for arbitrary Fock states using linear optics have been derived in [46]. The aim of this section is to derive a witness of non-Gaussianity tailored to the state $|\psi \rangle$ where the full knowledge of the probabilities distributions of each detector is used, and not only of two as in [46]. In order to witness such non-Gaussianity, we again need to specialize the witness over the free parameters of the coefficients $\textbf{c}(\theta )$. A first step is defining and computing the maximum mean value $w_g$ of the witness operator over all Gaussian states, i.e.,

$$\begin{aligned} w_g(\theta )=\max _{\forall ~~\rho _G}({{\textrm{Tr}}}\!\left( {\hat{W}}(\theta )\rho _G\right) ). \end{aligned}$$

(42)

We note one more time that this expression is linear in $\rho _G$, and thus, we can conclude in the same manner that its maximum is achieved by a pure state and that it is then sufficient to perform the optimization over the set of pure Gaussian states. In this case, as opposed to the witnessing of non-classicality via $w_c(\theta )$, the expression for $w_g(\theta )$ is more intricated and the optimization was performed numerically over all states of the form

$$\begin{aligned} \rho _{G} = {\hat{S}}_{s}{\hat{D}}_{\alpha }|0\rangle , \end{aligned}$$

(43)

i.e.,  squeezed coherent states, in which ${\hat{D}}_{\alpha }$ and ${\hat{S}}_{s}$ are the canonical displacement and squeezing operators. More details can be found in Appendix B. The second and last step is performing a further optimization, now over the set of the coefficient parameters $\theta$, of the difference

$$\begin{aligned} g({\theta })=\text {Tr}( \rho _{TPG}(\eta ){\hat{W}}({\theta }))-w_g({\theta }), \end{aligned}$$

(44)

where $\rho _{TPG}$ is the lossy state given by Eq. (37), in order to find $g_{\text {opt}}=\max _{{\theta }}(g({\theta }))$. Finding a positive value of $g_{\text {opt}}$ certifies that the mean value of the witness in state $\rho _{TPG}$ breaks the Gaussian bound and thus that the state $|\psi \rangle$ cannot be represented by a mixture of states of the form of Eq. (43), meaning that this state is non-Gaussian.

Fig. 19

Optimized mean values of $g_{\text {opt}}$. The optimization is performed numerically over the set of parameter coefficients $\theta$ for a range of efficiencies $\eta$ and for $\epsilon = 10^{-2}$. In the upper inset, we plot the expected minimum number of runs $N_{opt}$ necessary for non-Gaussianity certification. In the lower inset, we zoom in on the region of efficiency $\eta$ from 0 to 45$\%$, showing that we find positive values of $g_{\text {opt}}$ for all efficiencies

Figure 19 shows the values of $g_{\text {opt}}$ obtained by numerical optimizations performed over a range of efficiencies $\eta$ of the setup. We find that a violation of the Gaussian bound can be witnessed by the auto-correlation witness of the form of Eq. (32) over the range of all efficiencies, which again demonstrates the robustness of the method against photon losses. In order to estimate the number $N_{opt}$ of experimental runs needed for the certification, we one more time set

$$\begin{aligned} g_{opt}=3 \sigma _{W_s}, \end{aligned}$$

(45)

where $\sigma _{W_s}$ is given by Eq. (39), but now using the coefficients $c_i$ optimized for the non-Gaussianity witness. This estimation is plotted in the upper inset Fig. 19 for the range of efficiencies $\eta$.

5 Discussion and conclusion

In this article, we have reviewed our past work, both experimental and theoretical, from bulk crystal to KTP waveguide and from a simplistic quantum analysis extrapolated from second-order nonlinear process, to a deep understanding of peculiarities of quantum behavior introduced by the third-order nonlinear interaction. We thus highlighted these differences, such as the dependence of the classical and quantum behavior on the seeding intensity, and the emergence and constraints induced by the non-Gaussianity. Then, we presented original theoretical results and fixed one of the remaining important problems: how to experimentally conclude at the quantumness and the non-Gaussianity of the generated triple-photon states engaging a minimal resource budget. We have thus introduced quantum witnesses using the minimum number of photocounting detectors, optimizing thus losses and complexity. The spontaneous generation of triple photon statistics by the third-order nonlinear interaction is still elusive, but we feel now closer.

The following step is to demonstrate the ability of these states to exhibit stronger form of quantum correlation such as Wigner negativity or non-locality. It is then possible to use these behaviors in quantum information protocols. The ability of generating heralded pairs of photons can be used in quantum repeater protocols. Moreover, using photon detectors preceded by displacement operation on one of the three modes of the state $|\psi \rangle _3$, it is then possible to herald a state of the form $|00\rangle +\epsilon |11\rangle$ that has the ability to violate Bell inequalities [47]. Time-bin genuine entanglement and non-locality can be demonstrated on the state $|\psi \rangle _3$ using Franson-type measurement. Indeed, all the photons can be sent to a single imbalanced interferometer and look at threefold coincidences at the outputs of the interferometer. Then, if the arm length difference of the interferometers is smaller than the coherence length of the pump, it is by principle impossible to tell if all three photons have taken the short or the long arm, effectively generating a three-mode Greenberger-Horne-Zeilinger state (GHZ state). The long-term aim is to add TPG process to the quantum optics toolbox for quantum communication and computation.

Appendices

Appendix A: Non-classicality witness

A pure coherent state can be written in the Fock or number state basis as

$$\begin{aligned} |\alpha \rangle = \exp \left( -\frac{{|\alpha |}^2}{2}\right) \sum _{n=0}^{\infty }\frac{\alpha ^{n}}{\sqrt{n!}}|n\rangle , \end{aligned}$$

(A1)

where $\alpha$ is a parameter defining the specific state. The action of balanced beam-splitters at coherent states given by Eq. (A1) is straightforwardly computable. Actually, after a beam splitting, the state is represented by two pure coherent states attenuated as $\alpha ^{'} \rightarrow \alpha /\sqrt{2}$ at each output path, so that the probabilities $P_{i}$ of observing i clicks at the detectors of Fig. 17 can be written as

$$\begin{aligned} P_{i} = \left( {\begin{array}{c}4\\ 4-i\end{array}}\right) \left( \exp (-\frac{|\alpha |^2}{4})\right) ^{i}\left( 1 - \exp (-\frac{|\alpha |^2}{4})\right) ^{i},\nonumber \\ \end{aligned}$$

(A2)

for $i = 1,2,3,4$. The non-classicality witness will then simply be given by the summation

$$\begin{aligned} W(\theta ) = \sum _{i=1}^{4}c_{i}(\theta )P_{i}, \end{aligned}$$

(A3)

with $c_{i}(\theta )$ defined by Eq. (33), and the maximization of $w_c(\theta )$ of Eq. (34) will consist of a maximization over the sole parameter $\alpha$. If we first define the change of parameters $x = \exp (-\frac{|\alpha |^2}{4})$, the value of $\alpha$ which maximizes Eq. (A3) can be found by computing the roots of

$$\begin{aligned} \frac{\partial W(\theta )}{\partial x} = \sum _{i=1}^{4}c_{i}(\theta )\frac{\partial P_{i}}{\partial x} = 0, \end{aligned}$$

(A4)

so that $\alpha _{opt}$ will be given by $\pm \sqrt{-4\ln (x)}$, with x adequately picked among the found roots of Eq. (A4). As can easily be seen, due to the form of the $P_{i}$, Eq. (A4) is, in turn, a third-order polynomial in the new variable x, and thus, its roots can be routinely found. By computing the value of $W(\theta )$ at values $\alpha$ associated with each of the found roots, and verifying which of those points consist of $W(\theta )$ maxima ($\frac{\partial ^2 W(\theta )}{\partial ^2 \alpha } < 0$), the maximization of Eq. (34) can thus be completely computed analytically.

Let us focus on the multimode case, since we cannot have access to the coherence on the setup. A general multimode classical state can be written as:

$$\begin{aligned} \rho _m = \sum _\lambda p(\lambda )\, \varrho _\lambda =\sum _\lambda p(\lambda ) \bigotimes _k\rho ^{[k]}_\lambda \end{aligned}$$

(A5)

where $\rho ^{[k]}_\lambda =|\alpha _k\rangle \langle \alpha _k|.$ The POVM associated with the event ”i detector click and 4-i does not clicks” can be written as:

$$\begin{aligned} {\hat{P}}_{im} = \left( {\begin{array}{c}4\\ i\end{array}}\right) (1 - \bigotimes _k{\hat{P}}_{0})^{\otimes i}\otimes (\bigotimes _k{\hat{P}}_{0})^{\otimes (4 - i)} \end{aligned}$$

(A6)

The maximum of $\text {Tr}(W(\theta )\rho _m)$ is achieved by pure multimode states for which we have

$$\begin{aligned}{} & {} \text {Tr}({\hat{P}}_{im}|\alpha _k\rangle \langle \alpha _k|^{\otimes {k}}) \nonumber \\{} & {} \quad = \left( {\begin{array}{c}4\\ i\end{array}}\right) \left( 1 - \prod _{i=1}^k e^{-\frac{|\alpha _k|^2}{4}}\right) ^{ i}\left( \prod _{i=1}^k e^{-\frac{|\alpha _k|^2}{4}}\right) ^{ (4 - i)} \end{aligned}$$

(A7)

$$\begin{aligned}{} & {} \quad =\left( {\begin{array}{c}4\\ i\end{array}}\right) \left( 1 - e^{-\frac{\sum _{i=1}^k|\alpha _k|^2}{4}}\right) ^{ i}\left( e^{-\frac{\sum _{i=1}^k|\alpha _k|^2}{4}}\right) ^{ (4 - i)} \end{aligned}$$

(A8)

which is the same expression than (A2) if we take $|\alpha |=\sqrt{\sum _{i=1}^k|\alpha _k|^2}$. Thus, the bound for single mode holds for the multimode case.

Appendix B: Non-gaussianity witness

The expectation value of the probability $P_i$ of observing i out of 4 detectors clicking is associated with the projector operator $\hat{P_{i}}$ of Eq. (32) acting on the state after the unitary evolution U representing the beam-splitters, and for a general pure Gaussian state $|G\rangle$ arriving in the setup of Fig. 17 this can be written as:

$$\begin{aligned}&P_{i} = \langle G|U^{\dagger }{\hat{P}}_{i}U|G\rangle \nonumber \\&\quad = \langle 0|{\hat{D}}_{\alpha }^{\dagger }{\hat{S}}_{s}^{\dagger }U^{\dagger }{\hat{P}}_{i}U{\hat{S}}_{s}{\hat{D}}_{\alpha }|0\rangle \nonumber \\&\quad = \langle \alpha |{\hat{S}}_{s}^{\dagger }U^{\dagger }{\hat{P}}_{i}U{\hat{S}}_{s}|\alpha \rangle , \end{aligned}$$

(B1)

where ${\hat{D}}_{\alpha }$ and ${\hat{S}}_{s}$ are the canonical displacement and squeezing operators, with displacement and squeezing parameters equal to $\alpha$ and s, respectively, and with $\hat{P_{i}}$ given by

$$\begin{aligned} {\hat{P}}_{i} = \left( {\begin{array}{c}4\\ i\end{array}}\right) (\hat{{\mathbb {I}}} - {\hat{P}}_{0})^{i}({\hat{P}}_{0})^{(4 - i)}, \end{aligned}$$

(B2)

where $\hat{P_{0}} = |0\rangle \langle 0|$ is the projector onto vacuum at each detector. We use the fact that any Gaussian state $|G\rangle$ can be written as a squeezed coherent state and, without loss of generality, we can choose s to be real while keeping $\alpha$ generally complex.

Alternatively, and for convenience of calculation, we can reinterpret Eq. (B1) as a reverse evolution $U^{\dagger }$ acting on the $\hat{P_{i}}$ operators and compute the expectation value of $U^{\dagger }{\hat{P}}_{i}U$ in the incoming general pure Gaussian state $|G\rangle$. In accordance with Eq. (B2), this can be performed by deriving all the operators of the form $U^{\dagger }({\hat{P}}_{0})^{k}(\hat{{\mathbb {I}}})^{4-k}U$, each of those associated to having 0 clicks at k detectors without mention of what is observed at the other $4-k$ detectors. This can be done as follows.

For a Fock state $|n\rangle$, the probability of detecting a vacuum state (no click) at a detector placed after two balanced beam-splitters, without mention to what is observed at any remaining detectors, can be written as:

$$\begin{aligned} P_{0,n} = \left( \frac{1}{2}\right) ^n\sum _{k = 0}^{n} \left( {\begin{array}{c}n\\ k\end{array}}\right) \left( \frac{1}{2}\right) ^k = \left( \frac{3}{4}\right) ^n. \end{aligned}$$

(B3)

For any convex combination of Fock states $|n\rangle$, the associated projector onto vacuum at this detector ($U^{\dagger }({\hat{P}}_{0})^{1}(\hat{{\mathbb {I}}})^{3}U$) can then be written in terms of the number operator $a^{\dagger }a$ as:

$$\begin{aligned} {\hat{P}}_{0,n} = \left( \frac{3}{4}\right) ^{a^{\dagger }a}. \end{aligned}$$

(B4)

The operators associated with the detection of two or three vaccum states after the beam-splitters can be derived in the same manner, and are given, respectively, by:

$$\begin{aligned} {\hat{P}}_{00,n}&= \left( \frac{1}{2}\right) ^{a^{\dagger }a}, \nonumber \\ {\hat{P}}_{000,n}&= \left( \frac{1}{4}\right) ^{a^{\dagger }a}. \end{aligned}$$

(B5)

Finally, the operator associated with all four detections not clicking (${\hat{P}}_{0000,n} = U^{\dagger }({\hat{P}}_{0})^{4}U$) will just be the vacuum operator $|0\rangle \langle 0|$, with associated probability being the modulus squared of the overlap of the incoming Gaussian state with the vaccum, that is $\langle G|0\rangle \langle 0|G\rangle = |\langle 0|G\rangle |^2$. As derived in ref.[48], we have that:

$$\begin{aligned} \langle 0|G\rangle = \langle 0|{\hat{S}}_{s}{\hat{D}}_{\alpha }|0\rangle = \exp \left( {-\frac{1}{2}|\alpha |^2 + \frac{1}{2}\alpha ^2\tanh {(s)}}\right) .\nonumber \\ \end{aligned}$$

(B6)

Again, instead of directly computing the expectation value of such projection operators in a general Gaussian state, in accordance with Eq. (B1), we can apply the reversed squeezing operator to these projectors and compute their expectation values on a coherent state $|\alpha \rangle$. Following the result in Eq. (9) of ref. [49], and the fact that $e^{(k a^\dagger a)}{=}{:}e^{((e^k-1)a^\dagger a)}:$, where  :  :  represents normal ordering, we have

$$\begin{aligned}&{\hat{S}}_{s}^{\dagger }e^{k a^{\dagger } a}{\hat{S}}_{s} = e^{-\frac{k}{2}}(e^{\frac{T_s}{2}(\frac{e^{2k}}{C_s^{2} - S_{s}^{2}e^{2k}}-1)a^{\dagger 2}}\nonumber \\&\quad \times :e^{(e^{-\ln {F_s}}-1)a^{\dagger } a} : \times e^{\frac{T_s}{2}(\frac{e^{2k}}{C_s^{2} - S_{s}^{2}e^{2k}}-1)a^{2}})/\sqrt{F_s}, \end{aligned}$$

(B7)

where $S_s = \sinh {(s)}$, $C_s = \cosh {(s)}$, $T_s = \tanh {(s)}$ and $F_s = e^{-k}C_s^{2} - e^{k}S_s^{2}$, and, to be consistent with ref. [49] results, we have to take s to $-s$. By taking values for the parameter k in accordance with each of the projectors of Eqs. (B4) and (B5), we will have all needed terms of the form $S^{\dagger }(s)U^{\dagger }({\hat{P}}_{0})^{k}(\hat{{\mathbb {I}}})^{4-k}US(s)$, and we are ready to compute their expectation values on the coherent state $|\alpha \rangle$: as Eq. (B7) is normal ordered in the field operators, it can be directly applied between $\langle \alpha |$ and $|\alpha \rangle$ in Eq. (B1) using $\langle \alpha |a^{\dagger 2}|\alpha \rangle = \alpha ^{* 2}$, $\langle \alpha |a^2|\alpha \rangle = \alpha ^2$ and $\langle \alpha |a^{\dagger }a|\alpha \rangle = |\alpha |^2$.

The witness of Eq. (32) of a Gaussian state can then be readily computed by summing the results as:

$$\begin{aligned} \langle G|\hat{W(\theta )}|G\rangle = \sum _{i=1}^{4} c_{i}\langle G|\hat{P_{i}}|G\rangle \end{aligned}$$

(B8)

Finally, we witness non-Gaussianity of state $|\psi \rangle$ whenever we find $\theta$ so that:

$$\begin{aligned} g(\theta )= & {} \langle \psi |{\hat{W}}(\theta )|\psi \rangle - \max _{\forall ~~\alpha ,s}\nonumber \\{} & {} \times (\langle G(\alpha ,s)|{\hat{W}}(\theta )|G(\alpha ,s)\rangle ) > 0. \end{aligned}$$

(B9)

Moreover, we can optimize the witness by computing $g_{\text {opt}}=\max _{{\theta }}(g({\theta }))$.