Skip to main content
SpringerLink
Log in

Anonymous quantum voting protocol based on Chinese remainder theorem

  • Regular Article - Quantum Information
  • Published:
The European Physical Journal D Aims and scope Submit manuscript

Abstract

Electronic voting is an essential tool in modern society. In this paper, we investigate anonymous quantum voting for the travelling ballot. At present, there exist some anonymous quantum travelling ballot protocols, but these protocols are not practical because of the lack of non-reusability or verifiability. Based on Chinese Remainder Theorem, an anonymous quantum voting protocol of the travelling ballot is proposed with an entanglement state, where the partial qubits of the entangled state as the quantum ballot are sent to each voter one-by-one and the other as the corresponding quantum certificate to the tallyman. The proposed protocol can not only ensure non-reusability but also can verify the correctness of the votes.

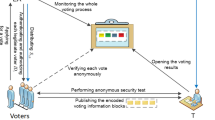
Graphic Abstract

(1) Define phase operators as voting operators based on Chinese Remainder Theorem; (2) Present an anonymous quantum voting protocol for the travelling ballot; (3) Meet more security requirements, e.g., verifiability, non-reusability and anonymity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Data Availability Statement

This manuscript has no associated data or the data will not be deposited. [Authors’ comment: All data generated or analyzed during this study are included in this published article.].

References

  1. M. Christandl, S. Wehner, Quantum anonymous transmissions. In Proceedings of 11th ASIACRYPT, Lecture Notes in Computer Science, vol. 3788. Springer, Berlin, pp. 217–235 (2005)

  2. M. Hillery, Quantum voting and privacy protection: first steps. Int. Soc. Opt. Eng (2006). https://doi.org/10.1117/2.1200610.0419

    Article  Google Scholar 

  3. J.A. Vaccaro, J. Spring, A. Chefles, Quantum protocols for anonymous voting and surveying. Phys. Rev. A 75, 012333 (2007)

    Article  ADS  Google Scholar 

  4. Y. Li, G. Zeng, Quantum anonymous voting systems based on entangled state. Opt. Rev. 15, 219–223 (2008)

    Article  Google Scholar 

  5. M. Bonanome, V. Bužek, M. Hillery, M. Ziman, Toward protocols for quantum-ensured privacy and secure voting. Phys. Rev. A 84, 022331 (2011)

    Article  ADS  Google Scholar 

  6. D. Horoshko, S. Kilin, Quantum anonymous voting with anonymity check. Phys. Lett. A 375, 1172–1175 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  7. Q.J. Xu, S.Y. Zhang, Improvement of the security of quantum protocols for anonymous voting and surveying. Sci. China Phys. Mech. Astron. 53, 2131–2134 (2010)

    Article  ADS  Google Scholar 

  8. Y. Li, G. Zeng, Anonymous quantum network voting scheme. Opt. Rev. 19, 121–124 (2012)

  9. L. Jiang, G. He, D. Nie et al., Quantum anonymous voting for continuous variables. Phys. Rev. A 85, 9335–9340 (2012)

    Google Scholar 

  10. Y.W. Wang, Quantum voting protocols based on the non-symmetric quantum channel with controlled quantum operation teleportation. Acta Phys. Sin. 62, 581–586 (2013)

    Google Scholar 

  11. D.S. Sundar, N. Narayan, A novel voting scheme using quantum cryptography (In Proc. Open Systems, 2015). IEEE, pp. 66–71

  12. H.J. Cao, L.Y. Ding, Y.F. Yu et al., An electronic voting scheme achieved by using quantum proxy signature. Int. J. Theor. Phys. 55, 1–8 (2016)

    Article  MathSciNet  Google Scholar 

  13. J.H. Tian, J.Z. Zhang, Y.P. Li, A voting protocol based on the controlled quantum operation teleportation. Int. J. Theor. Phys. 55, 2303–2310 (2016)

    Article  MathSciNet  Google Scholar 

  14. K. Thapliyal, R.D. Sharma, A. Pathak, Analysis and improvement of Tian-Zhang-Li voting protocol based on controlled quantum teleportation. arXiv:1602.00791 (2016)

  15. K. Thapliyal, R.D. Sharma, A. Pathak, Protocols for quantum binary voting. Int. J. Quantum Inf. 15, 175–179 (2016)

    MATH  Google Scholar 

  16. Q. Wang, C. Yu, F. Gao et al., Self-tallying quantum anonymous voting. Phys. Rev. A 94, 022333 (2016)

    Article  ADS  Google Scholar 

  17. J.L. Zhang, S.C. Xie, J.Z. Zhang, An elaborate secure quantum voting scheme. Int. J. Theor. Phys. 56, 1–10 (2017)

    Article  ADS  Google Scholar 

  18. P. Xue, X. Zhang, A simple quantum voting scheme with multi-qubit entanglement. Sci. Rep. 7, 7586 (2017)

    Article  ADS  Google Scholar 

  19. R.H. Shi, Y. Mu, H. Zhong et al., Quantum oblivious set-member decision protocol. Phys. Rev. A 92, 022309 (2015)

    Article  ADS  Google Scholar 

  20. R.H. Shi, Y. Mu, H. Zhong et al., Quantum private set intersection cardinality and its application to anonymous authentication. Inf. Sci. 370–371, 147–158 (2016)

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by National Natural Science Foundation of China (No. 61772001 and 61672010).

Author information

Authors and Affiliations

  1. School of Computer Science, Hubei University of Technology, Wuhan City, 430068, China

    Run-hua Shi, Bai Liu & Mingwu Zhang

  2. School of Control and Computer Engineering, North China Electric Power University, Beijing City, 102206, China

    Run-hua Shi

  3. School of Computer Science and Technology, Anhui University, Hefei City, 230601, China

    Jia-qi Qin

Authors
  1. Run-hua Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jia-qi Qin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Bai Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mingwu Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Run-hua Shi or Mingwu Zhang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shi, Rh., Qin, Jq., Liu, B. et al. Anonymous quantum voting protocol based on Chinese remainder theorem. Eur. Phys. J. D 75, 20 (2021). https://doi.org/10.1140/epjd/s10053-020-00014-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjd/s10053-020-00014-2

Search

Navigation