Effects of spin-orbital coupling on the propagation of whistler waves in the magnetized plasma

Abstract

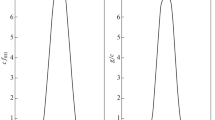
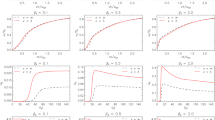
We study the spin-orbital corrections to the propagation of the whistler waves in a astrophysical quantum magnetoplasma composed by mobile ions and electrons. We use a fluid formalism to include weakly relativistic corrections due to the spin-orbital interactions and spin correction due to the magnetization energy of electrons and to the Bohm potential. We explicate a method of quantum magnetohydrodynamics (QMHD) for the study of the evolution of whistlers. The presented method is based upon the Schrödinger equation. Fundamental QMHD equations for electron-ion plasma were derived from the many-particle microscopic Schrödinger equation. We have applied the renormalization group method to obtain more general dynamical equations for the slowly varying amplitudes of whistler waves which involve the spin correction due to the Bohm potential and to magnetization energy of electrons, but also the spin-orbital corrections. We have found that the spin-orbital contributions to the whistler mode depends on the frequency due to its spin and must meaningful for the external magnetic field is below the quantum critical magnetic field strength.