1 Introduction

When considering the focus areas of cosmology and relativistic astrophysics, we focus on radiating stars in which the centre of attention is gravitational collapse amongst many other vital components such as stability, luminosity and temperature profiles. The use of spherically symmetric spacetime geometries render them even more useful when describing dense objects such as neutron stars, pulsars and ultra-compact strange stars in the strong gravity regime. Earlier pioneering works by Vaidya [1], Santos [2], Kolassis et al. [3] and Bonnor et al. [4] have subsequently led to the development of numerous ideas furthering our understanding of non-adiabatic gravitational collapse, the formation of super dense stars, black holes and the Cosmic Censorship Conjecture (CCC). Di Prisco et al. [5], studied non-adiabatic collapse processes on time scales shorter than the relaxation period. The relativistic heat equation was analysed and it was found that the luminosity during the early pre-relaxation stage was substantially different from that measured in the absence of relaxation. In an earlier treatment Tomimura and Nunes [6] investigated a model for a spherical radiating fluid with shear and expansion. By performing a process of matching across the surface they were able to show that at this interface, the energy density of the outgoing null radiation is exactly equal to the pressure. An imperfect stellar fluid with zero shear and zero acceleration was considered as the basis for a collapse scenario presented by Govender et al. [7]. They employed an exact solution to compute the fluid temperature for constant as well as variable collision time, and demonstrated that the central temperature in the causal limit is significantly higher than that measured in the non-causal case. A generalisation of this work which included the influence of shearing stresses was later carried out by Chan [8]. It was suggested that in the initial stages of radiative collapse the pressure of the stellar fluid is isotropic and that it becomes increasingly more anisotropic as the collapse proceeds. This is attributed to the effect of the shearing motion of the fluid distribution. The solution therein was used to comment on the physical features of a six times solar mass star. Relativistic models that are to be utilized in the description of systems with astrophysical importance should also include an acceptable equation of state (EoS). Consequently, numerous efforts have been made to incorporate an EoS along with other reasonable conditions that are suitable for more detailed investigations. Govender et al. [9] focused on radiative gravitational collapse with radial heat flux which described the stages that were close to the formation of a super dense cold star. In their model, they specified the temporal evolution by solving the junction conditions for radiating gravitational collapse. Their model also generates solutions for the earlier evolution stages of the star by a perturbative approach given that there is a known static configuration of a star. Hussain [10] generated exact solutions for a collapsing null fluid with pressure P, and density \(\rho \) related by a polytropic (EoS) of the form \( P = k \rho ^{a}\). All of the reported solutions were in good agreement with the CCC. Static spherically symmetric relativistic stars were explored by Sharma and Maharaj [11]. They assumed pressure anisotropy along with a linear equation of state \(p = n(\rho -\rho _{s})\), formulated earlier by Dey et al. [12], for applications to strange stars consisting of a quark gluon mixture. Non-singular and regular solutions for the stellar interior were generated by solving the modified Tolman–Oppenheimer–Volkoff (TOV) equation. The imposing of an arbitrarily linear barotropic EoS was a key factor in a shear-free model having nonzero radial heat flux proposed by Wagh et al. [13]. The exact solution resulting from the analysis of the simplified junction condition \(p = qB\) was used to probe the temporal evolution of the thermodynamic and matter variables. A recent project by Brassel et al. [14] involved a comprehensive examination of collapsing stars while considering a wide variety of equations of state. The mass function corresponding to each EoS was interrogated and localised naked singularities were predicted for the end stage of the collapse process. Some work, although not much, has also been devoted to special cases of the more general and astrophysically relevant polytropic equation of state, mentioned earlier. Mafa Takisa and Maharaj [15] studied static (non-rotating and adiabatic) spherical fluid masses with the inclusion of electric field and anisotropic pressure effects. They closed the Einstein–Maxwell system of equations with a general polytropic equation of state and were successful in obtaining new classes of solutions which interestingly, contained the earlier results of Feroze and Siddiqui [16] and Maharaj and Mafa Takisa [17] in the uncharged limit. In a subsequent investigation, Ngubelanga and Maharaj [18] imposed a polytropic equation of state to study compact stars. Their results contained the mass of the star PSR J1903+327.

Much recent investigations which coupled the gravitational collapse and dissipative processes were explored in greater detail by Ivanov [19] and Tewari [20, 21], Sarwe and Tikekar [22] and Sharma and Tikekar [23]. These investigations focused on the interior energy momentum tensor which was a neutral relativistic anisotropic fluid with heat flow. This then led to the understanding of there being an electromagnetic field which could possibly alter the physical features in a relativistic radiating star and in turn will disrupt the nature of gravitational interactions. The junction conditions which matched the interior radiating matter distribution to the Vaidya exterior for neutral matter were achieved by Santos [2]. A generalization of the junction conditions were completed by De Oliveira and Santos [24] which consisted of the electromagnetic field. Di Prisco et al. [25] in their work utilized a systematic approach in their investigation of nonadiabatic charged spherical gravitational collapse for diffusion and free-streaming limits. A class of charged anisotropic collapsing models were established by Cipolletta and Giambo [26] in which it was revealed that the shell focussing singularities could be avoided. When looking at the Karmarkar condition [27], it is important to note indirectly, a curved four-dimensional metric can be embedded within a five-dimensional pseudo-Euclidean space-time. This valuable condition gives a geometric relationship between the metric functions and their derivatives respectively. This allows one of the metric functions to be selected and the other can be determined. The Karmarkar condition gives a Kohler–Chao solution which is a non-conformally flat unbounded solution [28] or the Schwarzschild solution which is the homogeneous conformally flat bounded solution for the case in which one is presented with an isotropic static fluid sphere. When looking at static anisotropic matter, these arrangements give a geometrical mechanism in which equations of state can form a relationship between the radial and tangential pressures.

In more recent works established in the literature, Naidu et al. [29] engaged the Karmarkar condition in their model which consisted of a spherically symmetric radiating star undergoing dissipative gravitational collapse in the form of a radial heat flux. This gives more detailed insight into the Karmarkar condition as they determined a particular solution of the boundary condition which made the Karmarkar condition independent of time. Govender et al. [30] presented in their model that the dissipative gravitational collapse as a result from an initial static core satisfies the Karmarkar condition in isotropic coordinates, and proceeds non-adiabatically by releasing energy in the form of a radial heat flux to the exterior Vaidya spacetime. The Karmarkar scalar condition was used in the model by Ospino et al. [31], where they had executed a method to obtain all possible embedding class I static spherical solutions. An analysis was carried out on the incompatibility of the Kamarkar condition with several commonly assumed simplifications to the study of gravitational collapse. In the work done by Jaryal [32], a class of exact spherical symmetric solutions of the Einstein equations was presented which revealed heat conducting anisotropic fluid as a collapsing matter. The class of solutions presented not only satisfy all energy conditions throughout the interior of the star but also show that the luminosity is independent of time. Radiating collapse invoking the Karmarkar condition in modfied gravity theories such as f(R) and f(R, T) gravity have also been explored [33,34,35]. The dynamics of dissipative collapse in f(R) gravity has been investigated by Abbas et al. [36] in which they employed a full causal heat transport equation coupled to the matter profiles. In the model established by Herrera [37], the conditions for instability/stability of the isotropic pressure condition for collapsing spherically symmetric, dissipative fluid distributions were looked at. In this model, he found that dissipative fluxes, energy density inhomogeneities as well as the appearance of shear in the fluid flow, forces any initially isotropic configuration to relinquish that condition which then generates anisotropy in the pressure. Pretel et al. [38] configured a model in which they discussed the stability and constructed dynamical configurations describing the gravitational collapse of unstable neutron stars with realistic equations of state that are compatible with the LIGO-Virgo constraints. They carried out an analysis on stellar stability for equations of state. Numerical solutions were found that agree with the temporal and radial behaviour during the evolution of the collapse for precise relevant physical quantities which included the mass, luminosity and energy density amongst many others.

This paper is structured as follows. In Sect. 2 we introduce the field equations describing the geometry and matter content for a star undergoing gravitational collapse. In Sect. 3 we present the Riemann tensor components and show how the Karmarkar condition for the shear-free metric can be written. In Sect. 4 the exterior spacetime together with the junction conditions are presented. In Sect. 5 the perturbed equations are determined and the metric functions and the material functions are presented. In Sect. 6 the perturbation of the Karmarkar condition is carried out. In Sect. 7 we present the radiating solution in which we model a radiating star that collapses from an initial static configuration. In Sect. 8 we consider the physical viability of our model coupled with graphical representations of our results. Some concluding comments are made in Sect. 9.

2 Interior spacetime

The line element for the interior of the collapsing star is given by the general spherically symmetric, shear-free metric in comoving coordinates

$$\begin{aligned} ds^2 = -A^2dt^2 + B^2[dr^2 + r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2)], \end{aligned}$$
(1)

where \(A = A(r,t)\) and \(B = B(r,t)\).

The interior matter content is that of an isotropic spherical fluid undergoing dissipation in the form of a radial heat flow and producing pure radiation. The energy momentum tensor for the interior matter distribution is given by

$$\begin{aligned} T_{ab}= & {} (\mu + p_t)w_a w_b + p_tg_{ab} + (p_r - p_t)X_aX_b \nonumber \\&+ q_aw_b + q_b w_a, \end{aligned}$$
(2)

where \(\mu \) is the energy density, \(p_r\) the radial pressure, \(p_t\) the tangential pressure and \(q_a\) the heat flux, \(w_a\) is the four-velocity of the fluid and \(X_a\) is a unit four-vector along the radial direction. These quantities must satisfy \(w_aw^a = -1\), \(w_aq^a = 0\), \(X_aX^a = 1\) and \(X_aw^a = 0\). Furthermore, in comoving coordinates we have

$$\begin{aligned} w^a= & {} A^{-1}\delta ^a_0 , \end{aligned}$$
(3)
$$\begin{aligned} q^a= & {} q\delta ^a_1 , \end{aligned}$$
(4)

and

$$\begin{aligned} X^a = B^{-1}\delta ^a_1 . \end{aligned}$$
(5)

The nonzero components of the Einstein field equations for the line element (1) and the energy momentum (2) are

$$\begin{aligned} \mu= & {} - \frac{1}{B^2}\left[ 2\frac{B^{\prime \prime }}{B} - \left( \frac{B^{\prime }}{B}\right) ^2 +\frac{4}{r}\frac{B^{\prime }}{B}\right] +\frac{3}{A^2}\left( \frac{{\dot{B}}}{B}\right) ^2 , \end{aligned}$$
(6)
$$\begin{aligned} p_r= & {} \frac{1}{B^2}\left[ \left( \frac{B^{\prime }}{B}\right) ^2 + \frac{2}{r}\left( \frac{A^{\prime }}{A}+ \frac{B^{\prime }}{B}\right) + 2\frac{A^{\prime }}{A}\frac{B^{\prime }}{B}\right] \nonumber \\&+ \frac{1}{A^2}\left[ -2\frac{{\ddot{B}}}{B} - \left( \frac{\dot{B}}{B}\right) ^2 + 2\frac{\dot{A}}{A}\frac{\dot{B}}{B}\right] , \end{aligned}$$
(7)
$$\begin{aligned} p_t= & {} \frac{1}{A^2}\left[ -2\frac{{\ddot{B}}}{B} -\left( \frac{\dot{B}}{B}\right) ^2 +2 \frac{\dot{A}}{A}\frac{\dot{B}}{B}\right] \nonumber \\&+ \frac{1}{B^2}\left[ \frac{B^{\prime \prime }}{B}-\left( \frac{B^{\prime }}{B}\right) ^2+\frac{1}{r}\left( \frac{A^{\prime }}{A}+\frac{B^{\prime }}{B}\right) +\frac{A^{\prime \prime }}{A}\right] , \end{aligned}$$
(8)
$$\begin{aligned} q= & {} \frac{2}{AB^2}\left[ \frac{{\dot{B}}^{\prime }}{B}-\frac{\dot{B}}{B}\left( \frac{B^{\prime }}{B}+\frac{A^{\prime }}{A}\right) \right] , \end{aligned}$$
(9)

where the dots and primes represent the partial derivatives with respect to t and r respectively.

3 Karmarkar condition

The Riemann tensor components which are nonzero are given by

$$\begin{aligned} {\mathscr {R}}_{1212}= & {} \frac{r}{A^2} \biggl (r A^2 B^{\prime 2} -A^2 B B^{\prime }-r A^2 B B^{\prime \prime }+r B^2 {\dot{B}}^2\biggr ) , \end{aligned}$$
(10)
$$\begin{aligned} {\mathscr {R}}_{1220}= & {} \frac{r^2}{A} \biggl (AB{\dot{B}}^{\prime }-A^{\prime }B{\dot{B}}-A B^{\prime } {\dot{B}}\biggr ) , \end{aligned}$$
(11)
$$\begin{aligned} {\mathscr {R}}_{1313}= & {} \frac{r\sin ^2{\theta }}{A^2} \biggl (r A^2 B^{\prime 2} - A^2 B B^{\prime }- r A^2 B B^{\prime \prime } + r B^2 {\dot{B}}^2 \biggr ), \end{aligned}$$
(12)
$$\begin{aligned} {\mathscr {R}}_{1330}= & {} \frac{r^2 \sin ^2{\theta }}{A} \biggl (-A^{\prime }B {\dot{B}}-A B^{\prime } {\dot{B}}+A B {\dot{B}}^{\prime }\biggr ), \end{aligned}$$
(13)
$$\begin{aligned} {\mathscr {R}}_{1010}= & {} \frac{-1}{AB}\biggl (A^{\prime } A^2 B^{\prime }-{\dot{A}} B^2 {\dot{B}}-A^{\prime \prime } A^2 B+A B^2 {\ddot{B}}\biggr ), \end{aligned}$$
(14)
$$\begin{aligned} {\mathscr {R}}_{2323}= & {} \frac{r^3 \sin ^2{\theta }}{A^2} \biggl (-r A^2 B^{\prime 2} -2 A^2 B B^{\prime }+r B^2 {\dot{B}}^2\biggr ), \end{aligned}$$
(15)
$$\begin{aligned} {\mathscr {R}}_{2020}= & {} \frac{-r}{A B} \biggl (-rA^{\prime } A^2 B^{\prime }-r {\dot{A}} B^2 {\dot{B}}-A^{\prime } A^2B+r A B^2 {\ddot{B}}\biggr ), \end{aligned}$$
(16)
$$\begin{aligned} {\mathscr {R}}_{3030}= & {} \frac{-r\sin ^2{\theta }}{A B} \biggl (-r A^{\prime }A^2 B^{\prime }-r {\dot{A}} B^2 {\dot{B}}-A^{\prime } A^2 B +r A B^2 {\ddot{B}}\biggr ) , \nonumber \\ \end{aligned}$$
(17)

for the shear-free metric (1).

The Karmarkar condition for the shear-free metric (1) can be written as

$$\begin{aligned} {\mathscr {R}}_{1220} {\mathscr {R}}_{1330} + {\mathscr {R}}_{1010} {\mathscr {R}}_{2323} -{\mathscr {R}}_{1212}{\mathscr {R}}_{3030}=0 . \end{aligned}$$
(18)

From the component equations (10)–(17), the Karmarkar condition (18) takes the form

$$\begin{aligned} 0= & {} r^2 A B \left( -A^{\prime }B {\dot{B}}-A B^{\prime } {\dot{B}}+A B{\dot{B}}^{\prime }\right) ^2 \nonumber \\&-r \left( -r A^2 B^{\prime 2} -2 A^2 B B^{\prime }+r B^2 {\dot{B}}^2\right) \nonumber \\&\times \left( A^{\prime } A^2 B^{\prime }-{\dot{A}} B^2 {\dot{B}}-A^{\prime \prime } A^2 B+A B^2 {\ddot{B}}\right) \nonumber \\&+\left( r A^2B^{\prime 2} -A^2 B B^{\prime }-r A^2 B B^{\prime \prime }+r B^2 {\dot{B}}^2\right) \nonumber \\&\times \left( -r A^{\prime } A^2 B^{\prime }-r {\dot{A}} B^2 {\dot{B}}-A^{\prime } A^2B+r A B^2 {\ddot{B}}\right) , \end{aligned}$$
(19)

a highly nonlinear equation.

4 Exterior spacetime and junction conditions

Spacetime is divided by the boundary of a star into two distinct regions, the interior spacetime described by the metric (1) and the exterior spacetime. Since the collapsing star is radiating energy, the exterior spacetime is not a vacuum and is therefore described by Vaidya’s metric

$$\begin{aligned} ds^2_+= & {} -\left[ 1 - \frac{2m(v)}{\texttt {r}}\right] dv^2 - 2dvd\texttt {r} + \texttt {r}^2 d\theta ^2 \nonumber \\&+ \texttt {r}^2\sin ^2\theta d\phi ^2 , \end{aligned}$$
(20)

where m(v), the total energy inside \(\Sigma \), is a function of the retarded time v.

The two junction conditions to be satisfied across the boundary are

$$\begin{aligned} \left( K^+_{ij} - K^-_{ij}\right) _{\Sigma } = 0, \end{aligned}$$
(21)

and

$$\begin{aligned} \left( ds^2_+ - ds^2_-\right) _{\Sigma } =0, \end{aligned}$$
(22)

where \(K_{ij}\) is the extrinsic curvature on the two sides of the boundary. Following similar calculations as in de Oliveira et al [24] we obtain

$$\begin{aligned} \left( p_r\right) _{\Sigma }= & {} \left( qB\right) _{\Sigma }, \end{aligned}$$
(23)
$$\begin{aligned} \left( qB\right) _{\Sigma }= & {} -\left( \frac{2}{\texttt {r}^2}{{\dot{v}}^2}\frac{dm}{dv}\right) _{\Sigma } , \end{aligned}$$
(24)
$$\begin{aligned} \left( rB\right) _{\Sigma }= & {} \texttt {r}_{\Sigma } , \end{aligned}$$
(25)
$$\begin{aligned} m(v)= & {} \left( \frac{r^3B{\dot{B}}^2}{2A^2} - r^2{B^{\prime }} - \frac{r^3{{B^{\prime }}^2}}{2B}\right) _{\Sigma } , \end{aligned}$$
(26)

and

$$\begin{aligned} \left( A dt\right) _{\Sigma } = \left( 1 - \frac{2m}{\texttt {r}} + 2\frac{d\texttt {r}}{dv}\right) ^{1/2}_{\Sigma } dv . \end{aligned}$$
(27)

Equations (23)–(27) represent respectively the following conditions across the boundary \({\Sigma }\): conservation of momentum flux, conservation of radiation flux, radius of \(\Sigma \) in both coordinate systems, total energy inside \(\Sigma \) and the relationship between the two times t and v. The total energy entrapped up to a radius of r inside \(\Sigma \) is given by

$$\begin{aligned} m(r,t) = \frac{r^3B{\dot{B}}^2}{2A^2} - r^2{B^{\prime }} - \frac{r^3{{B^{\prime }}^2}}{2B} . \end{aligned}$$
(28)

5 The perturbed equations

We assume that the fluid is initially in static equilibrium, hence the fluid is described by quantities that have radial dependence only. We then assert that the static system is perturbed, undergoing slow shear-free collapse and producing pure radiation. We denote the quantities such as energy density, radial pressure and tangential pressure of the static system by a zero subscript and those of the perturbed fluid by an overhead bar. We further assume that the metric functions A(r, t) and B(r, t) have the same time dependence in their perturbations. This assumption would imply that the perturbed material functions also have the same time dependence. Therefore the metric functions and the material functions are given by

$$\begin{aligned} A(r,t)= & {} A_0(r) + \epsilon a(r)T(t), \end{aligned}$$
(29)
$$\begin{aligned} B(r,t)= & {} B_0(r) + \epsilon b(r)T(t) ,\end{aligned}$$
(30)
$$\begin{aligned} \mu (r,t)= & {} \mu _0(r) + \epsilon {\bar{\mu }}(r,t) , \end{aligned}$$
(31)
$$\begin{aligned} p_r(r,t)= & {} p_{r0}(r) + \epsilon {{\bar{p}}}_r(r,t) ,\end{aligned}$$
(32)
$$\begin{aligned} p_t(r,t)= & {} p_{t0}(r) + \epsilon {{\bar{p}}}_t(r,t) ,\end{aligned}$$
(33)
$$\begin{aligned} m(r,t)= & {} m_0(r) + \epsilon {\bar{m}}(r,t) , \end{aligned}$$
(34)

where we assume that \(0<\epsilon \ll 1\).

Einstein’s field equations for the static configuration are

$$\begin{aligned} \mu _0= & {} - \frac{1}{B_0^2}\left[ 2\frac{B_0^{\prime \prime }}{B_0} - \left( \frac{B_0^{\prime }}{B_0}\right) ^2 +\frac{4}{r}\frac{B_0^{\prime }}{B_0}\right] , \end{aligned}$$
(35)
$$\begin{aligned} p_{r0}= & {} \frac{1}{B_0^2}\left[ \left( \frac{B_0^{\prime }}{B_0}\right) ^2 + \frac{2}{r}\left( \frac{A_0^{\prime }}{A_0}+ \frac{B_0^{\prime }}{B_0}\right) + 2\frac{A_0^{\prime }}{A_0}\frac{B_0^{\prime }}{B_0}\right] , \end{aligned}$$
(36)
$$\begin{aligned} p_{t0}= & {} \frac{1}{B_0^2}\left[ \frac{B_0^{\prime \prime }}{B_0}-\left( \frac{B_0^{\prime }}{B_0}\right) ^2+\frac{1}{r}\left( \frac{A_0^{\prime }}{A_0}+\frac{B_0^{\prime }}{B_0}\right) +\frac{A_0^{\prime \prime }}{A_0}\right] .\nonumber \\ \end{aligned}$$
(37)

The perturbed field equations up to first order in \(\epsilon \) can be written as

$$\begin{aligned} {\bar{\mu }}= & {} -3\mu _0\frac{b}{B_0}T + \frac{1}{B_0^3} \nonumber \\&\times \biggl [-\left( \frac{B_0^{\prime }}{B_0}\right) ^2 b + 2\left( \frac{B_0^{\prime }}{B_0} -\frac{2}{r}\right) b^{\prime } -2b^{\prime \prime }\biggr ]T , \end{aligned}$$
(38)
$$\begin{aligned} {\bar{p}}_r= & {} -2p_{r0}\frac{b}{B_0}T + \frac{2}{B_0^2}\biggl [\left( \frac{B_0^{\prime }}{B_0} + \frac{1}{r} + \frac{A_0^{\prime }}{A_0}\right) \left( \frac{b}{B_0}\right) ^{\prime } \nonumber \\&+\left( \frac{B_0^{\prime }}{B_0}+ \frac{1}{r}\right) \left( \frac{a}{A_0}\right) ^{\prime }\biggr ]T- 2\frac{b}{{A_0^2}B_0}{{\ddot{T}}} , \end{aligned}$$
(39)
$$\begin{aligned} {\bar{p}}_t= & {} -2p_{t0}\frac{b}{B_0}T \nonumber \\&+ \frac{1}{B_0^2}\biggl [\left( \frac{b}{B_0}\right) ^{\prime \prime } + \frac{1}{r}\left( \frac{b}{B_0}\right) ^{\prime } + 2\frac{A_0^{\prime }}{A_0}\left( \frac{a}{A_0}\right) ^{\prime } +\left( \frac{a}{A_0}\right) ^{\prime \prime } \nonumber \\&+ \frac{1}{r}\left( \frac{a}{A_0}\right) ^{\prime }\biggr ]T - 2\frac{b}{{A_0^2}B_0}{{\ddot{T}}} , \end{aligned}$$
(40)
$$\begin{aligned} qB= & {} \frac{2}{B_0}\left( \frac{b}{A_0 B_0}\right) ^{\prime }{\dot{T}} . \end{aligned}$$
(41)

The total energy entrapped up to radius r inside \(\Sigma \) for the static and perturbed configurations are respectively given by

$$\begin{aligned} m_0(r_{\Sigma })= & {} -\left( r^2{B_0^{\prime }} + \frac{r^3{{B_0^{\prime }}^2}}{2B_0}\right) _{\Sigma }, \end{aligned}$$
(42)
$$\begin{aligned} {\bar{m}}(r_{\Sigma },t)= & {} -\left( \left[ {r^2}b^{\prime } + \frac{r^3{{B_0^{\prime }}^2}}{2B_0} \left( 2\frac{b^{\prime }}{B_0^{\prime }}-\frac{b}{B_0}\right) \right] T(t)\right) _{\Sigma }. \nonumber \\ \end{aligned}$$
(43)

The smooth matching of the interior spacetime to the Vaidya exterior is facilitated by using the junction conditions derived by Santos [2], and we may rewrite Eqs. (39) and (41) as

$$\begin{aligned} {\bar{p}}_r = -2p_{r0}\frac{b}{B_0}T +\frac{2b}{{A_0^2}B_0}\left( {\alpha }T - {{\ddot{T}}}\right) , \end{aligned}$$
(44)

and

$$\begin{aligned} qB = \frac{4b}{{A_0^2}B_0}{\beta }{\dot{T}}, \end{aligned}$$
(45)

where

$$\begin{aligned} \alpha (r)= & {} \frac{A_0^2}{B_0 b}\biggl [\left( \frac{B_0^{\prime }}{B_0} + \frac{1}{r} + \frac{A_0^{\prime }}{A_0}\right) \left( \frac{b}{B_0}\right) ^{\prime } \nonumber \\&+ \left( \frac{B_0^{\prime }}{B_0}+ \frac{1}{r}\right) \left( \frac{a}{A_0}\right) ^{\prime }\biggr ], \end{aligned}$$
(46)

and

$$\begin{aligned} \beta (r) = \frac{A_0^2}{2b}\left( \frac{b}{A_0B_0}\right) ^{\prime }. \end{aligned}$$
(47)

6 Perturbed Karmarkar condition

Using (19) together with Eqs. (30) and (31) yields

$$\begin{aligned} 0= & {} \Biggl [{A_0}^4B_0\biggl [{B_0}^{\prime }\biggl ({A_0}^{\prime }\bigl (B_0+2r{B_0}^{\prime }\bigr )-r\bigl (2B_0+r{B_0}^{\prime }\bigr ){A_0}^{{\prime }{\prime }}\biggr ) \nonumber \\&+r{A_0}^{\prime }\bigl (B_0+r{B_0}^{\prime }\bigr ){B_0}^{{\prime }{\prime }}\biggr ]\Biggr ]_{Static Karmarkar}\nonumber \\&+ \epsilon \Biggl [ rb{A_0}^3{B_0}^2{{\ddot{T}}}\bigl (2r{{B_0}^{\prime }}^2+B_0[{B_0}^{\prime }-r{B_0}^{{\prime }{\prime }}]\bigr )\nonumber \\&+{A_0}^3T\Biggl [4aB_0\Bigl [{B_0}^{\prime }\bigl ({A_0}^{\prime }[B_0+2r{B_0}^{\prime }]-r[2B_0+r{B_0}^{\prime }]{A_0}^{{\prime }{\prime }}\bigr ) \nonumber \\&+ r{A_0}^{\prime }[B_0+r{B_0}^{\prime }]{B_0}^{{\prime }{\prime }}\Bigr ]\nonumber \\&+A_0\Bigl [B_0\biggl ({B_0}^{\prime }\bigl (2b[{A_0}^{\prime }-2r{A_0}^{{\prime }{\prime }}]+r\bigl ({B_0}^{\prime }[2{a}^{\prime }-r{a}^{{\prime }{\prime }}] \nonumber \\&-2r{b}^{\prime }{A_0}^{{\prime }{\prime }}\bigr )\bigr )+\bigl ([2b+r{b}^{\prime }]{A_0}^{\prime }+r{a}^{\prime }{B_0}^{\prime }\bigr ){B_0}^{{\prime }{\prime }}\biggr ) \nonumber \\&+rb{B_0}^{\prime }\bigl (-r{B_0}^{\prime }{A_0}^{{\prime }{\prime }}+{A_0}^{\prime }[2{B_0}^{\prime }+r{B_0}^{{\prime }{\prime }}]\bigr ) \nonumber \\&+{B_0}^2\bigl ({B_0}^{\prime }[{a}^{\prime }-2r{a}^{{\prime }{\prime }}]+{b}^{\prime }[{A_0}^{\prime }-2r{A_0}^{{\prime }{\prime }}] \nonumber \\&+r[{A_0}^{\prime }{b}^{{\prime }{\prime }}+{a}^{\prime }{B_0}^{{\prime }{\prime }}]\bigr )\Bigr ]\Biggr ]\Biggr ]_{Time Dependent Karmarkar}. \nonumber \\ \end{aligned}$$
(48)

At this point we should point out that the time-dependent Karmarkar condition is a nonlinear partial differential equation. It is highly nonlinear in the radial component and holds at each interior point of the collapsing sphere. It is also evident from (48) that the Karmarkar condition separates out into a static part and a nonstatic part. If we assume that the initial static configuration (\(A_0,B_0\)) satisfies the static part of the Karmarkar condition (48), then we are able to write

$$\begin{aligned} A_0= k_1 + k_2\int {\sqrt{(r^2{B_0})'{B_0}'}}dr , \end{aligned}$$
(49)

which relates the potentials \(A_0(r)\) and \(B_0(r)\) with \(k_1\) and \(k_2\) being integration constants. Substituting (49) into (48) yields

$$\begin{aligned} 0= & {} \Biggl [ rb{A_0}^3{B_0}^2{{\ddot{T}}}\bigl (2r{{B_0}^{\prime }}^2+B_0[{B_0}^{\prime }-r{B_0}^{{\prime }{\prime }}]\bigr )\nonumber \\&+{A_0}^3T\Biggl [4aB_0\Bigl [{B_0}^{\prime }\bigl ({A_0}^{\prime }[B_0+2r{B_0}^{\prime }]-r[2B_0+r{B_0}^{\prime }]{A_0}^{{\prime }{\prime }}\bigr ) \nonumber \\&+ r{A_0}^{\prime }[B_0+r{B_0}^{\prime }]{B_0}^{{\prime }{\prime }}\Bigr ]\nonumber \\&+A_0\Bigl [B_0\biggl ({B_0}^{\prime }\bigl (2b[{A_0}^{\prime }-2r{A_0}^{{\prime }{\prime }}]+r\bigl ({B_0}^{\prime }[2{a}^{\prime }-r{a}^{{\prime }{\prime }}] \nonumber \\&-2r{b}^{\prime }{A_0}^{{\prime }{\prime }}\bigr )\bigr )+\bigl ([2b+r{b}^{\prime }]{A_0}^{\prime }+r{a}^{\prime }{B_0}^{\prime }\bigr ){B_0}^{{\prime }{\prime }}\biggr ) \nonumber \\&+rb{B_0}^{\prime }\bigl (-r{B_0}^{\prime }{A_0}^{{\prime }{\prime }}+{A_0}^{\prime }[2{B_0}^{\prime }+r{B_0}^{{\prime }{\prime }}]\bigr ) \nonumber \\&+{B_0}^2\bigl ({B_0}^{\prime }[{a}^{\prime }-2r{a}^{{\prime }{\prime }}]+{b}^{\prime }[{A_0}^{\prime }-2r{A_0}^{{\prime }{\prime }}] \nonumber \\&+r[{A_0}^{\prime }{b}^{{\prime }{\prime }}+{a}^{\prime }{B_0}^{{\prime }{\prime }}]\bigr )\Bigr ]\Biggr ]\Biggr ]_{Time Dependent Karmarkar}. \end{aligned}$$
(50)

This has the separable form

$$\begin{aligned} {\ddot{T}}f(r)+Tg(r)=0 , \end{aligned}$$
(51)

or

$$\begin{aligned} \frac{{\ddot{T}}}{T}=-\frac{g(r)}{f(r)} = \psi , \end{aligned}$$
(52)

where \(\psi \) is a dimensionless constant and the functions f(r) and g(r) are given by

$$\begin{aligned} f(r)= & {} rbB_0\sqrt{(r^2{B_0})'{B_0}'} \nonumber \\&\times \bigl [-2r{{B_0}'}^2 + B_0(-B_0'+r{B_0}'')\bigr ], \end{aligned}$$
(53)

and

$$\begin{aligned} g(r)= & {} \Bigg (k_1+k_2\int {\sqrt{(r^2{B_0})'{B_0}'}dr}\Biggr )\nonumber \\&\times \Biggl [2k_2r^2{B_0}^2(-{B_0}'{b}''+{b}'{B_0}'') \nonumber \\&+ B_0\Biggl (r{B_0}'\biggl [2\sqrt{(r^2{B_0})'{B_0}'}{a}'' -3cr^2{B_0}'{b}''\biggr ] \nonumber \\&-{a}'\sqrt{(r^2{B_0})'{B_0}'}({B_0}'+r{B_0}'') \nonumber \\&+cr^2{b}'{B_0}'(-3{B_0}'+2r{B_0}'')\Biggr ) \nonumber \\&+r{B_0}'\Biggl [-a'\sqrt{(r^2{B_0})'{B_0}'}(2{B_0}'+r{B_0}'')\nonumber \\&+crb{B_0}'(3{B_0}'+r{B_0}'')+ r{B_0}'\Bigl (\sqrt{(r^2{B_0})'{B_0}'}{a}''\nonumber \\&+cr^2(-B_0'{b}''+b'{B_0}'')\Bigr )\Biggr ]\Biggr ]. \end{aligned}$$
(54)

It is worthwhile noting that (52) is true for all r, and not just at the boundary of the star. This result is purely geometric in nature and holds true for any energy momentum tensor. This allows us to state our result in the form:

Theorem 1

Any perturbed spherically symmetric shear-free metric of the form

$$\begin{aligned} ds^2= & {} -(A_0+\epsilon a(r)T(t))^2dt^2 \nonumber \\&+ (B_0 +\epsilon b(r)T(t))^2[dr^2 + r^2(d\Omega ^2)] , \end{aligned}$$
(55)

where \((A_0(r), B_0(r))\) satisfies the static Karmarkar condition, the temporal dependence, T(t) always satisfies

$$\begin{aligned}{\ddot{T}} = \psi T,\end{aligned}$$

where \(\psi \) is a constant.

7 A radiating model

In this section we seek to model a radiating star collapsing from an initial static configuration. As the star collapses the core is always close to quasi-static equilibrium while dissipating energy to the exterior spacetime in the form of a radial heat flux. The interior spacetime must match smoothly to the Vaidya exterior. We make use of the junction condition \(\left( {{\bar{p}}}_r\right) _{\Sigma } = \left( qB\right) _{\Sigma }\) together with the fact that \(\left( p_{r0}\right) _{\Sigma } = 0\) to obtain

$$\begin{aligned} \alpha _{\Sigma }T - {{\ddot{T}}} = 2 {\beta }_{\Sigma }{\dot{T}}, \end{aligned}$$
(56)

which has the general solution given by

$$\begin{aligned} T(t) = -\exp \left[ \left( -\beta _{\Sigma }+\sqrt{\alpha _{\Sigma }+\beta ^2_{\Sigma }}\right) t\right] , \end{aligned}$$
(57)

where we have assumed that \(\alpha _{\Sigma } > 0\) and \(\beta _{\Sigma } < 0\). This solution represents a system in static equilibrium that starts to collapse at \(t = -\infty \) and continues to collapse as t increases. We choose the Schwarzschild interior solution as the initial static configuration of our model. The gravitational potentials for the interior Schwarzschild solution are [40]

$$\begin{aligned} A_0(r)= & {} c_1 - \frac{c_2\left( 1-r^2\right) }{1+r^2}, \end{aligned}$$
(58)
$$\begin{aligned} B_0(r)= & {} \frac{2R}{1+r^2} , \end{aligned}$$
(59)

where \(c_1\) , \(c_2\) and R are constants. We immediately obtain the thermodynamical quantities for the static solution. Then (36), (37), (37) and (43) can be written as

$$\begin{aligned}&\mu _0 = \frac{3}{R^2} ,\end{aligned}$$
(60)
$$\begin{aligned}&p_{r0} =p_{t0}= -\frac{c_1 - 3c_2 + r^2\left( c_1 + 3c_2\right) }{R^2\left( c_1 -c_2 +r^2\left( c_1 + c_2\right) \right) } , \end{aligned}$$
(61)
$$\begin{aligned}&m_0(r) = \frac{4 r^3 R}{\left( r^2+1\right) ^3}. \end{aligned}$$
(62)

The initial static configuration is isotropic with constant density and slowly exits an anisotropic regime as the collapse proceeds. The instability of the isotropy condition has been pointed out in a recent paper by Herrera [37]. It was shown that an initially isotropic configuration will evolve towards an anisotropic regime as the system loses equilibrium. The degree of anisotropy is driven by contributions from the Weyl stresses, dissipative fluxes and density inhomogeneities.

Study of static class I spacetimes via an embedding approach show that the only bounded solution that satisfies both the pressure isotropy condition and the Karmarkar condition is the interior Schwarzschild solution. Substituting Eq. (58) and (59) into (50) yields

$$\begin{aligned} 0= & {} 8r^3bc_2+2\bigl (1-3r^2\bigr )R{a}^{\prime }+c_2{b}^{\prime } \nonumber \\&+r\biggl (-2\bigl (1+r^2\bigr )R{a}^{{\prime }{\prime }}+c_2\bigl [7r^3{b}^{\prime } +(r^4-1){b}^{{\prime }{\prime }}\bigr ]\biggr ) . \end{aligned}$$
(63)

Using a well motivated form for b(r) [40, 41] , viz.

$$\begin{aligned} b(r)=\bigl (1+\zeta r^2\bigr )A_0(r)B_0(r), \end{aligned}$$
(64)

where \(\zeta \) is a constant, and we are in a position to solve equation (63) to obtain

$$\begin{aligned} a(r)= & {} \zeta c_2\bigl (c_1 + c_2\bigr )(1+r^2)-\frac{c_3}{2(1+r^2)} \nonumber \\&-\frac{4(\zeta -1){c_2}^2}{(1+r^2)^2}+c_4, \end{aligned}$$
(65)

where \(c_3\) and \(c_4\) are constants of integration. With the potentials (58), (59), (64) and (65) the radial dependence of our model is fully determined. The matter variables become

$$\begin{aligned}&\mu (r,t)=\frac{\epsilon e^{\lambda t}}{R^2} \biggl (c_1 \left( \zeta \left( r^4+10 r^2+3\right) +6\right) \nonumber \\&\quad +c_2 \zeta \left( r^4+10r^2-3\right) \biggr )+\frac{3}{R^2}, \end{aligned}$$
(66)
$$\begin{aligned}&p_r(r,t)= \Biggr (2 R^2 \left( c_1 \left( r^2+1\right) +c_2 \left( r^2-1\right) \right) {}^2\Biggr )^{-1} \nonumber \\&\quad \times \biggl (\epsilon e^{\lambda t} \biggl (2 c_1^3 \left( r^2+1\right) ^2 \left( \zeta \left( r^4-2r^2-1\right) -2\right) \nonumber \\&\quad +c_1 \biggl (c_3 \left( r^4-1\right) +2 c_2^2 \biggl (-9 \zeta +r^2 \nonumber \\&\quad \times \left( 12 \zeta +r^2\left( \zeta \left( 5 r^4-24 r^2+8\right) -10\right) +4\right) -2\biggr ) \nonumber \\&\quad +4 \lambda ^2 \left( r^2+1\right) ^2 R^2\left( \zeta r^2+1\right) \biggr ) \nonumber \\&\quad +c_2 \left( r^2-1\right) \biggl (\left( r^2+1\right) (c_3-4 c_4 \nonumber \\&\quad +4 \lambda ^2R^2 \left( \zeta r^2+1\right) ) \nonumber \\&\quad +4 c_2^2 \left( r^2 \left( \zeta \left( r^4-6 r^2+3\right) -2\right) -2 (\zeta +1)\right) \biggr ) \nonumber \\&\quad +4 c_2 c_1^2 \left( r^2+1\right) \left( \zeta +2 \zeta r^6-7 \zeta r^4-4r^2+4\right) \biggr ) \nonumber \\&\quad -2\left( c_1 \left( r^2+1\right) +c_2 \left( r^2-1\right) \right) (c_1 \left( r^2+1\right) \nonumber \\&\quad +3 c_2\left( r^2-1\right) \biggr )\biggr ), \end{aligned}$$
(67)
$$\begin{aligned}&\quad p_t(r,t) = \biggl (2R^2 \left( c_1 \left( r^2+1\right) +c_2 \left( r^2-1\right) \right) {}^2\Biggr )^{-1} \nonumber \\&\quad \times \biggl (\epsilon e^{\lambda t} \biggl (-2 c_1^3 \left( r^2+1\right) ^2 \left( \zeta \left( r^4+4 r^2+1\right) +2\right) \nonumber \\&\quad -4 c_2 c_1^2 \left( r^2+1\right) \biggl (-\zeta +r^2 (\zeta (2 r^4+9 r^2-2) \nonumber \\&\quad +4)-4\biggr ) +c_2 \left( r^2-1\right) \biggl (\left( r^2+1\right) \biggl (c_3-4 c_4 \nonumber \\&\quad +4 \lambda ^2 R^2 \left( \zeta r^2+1\right) \biggr )-4 c_2^2 \biggl (2 (\zeta +1) \nonumber \\&\quad +r^2 \left( \zeta \left( r^4+6 r^2-5\right) +2\right) \biggr )\biggr ) \nonumber \\&\quad +c_1 \biggl (c_3 \left( r^4-1\right) -2 c_2^2 \biggl (9 \zeta +5 \zeta r^8+26 \zeta r^6 \nonumber \\&\quad +2 (5-9 \zeta ) r^4 -2 (7 \zeta +2) r^2+2\biggr ) \nonumber \\&\quad +4 \lambda ^2 \left( r^2+1\right) ^2 R^2 \left( \zeta r^2+1\right) \biggr )\biggr )\nonumber \\&\quad -2 (c_1\left( r^2+1\right) +c_2 \left( r^2-1\right) ) \biggl (c_1 \left( r^2+1\right) \nonumber \\&\quad +3 c_2 \left( r^2-1\right) \biggr )\biggr ), \end{aligned}$$
(68)
$$\begin{aligned}&\Delta (r,t) = \frac{1}{R^2 \left( c_1 \left( r^2+1\right) +c_2 \left( r^2-1\right) \right) } \nonumber \\&\quad \times \biggl [2 \left( c_1+c_2\right) \zeta r^2 \left( r^2+1\right) \epsilon \biggl (c_1 \left( r^2+1\right) \nonumber \\&\quad +2 c_2 \left( r^2-1\right) \biggr ) e^{\lambda t}\biggr ], \end{aligned}$$
(69)
$$\begin{aligned}&qB(r,t) = -{R}^{-1}\Bigr (2 \zeta \lambda r \left( r^2+1\right) e^{\lambda t}\Bigr ), \end{aligned}$$
(70)
$$\begin{aligned}&m(r,t) = \frac{4 r^3 R}{\left( r^2+1\right) ^4} \nonumber \\&\quad \times \biggl (\biggl (-\epsilon e^{\lambda t} \biggl (c_2 \left( r^2-1\right) \biggl (\zeta \left( r^4+3 r^2-1\right) +3\biggr ) \nonumber \\&\quad +c_1 \left( r^2+\zeta \left( r^6+2 r^4-1\right) +1\right) \biggr )+r^2+1\biggr )\biggr ) ,\nonumber \\ \end{aligned}$$
(71)

where \(\lambda \) is given by

$$\begin{aligned} \lambda =-\beta _1(r_0)+\sqrt{\alpha _1(r_0)+{{\beta _1}^2(r_0)}}, \end{aligned}$$
(72)

where \(r = r_{0}\) defines the boundary of the star. We are in position to write

$$\begin{aligned} \alpha _1(r_0)= & {} -\Biggl (4\left( r_0^2+1\right) {}^2 R^2 (\left( c_1+c_2\right) r_0^2+c_1-c_2) \nonumber \\&\times (\zeta r_0^2+1)\Biggr )^{-1} \biggl ( 2 c_1^3 \zeta \left( r_0^2-1\right) \left( r_0^2+1\right) {}^4 \nonumber \\&+4 c_1^2 c_2 (r_0^2+1){}^2 (\zeta +r_0^2 (-5 \zeta +2 \zeta \left( r_0^2-1\right) r_0^2 \nonumber \\&+1)-1)+c_1 \left( r_0^2+1\right) \nonumber \\&\times \biggl (2 c_2^2 \biggl (-9 \zeta +r_0^2 \biggl (26 \zeta +r_0^2 \biggl (-20 \zeta +5 \zeta \left( r_0^2-2\right) \nonumber \\&r_0^2+4\biggr ) -24\biggr )+12\biggr )+c_3 \left( r_0^4-1\right) \biggr ) \nonumber \\&+c_2 \left( r_0^2-1\right) \biggl (4 c_2^2 \biggl (-2 \zeta +r_0^2 \biggl (4 \zeta +r_0^2 (-9 \zeta \nonumber \\&+\zeta \left( r_0^2-2\right) r_0^2+1) -10\biggr )+1\biggr )+\left( c_3-4 c_4\right) \nonumber \\&\times \left( r_0^2+1\right) {}^2\biggr )\biggr ), \end{aligned}$$
(73)
$$\begin{aligned} \beta _1(r_0)= & {} \frac{\zeta r_0 \left( \left( c_1+c_2\right) r_0^2+c_1-c_2\right) }{2 \left( \zeta r_0^2 R+R\right) }, \end{aligned}$$
(74)

for our model.

8 Physical viability

In order to test the physical viability of our model, we have plotted the relevant thermodynamical quantities which allow us to gain insight into the collapse process.

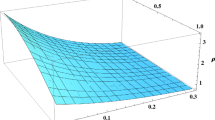
In Fig. 1 we present the density as a function of the radial and temporal coordinates. We observe that the density remains fairly constant for a large period of the collapse epoch. This is expected as the fluid is always close to hydrostatic equilibrium. For late times we observe an increase in the density. This is a result of the collapsing core where the mass becomes confined to smaller volumes as the collapse proceeds.

An observation of the radial pressure plotted in Fig. 2 shows that the pressure is regular at each interior point of the collapsing core. The pressure decreases smoothly to the boundary. A time slice of Fig. 2 (\(r = \text{ constant }\)) shows that the radial pressure remains fairly constant for a large portion of the collapse. During this period the heat generated will be very little as the core is in quasi-static equilibrium. For late times the generation of heat resulting from a denser core leads to higher pressure. This pressure is reduced as core radiates to the exterior in the form of a radial heat flux.

Fig. 1
figure 1

Total density, \(c_1=0.81\), \(c_2=0.5\), \(c_3=-10\), \(c_4=-10\), \(\zeta =-0.2\), \(R=6.62\), \(r_0=0.55\) and \(\epsilon =0.1\)

Full size image
Fig. 2
figure 2

Total radial pressure, \(c_1=0.81\), \(c_2=0.5\), \(c_3=-10\), \(c_4=-10\), \(\zeta =-0.2\), \(R=6.62\), \(r_0=0.55\) and \(\epsilon =0.1\)

Full size image
Fig. 3
figure 3

Total tangential pressure, \(c_1=0.81\), \(c_2=0.5\), \(c_3=-10\), \(c_4=-10\), \(\zeta =-0.2\), \(R=6.62\), \(r_0=0.55\) and \(\epsilon =0.1\)

Full size image
Fig. 4
figure 4

Heat flow, \(c_1=0.81\), \(c_2=0.5\), \(c_3=-10\), \(c_4=-10\), \(\zeta =-0.2\), \(R=6.62\), \(r_0=0.55\) and \(\epsilon =0.1\)

Full size image
Fig. 5
figure 5

Total mass, \(c_1=0.81\), \(c_2=0.5\), \(c_3=-10\), \(c_4=-10\), \(\zeta =-0.2\), \(R=6.62\), \(r_0=0.55\) and \(\epsilon =0.1\)

Full size image
Fig. 6
figure 6

\(\Delta =p_{r}- p_{t}\), \(c_1=0.81\), \(c_2=0.5\), \(c_3=-10\), \(c_4=-10\), \(\zeta =-0.2\), \(R=6.62\), \(r_0=0.55\) and \(\epsilon =0.1\)

Full size image
Fig. 7
figure 7

Energy condition 1, \(c_1=0.81\), \(c_2=0.5\), \(c_3=-10\), \(c_4=-10\), \(\zeta =-0.2\), \(R=6.62\), \(r_0=0.55\) and \(\epsilon =0.1\)

Full size image
Fig. 8
figure 8

Energy condition 2, \(c_1=0.81\), \(c_2=0.5\), \(c_3=-10\), \(c_4=-10\), \(\zeta =-0.2\), \(R=6.62\), \(r_0=0.55\) and \(\epsilon =0.1\)

Full size image
Fig. 9
figure 9

Energy condition 3, \(c_1=0.81\), \(c_2=0.5\), \(c_3=-10\), \(c_4=-10\), \(\zeta =-0.2\), \(R=6.62\), \(r_0=0.55\) and \(\epsilon =0.1\)

Full size image

A snapshot of Fig. 3 in time shows that the tangential pressure decreases smoothly towards the boundary of the star. As the collapse proceeds, the tangential pressure decreases, almost mimicking the temporal trend in the radial pressure. We can understand this by observing that for a collapsing core the inner shells (smaller radii) would possess a higher surface tension which can be ascribed to a higher tangential pressure. Since the core is collapsing and simultaneously radiating energy, each concentric shell relaxes thus resulting in a decrease in the tangential pressure.

The heat flow is displayed in Fig. 4. The heat generation is highest at the center (highest density) and decreases in the cooler surface layers of the stellar configuration. The heat production increases as the collapse proceeds.

The mass profile of the collapsing core is presented in Fig. 5. The mass increases radially outwards as we expect as larger concentric shells contain more mass. The mass decreases as a function of time since the star is radiating and losing mass in the form of a radial heat flux.

The anisotropy parameter is presented in Fig. 6. We observe that for early times the anisotropy parameter vanishes. This is expected as the collapse starts off from an isotropic static core. As the collapses proceeds and heat is generated, the anisotropy increases. When \(\Delta > 0\), it signifies that the radial pressure dominates the tangential pressure thus making the force due to anisotropy attractive. This attractive force couples with the inwardly driven gravitational interaction thus enhancing collapse for late times.

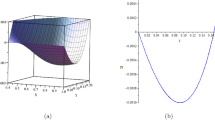
From Figs. 7, 8, 9, we observe that all three energy conditions

$$\begin{aligned} E_{1}= & {} (\mu + P_{r})^2 - 4q^2 \ge 0, \end{aligned}$$
(75)
$$\begin{aligned} E_{2}= & {} \mu - P_{r} \ge 0, \end{aligned}$$
(76)
$$\begin{aligned} E_{3}= & {} \mu - P_{r} - 2 P_{t} + \sqrt{(\mu + P_{r})^2 - 4q^2 } \ge 0, \end{aligned}$$
(77)

are satisfied throughout the stellar configuration.

9 Discussion

The Karmarkar embedding condition is an interesting geometrical condition that relates the two gravitational potentials. This has been extensively studied in static relativistic spheres, see for example the recent work by Ospino and Nunez [31] and Hansraj and Moodly [39]. The solutions of Naidu et al. [29] and Jaryal [32] show that nonstatic models are possible, and these can be used to describe radiating relativistic spheres. We have showed that a perturbative approach can be used to find a new radiating model which has a simple time dependence. The physical analysis shows that the criteria for physical acceptability are satisfied. The advantage of the perturbative approach is a clear physical representation corresponding to a realistic model: a model that is initially static and then perturbations lead to loss of radiation as is observed in real astronomical bodies.