1 Introduction

The Einstein–Rosen bridge was developed in order to explain the particle problem in General Relativity, more precisely to try to explain fundamental particles such as electrons in terms of space-time tunnels threaded by electric lines of force [1]. However, a major problem is the instability of the geometric structure present in this kind of solutions within the arena of General Relativity. This means that the bridge is not able to remain open long enough for an object to pass through it (not even a photon). As far as this is concerned, Wheeler [2] tried to explain Einstein–Rosen bridge (today known as wormholes) in terms of topological entities called geons and, incidentally, provided the first (now familiar) diagram of a wormhole as a tunnel connecting two openings in different regions of space-time. Basically, the geometry of a wormhole is formed by two mouths joined by a throat connecting two parallel Universes or two far away regions of the space-time. Following Morris and Thorne pioneering work [3, 4] the wormhole exists only if the wormhole throat is supported by the so-called exotic matter field. By exotic matter Morris and Thorne mean negative radial pressure \(p_{r}\), which entails the violation of null energy condition due to \(|p_{r}|>|\rho |\) in the throat of the wormhole. What is more if an observer crosses the tunnel it will see a negative energy density \(\rho \). Regarding this, many works available in the literature have addressed the energy violation problem at the wormhole throat, for example working out dynamical wormholes [5, 6]. Moreover, theories containing high derivative terms in the gravitational sector through functions of the scalar curvature, enable to construct thin-shell structures driven by normal matter distributions [7, 8]. Other interesting works concerning the study and analysis of wormholes in gravity theories include scalar–tensor gravity, such as Brans–Dicke theory, non-linear electrodynamics such as Born–Infield theory or higher dimensional theories like Kaluza–Klein, Einstein-Gauss–Bonnet or Einstein–Cartan theories [9,10,11,12,13,14,15,16,17,18,19,20,21,22].

Besides, modified gravity theories such as f(R) and f(R, T) gravity are promised scenarios to investigate wormhole regions satisfying energy conditions. These theories attempt to explain the most recent data about the accelerated expansion of the Universe. This phenomenon has not been explained from the point of view of General Relativity and it is confirmed and supported by numerous observational data from Supernova type Ia [23], high Planck data [24] and large scale structure [25,26,27,28,29,30,31,32,33,34,35,36]. On the other hand, a possible explanation of this phenomenon is the so-called dark energy [37] a mysterious cosmic fluid, which has uniform density distribution and negative pressure.

So, as stated before, modified gravity theories are an alternative way to explain the above issue. f(R)-gravity [38] was the first modified gravity theory employed to explain the singularities introduced by the isotropic homogeneous cosmological model. After its presentation in the early 80’s, Starobinsky [39] used this theory to face questions related to cosmic inflationary models. The main point of this theory is to introduce a function f(R) of the Ricci scalar R. Its consequence is the presence of high derivative terms, which could in principle explain the accelerated expansion and the existence of dark energy or dark matter without the addition of extra matter fields. Besides f(R, T) gravity theory [40] can be seen as a generalization of f(R)-gravity. Particularly, f(R, T) theory also modifies the material sector by including the trace T of the energy-momentum tensor, which breaks down the minimal-coupling matter principle between the gravitational sector and the material one. The study of wormhole solutions satisfying energy conditions in the arena of f(R, T) theory was considered in [22, 41,42,43,44]. However, the study of wormhole geometries is more robust in the context of f(R)-gravity than it is performed in f(R, T) theory. For example, it was found in [45,46,47] that high derivative terms coming from the f(R) function regularize energy conditions. In [48, 49] the study of static wormhole solutions using power-law models \(R^{n}\) was performed. Cosmological evolution and non-commutative techniques were treated in [50,51,52,53]. More recently the matching condition formalism to build thin-shell was done in [54,55,56] and the study of new wormhole solutions was performed in [57].

In a broader cosmological context, f(R)-gravity is a viable theory to address at the same footing the early-time inflation with the late-time acceleration process [58,59,60,61,62]. To face the ultra accelerated expansion or inflationary age of the Universe, the seminal work by Starobinsky [39] is considered as the building block in this direction. On the other hand, the present accelerated era of the Universe represents nowadays a great challenge to the astrophysical and cosmological community. Several works available in the literature have attempted to tackle this problem by proposing different f(R)-gravity models [63,64,65,66,67,68,69,70,71,72,73,74,75,76]. To be a viable models with a physical meaning, all these proposal should fulfill some general requirements [77]. What is more if the scalar curvature is convariantly constant ı.e, \(R\equiv R_{0}\) where \(R_{0}\) is representing the scalar curvature at the present epoch, the model contains a special kind of solutions: vacuum solutions, including the vacuum de Sitter space-time with cosmological constant (General Relativity solution) [78].

Motivated by these prior studies, we investigate the existence of wormhole solutions in the arena of f(R)-gravity. In order to achieve it we propose a new ansatz for the shape function b(r) depending on two parameters m and \(\beta \), and also impose an equation of state relating the components of the energy–momentum tensor threading the throat of the wormhole, specifically \(\rho _{\perp }=-\rho \). These components allow us to solve a first order differential equation for F(R(r)) and also find an explicit expression for the null energy condition (NEC). To facilitate the mathematical treatment of the field equations we have set the red-shift function to be null. The resulting model satisfies all the basic requirements to be an asymptotically and traversable wormhole. Moreover, it is found that the matter content threading the throat satisfies the NEC in one case while in the second case this condition is partially violated near the throat, although it is satisfied away from it. To complete the study we emphasize that the main result on this scenario is the non-existence theorem proved in [79] and extended in [80, 81]. It was proved in the Einstein frame in [79] and extended to scalar tensor theories and f(R)-gravity by performing a conformal map from the Jordan frame to the Einstein one [80, 81]. The main point is that the wormhole topology together with the asymptotically flat spaces on both sides of the throat are preserved on the conformal map together with the NEC. In this concern, the feasibility of the existence of wormhole solutions in f(R) theory without ghost fields is subject to the violation of NEC at least on the throat of the wormhole. In this context one class of solutions we are going to present satisfies the null energy condition away from the throat, where the function F(R) is everywhere positive and together with dF(R)/dR vanish at the throat of the wormhole. This fact is beyond the scope of the nonexistence theorem, since the conformal map from the Jordan frame to the Einstein frame is not well defined at the throat. In this concern, the incompatibility between both frames was previously noted in the cosmological scenario, in the treatment of f(R) singularities (see [82] for a recent and detailed discussion about the correspondence of f(R)-gravity singularities in Jordan and Einstein frames in the cosmological context) and then translated into the wormhole studies. On the other hand, to check the feasibility of our model, we have explored the cosmological properties of the obtained f(R) models to address the late-time cosmic acceleration of the Universe (issue related with the dark energy problem). In this regard, the resulting f(R) Lagrangian satisfies the general requirements to face this point [77], such as: (i) ghost free consistency, (ii) consistency with local gravity and stability under cosmological perturbations, (iii) stability at late-time de Sitter point. On the other hand, we have extended our model to include the inflationary phase, adding a two step model [62], although it represents a toy inflationary-accelerated unification model to describe the early and late time epochs of our Universe. However, it shows the possibility of a natural extension of our model to address this problem. Furthermore, we have solved the field equations in the cosmological scenario to obtain the Hubble rate H(t) and scale factor a(t). To do it, we have imposed a flat Friedmann–Lemaitre–Robertson–Walker (FLRW) metric accompanied with an isotropic perfect fluid distribution. It is worth mentioning that f(R)-gravity offers in the cosmological framework a natural scenario to address the existence of an effective dark energy, without the need to introduce a negative pressure ideal fluid [59, 83].

The article is organized as follows: Sect. 2 presents the wormhole anatomy. Section 3 develops the f(R) formalism, presenting the geometry and field equations. In Sect. 4 the field equations are solved and the model is studied in details. In Sect. 5 the main features of the models are discussed and in Sect. 6 some cosmological properties related with the accelerated expansion at late time of the Universe (dark energy) are discussed, and the Hubble rate and scale factor satisfying the field equations in the flat FLRW regime with an isotropic fluid are shown. Furthermore, the connection with the inflationary stage is also addressed. Finally Sect. 7 provides some conclusions.

2 A quick review: WormHoles (WH) generalities

In curvature coordinates, the static and spherically symmetric line element describing a WH region is given by

$$\begin{aligned} ds^{2}=-e^{2\Phi }dt^{2}+e^{\Lambda }dr^{2}+r^{2}d\Omega ^{2}, \end{aligned}$$
(1)

where \(d\Omega ^{2}\equiv sin^{2}\theta d\phi ^{2}+d\theta ^{2}\). In Eq. (1) the metric functions depend only on the radial coordinate ı.e, \(\Phi =\Phi (r)\) and \(\Lambda =\Lambda (r)\). The function \(\Phi \) is referred as the red-shift function while \(e^{\Lambda }\) is related with the so called shape function b(r), explicitly

$$\begin{aligned} e^{\Lambda (r)}=\frac{1}{1-\frac{b(r)}{r}}. \end{aligned}$$
(2)

To be a traversable and asymptotically flat space-time we assume the WH geometry must satisfy the following general requirements [3, 84]

  1. 1.

    The radius of the WH throat is defined as

    $$\begin{aligned} r_{0}=\text {min} \{r\left( l\right) \}. \end{aligned}$$

    It is assumed that there is only one global minimum. Furthermore, the proper distant l is related with radial coordinate r by

    $$\begin{aligned} l(r)=\pm \int ^{r}_{r_{0}}\frac{dx}{\sqrt{1-b_{\pm }(x)/x}}, \end{aligned}$$

    where \(l\in (-\infty ,+\infty )\). The ± refer to both mouths of the WH.

  2. 2.

    For comparison with Schwarzschild solution the mass of the WH as seen for spatial infinity is given by \(b_{\pm }\rightarrow 2GM_{\pm }\).

  3. 3.

    There are two coordinate patches covering the range \(r\in [r_{0},+\infty )\). Each patch covers an asymptotically flat region, and both match at \(r_{0}\), the throat of the WH.

  4. 4.

    The red-shift function \(\Phi \) must be finite everywhere, for \(r\ge r_{0}\), in order to avoid an event horizon, so \(e^{\Phi }>0\) for all \(r>r_{0}\). Moreover,

    $$\begin{aligned} \lim _{r\rightarrow \infty } \Phi (r)=\Phi _{0}, \end{aligned}$$

    where \(\Phi _{0}\) a finite real number.

  5. 5.

    The shape function b(r) must fulfill \(b(r_{0})=r_{0}\), where the throat \(r_{0}\) of the WH defines the spherical surface \(r=r_{0}\).

  6. 6.

    For all \(r>r_{0}\) \(\Rightarrow \) \(b(r)<r\) and \(b^{\prime }(r_{0})< 1\) or equivalently \(b^{\prime }(r)<b(r)/r\). This condition is known as the flare-out condition. Here \(b^{\prime }(r)\) means db(r)/dr.

In the next section we discuss the explicit form of the field equations and the matter content surrounding the WH throat.

3 The f(R) formalism

In this section we present the f(R)-gravity formalism. The starting point is the modified Einstein-Hilbert action minimally coupled to a generic matter field given by

$$\begin{aligned} S=\frac{1}{2\kappa }\int d^{4}x\sqrt{-g}f(R)+\int d^{4}x\sqrt{-g}\mathcal {L}_{m}\left( g^{\mu \nu },\Psi \right) , \end{aligned}$$
(3)

where f(R) is an arbitrary smooth function of the Ricci’s scalar R, g is the determinant of the metric tensor \(g_{\mu \nu }\) (\(g^{\mu \nu }\) its inverse), \(\mathcal {L}_{m}\) is the matter Lagrangian density, \(\Psi \) encodes the matter fields and \(\kappa =8\pi G/c^{4}\)Footnote 1. So, by taking variations with respect to \(g^{\mu \nu }\) in the action (3) we arrive at the following general field equations

$$\begin{aligned} FR_{\mu \nu }-\frac{1}{2}fg_{\mu \nu }-\nabla _{\mu }\nabla _{\nu }F+g_{\mu \nu }\Box F=T^{(\text {m})}_{\mu \nu }, \end{aligned}$$
(4)

where as always \(F\equiv df/dR\). Moreover, the right hand side of Eq. (4) represents the usual matter content. Considering the trace of the Eq. (4) we obtain

$$\begin{aligned} FR-2f+3\Box F=T^{(\text {m})}, \end{aligned}$$
(5)

where \(\Box \) is the D’alembertian differential operator defined by

$$\begin{aligned} \Box \equiv \nabla _{\mu }\nabla ^{\mu }=\frac{1}{\sqrt{-g}}\partial _{\mu }\left( \sqrt{-g}g^{\mu \nu }\partial _{\nu }\right) . \end{aligned}$$
(6)

The Eq. (5) shows that F(R) has a dynamical role in the theory ı.e, it is a fully dynamical degree of freedom. Furthermore, we have denoted the trace of the energy–momentum tensor by \(T^{(\text {m})}=T^{{\mu }(\text {m})}_{\ \mu }\).

In the following we shall consider that the matter content threading the wormhole throat is taken to be an imperfect fluid distribution described by the following energy–momentum tensor

$$\begin{aligned} T^{(\text {m})}_{\mu \nu }=\left( \rho +p_{\perp }\right) u_{\mu }u_{\nu }+g_{\mu \nu }p_{\perp }+\left( p_{r}-p_{\perp }\right) \chi _{\mu }\chi _{\nu }, \end{aligned}$$
(7)

with \(\rho \) the energy density, \(p_{r}\) and \(p_{\perp }\) being the pressure waves in the principal directions ı.e, the radial and tangential ones respectively. The four-velocity of the above fluid distribution is characterized by the time-like vector \(u^{\nu }\). Moreover \(\chi ^{\nu }\) is a unit space-like vector in the radial direction (orthogonal to \(u^{\nu }\)) that is, \(\chi ^{\nu }=\sqrt{1-b/r}\delta ^{\nu }_{r}\). Besides, throughout the study we shall assume a constant red-shift function, specifically \(\Phi =0\). This assumption implies that the gravitational red-shift z is totally vanishing, of course

$$\begin{aligned} z=\frac{1}{\sqrt{g_{tt}}}-1, \quad \text{ with } \quad g_{tt}=e^{2\Phi }=1 \quad (\text{ for } \quad \Phi =0). \end{aligned}$$
(8)

Furthermore, from the mathematical point of view a vanishing red-shift function reduces the complexity of the field equations to be solved. So, taking into account the above considerations Eqs. (4) and (7) yield to the following field equations

$$\begin{aligned} \rho= & {} \frac{1}{2}f-\Box F, \end{aligned}$$
(9)
$$\begin{aligned} p_{r}= & {} \frac{\left( rb^{\prime }-b\right) }{r^{3}}F+\frac{2\left( r-b\right) }{r^{2}}F^{\prime }-\frac{1}{2}f, \end{aligned}$$
(10)
$$\begin{aligned} p_{\perp }= & {} \frac{\left( rb^{\prime }+b\right) }{2r^{3}}F-\frac{\left( r-b\right) }{r^{2}}F^{\prime }-\frac{f}{2}+\Box F, \end{aligned}$$
(11)

where \(\Box F\) using Eqs. (1) and (6) is given by

$$\begin{aligned} \Box F=\left[ \frac{r-b}{r}\right] \left[ F^{\prime \prime }+F^{\prime }\left( \frac{4r-3b-rb^{\prime }}{2r\left( r-b\right) }\right) \right] , \end{aligned}$$
(12)

where primes denote differentiation with respect to the radial coordinate r. There are many ways to tackle the system (9)-(11). One possibility is to impose an adequate f(R) model supplemented by a suitable shape-function b(r) or supplement the system with an equation of state relating the thermodynamic variables and impose a suitable shape function. In this regard we follow the second approach. Nevertheless, among all the equations of state or possible equivalent relationships, only some are mathematically treatable, because the resulting expressions are highly complex to solve (at least analytically). So, following [47] we established \(p_{\perp }=-\rho \) as a supplementary equation of state.

4 The Model

As was discussed in the previous section, in order to solve the f(R)-gravity system of equations (9)-(11), we impose the following shape function b(r),

$$\begin{aligned} b(r)=\alpha +\beta \frac{r_{0}}{r^{m+1}}, \quad \text{ with } \quad m+1>0 \end{aligned}$$
(13)

where m, \(\alpha \) and \(\beta \) are constant parameters. The parameter \(\alpha \) and \(\beta \) have units of \([\text {length}]\) and \({[\text {length}]^{1+m}}\) respectively. To ensure the fulfillment of \(b(r_{0})=r_{0}\) and \(b^{\prime }(r_{0})<1\) at the throat of the WH one has

$$\begin{aligned} b(r_{0})=\alpha +\beta r_{0}^{-m}=r_{0} \Rightarrow \alpha = r_{0}\left( 1-\frac{\beta }{r^{m+1}_{0}}\right) , \end{aligned}$$
(14)

then

$$\begin{aligned} b(r)=r_{0}\left( 1-\frac{\beta }{r^{m+1}_{0}}\right) +\beta \frac{r_{0}}{r^{m+1}}. \end{aligned}$$
(15)

Furthermore, from the flare-out condition one obtains a bound on the constant parameter \(\beta \) as follows

$$\begin{aligned} b^{\prime }(r_{0})<1 \Rightarrow \beta >-\frac{r^{m+1}_{0}}{m+1}. \end{aligned}$$
(16)

Besides, in to order to satisfy the condition \(b(r)<r\) for all \(r>r_{0}\) we have for \(m\ne 0\)

$$\begin{aligned} r_{0}\left[ 1+\beta \left( \frac{1}{r^{m+1}}-\frac{1}{r^{m+1}_{0}}\right) \right] <r. \end{aligned}$$
(17)

It follows that for all \(\beta >0\), Eq. (17) is always satisfied. We shall then restrict \(\beta \) to be strictly positive. Then the line element (1) representing the WH geometry is given by

$$\begin{aligned} ds^{2}=-dt^{2}+\frac{dr^{2}}{1-\frac{r_{0}}{r}\left( 1-\frac{\beta }{r^{m+1}_{0}}\right) +\frac{\beta r_{0}}{r^{m+2}}}+r^{2}d\Omega ^{2}. \end{aligned}$$
(18)

The above geometry reproduces the Minkowski space-time geometry when \(r\rightarrow \infty \). Furthermore, it represents a family of WH depending on the choice of the m parameter. In this respect, power law shape functions have been considered by several authors in the arena of WH solutions.

Next, by using Eq. (15) and the equation of state \(p_{\perp }=-\rho \) into the set of Eqs. (9)–(11) one arrives at the following first order differential equation for F(R(r)),

$$\begin{aligned} F^{\prime }\left( 1-\frac{b}{r}\right) -\frac{F}{2r^{2}}\left[ b+b^{\prime }r\right] =0. \end{aligned}$$
(19)

The general solution of (19) is given by

$$\begin{aligned} F(R(r))= & {} F_{0}\text {Exp}\left[ -\frac{1}{2}\int \right. \nonumber \\&\left. \frac{r_{0}\left( -\beta mr^{m}_{0}+r^{m}_{0}r^{m}+\beta r^{m}_{0}-\beta r\right) }{r\left( r^{1+m}_{0}r^{m}-r^{m}_{0}r^{1+m}+\beta r^{1+m}_{0}-\beta r_{0}r^{m}\right) }dr\right] ,\nonumber \\ \end{aligned}$$
(20)

being \(F_{0}\) an integration constant. Now we examined the output expressions obtained from Eq. (20) by taking different values for the running constant parameters m and \(\beta \) satisfying the mentioned requirements.

4.1 Solution \(\#\)1: \(m=1\)

The election \(m=1\) yields from Eq. (20) to

$$\begin{aligned} F(R(r))= & {} F_{0}\sqrt{r}\left( r-r_{0}\right) ^{A}\left( r_{0}r^{2}+\beta r+\beta r_{0}\right) ^{B}\nonumber \\&\qquad \text {Exp}\Bigg [-\frac{2\text {arctan}\left( \frac{2 r_{0}r+\beta }{\sqrt{4\beta r^{2}_{0}-\beta ^{2}}}\right) \beta \left( \beta -r^{2}_{0}\right) }{\nonumber }\\&\qquad {\left( 2\beta +r^{2}_{0}\right) \sqrt{4\beta r^{2}_{0}-\beta ^{2}}}\Bigg ], \end{aligned}$$
(21)

where A and B are defined by

$$\begin{aligned} A\equiv \frac{r^{2}_{0}-2\beta }{2\left( r^{2}_{0}+2\beta \right) }, \quad B\equiv -\frac{r^{2}_{0}}{2\left( r^{2}_{0}+2\beta \right) }. \end{aligned}$$
(22)

As it is observed from Eq. (21) the sign of the F(R(r)) function depends on the sign of the integration constant \(F_{0}\). If the sign of the F(R(r)) function is positive or negative is a very important issue regarding the existence of WH solutions in the arena of f(R)-gravity theory. As we will see later this fact is related with the fulfillment of energy conditions and ghost fields existence in the model. It should be noted that in order to have a dimensionless F(R(r)) function the dimensionality of the integration constant \(F_{0}\) depends on the factors A and B.

4.2 Solution \(\#\)2: \(m=0\)

This simple choice provides from Eq. (15)

$$\begin{aligned} b(r)=r_{0}\left( 1-\frac{\beta }{r_{0}}\right) +\beta \frac{r_{0}}{r}. \end{aligned}$$
(23)

In this case, in order to satisfy the flare-out condition one can express \(\beta =\gamma r_{0}\), where \(\gamma \) is a constant parameter. To satisfy \(b^{\prime }(r_{0})<1\), \(\gamma \) must be restricted to be \(\gamma > -1\). Furthermore, from \(b(r)<r\) we get

$$\begin{aligned} r^{2}-r_{0}\left( 1-\gamma \right) r-\gamma r^{2}_{0}>0. \end{aligned}$$
(24)

The roots of the above inequality are \(r_{+}=r_{0}\) and \(r_{-}=-\gamma r_{0}\). It is clear that \(r_{+}>r_{-}\), then to cover the range \([r_{0},+\infty )\) is enough to take \(\gamma >-1\). So, F(R(r)) function is given by

$$\begin{aligned} F(R(r))=F_{0}\left( \frac{r+\beta }{r-r_{0}}\right) ^{C}, \end{aligned}$$
(25)

being \(C\equiv (\beta -r_{0})/2(\beta +r_{0})\). Again, the sign of the F(R(r)) function depends on the integration constant \(F_{0}\), however this time \(F_{0}\) is dimensionless. It should be noted that the point \(r=r_{0}\) makes the expressions (21) and (25) singular or null. This depends on the relation between \(r_{0}\) and \(\beta \) which determine the sign of A, B and C.

Fig. 1
figure 1

The trend of the dimensionless \(f(R(r))/f(R(r_{0}))\) function and Ricci’s scalar R(r) against the dimensionless radial coordinate \(r/r_{0}\) for \(m=1\), \(\beta =r^{2}_{0}=1\), \(F_{0}=-1\) and \(f_{0}=10\) (red curves) and \(m=0\), \(\beta =-r_{0}/2\), \(r_{0}=1\), \(F_{0}=-1\) and \(f_{0}=20\) (blue curves). It is worth mentioning that from now on throughout the analysis the numerical value assigned to the throat of the WH will be \(r_{0}=1\)

Full size image

Next, the f(R(r)) function can be obtained from

$$\begin{aligned} F=\frac{df}{dR}=\frac{df/dr}{dR/dr}\Rightarrow f(R(r))=\int F(R(r))\frac{dR(r)}{dr}dr, \end{aligned}$$
(26)

where the general expression for the Ricci scalar corresponding to the line element (18) is given by

$$\begin{aligned} R(r)=\frac{2b^{\prime }(r)}{r^{2}}\Rightarrow R(r)=-\frac{2\beta r_{0}\left( m+1\right) }{r^{m+4}}. \end{aligned}$$
(27)

To reduce the mathematical complications in the case \(m=1\) we shall assume \(\beta =r^{2}_{0}\). In this way the expression (21) becomes

$$\begin{aligned} F(R(r))=F_{0}\left[ \frac{r^{3}}{(r-r_{0})(r_{0}r^{2}+r^{2}_{0}r+r^{3}_{0})}\right] ^{1/6}, \end{aligned}$$
(28)

where the above choice leads to \(A=B=-1/6\) and the resulting scalar curvature is

$$\begin{aligned} R(r)=-\frac{4r^{3}_{0}}{r^{5}}. \end{aligned}$$
(29)

So, combining Eqs. (26), (28) and (29) one gets

$$\begin{aligned} f(R(r))= & {} -\frac{40}{81}\frac{F_{0}}{r^{3}_{0}r^5} \left[ \frac{r^{3}}{r^{3}r_{0}-r^{4}_{0}}\right] ^{1/6}\bigg [9r^{6}_{0}+3r^{3}_{0}r^{3}\nonumber \\&\quad -12r^{6}+8r^{6}\left( 1-\frac{r^{3}}{r^{3}_{0}}\right) ^{1/6}{}_2F_{1}\nonumber \\&\quad \left( \frac{1}{6};\frac{1}{2};\frac{3}{2};\frac{r^{3}}{r^{3}_{0}}\right) \bigg ] + f_{0}, \end{aligned}$$
(30)

being \(f_{0}\) an integration constant with units of \(\text {length}^{-2}\). For the case \(m=0\) we shall assume \(\gamma =-1/2\), then \(\beta =-r_{0}/2\). So, from Eqs. (25) and (27) the following F(R(r)) function and Ricci scalar are obtained

$$\begin{aligned} F(R(r))=\left( \frac{r-r_{0}}{2r-r_{0}}\right) ^{3/2}F_{0}, \end{aligned}$$
(31)
$$\begin{aligned} R(r)=\frac{r^{2}_{0}}{r^{4}}. \end{aligned}$$
(32)

Thus, putting together Eqs. (26), (31) and (32) one arrives to

$$\begin{aligned} f(R(r))=\frac{ r^{2}_{0} F_{0}}{r^{4}}\text {Appell}F_{1}\left( 4;-\frac{3}{2};\frac{3}{2};5;\frac{r_{0}}{r};\frac{r_{0}}{2r}\right) +f_{0}. \end{aligned}$$
(33)

The trend of the f(R(r)) function and the Ricci scalar R(r) are depicted in Fig. 1. It is appreciated that R vanishes when r tends to infinity as expected (flat space-time).

Fig. 2
figure 2

These plots show the trend of the shape function (blue line), its first derivative (green line) and the curve \(b(r)-r\) defining the WH throat (red line), for \(m=1\) and \(\beta =r^{2}_{0}=1\) (left panel) and \(m=0\) and \(\beta =-r_{0}/2\) (right panel)

Full size image

5 Results and discussions

In this section, we discuss the behavior of the shape function b(r), energy conditions and the presence of ghost fields of the WH models we have obtained.

5.1 Shape function behavior

As was pointed out in Sect. 2 the shape function b(r) must respect some basic requirements in order to have an asymptotically and traversable WH space-time. So, taking into account these rules, the proposed ansatz given by (15) fulfills all the formalities. Furthermore, the above requirements are ensured only in the range \(m+1>0 \Rightarrow m>-1\). This is so because, if m is taken to be less than \(-1\), then the shape function will not be finite when r goes to infinity. Moreover, the limit of b/r when r tends to infinity will be divergent. Besides, we discard the condition \(m+1=0 \Rightarrow m=-1\) because it does not lead to the Minkowski space-time in the mentioned limit, because the coefficient in front of \(dr^{2}\) term in the line element will not be 1. In that case one needs to redefine the radial coordinate r but the solid angle is altered.

As shown Fig. 2 for the chosen m the shape function b(r) (blue line) remains finite everywhere. Moreover, the flare-out condition is also satisfied, it is depicted by the green line, where \(b^{\prime }(r)\) is always less than the straight line \(r=1\) at the neighborhood of the throat \(r_{0}\), and the blue line is representing the WH throat, as can be seen this curve cuts the radial axis just at \(r=1\) the throat of the WH geometry.

5.2 Thermodynamic variables and energy conditions

It is well known that the matter distribution surrounding the space-time can be composed of a large number of material fields. While one has an idea of how the matter content described by the energy–momentum tensor behaves, obtaining an exact description of it can be a very complex task. As far as this is concerned, the so-called energy conditions constitute a way of testing the positivity of energy density \(\rho \), as is required by a real and well behaved matter content.

Despite energy conditions are not part of fundamental physics, they are useful to characterize the type of fluid distribution one deals with [84]. As it is well known in the framework of General Relativity, the so called null energy condition (NEC): \(\rho +p_{r}\ge 0\) and \(\rho +p_{\perp }\ge 0\) (for anisotropic matter distributions) is violated in order to have a spherically and static traversable WH space-time. Since, in that case the radial pressure \(p_{r}\) is negative and greater in magnitude than the energy density \(\rho \). It may also occur that the energy density \(\rho \) becomes not strictly positive at all points. Besides, in General Relativity the energy conditions establish that gravity should be attractive and they can be derived from the Raychaudhuri equation which is given by

$$\begin{aligned} \frac{d\theta }{d\tau }=-\frac{\theta ^{2}}{3}-\sigma ^{\mu \nu }\sigma _{\mu \nu }+\omega ^{\mu \nu }\omega _{\mu \nu }-R_{\mu \nu }u^{\mu }u^{\mu } \end{aligned}$$
(34)

where \(\theta \), \(\sigma _{\mu \nu }\), \(\omega _{\mu \nu }\) are respectively the expansion, shear and rotation associated with the congruence of time-like geodesics specified by the vector field \(u^{\nu }\). So, the Raychaudhuri equation for the congruence of null geodesics (defined by the null vector \(k^{\mu }\)) is as follows

$$\begin{aligned} \frac{d\theta }{d\tau }=-\frac{\theta ^{2}}{2}-\sigma ^{\mu \nu }\sigma _{\mu \nu }+\omega ^{\mu \nu }\omega _{\mu \nu }-R_{\mu \nu }k^{\mu }k^{\mu }. \end{aligned}$$
(35)

So, to satisfy the attractive gravitational force condition one needs \(R_{\mu \nu }u^{\mu }u^{\nu }\ge 0\) and \(R_{\mu \nu }k^{\mu }k^{\nu }\ge 0\) [85]. It should be noted that the Raychaudhari equations are purely geometric description. Since Einstein fields equations relate the geometry of the space-time \(R_{\mu \nu }\) with the matter content \(T_{\mu \nu }\), Raychaudhuri equations can be combined with the General Relativity ones to impose certain conditions on the energy–momentum tensor for its physical viability. Hence, in Einstein theory one requires \(R_{\mu \nu }k^{\mu }k^{\nu }\ge 0\), which implies \(T_{\mu \nu }k^{\mu }k^{\nu }\ge 0\) (NEC). Nevertheless, in the arena of modified gravity theories, such constraints are not straightforward. Specifically, in f(R) gravity the geometric sector is too complicated due to the introduction of high power terms of the Ricci scalar R. Therefore, to deal with energy conditions in this case one takes the total or effective thermodynamic quantities, that is those formed by the combination of the normal matter sector described by \(T^{\text {m}}_{\mu \nu }\) and the curvature energy–momentum tensor \(T^{\text {c}}_{\mu \nu }\).

It should be noted that violations of the energy conditions have sometimes been presented as only being produced by nonphysical stress energy tensors. Nevertheless, they can be violated in many cases, for example the minimally coupled scalar field and curvature-coupled scalar field theories. As was discussed in [81] the possibilities to obtain WH solutions in f(R)-gravity theory can be analyzed by performing a conformal map from the Jordan frame to the Einstein one and apply there the known results given in [79]. Nevertheless, there are possibilities of getting geometries connecting two far away flat or infinity regions that is, wormholes, driven by normal matter that is, matter satisfying the NEC [57]. However, the price to pay is the presence of ghost fields [80, 81].

So, to check the energy conditions it is necessary to know the behavior of the principal thermodynamic variables that characterize the fluid distribution, namely the density \(\rho \), the radial \(p_{r}\) and tangential \(p_{\perp }\) pressures. These physical quantities are given by Eqs. (9)–(11), where the f(R(r)) function for each model are expressed by Eqs. (30) and (33).

Fig. 3
figure 3

Upper row: (\(m=0\)) The dimensionless density and radial and tangential pressure against the ratio \(r/r_{0}\). Lower row: (\(m=1\)) The trend of the dimensionless thermodynamic variables versus the dimensionless radial coordinate \(r/r_{0}\)

Full size image
Fig. 4
figure 4

The dimensionless null energy condition against the dimensionless radial coordinate \(r/r_{0}\) for \(m=1\) (left panel) and \(m=0\) (right panel)

Full size image

For \(m=1\) we have

$$\begin{aligned} \rho (r)= & {} \frac{20}{81}\frac{F_{0}}{r^{3}_{0}r^5} \left[ \frac{r^{3}}{r^{3}r_{0}-r^{4}_{0}}\right] ^{1/6}\nonumber \\&\quad \bigg [9r^{6}_{0}+3r^{3}_{0}r^{3}-12r^{6}+8r^{6}\left( 1-\frac{r^{3}}{r^{3}_{0}}\right) ^{1/6} {}_2F_{1}\nonumber \\&\quad \left( \frac{1}{6};\frac{1}{2};\frac{3}{2};\frac{r^{3}}{r^{3}_{0}}\right) \bigg ]\nonumber \\&+f_{0}-\left( \frac{r^{3}r_{0}-r^{4}_{0}}{r^{3}}\right) ^{5/6}\frac{rr^{2}_{0}}{\left( r^{3}_{0}-r^{3}\right) ^{2}}F_{0},\end{aligned}$$
(36)
$$\begin{aligned} p_{r}(r)= & {} \frac{20}{81}\frac{F_{0}}{r^{3}_{0}r^5} \left[ \frac{r^{3}}{r^{3}r_{0}-r^{4}_{0}}\right] ^{1/6}\nonumber \\&\quad \bigg [9r^{6}_{0}+3r^{3}_{0}r^{3}-12r^{6}+8r^{6}\left( 1-\frac{r^{3}}{r^{3}_{0}}\right) ^{1/6} {}_2F_{1}\nonumber \\&\quad \left( \frac{1}{6};\frac{1}{2};\frac{3}{2};\frac{r^{3}}{r^{3}_{0}}\right) \bigg ]\nonumber \\&-f_{0}-\frac{4r^{3}_{0}}{r^{5}}\left( \frac{r^{3}}{r^{3}r_{0}-r^{4}_{0}}\right) ^{1/6}F_{0}, \end{aligned}$$
(37)

and for \(m=0\) one arrives to

$$\begin{aligned} \rho (r)= & {} \frac{ r^{2}_{0} F_{0}}{2r^{4}}\text {Appell}F_{1}\left( 4;-\frac{3}{2};\frac{3}{2};5;\frac{r_{0}}{r};\frac{r_{0}}{2r}\right) \nonumber \\&+f_{0}+\frac{3r^{3}_{0}}{4\left( r_{0}-r\right) \left( 2r-r_{0}\right) r^{3}}\left( \frac{r-r_{0}}{2r-r_{0}}\right) ^{3/2}F_{0}, \end{aligned}$$
(38)
$$\begin{aligned} p_{r}(r)= & {} -\frac{ r^{2}_{0} F_{0}}{2r^{4}}\text {Appell}F_{1}\left( 4;-\frac{3}{2};\frac{3}{2};5;\frac{r_{0}}{r};\frac{r_{0}}{2r}\right) \nonumber \\&+f_{0}+\frac{r^{2}_{0}}{r^{4}}\left( \frac{r-r_{0}}{2r-r_{0}}\right) ^{3/2}F_{0}. \end{aligned}$$
(39)

In both cases the tangential pressure is determined by the condition \(p_{\perp }=-\rho \). As can be seen the behavior of the principal thermodynamic variables depends on the integration constants \(F_{0}\) and \(f_{0}\). The Fig. 3 displays the behavior of the main physical quantities for both models. As can be seen in the upper left panel for \(m=0\) the density \(\rho \) is positive defined everywhere for all \(r\in [r_{0},+\infty )\), while the upper right panel shows the trend of the radial \(p_{r}\) and tangential \(p_{\perp }\) pressures, being both quantities negative everywhere. As it is well known a negative radial pressure causes a repulsive gravitational force maintaining the throat of the WH open. In comparing the density and radial pressure in magnitude it is observed that the former is greater than the second one, namely \(|\rho |>|p_{r}|\). This fact as we will see soon ensure the satisfaction of the null and weak energy conditions at least at the throat of the WH and its neighborhood. On the other hand for the case \(m=1\) the situation concerning the density is similar to the previous case, that is, positive defined everywhere. However, the radial pressure is positive at the throat but takes negative values away of it.

Now, we proceed to analyze the behavior of the NEC and WEC. So, combining Eqs. (5) and (9) we get

$$\begin{aligned} FR-\frac{1}{2}f=p_{r}. \end{aligned}$$
(40)

Next, adding Eqs. (9) and (40) we obtain

$$\begin{aligned} \rho +p_{r}=FR-\Box F. \end{aligned}$$
(41)

The above equation is just the NEC. As can be seen this expression is independent of f(R(r)). For the present models the respective NEC expressions are given by

\(m=1\)

$$\begin{aligned} \rho +p_{r}=F_{0}\frac{\left( 4r^{5}_{0}-5r^{3}r^{2}_{0}\right) }{\left( r^{4}-rr^{3}_{0}\right) ^{2}}\left( \frac{r^{3}r_{0}-r^{4}_{0}}{r^{3}}\right) ^{5/6}, \end{aligned}$$
(42)

\(m=0\)

$$\begin{aligned} \rho +p_{r}= & {} F_{0}\frac{r_{0}\beta \left( r_{0}-\beta \right) \left( 5rr_{0}-4r^{2}+4\beta r_{0}-5r\beta \right) }{2\left( r_{0}-r\right) \left( r+\beta \right) r^{3}}\nonumber \\&\quad \left( \frac{r-r_{0}}{r+\beta }\right) ^{\frac{3r_{0}+\beta }{2\left( r_{0}+\beta \right) }} \end{aligned}$$
(43)

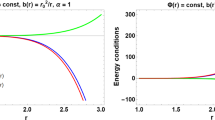
It is clear from the previous expressions (42) and (43) that \(\rho +p_{r}>0\) for \(F_{0}<0\). In this case to contrast the implications of having a WH solution that satisfies NEC and another that violates it, we consider \(F_{0}=-1\) for both cases ı.e, \(m=1\) and \(m=0\). It is worth mentioning that to satisfy the positiveness of \(\rho +p_{r}\) in the case \(m=0\) there are several more restrictions than just considering \(F_{0}<0\). Due to the \(r>r_{0}\) for all \(r\in [r_{0},+\infty )\) the denominator of Eq. (43) is always negative, but this negative sign is cancel out by the global factor \(\beta \) taking into account that \(\beta <0\). Nevertheless, on the numerator appears the term \((r_{0}-\beta )\), thus to assure a positive \(\rho +p_{r}\) quantity \(r_{0}\) must be greater than \(\beta \) in modulus. Therefore, our choice \(\beta =-r_{0}/2\) satisfies the above requirement. Finally, the term \(-4r^{2}\) dominates over the rest part, then the previous choice on \(F_{0}\) is necessary to satisfy the mentioned condition. Figure 4 shows the trend of the NEC for both cases. The left panel corresponds to \(m=1\), as illustrated the NEC is positive for all r belonging to \([r_{0},+\infty )\). Moreover, at large distance the NEC is saturated ı.e, \(\rho +p_{r}=0\). On the other hand the right panel displays a different situation for the \(m=0\) case. In this opportunity the NEC is satisfied at the throat of the WH (see Eq. (43)) and its neighborhood, after that takes negative values, this means violation of the NEC. However, far away from the throat is saturated. Furthermore, as was pointed out earlier, in both cases \(\rho >0\), hence the WEC \( (\rho \ge 0 \quad \& \quad \rho +p_{r}\ge 0)\) is also satisfied everywhere for \(m=1\) and partially for \(m=0\), because the NEC is violated in some regions. The fulfilment of NEC and WEC in the model \(m=1\) implies that the dominant energy condition (DEC) is also satisfied, that is, \(\rho \ge |p_{r}|\). In considering the NEC, WEC and DEC in the tangential direction all are satisfied for \(m=1\) and \(m=0\), while the strong energy condition (SEC) ı.e, \(\rho +p_{r}+2p_{\perp }\ge 0\) is violated for each model due to the condition \(p_{\perp }=-\rho \).

5.3 Ghost fields

The existence of WH regions, at least from the theoretical point of view in the context of f(R)-gravity theory should be supplemented with an additional analysis. As was pointed out by Bronnikov and Starobinsky [80, 81] a WH space-time with matter fields satisfying the NEC cannot exist if

$$\begin{aligned} F(R)\equiv \frac{df(R)}{dR}>0 \quad \text{ and } \quad \frac{d^{2}f(R)}{dR^{2}}=\frac{dF(R)}{dR}\ne 0. \end{aligned}$$
(44)

This implies that the existence of such solutions violates the NEC (like in General Relativity). The first statement of (44) assures that ghost fields (gravitons with negative kinetic energy) are absent in the solution. Hence, if \(F(R)<0\) then the theory propagates ghost fields (for a detailed discussion about this subject in modify gravity theories see [58] and Appendix A). The second statement of (44) is refereed to the stability of the WH throat.Footnote 2

So, to have a better understanding of how (44) works we will re-express Eqs. (21) and (25) as functions of the Ricci scalar and its value at the throat. So, from the expressions (29) and (32) we get

\(m=1\)

$$\begin{aligned} r(R)=\sqrt{-4}\left( \frac{1}{RR^{3/2}_{0}}\right) ^{1/5} \quad \text{ and } \quad r_{0}(R_{0})=\left( \frac{-4}{R_{0}}\right) ^{1/2}, \end{aligned}$$
(45)

where in order to avoid complex numbers \(R_{0}<0\). For \(m=0\) we have

$$\begin{aligned} r(R)= \left( \frac{1}{RR_{0}}\right) ^{1/4} \quad \text{ and } \quad r_{0}(R_{0})=\left( \frac{1}{R_{0}}\right) ^{1/2}. \end{aligned}$$
(46)

So, using Eqs. (28), (30), (31), (33), (45) and (46) one arrives to

$$\begin{aligned} f(R)= & {} -\frac{5F_{0}}{162}RR^{3}_{0} \left[ \frac{1}{\sqrt{-4}\left( R^{-1/2}_{0}-R^{3/5}R^{-11/10}_{0}\right) }\right] ^{1/6}\nonumber \\&\qquad \Bigg [9\left( \frac{-4}{R_{0}}\right) ^{3}+\frac{192}{R^{3/5}R^{12/5}_{0}}\nonumber \\&+768\left( \frac{1}{RR^{3/2}_{0}}\right) ^{6/5}-512\left( \frac{1}{RR^{3/2}_{0}}\right) ^{6/5}\nonumber \\&\left( 1-\frac{R^{3/5}_{0}}{R^{3/5}}\right) ^{1/6}{}_2F_{1}\left( \frac{1}{6};\frac{1}{2}; \frac{3}{2};\frac{R^{3/5}_{0}}{R^{3/5}}\right) \Bigg ]+ f_{0}, \end{aligned}$$
(47)
$$\begin{aligned} F(R)= & {} \left[ \frac{\frac{1}{R^{3/5}R^{9/10}_{0}}}{\left( \frac{\left( -4\right) ^{1/2}}{R^{1/5}R^{3/10}_{0}}-\frac{\left( -4\right) ^{1/2}}{R^{1/2}_{0}}\right) \left( \frac{1}{R^{2/5}R^{11/10}_{0}} +\frac{1}{R^{1/5}R^{13/10}_{0}}+\frac{1}{R^{3/2}_{0}}\right) }\right] ^{1/6}F_{0},\nonumber \\ \end{aligned}$$
(48)

for \(m=1\) and

$$\begin{aligned} f(R)= & {} \text {Appell}F_{1}\left( 4;-\frac{3}{2};\frac{3}{2};5;\right. \nonumber \\&\quad \left. \frac{R^{1/4}}{R^{1/4}_{0}};\frac{R^{1/4}}{2R^{1/4}_{0}}\right) RF_{0}+f_{0}. \end{aligned}$$
(49)
$$\begin{aligned} F(R)= & {} \left[ \frac{\left( \frac{1}{RR_{0}}\right) ^{1/4} -\left( \frac{1}{R_{0}}\right) ^{1/2}}{2\left( \frac{1}{RR_{0}}\right) ^{1/4}-\left( \frac{1}{R_{0}}\right) ^{1/2}}\right] ^{3/2}F_{0}, \end{aligned}$$
(50)
Fig. 5
figure 5

Upper row: the trend of the dimensionless f(R) function (left panel) and its first derivative F(R) (right panel) against the dimensionless quantity \(R/R_{0}\) for \(m=1\). Lower row: the behavior of the quantities \(f(R)/f(R_{0})\) and F(R) versus \(R/R_{0}\) for \(m=0\)

Full size image
Fig. 6
figure 6

The trend of dF/dR versus \(R/R_{0}\) for \(m=1\) (left panel) and \(m=0\) (right panel)

Full size image

for \(m=0\). As it is depicted in Fig. 5 (right upper panel) in the \(m=1\) case F(R) is negative for all R. This means that the first statement of (44) is not met. A negative F(R) implies the present of ghost fields in the solution. However, as was stated in [80, 81] it is not possible to obtain a free ghost field WH solution satisfying NEC. Of, course as pointed out earlier, the case \(m=1\) satisfies the NEC but contains states with negative kinetic energy. The second requirement of (44) is satisfied for this model as shows the left panel of Fig. 6. The case \(m=0\) entails a more interesting situation. As it is appreciated from expression (50) the F(R) function is everywhere positive and zero at \(R=R_{0}=1\) (or equivalently at \(r=r_{0}\), since there is a one to one relation between r and R). This implies that at the throat the gravitational forces become infinite. Moreover, from the right panel in Fig. 6 is evident that \(dF/dR=0\) at \(R=R_{0}=1\). This particular model is not within the scope of the analysis given in [80, 81], because in these works only the case \(F(R)=0\) and \(dF/dR\ne 0\) is studied. In general, for the case \(m=0\) the expression of dF/dR reads

$$\begin{aligned}&\frac{dF(R)}{dR}=-\frac{3}{8}\nonumber \\&\quad \times \frac{\left[ \left( \frac{1}{RR_{0}}\right) ^{1/4}-\left( \frac{1}{R_{0}}\right) ^{1/2} \right] ^{1/2}\left( \frac{1}{R_{0}}\right) ^{1/2}}{\left[ 2\left( \frac{1}{RR_{0}}\right) ^{1/4} -\left( \frac{1}{R_{0}}\right) ^{1/2}\right] ^{5/2}\left( \frac{1}{RR_{0}}\right) ^{3/4}R^{2}R_{0}} F_{0}, \end{aligned}$$
(51)

as can be seen the numerator of the above expression vanishes for every \(R=R_{0}\). Besides, this solution constrains ghost fields as Fig. 5 illustrates (right panel in the lower row) and partially violates the NEC as can be seen from the left panel in Fig. 4. In this case, ghosts appear because the NEC is satisfied in some regions. At this point, it is worth mentioning that the general solution of (20) with \(m=0\) and without any specification about the values of \(\gamma \) and \(r_{0}\) is given by

$$\begin{aligned} F(R(r))=\left[ \frac{r-r_{0}}{\beta +r}\right] ^{\frac{r_{0}-\beta }{2\left( r_{0}+\beta \right) }}F_{0}, \end{aligned}$$
(52)

so regardless of which values are chosen for the parameters \(\gamma \) and \(r_{0}\) this particular model always leads to \(F(R(r))=0\) at the throat, or using (50) in terms of the scalar curvature R, one obtains at \(R_{0}\): \(F(R)=0\) and \(dF(R)/dR=0\).

6 Cosmological properties

In this section we discuss some cosmological aspects associated to f(R)-gravity. As it is well known this modify gravity theory emerges as an alternative for a unified description of the early-time inflation with late-time cosmic acceleration, without adding unknown forms of dark components ı.e, dark energy and dark matter [59]. Although several models of gravity f(R) have been proposed to unify the aforementioned problems [60,61,62], there are models that only address either early or late stage of the Universe. Considering, the latter a wide range of works available in the literature have faced the accelerated expansion of the Universe to give an explanation to the existence of dark energy from the perspective of f(R)-gravity [63,64,65,66,67,68,69,70,71,72,73,74,75,76].

6.1 Early and late time phases

To tackle the dark energy issue from the arena of f(R)-gravity there some general requirement that any viable f(R) model should satisfy [77]

  1. 1.

    \(F(R)>0\) for \(R \ge \tilde{R}\) (\(\tilde{R}> 0\)), where \(\tilde{R}\) is the Ricci scalar at the present epoch.

  2. 2.

    \(\frac{dF(R)}{dR}>0\) for \(R \ge \tilde{R}\). This is required for consistency with local gravity tests, for the presence of the matter-dominated epoch and for the stability of cosmological perturbations.

  3. 3.

    \(f(R)\rightarrow R\) for \(R>>\tilde{R}\). This is required for consistency with local gravity tests and for the presence of the matter-dominated epoch.

  4. 4.

    \(0<\frac{R}{F(R)}\frac{dF(R)}{dR}(\Delta =-2)<1\) at \(\Delta \equiv -\frac{RF(R)}{f(R)}=-2\). This is required for the stability of the late-time de Sitter point.

To check the feasibility and viability of our model, we have analyzed in details the above criteria for the case given by \(m=0\) (the case \(m=1\) is not analyzed due to the general F(R) function without any specification about \(\beta \) and \(r_{0}\) cannot be integrated to obtain the f(R) function). So, from expression (52) one has

$$\begin{aligned} F(R)=\left[ \frac{\left( \frac{-2c\beta }{R}\right) ^{1/4}-c}{\left( \frac{-2c\beta }{R}\right) ^{1/4}+\beta }\right] ^{\frac{c-\beta }{2\left( c+\beta \right) }} F_{0}, \end{aligned}$$
(53)

where c is a constant parameter replacing \(r_{0}\). Integration of (53) with respect to R leads to

$$\begin{aligned}&f(R)=F_{0}\text {Appell}F_{1}\nonumber \\&\quad \times \left( 4;-\frac{c-\beta }{2\left( c+\beta \right) };\frac{c-\beta }{2\left( c+\beta \right) };5;\frac{cR^{1/4}}{\left( -2\beta c\right) ^{1/4}}; -\frac{\beta R^{1/4}}{\left( -2\beta c\right) ^{1/4}}\right) R+f_{0}.\nonumber \\ \end{aligned}$$
(54)

Next, from (53) the condition 1 is fulfilled if for all \(R \ge \tilde{R}>0\) iff \(F_{0}>0\) and \(c\beta <0\) where \(\beta >0\) and \(c<0\), thus \(F(R)>0\). To check the second condition from Eq. (53) one gets

$$\begin{aligned}&\frac{dF(R)}{dR}\nonumber \\&\quad =\frac{\left( \beta -c\right) }{4R\left( 2\beta -2c+2\left( \frac{-2c\beta }{R}\right) ^{1/4} +R\left( \frac{-2c\beta }{R}\right) ^{3/4}\right) }F(R).\nonumber \\ \end{aligned}$$
(55)

As before, this condition is satisfied for all \(\beta >0\) and \(c<0\). Next, when \(R>>\tilde{R}\) the special function tends to a real positive number, namely K. Then from (54) we have

$$\begin{aligned} f(R)\sim F_{0}KR+f_{0}. \end{aligned}$$
(56)

Now choosing \(F_{0}K=1\), Eq. (56) becomes

$$\begin{aligned} f(R)\sim R, \end{aligned}$$
(57)

where at large scalar curvature R the constants \(f_{0}\) can be neglected, or it can be interpreted as \(f_{0}=-2\Lambda \), thus one ends with Einstein theory including the cosmological constant term. Then condition 3 is satisfied. As can be seen from (57) in the limit \(R>>\tilde{R}\) Einstein’s gravity is recovered as expected for viable and realistic f(R) models going from a matter-dominated epoch to a dark energy Universe [86]. The last condition entails a special kind of solutions within the f(R)-gravity background, those are the so-called de Sitter point class of solutions. This class of solutions satisfy the following constraint obtained from the trace of the equations of motion (5), which is trivial in the Einstein theory but gives precious dynamical information in the modified gravitational models [62]. So, this condition reads

$$\begin{aligned} F(\tilde{R})\tilde{R}-2f(\tilde{R})=0. \end{aligned}$$
(58)

This constraint reveals the existence of maximally symmetric vacuum solutions in the theory [78]. So, if a covariantly constant scalar curvature \(R\equiv \tilde{R}=\text {constant}\) satisfies (58) given any f(R)-gravity model, then the theory contains the General Relativity de Sitter solution with constant curvature \(\tilde{R}\). Therefore, by replacing in Eq. (58) one arrives to

$$\begin{aligned}&-2F_{0}\text {Appell}F_{1}\left( 4;-\frac{c-\beta }{2\left( c+\beta \right) };\frac{c-\beta }{2\left( c+\beta \right) };\right. \nonumber \\&\qquad \left. 5;\frac{c\tilde{R}^{1/4}}{\left( -2\beta c\right) ^{1/4}};-\frac{\beta \tilde{R}^{1/4}}{\left( -2\beta c\right) ^{1/4}}\right) \tilde{R}\nonumber \\&\quad +\tilde{R}\left[ \frac{\left( \frac{-2c\beta }{\tilde{R}}\right) ^{1/4}-c}{\left( \frac{-2c\beta }{\tilde{R}}\right) ^{1/4}+\beta }\right] ^{\frac{c-\beta }{2\left( c+\beta \right) }}F_{0}-2f_{0}=0. \end{aligned}$$
(59)

It is obvious that the previous equation has always a solution which depends on three parameters, namely \(\{c,\beta ,\tilde{R}\}\). Next, the stability condition 4: \(0<\frac{R}{F}\frac{dF}{dR}<1\) is always satisfied. In the present case this condition reads

$$\begin{aligned} \frac{R}{F(R)}\frac{dF(R)}{dR}=\frac{\left( \beta -c\right) }{4\left( 2\beta -2c+2\left( \frac{-2c\beta }{R}\right) ^{1/4}+R\left( \frac{-2c\beta }{R}\right) ^{3/4}\right) }. \end{aligned}$$
(60)

Indeed, from (60) the denominator is always greater than the numerator, hence the expression is always positive and less than 1 for every c and \(\beta \).

It is clear from (54) that the model reproduces the dominated matter epoch expressed by (57). As it is well-known, this stage corresponds to early times or equivalently large curvature [86]. On the other hand, the late time stage (small curvature) described by (54) can be stated as followsFootnote 3

$$\begin{aligned} f(R)\sim F_{0}R\left[ 1+\frac{2\left( \beta -c\right) }{5\left( -2\beta c\right) ^{1/4}}R^{1/4}+O\left( R^{1/2}\right) \right] +f_{0}. \end{aligned}$$
(61)

As can be seen at late times the asymptotic behavior of the present model leads to a model with positive powers of curvature [86].

At this point, it is worth mentioning that the present model does not unify the inflationary stage with the accelerated expansion. Notwithstanding, without loss of generality Eq. (53) can be generalized as follows

$$\begin{aligned} F(R)= & {} \left[ \frac{\left( \frac{-2c\beta }{R}\right) ^{1/4}-c}{\left( \frac{-2c\beta }{R}\right) ^{1/4}+\beta }\right] ^{\frac{c-\beta }{2\left( c+\beta \right) }}\nonumber \\&F_{0}-2\Lambda _{0}\delta \left( R-R_{0}\right) -2\Lambda _{I}\delta (R-R_{I}), \end{aligned}$$
(62)

being \(\delta \) the delta Dirac function and \(R_{0}\) and \(R_{I}\) (\(R_{I}>>R_{0}\)) are representing transition scalar curvatures (for further details see [62]). The above extension is completely plausible, since the functional given by (62) is valid for all \(R\ne R_{0}\) and \(R\ne \ R_{I}\), being \(\delta (R-R_{0})\) and \(\delta (R-R_{I})\) vanishing. So, integrating the above expression one gets

$$\begin{aligned} f(R)= & {} F_{0}\text {Appell}F_{1}\left( 4;-\frac{c-\beta }{2\left( c+\beta \right) };\frac{c-\beta }{2\left( c+\beta \right) };\right. \nonumber \\&\qquad \left. 5;\frac{cR^{1/4}}{\left( -2\beta c\right) ^{1/4}};-\frac{\beta R^{1/4}}{\left( -2\beta c\right) ^{1/4}}\right) R \nonumber \\&-2\Lambda _{0}\Theta (R-R_{0})-2\Lambda _{I}\Theta (R-R_{I}) + f_0, \end{aligned}$$
(63)

where \(\Theta \) is the Heaviside step function. As stated in [59, 62] any viable f(R) model unifying inflationary phase with accelerated stage must satisfy the following requirements

$$\begin{aligned} f(0)=0 \quad \text{ and }\quad \lim _{R\rightarrow \hat{R}}f(R)=-2\left( \Lambda _{0}+\Lambda _{I}\right) , \end{aligned}$$
(64)

with \(\hat{R}>>R_{I}>>R_{0}\). Of course when \(R=0\) the special function tends to 1 and (63) provides \(f(0)=0\), ensuring the disappearance of the cosmological constant in the limit of flat space-time [62]. On the other hand, in the limit \(R\rightarrow \hat{R}\) Eq. (63) yields to \(-2\left( \Lambda _{0}+\Lambda _{I}\right) \), where \(\Lambda _{I}\) is the inflation cosmological constant and \(\hat{R}\) being the corresponding transition large scalar curvature. Despite the coupling between our model and the two step model provides a well posed scenario to unify the early and late time stages of the Universe, the introduction of Heaviside and Dirac distributions makes it a simply toy model [62]. However it shows a natural way to extend our model to address this point.

Fig. 7
figure 7

The evolution of the density \(\rho (t)\) versus the cosmic time variable t (left panel) and the scale factor a(t) (right panel)

Full size image

6.2 Late time accelerated phase in the flat FLRW space-time

To explore the late time accelerated phase of our Universe, we shall consider that the geometric background is described by a flat Friedmann–Lemaitre–Robertson–Walker (FLRW) metric [59, 83], with line element given by,

$$\begin{aligned} ds^{2}=-dt^{2}+a(t)^{2}\sum _{i=1,2,3}\left( dx^{i}\right) ^{2}, \end{aligned}$$
(65)

with a(t) denoting as usual the scale factor. Next, taking into account a perfect fluid matter distribution

$$\begin{aligned} T^{{\mu }(\text {m})}_{\ \nu }=\text {diag}\left[ -\rho (t),p(t),p(t),p(t)\right] , \end{aligned}$$
(66)

the field equation (4) adopt the following form

$$\begin{aligned}&-\frac{f}{2}+3\left( H^{2}+\dot{H}\right) F\nonumber \\&\qquad -18\left( 4H^{2}\dot{H}+H\ddot{H}\right) \frac{dF}{dR}+\rho =0 \end{aligned}$$
(67)
$$\begin{aligned}&\frac{f}{2}-\left( \dot{H}+3H^{2}\right) F\nonumber \\&\qquad +6\left( 8H^{2}\dot{H}+4\dot{H}^{2}+6H\ddot{H} +\dddot{H}\right) \frac{dF}{dR}\nonumber \\&\qquad +36\left( 4H\dot{H}+\ddot{H}\right) ^{2}\frac{d^{2}F}{dR^{2}}+p=0, \end{aligned}$$
(68)

where dots represent differentiation with respect to the cosmic time t and being H the Hubble rate defined as \(H(t)\equiv \dot{a}(t)/a(t)\). As usual we shall assume that \(\rho \) and p are related by the following equation of state

$$\begin{aligned} p=\omega \rho , \end{aligned}$$
(69)

being \(\omega \) a constant parameter, namely the equation of state parameter. So, plugging the model expressed by (61)Footnote 4 with the previous ingredients into the field equation (67) one gets

$$\begin{aligned}&-\frac{1}{2}\left( F_{0}R+DR^{5/4}\right) +3\left( H^{2}+\dot{H}\right) \left( F_{0}+\frac{5D}{4}R^{1/4}\right) \nonumber \\&\quad -\frac{45D}{8}\left( 4H^{2}\dot{H}+H\ddot{H}\right) R^{-3/4}\nonumber \\&\qquad +\rho _{0}a^{-3\left( 1+\omega \right) }=0, \end{aligned}$$
(70)

where \(D\equiv 2F_{0}\left( \beta -c\right) /5\left( -2\beta c\right) ^{1/4}\). Besides, for the sake of simplicity we have fixed \(f_{0}=0\). The FLRW line element given by (65) leads to

$$\begin{aligned} R=12H^{2}+6\dot{H}. \end{aligned}$$
(71)

So, Eq. (70) can be written as

$$\begin{aligned}&-\frac{1}{2}\left[ F_{0}\left( 12H^{2}+6\dot{H}\right) +D\left( 12H^{2}+6\dot{H}\right) ^{5/4} \right] \nonumber \\&\quad +3\left[ H^{2}+\dot{H}\right] \left[ F_{0}+\frac{5D}{4}\left( 12H^{2}+6\dot{H}\right) ^{1/4}\right] \nonumber \\&\quad -\frac{45D}{8}\left[ 4H^{2}\dot{H}+H\ddot{H}\right] \left[ 12H^{2}+6\dot{H}\right] ^{-3/4}\nonumber \\&\quad +\rho _{0}a^{-3\left( 1+\omega \right) }=0. \end{aligned}$$
(72)

The above equation admits the following solution in inverse powers of t for the Hubble rate H(t) as follows

$$\begin{aligned} H(t)=\frac{I}{t}+\frac{J}{t^{3/2}}, \end{aligned}$$
(73)

where I and J are given by

$$\begin{aligned} I= & {} \frac{2}{3\left( 1+\omega \right) }, \quad J=-\frac{1}{10}\frac{\left( \beta -c\right) }{\left( -2\beta c\right) ^{1/4}}\left[ \frac{4\left( 1-3\omega \right) }{3\left( 1+\omega \right) ^{2}}\right] ^{1/4}\nonumber \\&\qquad \times \left[ \frac{11+87\omega }{36\left( 1+\omega \right) }\right] , \end{aligned}$$
(74)

then the scale factor a(t) is

$$\begin{aligned} a(t)=a_{0}t^{2/3\left( 1+\omega \right) }\text {Exp}\left[ -\frac{2J}{t^{1/2}}\right] , \end{aligned}$$
(75)

being

$$\begin{aligned} a_{0}=\left[ \frac{4F_{0}}{3\rho _{0}\left( 1+\omega \right) ^{2}}\right] ^{-\frac{1}{3\left( 1+\omega \right) }}. \end{aligned}$$
(76)

It should be noted that the first terms of (73) and (75) yield to the well-known results provided by General Relativity [87], hence next terms can be seen as corrections introduced by f(R)-gravity. Now, from the field equations given above (67)–(68) the acceleration equation reads

$$\begin{aligned} \frac{\ddot{a}}{a}=-\frac{1}{6}\left( \rho _{\text {eff}}+3p_{\text {eff}}\right) , \end{aligned}$$
(77)

being \(\rho _{\text {eff}}\equiv \rho +\rho _{R}\) and \(p_{\text {eff}}\equiv p+p_{R}\), where

$$\begin{aligned} \rho _{R}=\frac{1}{F}\left[ \frac{1}{2}\left( f-RF\right) -3H\dot{R}\frac{dF}{dR}\right] , \end{aligned}$$
(78)

and

$$\begin{aligned} p_{R}=\frac{1}{F}\left[ 2H\dot{R}\frac{dF}{dR}+\ddot{R}\frac{dF}{dR}+\dot{R}^{2}\frac{d^{2}F}{dR^{2}}-\frac{1}{2}\left( f-RF\right) \right] . \end{aligned}$$
(79)

From Eqs. (77)–(79), the acceleration condition, for a dust dominated model (\(p=0 \Rightarrow \omega =0\) ), leads to [88]

$$\begin{aligned} \omega _{\text {eff}}=-1-\frac{2\dot{H}}{3H^{2}}<-\frac{1}{3}, \end{aligned}$$
(80)

where we have defined \(\omega _{\text {eff}}\) as

$$\begin{aligned} \omega _{\text {eff}}\equiv \frac{p_{\text {eff}}}{\rho _{\text {eff}}}. \end{aligned}$$
(81)

the above condition can be cast in terms of the curvature contributions as follows

$$\begin{aligned} \omega _{R}\equiv \frac{p_{R}}{\rho _{R}}<-\frac{\rho _{\text {eff}}}{3\rho _{R}}. \end{aligned}$$
(82)

In Fig. 7 are displayed the evolution of the density \(\rho (t)\) (left panel) against the cosmic time t and the trend of the scale factor a(t) (right panel). On the other hand Fig. 8 shows the behavior of the effective equation of state parameter \(\omega _{\text {eff}}\). As can be seen the condition (80) is satisfied. Then the model describe a Universe in an accelerated phase as desired [88].

Fig. 8
figure 8

The trend of the effective equation of state parameter \(\omega _{\text {eff}}\)

Full size image

7 Concluding remarks

In this work a spherically and static wormhole family with vanishing red-shift function was studied in the arena of f(R)-gravity theory. The field equations were solved by imposing a suitable shape function satisfying all the requirements to describe a traversable wormhole and asymptotically flat space-time at infinity and an equation of state, specifically \(p_{\perp }=-\rho \). The imposition of this relation leads to a first order differential equation for F(R(r)) function. Once the F(R(r)) function is obtained it can be expressed in the form F(R) by inverting the radial coordinate r from the Ricci scalar expression.

As it is well known in the context of General Relativity a wormhole space-time is only possible if the NEC is not satisfied at the throat and its neighborhood [79]. The same argument is translated into the f(R)-gravity theory in the absence of ghost fields. Moreover, under some special conditions wormhole geometries respecting NEC are possible in the background of f(R)-gravity. Regarding the present study we can summarize the main results for each model as follows:

\(m=0\)

  1. 1.

    For the considered space parameter, that is \(\{r_{0},\beta ,F_{0}\}=\{1,-\frac{1}{2},-1\}\), it can be seen from Fig. 3 (upper panels) that the density \(\rho \) is positive defined everywhere, contrarily to what happens with the radial pressure \(p_{r}\) which is negative for all \(r\in [r_{0},+\infty )\), so the WH geometry is supported by a repulsive gravitational force introduced by this negative radial pressure. However, it should be noted that there are some points where \(|p_{r}|>|\rho |\), then the NEC and WEC are locally violated as it is illustrated in Fig. 4 (left panel).

  2. 2.

    As Fig. 5 shows (right panel in the lower row ) F(R) is strictly negative everywhere. One should take into account that as stated in [80, 81] in the framework of f(R)-gravity theory it is not possible to obtain a wormhole solution respecting energy conditions (not supported by exotic matter) without the presence of ghost fields.

\(m=1\)

  1. 1.

    In this case the space parameter was fixed to \(\{r_{0},\beta ,F_{0}\}=\{1,1,-1\}\) and in distinction with the previous case the the WEC and NEC are satisfied everywhere. This is so because the density \(\rho \) is positive defined at all points \(r\in [r_{0},+\infty )\) and greater in magnitude than the radial pressure \(p_{r}\), which is negative everywhere. The fact of fulfilling the energy conditions (WEC and NEC) makes the f(R)-gravity arena an interesting and promising field to study the main properties of wormhole structures without any exotic matter distribution as occurs in General Relativity.

  2. 2.

    Although this case satisfies the WEC and NEC everywhere, as stated before then the theory can not have absence of ghosts. In fact, if the wormhole structure is threading at its throat by normal matter distribution respecting the mentioned energy conditions, then the solution must have ghost fields. The main problem with the ghost fields is that the f(R)-gravity model associated with the wormhole geometry can not describe or explain cosmological issues, since this requires a positive defined energy.

To close the wormhole scenario, we remark that it is possible to build viable wormholes space-time in the f(R)-gravity context respecting all the general requirements to be a traversable region connecting two asymptotically Minkowskian or infinite spaces, either violating or satisfying NEC. However, in the latter case, the conformal map [80, 81] must be ill defined at some points since in the Einstein frame there are not wormholes satisfying NEC [79].

An important property of one of our models is the cosmological viability to address the late-time accelerated epoch of our Universe. This point was analyzed by checking that the f(R)-gravity models satisfy the general requirements given in [77]. It is worth mentioning that to study the cosmological implications described by the resulting models with \(m=0\) and \(m=1\), the space parameter \(\{r_{0},\beta ,F_{0}\}\) should be reset, because the previous assignation was to describe an asymptotically and traversable wormhole geometry satisfying the energy conditions (partially or totally). For the case \(m=1\) it is not possible in general to analyze its cosmological viability, because the general expression given by (21) is not tractable mathematically. in distinction, the case \(m=0\), as was shown in Sect. 6 has good properties to address the late-time acceleration era of the Universe. In this concern, we have checked the general criteria [77] to confirm these good properties. Among these features, the model f(R) corresponding to \(m=0\) respects: (i) consistency with local gravity tests, (ii) stability under cosmological perturbations, (iii) ghosts free and (iv) stability of the de Sitter point. In considering the last point, it is remarkably that this model contains vacuum solutions ı.e, solutions with constant curvature \(R_{0}\) and null energy–momentum tensor \(T_{\mu \nu }=0\), which also include the de Sitter’s solution to the vacuum Einstein field equations with cosmological constant [78]. Furthermore, to check the accelerated phase of our Universe at late time for the present model, we have explored the behaviour of the scale factor a(t) and effective equation of state parameter \(\omega _{\text {eff}}\) on the background of a flat Friedmann–Lemaitre–Robertson–Walker space-time. As it is corroborated in Fig. 8 the equation of state parameter satisfies the condition \(\omega _{\text {eff}}<-1/3\) as desired for an accelerated expanding Universe [88]. At this point it should be noted that the present model is in accordance with some well-known recognize models previously reported [59, 62, 86] in the arena of f(R)-gravity theory to deal with cosmological open issues, facing both: the early and late time epochs of our evolving Universe. In considering the former, our model does not include early time phase (inflationary phase), since the model is not capable to produces the minimal ingredients to describe this stage of the Universe [59]. Nevertheless, as was discussed in Sect. 6, the model can be consistently coupled with a two step model [62] to unify both stages, although the output is only a toy model it shows a natural way to extend our model to address this point. For these reasons we only explore in some details the late time accelerated phase, which in the limit of high curvature reproduces Einstein gravity theory. Finally, we want to highlight that the model obtained in this work is able to describe for certain values of the parameters \(\{m,\beta , r_{0},F_{0}\}\) a wormhole structure without ghost, partially satisfying the NEC, while for other values of aforementioned parameters, describes a consistent and viable cosmological model to explain late stages of the cosmic evolution of the Universe in a flat FRLW background.