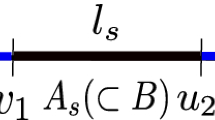1 Introduction

Gauge-gravity duality [1,2,3,4] has been one of the major areas of research in theoretical physics in the last two decades. The reason for this intense focus is for its success in explaining the physics of strongly coupled field theories [5,6,7,8,9,10,11,12]. The duality makes a connection between a strongly coupled gauge field theory in d-dimensional spacetime and a classical gravity theory in \((d+1)\)-dimensional spacetime, with the field theory living on the boundary of the \((d+1)\)-dimensional spacetime. The advantage of the connection is evident at once. Perturbative calculations which could not be performed on the field theory side due to the strong coupling, can now be carried out in the gravitational side since the bulk theory is a weakly coupled theory in a classical gravity background. The duality then translates the information obtained on the gravity side to a lot of valuable information about the strongly coupled field theories.

The gravitational dual gives tractable prescriptions to describe a wide range of properties of strongly coupled field theories. For instance, a very neat and simple proposal was put forward in [5, 6], to compute the entanglement entropy (EE) in field theories. In particular, the holographic description of quantum entanglement known as holographic EE (HEE) have proven to be elegant in computing the EE of quantum field theories with conformal symmetry [13, 14]. The result for EE in two dimensional conformal field theories is well known, however the result in higher dimensions would be extremely difficult to compute. The holographic prescription gives a handle to compute such quantities. The holographic calculation of EE starts with the Ryu–Takayanagi (RT) proposal which states that the HEE of an asymptotically \(AdS_{(d+1)}\) spacetime is equal to EE of a d- dimensional CFT living on the boundary of the gravitational theory in the bulk. The formula for the HEE reads [13, 14]

$$\begin{aligned} S_{HEE}= \frac{Area (\gamma _A)}{4 G_{(d+1)}} \end{aligned}$$
(1)

where \(\gamma _A\) corresponds to the static minimal surface extending from the subsystem A, at the boundary of the asymptotically AdS spacetime to the bulk. Thereafter, HEE calculation in various scenarios has been carried out extensively [15,16,17,18,19,20,21].

It has also been realized that EE is useful in studying systems away from equilibrium. An important question that can be raised in this context is whether there exists a relation analogous to the first law of thermodynamics. In [15, 16], the question was answered in the affirmative. It was found there that in the ultra-violet (UV) limit, the HEE gives a thermodynamics like relation. It was named as entanglement thermodynamics and a notion of entanglement temperature came up with this observation. However, the entanglement temperature definition arising in the UV limit is quite different from the well known thermodynamic temperature. This has lead to the investigation of finding a generalized temperature that agrees with the entanglement temperature in the UV limit and the Hawking temperature of the black hole in the infra-red (IR) limit [22, 23].

Quantum complexity is another important quantity in the theory of quantum information. The quantity gives a measure of difficulty in performing a particular task. The proposal with which computations are usually carried out is the holographic subregion complexity proposal (HSC) [24]. It states that for a subsystem A in the boundary, the HSC can be calculated from the formula

$$\begin{aligned} C_V=\frac{V(\gamma _A)}{8\pi R G_{(d+1)}} \end{aligned}$$
(2)

where \(V(\gamma _A)\) is the maximal volume enclosed by the RT surface in the bulk, and R is the radius of curvature of the spacetime.

There are other proposals as well to compute the complexity holographically. The proposal was put forward in [25, 26]. The prescription to obtain the complexity of a state is to calculate the volume of the Einstein–Rosen bridge (ERB) and is given by

$$\begin{aligned} C_V(t_L, t_R)=\frac{V(t_L, t_R)}{RG_{(d+1)}} \end{aligned}$$
(3)

where V represents the spatial volume of the ERB. This volume is the maximum volume bounded by the CFT spatial slices at times \(t_L\), \(t_R\) on the two boundaries.

Then other proposal to calculate the holographic complexity is that of the bulk action computed on the Wheeler–De Witt patch [27]

$$\begin{aligned} C_W=\frac{A(W)}{\pi \hbar } \end{aligned}$$
(4)

where A(W) is the action calculated on the Wheeler–De Witt patch W.

The majority of the analyses of the quantities described above have been carried out for systems which are relativistic in nature [28,29,30,31,32,33,34,35,36,37,38,39]. Relatively few investigations has been done for non-relativistic systems. In [40], the Lifshitz system in \(3+1\)- dimensions, which is a well known non-relativistic system, was studied and thermodynamics like law for entanglement entropy of perturbed Lifshitz spacetime was obtained. In [41], the HSC of the perturbed Lifshitz spacetime was computed, and a relation analogous to entanglement thermodynamics was obtained in the context of HSC.

In this paper, we set out to investigate the holographic quantities for a Lifshitz black hole [42] in \(3+1\)-dimensions with the dynamical exponent \(z=2\). The motivation for looking at this gravity solution with Lifshitz-type scale invariance is the following. Indeed, several attempts have been made to use the holographic principle to analyse condensed matter systems near their critical points [43]. To study such critical points, scale invariant theories which are not Lorentz invariant are of primary importance. Time and space can scale differently under dilations in such a theory. A Lifshitz theory exhibits such a scale invariance. However, it is to be noted that numerous analytic solutions of Lifshitz black hole are present in the literature [44,45,46,47,48] other than that mentioned in [42]. Despite this fact, we have chosen this particular background because this is a remarkably simple analytic solution in \(3+1\)-dimensions with \(z=2\). We first obtain the finite part of the HEE of the Lifshitz black hole, and then study its infrared (IR) and ultra-violet (UV) limits. We then proceed to investigate the near horizon behavior of the HEE to study the divergence structure. Next we obtain the change in HEE between a Lifshitz black hole and a pure Lifshitz spacetime. This we call the renormalized EE. Then we proceed to write down a thermodynamic like relation involving the change in HEE by introducing the notion of generalized temperature. The generalized temperature is defined in such a way that it gives the Hawking temperature of the Lifshitz black hole in the IR limit. In the UV limit, it gives rise to the entanglement temperature.

We then look into other information theoretic quantities holographically. We start by computing the HSC and then look at its near horizon limit. Interestingly we see that the HSC has a logarithmic divergence in addition to the UV divergence. The logarithmic divergence is absent in the Schwarzschild-AdS case in \((3+1)\)-dimensions [49]. The logarithmic divergence owes its origin to the power of the blackening factor appearing in the spacetime metric. Then we compute the Fisher information metric holographically by following the prescription in [50]. Then we compute the fidelity susceptibility from the fidelity expanded upto second order in the perturbation. We observe that the fidelity susceptibility can be related to the Fisher information metric upto a dimensional dependent constant. Finally, we compute the fidelity susceptibility by following the proposal in [51]. We observe that this does not match with the Fisher information metric computed holographically.

The organization of the paper is as follows. The basic setup is discussed in Sect. 2. This contains a short description of Lifshitz black hole metric and integrals related to computation of HEE and HSC. We have computed the HEE for Lifshitz black hole in Sect. 3. Firstly, the HEE has been computed analytically without any approximation then it has been analyzed for IR and UV approximation. Then the near horizon behavior of HEE has been checked in this section. The concept of generalized temperature has been introduced in Sect. 3.1. In this section we have clearly shown that in IR regime the generalized temperature is equal to the black hole temperature plus some correction terms. Those correction terms becomes negligible when the subsystem length becomes very large. The HSC has been computed in Sect. 4. The holographic Fisher information metric and fidelity susceptibility has been discussed in Sect. 5.

2 Lifshitz black hole

We are interested in computing HEE and HC for Lifshitz black hole which asymptotically approaches to Lifshitz spacetime in near boundary limit. For Lifshitz black hole one may consider the following \(3+1\)-dimensional action [42]

$$\begin{aligned} {} S= & {} \frac{1}{2}\int d^4x ~ \sqrt{-g}(R-2\varLambda ) \nonumber \\&-\int d^4x \sqrt{-g}\left( e^{-2 \Phi } \frac{F^2}{4} +\frac{m^2 }{2}A^2+ (e^{-2\Phi }-1)\right) .\nonumber \\ \end{aligned}$$
(5)

A solution to this action is given by

$$\begin{aligned} {} ds^2= & {} -f(r)\frac{dt^2}{r^{2z}}+\frac{dx^2 + dy^2}{r^2}+\frac{dr^2}{r^2 f(r)} \nonumber \\ \varLambda= & {} -\frac{z^2+z+4}{2}; \quad \Phi =-\frac{1}{2} \log (1+\frac{r^2}{r_h^2}); \quad \nonumber \\ A= & {} \frac{f(r)}{r^2}dt \end{aligned}$$
(6)

with

$$\begin{aligned} {} f(r)=1-\frac{r^2}{r_h^2} \end{aligned}$$
(7)

where \(r_h\) is the horizon radius of the black hole. This solution enjoys an anisotropic scaling with the space and time scaling as \((x,y) \rightarrow (\lambda x, \lambda y)\) and \(t \rightarrow \lambda ^z t\). As mentioned earlier, z is called the dynamical exponent, and in the subsequent discussion we shall work with \(z=2\). Such theories are non relativistic as they do not obey Lorentz invariance and have a lot of importance in the study of condensed matter systems near the quantum critical point. The spacetime metric (6) reduces to that of pure Lifshitz spacetime (vacuum solution) in the near boundary limit (\(r \rightarrow 0\)). Note that the solution (6) with \(z=2\) in \((3+1)\)-dimensions does not have the kinetic term for the scalar, as the scalar is strongly coupled. However, the solution is very simple and the scalar wave equation can be solved exactly.

The Hawking temperature and entropy of the black hole are given by

$$\begin{aligned} T_{h}=\frac{1}{2\pi r_h^2}; ~~~~~~ S_h = \frac{lL}{4G_{(4)} r_h^2}. \end{aligned}$$
(8)

We now choose the shape of the subsystem to be strip like for computing the HEE and subregion HC. The strip like subsystem lies at the boundary of the Lifshitz black hole with the specifications \(-\frac{l}{2}\le x\le \frac{l}{2}\); \(0\le y \le L\). According to the prescription in [13, 14] the HEE is proportional to the static minimal area of the hypersurface in the bulk whose boundary coincides with the boundary of the subsystem at \(r=0\). To evaluate that minimal area we parametrize the hypersurface as \(r= r(x)\) and leave the y-direction independent. With this parametrization we get the area of the hypersurface to be

$$\begin{aligned} A=L\int _{-l/2}^{l/2} dx\;\; \frac{1}{r^2}\sqrt{1+\frac{r'(x)^2}{f(r)}} \end{aligned}$$
(9)

where \(r'(x)\equiv \frac{dr(x)}{dx}\). Using the standard procedure of minimization, we obtain the minimal surface specified by the following equation

$$\begin{aligned} \frac{dr(x)}{dx}=\sqrt{f(r)\left( \frac{r_t^4}{r^4}-1 \right) } \end{aligned}$$
(10)

where \(r_t\) is the turning point of the minimal surface. This condition for minimal surface can be used to get the minimal surface area and the subsystem length as

$$\begin{aligned} A= & {} 2L\int _{r_c}^{r_t}dr\; \frac{1}{r^2 \sqrt{f(r) (1-r^4/r_t^4)}};~~~~ \nonumber \\ l= & {} 2\int _0^{r_t} dr\; \frac{(r/r_t)^2}{\sqrt{f(r) (1-r^4/r_t^4)}} \end{aligned}$$
(11)

where \(r_c\) is the UV cutoff. The minimal volume under the same hypersurface is given by

$$\begin{aligned} V= & {} 2L \int _{r_c}^{r_t} dr\; \frac{1}{r^3 \sqrt{f(r)}}\; x(r) \nonumber \\= & {} 2L \int _{r_c}^{r_t} dr\; \frac{1}{r^3 \sqrt{f(r)}}\; \int _r^{r_t} ds \frac{(s/r_t)^2}{\sqrt{f(s) (1-s^4/r_t^4)}}. \end{aligned}$$
(12)

For the sake of simplicity we choose a new coordinate \(u=r/r_t\). With this change of variables, the lapse function takes the form \(f(u)=1-u^2/u_0^2\), where \(u_0=r_h/r_t\) and the scaled UV cutoff \(\delta \) is defined as \(\delta =r_c/r_t\). Therefore, the expressions for the subsystem length, minimal hypersurface area, minimal volume takes the form

$$\begin{aligned} l= & {} 2r_t \int _0^1 du\; \frac{u^2}{\sqrt{(1-u^4)f(u)}} \end{aligned}$$
(13)
$$\begin{aligned} A= & {} \frac{2L}{r_t}\int _{\delta }^{1}du \; \frac{1}{u^2\sqrt{(1-u^4)f(u)}} \end{aligned}$$
(14)
$$\begin{aligned} V= & {} \frac{2L}{r_t}\int _{\delta }^{1}du \; \frac{1}{u^3\sqrt{f(u)}} \int _u^1 ds\;\frac{s^2}{\sqrt{(1-s^4)f(s)}}. \end{aligned}$$
(15)

In the rest of the paper we have used the above expressions for computing different holographic quantities.

3 Holographic entanglement entropy

The integrals involved in the expressions for subsystem length (13) and area (14) integrals contains a term \(1/\sqrt{f(u)}\). When \(f(u)=1\), the background geometry reduces to that of \((3+1)\)-dimensional pure Lifshitz spacetime [42, 52]. The computation of HEE for such a system is easy due to the absence of \(1/\sqrt{f(u)}\) term. In the case of the Lifshitz black hole, the integrals become non-trivial, but can be done analytically. For that we have to expand \(1/\sqrt{f(u)}\) binomially as

$$\begin{aligned} \frac{1}{\sqrt{f(u)}}=\sum _{n=0}^{\infty } \frac{\Gamma (n+\frac{1}{2})}{\sqrt{\pi }\Gamma (n+1)}u^n. \end{aligned}$$
(16)

Using the above expression we obtain the subsystem length from Eq.(13), which reads

$$\begin{aligned} \frac{l}{r_t}=\sum _{n=0}^{\infty }\frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}+\frac{3}{4})}{2\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{5}{4})} \left( \frac{r_t}{r_h} \right) ^{2n}. \end{aligned}$$
(17)

When the subsystem length l is small, that is, \(l/r_h \ll 1\) with \(r_h\) kept fixed, we have \(r_t \ll r_h\). The above sum can then be terminated for some value of n as the higher order terms can be neglected. However, in the \(r_t\rightarrow r_h\) limit, one cannot terminate the series unlike the previous case. We need to check the behavior of l for large values of n. The expression (17) goes as \(\sim \frac{1}{n}\left( \frac{r_t}{r_h}\right) ^{2n}\) for large values of n. The expression for the subsystem length given in Eq. (17) can be written as

$$\begin{aligned} \frac{l}{r_t} = \frac{\sqrt{\pi }\Gamma (3/4)}{2\Gamma (5/4)} +\sum _{n=1}^{\infty } \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}+\frac{3}{4})}{2\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{5}{4})} \left( \frac{r_t}{r_h} \right) ^{2n}.\nonumber \\ \end{aligned}$$
(18)

For large values of n the second term goes as \(\sim \frac{1}{2\sqrt{2}\;n}\; \). Therefore the comparison test for infinite series implies that the series is divergent in \(r_t \rightarrow r_h\) limit. We separate the divergence part to rewrite the above expression as

$$\begin{aligned} \frac{l}{r_t}= & {} \frac{\sqrt{\pi }\Gamma (3/4)}{2\Gamma (5/4)}\nonumber \\&+\sum _{n=1}^{\infty } \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}+\frac{3}{4})}{2\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{5}{4})} \left( 1-\frac{1}{\sqrt{2}n} \right) \left( \frac{r_t}{r_h} \right) ^{2n} \nonumber \\&-\frac{1}{\sqrt{2}} \log \left( 1-r_t^2/r_h^2 \right) . \end{aligned}$$
(19)

In the above expression, the divergent piece \(\frac{1}{\sqrt{2}} \log \left( 1-r_t^2/r_h^2 \right) \) has been separated out. Now since the hypersurface cannot penetrate the black hole horizon [18], we use the approximation \(r_t \simeq r_h(1-\epsilon )\), where \(\epsilon \) is very small, and obtain

$$\begin{aligned} \frac{l}{r_h}=k_1 -\frac{1}{\sqrt{2}}\log (2 \epsilon )+ \mathcal {O}(\epsilon ) \end{aligned}$$
(20)

with

$$\begin{aligned} k_1= & {} \frac{\sqrt{\pi }\Gamma (3/4)}{2\Gamma (5/4)} \nonumber \\&+\sum _{n=1}^{\infty } \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}+\frac{3}{4})}{2\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{5}{4})} \left( 1-\frac{1}{\sqrt{2}n} \right) . \end{aligned}$$
(21)

We now proceed to compute the area (14) using the same expansion of the lapse factor (Eq. 16). This gives

$$\begin{aligned} A=\frac{2L}{r_t}\sum _{n=0}^{\infty } \frac{\Gamma (n+\frac{1}{2})}{\sqrt{\pi }\Gamma (n+1) u_0^{2n}} \int _{\delta }^{1} du\; \frac{u^{2n-2}}{\sqrt{1-u^4}}. \end{aligned}$$
(22)

Looking at the above expression one can see that the integral is divergent for \(n=0\) in the \(\delta \rightarrow 0\) limit. Performing the computation for the \(n=0\) term separately, we get

$$\begin{aligned} A_{n=0}=\frac{2L}{r_t}\left( \frac{1}{\delta } -\frac{\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)} \right) . \end{aligned}$$
(23)

We observe that the first term in the above expression is divergent. After computing the \(A_{n\ge 1}\) terms, we combine them to get the total area as

$$\begin{aligned} A= & {} \frac{2L}{r_t}\left( \frac{1}{\delta } -\frac{\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)}\right. \nonumber \\&\left. + \sum _{n=1}^{\infty } \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}-\frac{1}{4})}{4\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{1}{4})}\right. \nonumber \\&\qquad \left. \left( 1-\frac{4 \Gamma (\frac{n}{2}+\frac{1}{4}) \delta ^{2n-1}}{\sqrt{\pi }\Gamma (\frac{n}{2}-\frac{1}{4})} \right) \left( \frac{r_t}{r_h} \right) ^{2n}\right) . \end{aligned}$$
(24)

The above expression shows that area has an UV divergence going as \(\sim \frac{1}{\delta }\). This UV divergence is exactly similar to that of the \((3+1)\)-dimensional AdS black brane. So this divergence is universal irrespective of the underlying theory being relativistic or non-relativistic. Further, \(A_{n=0}\) is the minimal area of the hypersurface for the pure Lifshitz spacetime, which expectedly has a UV divergent term. From Eqs. (23, 24), we can now obtain the finite part of the minimal area of the hypersurface to be

$$\begin{aligned} A_{finite}= & {} \frac{2L}{r_t}\left( -\frac{\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)}\right. \nonumber \\&\left. + \sum _{n=1}^{\infty } \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}-\frac{1}{4})}{4\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{1}{4})}\left( \frac{r_t}{r_h} \right) ^{2n}\right) . \end{aligned}$$
(25)

where we have taken the \(\delta \rightarrow 0\) limit and also subtracted the divergent term proportional to \(1/\delta \).

We now use the gamma function identity \(\Gamma (p+1)=p \;\Gamma (p)\) to rewrite the above result as

$$\begin{aligned}&A_{finite} = \frac{2L}{r_t}\left( -\frac{\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)}\right. \nonumber \\&\qquad \left. + \sum _{n=1}^{\infty }\frac{1}{4}\left( 1+\frac{2}{2n-1} \right) \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}+\frac{3}{4})}{\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{5}{4})}\left( \frac{r_t}{r_h} \right) ^{2n}\right) \nonumber \\&\quad = \frac{2L}{r_t}\left( -\frac{2\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)}+\frac{l}{2 r_t}\right. \nonumber \\&\qquad \left. + \sum _{n=1}^{\infty }\frac{1}{2(2n-1)} \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}+\frac{3}{4})}{\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{5}{4})}\left( \frac{r_t}{r_h} \right) ^{2n}\right) \end{aligned}$$
(26)

where in the second line of the equality we have used the expression for subsystem length (17). The third term in the above expression, for large values of n goes as \(\sim \frac{1}{2\sqrt{2} n^2}\left( \frac{r_t}{r_h} \right) ^{2n}\). Using this fact, \(A_{finite}\) can be recast as

$$\begin{aligned}&A_{finite}=\frac{2L}{r_t}\left( -\frac{2\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)}+\frac{l}{2 r_t}\right. \nonumber \\&\qquad \left. + \sum _{n=1}^{\infty }\left( \frac{1}{2(2n-1)} \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}+\frac{3}{4})}{\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{5}{4})}-\frac{1}{2\sqrt{2}n^2}\right) \left( \frac{r_t}{r_h} \right) ^{2n} \right. \nonumber \\&\qquad \left. +\sum _{n=1}^{\infty } \frac{1}{2\sqrt{2}n^2}\left( \frac{r_t}{r_h} \right) ^{2n} \right) \nonumber \\&\quad = \frac{2L}{r_t}\left( -\frac{2\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)}+\frac{l}{ 2 r_t}\right. \nonumber \\&\qquad \left. + \sum _{n=1}^{\infty }\left( \frac{1}{2(2n-1)} \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}+\frac{3}{4})}{\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{5}{4})}-\frac{1}{2\sqrt{2}n^2}\right) \left( \frac{r_t}{r_h} \right) ^{2n} \right. \nonumber \\&\qquad \left. + \frac{1}{2\sqrt{2}}Li_{2}\left[ \left( \frac{r_t}{r_h}\right) ^2\right] \right) . \end{aligned}$$
(27)

This leads to the finite EE

$$\begin{aligned}&S_{finite}= \frac{A_{finite}}{4G_{(4)}} \nonumber \\&\quad = \frac{L}{2G_{(4)} r_t}\left( -\frac{2\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)}+\frac{l}{ 2 r_t}\right. \nonumber \\&\qquad \left. + \sum _{n=1}^{\infty }\left( \frac{1}{2(2n-1)} \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}+\frac{3}{4})}{\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{5}{4})}-\frac{1}{2\sqrt{2}n^2}\right) \left( \frac{r_t}{r_h} \right) ^{2n} \right. \nonumber \\&\qquad \left. + \frac{1}{2\sqrt{2}}Li_{2}\left[ \left( \frac{r_t}{r_h}\right) ^2\right] \right) . \end{aligned}$$
(28)

It is to be noted once again that the radius of the horizon \(r_h\) is kept fixed and the length of the subsystem (l) is varied which in turn implies by Eq. (17) that the turning point of the RT surface (\(r_t\)) also changes. If the subsystem length is large (\(l/r_h\gg 1\)), then the turning point will be near to the horizon. This means that turning point lies in IR region. Using the approximation \(r_t=r_h(1-\epsilon )\) (IR limit), we have

$$\begin{aligned} S_{finite}^{(IR)}= & {} S_h + \frac{L}{2G_{(4)} r_h} \left( k_2 + k_3 \; \epsilon +k_4 \; \epsilon \log \epsilon \right) \nonumber \\\simeq & {} S_h +\frac{L}{2G_{(4)} r_h} k_2+ \mathcal {O}(\epsilon ) \end{aligned}$$
(29)

where

$$\begin{aligned} S_h= \frac{lL}{4G_{(4)} r_h^2} \end{aligned}$$
(30)

is the Bekenstein–Hawking entropy of the Lifshitz black hole and

$$\begin{aligned} k_2= & {} -\frac{2\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)}\nonumber \\&+ \sum _{n=1}^{\infty }\left( \frac{1}{2(2n-1)} \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}+\frac{3}{4})}{\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{5}{4})}-\frac{1}{2\sqrt{2}n^2}\right) \nonumber \\&+\frac{1}{2\sqrt{2}}\xi (2), \nonumber \\ k_3= & {} \frac{2( \log 2 -1)}{2\sqrt{2}};~~~~~~~ k_4= \frac{1}{\sqrt{2}} \end{aligned}$$
(31)

with \(\xi (2)\) being the Riemann zeta function. Thus, we find that the holographic entanglement entropy in the IR limit is the thermal entropy plus correction terms. Since the black hole temperature goes as \(T_{h} \sim 1/r_h^2\), so in terms of the black hole temperature the finite part of HEE reads

$$\begin{aligned} S_A^{finite} \sim T_h\left( 1 +c_1 \frac{1}{\sqrt{T_h}}\right) \end{aligned}$$
(32)

with \(c_1\) being some numerical constant.

If on the other hand the subsystem length l is small \(\left( l/r_h<<1\right) \), then the bulk extension will be near the boundary. Therefore, the turning point \(r_t\) of the RT surface will be far away from the black hole horizon \(r_h\). In this approximation \(r_t/r_h \ll 1\), we need to take only first few terms of the binomial expansion of \(1/\sqrt{f(u)}\) in the expression (16). This approximation may be called the UV limit. In the UV limit, that is \(l\rightarrow 0\), the expression for finite part of HEE is given by

$$\begin{aligned} S_{finite}^{(UV)}= & {} \frac{L}{4G_{(4)} l}\left( -4\pi \left( \frac{\Gamma (3/4)}{\Gamma (1/4)} \right) ^2 +\frac{l^2}{r_h^2}\frac{1}{12}\left( \frac{\Gamma (1/4)}{\Gamma (3/4)}\right) ^2 \right. \nonumber \\&\left. + \frac{l^4}{r_h^4}\frac{3}{80\pi }\left( \frac{\Gamma (1/4)}{\Gamma (3/4)}\right) ^2\left( 1-\frac{5}{432}\left( \frac{\Gamma (1/4)}{\Gamma (3/4)}\right) ^4\right) \right) .\nonumber \\ \end{aligned}$$
(33)

We would like to point out that the expressions for subsystem length (17) and hypersurface area (24) are exact in the sense that no approximations were made.

We now proceed to see the behaviour of the UV cutoff dependent divergences in the near horizon approximation. The near horizon approximation is important when we deal with high temperature black holes. In this case the horizon approaches the turning point of the hypersurface (\(r_h \rightarrow r_t\)). This approximation therefore implies \(u_0 \sim 1\). Hence the integrals in Eqs. (13, 14) receives most of the contribution when \(u \sim 1\). We therefore make a Taylor expansion of the lapse function around \(u \sim u_0\) to get

$$\begin{aligned} f(u)= & {} f(u_0)+(u-u_0)f'(u_0)+\frac{(u-u_0)^2}{2}f''(u_0)+ \cdots \nonumber \\\approx & {} 2\left( 1-\frac{u}{u_0} \right) \end{aligned}$$
(34)

where we have neglected the higher order terms as \(u-u_0\ll 1\). With this approximation the subsystem length is as follows

$$\begin{aligned} \frac{l}{r_t}=\frac{\sqrt{\pi }}{2\sqrt{2}}\frac{\Gamma (3/4)}{\Gamma (5/4)}+\sum _{n=1}^{\infty }\frac{\Gamma (n+\frac{1}{2}) \Gamma (\frac{n+3}{4})}{2\sqrt{2}\;\Gamma (n+1)\Gamma (\frac{n+5}{4})} \left( \frac{r_t}{r_h} \right) ^{n}.\nonumber \\ \end{aligned}$$
(35)

For large values of n the second term in the above expression goes as \(\sim \frac{1}{n}\left( \frac{r_t}{r_h} \right) ^{n}\). The comparison test for infinite series suggests that term is divergent in the limit \(r_h \rightarrow r_t\). We separate out the divergent term and rewrite Eq. (35) in the following form

$$\begin{aligned} \frac{l}{r_t}= & {} \frac{\sqrt{\pi }}{2\sqrt{2}}\frac{\Gamma (3/4)}{\Gamma (5/4)}\nonumber \\&+\sum _{n=1}^{\infty }\left( \frac{\Gamma (n+\frac{1}{2}) \Gamma (\frac{n+3}{4})}{2\sqrt{2}\;\Gamma (n+1)\Gamma (\frac{n+5}{4})}-\frac{1}{\sqrt{2}\;n}\right) \left( \frac{r_t}{r_h} \right) ^{n} \nonumber \\&-\frac{1}{\sqrt{2}}\log \left( 1-\frac{r_t}{r_h} \right) . \end{aligned}$$
(36)

Once again we can use the approximation \(r_t \simeq r_h(1-\epsilon )\), as the hypersurface cannot penetrate the black hole horizon [18], to have

$$\begin{aligned} \frac{l}{r_h}=c_1 -\frac{1}{\sqrt{2}}\log \epsilon +\mathcal {O}(\epsilon ) \end{aligned}$$
(37)

with

$$\begin{aligned} c_1=\frac{\sqrt{\pi }}{2\sqrt{2}}\frac{\Gamma (3/4)}{\Gamma (5/4)}+ \sum _{n=1}^{\infty }\left( \frac{\Gamma (n+\frac{1}{2}) \Gamma (\frac{n+3}{4})}{2\sqrt{2}\;\Gamma (n+1)\Gamma (\frac{n+5}{4})}-\frac{1}{\sqrt{2}\;n}\right) .\nonumber \\ \end{aligned}$$
(38)

The area integral under the near horizon approximation is given by

$$\begin{aligned} A=\frac{L}{r_t}\sum _{n=0}^{\infty }\frac{\sqrt{2}\Gamma (n+\frac{1}{2})}{\sqrt{\pi }\Gamma (n+1)}\frac{1}{u_0^n} \int _{\delta }^{1} du\; \frac{u^{n-2}}{\sqrt{1-u^4}}. \end{aligned}$$
(39)

The above expression contains integrals which are divergent for \(n=0,1\). We compute them separately now. These reads

$$\begin{aligned} A_{n=0}= & {} \frac{\sqrt{2}L}{r_t}\left( \frac{1}{\delta } -\frac{\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)} \right) \nonumber \\ A_{n=1}= & {} \frac{L}{\sqrt{2}r_h} \left[ \int _{\delta }^{1}du\; \frac{1}{u} + \sum _{m=1}^{\infty }\frac{\Gamma (m+\frac{1}{2})}{\sqrt{\pi }\Gamma (m+1)}\int _{\delta }^{1}du\; u^{4m-1} \right] \nonumber \\= & {} \frac{L}{\sqrt{2}r_h}\left( - \log \delta +\frac{\log 4}{4} \right) \end{aligned}$$
(40)

where we have used the expansion

$$\begin{aligned} 1/\sqrt{1-u^4} = \sum _{n=0}^{\infty } \frac{\Gamma (n+\frac{1}{2})}{\sqrt{\pi }\Gamma (n+1)}u^{4n}. \end{aligned}$$
(41)

Now computing \(A_{n\ge 2}\) terms and gathering all terms, we write the expression for area in the near horizon approximation to be

$$\begin{aligned} A= & {} \frac{\sqrt{2}L}{r_t} \left( \frac{1}{\delta }- \frac{r_t}{2r_h} \log \delta -\frac{\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)} + \frac{r_t}{8r_h}\log 4\nonumber \right. \\&\left. +\sum _{n=2}^{\infty }\frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n-1}{4})}{4 \Gamma (n+1)\Gamma (\frac{n+1}{4})} \left( \frac{r_t}{r_h} \right) ^n\right) . \end{aligned}$$
(42)

Interestingly, we observe that in the near horizon approximation, the expression for the area contains logarithmic divergence term in addition to the usual \(1/\delta \) divergence term. It has been reported earlier in [49] that spurious divergences such as the logarithmic divergence in this case can arise in the near horizon approximation and these divergences may be artifacts of this approximation. Neglecting the UV divergent part and using the formula \(\Gamma (p+1)=p \;\Gamma (p)\), we can write the finite part of the area under RT hypersurface as

$$\begin{aligned}&A_{finite}= \frac{\sqrt{2}L}{r_t} \left( -\frac{\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)} + \frac{r_t}{8r_h}\log 4\right. \nonumber \\&\qquad \left. +\sum _{n=2}^{\infty }\left( 1+\frac{2}{n-1}\right) \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n-1}{4})}{4 \Gamma (n+1)\Gamma (\frac{n+1}{4})} \left( \frac{r_t}{r_h} \right) ^n\right) \nonumber \\&\quad = \frac{\sqrt{2}L}{r_t} \left( \frac{l}{\sqrt{2}r_t}-\frac{2\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)} - \frac{r_t}{8r_h}(2-\log 4) \right. \nonumber \\&\qquad \left. +\sum _{n=2}^{\infty }\frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n-1}{4})}{2(n-1) \Gamma (n+1)\Gamma (\frac{n+1}{4})} \left( \frac{r_t}{r_h} \right) ^n\right) \end{aligned}$$
(43)

where in the last step we have used the relation (35). The last term of the above equation goes as \(\sim \frac{1}{n^2}\left( \frac{r_t}{r_h} \right) ^{n}\). Using this fact we recast the expression for the finite part of area as

$$\begin{aligned}&A_{finite}= \frac{L l}{r_t^2} + \frac{\sqrt{2}L}{r_t} \left[ -\frac{2\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)}\right. \nonumber \\&\qquad \left. -\left( \frac{5}{4}-\frac{\log 4}{8} \right) \frac{r_t}{r_h}+Li_{2}\left[ \left( \frac{r_t}{r_h}\right) \right] \right. \nonumber \\&\qquad \left. +\sum _{n=2}^{\infty }\left( \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n-1}{4})}{2(n-1) \Gamma (n+1)\Gamma (\frac{n+1}{4})}-\frac{1}{n^2} \right) \left( \frac{r_t}{r_h} \right) ^n \right] .\nonumber \\ \end{aligned}$$
(44)

Now using the approximation \(r_t \simeq r_h(1-\epsilon )\) and the definition of HEE, we get

$$\begin{aligned} {} S_{finite}= & {} \frac{A_{finite}}{4 G_{(4)}} \nonumber \\= & {} S_h + \frac{L}{2\sqrt{2}\;G_{(4)}r_h} (c_2+c_3 \epsilon + \epsilon \log \epsilon ) \end{aligned}$$
(45)

where

$$\begin{aligned} S_h= \frac{lL}{4G_{(4)} r_h^2} \end{aligned}$$
(46)

is the Bekenstein–Hawking entropy of the Lifshitz black hole and

$$\begin{aligned} c_2= & {} -\frac{2\sqrt{\pi } \Gamma (3/4)}{\Gamma (1/4)}-\left( \frac{5}{4}-\frac{\log 4}{8} \right) \nonumber \\&+ \sum _{n=2}^{\infty }\left( \frac{1}{2(n-1)} \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}+\frac{3}{4})}{\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{5}{4})}-\frac{1}{n^2}\right) +\xi (2), \nonumber \\ c_3= & {} \frac{1}{4}-\frac{\log 4}{8}. \end{aligned}$$
(47)

Note that the finite part of the HEE in the near horizon approximation as shown in Eq. ((45)) has the same form as the finite part part of the HEE in the IR limit. This is in turn implies that the finite part of the HEE in the near horizon approximation have similar temperature dependence as in Eq. (32).

3.1 Generalized temperature

The Lifshitz black hole as described in Sect. 2 satisfies the first law of black hole thermodynamics [42]

$$\begin{aligned} dE =T_h \; dS_h \end{aligned}$$
(48)

leading to

$$\begin{aligned} E=\int T_h \; dS_h = T_h S_h/2 \end{aligned}$$
(49)

where the energy E is given by

$$\begin{aligned} {} E=\frac{lL}{16 \pi G_{(4)} r_h^4}. \end{aligned}$$
(50)

The relation is important since it relates the near boundary quantity (E) to the near horizon quantities (\(S_h, T_h\)). It can be seen from Eq. (29) that in the IR limit (\(r_t \rightarrow r_h\)) the leading contribution to the HEE comes from the thermal entropy \(S_h\). As we depart from the IR limit, the HEE gets quantum corrections due to microscopic properties of the underlying quantum system. Keeping this point in mind we may ask for a quantity called the generalized temperature (\(T_g\)) which is different from the black hole temperature \(T_h\). We define the generalized temperature in the following way

$$\begin{aligned} \frac{1}{T_g}= \frac{S_{REE}}{2E};~~~~ S_{REE}=S_A - S_A^{(0)}=\frac{1}{4G_{(4)}}\left( A-A^{(0)} \right) \nonumber \\ \end{aligned}$$
(51)

where \(S_{REE}\) is the HEE of the Lifshitz black hole and \(S_A^{(0)}\) is the HEE of the pure Lifshitz spacetime. The hypersurface area and subsystem length as obtained for pure Lifshitz spacetime are given by [41]

$$\begin{aligned} A_0=\frac{2L}{\delta r_t^{(0)}}- \frac{4 \pi L }{ l}\left( \frac{\Gamma (3/4)}{\Gamma (1/4)}\right) ^2; ~~~~ \frac{l}{r_t^{(0)}}=\frac{\sqrt{\pi }\Gamma (3/4)}{2 \; \Gamma (5/4)}\nonumber \\ \end{aligned}$$
(52)

Using this and Eq. ((50)), the generalized temperature reads

$$\begin{aligned} {} \frac{1}{T_g}= & {} \frac{2\pi r_h^2}{l}\left( \frac{4 \pi }{ l}\left( \frac{\Gamma (3/4)}{\Gamma (1/4)}\right) ^2 -\frac{2\sqrt{\pi } \Gamma (3/4)}{r_t \; \Gamma (1/4)} \nonumber \right. \\&\left. +\frac{1}{2r_t} \sum _{n=1}^{\infty } \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{n}{2}-\frac{1}{4})}{4\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{1}{4})}\left( \frac{r_t}{r_h} \right) ^{2n}\right) . \end{aligned}$$
(53)

From the above expression we see that \(T_g\) is a function of l and \(r_t\), but \(r_t\) itself depends on the subsystem length l. So we conclude that \(T_g\) is a function of l alone. Therefore the generalized temperature depends on the subsystem size. We now discuss the behavior of the generalized temperature in extreme limits. In the IR limit (\(r_t \rightarrow r_h\)), the generalized temperature takes the form

$$\begin{aligned} {} \frac{1}{T_g}= \frac{1}{T_h} + \frac{r_h^3}{l} \alpha +\frac{r_h^4}{l^2}\beta \end{aligned}$$
(54)

with

$$\begin{aligned} \alpha= & {} 2\pi \left( -\frac{4\sqrt{\pi }\Gamma (3/4)}{\Gamma (1/4)}+ \sum _{n=1}^{\infty } \frac{\Gamma (n+\frac{1}{2}) \Gamma (\frac{n}{2}+\frac{3}{4})}{(2n-1)\Gamma (n+1)\Gamma (\frac{n}{2}+\frac{5}{4})}\right) \nonumber \\ \beta= & {} 8 \pi ^2\left( \frac{\Gamma (3/4)}{\Gamma (1/4)}\right) ^2. \end{aligned}$$
(55)

It is evident from Eq. (54) that the generalized temperature yields the thermodynamic temperature \(T_h\) in the large subsystem size limit (\(l/r_h \gg 1\)). The sub-leading terms are due to quantum entanglement. In the UV limit (\(l\rightarrow 0\), \(r_t \rightarrow 0\)), the generalized temperature is given by

$$\begin{aligned} {} \frac{1}{T_g}=\frac{\pi r_h^2}{6}\left( \frac{\Gamma (1/4)}{\Gamma (3/4)}\right) ^2 \left( 1 +\frac{l^2}{r_h^2}\gamma \right) \end{aligned}$$
(56)

where

$$\begin{aligned} \gamma =\frac{9}{20 \pi } -\frac{1}{192 \pi } \left( \frac{\Gamma (1/4)}{\Gamma (3/4)}\right) ^4. \end{aligned}$$
(57)

In the \(l/r_h \rightarrow 0\) limit (that is the UV limit) with \(r_h\) kept fixed, the generalized temperature temperature behaves as \(\sim c+ \frac{1}{l^2}\). Although the \(1/l^2\) dependence is similar as in [15] but the constant term is not present in [15] which may be due to the fact that the non-relativistic gravity dual considered there is the hyperscaling violating black brane geometry which is different than the Lifshitz black hole. Further, we observe that \(T_g\ne 0\) when \(l/r_h =0\) (\(r_h \ne 0\)). It is a non-relativistic phenomena in contrast to relativistic systems for which the inverse of the generalized temperature becomes zero when \(l/r_h =0\) (\(r_h \ne 0\)) [22, 23]). This is one of the important findings in our paper. This non-zero generalized temperature (\(T_g\)) in \(l \rightarrow 0\) limit can be called “entanglement temperature”(\(T_{ent}\)). The origin of this entanglement temperature is solely microscopic (quantum entanglement) and has nothing to do with the macroscopic properties of the system. The expression for the entanglement temperature follows from eq.(56) and is given by

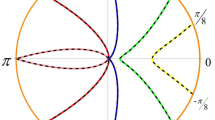
$$\begin{aligned} T_{ent}= \frac{6}{\pi r_h^2}\left( \frac{\Gamma (3/4)}{\Gamma (1/4)}\right) ^2. \end{aligned}$$
(58)

Figure 1a and our analysis in the IR regime, it is evident that the generalized temperature (\(T_g\)) becomes the Hawking temperature (\(T_h\)) for large subsystem length. To characterize the thermal and quantum nature of the system we study the flow of \(\beta _g=1/T_g\). We study the flow of the generalized temperature by studying the variation of \(\frac{d \beta _g}{d \log l}\) with l. This has been shown in Fig. 1b. From the flow, we observe that it has a maximum near a critical value \(\frac{l_c}{r_h}=4.91\). Above this value of the subsystem size, the system behave as a thermal system and below this value the system behaves as a quantum system.

Fig. 1
figure 1

a Variation of \(\frac{\beta _g}{r_h^2}=\frac{1}{T_g r_h^2}\) with subsystem length, b variation of \(\frac{d \beta _g}{d \log l}\) with subsystem length (the \(\frac{d \beta _g}{d \log l}\) axis has been scaled five times for visualization purpose)

Full size image

4 Holographic subregion complexity

The subregion HC is proportional to the volume under the minimal hypersurface whose boundary coincides with the the boundary of the subsystem lying at the boundary at a fixed time. Using the approximation (16) in the expression for volume (15), we get

$$\begin{aligned} V=\frac{L}{r_t}\sum _{n=0}^{\infty } \sum _{m=0}^{\infty } \left( V_1 +V_2+V_3 \right) \left( \frac{r_t}{r_h} \right) ^{2n+2m} \end{aligned}$$
(59)

where

$$\begin{aligned} V_1= & {} \frac{2\Gamma (n+\frac{1}{2})\Gamma (m+\frac{1}{2})}{\pi \;(2n+3)(2m+2n+1) \Gamma (n+1) \Gamma (m+1)} \delta ^{2m+2n+1} \nonumber \\ V_2= & {} -\frac{\Gamma (n+\frac{1}{2})\Gamma (m+\frac{1}{2})\Gamma (\frac{2n+3}{4})}{4 \sqrt{\pi }(m-1)\Gamma (n+1)\Gamma (m+1)\Gamma \left( \frac{2n+5}{4} \right) } \delta ^{2m-2} \nonumber \\ V_3= & {} \frac{\Gamma (n+\frac{1}{2})\Gamma (m+\frac{1}{2})\Gamma \left( \frac{2m+2n+1}{4}\right) }{4 \sqrt{\pi }(m-1)\Gamma (n+1)\Gamma (m+1)\Gamma \left( \frac{2m+2n+3}{4}\right) }. \end{aligned}$$
(60)

Now we should checkout for the divergences in the above mentioned terms as the expression for volume contains double sum which extends from \(m, n =0\) to \(\infty \). Due to the presence of the term \(\left( \frac{r_t}{r_h} \right) ^{2n+2m}\), we expect the divergence to occur near \(r_t \rightarrow r_h\). We start analyzing the \(V_1\) term. For large values of (m, n), \(V_1\) varies as

$$\begin{aligned} V_1 \sim \frac{1}{n^{\frac{3}{2}} m^{\frac{1}{2}}(n+m)} < \frac{1}{n^{\frac{3}{2}} m^{\frac{3}{2}}}. \end{aligned}$$
(61)

We can now argue that \(\sum _{n,m=0}^{\infty } V_1\left( \frac{r_t}{r_h} \right) ^{2n+2m}\) is convergent. If p(m, n) and q(m, n) are two sequences of real numbers with m and n being positive integers, then the series \(\sum _{n,m=0}^{\infty }p(m,n)\) is convergent if for each values of (m, n) we have \(|p(m,n)| \le |q(m,n)|\). If we choose \(q(m,n)=\frac{1}{n^{\frac{3}{2}} m^{\frac{3}{2}}}\), then \(\sum _{n,m=0}^{\infty }\frac{1}{n^{\frac{3}{2}} m^{\frac{3}{2}}}=1/(\xi (3/2))^2 \), where \(\xi (3/2)\) is the Riemann zeta function. Therefore the double sum over \(V_1\) term converges absolutely. Moreover it is multiplied by \(\delta ^{2m+2n+1}\), which tends to zero. So we can neglect the contribution from \(V_1\). Let us now look at the \(V_2\) term which has a UV cutoff dependent term \(\delta ^{2m-2}\). For \(m\ge 2\), this term will have negligible contribution but for \(m=0, 1\), this term is UV divergent. To get the exact form of UV divergence we compute the volume for \(m=0\) and 1 separately. It is expected that the \(m=1\) term should give a logarithmic UV divergence. The volume integral for \(m=0\) and \(m=1\) are given by

$$\begin{aligned} V_{m=0}= & {} \frac{L}{r_t}\sum _{n=0}^{\infty }\left( \frac{r_t}{r_h}\right) ^{2n} \left( \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{3}{4}+\frac{n}{2})}{4\Gamma (n+1)\Gamma (\frac{5}{4}+\frac{n}{2})}\frac{1}{\delta ^2}\nonumber \right. \\&-\frac{\Gamma (n+\frac{1}{2})}{\sqrt{\pi }(2n+3)\Gamma (n+1)}\delta ^{2n+1} \nonumber \\&-\left. \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{1}{4}+\frac{n}{2})}{4 \Gamma (n+1) \Gamma (\frac{3}{4}+\frac{n}{2})}\right) \nonumber \\ V_{m=1}= & {} \frac{L}{r_t}\sum _{n=0}^{\infty }\left( \frac{r_t}{r_h}\right) ^{2n} \left( - \frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{3}{4}+\frac{n}{2})}{4\Gamma (n+1)\Gamma (\frac{5}{4}+\frac{n}{2})} \log \delta \nonumber \right. \\&+\frac{\Gamma (n+\frac{1}{2})}{\sqrt{\pi }(2n+3)\Gamma (n+1)}\delta ^{2n+3}\log \delta \nonumber \\&\left. +\frac{\Gamma (n+\frac{1}{2})\Gamma (\frac{3}{4}+\frac{n}{2})}{16\Gamma (n+1)\Gamma (\frac{5}{4}+\frac{n}{2})} \left( H_n\left[ \frac{n}{2}-\frac{1}{4} \right] \right. \right. \nonumber \\&\left. \left. -H_n\left[ \frac{n}{2}+\frac{1}{4} \right] \right) \right) . \end{aligned}$$
(62)

In the \(r_t \rightarrow r_h\) limit, we use the expression for subsystem length (17) to get

$$\begin{aligned}&V_{m=0} \sim \frac{L}{r_h}\left( \frac{l}{2 r_h}\frac{1}{\delta ^2} +b_1 \right) ;~~~ \nonumber \\&V_{m=1}\sim \frac{L}{r_h}\left( -\frac{l}{2r_h}\log \delta + b_2\right) \end{aligned}$$
(63)

where \(b_1\) and \(b_2\) are numerical constants. Finally we look at the \(V_3\) term. The analysis for \(V_3\) term is more complicated. The detailed analysis is given in Appendix A. This term in the \(r_t \rightarrow r_h\) limit varies as

$$\begin{aligned} {}&\frac{L}{r_t}\sum _{n=0}^{\infty } \sum _{m=0}^{\infty } \left( \frac{r_t}{r_h} \right) ^{2n+2m} \nonumber \\&\quad V_3 \sim \frac{L}{r_h}\left( b_3 \frac{l}{r_h}+b_4+b_5 \epsilon +b_6 \epsilon \log \epsilon +b_7 \log \epsilon \right) . \end{aligned}$$
(64)

Combining all these terms, we get the volume to be

$$\begin{aligned}&V \sim \frac{lL}{(r_h)^2}\left( \frac{1}{2 \delta ^2}-\frac{\log \delta }{2}+b_4 \frac{r_h}{l}+b_8\right) \nonumber \\&\quad + \frac{L}{r_h}\left( b_5 \epsilon +b_6 \epsilon \log \epsilon +b_7 \log \epsilon \right) \end{aligned}$$
(65)

where \(b_i\) for \(i=3\) to 8 are numerical constants. The above expression clearly shows the presence of the UV cutoff \(\delta \) and the parameter \(\epsilon \) arising in the IR limit from the relation \(r_t =r_h (1-\epsilon )\) with \(r_h\) being kept fixed. In terms of the black hole temperature, the expression for the finite part of holographic subregion complexity (which is the volume divided by the factor of \(8\pi R G\)) varies as

$$\begin{aligned} C_{finite} \sim T_h\left( b_8 +b_4\frac{1}{ \sqrt{T_h}}\right) . \end{aligned}$$
(66)

Therefore, the holographic entanglement entropy (32) and holographic subregion complexity (66) have the same kind of temperature dependence.

We now proceed to evaluate the volume integral in the near horizon limit. In this limit the volume becomes

$$\begin{aligned} V=\frac{L}{r_t}\sum _{n=0}^{\infty } \sum _{m=0}^{\infty } \left( V_1 +V_2+V_3 \right) \left( \frac{r_t}{r_h} \right) ^{n+m} \end{aligned}$$
(67)

where

$$\begin{aligned} V_1= & {} \frac{\Gamma (n+\frac{1}{2})\Gamma (m+\frac{1}{2})}{\pi \;(n+3)(m+n+1) \Gamma (n+1) \Gamma (m+1)} \delta ^{m+n+1} \nonumber \\ V_2= & {} -\frac{\Gamma (n+\frac{1}{2})\Gamma (m+\frac{1}{2})\Gamma \left( \frac{n+3}{4} \right) }{4 \sqrt{\pi }(m-2)\Gamma (n+1)\Gamma (m+1)\Gamma \left( \frac{n+5}{4} \right) } \delta ^{m-2} \nonumber \\ V_3= & {} \frac{\Gamma (n+\frac{1}{2})\Gamma (m+\frac{1}{2})\Gamma \left( \frac{m+n+1}{4}\right) }{4 \sqrt{\pi }(m-2)\Gamma (n+1)\Gamma (m+1)\Gamma \left( \frac{m+n+3}{4}\right) }~. \end{aligned}$$
(68)

The terms \(V_1\) and \(V_3\) have almost the same pattern as in the previous case. So we can say that the term \(V_1\) is convergent and have negligible contribution due to the UV cutoff \(\delta ^{m+n+1}\) and the term \(V_3\) would have the same form as presented in Eq. (64). On the other hand the term \(V_2\) is divergent for \(m \le 2\), so we compute the volume term for \(m=0, 1, 2\) separately (see Appendix B). In the limit \(r_h \rightarrow r_t\), they behave as

$$\begin{aligned} V_{m=0} \sim \frac{lL}{(r_h)^2} \left( \frac{1}{2\sqrt{2}}\frac{1}{\delta ^2}+ d_1\right) \nonumber \\ V_{m=1} \sim \frac{lL}{(r_h)^2} \left( \frac{1}{2\sqrt{2}}\frac{1}{\delta }+ d_2 \right) \nonumber \\ V_{m=2} \sim \frac{lL}{(r_h)^2} \left( -\frac{3\sqrt{2}}{16}\log \delta + d_3 \right) . \end{aligned}$$
(69)

Combining all the volume terms, we get

$$\begin{aligned}&V \sim \frac{lL}{(r_h)^2}\left( \frac{1}{2\sqrt{2} \delta ^2}+\frac{1}{2\sqrt{2} \delta } -\frac{3\sqrt{2}\log \delta }{16}+d_4 \frac{r_h}{l}+d_5\right) \nonumber \\&\quad + \frac{L}{r_h}\left( d_6 \epsilon +d_7 \epsilon \log \epsilon +d_8 \log \epsilon \right) \end{aligned}$$
(70)

where \(d_i\) for \(i=1\) to 8 are numerical constants. So the finite part of the holographic subregion complexity varies with the black hole temperature as

$$\begin{aligned} C_{finite}\sim T_h\left( d_{5} +d_4 \frac{1}{\sqrt{T_h}}\right) . \end{aligned}$$
(71)

5 Fisher information metric and fidelity susceptibility

In this section, we shall compute the Fisher information metric and the fidelity susceptibility for the Lifshitz black hole using holographic prescriptions [50, 51, 53]. In the context of quantum information theory there exists two well notions of distance between two quantum states. They are the Fisher information metric [54] and the fidelity susceptibility [55] (or called the Bures metric). From the literature [53], the definition of the Fisher information metric is given by

$$\begin{aligned} G_{F,\lambda \lambda }=\langle \delta \rho \; \delta \rho \rangle _{\lambda \lambda }^{(\sigma )}= \frac{1}{2}tr \left( \delta \rho \frac{d}{d(\delta \lambda )} \log (\sigma + \delta \lambda \delta \rho )|_{\delta \lambda =0} \right) \nonumber \\ \end{aligned}$$
(72)

where \(\delta \rho \) is a small deviation from the density matrix \(\sigma \).

On the other hand the fidelity susceptibility is given by

$$\begin{aligned} G_{\lambda \lambda }= \partial ^2_{\lambda } F ;~~~~F= tr\sqrt{\sqrt{\sigma _{\lambda }} \rho _{\lambda + \delta \lambda } \sqrt{\sigma _{\lambda }}} \end{aligned}$$
(73)

where \(\rho \) and \(\sigma \) are the final and initial density matrices, F is called the fidelity between the two states.

The holographic computation of the Fisher information metric from relative EE was put forward in [50]. The Fisher information metric is given by

$$\begin{aligned} {} G_{F,mm}= & {} \frac{\partial ^2 }{\partial m^2}S_{rel}(\rho _m \parallel \rho _0);~~~~~~~ \nonumber \\ S_{rel}(\rho _m \parallel \rho _0)= & {} \Delta \langle H_{\rho _0} \rangle -\Delta S \end{aligned}$$
(74)

where m is a perturbation parameter, \(\Delta S\) is the change in entanglement entropy from the vacuum state and \(\Delta \langle H_{\rho _0} \rangle \) is the change in modular Hamiltonian. With this basic background in place we first compute the Fisher information metric for the Lifshitz black hole. It should be noted however that the above formulations rely heavily on the symmetries of the holographic conformal field theories, and the fact that they can also be used in the non-relativistic case is the working assumption in this paper. We consider that the background is slightly perturbed from the pure Lifshitz spacetime but the subsystem length l fixed. Then the inverse of the lapse function 7 can be written as

$$\begin{aligned} \frac{1}{f(r)}=\frac{1}{1-{r^2\over r_h^2}}=1+m r^2+ m^2 r^4. \end{aligned}$$
(75)

where \(m=\frac{1}{r_h^2}\), is the perturbation parameter in the bulk. As the underlying geometry has been changed from Lifshitz spacetime to asymptotic Lifshitz spacetime and we have not changed the subsystem length the turning point of the bulk extension will change as

$$\begin{aligned} {} r_t=r_t^{(0)}+m~r_t^{(1)}+m^2~r_t^{(2)} \end{aligned}$$
(76)

where \(r_t^{(0)}\) is the turning point for pure Lifshitz spacetime and \(r_t^{(1)}\), \(r_t^{(2)}\) are first and second order corrections to the turning point.On the other hand the subsystem length l can be obtained from (13,17) upto second order in perturbation as

$$\begin{aligned} {} \frac{l}{r_t}=a_0 +m~a_1 r_t^2 +m^2~ a_2 r_t^4 \end{aligned}$$
(77)

with

$$\begin{aligned} a_0= & {} \frac{\sqrt{\pi }\Gamma \left( \frac{3}{4}\right) }{2~\Gamma \left( \frac{5}{4} \right) };~ a_1 = \frac{\Gamma \left( \frac{3}{2}\right) \Gamma \left( \frac{5}{4}\right) }{2~\Gamma \left( \frac{7}{4} \right) };~\nonumber \\ a_2= & {} \frac{\Gamma \left( \frac{5}{2}\right) \Gamma \left( \frac{7}{4}\right) }{4~\Gamma \left( \frac{9}{4} \right) }. \end{aligned}$$
(78)

Using the fact that the subsystem length is unchanged we obtain from Eqs. (76, 77), expressions for \(r_t^{(0)}\), \(r_t^{(1)}\) and \(r_t^{(2)}\) as given below

$$\begin{aligned} \frac{l}{r_t^{(0)}}= & {} a_0,~~ r_t^{(1)}=-\frac{a_1}{a_0}(r_t^{(0)})^3,~~\nonumber \\ r_t^{(2)}= & {} \left( 3\frac{a_1^2}{a_0^2}-\frac{a_2}{a_0}\right) (r_t^{(0)})^5~~. \end{aligned}$$
(79)

The expression for extremal area of the bulk extension upto second order in perturbation parameter can be obtained from Eqs. (14, 24) as

$$\begin{aligned} A=\frac{2L}{r_c}-a_0 \frac{L}{r_t}+ 3a_1Lr_t m+\frac{5}{3}a_2 Lr_t^3 m^2. \end{aligned}$$
(80)

As we are interested in computing the change in area due to a slight change in background we use (76) to recast the above expression for area in the following form

$$\begin{aligned} A=A^{(0)}+m~A^{(1)}+m^2~A^{(2)} \end{aligned}$$
(81)

where \(A^{(0)}\), \(A^{(1)}\) and \(A^{(2)}\) are area for pure Lifshitz spacetime, first order and second order corrections to the area for change in background. They have the following expressions

$$\begin{aligned} A^{(0)}= & {} \frac{2L}{r_c}-a_0 \frac{L}{r_t^{(0)}},~~ A^{(1)} =2a_1 Lr_t^{(0)},~~ \nonumber \\ A^{(2)}= & {} \left( \frac{2}{3}a_2 -\frac{a_1^2}{a_0} \right) L(r_t^{(0)})^3. \end{aligned}$$
(82)

It has been shown in [50] that at first order in m the relative entropy vanishes and in second order in m the relative entropy is given by \(S_{rel}=-\Delta S\). Hence,

$$\begin{aligned} S_{rel}= -m^2\frac{A^{(2)}}{4G} =m^2 \frac{L l^3}{4G}\left( \frac{3a_1^2 -2a_0 a_2}{3a_0^4} \right) . \end{aligned}$$
(83)

From Eq. (74), the Fisher information metric therefore reads

$$\begin{aligned} G_{F,mm}= \frac{L l^3}{2G}\left( \frac{3a_1^2 -2a_0 a_2}{3a_0^4} \right) . \end{aligned}$$
(84)

In [53], a proposal for computing the above quantity was given. The proposal is to consider the difference of two volumes yielding a finite expression

$$\begin{aligned} \mathcal {F}=C_d(V-V_{(0)}) \end{aligned}$$
(85)

where V is evaluated for a second order perturbation around pure Lifshitz spacetime . \(C_d\) is a dimensionless constant which cannot be fixed from the first principles of the gravity side. We shall now apply this proposal to compute the Fisher information metric for the Lifshitz black hole. The change in volume under Ryu–Takayanagi minimal surface at second order in perturbation takes the form

$$\begin{aligned} V=V^{(0)}+m V^{(1)}+m^2 V^{(2)} \end{aligned}$$
(86)

with

$$\begin{aligned} V^{(0)}= & {} \frac{L l}{2 r_c^2} -\frac{a_0^2 L}{2l}, ~~V^{(1)}= - mL l \left( \frac{a_1}{2a_0}+\frac{6-\pi }{8}\right) ,~~ \nonumber \\ V^{(2)}= & {} m^2 \frac{Ll^3}{a_0^3}\left( \frac{a_1^2}{a_0}-\frac{a_2}{2}+\frac{13-3\pi }{12}a_1 \right) . \end{aligned}$$
(87)

The holographic dual of Fisher information metric is now defined as

$$\begin{aligned} {} G_{F,mm}=\partial _m^2 \mathcal {F};~~~~~~\mathcal {F}= C_d \left( V-V_{(0)} \right) \end{aligned}$$
(88)

with the constant \(C_d\) to be determined by requiring that the holographic dual Fisher information metric from the above equation must agree with that obtained from the relative entropy (84). The constant \(C_d\) is therefore given by

$$\begin{aligned} {} C_d=\frac{3a_1^2 -2a_0 a_2}{G(12a_1^2 -6a_0a_2 +(13-3\pi )a_0a_1)} . \end{aligned}$$
(89)

We now look forward to compute the fidelity susceptibility holographically. If one assumes that the states depend on a single parameter \(\lambda \) then for pure states the fidelity (73) reduces to

$$\begin{aligned} \langle \Psi (\lambda ) | \Psi (\lambda + \delta \lambda ) \rangle =1-G_{\lambda \lambda } (\delta \lambda )^2+ \cdots . \end{aligned}$$
(90)

The above expression immediately suggests that \(G_{\lambda \lambda }\) is a measure of distance between two quantum states called the fidelity susceptibility . The holographic prescription for evaluating the fidelity susceptibility in (\(d+1\))-dimensional AdS spacetime is given by [51]

$$\begin{aligned} {} G_{\lambda \lambda } = n_{d-1} \frac{Vol(\Sigma _{max})}{R^{d}} \end{aligned}$$
(91)

where \(\Sigma _{max}\) is the maximum volume in the bulk that ends at the boundary of the bulk at a fixed time slice. R is the radius of curvature of AdS spacetime and \(n_{d-1}\) is a \(\mathcal {O}(1)\) constant.

For our case the fidelity susceptibility reads

$$\begin{aligned} G_{\lambda \lambda }= & {} n_{2} L l \int _{r_c}^{r_h} dr \frac{1}{r^3 \sqrt{1-{r^2\over r_h^2}}} \nonumber \\= & {} \frac{n_{2} Ll}{r_h^2}\left( \frac{r_h^2}{2r_c^2}+B(-1,\frac{1}{2}) \right) . \end{aligned}$$
(92)

We see that the above expression for the fidelity susceptibility does not agree with the Fisher information metric obtained in Eq. (84). We end this section by making a few observations. It is to be noted that the Fisher information metric [54] and the fidelity susceptibility [55] (also known as the Bures metric) are two well established notion of distance between two quantum states in quantum information literature. In quantum information theory it is known that both of the quantities are either same ([56,57,58,59]) or related to each other [60]. The possible reason for the disagreement in holographic theory may lie in the definitions of the two quantities in holographic theory. The holographic definition of fidelity susceptibility, as mentioned in [51], is exact in the sense it depends on an integration from the boundary upto the horizon of the black hole. Therefore, it contains the information of the underlying geometry from UV to IR region. On the other hand, the definition of the Fisher information metric as prescribed in [53], depends upon the integration from the boundary upto the turning point of RT surface. This computation is carried out perturbatively upto second order in the perturbation parameter. Hence, it contains the information of the UV structure of the underlying geometry only.

6 Conclusion

In this paper, we have computed different information theoretic quantities holographically in the context of a non-relativistic (\(3+1\))-dimensional Lifshitz black hole with \(z=2\). Our main focus has been the following. To begin with we have looked at the Ryu–Takayanagi area which is related to the holographic entanglement entropy and second is the minimal volume under the Ryu–Takayanagi area which is related to holographic subregion complexity. The finite part of the holographic entanglement entropy approaches the black hole entropy in the infrared regime. This clearly depicts that the entanglement entropy becomes thermal entropy in the high temperature limit even in the non-relativistic background. In the ultra-violet limit, the finite part of holographic entanglement entropy goes as \(S_{finite}^{(UV)} \sim \frac{1}{l}\left( constant + \mathcal {O}(l^2)\right) \). This result departs with respect to the subleading terms from the relativistic counterpart comprising the \((3+1)\)-dimensional SAdS black hole where \(S_{finite}^{(UV)} \sim \frac{1}{l}\left( constant + \mathcal {O}(l^3) \right) \). Further, the holographic entanglement entropy has a logarithmic divergence in addition to the usual \(1/\delta \) divergence in the near horizon approximation. We have then introduced the notion of a generalized temperature in terms of the renormalized holographic entanglement entropy. The variation of the generalized temperature with the subsystem length l shows that the generalized temperature reduces to the black hole temperature, that is the Hawking temperature, at large subsystem length (infrared limit). This therefore implies that our choice of the definition for the generalized temperature is correct. It has been observed that the generalized temperature leads to a thermodynamics like law \(E=\frac{1}{2}T_g S_{REE}\). It is also interesting to note that the generalized temperature does not reduces to zero when \(l/r_h =0\) (\(r_h \ne 0\)). This is a new result which does not have any counterpart in the relativistic background, namely, the \((3+1)\)-dimensional SAdS black hole. We have then observed departures from relativistic results in case of the holographic subregion complexity. Both in the \(3+1\)-dimensional relativistic and non-relativistic (Lifshitz black hole with \(z=2\)) cases, the holographic subregion complexity suffers \(1/\delta ^2\) divergences, but in the non-relativistic case we have \(\log \delta \) divergence which was absent in the relativistic case [49]. The logarithmic divergence may be spurious in nature as pointed out earlier in [49]. If it is not spurious, then it would require an interpretation from the field theory side. At present it is not clear what this divergence mean in the field theory side but one may speculate that it may correspond to some power law like behaviour for a correlation function of some physical quantity. The near horizon approximation have the same type of divergences in both the cases. The holographic Fisher information metric has been computed next from the concept of relative entropy [50]. We have also computed the holographic subregion complexity in the ultra-violet limit upto second order in the perturbation parameter. Using the proposal in [53], we have used this result to obtain an expression for the Fisher information metric upto an undetermined constant. We have equated this result of the Fisher information metric with that obtained from the relative entropy to determine the undetermined constant. The constant is found to be a number. The holographic fidelity susceptibility has also been computed. We find that there is a mismatch between the expressions for the Fisher information metric and the holographic fidelity susceptibility. These two quantities are related in the context of quantum information. A similar observation has already been made in the relativistic background in [39]. It would be therefore be interesting to find a reason for this mismatch.