Stellar modelling of isotropic Einstein–Maxwell perfect fluid spheres of embedding class one

Abstract

It is indeed remarkable that while charged anisotropic models with the embedding class one property are abundant, there are no reports of the physically important isotropic case despite its simplicity. In fact, the Karmarkar condition turns out to be the only avenue to generate all such stellar models algorithmically. The process of determining exact solutions is almost trivial: either specify the spatial potential and perform a single integration to obtain the temporal potential or simply select any temporal potential and get the space potential without any integrations. Then the model is completely determined and all dynamical quantities may be calculated. The difficulty lies in ascertaining whether such models satisfy elementary physical requisites. A number of physically relevant models are considered though not exhaustively. We prove that conformally flat charged isotropic stars of embedding class one do not exist. If spacetime admits conformal symmetries then the space potential must be of the Finch–Skea type in this context. A general metric ansatz is stated which contains interesting special cases. The Finch–Skea special case is shown to be consistent with the expectations of a stellar model while the Vaidya–Tikekar special case generates a physically viable cosmological fluid. The case of an isothermal sphere with charge and the Karmarkar property is examined and is shown to be defective. When the Karmarkar property is abandoned for isothermal charged fluids, the spacetimes are necessarily flat.

1 Introduction

Interest in higher dimensional geometry commenced with the pioneering work of Riemann, Cayley and seminal ideas of Schlaefli [1] who examined the question of embedding a lower dimensional Riemannian manifold in a higher dimensional Euclidean manifold. Essentially this is accomplished by solving the well known Gauss–Codacci–Ricci equations (see the Appendix for a brief review). It has been suggested that higher dimensions which are not observable exist as topologically curled and have very small value. In 1948 Karmarkar [3] established a necessary condition restricting components of the Riemann tensor and later a sufficiency condition was added by Pandey and Sharma [4]. Of relevance to relativistic astrophysics the Karmarkar condition establishes a direct relationship between the metric potential functions for spherically symmetric spacetimes. It is known that spherical metrics are in general class two and any four dimensional metric may be embedded into a six dimensional Euclidean spacetime, however, the imposing of the Karmarkar condition allows spherical metrics to be of class one and embeddable in five dimensional Euclidean spacetimes. Taken together with the isotropy of pressure condition the equations of motion have the unique solutions of the Schwarzschild interior metric (bounded) or the unbounded Kohler–Chao [5] solution. Further significant advances in this area were made by Nash [6] who posed the problem equivalently as of finding to what extent Riemannian manifolds are submanifolds of Euclidean spaces. Nash proved that every Riemannian manifold can be isometrically embedded into some Euclidean space for continuously differentiable ($C^1$) embeddings. He further showed that for analytic embeddings or embeddings that are smooth of class $C^k, 3 \le k < \infty$ such an isometric embedding is always possible. In 1973 Barnes [7] established that class one perfect fluids are either conformally flat (such as the Schwarzschild interior), exhibit geodesic flow or admit a three dimensional group of isometries with two dimensional space-like trajectories.

The natural question that arises is: what importance do the embedding theorems hold for current investigations in relativistic astrophysics and cosmology in general. Firstly, the search for a grand unified theory merging the quantum theory with gravitational physics strongly suggests that gravitation should incorporate higher dimensions in order to be compatible with quantum field theory. In addition, in order to address some shortcomings of general relativity without the need to resort to exotic matter fields, there are many modified theories of gravity on the market. Admittedly not all require higher dimensions. However, brane world [8] ideas, Kaluza–Klein [9, 10] theory and the more recent vigorously pursued Lovelock gravity [11, 12], including its special case Einstein–Gauss–Bonnet gravity [13,14,15], all demand extra spacetime dimensions. Note that Lovelock gravity is a quintessentially higher dimensional theory which is simply the standard Einstein theory in dimensions less than five. Therefore it is of immense interest to investigate the embedding prospects of spacetimes in the context of a variety of matter fields.

Spacetimes with pressure isotropy are of particular significance since they have been shown to be reasonable in describing various physical phenomena such as stars and cold fluid planets. As remarked above, the isotropic exact solution of embedding class one is unique and known. However, when the electromagnetic field is introduced there is no unique isotropic solution for charged stars of embedding class one since the field equations are under-determined. It is already known that no exact solution to the neutral Einstein field equations can generate a charged stellar model [16]. This point is corroborated by Maurya et al. [17] and Singh et al. [18]. Our interest lies in detecting new classes of isotropic spherically symmetric charged fluid distributions which may be embedded in five dimensional Euclidean space.

It is remarkable that a literature search returned zero results for isotropic charged spheres of embedding class one. There are a number of charged isotropic solutions investigated in the literature without the embedding class one property. These include the work of Kileba Matondo et al. [19] with the imposition of conformal symmetry, Prasad et al. [20] with isotropic solutions of compact stars and the work of Herrera and Ponce de León [21] with charged isotropic spheres admitting a oneparameter group of conformal motions. Several authors generating anisotropic models claim that it is trivial to switch off the anistropy thus yielding an isotropic fluid. This is misleading as the vanishing of anisotropy induces a further constraint on the metric potentials in addition to the Karmarkar condition.

There exists a plethora of anisotropic models with electric charge and with the embedding property. For example, the reader may consult [22,23,24,25,26,27,28,29,30]. The introduction of anisotropic stresses further weakens the mathematical problem as an extra choice is now available. For example for spherical symmetry the equations of motion number four in total but the number of variables is up to 7 (density, radial pressure, tangential pressure, electrostatic field intensity, proper charge density, spatial and temporal potentials) for anisotropy and charge. Even if one imposes the Karmarkar condition there still remains two prescriptions to be made. Frankly it is possible to write solutions for such a problem at will without even having to solve any complicated system of partial differential equations and dozens of such solutions and their associated graphical analyses have flooded the literature. Models which satisfy important physical constraints such as an equation of state are more likely to be physically relevant. This method has been used by Bhar et al. [31], Maurya et al. [32,33,34,35] and Singh et al. [36, 37] to generate anisotropic solutions of embedding class 1.

The approach taken in this article is to consider a wide class of generalised Buchdahl spacetimes which contain a number of interesting physically reasonable special cases such as the Schwarzschild interior metric [38], the isothermal fluid sphere [39], the Vaidya–Tikekar [40] superdense stars and the Finch–Skea [41] static star model shown to be consistent with Walecka’s [42] astrophysical theory. We are able to present the most general solution however it is given in terms of elliptic functions. The important special cases however, have remarkably simple forms worthy of attention. In addition we also address the coupling of the embedding problem with the conformal flatness scenario and separately with the existence of conformal symmetries.

2 Einstein–Maxwell field equations

It is reasonable to assume that the interior of a spherically symmetric charged star is described by the line element

$$\begin{aligned} ds^2 = -e^{2\nu (r)} dt^2 + e^{2\lambda (r)} dr^2 + r^2\left( d\theta ^2 + \sin ^2 \theta d\phi ^2 \right) \end{aligned}$$

(1)

where the functions $\nu (r)$ and $\lambda (r)$ are gravitational potentials and we specify a co-moving fluid four–velocity field $u^a = e^{-\nu }\delta _0{}^{a}$. It has been extensively shown in the literature (for example see [43]) that the Einstein–Maxwell field equations are given by the nonlinear system

$$\begin{aligned}&\left[ r\left( 1-e^{-2\lambda }\right) \right] '=r^2\rho + \frac{1}{2}r^2E^2 \end{aligned}$$

(2)

$$\begin{aligned}&-\left( 1-e^{-2\lambda }\right) +2\nu 're^{-2\lambda }= pr^2 -\frac{1}{2}r^2E^2 \end{aligned}$$

(3)

$$\begin{aligned}&e^{-2\lambda }\left[ \frac{r\nu '}{\nu }{-}\frac{r\lambda '}{\lambda }{+}r^2\left( \nu ''{-}\nu '\lambda ' {+}\nu '^2\right) \right] {=}pr^2+\frac{1}{2}E^2r^2 \end{aligned}$$

(4)

$$\begin{aligned}&r^2 \sigma = e^{-\lambda } \left( r^2 E\right) ' \end{aligned}$$

(5)

where $\rho$ is the energy density, p the isotropic particle pressure, E the electric field intensity and $\sigma$ the proper charge density. Note that $'$ denotes differentiation with respect to the variable r. The conservation laws $T^{ab}_{}{}_{;b} = 0$ generate the condition

$$\begin{aligned} p' + (\rho + p)\nu ' = \frac{E}{r^2}\left[ r^2 E\right] ' \end{aligned}$$

(6)

which may substitute one of the independent field equations in the system (2). However since (6) incorporates four physical quantities, it has limited use. It is convenient to invoke the following transformations to simplify the field equations: $x = Cr^2$, $Z(x) = e^{-2\lambda (r)}$, $y^2(x) = e^{2\nu (r)}$. With these transformations the Einstein–Maxwell field equations (2) to (5) may be expressed in the following equivalent form

$$\begin{aligned}&\frac{1-Z}{x}-2\dot{Z}=\frac{\rho }{C}+\frac{E^2}{2C}\end{aligned}$$

(7)

$$\begin{aligned}&\frac{Z-1}{x} + \frac{4Z\dot{y}}{y}=\frac{p}{C}-\frac{E^2}{2C} \end{aligned}$$

(8)

$$\begin{aligned}&4x^2Z\ddot{y} + 2x^2\dot{Z}\dot{y}+\left( \dot{Z}x-Z+1-\frac{E^2x}{C}\right) y=0 \end{aligned}$$

(9)

$$\begin{aligned}&\frac{\sigma ^2}{C}=\frac{4Z}{x}\left( x\dot{E} + E \right) ^2 \end{aligned}$$

(10)

where dots represent differentiation with respect to x. This version has the distinct advantage that the equation of pressure isotropy (9) is now linear in one of the potentials y. This is bound to greatly assist in the process of locating exact solutions.

The exterior gravitational field for a static, spherically symmetric charged distribution is governed by the Reissner–Nordstrom [44, 45] solution. The Reissner–Nordstrom exterior line element has the form

$$\begin{aligned} ds^2= & {} -\left( 1-\frac{2M}{r} + \frac{Q^2}{r^2}\right) dt^2 + \left( 1-\frac{2M}{r} + \frac{Q^2}{r^2}\right) ^{-1} dr^2 \nonumber \\&+ r^2(d\theta ^2 + \sin ^2 \theta d\phi ^2) \end{aligned}$$

(11)

where M and Q are associated with the mass and charge of the sphere respectively as measured by an observer at spatial infinity. For the Reissner–Nordstrom solution (11) the radial electric field is described by

$$\begin{aligned} E=\frac{Q}{r^2} \end{aligned}$$

(12)

and consequently the proper charge density is $\sigma = 0$ in the exterior by (5). Observe that upon setting $Q=0$ in (11) we regain the exterior Schwarzschild [46] solution. When the gravitational field is generated by a massless electromagnetic field, then such an exterior metric is referred to as an electrovacuum solution.

3 Embedding class one

In order to embed a lower dimensional Riemannian spacetime into a higher dimensional Euclidean one, Karmarkar [3] established the necessary condition between the metric potentials. These spacetimes are referred to as being of embedding class 1 and the Riemann tensor components must obey

$$\begin{aligned} R_{0303} = \frac{R_{0101}R_{2323}+R_{0113}+R_{0223}}{R_{1212}} \end{aligned}$$

(13)

with $R_{1212} \ne 0$ [4]. The Karmarkar condition constrains the metric potentials according to the relationship

$$\begin{aligned} y = A + B\int {\sqrt{\frac{1-Z}{Zx}}}dx \end{aligned}$$

(14)

where A and B are arbitrary constants. By specifying a metric potential Z, we are theoretically able to find a solution for y. The condition for pressure isotropy remains unchanged and can be rearranged in the following form

$$\begin{aligned} \frac{E^2}{C} = \frac{4 x^2 Z \ddot{y} +x \left( 2 x \dot{y}+y\right) \dot{Z}+y\left( 1-Z\right) }{x y} \end{aligned}$$

(15)

from which we can obtain the electric field intensity E once Z and y are known.

Revisiting (7), (8) and (10) the remaining dynamical quantities $\rho$, p and $\sigma$ assume the forms

$$\begin{aligned} \frac{\rho }{C}= & {} \frac{ 2y\left( 1-Z\right) -4xy \dot{Z} -4 x^2 Z \ddot{y} -x \left( 2 x \dot{y}+y\right) \dot{Z} -y (Z-1)}{2 x y} \end{aligned}$$

(16)

$$\begin{aligned} \frac{p}{C}= & {} \frac{2y\left( Z-1\right) +8xZ\dot{y} + 4 x^2 Z \ddot{y}+x \left( 2 x \dot{y}+y\right) \dot{Z}+y (Z-1)}{2 x y} \end{aligned}$$

(17)

$$\begin{aligned} \frac{\sigma ^2}{C}= & {} \frac{4Z}{x} \left( x\dot{E}+E\right) ^2. \end{aligned}$$

(18)

The exercise of finding suitable metrics for charged perfect fluids of embedding class 1 reduces to finding Z, y functions satisfying (14). There is no other reasonable avenue to go forward but to work with (14) since each of Eqs. (7)–(10) consists of at least 3 of the dynamical or geometrical variables. Now given that the model comprises 5 equations in six unknowns and there remains only one prescription left, it follows that (14) serves as an algorithm to detect all isotropic charged spheres of embedding class one. Notice also that (14) may be differentiated and it is easy to find Z in terms of y. Now it is trivial to pick any y function to generate an exact model. Theoretically this is a straight forward exercise, however, the challenge lies in locating solutions that satisfy the elementary physical requirements.

4 Embedding and conformal flatness

Conformal flatness is an indication that a spacetime tends to flatness at spatial infinity and is characterised by the vanishing of the Weyl conformal tensor. In our coordinates, this is tantamount to the constraint equation

$$\begin{aligned} 4x^2 Z\ddot{y} +2x^2 \dot{Z}\dot{y} - (\dot{Z}x -Z +1)y = 0 \end{aligned}$$

(19)

which bears an uncanny resemblance to the isotropy of pressure equation (9) when the electric field E vanishes. Consequently it is simple to deduce that conformal flatness for neutral isotropic spheres is satisfied only by the Schwarzschild interior metric [16]. However, with the introduction of charge the situation is different. There still remains one choice to be made in order to close the system of field equations and a large number of models may thus be found in general. Imposing the requirement for the spacetime to be of embedding class one together with conformal flatness fixes the variables and a unique solution may be found if it exists. Inserting the Karmarkar condition (14) into (19) generates the remarkably simple equation

$$\begin{aligned} -2\sqrt{\frac{1-Z}{Zx}} = \frac{A}{B} + \int \sqrt{\frac{1-Z}{Zx}} dx \end{aligned}$$

(20)

after several simplifications. Differentiating Eq. (20) with respect to x gives

$$\begin{aligned} \dot{Z}x - Z + 1 = 0 \end{aligned}$$

(21)

on rearranging. The general solution to (21) is

$$\begin{aligned} Z = 1 + kx \end{aligned}$$

(22)

which corresponds to the interior Schwarzschild potential which corroborates the result of Barnes [7]. Substituting (22) into (15) gives $E = 0$ and the charge disappears. So the embedding requirement and conformal flatness condition together generate the interior Schwarzschild metric applicable to neutral incompressible spherically symmetric fluids. Consequently we have proved the

Theorem

There exists no nontrivial conformally flat charged isotropic fluid sphere of embedding class one.

5 Embedding and conformal symmetry

It has long been established that for a spacetime to admit a one-parameter group of conformal motions then the temporal metric potential should have the quadratic form $e^{2\nu } \sim r^2$ [47] which in our scheme may be expressed as

$$\begin{aligned} {y = ax } \end{aligned}$$

(23)

for some constant a. With this stipulation the embedding condition (15) requires that the equation

$$\begin{aligned} {A + B \int \sqrt{\frac{1-Z}{Zx}} = ax } \end{aligned}$$

(24)

be satisfied. Equation (24) results in the spatial potential

$$\begin{aligned} Z = \frac{1}{1 + \frac{a^2}{B^2} x} \end{aligned}$$

(25)

which corresponds to the Finch–Skea potential. This case will be examined in greater detail later in this article however it is interesting to note that for a charged isotropic sphere to be of embedding class one and to admit a one-parameter group of conformal motions the unique solution is the Finch–Skea class of spatial potentials. This class of potentials belongs to a wider class which we propose to study next.

6 A general class of spacetimes

While the relationship (14) admits large classes of solutions for choices of the metric potentials, we are interested in those classes which contain important special cases of metric ansatze that have been studied in the literature. Of course these prescriptions will generate new line elements in view of the Karmarkar condition. It is already known that exact solutions of Einstein’s equations cannot model charged stars as the electric field will always vanish [16].

Consider the spatial metric potential in the form

$$\begin{aligned} Z=\frac{1+ax}{1+bx +cx^2} \end{aligned}$$

(26)

and the associated temporal potential

$$\begin{aligned} y= & {} B\frac{\sqrt{ac(1+ax)(b-a+cx)} - (a^2 - ab+c) \sinh ^{-1} \sqrt{\frac{c(1+ax)}{ab-a^2-c}}}{\sqrt{a^3 c}} + A \nonumber \\ \end{aligned}$$

(27)

with the help of (14). Note that introducing general quadratics into the numerator and denominator of (26) leads to a solvable integral but in the form of elliptic functions. These solutions are not compatible with the process of model building. We now consider in turn some well known metric prescriptions and the behavior of their complete geometry and dynamics.

6.1 Isothermal behavior

We commence with the simple prescription of Z being a constant. Aside from the trivial case of $k = 1$ the general case does not actually fall into the class of solutions (27). Nevertheless it is simple to generate the solution on its own. The importance of this selection of a constant space potential lies in its relation to the isothermal behaviour of static neutral spheres. By isothermal behaviour we mean that the density and pressure both obey an inverse square law relation to the radius of the sphere. By construction such spheres do not represent isolated spheres but have application to cosmological fluids since no surface of vanishing pressure demarcating a boundary is possible. An additional drawback of such models is a persistent singularity at the centre of the distribution. Nevertheless outside of these extremes such fluids have been thoroughly analysed in the literature [39]. It is also known that constant spatial potentials generate isothermal fluid spheres in both regular Einstein theory and also in the generalised version Lovelock gravity [48]. However, it is interesting to see if isothermal behaviour is preserved in view of the embedding restriction. The stipulation $Z = k$, for some positive constant k, in (14) yields

$$\begin{aligned} y = A+2 B \sqrt{\frac{x\left( 1-k\right) }{k}} \end{aligned}$$

(28)

where A and B are arbitrary constants for the temporal potential. Clearly the interval of validity for a realistic model reduces to the window $0< k < 1$ from (28). The dynamical quantities then assume the form

$$\begin{aligned} \frac{\rho }{C}= & {} \frac{(k-1) \left( A k \alpha \sqrt{ x}+2 B x\right) }{2 x \left( 2 B (k-1) x-A k \alpha \sqrt{x}\right) } \end{aligned}$$

(29)

$$\begin{aligned} \frac{p}{C}= & {} \frac{A^2 (k-1) k+6 A B k^2 \alpha \sqrt{ x}+4 B^2 (k-1) (4 k-1) x}{2 x \left( A^2 k+4 B^2 (k-1) x\right) }\end{aligned}$$

(30)

$$\begin{aligned} \frac{E^2}{C }= & {} \frac{(k-1) \left( 2 B (2 k-1) x-A k \alpha \sqrt{x}\right) }{x \left( A k \alpha \sqrt{ x}-2 B (k-1) x\right) }\end{aligned}$$

(31)

$$\begin{aligned} \frac{\sigma ^2}{C}= & {} (k-1)^2 k^2 x \left( A^3 (k-1) k+3 A^2 B k (3 k-2) \alpha \sqrt{ x} \right. \nonumber \\&\left. -2 A B^2 (k-1) (11 k-6) x -8 B^3 (k-1) (2 k-1) x \alpha \sqrt{ x}\right) ^2 \big / \nonumber \\&\left( 2 B (k-1) x-A k \alpha \sqrt{\ x}\right) ^5 \left( 2 B (2 k-1) x-A k \alpha \sqrt{ x}\right) \end{aligned}$$

(32)

where we have set $\alpha = \sqrt{\left( \frac{1}{k}-1\right) }$ for simplicity. What may be observed is that the solution is not in general isothermal except when $A=0$, in which case $\rho$ and p vary as $\frac{1}{r^2}$. However, $A=0$ leads to a constant potential y which is not physically viable and is indicative of the defective Einstein universe model. Therefore we conclude that the embedding requirement does not guarantee isothermal behaviour for constant space potentials in general. It is worth noting that imposing an inverse square fall-off on the density and pressure fixes the model in the presence of charge and theoretically a unique solution exists. We consider this problem next.

6.2 Isothermal charged fluid without embedding

Using $\frac{\rho }{c} = \frac{G}{x}$ and $\frac{p}{c} = \frac{H}{x}$ for some constants G and H, we get the resulting equations

$$\begin{aligned}&\frac{1-Z}{x}-2\dot{Z} = \frac{G}{x} + \frac{E^2}{2C} \end{aligned}$$

(33)

$$\begin{aligned}&\frac{Z-1}{x} + \frac{4Z\dot{y}}{y} = \frac{H}{x} - \frac{E^2}{2C} \end{aligned}$$

(34)

$$\begin{aligned}&\frac{4x^2Z\ddot{y} + 2x^2\dot{Z}\dot{y} + (\dot{Z}x-Z+1 )y}{2xy} = \frac{E^2}{2C} \end{aligned}$$

(35)

which are three independent differential equations uniquely determining the structure of the isothermal sphere. We can convert (33) to (35) to an equivalent more transparent system. Adding (33) and (34) gives

$$\begin{aligned} \frac{\dot{y}}{y} = \frac{2\dot{Z}x + G + H}{4xZ} \end{aligned}$$

(36)

while (34) and (35) together imply

$$\begin{aligned} 4x^2Z\ddot{y} + (8xZ + 2x^2\dot{Z})\dot{y} + (x\dot{Z} + Z - 1 - 2H)y = 0 \end{aligned}$$

(37)

and subtracting (33) from (35) gives the equation

$$\begin{aligned} 4x^2 Z \ddot{y} + 2x^2 \dot{Z} \dot{y} + (5x\dot{Z} - Z + 1 + 2G)y = 0. \end{aligned}$$

(38)

Now Eqs. (36) to (38) constitute an equivalent set of independent equations for the system (33) to (35). Now comparing (37) and (38) the relationship

$$\begin{aligned} \frac{\dot{y}}{y} = \frac{2x\dot{Z} -Z +1 + G + H}{4xZ} \end{aligned}$$

(39)

results. Finally it is evident from (36) and (39) that the only solution the system admits is

$$\begin{aligned} {Z = 1} \end{aligned}$$

(40)

which is physically unacceptable. From (14) we get $y =$ a constant. Thus we have a trivial flat spacetime. In other words we have the

Theorem

Electrically charged isotropic static fluid spheres with isothermal behaviour, that is where density and pressure both decrease as $1/r^2$ generate flat spacetimes.

6.3 Geodesic flow

The results above raise the question of whether a constant temporal potential always gives a flat spacetime. The case $y =$ a constant corresponds to geodesic flow and from (14) the space potential is $Z = 1$ effectively corresponding to $a = b = c = 0$ in the ansatz (26). Thus we have a defective universe model such as was proposed by Einstein. Conversely $Z = 1$ gives $y =$ a constant. Thus a nontrivial static geodesic flow model satisfying the embedding property does not exist.

6.4 $Z = 1+x$ – the Schwarzschild interior ansatz

Although we have inspected this case already – we check it for completeness. Setting $a = 1$, $b = c = 0$ in (26) gives $Z = 1+x$ known to generate the Schwarzschild incompressible fluid sphere in general relativity. Plugging this into (14) we get

$$\begin{aligned} y = A + 2B \sqrt{1+x} \end{aligned}$$

(41)

where A and B are arbitrary constants. But it is known that the Schwarzschild interior metric cannot be valid for charged stars as shown by Hansraj et al. [16] since the electric field vanishes.

6.5 $Z = \frac{1}{1+x}$ – The Finch–Skea metric ansatz

The extensively studied Finch–Skea [41] stellar model is generated by the potential choice $Z =$$\frac{1}{1+x}$ corresponding to $a = 0$, $b = 1$ and $c = 0$. The general solution to Eq. (14) has the remarkably simple form

$$\begin{aligned} y = A + Bx \end{aligned}$$

(42)

where A and B are arbitrary constants. It is convenient to let $\beta = \frac{A}{B}$, and so the dynamical quantities may be expressed as

$$\begin{aligned} \frac{\rho }{C} = \frac{\beta (x+6)+ x (x+8)}{2 (x+1)^2 (\beta + x)} \end{aligned}$$

(43)

and at the centre

$$\begin{aligned} \left( \frac{\rho }{C}\right) _0 = 3&\end{aligned}$$

(44)

where the subscript 0 is used to denote quantity values at the stellar centre $x=0$. For the pressure

$$\begin{aligned} \frac{p}{C}= \frac{ (-x^2 +4x + 8 )-\beta (x+2)}{2 (x+1)^2 (\beta + x)} \end{aligned}$$

(45)

and at the centre

$$\begin{aligned} \left( \frac{p}{C}\right) _0 = \frac{8-2\beta }{2\beta } \end{aligned}$$

(46)

for $x=0$. Positivity of the central pressure demands

$$\begin{aligned} 0< \beta < 4 \end{aligned}$$

(47)

as a constraint on $\beta$. The electric field intensity is given by

$$\begin{aligned} \frac{E^2}{C} = \frac{x [\beta + (x-2)]}{(x+1)^2 (\beta + x)} \end{aligned}$$

(48)

and this quantity vanishes at the centre, as expected. The charge density has the form

$$\begin{aligned} \left( \frac{\sigma ^2}{C}\right) = \frac{\left[ \beta ^2 (x+3)+2 \beta (x-1) (x+3)+ (x-1) x (x+4)\right] ^2}{(x+1)^5 (\beta + x-2) (\beta + x)^3} \end{aligned}$$

(49)

and at the centre

$$\begin{aligned} \left( \frac{\sigma ^2}{C}\right) _0 = \frac{3}{\beta ^2} \end{aligned}$$

(50)

which is positive for all $\beta$ values. The expressions for the energy conditions are given by

$$\begin{aligned} \rho -p= & {} \frac{\beta (x+4)+\left( x^2+2 x-4\right) }{(x+1)^2 (\beta + x)} \end{aligned}$$

(51)

$$\begin{aligned} \rho +p= & {} \frac{2 (\beta + (3 x+2))}{(x+1)^2 (\beta + x)}\end{aligned}$$

(52)

$$\begin{aligned} \rho +3p= & {} \frac{ \left( -x^2+10 x+12\right) -\beta x}{(x+1)^2 (\beta + x)} \end{aligned}$$

(53)

and these are all expected to be positive. The square of the speed of sound index is given by

$$\begin{aligned} \left( \frac{dp}{d\rho }\right)= & {} \frac{-\beta ^2 (x+3)-2 \beta \left( x^2-5\right) + \left( -x^3+9 x^2+24 x+8\right) }{\beta ^2 (x+11)+2\beta \left( x^2+12 x-1\right) + x^2 (x+15)}\nonumber \\ \end{aligned}$$

(54)

and at the centre $(x=0)$:

$$\begin{aligned} \left( \frac{dp}{d\rho }\right) _0= & {} \frac{-3\beta ^2+10\beta +8}{11\beta ^2 -2\beta } \end{aligned}$$

(55)

which places a further restriction on $\beta$, namely

$$\begin{aligned} 1.3<\beta <4 . \end{aligned}$$

(56)

The adiabatic stability index has the form

$$\begin{aligned}&\left( \frac{\rho +p}{p}\right) \frac{dp}{d\rho }\nonumber \\&= \frac{4 (\beta + 3 x+2) \left( \beta ^2 (x+3)+2 \beta \left( x^2-5\right) + (x (x^2-9x-24)-8)\right) }{(\beta x + 2\beta + x^2-4x-8) \left( \beta ^2 (x+11)+2 \beta (x^2+12x-1)+ x^3 +15x\right) }\nonumber \\ \end{aligned}$$

(57)

and at the centre $(x=0)$:

$$\begin{aligned} \left[ \left( \frac{\rho +p}{p}\right) \frac{dp}{d\rho }\right] _0 = \frac{4(\beta +2)(3\beta ^2-10\beta -8) }{(2\beta -8)(11\beta ^2-2\beta )} > \frac{4}{3} \end{aligned}$$

(58)

giving

$$\begin{aligned} 0.18<\beta < 2.52 \end{aligned}$$

(59)

as a restriction on $\beta$. Finally harmonising all the restrictions we have established, we obtain the window

$$\begin{aligned} 1.3< \beta < 2.52 \end{aligned}$$

(60)

on $\beta$ which we will use when choosing suitable constants to model stars. The mass profile is given by

$$\begin{aligned} M= & {} \left\{ (x+1) \left( 4 A^{3/2} \sqrt{B} \tan ^{-1}\left( \sqrt{\frac{Bx}{A}}\right) \right. \right. \nonumber \\&\left. +\left( 3 A^2-12 A B+5 B^2\right) \tan ^{-1}\left( \sqrt{x}\right) \right) \nonumber \\&\left. +\sqrt{x} (A-B) (A (2 x-3)+B (5-2 x))\right\} \nonumber \\&\div \left[ 4 (x+1) (A-B)^2\right] \end{aligned}$$

(61)

and the compactification expression $\frac{m}{r}$ reduces to

$$\begin{aligned} \frac{M}{\sqrt{x}}= & {} \left\{ (x+1) \left( 4 A^{3/2} \sqrt{B} \tan ^{-1}\left( \sqrt{\frac{Bx}{A}}\right) \right. \right. \nonumber \\&\left. +\left( 3 A^2-12 A B+5 B^2\right) \tan ^{-1}\left( \sqrt{x}\right) \right) \nonumber \\&\left. +\sqrt{x} (A-B) (A (2 x-3)+B (5-2 x))\right\} \nonumber \\&\div \left[ 4\sqrt{x} (x+1) (A-B)^2\right] . \end{aligned}$$

(62)

Finally, the equation of state expression $\frac{p}{\rho }$ has the form

$$\begin{aligned} \frac{p}{\rho }= \frac{4 (\beta + 3 x+2)}{\beta (x+6)+ x (x+8)}-1 \end{aligned}$$

(63)

6.6 Hydrostatic equilibrium and stability

In order to study the balance of forces or state of hydrostatic equilibrium inherent in this model we analyse the Tolman–Oppenheimer–Volkoff (TOV) equation

$$\begin{aligned} (\rho + p)\dot{\nu } + \dot{p} - \frac{E}{x} (x\dot{E} +E) = 0 \end{aligned}$$

(64)

obtained from the vanishing covariant divergence of the energy momentum tensor. This is a statement about the energy conservation of the system. The gravitational force is defined as $F_g = - (\rho + p)\dot{\nu }$, the hydrostatic force is given by $F_h = - \dot{p}$ and the electrostatic force has the formula $F_e = \frac{E}{x} (x\dot{E} +E)$. The expressions for these three quantities are given by

$$\begin{aligned} F_g= & {} -\frac{2 B (A+B (3 x+2))}{(x+1)^2 (A+B x)^2} \end{aligned}$$

(65)

$$\begin{aligned} F_h= & {} -\frac{A^2 (x+3)+2 A B \left( x^2-5\right) +B^2 (x ((x-9) x-24)-8)}{2 (x+1)^3 (A+B x)^2} \end{aligned}$$

(66)

$$\begin{aligned} F_e= & {} \frac{A^2 (x+3)+2 A B (x-1) (x+3)+B^2 (x-1) x (x+4)}{2 (x+1)^3 (A+B x)^2} \end{aligned}$$

(67)

for our line element. These quantities will be examined with the aid of plots below.

In the area of stellar structure there are several notions of stability of the model. For example, the causality criterion is understood to be a stability test. We shall analyse this in what follows. The Harrison–Zeldovich–Novikov (HZN) [49, 50] sense of stability demands the inequality

$$\begin{aligned} \frac{d M(\rho _0)}{d\rho _0} \ge 0 \end{aligned}$$

be satisfied where $M(\rho _0)$ is the mass of a star and $\rho _0$ is the central energy density. The HZN stability asserts that the mass increases with the value of the density at the stellar centre. Defining the mass as $M = \frac{1}{2C^\frac{3}{2}} \int ^{\rho _0}_0 \rho \sqrt{v} dv$ in our coordinates we obtain the expression

$$\begin{aligned} \frac{dM(\rho _0)}{d \rho _0} = \frac{\sqrt{\rho _0}\left( \beta (6 + \rho _0) +\rho _0(\rho _0 + 8)\right) }{2(1+ \rho _0)^2 (\beta + \rho _0)} \end{aligned}$$

(68)

for the HZN quantity. Given that $\beta = 2 > 0$ and $\rho _0 \ge 0$ it easily follows that the right hand side of (68) is positive and the HZN stability condition is satisfied. That is the mass increases with increasing central density value. Figure 7 below confirms this result. In addition it can be seen that the ratio of central pressure to central density

$$\begin{aligned} \frac{p_0}{\rho _0} = \frac{1}{3} \end{aligned}$$

(69)

satisfies the Zeldovich [51] stability criterion $\frac{p_0}{\rho _0} < 1$ which essentially follows from the energy conditions. Further the Chandrasekhar adiabatic stability condition [52,53,54]

$$\begin{aligned} \left( \frac{\rho + p}{p} \right) \frac{dp}{d\rho } > \frac{4}{3} \end{aligned}$$

will be examined with the help of the plots.

6.7 Physical analysis

In the Finch–Skea case, from (43) we see that the density is always positive. From Eq. (45) it is possible to infer the existence of a finite boundary $p(R) = 0$ on account of the existence of a zero of the numerator. The electric field intensity and charge density are well behaved functions, decreasing outwardly from the centre. We now analyse graphical plots of the dynamical quantities. These plots have been constructed using parameter values $A = 1$ and $B = 0.5$, so $\beta = 2$ which fall within the accepted range shown in (60).

Fig. 1

Density $\rho$ versus the radial variable x

Fig. 2

Pressure p versus the radial variable x

Fig. 3

Square of sound speed $\frac{dp}{d\rho }$ versus the radial variable x

Fig. 4

Energy conditions versus the radial variable x

Fig. 5

Chandrasekhar adiabatic stability index versus the radial variable x

Fig. 6

Mass profile versus the radial variable x

Fig. 7

Change in mass $\frac{dM}{d\rho _0}$ versus the central density $\rho _0$

Fig. 8

Compactification versus the radial variable x

Fig. 9

Equation of state $\frac{p}{\rho }$ versus the radial variable x

Fig. 10

Variation of forces in TOV-equation versus the radial variable x

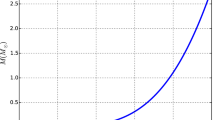
From Figs. 1 and 2 we see that the pressure and density are both monotonically decreasing, which is expected. We also note that the pressure cuts the x-axis at $x=3.23$, which determines the radius of the star. The sound speed index shown in Fig. 3 is less than 1 which confirms the model as causal. It can be observed from Fig. 4 that all the energy conditions are positive and hence satisfied. The adiabatic index demonstrated in Fig. 5 is positive and is in the accepted range of being more than $\frac{4}{3}$ for the radius of the star. In Fig. 6 we see that the mass profile appears well behaved as an increasing function of the radius with a value of $M = 1.27$ at the radius. As previously noted the HZN stability quantity is depicted in Fig. 7 and its positivity is established for this model. The compactification curve displayed in Fig. 8 is a smooth, increasing function. The equation of state profile against the radial variable in Fig. 9 is almost linear and decreasing. Finally Fig. 10 depicts the balance of forces in the TOV equation and confirms that the system is in hydrostatic equilibrium.

The line element for the star at the boundary $(r=R)$ has the form

$$\begin{aligned} ds^2= & {} -\left( A + BCR^{2} \right) ^{2} dt^2 + \left( 1 + CR^{2}\right) dr^2 \nonumber \\&+ r^2(d\theta ^2 + \sin ^2 \theta d\phi ^2) \end{aligned}$$

(70)

which can be matched with the Reissner–Nordstrom exterior line element [44, 45] shown in (11). This gives

$$\begin{aligned} \frac{1}{1 + CR^{2}} = \left( A + BCR^{2} \right) ^{2} = 1-\frac{2M}{R}+\frac{Q^2}{R^2}. \end{aligned}$$

(71)

The pressure vanishing at the boundary results in the following condition

$$\begin{aligned} \left( -C^2R^4 +4CR^2 +8\right) - \frac{A}{B}\left( CR^2+2 \right) =0 \end{aligned}$$

(72)

from which we can get a relation on the integration constants as

$$\begin{aligned} A = \frac{B \left( -C^2R^4 +4CR^2 +8\right) }{CR^2+2 } \end{aligned}$$

(73)

and using the condition from (71) we are able to write B as

$$\begin{aligned} B = \left( 1-\frac{2M}{R}+\frac{Q^2}{R^2}\right) ^{\frac{1}{2}} \left[ 6-\frac{4}{C R^2+2}\right] ^{-1} \end{aligned}$$

(74)

which settles the integration constants A and B. We are now able to proceed to use numerical values to settle the other constants and find the relevant ratios. From (72) using our careful selection of $A=1$ and $B=0.5$ which yielded a radius at the boundary of $R=3.23$, we obtain $C=0.31$. Taking into consideration the radial electric field (12) we get the following expression

$$\begin{aligned} \frac{CR^2\left( \frac{A}{B} +CR^2 -2\right) }{\left( CR^2+1\right) ^{2} \left( \frac{A}{B} +CR^2 \right) } = \frac{Q}{R^2} \end{aligned}$$

(75)

where the numerical values are again used to obtain $Q=1.16$. A maximum mass–radius ratio of 0.79 was determined and this is less than $\frac{8}{9}$ as required by Buchdahl [55]. The Böhmer and Harko [56] upper bound is also satisfied with a left hand side of 0.19 which is less than the limit 0.79. The Andréasson [57] limit has also been satisfied, with the left hand side value of 1.13 being less than the limit of 1.30. Finally, we obtain a mass–charge ratio of 1.09 which is greater than 1 as demanded by Cooperstock and de la Cruz [58]. We can now state that this model satisfies all requirements for physical viability.

6.8 Vaidya–Tikekar superdense star ansatz

Another interesting case is that proposed by Vaidya and Tikekar [40] and in our scheme is generated by setting $a = 1$, $b = 2$ and $c = 0$. It was shown that this model generates superdense isotropic stars, however, will this be the case when charge is involved and when the geometric restriction of embedding class one is imposed? We shall see that the answer is negative and that a bounded distribution does not exist. Instead a cosmological fluid results under the embedding requirement. Using the metric ansatz $Z = \frac{1+x}{1+2x}$, the general solution has the form

$$\begin{aligned} y = A+{2 B} \sqrt{x+1} \end{aligned}$$

(76)

which turns out to be the Schwarzschild interior temporal potential – see (41). For simplicity, we now set $\sqrt{1+x} = u$ and we let $\beta = \frac{A}{B}$. The dynamical quantities have the form

$$\begin{aligned} \left( \frac{\rho }{C}\right) = \frac{\beta (x+3) u+ (4 x+6)}{(2 x+1)^2 \left( \beta u+2 \right) } \end{aligned}$$

(77)

and at the centre $(x=0)$:

$$\begin{aligned} \left( \frac{\rho }{C}\right) _0 = 3. \end{aligned}$$

(78)

The pressure

$$\begin{aligned} \left( \frac{p}{C}\right) = \frac{u (4 x+2)-\beta }{(2 x+1)^2 \left( \beta u+2 \right) } \end{aligned}$$

(79)

should vanish at the radius, giving us the roots

$$\begin{aligned} x_0= & {} \frac{1}{12} \left( \root 3 \of {54 \beta ^2+6 \beta \sqrt{3 \left( 27 \beta ^2-8\right) }-8} \right. \nonumber \\&\left. +\frac{ 2^{5/3}}{\root 3 \of {27 \beta ^2+3 \beta \sqrt{3 \left( 27 \beta ^2-8\right) }-4}}-8\right) \end{aligned}$$

(80)

$$\begin{aligned} x_{1,2}= & {} \frac{1}{24} \left[ \left( \pm i\sqrt{3}-1\right) \root 3 \of {54 \beta ^2+6 \sqrt{3} \sqrt{\beta ^2 \left( 27 \beta ^2-8\right) }-8} \right. \nonumber \\&\left. \mp \frac{2\ 2^{2/3} \left( \pm 1+i \sqrt{3}\right) }{\root 3 \of {27 \beta ^2+3 \sqrt{3} \sqrt{\beta ^2 \left( 27 \beta ^2-8\right) }-4}}-16\right] \end{aligned}$$

(81)

consequently, for the real root (80) to be positive it is required that

$$\begin{aligned} \beta < -2 \vee \beta >2 . \end{aligned}$$

(82)

Moreover at the centre $(x=0)$:

$$\begin{aligned} \left( \frac{p}{C}\right) _0 = \frac{2-\beta }{2+\beta } \end{aligned}$$

(83)

and positivity of the pressure demands

$$\begin{aligned} -2< \beta < 2 \end{aligned}$$

(84)

which contradicts (82). Immediately we are alerted to the possibility that the physical requirements for a closed compact object will be violated at some level. The electric field intensity is given by

$$\begin{aligned} \frac{E^2}{C} = \frac{2 \beta u x }{(2 x+1)^2 \left( \beta u+2 \right) } \end{aligned}$$

(85)

and this has a 0 value at the centre. The charge density has the form

$$\begin{aligned} \left( \frac{\sigma ^2}{C}\right) = \frac{2 \beta u^3 \left( \beta ^2 (2 x+3)+\beta (6 x^2+19x+12) u +2 (2 x^2+9x+6)\right) ^2}{(2 x+1)^5 \left( \beta u+2 \right) ^5}\nonumber \\ \end{aligned}$$

(86)

which simplifies to

$$\begin{aligned} \left( \frac{\sigma ^2}{C}\right) _0 = \frac{2 \beta \left( 3\beta ^2 +12\beta +12\right) ^2 }{\left( \beta +2\right) ^5} \end{aligned}$$

(87)

at the centre of a charged star. The expressions for the energy conditions are given by

$$\begin{aligned} \rho -p= & {} \frac{2 \beta (x+2) u+4 }{(2 x+1)^2 \left( \beta u+2 \right) } \end{aligned}$$

(88)

$$\begin{aligned} \rho +p= & {} \frac{2 \beta u+8 (x+1)}{(2 x+1)^2 \left( \beta u+2 \right) }\end{aligned}$$

(89)

$$\begin{aligned} \rho +3p= & {} \frac{2 \left( 8 x+6-\beta u x\right) }{(2 x+1)^2 \left( \beta u+2 \right) } \end{aligned}$$

(90)

and these are all expected to be positive.

The speed of sound squared index is given by

$$\begin{aligned} \left( \frac{dp}{d\rho }\right) = \frac{\beta ^2 (2 x+3)+\beta \left( 2 x^2+5 x+4\right) u-8 \left( 2 x^2+3 x+1\right) }{\beta ^2 (2 x+11)+\beta \left( 10 x^2+53 x+42\right) u+8 \left( 2 x^2+7 x+5\right) } \end{aligned}$$

(91)

and is reduced to

$$\begin{aligned} \left( \frac{dp}{d\rho }\right) _0 = \frac{3\beta ^2 + 4\beta -8}{11\beta ^2 +42\beta +40} \end{aligned}$$

(92)

at the centre, which places a further restriction on $\beta$

$$\begin{aligned} \beta < -2.43 \vee \beta >1.09 \end{aligned}$$

(93)

to ensure a subluminal sound speed $0<\frac{dp}{d\rho } <1$ at $x=0$. The adiabatic stability index given by

$$\begin{aligned}&\left( \frac{\rho +p}{p}\right) \frac{dp}{d\rho }\nonumber \\&= \frac{-u \left( 2\beta u+8 (x+1)\right) \left( \beta ^2 (2 x+3)+u \beta (2 x^2+5x+4) -8 (2x^2+3x+1)\right) }{\left( u (4 x+2)-\beta \right) \left( \beta ^2 (2 x+11)+ u \beta (10 x^2+53x+42) +8 (2x^2 +7x +5)\right) }\nonumber \\ \end{aligned}$$

(94)

evaluates to

$$\begin{aligned} \left[ \left( \frac{\rho +p}{p}\right) \frac{dp}{d\rho } \right] _0 = \frac{\left( -2\beta -8\right) \left( 3\beta ^2 +4\beta -8 \right) }{\left( 2-\beta \right) \left( 11\beta ^2 +42 \beta +40\right) } > \frac{4}{3}\nonumber \\ \end{aligned}$$

(95)

at the centre. This inequality is satisfied provided

$$\begin{aligned} -2.25<\beta<-2 \vee -1.81<\beta<-0.62 \vee 2< \beta < 3.49.\nonumber \\ \end{aligned}$$

(96)

From our restrictions on $\beta$, it is evident that no parameter space exists that generates a physically viable closed compact star. Nevertheless the model does display pleasing properties that may have significance as an unbounded cosmological fluid. The mass profile is given by

$$\begin{aligned} M= & {} \left[ \frac{2 \sqrt{x}}{2 x+1} \left( A^2-2 B^2\right) \left( A^2 (8 x-1)+\frac{2 A B}{u}-16 B^2 x\right) \right. \nonumber \\&+\frac{A}{B} \left[ -2 \left( A^2-2 B^2\right) ^2 \log \left( u\sqrt{x}+x +u\right) \right. \nonumber \\&\left. +2 A \left( 4 B^2-A^2\right) ^{3/2} \tan ^{-1}\left( \frac{2 B \sqrt{x}}{\sqrt{4 B^2-A^2}}\right) \right. \nonumber \\&\left. -8 A B^2 \sqrt{4 B^2-A^2} \tan ^{-1}\left( \frac{A u \sqrt{x} }{\sqrt{4 B^2-A^2}}\right) \right. \nonumber \\&\left. -4 B^2 \left( A^2-4 B^2\right) \tan ^{-1}\left( u\sqrt{x} \right) \right. \nonumber \\&+\sqrt{2} A B \left( 3 A^2-10 B^2\right) \tan ^{-1}\left( \sqrt{2} \sqrt{x}\right) \nonumber \\&\left. \left. +2 A^3 \sqrt{4 B^2-A^2} \tan ^{-1}\left( \frac{A u \sqrt{x} }{\sqrt{4 B^2-A^2}}\right) \right] \right] \nonumber \\&\div {16 \left( A^2-2 B^2\right) ^2} \end{aligned}$$

(97)

and the compactification expression takes the form

$$\begin{aligned} \frac{M}{\sqrt{x}}= & {} \left[ \frac{2 \sqrt{x}}{2 {x}+1} \left( A^2-2 B^2\right) \left( A^2 (8 x{-}1){+}\frac{2 A B}{u}{-}16 B^2 x\right) \right. \nonumber \\&+\frac{A}{B} \left[ -2 \left( A^2-2 B^2\right) ^2 \log \left( u\sqrt{x}+x +u\right) \right. \nonumber \\&\left. +2 A \left( 4 B^2-A^2\right) ^{3/2} \tan ^{-1}\left( \frac{2 B \sqrt{x}}{\sqrt{4 B^2-A^2}}\right) \right. \nonumber \\&\left. -8 A B^2 \sqrt{4 B^2-A^2} \tan ^{-1}\left( \frac{A u \sqrt{x} }{\sqrt{4 B^2-A^2}}\right) \right. \nonumber \\ s&\left. -4 B^2 \left( A^2-4 B^2\right) \tan ^{-1}\left( u\sqrt{x} \right) \right. \nonumber \\&+\sqrt{2} A B \left( 3 A^2-10 B^2\right) \tan ^{-1}\left( \sqrt{2} \sqrt{x}\right) \nonumber \\&\left. \left. +2 A^3 \sqrt{4 B^2-A^2} \tan ^{-1}\left( \frac{A u \sqrt{x} }{\sqrt{4 B^2-A^2}}\right) \right] \right] \nonumber \\&\div {16\sqrt{x} \left( A^2-2 B^2\right) ^2}. \end{aligned}$$

(98)

Finally, the ratio $\frac{p}{\rho }$ given by

$$\begin{aligned} \frac{p}{\rho } = \frac{u (4 x+2)-\beta }{ u \left[ u \beta (x+3) + (4 x+6)\right] }. \end{aligned}$$

(99)

gives an indication of the equation of state.

6.9 Hydrostatic equilibrium and stability

The components of the TOV equation evaluate to

$$\begin{aligned} F_g= & {} -\frac{2 B \left( A \left( \frac{1}{x+1}\right) ^{3/2}+4 B\right) }{(2 x+1)^2 \left( A \sqrt{\frac{1}{x+1}}+2 B\right) ^2} \end{aligned}$$

(100)

$$\begin{aligned} F_h= & {} -\frac{A^2 (2 x+3)+A B (x (2 x+5)+4) \sqrt{\frac{1}{x+1}}-8 B^2 (x+1) (2 x+1)}{(x+1) (2 x+1)^3 \left( A \sqrt{\frac{1}{x+1}}+2 B\right) ^2} \end{aligned}$$

(101)

$$\begin{aligned} F_e= & {} \frac{A \left( x+1\right) ^{-3/2} \left( A^2 (2 x+3)+A B (x (6 x+19)+12) \sqrt{\frac{1}{x+1}}+2 B^2 (x (2 x+9)+6)\right) }{(2 x+1)^3 \left( A \sqrt{\frac{1}{x+1}}+2 B\right) ^3}\nonumber \\ \end{aligned}$$

(102)

for this model. We comment on the state of equilibrium of the model on the basis of the graphical plots below. For the present model the HZN stability quantity assumes the form

$$\begin{aligned} \frac{dM(\rho _0)}{d\rho _0} = \frac{\sqrt{\rho _0} \left( \beta (\rho _0 +3)\sqrt{\rho _0 +1} + (4\rho _0 +6) \right) }{(2\rho _0 +1)^2 \left( \beta \sqrt{\rho _0 +1} +2 \right) } \end{aligned}$$

(103)

which can be seen to be positive by examining Fig. 17. Observe that we are utilising a negative value for $\beta$ in this model hence we depend on the plot to verify the HZN stability criterion. Moreover, the ratio of central pressure to central density is given by

$$\begin{aligned} \left( \frac{p}{\rho } \right) _0 = 0.7 \end{aligned}$$

and is below unity as required.

6.10 Physical analysis

We now analyse graphical plots of the dynamical quantities. These plots have been constructed using parameter values $A = -7$ and $B = 10$ for illustrative purposes. Note that $\beta = -0.7$, which violates the requirement for the existence of a boundary $\beta <-2$ or $\beta >2$. In other words we sacrifice the boundedness property and consequently the fluid must have a cosmological application.

Fig. 11

Density $\rho$ versus the radial variable x

Fig. 12

Pressure p versus the radial variable x

Fig. 13

Square of sound speed $\frac{dp}{d\rho }$ versus the radial variable x

Fig. 14

Energy conditions versus the radial variable x

Fig. 15

Chandrasekhar adiabatic stability index versus the radial variable x

Fig. 16

Mass profile versus the radial variable x

Fig. 17

Change in mass $\frac{dM}{d\rho _0}$ versus the central density $\rho _0$

Fig. 18

Compactification versus the radial variable x

Fig. 19

Equation of state $\frac{p}{\rho }$ versus the radial variable x

Fig. 20

Variation of forces in TOV-equation versus the radial variable x

Figures 11 and 12 depict that the pressure and density are both monotonically decreasing, which is expected. We also note that the pressure is asymptotic hence the model may be interpreted as a cosmological fluid. The sound speed index in Fig. 13 is less than 1 which confirms the model as causal. It can be observed from Fig. 14 that all the energy conditions are positive and hence satisfied. The adiabatic index shown in Fig. 15 is positive and is in the accepted range of being more than $\frac{4}{3}$ for the radius of the star. The mass profile and compactification displayed in Figs. 16 and 18 respectively appears well behaved as increasing functions of the radius. As already noted the rate of change of mass with respect to the central density shown in Fig. 17 is always positive and corroborates the HZN stability requirement. The equation of state profile demonstrated in Fig. 19 is a smooth and increasing function. Finally Fig. 20 depicts the balance of the forces for hydrodynamical equilibrium as expressed in the TOV equation. This model therefore satisfies most requirements for physical viability as a cosmological fluid in view of the absence of a vanishing pressure surface.

Table 1 Viable metric potentials for embedding class 1 spacetimes

6.11 Other solvable cases

There exists a large number of exact models for charged isotropic fluid spheres of embedding class 1. We tabulate a few solutions which ostensibly have no singularities (at least in the metric) in Table 1 but do not engage in a study of any, as we have exhibited two simple models that satisfy all or most physical requirements.

The table contains a small sample of exact solutions with at least no singularities in the metric. A much wider class exists for charged spheres of embedding class 1.

7 Discussion

We have considered for the first time in the literature charged isotropic stars of embedding class one. The analysis boiled down to nominating one of the gravitational potentials and establishing the other via the Karmarkar condition for embedding a four dimensional curved spacetime into a 5 dimensional Euclidean spacetime. This process is virtually trivial, however, the caveat is whether the model would satisfy elementary conditions demanded of stellar models. To this end we commenced by analysing physically important geometric restrictions such as conformal flatness and the existence of conformal symmetries. In the former case we proved that no nontrivial conformally flat charged spacetimes of embedding class one exist for isotropic spheres. In the latter case, conformal symmetries were admitted by spacetimes with a Finch–skea spatial potential. An ansatz of a gravitational potential was made and the exact solution explicitly found. This metric contained a number of interesting special cases such as the Finch–Skea and Vaidya–Tikekar potentials. The charged Finch–Skea potential of embedding class one generated an astrophysical model that satisfied all the physical constraints imposed on it. The Vaidya–Tikekar proposal generated a fluid model with pleasing physical properties but did not admit a surface of vanishing pressure required for a bound model and accordingly has the interpretation of a cosmological fluid. While considering our general class of spacetimes we inspected the case of a charged isothermal fluid sphere of embedding class one and proved the non-existence of same. When the embedding property was removed, the fluid was shown to be flat. Finally we exhibited a set of metrics all of which satisfy the Karmarkar condition and which generate charged star models.

Appendix

We give a very brief explanation of the connection between the Gauss–Codacci–Ricci equations of surface theory and the concept of Gaussian curvature which generate the Kamarkar embedding condition. In Riemannian geometry the problem of embedding a d-dimensional Riemannian manifold into a higher dimensional Euclidean space $\mathbb {R}^N$ may be reduced to the solvability of the Gauss–Codacci–Ricci system of nonlinear partial differential equations. Denoting $g_{ij}$ as the metric tensor, $\Gamma ^k_{ij}$ as the Christoffel symbols or affine metric connection, $R_{ijkl}$ as the Riemann tensor, $h^a_{ij}$ as the coefficients of the second fundamental form and finally $\kappa ^a_{lb}$ as the coefficients of the connection form on the normal bundle, the Gauss–Codacci–Ricci system may be expressed in the form

$$\begin{aligned}&h^a_{ji} h^a_{kl} -h^a_{ki} h^a_{jl} = R_{ijkl} \nonumber \\&h^a_{lj,k} - h^a_{kj,l} +\Gamma ^m_{lj} h^a_{km} -\Gamma ^m_{kj} h^a_{lm} +\kappa ^a_{kb} h^b_{lj} -\kappa ^a_{lb} h^b_{kj} =0 \nonumber \\&\kappa ^a_{lb,k} -\kappa ^a_{kb,l} -g^{mn} \left( h^a_{ml} h^b_{kn} -h^a_{mk} h^b_{ln} \right) + \kappa ^a_{kc} \kappa ^c_{lb} -\kappa ^a_{lc} \kappa ^c_{kb} = 0\nonumber \\ \end{aligned}$$

(104)

known respectively as the Gauss, Codacci and Ricci equations and where “,” refers to ordinary partial differentiation with respect to the relevant index. The equations relate the components of the intrinsic and extrinsic curvature of the manifolds. A significant theorem due to Günther [2] asserts that any smooth d-dimensional compact Riemannian manifold admits a smooth ($C^{\infty }$) isometric embedding in $\mathbb {R}^N$ for $N = \frac{1}{2} \text{ max } \left\{ d(d+5), d(d+3) +10\right\}$. The Riemann tensor of a $d +1$ dimensional manifold can be expressed entirely in terms of the extrinsic curvature of the d- dimensional manifolds via the Gauss–Codacci–Ricci equations. In his famous Theorema Egregium Gauss proved remarkably that the Gaussian curvature of a surface is an intrinsic invariant, i.e. Gaussian curvature is independent of the embedding. In this context we are embedding into a flat manifold and so its Gaussian curvature and indeed Riemann tensor vanish. The equations show that the components of the second fundamental form and its derivatives along the surface completely classify the surface up to a Euclidean transformation.

In the work of Kamarkar the vanishing of the Gaussian curvature gives relationship (14) in our coordinates. Of course at that time the first integration which we are now exploiting was not known. Additionally Kamarkar utilised the fact that a four dimensional manifold admits a symmetric tensor $b_{ij}$ such that

$$\begin{aligned} R_{hijk} = \pm (b_{hj}b_{ik} -b_{ij}b_{hk}) \end{aligned}$$

(105)

when it is of class one; that is it can be immersed in a 5 dimensional flat manifold. Only 8 of 20 Riemann tensor components survive for a spherical line element. Consequently only the diagonal terms $b_{ii}$ and $b_{03}=b_{30}$ are nonzero and it may be deduced that $b_{22} = b_{11} \sin ^2 \theta$. Finally on plugging in the components of $b_{ij}$ into (105) the result (13) emerges.